Thermodynamic and Electrochemical Characterization of Nd* (III) Ion Diffusion in (LiF-CaF2)-Nd2O3 Molten Salts
Abstract
:1. Introduction
2. Experimental and Computational Methods
2.1. Experimental Methods
2.1.1. Solubility of Nd2O3
2.1.2. Measurement of Conductivity and Density of Saturated (LiF-CaF2)eut.-Nd2O3 Molten Salt
2.1.3. Measurement of Dissolved Nd* (III) Ion Migration Number
2.2. Ab Initio Molecular Dynamics Method
3. Results and Discussion
3.1. Conductivity and Density of Saturated (LiF-CaF2)eut.-Nd2O3 Molten Salt
3.2. Migration Number of Solvated Nd* (III) Ions in the Saturated (LiF-CaF2)eut.–Nd2O3 System
3.3. Diffusion Coefficients of Nd* (III) Ions in the Saturated (LiF-CaF2)eut.–Nd2O3 System
3.3.1. Ab Initio Molecular Dynamics of the Saturated (LiF-CaF2)eut.–Nd2O3 System
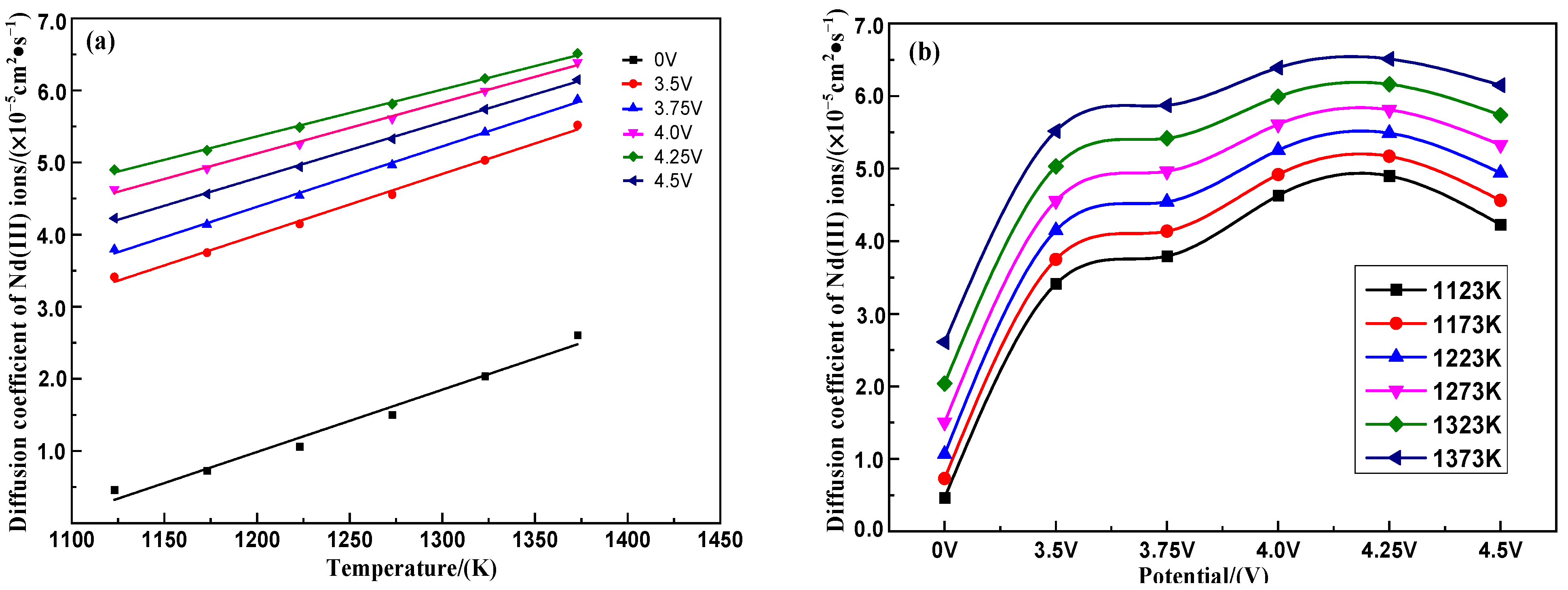
3.3.2. Calculation and Analysis of Diffusion Coefficients of Nd* (III) Ions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, W.; Li, M.; Zhang, M.L.; Yan, Y.D. Progress in preparation of rare earth metals and alloys by electrodeposition in molten salts. Rare Met. 2016, 35, 811–825. [Google Scholar] [CrossRef]
- Zhadan, A.; Sarou-Kanian, V.; Del Campo, L.; Cosson, L.; Malki, M.; Bessada, C. Transport properties in molten carbonates: Self-diffusion and conductivity measurements at high temperature. Int. J. Hydrogen Energy 2021, 46, 15059–15065. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Yue, B.; Yan, L.; Jiang, T.; Peng, S. Unifying the diffusion coefficients of lanthanides and actinides in binary molten salt mixtures: A data review. J. Mol. Liq. 2020, 297, 112106. [Google Scholar] [CrossRef]
- Seki, S.; Hayamizu, K.; Tsuzuki, S.; Takahashi, K.; Ishino, Y.; Kato, M.; Nozaki, E.; Watanabe, H.; Umebayashi, Y. Density, viscosity, ionic conductivity, and self-diffusion coefficient of organic liquid electrolytes: Part I. Propylene carbonate+ Li, Na, Mg and Ca cation salts. J. Electrochem. Soc. 2018, 165, A542–A546. [Google Scholar] [CrossRef]
- Wang, Y.F.; Yang, Q.; Zhang, J. Transport and kinetics properties of LaF3 in FLiNaK molten salt determined by electrochemical methods. J. Fluor. Chem. 2020, 233, 109502. [Google Scholar] [CrossRef]
- Rollet, A.L.; Sarou-Kanian, V.; Bessada, C. Self-diffusion coefficient measurements at high temperature by PFG NMR. Comptes Rendus Chimie 2010, 13, 399–404. [Google Scholar] [CrossRef]
- He, M.G.; Zhang, S.; Zhang, Y.; Peng, S.G. Development of measuring diffusion coefficients by digital holographic interferometry in transparent liquid mixtures. Opt. Express. 2015, 23, 10884–10899. [Google Scholar] [CrossRef]
- Kim, C.M.; Yoon, S.P.; Cho, S.K. Determination of diffusion coefficient in high temperature molten salt using cyclic voltammetry on microwire electrode: Its validity and limitation. J. Electroanal. Chem. 2021, 894, 115353. [Google Scholar] [CrossRef]
- Chen, C.; Li, J.; Luo, R.M.; Zhang, H.L. Ab initio Molecular Dynamics Study on microstructure and Diffusion Properties of CaF2-2.2NaF-AlF3 System. Chem. Phys. 2021, 550, 111294. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Sun, Z.; Lu, G.M.; Guimin; Yu, J.G. Molecular dynamics study of the transport properties and local structures of molten binary systems (Li, Na)Cl, (Li, K)Cl and (Na, K)Cl. J. Mol. Liq. 2015, 209, 498507. [Google Scholar] [CrossRef]
- Xie, Y.; Bu, M.; Zhang, Y.; Lu, G. Effect of composition and temperature on microstructure and thermophysical properties of LiCl-CaCl2 molten salt based on machine learning potentials. J. Mol. Liq. 2023, 383, 2112. [Google Scholar] [CrossRef]
- Vaidya, T.; Zhao, H. Solubility of Lanthanide Trichlorides in the Eutectic LiCl-KCl molten salt. Trans. Am. Nucl. Soc. 2022, 129, 119–121. [Google Scholar]
- Zhu, X.; Sun, S.; Sun, T.; Liu, C.; Tu, G.; Zhang, J. Electrical conductivity of REF3-LiF (RE = La and Nd) molten salts. J. Rare Earths 2020, 38, 676–682. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, X.F. Research progress of density measurement for high temperature melt. Bull. Chin. Ceram. Soc. 2013, 32, 1087–1091. [Google Scholar]
- Gheribi, A.E.; Machado, K.; Zanghi, D.; Bessada, C.; Salanne, M.; Chartrand, P. On the determination of ion transport numbers in molten salts using molecular dynamics. Electrochim. Acta. 2018, 274, 266–273. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3–21+G basis set for first-row elements, Li–F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Bengtson, A.; Nam, H.O.; Saha, S.; Sakidja, R.; Morgan, D. First-principles molecular dynamics modeling of the LiCl−KCl molten salt system. Comp. Mater. Sci. 2014, 83, 362–370. [Google Scholar] [CrossRef]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; Vandevondele, J. cp2k: Atomistic simulations of condensed matter systems. Wiley Interdiscip. Rev. Comp. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package-Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef] [PubMed]
- VandeVondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. [Google Scholar] [CrossRef]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B. 1996, 54, 1703–1710. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar]







| Ionic Species | Diffusion Coefficient Fits | lnD ~ 1/T Fit | Prefactor (J·mol−1) | DEA(J·mol−1) |
|---|---|---|---|---|
| Li(I) | 1.75 × 10−4 + 1.99 × 10−7T | 6.05 − 4357.29X | 2.36 × 10−3 | 36,226.51 |
| Ca(II) | 1.56 × 10−4 + 1.58×10−7T | 5.08 − 6310.64X | 6.22 × 10−3 | 52,466.66 |
| Nd(III) | DNd = 9.37 × 10−5 + 8.63 × 10−8T | 2.74 − 10,677.55X | 6.46 × 10−2 | 88,773.15 |
| O(II) | 1.27 × 10−4 + 1.21 × 10−7T | 3.90 − 8497.52X | 2.02 × 10−2 | 70,648.38 |
| F(I) | 2.27 × 10−4 + 2.31 × 10−7T | 4.77 − 6186.31X | 8.48 × 10−3 | 51,432.9 |
| M*-Nd* | Average Coordination Radius/Å | Cut-Off Radius/Å | V(r)/KJ·mol−1 |
|---|---|---|---|
| Li-Nd | 3.49 | 4.82 | 11.99 |
| Ca-Nd | 3.86 | 5.24 | 15.13 |
| F-Nd | 2.46 | 3.39 | 17.92 |
| O-Nd | 2.16 | 3.33 | 54.13 |
| Nd-Nd | 3.85 | 5.98 | 36.49 |
| Potential(V) | Diffusion Coefficient Fits | lnD ~ 1/T Fit | Prefactor (J·mol−1) | DEA (J·mol−1) |
|---|---|---|---|---|
| 0 | D = −9.37×10−5 + 8.63×10−8T | Y = −2.74 − 10,677.56X | 6.46×10−2 | 88,773.23 |
| 3.5 | D = −6.14×10−5 + 8.45×10−8T | Y = −7.65 − 2974.74X | 4.76×10−4 | 24,731.99 |
| 3.75 | D = −5.67×10−5 + 8.38×10−8T | Y = −7.77 − 2716.0X | 4.22×10−4 | 22,580.82 |
| 4.0 | D = −4.49×10−5 + 7.73×10−8T | Y = −8.21 − 1998.09X | 2.72×10−4 | 16,612.12 |
| 4.25 | D = −3.37×10−5 + 7.08×10−8T | Y = −8.36 − 1766.48X | 2.34×10−4 | 14,686.51 |
| 4.5 | D = −2.44×10−5 + 6.50×10−8T | Y = −8.01 − 2322.01X | 3.32×10−4 | 19,305.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, K.; Luo, L.; Wang, X. Thermodynamic and Electrochemical Characterization of Nd* (III) Ion Diffusion in (LiF-CaF2)-Nd2O3 Molten Salts. Materials 2025, 18, 706. https://doi.org/10.3390/ma18030706
Sun K, Luo L, Wang X. Thermodynamic and Electrochemical Characterization of Nd* (III) Ion Diffusion in (LiF-CaF2)-Nd2O3 Molten Salts. Materials. 2025; 18(3):706. https://doi.org/10.3390/ma18030706
Chicago/Turabian StyleSun, Kailei, Linsheng Luo, and Xu Wang. 2025. "Thermodynamic and Electrochemical Characterization of Nd* (III) Ion Diffusion in (LiF-CaF2)-Nd2O3 Molten Salts" Materials 18, no. 3: 706. https://doi.org/10.3390/ma18030706
APA StyleSun, K., Luo, L., & Wang, X. (2025). Thermodynamic and Electrochemical Characterization of Nd* (III) Ion Diffusion in (LiF-CaF2)-Nd2O3 Molten Salts. Materials, 18(3), 706. https://doi.org/10.3390/ma18030706





