Numerical Homogenization of Multi-Layered Corrugated Cardboard with Creasing or Perforation
Abstract
:1. Introduction
2. Materials and Methods
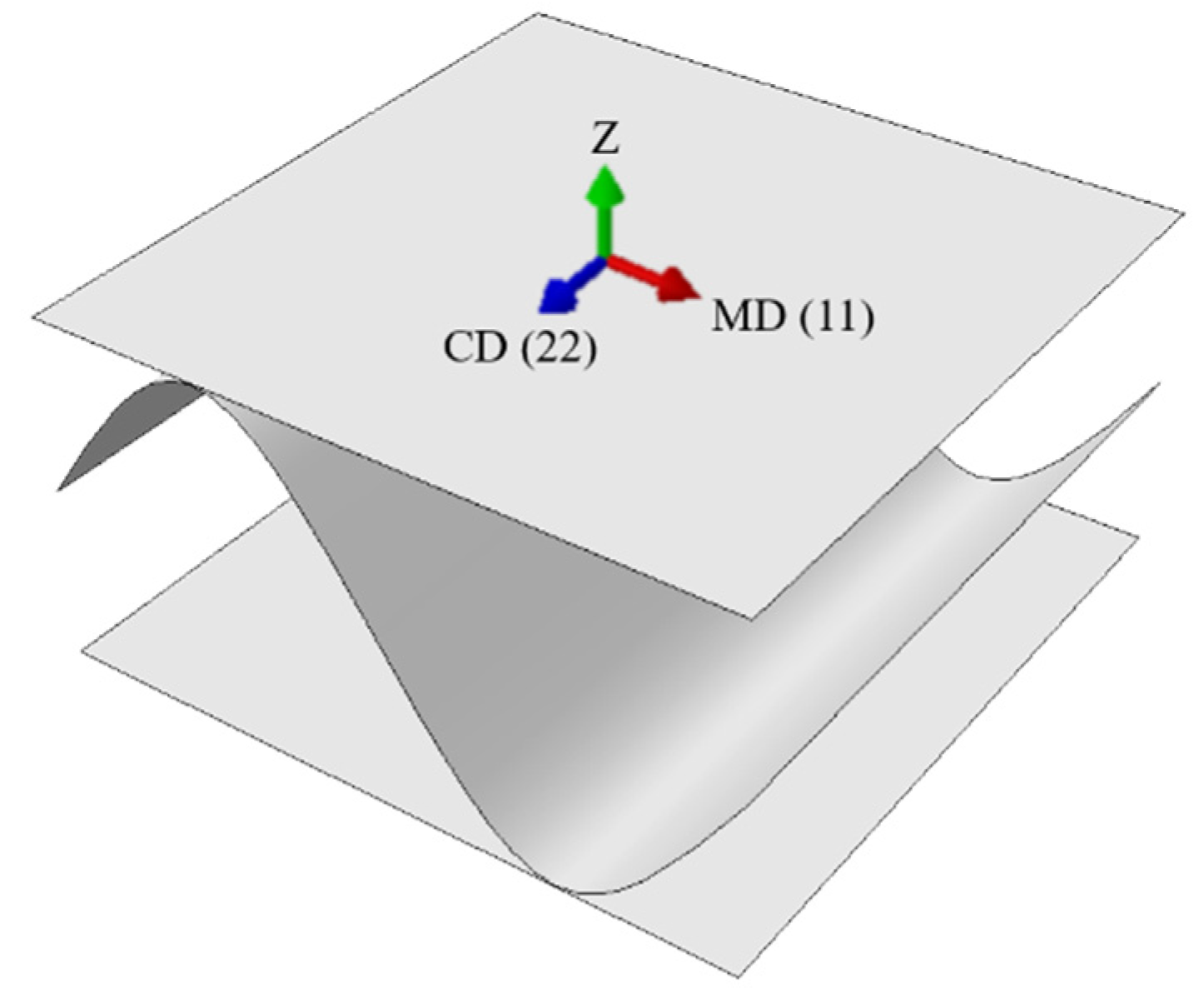
2.1. Corrugated Board—Material Definition
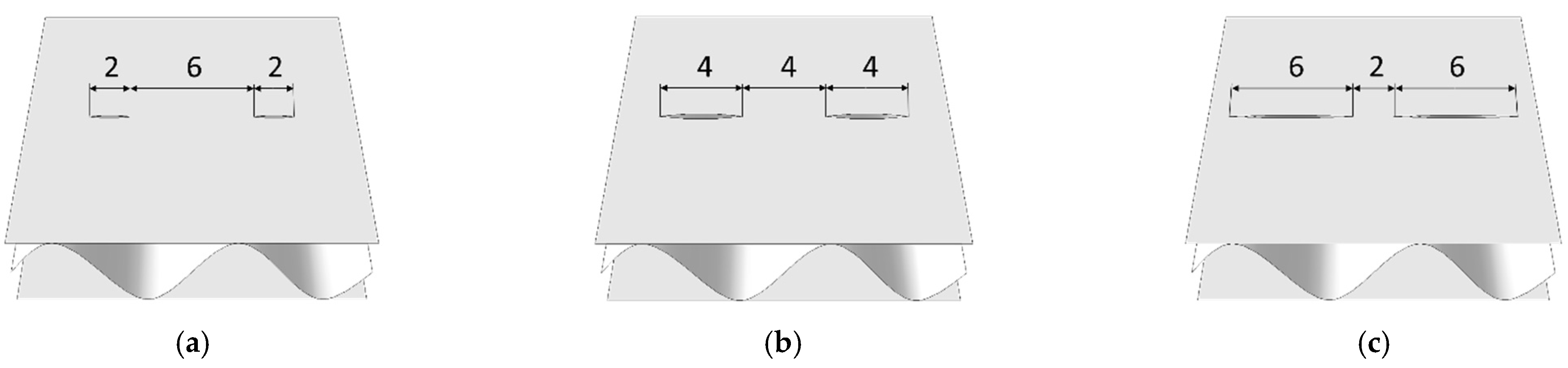
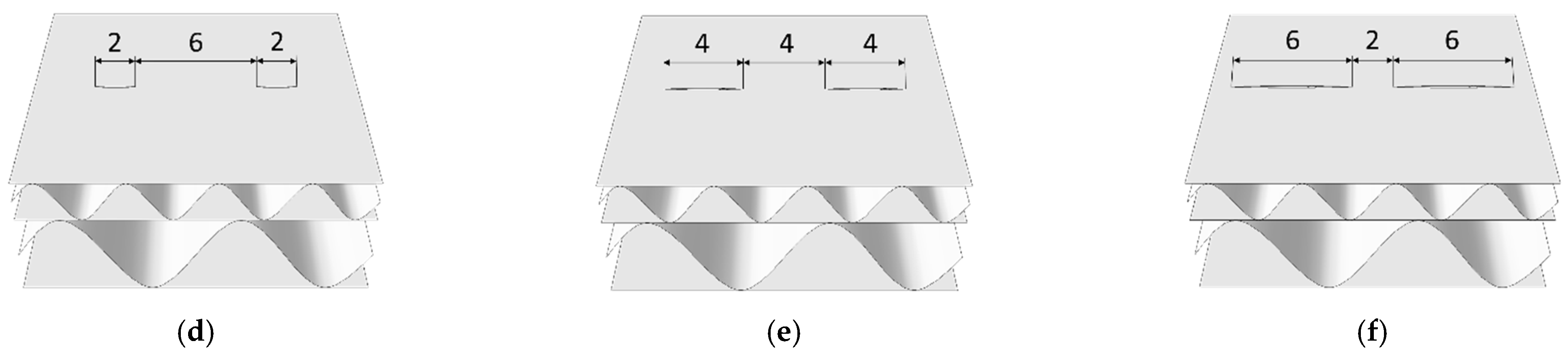
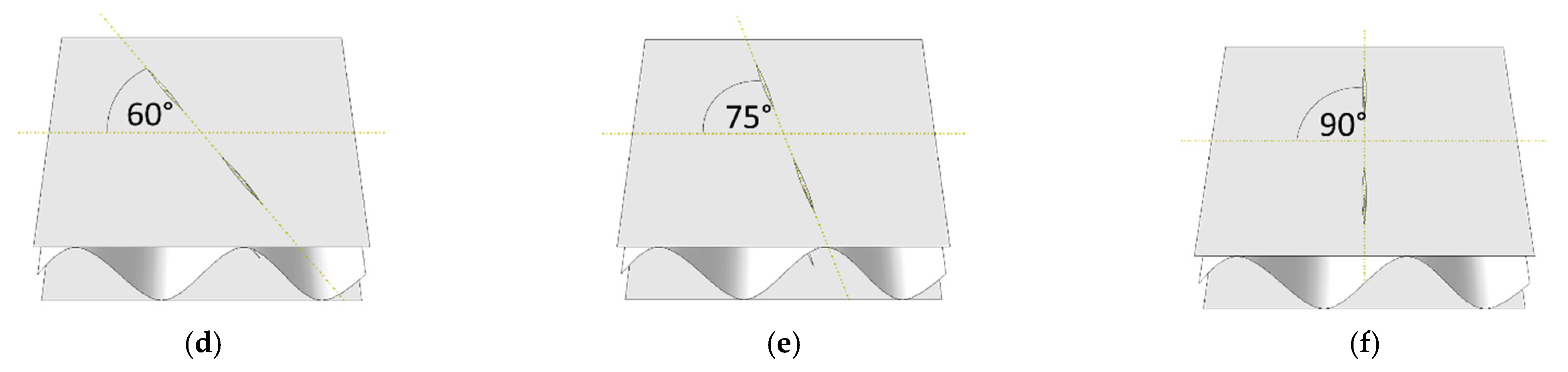
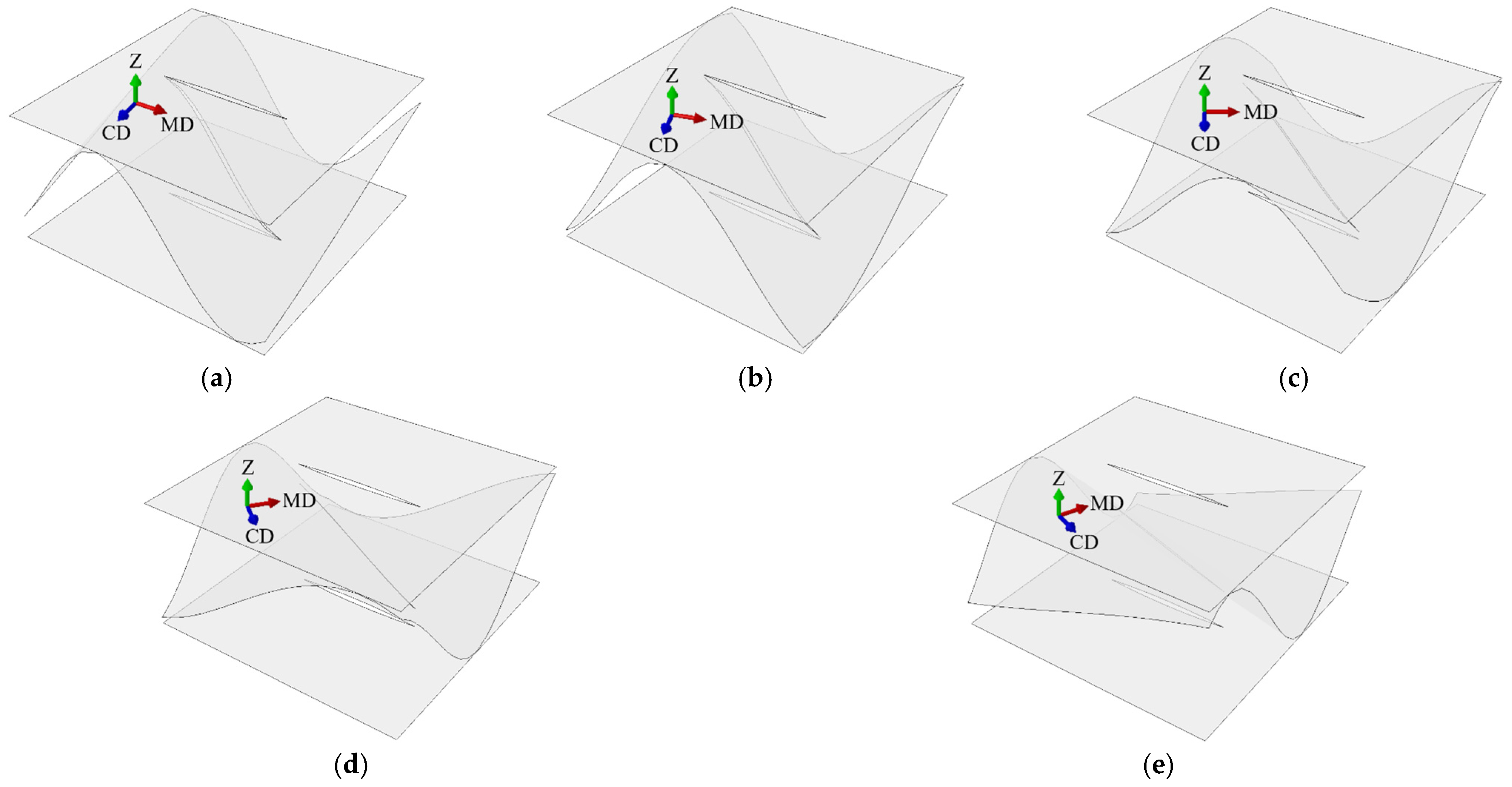
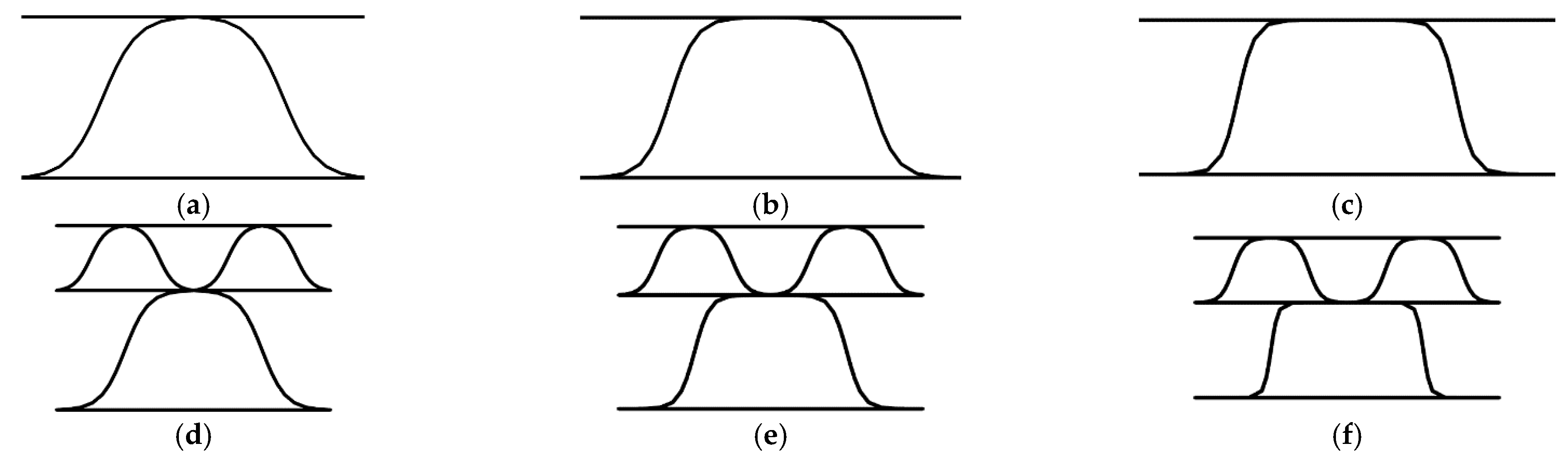
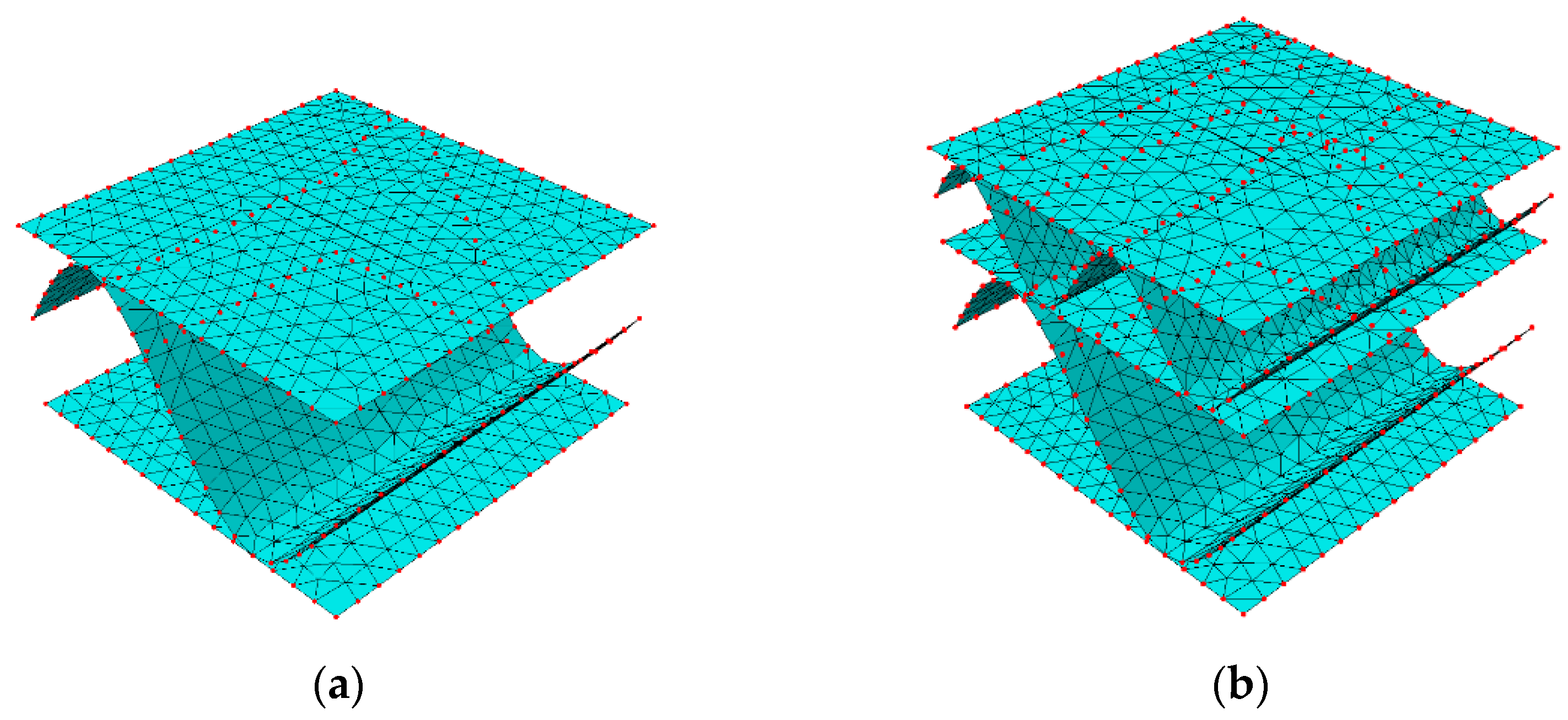
2.2. Creases and Perforations—Numerical Study
2.3. Homogenization Technique
3. Results
3.1. Validation of the Proposed Method
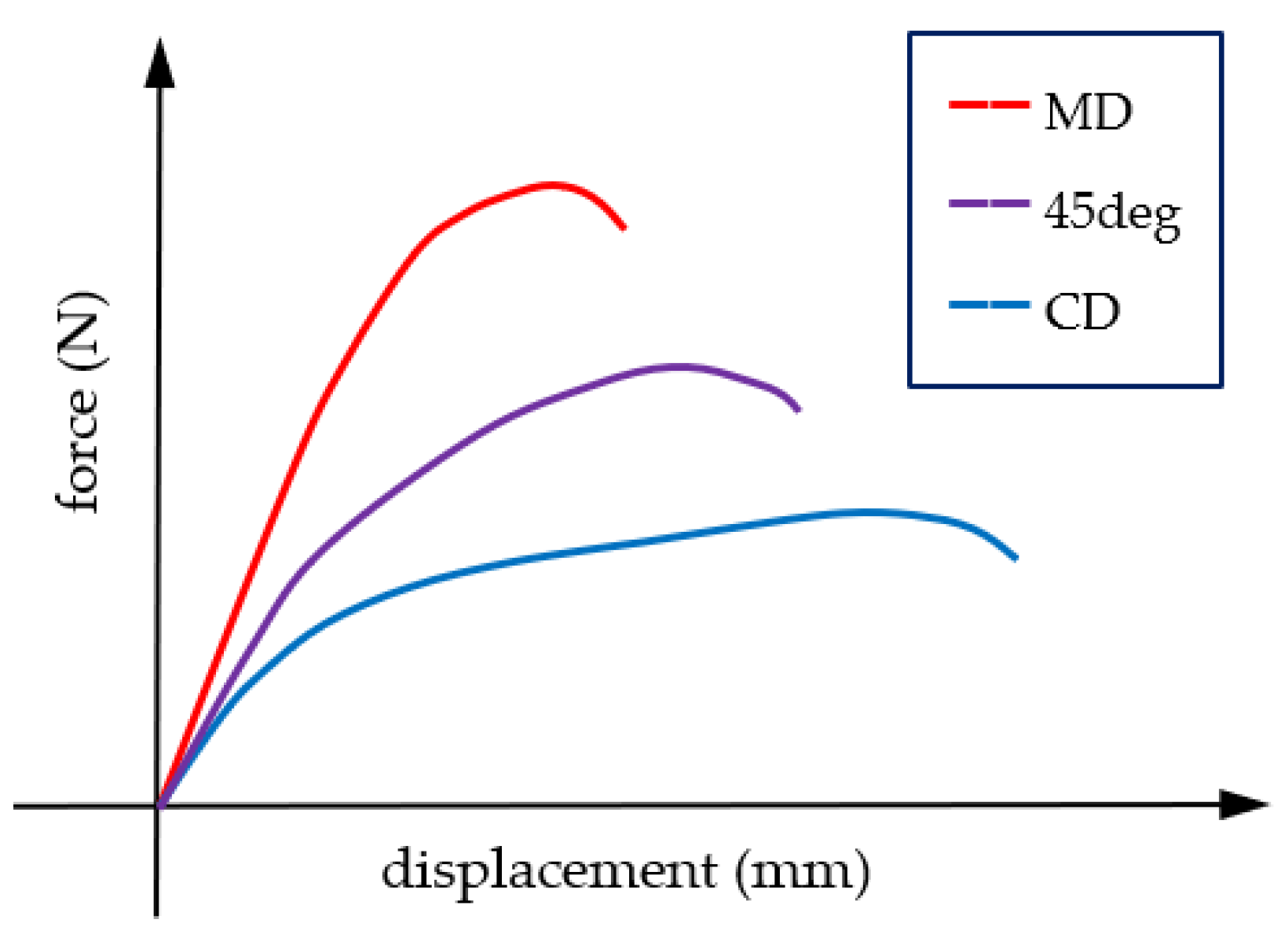
3.2. Detailed Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sohrabpour, V.; Hellström, D. Models and software for corrugated board and box design. In Proceedings of the 18th International Conference on Engineering Design (ICED 11), Copenhagen, Denmark, 15–18 October 2011. [Google Scholar]
- Kellicutt, K.; Landt, E. Development of design data for corrugated fiberboard shipping containers. Tappi J. 1952, 35, 398–402. [Google Scholar]
- Maltenfort, G. Compression strength of corrugated containers. Fibre Contain. 1956, 41, 106–121. [Google Scholar]
- McKee, R.C.; Gander, J.W.; Wachuta, J.R. Compression strength formula for corrugated boxes. Paperboard Packag. 1963, 48, 149–159. [Google Scholar]
- Allerby, I.M.; Laing, G.N.; Cardwell, R.D. Compressive strength—From components to corrugated containers. Appita Conf. Notes 1985, 1–11. [Google Scholar]
- Schrampfer, K.E.; Whitsitt, W.J.; Baum, G.A. Combined Board Edge Crush (ECT) Technology; Institute of Paper Chemistry: Appleton, WI, USA, 1987. [Google Scholar]
- Batelka, J.J.; Smith, C.N. Package Compression Model; Institute of Paper Science and Technology: Atlanta, GA, USA, 1993. [Google Scholar]
- Urbanik, T.J.; Frank, B. Box compression analysis of world-wide data spanning 46 years. Wood Fiber Sci. 2006, 38, 399–416. [Google Scholar]
- Avilés, F.; Carlsson, L.A.; May-Pat, A. A shear-corrected formulation of the sandwich twist specimen. Exp. Mech. 2012, 52, 17–23. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. The role of buckling in the estimation of compressive strength of corrugated cardboard boxes. Materials 2020, 13, 4578. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various openings. Energies 2021, 14, 155. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Estimation of the compressive strength of corrugated cardboard boxes with various perforations. Energies 2021, 14, 1095. [Google Scholar] [CrossRef]
- Wang, L.; Qian, Z. A meshfree stabilized collocation method (SCM) based on reproducing kernel approximation. Comput. Methods Appl. Mech. Eng. 2020, 371, 113303. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y.; Zhou, Y.; Yang, F. Static and dynamic analysis of thin functionally graded shell with in-plane material inhomogeneity. Int. J. Mech. Sci. 2021, 193, 106165. [Google Scholar] [CrossRef]
- Chu, F.; He, J.; Wang, L.; Zhong, Z. Buckling analysis of functionally graded thin plate with in-plane material inhomogeneity. Eng. Anal. Bound. Elem. 2016, 65, 112–125. [Google Scholar] [CrossRef]
- Frank, B. Corrugated box compression—A literature survey. Packag. Technol. Sci. 2014, 27, 105–128. [Google Scholar] [CrossRef]
- Stott, R.A. Compression and stacking strength of corrugated fibreboard containers. Appita J. 2017, 70, 76–82. [Google Scholar]
- Junli, W.; Quancheng, Z. Effect of moisture content of corrugated box on mechanical properties. J. Lanzhou Jiaotong Univ. 2006, 25, 134–136. [Google Scholar]
- Archaviboonyobul, T.; Chaveesuk, R.; Singh, J.; Jinkarn, T. An analysis of the influence of hand hole and ventilation hole design on compressive strength of corrugated fiberboard boxes by an artificial neural network model. Packag. Technol. Sci. 2020, 33, 171–181. [Google Scholar] [CrossRef]
- Zhang, Y.-L.; Chen, J.; Wu, Y.; Sun, J. Analysis of hazard factors of the use of corrugated carton in packaging low-temperature yogurt during logistics. Procedia Environ. Sci. 2011, 10, 968–973. [Google Scholar] [CrossRef] [Green Version]
- Gallo, J.; Cortés, F.; Alberdi, E.; Goti, A. Mechanical behavior modeling of containers and octabins made of corrugated cardboard subjected to vertical stacking loads. Materials 2021, 14, 2392. [Google Scholar] [CrossRef]
- Thakkar, B.K.; Gooren, L.G.J.; Peerlings, R.H.J.; Geers, M.G.D. Experimental and numerical investigation of creasing in corrugated paperboard. Philos. Mag. 2008, 88, 3299–3310. [Google Scholar] [CrossRef] [Green Version]
- Beex, L.A.A.; Peerlings, R.H.J. An experimental and computational study of laminated paperboard creasing and folding. Int. J. Solids Struct. 2009, 46, 4192–4207. [Google Scholar] [CrossRef] [Green Version]
- Giampieri, A.; Perego, U.; Borsari, R. A constitutive model for the mechanical response of the folding of creased paperboard. Int. J. Solids Struct. 2011, 48, 2275–2287. [Google Scholar] [CrossRef] [Green Version]
- Domaneschi, M.; Perego, U.; Borgqvist, E.; Borsari, R. An industry-oriented strategy for the finite element simulation of paperboard creasing and folding. Pack. Technol. Sci. 2017, 30, 269–294. [Google Scholar] [CrossRef]
- Awais, M.; Tanninen, P.; Leppänen, T.; Matthews, S.; Sorvari, J.; Varis, J.; Backfol, K. A computational and experimental analysis of crease behavior in press forming process. Procedia Manuf. 2018, 17, 835–842. [Google Scholar] [CrossRef]
- Leminena, V.; Tanninena, P.; Pesonena, A.; Varis, J. Effect of mechanical perforation on the press-forming process of paperboard. Procedia Manuf. 2019, 38, 1402–1408. [Google Scholar] [CrossRef]
- Nordstrand, T. Basic Testing and Strength Design of Corrugated Board and Containers. Ph.D. Thesis, Lund University, Lund, Sweden, 2003. [Google Scholar]
- Nordstrand, T.; Carlsson, L. Evaluation of transverse shear stiffness of structural core sandwich plates. Comp. Struct. 1997, 37, 145–153. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Role of transverse shear modulus in the performance of corrugated materials. Materials 2020, 13, 3791. [Google Scholar] [CrossRef]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Torsional and transversal stiffness of orthotropic sandwich panels. Materials 2020, 13, 5016. [Google Scholar] [CrossRef] [PubMed]
- Garbowski, T.; Gajewski, T. Determination of transverse shear stiffness of sandwich panels with a corrugated core by numerical homogenization. Materials 2021, 14, 1976. [Google Scholar] [CrossRef]
- Urbanik, T.J.; Saliklis, E.P. Finite element corroboration of buckling phenomena observed in corrugated boxes. Wood Fiber Sci. 2003, 35, 322–333. [Google Scholar]
- Garbowski, T.; Jarmuszczak, M. Homogenization of corrugated paperboard. Part 1. Analytical homogenization. Pol. Pap. Rev. 2014, 70, 345–349. (In Polish) [Google Scholar]
- Garbowski, T.; Jarmuszczak, M. Homogenization of corrugated paperboard. Part 2. Numerical homogenization. Pol. Pap. Rev. 2014, 70, 390–394. (In Polish) [Google Scholar]
- Marek, A.; Garbowski, T. Homogenization of sandwich panels. Comput. Assist. Methods Eng. Sci. 2015, 22, 39–50. [Google Scholar]
- Garbowski, T.; Marek, A. Homogenization of corrugated boards through inverse analysis. In Proceedings of the 1st International Conference on Engineering and Applied Sciences Optimization, Kos Island, Greece, 4–6 June 2014; pp. 1751–1766. [Google Scholar]
- Hohe, J. A direct homogenization approach for determination of the stiffness matrix for microheterogeneous plates with application to sandwich panels. Compos. Part B 2003, 34, 615–626. [Google Scholar] [CrossRef]
- Buannic, N.; Cartraud, P.; Quesnel, T. Homogenization of corrugated core sandwich panels. Comp. Struct. 2003, 59, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Biancolini, M.E. Evaluation of equivalent stiffness properties of corrugated board. Comp. Struct. 2005, 69, 322–328. [Google Scholar] [CrossRef]
- Abbès, B.; Guo, Y.Q. Analytic homogenization for torsion of orthotropic sandwich plates: Application to corrugated cardboard. Comp. Struct. 2010, 92, 699–706. [Google Scholar] [CrossRef]
- Ramírez-Torres, A.; Penta, R.; Rodríguez-Ramos, R.; Merodio, J.; Sabina, F.J.; Bravo-Castillero, J.; Guinovart-Díaz, R.; Preziosi, L.; Grillo, A. Three scales asymptotic homogenization and its application to layered hierarchical hard tissues. Int. J. Solids Struct. 2018, 130–131, 190–198. [Google Scholar] [CrossRef]
- Ramírez-Torres, A.; Di Stefano, S.; Grillo, A.; Rodríguez-Ramos, R.; Merodio, J.; Penta, R. An asymptotic homogenization approach to the microstructural evolution of heterogeneous media. Int. J. Non-Lin. Mech. 2018, 106, 245–257. [Google Scholar] [CrossRef] [Green Version]
- Garbowski, T.; Gajewski, T.; Mrówczyński, D.; Jędrzejczak, R. Crushing of single-walled corrugated board during converting: Experimental and numerical study. Energies 2021, 14, 3203. [Google Scholar] [CrossRef]
- Gajewski, T.; Garbowski, T.; Staszak, N.; Kuca, M. Crushing of double-walled corrugated board and its influence on the load capacity of various boxes. Preprints 2021, 2021050667. [Google Scholar] [CrossRef]
- Garbowski, T.; Grabski, J.K.; Marek, A. Full-field measurements in the edge crush test of a corrugated board—Analytical and numerical predictive models. Materials 2021, 14, 2840. [Google Scholar] [CrossRef] [PubMed]




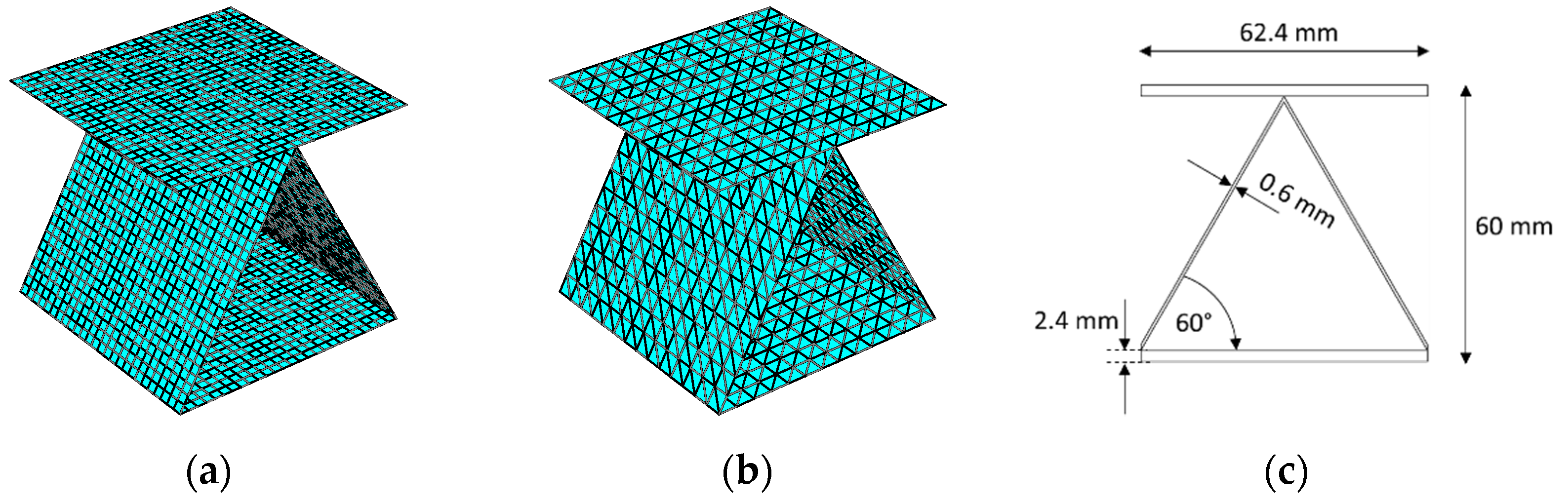

| Layers | ||||||
|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (-) | (MPa) | (MPa) | (MPa) | |
| liners | 3326 | 1694 | 0.34 | 859 | 429.5 | 429.5 |
| fluting | 2614 | 1532 | 0.32 | 724 | 362 | 362 |
| Perforation Type | Model SW | Model DW |
|---|---|---|
| 4 mm cut, 4 mm gap | SW-44-Y 1-xx 2 | DW-44-Y-xx |
| 2 mm cut, 6 mm gap | SW-26-Y-xx | DW-26-Y-xx |
| 6 mm cut, 2 mm gap | SW-62-Y-xx | DW-62-Y-xx |
| Stiffness | Ref. [39] | Corse Model | Fine Model |
|---|---|---|---|
| 1.108 106 | 1.118 106 | 1.118 106 | |
| 1.358 106 | 1.380 106 | 1.378 106 | |
| 3.324 105 | 3.449 105 | 3.448 105 | |
| 4.168 105 | 4.115 105 | 4.115 105 | |
| 9.195 108 | 9.211 108 | 9.210 108 | |
| 9.822 108 | 9.926 108 | 9.925 108 | |
| 2.758 108 | 2.777 108 | 2.777 108 | |
| 3.220 108 | 3.269 108 | 3.268 108 | |
| , | - | 5.194 104 | 5.184 104 |
| , | - | 7.408 104 | 7.376 104 |
| A & B | B & D | R | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | ||
| A & B | 1 | 2184.4 | 388.92 | 0 | 0 | 0 | 0 | ||
| 2 | 388.92 | 1756.9 | 0 | 0 | 0 | 0 | |||
| 3 | 0 | 0 | 667.81 | 0 | 0 | 0 | |||
| B & D | 1 | 0 | 0 | 0 | 8628.2 | 1506.5 | 0 | ||
| 2 | 0 | 0 | 0 | 1506.5 | 5469.3 | 0 | |||
| 3 | 0 | 0 | 0 | 0 | 0 | 2300.2 | |||
| R | 4 | 105.08 | 0 | ||||||
| 5 | 0 | 130.91 | |||||||
| A & B | B & D | R | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | ||
| A & B | 1 | 3313.8 | 593.33 | 0 | 1117.1 | 195.90 | 0 | ||
| 2 | 593.33 | 2967.5 | 0 | 196.36 | 1200.6 | 0 | |||
| 3 | 0 | 0 | 1077.8 | 0 | 0 | 409.89 | |||
| B & D | 1 | 1117.1 | 196.36 | 0 | 20 619 | 3620.8 | 0 | ||
| 2 | 195.90 | 1200.6 | 0 | 3620.8 | 15 042 | 0 | |||
| 3 | 0 | 0.0 | 409.89 | 0 | 0 | 5934.5 | |||
| R | 4 | 233.13 | 0 | ||||||
| 5 | 0 | 242.28 | |||||||
| SW-0-F-00 | SW-0-F-15 | SW-0-F-30 | SW-0-F-45 | SW-0-F-60 | SW-0-F-75 | SW-0-F-90 | |
|---|---|---|---|---|---|---|---|
| (MPa mm) | 2184.4 | 2127.2 | 1990.3 | 1854.2 | 1774.2 | 1751.5 | 1756.9 |
| (MPa mm) | 1756.9 | 1751.5 | 1774.2 | 1854.2 | 1990.3 | 2127.2 | 2184.4 |
| (MPa mm) | 667.81 | 699.26 | 760.50 | 792.80 | 760.50 | 699.30 | 667.80 |
| (MPa mm3) | 8628.2 | 8313.5 | 7480.9 | 6521.5 | 5897.3 | 5575.8 | 5469.3 |
| (MPa mm3) | 5469.3 | 5575.8 | 5897.3 | 6520.4 | 7480.9 | 8313.5 | 8628.2 |
| (MPa mm3) | 2300.2 | 2425.2 | 2650.1 | 2755.4 | 2650.1 | 2425.2 | 2300.2 |
| (MPa mm) | 105.08 | 108.15 | 119.80 | 132.90 | 127.20 | 126.20 | 130.90 |
| (MPa mm) | 130.91 | 126.16 | 127.20 | 132.80 | 119.80 | 108.10 | 105.10 |
| DW-0-F-00 | DW-0-F-15 | DW-0-F-30 | DW-0-F-45 | DW-0-F-60 | DW-0-F-75 | DW-0-F-90 | |
|---|---|---|---|---|---|---|---|
| (MPa mm) | 3313.8 | 3250.6 | 3090.4 | 2955.2 | 2912.0 | 2939.7 | 2967.5 |
| (MPa mm) | 2967.5 | 2939.7 | 2912.0 | 2955.3 | 3090.4 | 3250.6 | 3313.8 |
| (MPa mm) | 1077.8 | 1127.5 | 1225.3 | 1275.9 | 1225.3 | 1127.5 | 1077.8 |
| (MPa mm3) | 20,242 | 19,610 | 17,980 | 16,221 | 15,123 | 14,662 | 14,556 |
| (MPa mm3) | 14,556 | 14,662 | 15,123 | 16,220 | 17,980 | 19,610 | 20,242 |
| (MPa mm3) | 5778.6 | 6071.8 | 6634.3 | 6910.6 | 6634.3 | 6071.8 | 5778.6 |
| (MPa mm) | 233.13 | 240.21 | 246.71 | 257.56 | 247.51 | 242.88 | 242.28 |
| (MPa mm) | 242.28 | 242.88 | 247.51 | 257.43 | 246.71 | 240.21 | 233.13 |
| Stiffness | SW-0-F-15 | SW-26-F-15 | SW-44-F-15 | SW-62-F-15 |
|---|---|---|---|---|
| (MPa mm) | 2127.2 | 2116.1 | 2082.1 | 2052.3 |
| (MPa mm) | 1751.6 | 1609.1 | 1267.7 | 885.12 |
| (MPa mm) | 699.26 | 681.92 | 608.30 | 524.18 |
| (MPa mm3) | 8313.4 | 8276.1 | 8166.4 | 8048.5 |
| (MPa mm3) | 5575.8 | 5290.9 | 4291.8 | 2877.2 |
| (MPa mm3) | 2425.2 | 2384.5 | 2216.7 | 1968.9 |
| (MPa mm) | 108.15 | 107.68 | 106.48 | 106.77 |
| (MPa mm) | 126.16 | 120.04 | 94.100 | 83.465 |
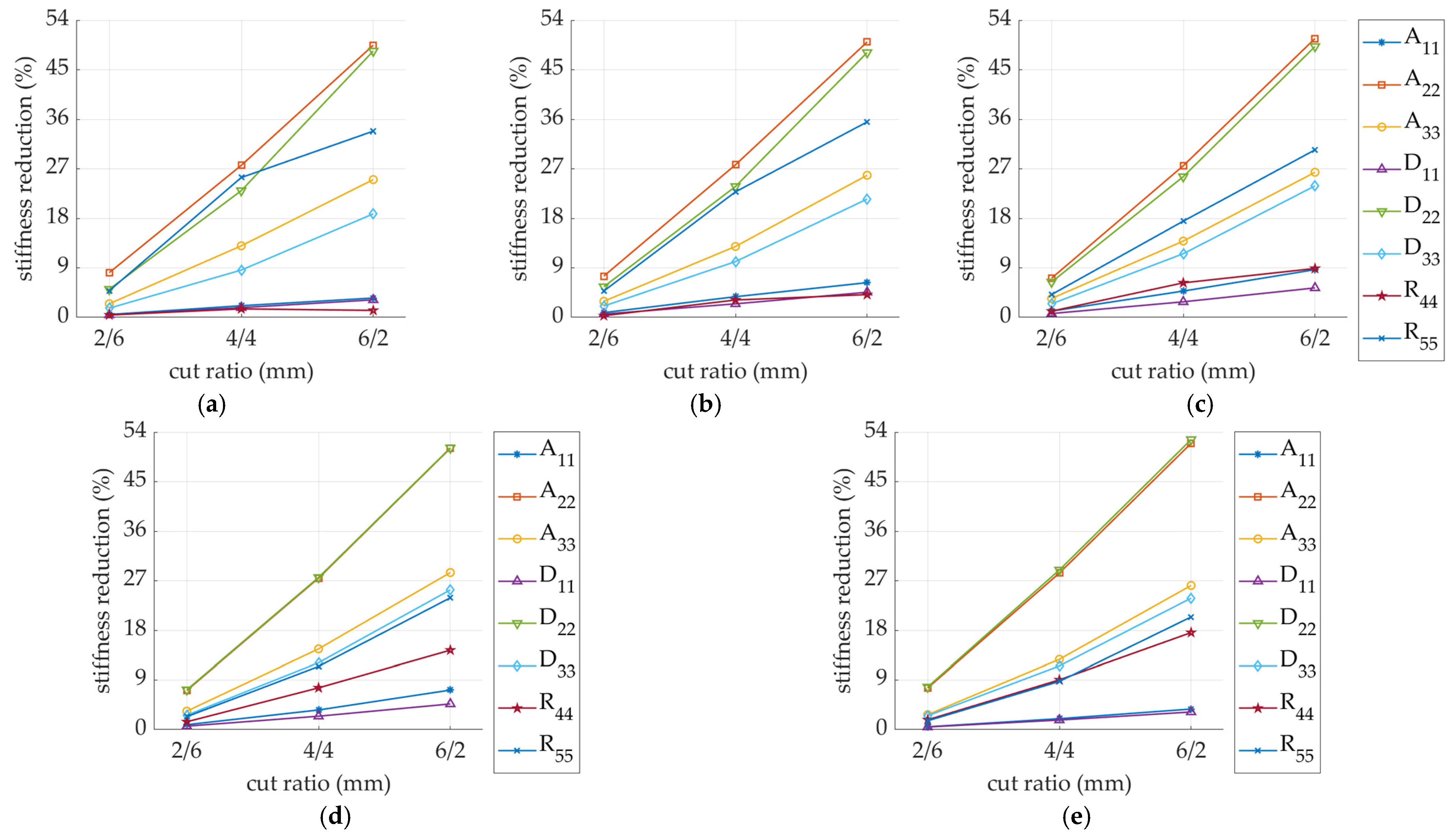
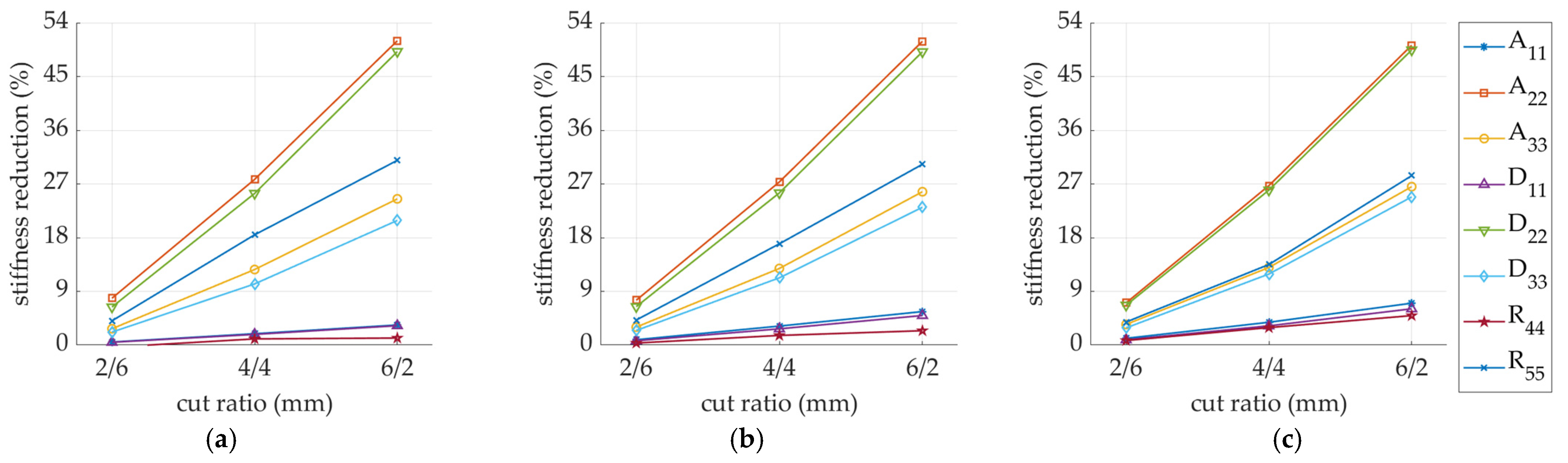
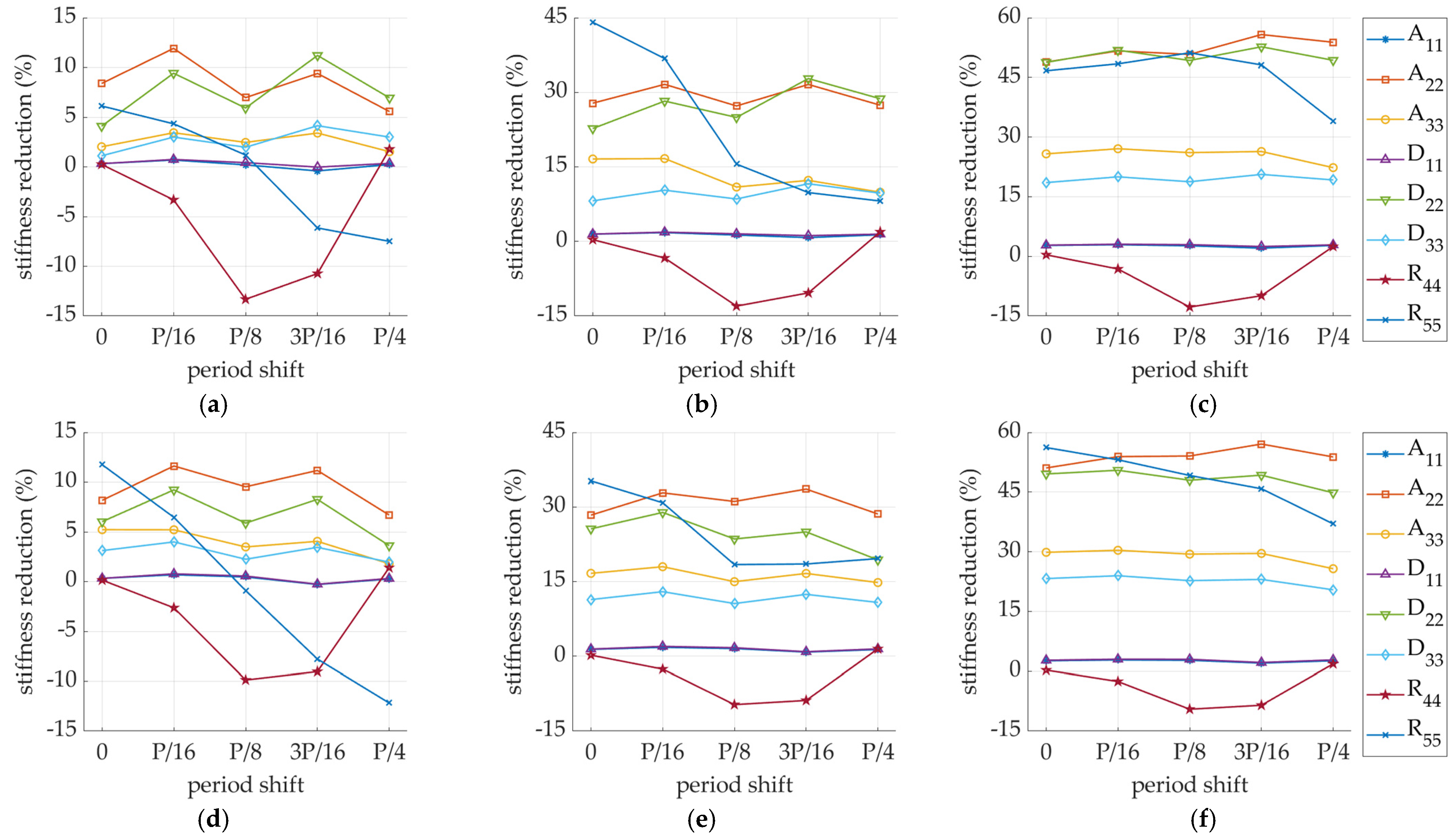
| Stiffness Reduction | SW-26-F-15 (%) | SW-44-F-15 (%) | SW-62-F-15 (%) | DW-26-F-15 (%) | DW-44-F-15 (%) | DW-62-F-15 (%) |
|---|---|---|---|---|---|---|
| 0.523 | 2.121 | 3.519 | 0.508 | 1.903 | 3.364 | |
| 8.133 | 27.66 | 49.46 | 7.852 | 27.77 | 50.98 | |
| 2.480 | 13.01 | 25.04 | 2.735 | 12.66 | 24.50 | |
| 0.449 | 1.769 | 3.187 | 0.467 | 1.786 | 3.247 | |
| 5.110 | 23.03 | 48.40 | 6.377 | 25.41 | 49.18 | |
| 1.677 | 8.598 | 18.81 | 2.171 | 10.25 | 20.88 | |
| 0.435 | 1.545 | 1.273 | −0.349 | 1.032 | 1.177 | |
| 4.851 | 25.41 | 33.84 | 4.060 | 18.48 | 30.95 |
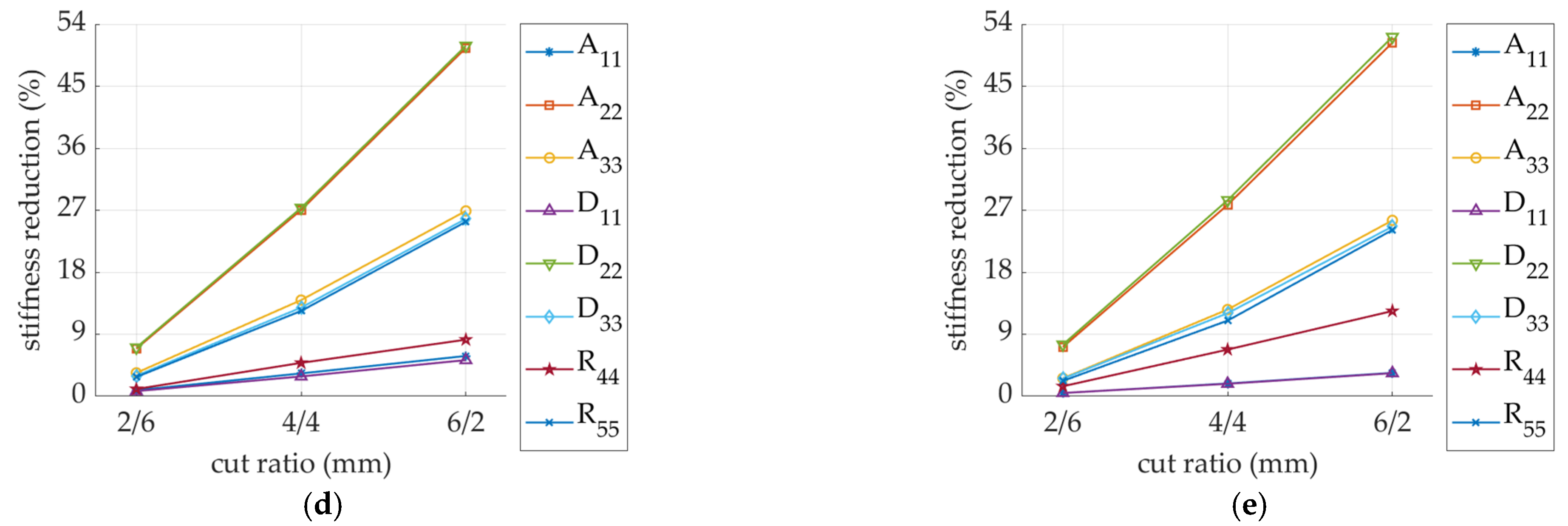
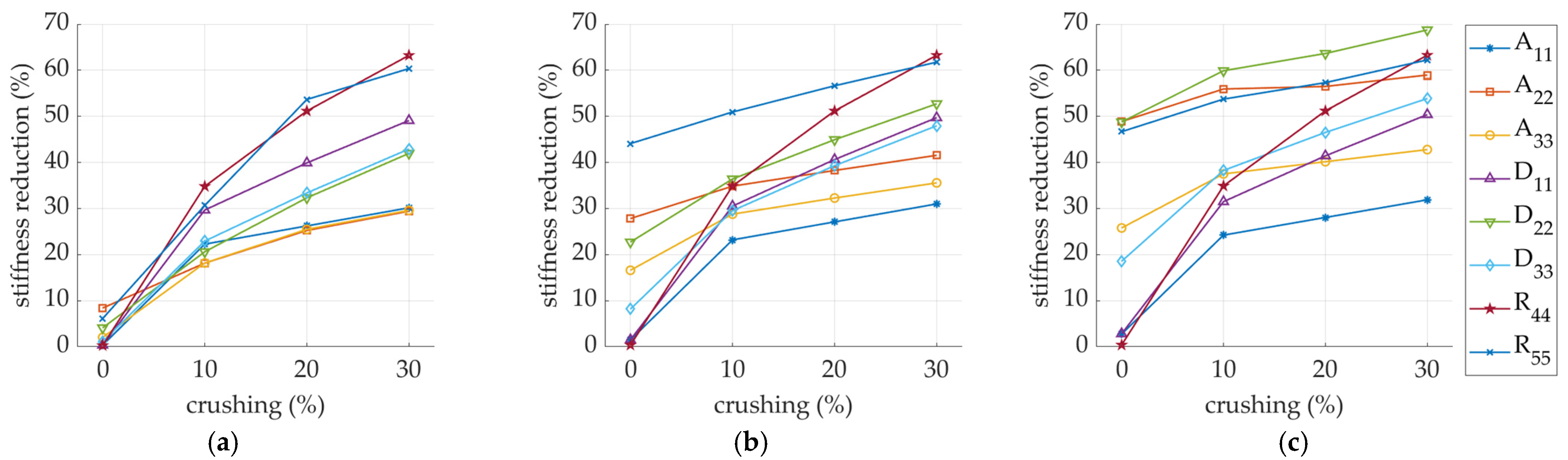
| Stiffness Reduction | 1/16 P (%) | 2/16 P (%) | 3/16 P (%) | 4/16 P (%) |
|---|---|---|---|---|
| −0.023 | −0.121 | −1.061 | −0.055 | |
| −0.018 | −0.061 | −0.086 | −0.003 | |
| −0.035 | −0.089 | −0.062 | 0.038 | |
| 0.023 | 0.099 | −0.687 | 0.059 | |
| 0.018 | 0.053 | −0.007 | 0.050 | |
| 0.124 | 0.495 | 1.102 | 1.720 | |
| 3.533 | 13.41 | 10.63 | 1.771 | |
| 1.286 | 4.036 | 8.186 | 8.956 |
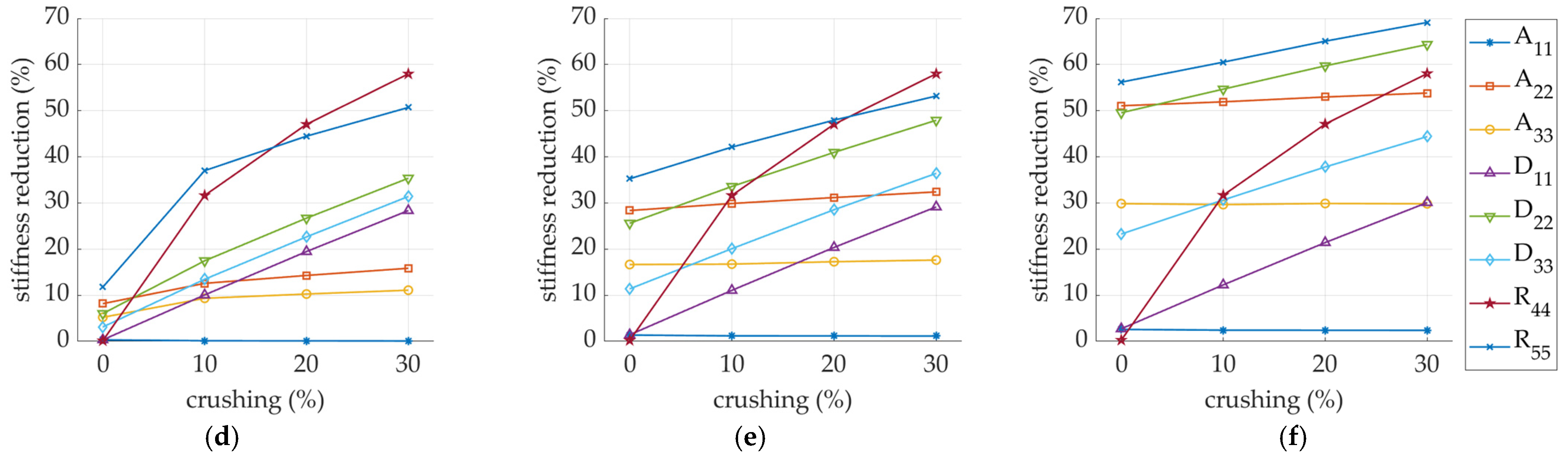
| Stiffness Reduction | 1/16 P (%) | 2/16 P (%) | 3/16 P (%) | 4/16 P (%) |
|---|---|---|---|---|
| −0.018 | −0.094 | −1.052 | −0.037 | |
| −0.013 | −0.044 | −0.075 | −0.003 | |
| −0.032 | −0.082 | −0.056 | 0.039 | |
| 0.012 | 0.029 | −1.048 | −0.012 | |
| 0.011 | 0.009 | −0.062 | 0.021 | |
| −0.029 | 0.110 | 0.459 | 0.880 | |
| 2.706 | 9.932 | 8.977 | 1.396 | |
| 2.378 | 6.572 | 11.88 | 15.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garbowski, T.; Knitter-Piątkowska, A.; Mrówczyński, D. Numerical Homogenization of Multi-Layered Corrugated Cardboard with Creasing or Perforation. Materials 2021, 14, 3786. https://doi.org/10.3390/ma14143786
Garbowski T, Knitter-Piątkowska A, Mrówczyński D. Numerical Homogenization of Multi-Layered Corrugated Cardboard with Creasing or Perforation. Materials. 2021; 14(14):3786. https://doi.org/10.3390/ma14143786
Chicago/Turabian StyleGarbowski, Tomasz, Anna Knitter-Piątkowska, and Damian Mrówczyński. 2021. "Numerical Homogenization of Multi-Layered Corrugated Cardboard with Creasing or Perforation" Materials 14, no. 14: 3786. https://doi.org/10.3390/ma14143786








