On Wrinkling in Sandwich Panels with an Orthotropic Core
Abstract
:1. Introduction
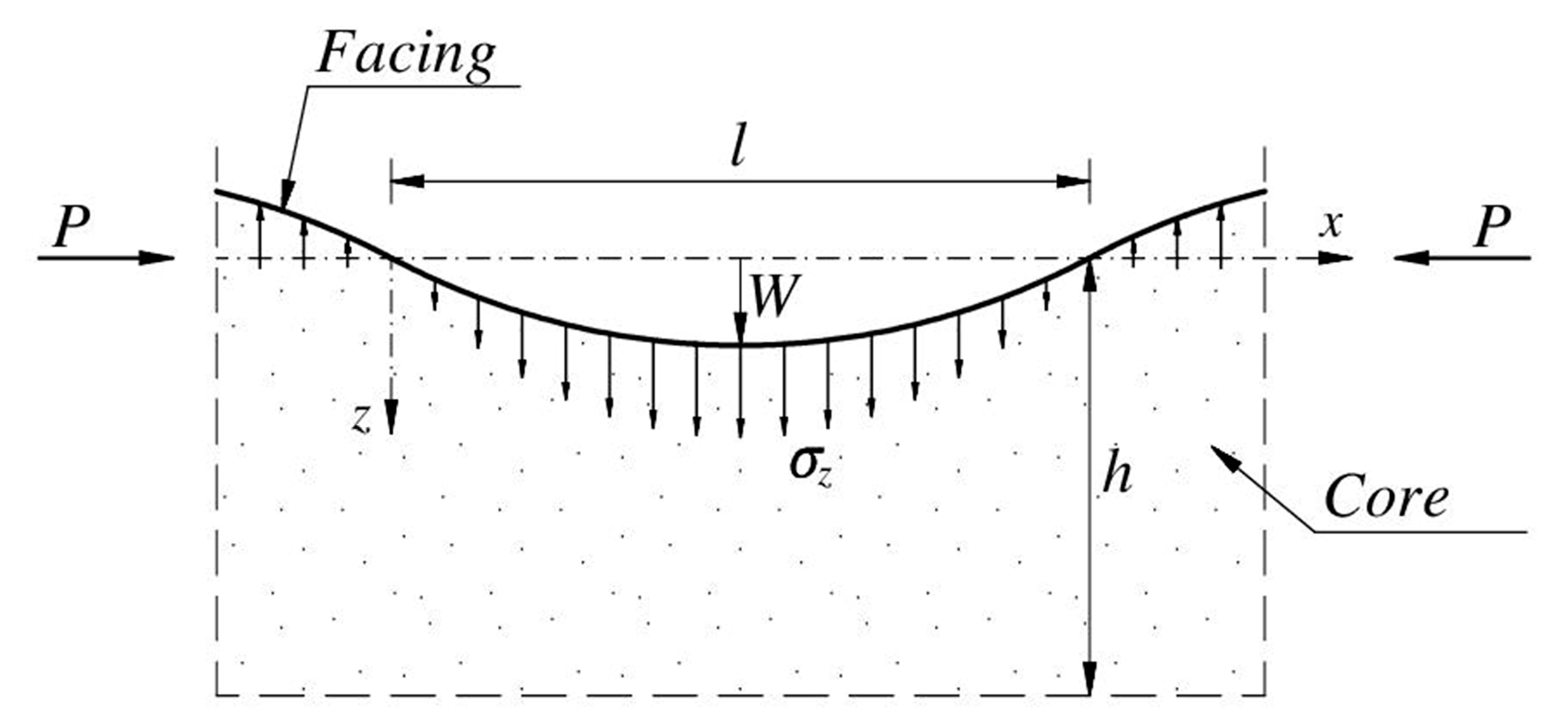
2. Formulation of the Problem
3. Classical Solutions of the Wrinkling Problem
3.1. Energy Method—Linear Decay Function
3.2. Energy Method—Exponential Decay Function
3.3. Differential Equation Method
3.4. Comparison of Classical Solutions
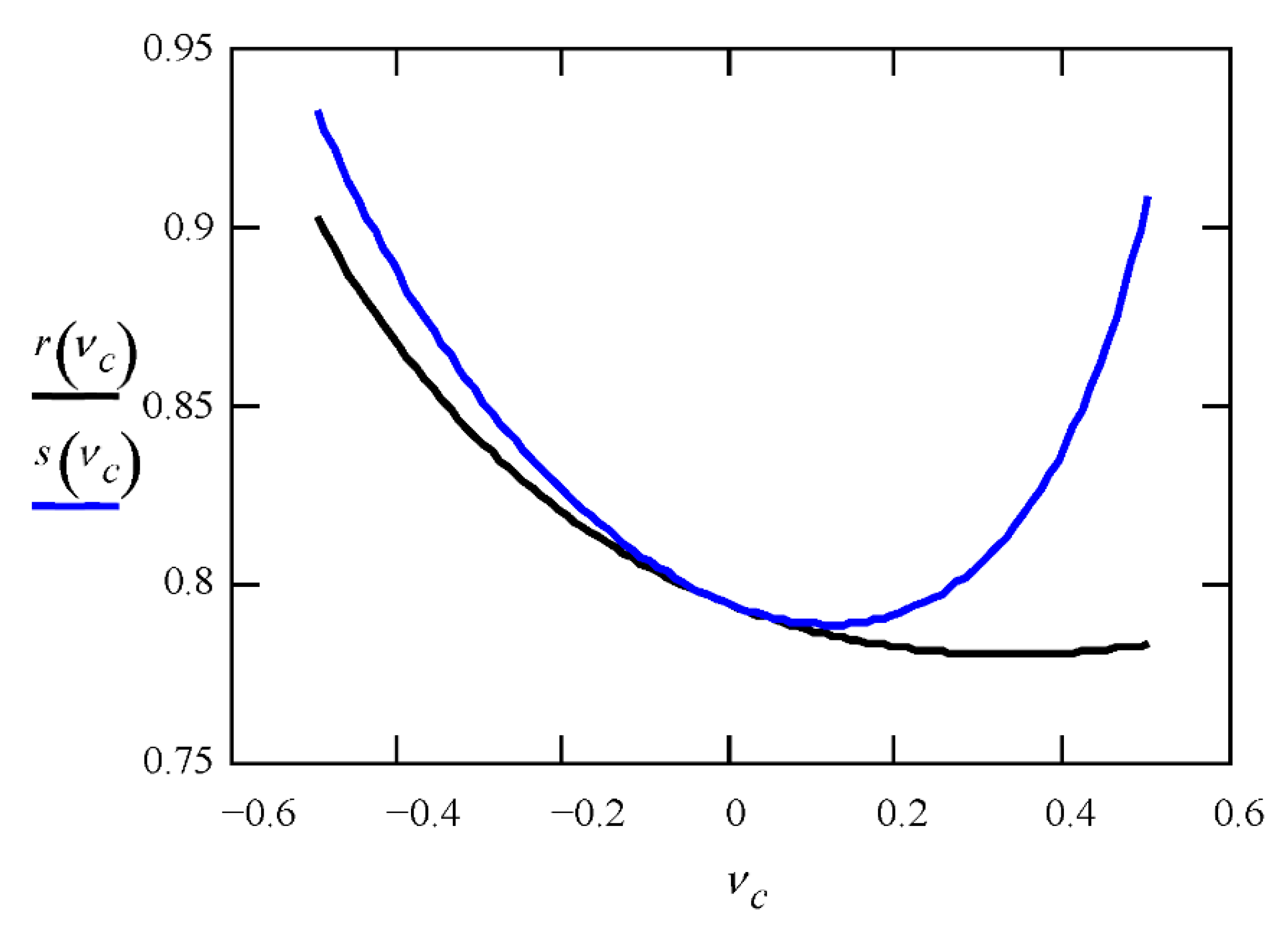
3.4.1. Influence of the Poisson Ratio
3.4.2. Assumptions and Strain Energy Considerations
4. Solution for the Orthotropic Core
4.1. Differential Equation
4.2. Solution of the Differential Equation
5. Examples
5.1. Analytical Solutions
5.2. Numerical Solutions
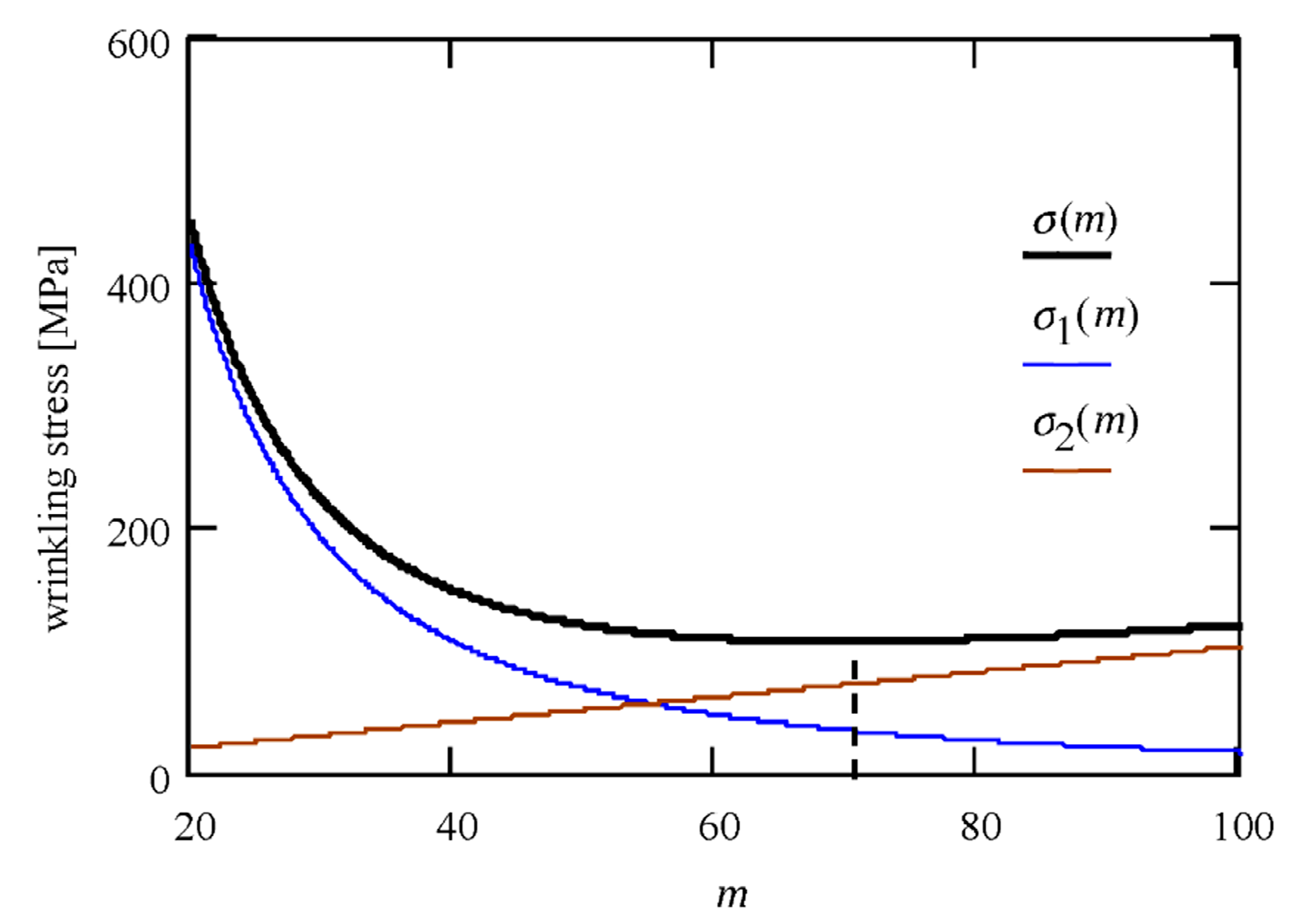
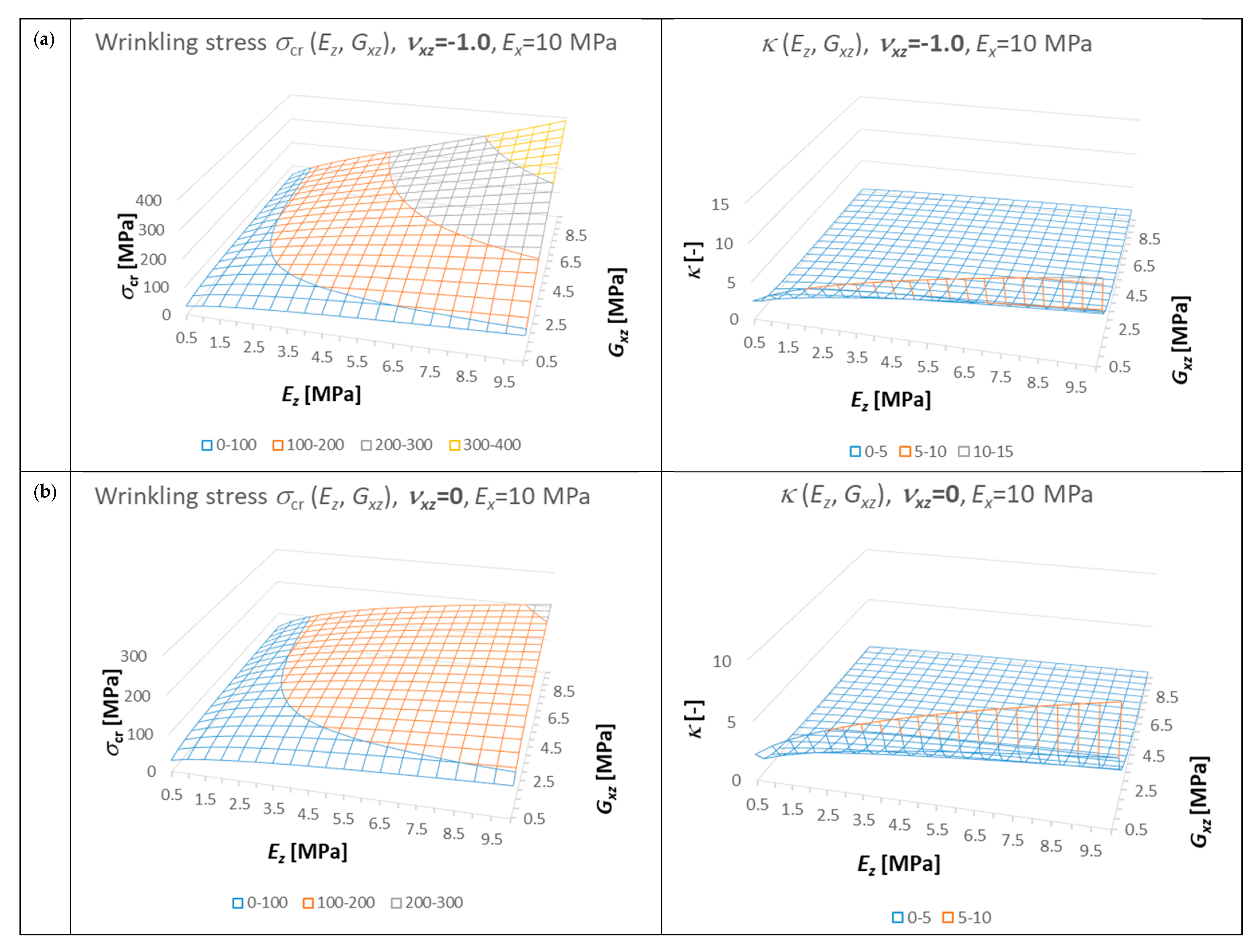
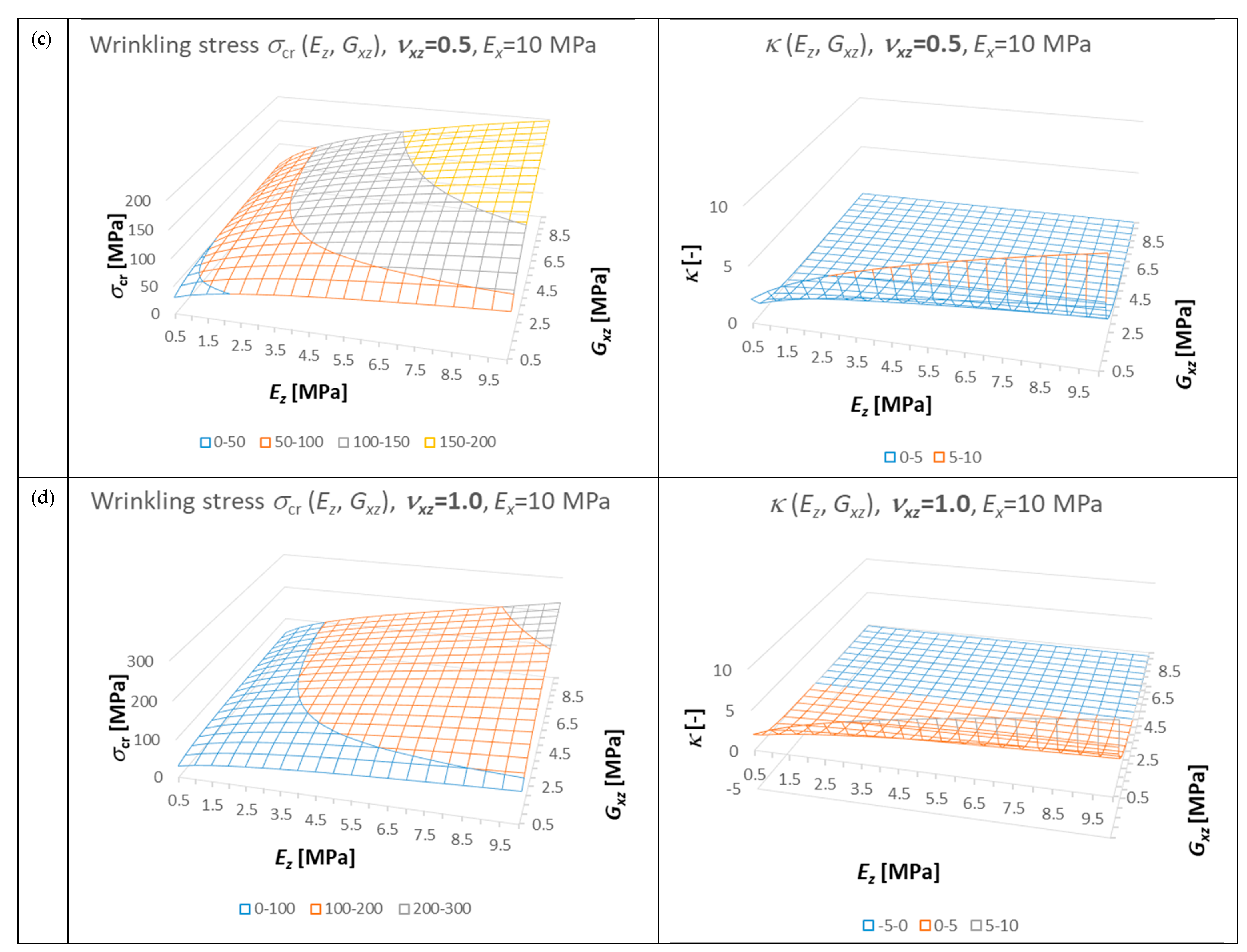
6. Parametric Analysis
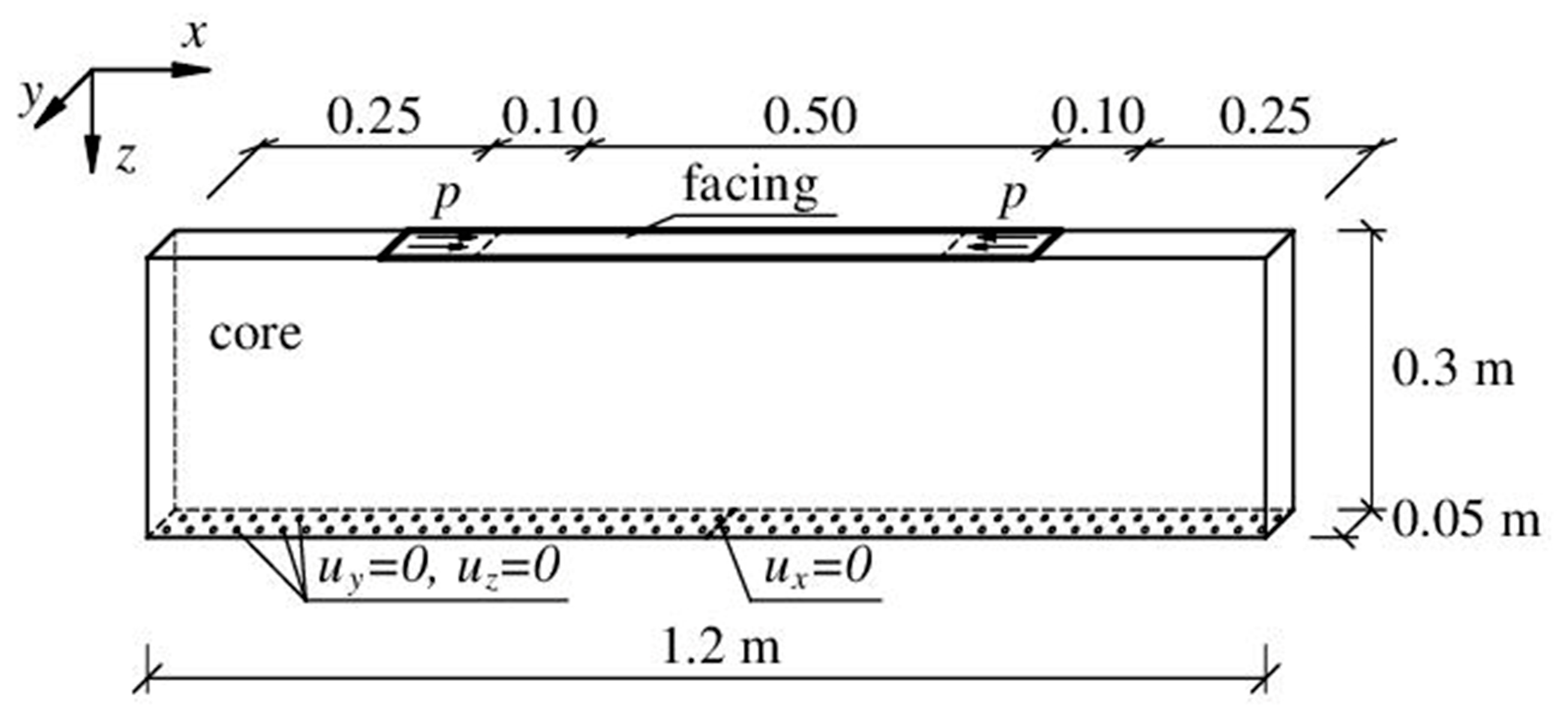
Description of the Models
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vescovini, R.; D’Ottavio, M.; Dozio, L.; Polit, O. Buckling and wrinkling of anisotropic sandwich plates. Int. J. Eng. Sci. 2018, 130, 136–156. [Google Scholar] [CrossRef] [Green Version]
- Studziński, R.; Gajewski, T.; Malendowski, M.; Sumelka, W.; Al-Rifaie, H.; Peksa, P.; Sielicki, P.W. Blast test and failure mechanisms of soft-core sandwich panels for storage halls applications. Materials 2021, 14, 70. [Google Scholar] [CrossRef] [PubMed]
- Zaharia, S.M.; Enescu, L.A.; Pop, M.A. Mechanical performances of lightweight sandwich structures produced by material extrusion-based additive manufacturing. Polymers 2020, 12, 1740. [Google Scholar] [CrossRef] [PubMed]
- Hoff, N.J.; Mautner, S.E. Buckling of Sandwich Type Panels. J. Aeronaut. Sci. 1945, 12, 285–297. [Google Scholar] [CrossRef]
- Plantema, F.J. Sandwich Construction; the Bending and Buckling of Sandwich Beams, Plates and Shells; John Wiley & Sons, Inc.: New York, NY, USA, 1966. [Google Scholar]
- Allen, H.G. Analysis and Design of Structural Sandwich Panels; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Norris, C.B.; Ericksen, W.S.; March, H.W.; Smith, C.B.; Boller, K.H. Wrinkling of the Facing of Sandwich Construction Subjected to Edgewise Compression, Report No. 1810; Forest Products Laboratory: Madison, WI, USA, 1961. [Google Scholar]
- Vonach, W.K.; Rammerstorfer, F.G. Wrinkling of thick orthotropic sandwich plates under general loading conditions. Arch. Appl. Mech. 2000, 70, 338–348. [Google Scholar] [CrossRef]
- Birman, V.; Bert, C.W. Wrinkling of composite-facing sandwich panels under biaxial loading. J. Sandw. Struct. Mater. 2004, 6, 217–237. [Google Scholar] [CrossRef]
- Lopatin, A.; Morozov, E. Symmetrical facing wrinkling of composite sandwich panels. J. Sandw. Struct. Mater. 2008, 10, 475–497. [Google Scholar] [CrossRef]
- Koissin, V.; Shipsha, A.; Skvortsov, V. Wrinkling in sandwich panels—An analytical approach. J. Sandw. Struct. Mater. 2011, 13, 705–730. [Google Scholar] [CrossRef]
- Fagerberg, L. The effect of local bending stiffness on wrinkling of sandwich panels. J. Eng. Marit. Environ. 2003, 217, 111–119. [Google Scholar] [CrossRef]
- Fagerberg, L.; Zenkert, D. Effects of anisotropy and multiaxial loading on the wrinkling of sandwich panels. J. Sandw. Struct. Mater. 2005, 7, 177–194. [Google Scholar] [CrossRef]
- Birman, V.; Vo, N. Wrinkling in sandwich structures with a functionally graded core. J. Appl. Mech. 2017, 84, 021002. [Google Scholar] [CrossRef]
- Frostig, Y. On wrinkling of a sandwich panel with a compliant core and self-equilibrated loads. J. Sandw. Struct. 2011, 13, 663–679. [Google Scholar] [CrossRef]
- Hohe, J.; Librescu, L. Recent results on the effect of the transverse core compressibility on the static and dynamic response of sandwich structures. Composites Part B Eng. 2008, 39, 108–119. [Google Scholar] [CrossRef]
- Phan, C.N.; Bailey, N.W.; Kardomateas, G.A.; Battley, M.A. Wrinkling of sandwich wide panels/beams based on the extended high-order sandwich panel theory: Formulation, comparison with elasticity and experiments. Arch. Appl. Mech. 2012, 82, 1585–1599. [Google Scholar] [CrossRef]
- EN 14509:2013 Self-Supporting Double Skin Metal Faced Insulating Panels—Factory Made Products—Specifications; British Standards Institution: London, UK, 2013.
- Pozorski, Z. Sandwich Panels in Civil Engineerin—Theory, Testing and Design; Wydawnictwo Politechniki Poznańskiej: Poznań, Poland, 2016. [Google Scholar]
- Garbowski, T.; Gajewski, T.; Grabski, J.K. Torsional and transversal stiffness of orthotropic sandwich panels. Materials 2020, 13, 5016. [Google Scholar] [CrossRef] [PubMed]
- Lempriere, B.M. Poisson’s Ratio in Orthotropic Materials. AIAA J. 1968, 6, 2226–2227. [Google Scholar] [CrossRef]
- Steeves, C.A.; Fleck, N.A. Collapse mechanisms of sandwich beams with composite faces and a foam core, loaded in three-point bending. Part II: Experimental investigation and numerical modelling. Int. J. Mech. Sci. 2004, 46, 585–608. [Google Scholar] [CrossRef]
- Smakosz, Ł.; Kreja, I.; Pozorski, Z. Flexural behavior of composite structural insulated panels with magnesium oxide board facings. Arch. Civ. Mech. Eng. 2020, 20, 1–21. [Google Scholar] [CrossRef]
- Pozorski, Z.; Wojciechowski, S. The influence of symmetrical boundary conditions on the structural behaviour of sandwich panels subjected to torsion. Symmetry 2020, 12, 2093. [Google Scholar] [CrossRef]
- Riks, E. An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Struct. 1979, 15, 524–551. [Google Scholar] [CrossRef]



| Load Increment | The Percentage Completion of the Load Step (LPF) | Theoretical Compressive Stress σx [MPa] | Extreme Compressive Stress Read in the Model Nodes σx [MPa] |
|---|---|---|---|
| 1 | 0.0156 | 6.24 | 6.72 |
| 2 | 0.0313 | 12.52 | 13.52 |
| 3 | 0.0547 | 21.88 | 23.88 |
| 4 | 0.0898 | 35.92 | 39.99 |
| 5 | 0.142 | 56.80 | 66.62 |
| 6 | 0.213 | 85.20 | 129.5 |
| 7 | 0.238 | 95.20 | 263.8 |
| 8 | 0.241 | 96.40 | 330.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pozorski, Z.; Pozorska, J.; Kreja, I.; Smakosz, Ł. On Wrinkling in Sandwich Panels with an Orthotropic Core. Materials 2021, 14, 5043. https://doi.org/10.3390/ma14175043
Pozorski Z, Pozorska J, Kreja I, Smakosz Ł. On Wrinkling in Sandwich Panels with an Orthotropic Core. Materials. 2021; 14(17):5043. https://doi.org/10.3390/ma14175043
Chicago/Turabian StylePozorski, Zbigniew, Jolanta Pozorska, Ireneusz Kreja, and Łukasz Smakosz. 2021. "On Wrinkling in Sandwich Panels with an Orthotropic Core" Materials 14, no. 17: 5043. https://doi.org/10.3390/ma14175043
APA StylePozorski, Z., Pozorska, J., Kreja, I., & Smakosz, Ł. (2021). On Wrinkling in Sandwich Panels with an Orthotropic Core. Materials, 14(17), 5043. https://doi.org/10.3390/ma14175043







