Stability Analysis of Multi-Discrete Delay Milling with Helix Effects Using a General Order Full-Discretization Method Updated with a Generalized Integral Quadrature
Abstract
1. Introduction
- Low order interpolation methods have been applied in handling milling states thus accuracy optimization has not been investigated holistically. In this regard, only [20] so far ventured further by exploiting a single case—involving third order interpolation of the delayed state—in the domain of hyper-first order methods.
- Stability analyses are mostly done manually thus needing re-analysis when interpolation parameters change.
- The distributed cutting force on helix tools has been mostly handled as zero-th order variations on discrete depth segments of the tools. Here again, re-analysis is needed when interpolation order of the variations change.
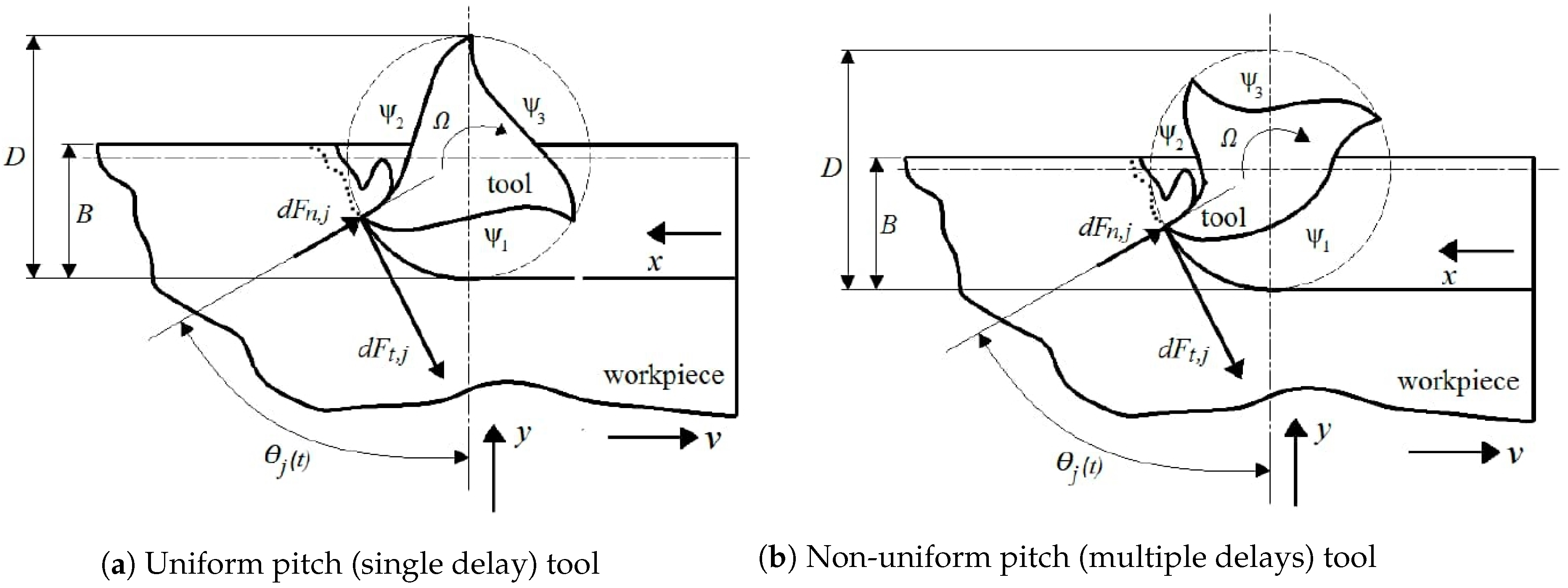
2. Regenerative Dynamics of Milling with Multi-Delay and Helix Effects
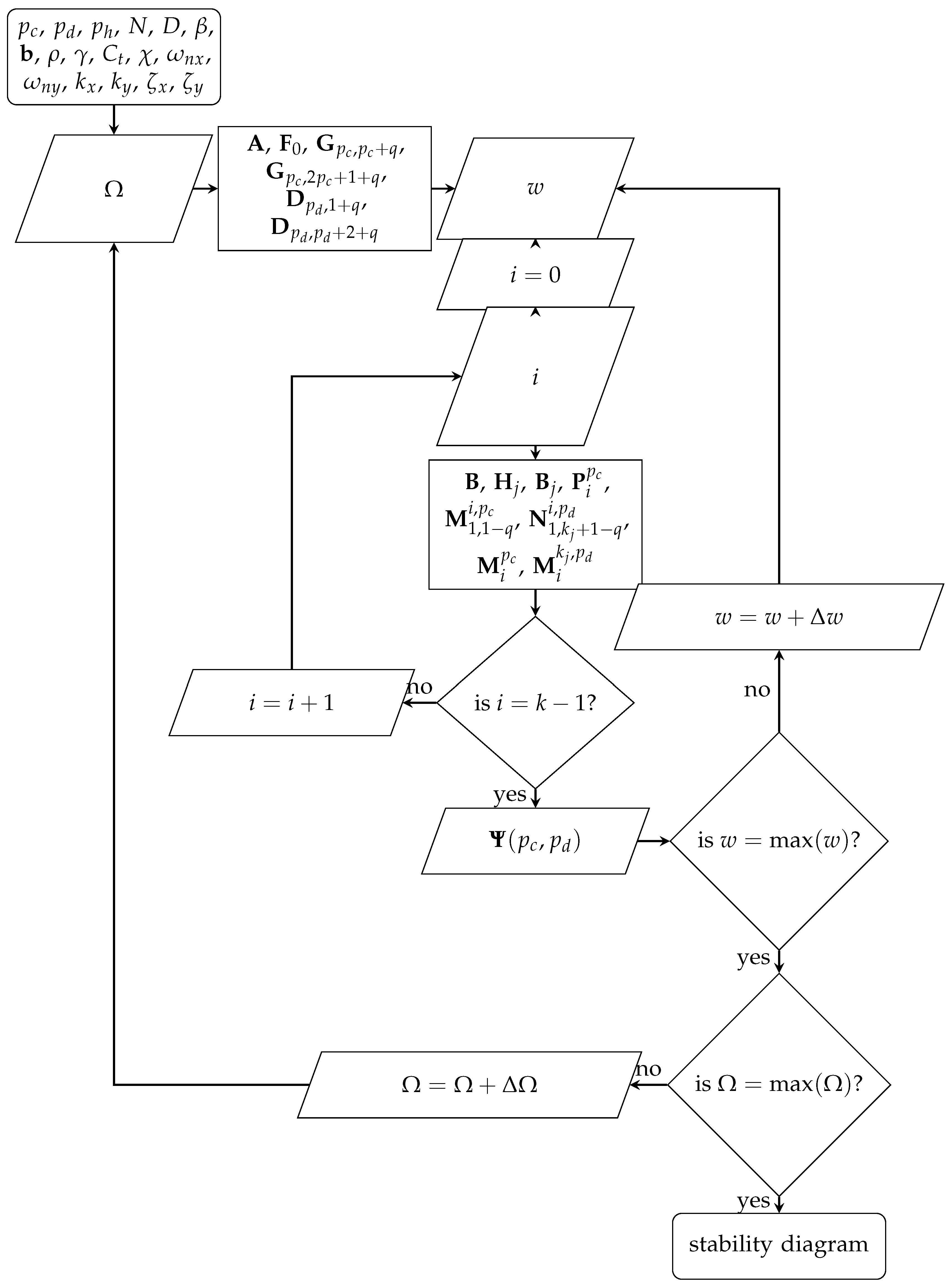
3. A Generalized Stability Analysis Considering Multiple Discrete Delays and the Helix Tool Angle
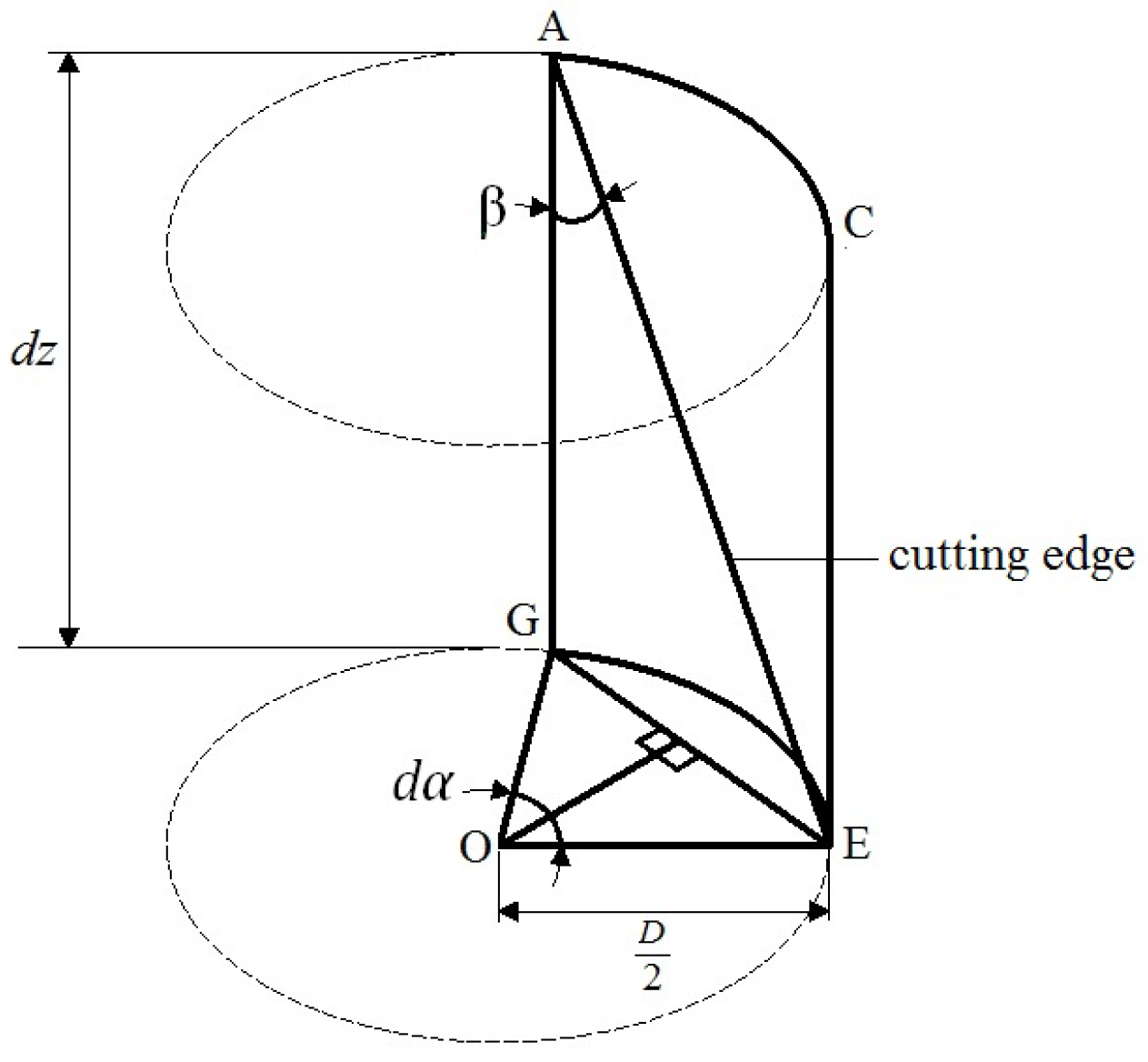
4. General Order Tensor-Based Interpolation and Integration of Helix-Induced
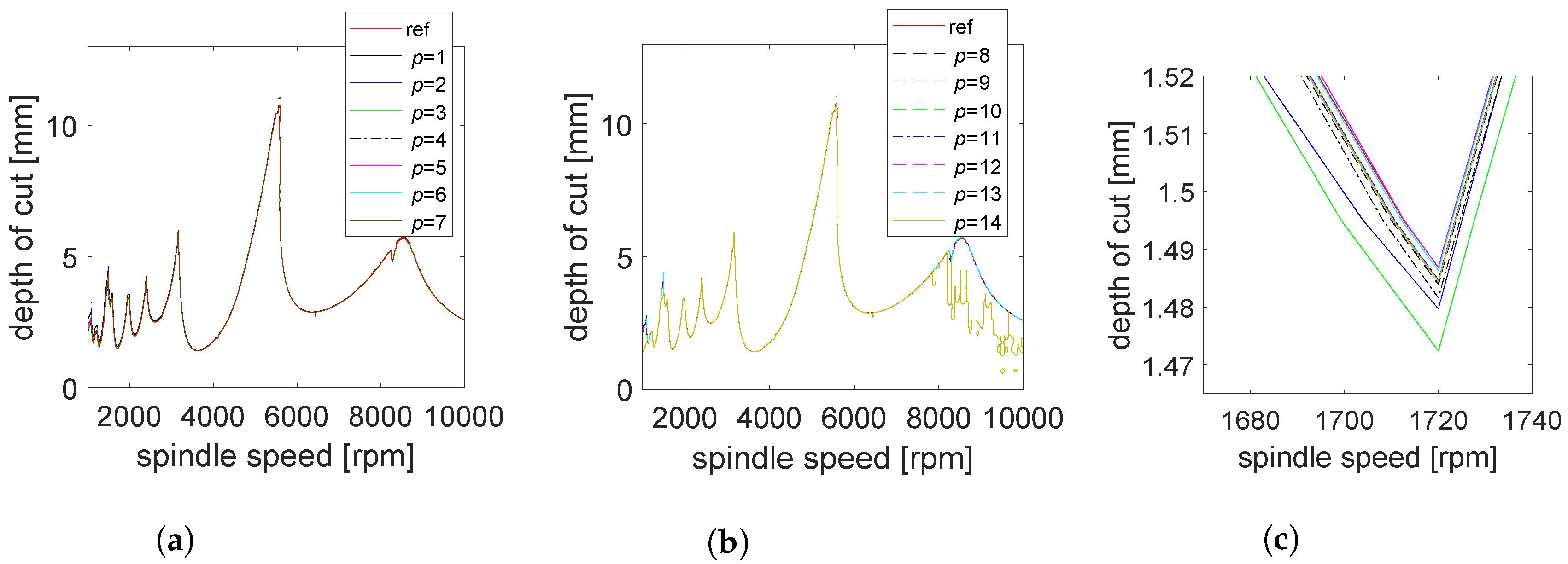
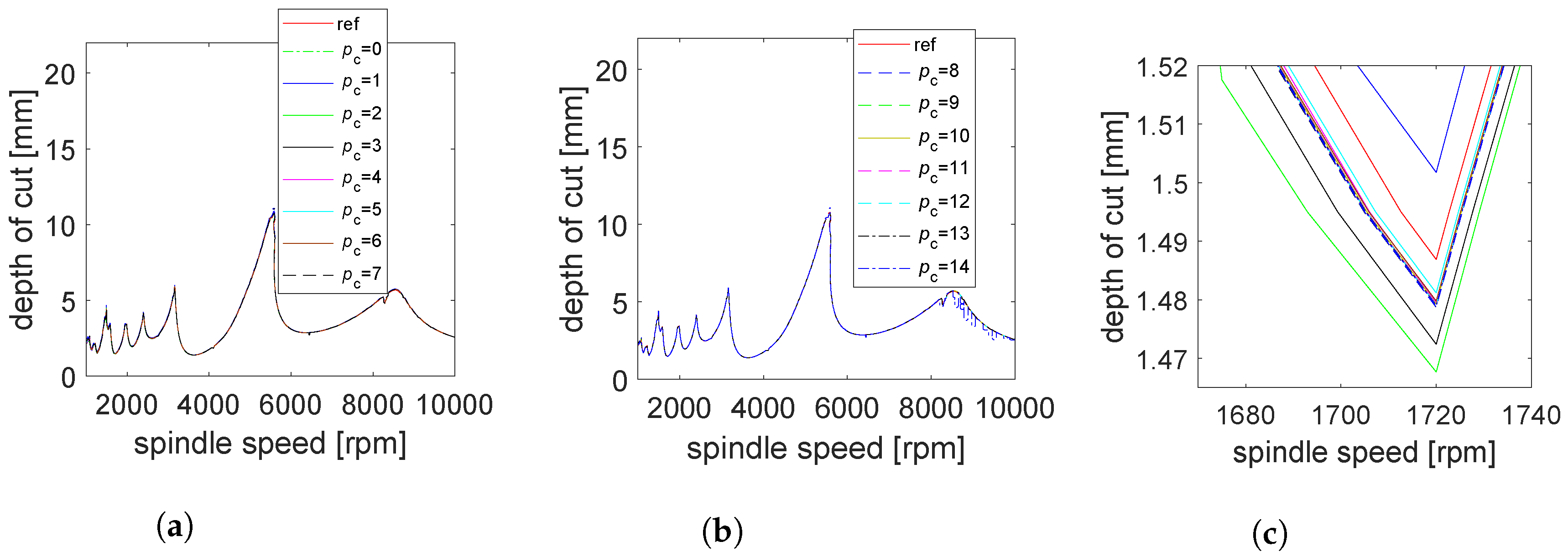
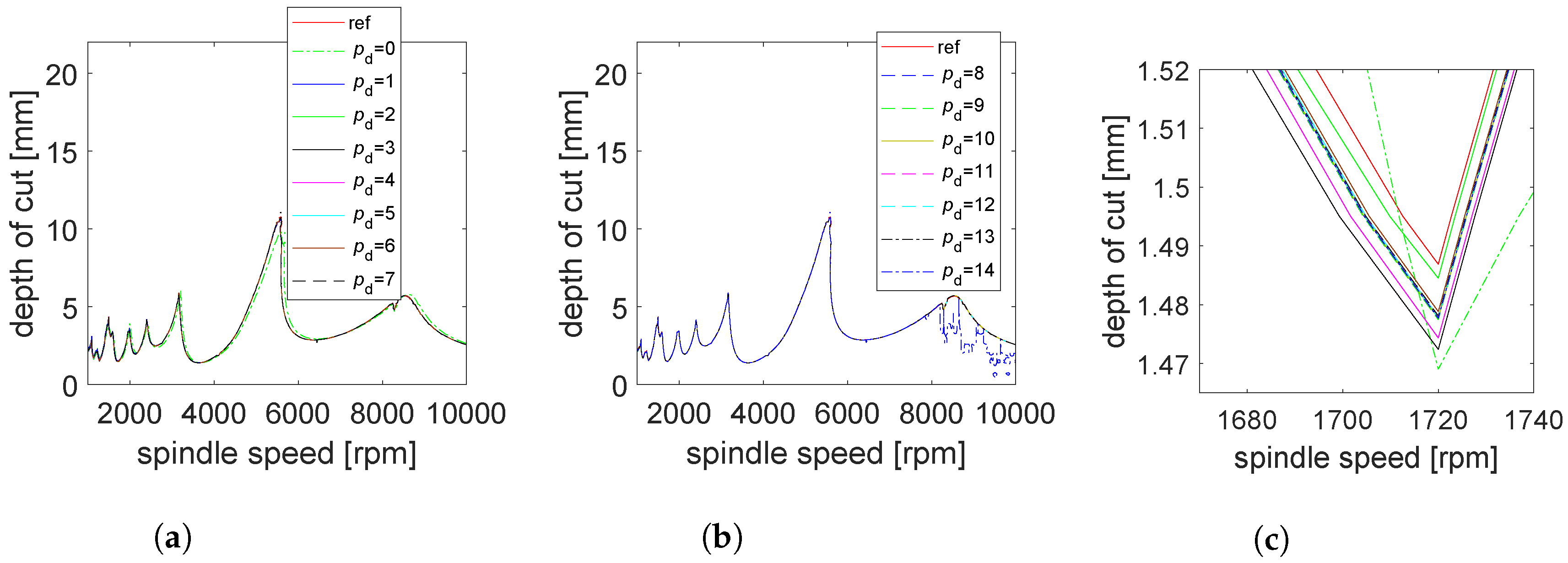
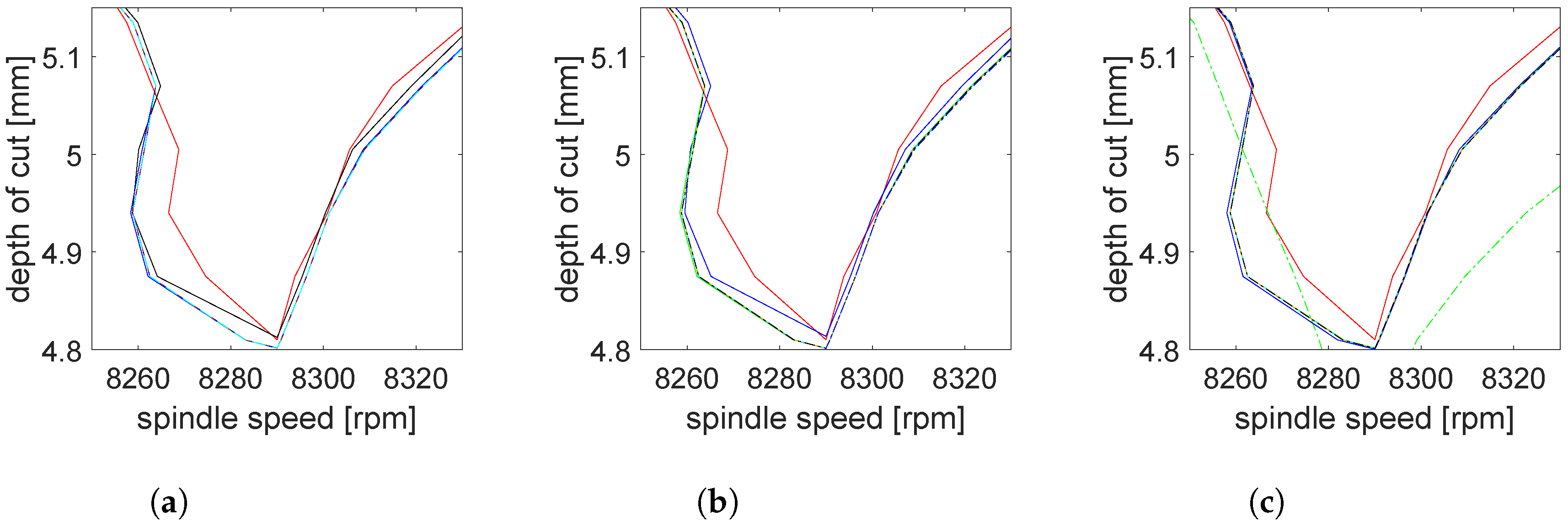
5. Numerical Simulation and Discussions
5.1. Two Degree of Freedom Tool
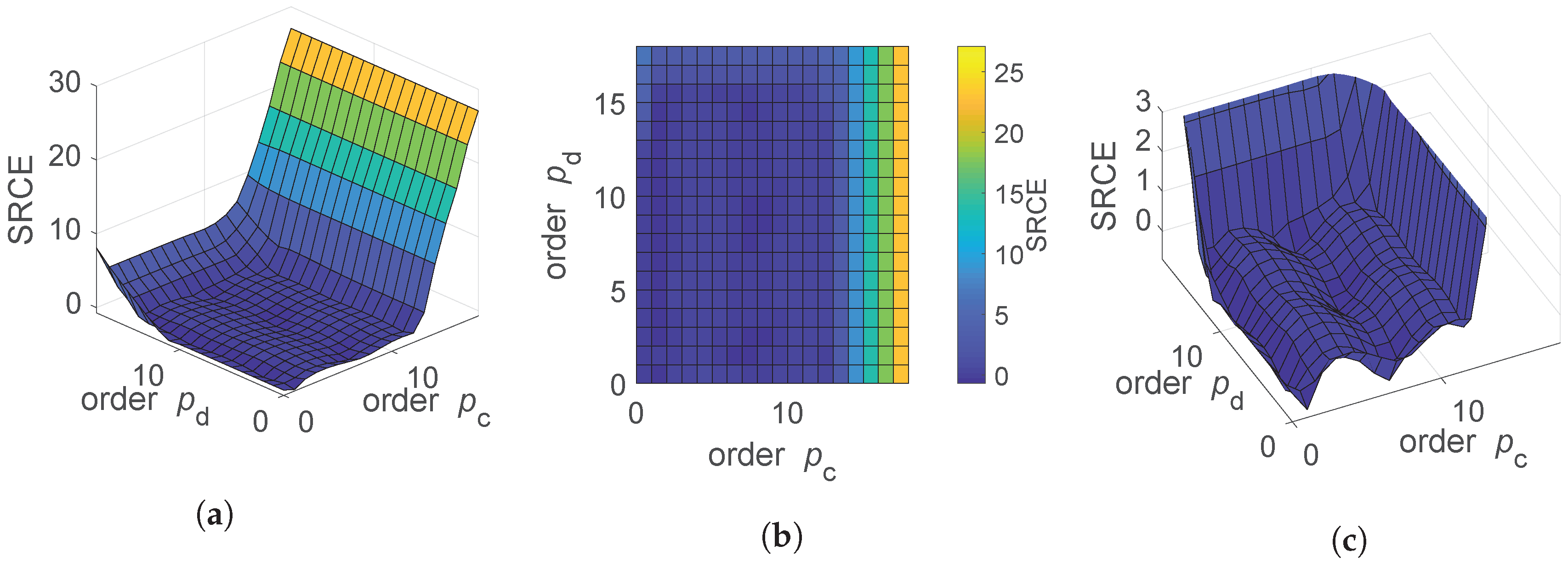
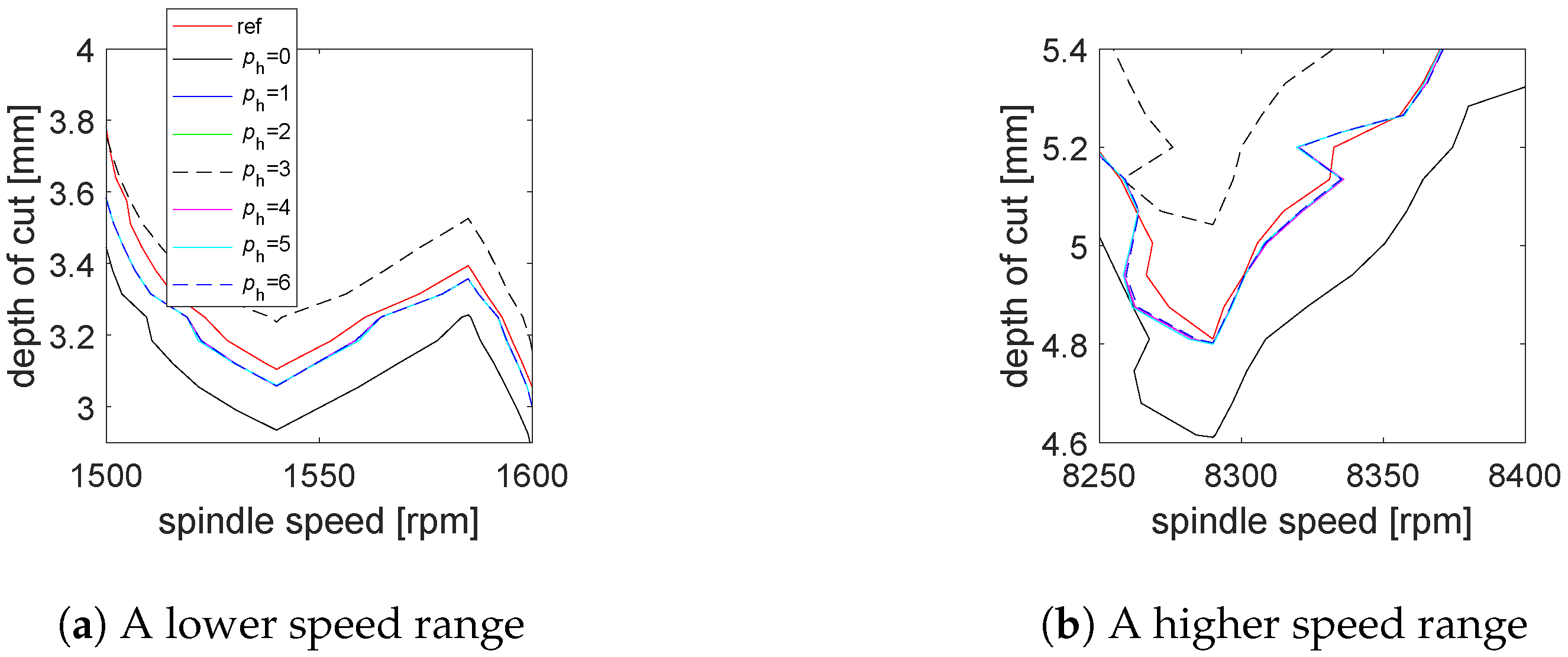
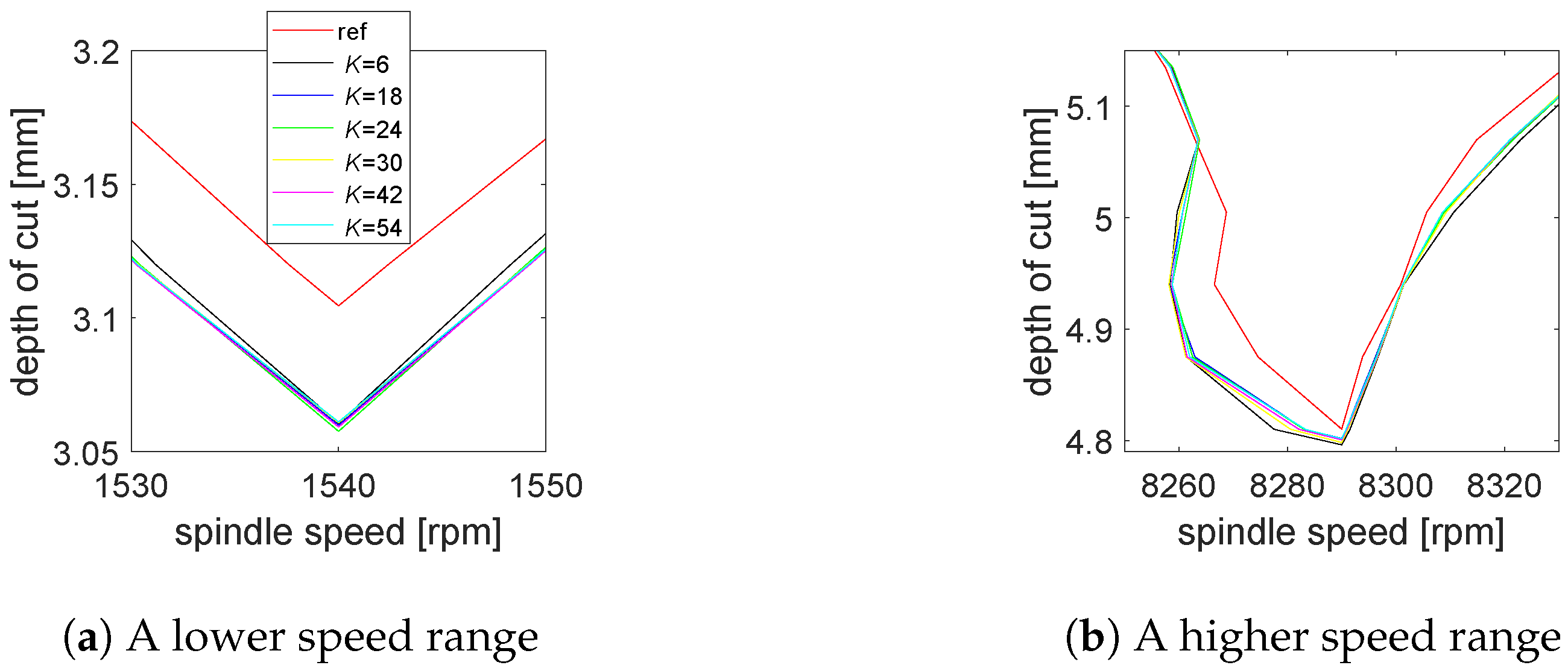
5.1.1. Convergence with Interpolation Orders
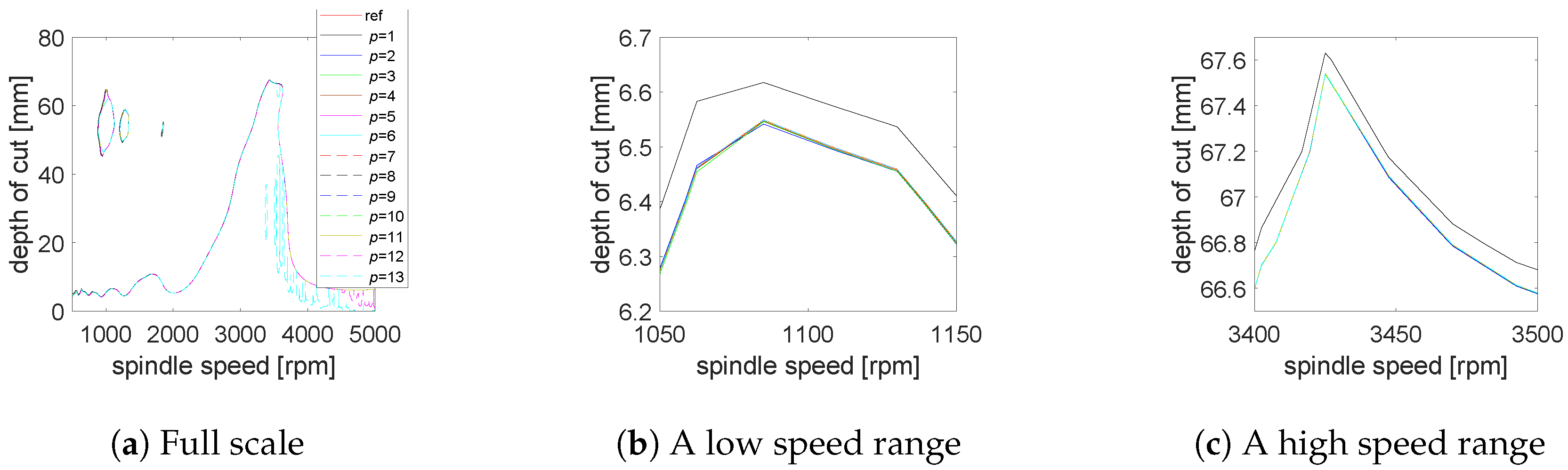
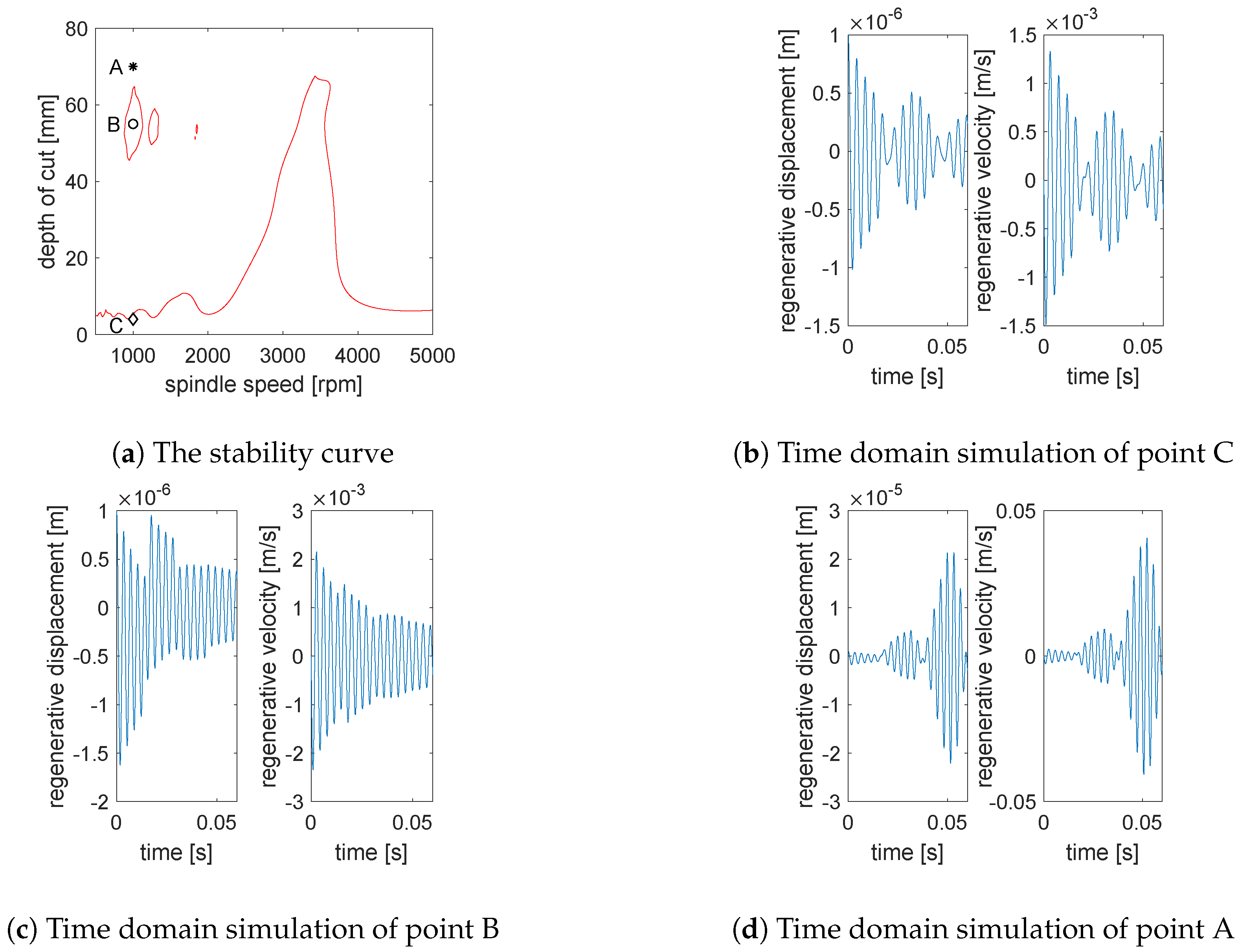
5.1.2. Stability Lobes Identification
5.2. Single Degree of Freedom Tool
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Altıntaş, Y.; Engin, S.; Budak, E. Analytical stability prediction and design of variable pitch cutters. J. Manuf. Sci. Eng. 1999, 121, 173–178. [Google Scholar] [CrossRef]
- Sims, N.D.; Mann, B.; Huyanan, S. Analytical prediction of chatter stability for variable pitch and variable helix milling tools. J. Sound Vib. 2008, 317, 664–686. [Google Scholar] [CrossRef]
- Dombovari, Z.; Altintas, Y.; Stepan, G. The effect of serration on mechanics and stability of milling cutters. Int. J. Mach. Tools Manuf. 2010, 50, 511–520. [Google Scholar] [CrossRef]
- Yusoff, A.R.; Sims, N.D. Optimisation of variable helix tool geometry for regenerative chatter mitigation. Int. J. Mach. Manuf. 2011, 51, 133–141. [Google Scholar] [CrossRef]
- Dombovari, Z.; Stepan, G. The effect of helix angle variation on milling stability. J. Manuf. Sci. Eng. 2012, 134, 1–6. [Google Scholar] [CrossRef]
- Altintaş, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann. Manuf. Technol. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Budak, E. An analytical design method for milling cutters with nonconstant pitch to increase stability, Part I: Theory. J. Manuf. Eng. 2003, 125, 29–34. [Google Scholar] [CrossRef]
- Olgac, N.; Sipahi, R. A unique methodology for chatter stability mapping in simultaneous machining. J. Manuf. Sci. Eng. 2005, 127, 791–800. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G. Updated semi-discretization method for periodic delay-differential equations with discrete delay. Int. J. Numer. Methods Eng. 2004, 61, 117–141. [Google Scholar] [CrossRef]
- Bayly, P.V.; Mann, B.P.; Peters, D.A.; Schmitz, T.L.; Stepan, G.; Insperger, T. Effects of Radial Immersion and Cutting Direction on Chatter Instability in End-Milling; ASME: New Orleans, LA, USA, 2002; pp. 1–13. [Google Scholar]
- Wan, M.; Zhang, W.H.; Dang, J.W.; Yang, Y. A unified stability prediction method for milling process with multiple delays. Int. Mach. Tools Manuf. 2010, 50, 29–41. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. A full-discretization method for prediction of milling stability. Int. J. Mach. Manuf. 2010, 50, 502–509. [Google Scholar] [CrossRef]
- Zhang, X.; Xiong, C.; Ding, Y. Improved full-discretization method for milling chatter stability prediction with multiple delays. In Proceedings of the International Conference on Intelligent Robotics and Applications—ICIRA 2010: Intelligent Robotics and Applications, Shanghai, China, 10–12 November 2010; pp. 541–552. [Google Scholar]
- Sellmeier, V.; Denkena, B. Stable islands in the stability chart of milling processes due to unequal tooth pitch. Int. J. Mach. Tools Manuf. 2011, 51, 152–164. [Google Scholar] [CrossRef]
- Zhang, X.; Xiong, C.; Ding, Y.; Xiong, Y. Variable-step integration method for milling chatter stability prediction with multiple delays. Sci. China Technol. Sci. 2011, 54, 3137–3154. [Google Scholar] [CrossRef]
- Suzuki, N.; Kojima, T.; Hino, R.; Shamoto, E. A novel design method of irregular pitch cutters to attain simultaneous suppression of multi-mode regenerations. Procedia CIRP 2012, 4, 98–102. [Google Scholar] [CrossRef]
- Jin, G.; Zhang, Q.; Hao, S.; Xie, Q. Stability prediction of milling process with variable pitch cutter. Math. Probl. Eng. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Zatarain, M.; Dombovari, Z. Stability analysis of milling with irregular pitch tools by the implicit subspace iteration method. Int. Dyn. Control 2014, 2, 26–34. [Google Scholar] [CrossRef][Green Version]
- Budak, E. An analytical design method for milling cutters with nonconstant pitch to increase stability, Part 2: Application. J. Manuf. Sci. Eng. 2003, 125, 35–38. [Google Scholar] [CrossRef]
- Guo, Q.; Sun, Y.; Jiang, Y.; Guo, D. Prediction of stability limit for multi-regenerative chatter in high performance milling. Int. Dyn. Control 2014, 2, 35–45. [Google Scholar] [CrossRef]
- Jin, G.; Zhang, Q.; Hao, S.; Xie, Q. Stability prediction of milling process with variable pitch and variable helix cutters. Proc. Inst. Mech. Eng. Part C J. Mech. Sci. 2014, 228, 281–293. [Google Scholar] [CrossRef]
- Comak, A.; Budak, E. Modeling dynamics and stability of variable pitch and helix milling tools for development of a design method to maximize chatter stability. Precis. Eng. 2017, 47, 459–468. [Google Scholar] [CrossRef]
- Ozoegwu, C.G. Least squares approximated stability boundaries of milling process. Int. J. Mach. Tools Manuf. 2014, 79, 24–30. [Google Scholar] [CrossRef]
- Ozoegwu, C.G.; Omenyi, S.N.; Ofochebe, S.M. Hyper-third order full-discretization methods in milling stability prediction. Int. J. Mach. Tools Manuf. 2015, 92, 1–9. [Google Scholar] [CrossRef]
- Ozoegwu, C.G. A general order full-discretization algorithm for chatter avoidance in milling. Adv. Mech. Eng. 2018, 10, 1–23. [Google Scholar] [CrossRef]
- Ozoegwu, C.G.; Eberhard, P. Tensor-based automatic arbitrary order computation of the full-discretization method for milling stability analysis. In Contributions to Advanced Dynamics and Continuum Mechanics; Altenbach, H., Irschik, H., Matveenko, V., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Chapter 11; pp. 179–205. [Google Scholar]
- Ozoegwu, C.G.; Eberhard, P. Automated Upgraded Generalized Full-Discretization Method: Application to the Stability Study of a Thin Walled Milling Process. In Mechanical Sciences; Dixit, U.S., Dwivedy, S.K., Eds.; Springer Nature Singapore Pte Ltd.: Singapore, 2020; in press. [Google Scholar]
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| number of flutes | N | 4 | - |
| tool diameter | D | 19.05 | mm |
| helix angle | 30 | deg | |
| tool pitch | deg | ||
| down-milling radial immersion | 0.5 | - | |
| power force law exponent | 1 | - | |
| tangential cutting coefficient | |||
| thrust to tangential force ratio | 255.799/697 | - | |
| natural frequency | 563.60 | Hz | |
| 516.21 | |||
| modal stiffness | 18,792,624.40 | N/m | |
| 12,613,387.75 | |||
| modal damping ratio | 5.5801% | - | |
| 2.5004% |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| number of flutes | N | 4 | - |
| tool diameter | D | 20 | mm |
| helix angle | 30 | deg | |
| tool pitch | deg | ||
| radial immersion | 1 | - | |
| power force law exponent | 1 | - | |
| tangential cutting coefficient | |||
| thrust to tangential force ratio | - | ||
| natural frequency | 227.66 | Hz | |
| modal stiffness | N/m | ||
| modal damping ratio | 3.23% | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozoegwu, C.; Eberhard, P. Stability Analysis of Multi-Discrete Delay Milling with Helix Effects Using a General Order Full-Discretization Method Updated with a Generalized Integral Quadrature. Mathematics 2020, 8, 1003. https://doi.org/10.3390/math8061003
Ozoegwu C, Eberhard P. Stability Analysis of Multi-Discrete Delay Milling with Helix Effects Using a General Order Full-Discretization Method Updated with a Generalized Integral Quadrature. Mathematics. 2020; 8(6):1003. https://doi.org/10.3390/math8061003
Chicago/Turabian StyleOzoegwu, Chigbogu, and Peter Eberhard. 2020. "Stability Analysis of Multi-Discrete Delay Milling with Helix Effects Using a General Order Full-Discretization Method Updated with a Generalized Integral Quadrature" Mathematics 8, no. 6: 1003. https://doi.org/10.3390/math8061003
APA StyleOzoegwu, C., & Eberhard, P. (2020). Stability Analysis of Multi-Discrete Delay Milling with Helix Effects Using a General Order Full-Discretization Method Updated with a Generalized Integral Quadrature. Mathematics, 8(6), 1003. https://doi.org/10.3390/math8061003





