A Novel Chaotic System with Two Circles of Equilibrium Points: Multistability, Electronic Circuit and FPGA Realization
Abstract
:1. Introduction
2. Dynamical Model of the New Chaotic System
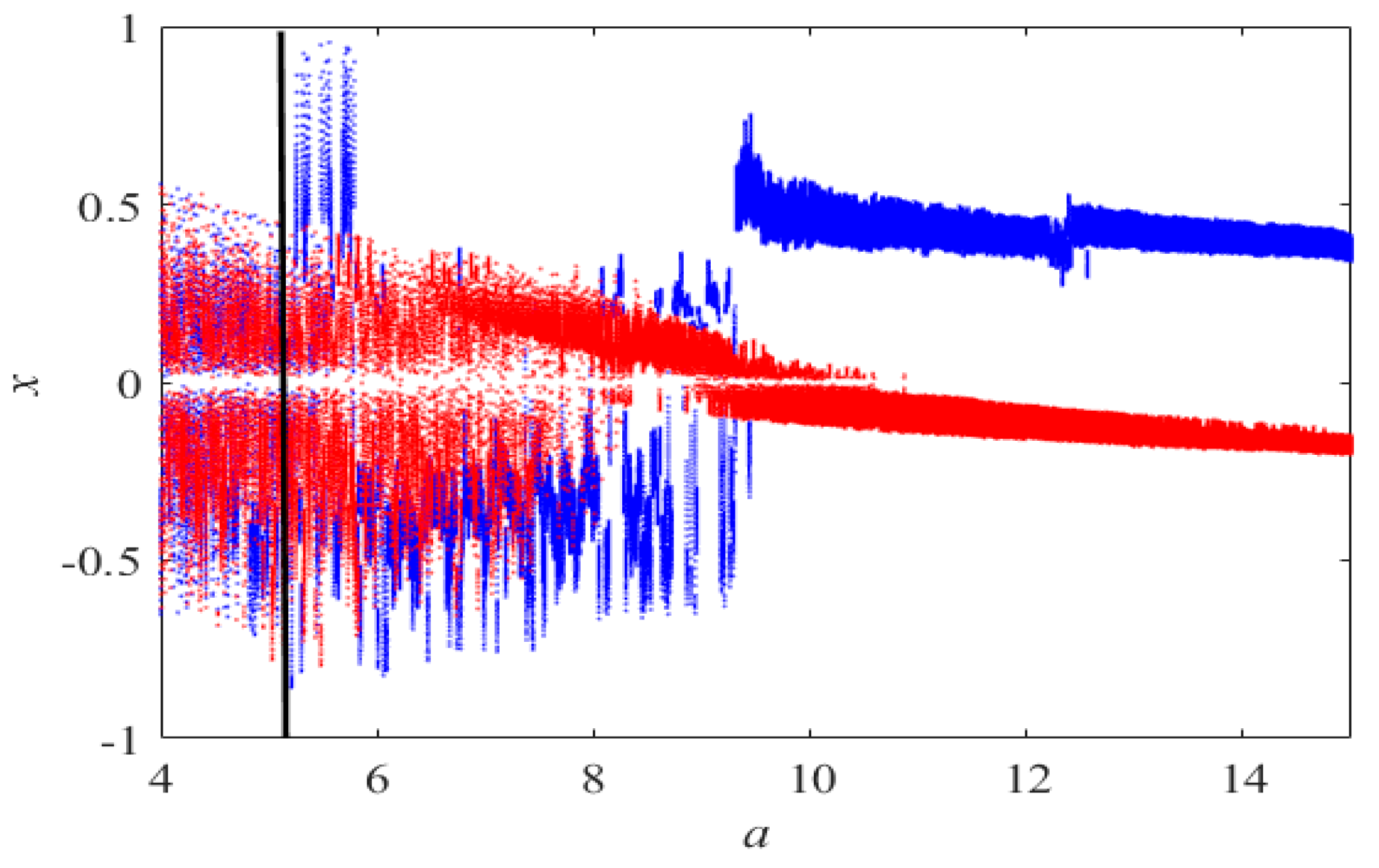
3. Multistability Analysis
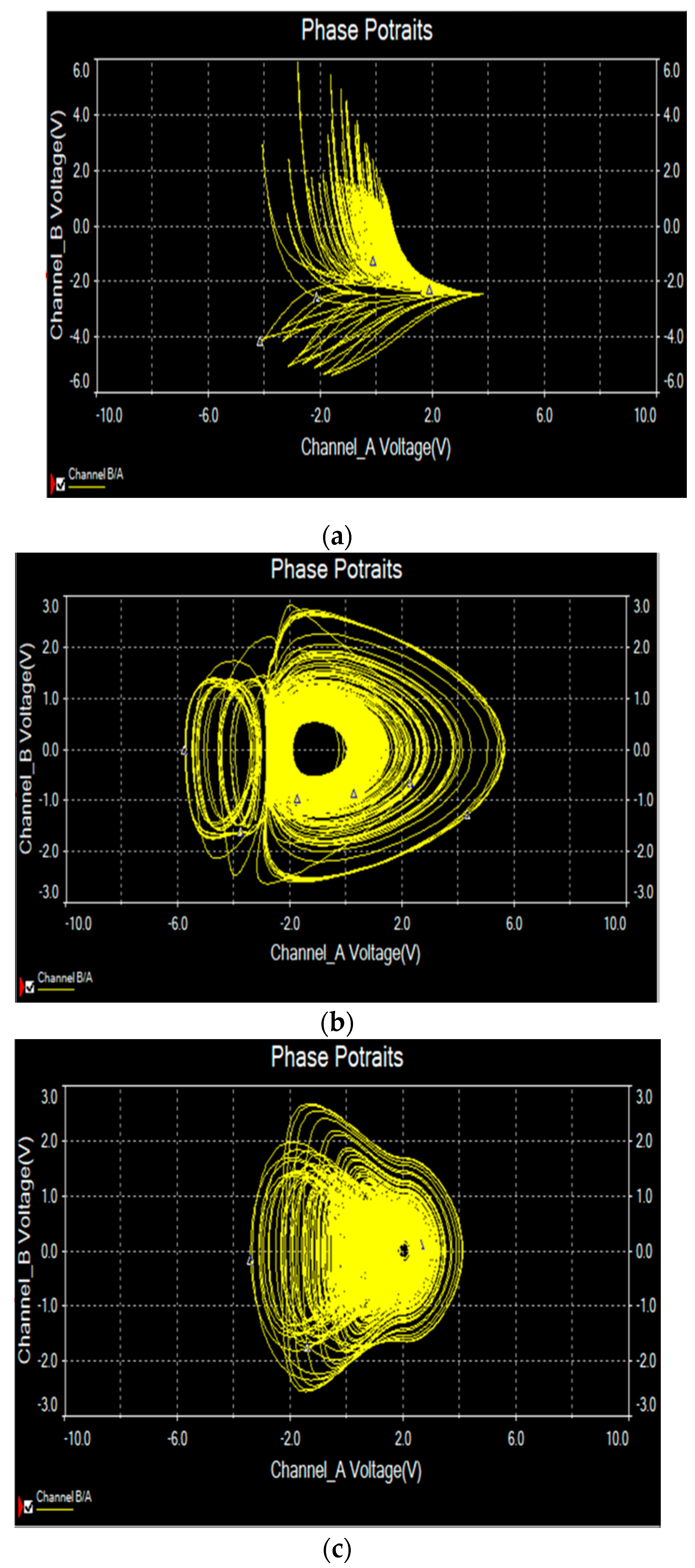
4. The Electronic Circuit Implementation
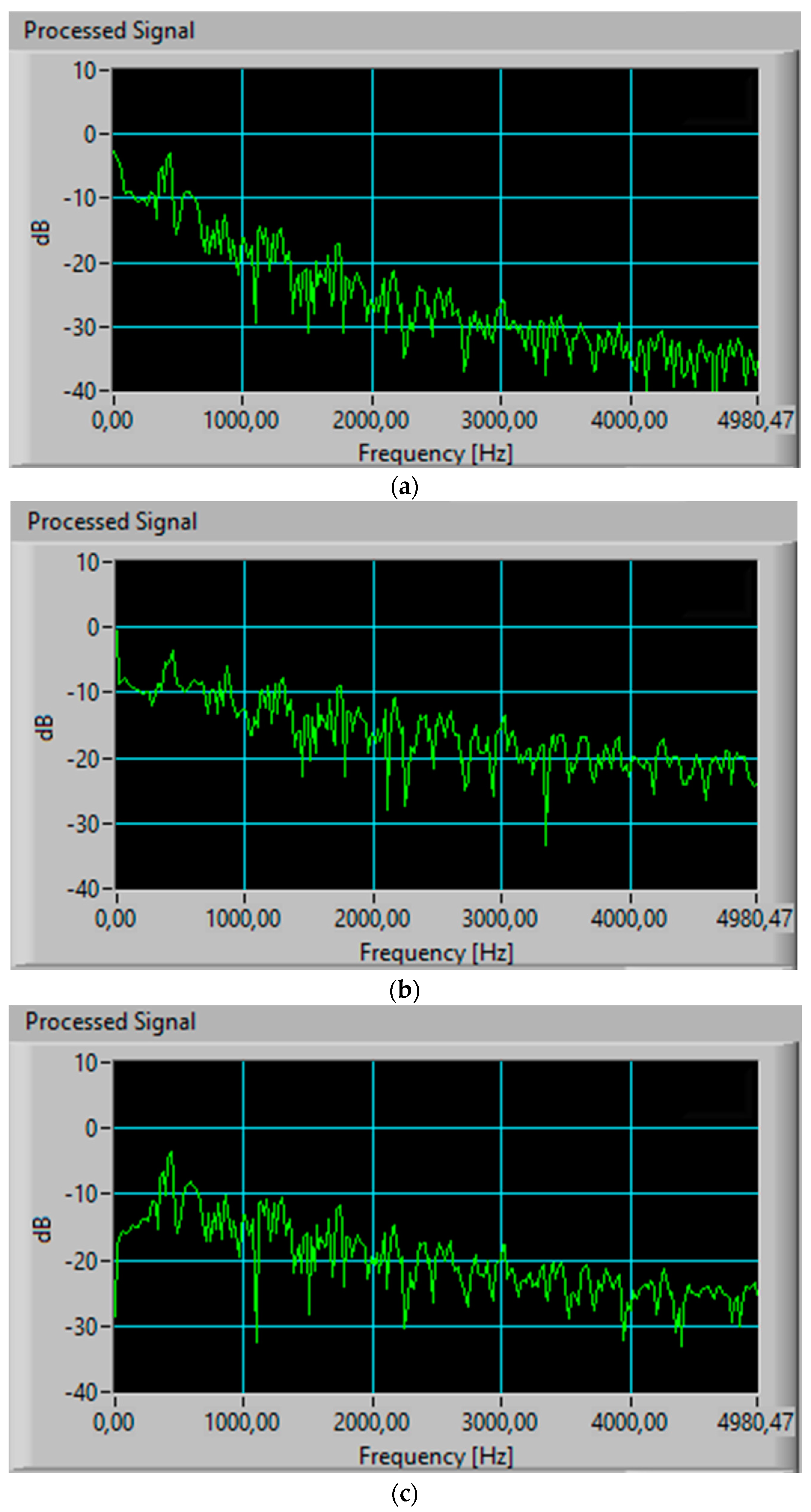
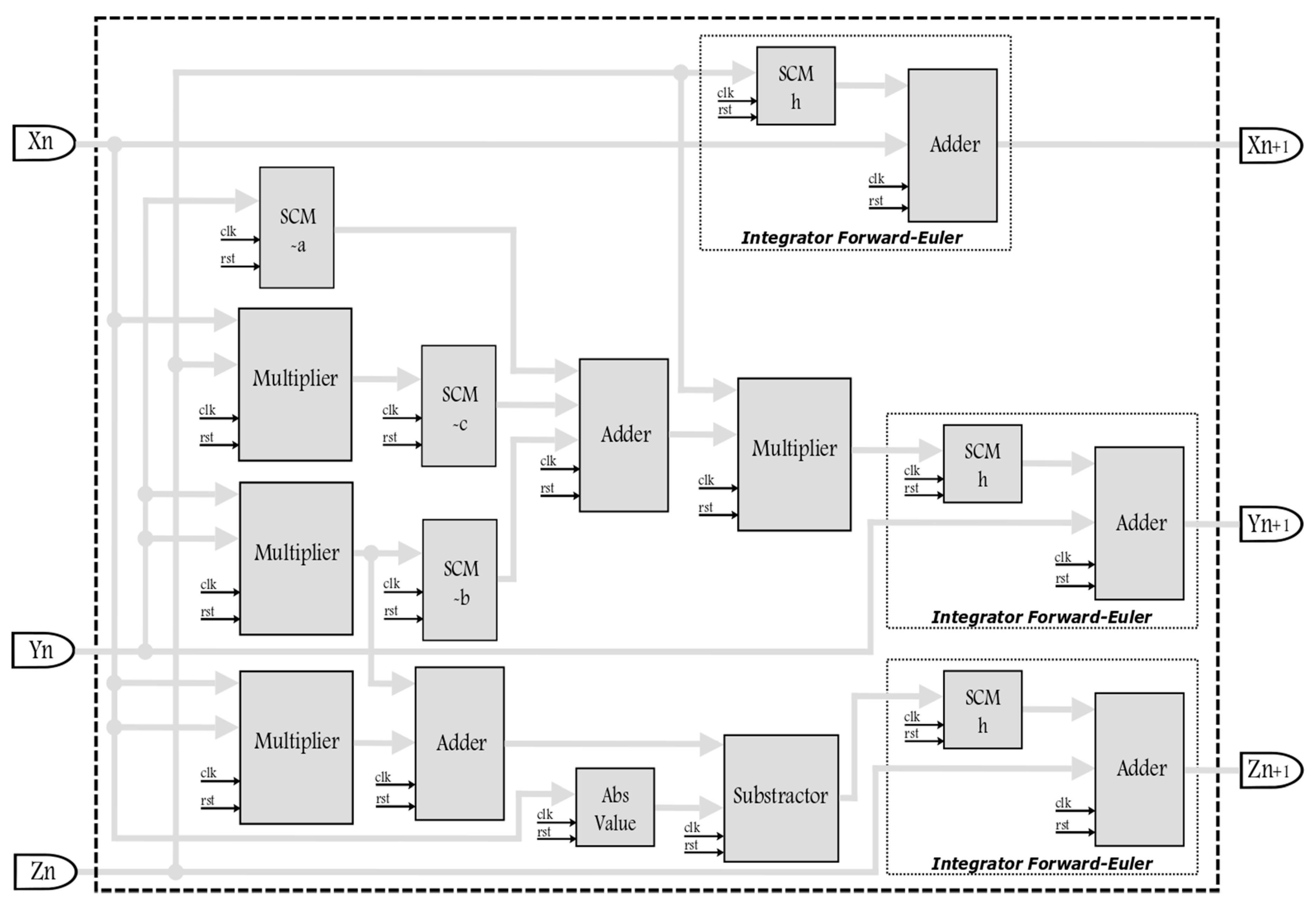
5. FPGA Realization
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering; Westview Press: Boulder, CO, USA, 2015. [Google Scholar]
- Vaidyanathan, S.; Volos, C. Advances and Applications in Chaotic Systems; Springer: Basel, Switzerland, 2016. [Google Scholar]
- Gotthans, T.; Petrzela, J. New class of chaotic systems with circular equilibrium. Nonlinear Dyn. 2015, 73, 429. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Wang, X.; Ma, J. A chaotic system with different shapes of equilibria. Int. J. Bifurc. Chaos 2016, 26, 1650069. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Volos, C. A novel chaotic system with heart-shaped equilibrium and its circuital implementation. Optik 2017, 131, 343–349. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Volos, C.; Giakoumis, A.; Vaidyanathan, S.; Kapitaniak, T. A chaotic system with equilibria located on the rounded square loop and its circuit implementation. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 878–882. [Google Scholar] [CrossRef]
- Mobayen, S.; Volos, C.; Kaçar, S.; Çavuşoğlu, Ü. New class of chaotic systems with equilibrium points like a three-leaved clover. Nonlinear Dyn. 2018, 91, 939–956. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Mamat, M.; Mohamed, M.A. A new chaotic system with a pear-shaped equilibrium and its circuit simulation. Int. J. Electr. Comput. Eng. 2018, 8, 4951. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Sambas, A.; Mamat, M. A new chaotic system with axe-shaped equilibrium, its circuit implementation and adaptive synchronization. Arch. Control Sci. 2018, 28, 443. [Google Scholar]
- Vaidyanathan, S.; Sambas, A.; Kaçar, S.; Çavuşoğlu, Ü. A new three-dimensional chaotic system with a cloud-shaped curve of equilibrium points, its circuit implementation and sound encryption. Int. J. Model. Identif. Control 2018, 30, 184. [Google Scholar] [CrossRef]
- Mobayen, S.; Vaidyanathan, S.; Sambas, A.; Kaçar, S.; Çavuşoğlu, Ü. A novel chaotic system with boomerang-shaped equilibrium, its circuit implementation and application to sound encryption. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 43, 1–12. [Google Scholar] [CrossRef]
- Matsumoto, T. A chaotic attractor from Chua’s circuit. IEEE Trans. Circuits Syst. 1984, 31, 1055. [Google Scholar] [CrossRef]
- Chua, L.O.; Komuro, M.; Matsumoto, T. The double-scroll family. IEEE Trans. Circuits Syst. 1986, 33, 1073. [Google Scholar] [CrossRef]
- Chua, L.O.; Lin, G.N. Canonical realization of Chua’s circuit family. IEEE Trans. Circuits Syst. 1990, 37, 885. [Google Scholar] [CrossRef]
- Chua, L.O.; Wu, C.W.; Huang, A. A universal circuit for studying and generating chaos—Part I. Routes to chaos. IEEE Trans. Circuits Syst. 1993, 40, 732. [Google Scholar] [CrossRef]
- Sprott, J.C. Simple chaotic systems and circuits. Am. J. Phys. 2000, 68, 758. [Google Scholar] [CrossRef]
- Kim, H.; Kim, Y.; Ji, H.; Park, H.; An, J.; Song, H.; Kim, Y.T.; Lee, H.; Kim, K. A single-chip FPGA holographic video processor. IEEE Trans. Ind. Electron. 2019, 66, 2066. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Zhang, S.; Zeng, Y.; Mohamed, M.A.; Mamat, M. A new double-wing chaotic system with coexisting attractors and line equilibrium: Bifurcation analysis and electronic circuit simulation. IEEE Access 2019, 7, 115454–115462. [Google Scholar] [CrossRef]
- Li, C.; Hu, W.; Sprott, J.C.; Wang, X. Multistability in symmetric chaotic systems. Eur. Phys. J. Spec. Top. 2015, 224, 1493–1506. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C. Coexisting hidden attractors in a 4-D simplified Lorenz system. Int. J. Bifurc. Chaos 2014, 24, 1450034. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Li, Z.; Wang, M.; Xiong, L. Generating one to four-wing hidden attractors in a novel 4D no-equilibrium chaotic system with extreme multistability. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 013113. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Li, Z. One to four-wing chaotic attractors coined from a novel 3D fractional-order chaotic system with complex dynamics. Chin. J. Phys. 2018, 56, 793–806. [Google Scholar] [CrossRef]
- Sun, K.; Wang, X.; Sprott, J.C. Bifurcations and chaos in fractional-order simplified Lorenz system. Int. J. Bifurc. Chaos 2010, 20, 1209–1219. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Fernandez, O.G.; Cano, A.M.; Cuautle, E.T.; Perez, J.C.N.; Magdaleno, J.J.R. On the synchronization techniques of chaotic oscillators and their FPGA-based implementation for secure image transmission. PLoS ONE 2019, 14, e0209618. [Google Scholar]
- Cuautle, E.T.; Fraga, L.G.; Magdaleno, J.R. Engineering Applications of FPGAs; Springer: Basel, Switzerland, 2016. [Google Scholar]








| Chaotic Systems | Closed Curve of Equilibrium Points |
|---|---|
| Gotthans and Petrzela [3] | Circle |
| Pham et al. [4] | Ellipse, Square and Rectangle |
| Pham et al. [5] | Heart |
| Pham et al. [6] | Rounded Square |
| Mobayen et al. [7] | Three-Leaved Clover |
| Sambas et al. [8] | Pear |
| Vaidyanathan et al. [9] | Axe |
| Vaidyanathan et al. [10] | Cloud |
| Mobayen et al. [11] | Boomerang |
| This Work | Two Circles |
| Resources | Numerical Method | Available | |
|---|---|---|---|
| Forward Euler | Runge-Kutta fourth Order | ||
| Logics Elements | 1,440 | 6,420 | 149,760 |
| Registers | 1,793 | 2,887 | 149,760 |
| 9*9 bits multipliers | 32 | 128 | 720 |
| Maximum Frequency (MHz) | 89.96 | 70.09 | 50 |
| Clock Cycles by Iteration | 10 | 34 | - |
| Latency by Iteration (ns) | 200 | 680 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sambas, A.; Vaidyanathan, S.; Tlelo-Cuautle, E.; Zhang, S.; Guillen-Fernandez, O.; Sukono; Hidayat, Y.; Gundara, G. A Novel Chaotic System with Two Circles of Equilibrium Points: Multistability, Electronic Circuit and FPGA Realization. Electronics 2019, 8, 1211. https://doi.org/10.3390/electronics8111211
Sambas A, Vaidyanathan S, Tlelo-Cuautle E, Zhang S, Guillen-Fernandez O, Sukono, Hidayat Y, Gundara G. A Novel Chaotic System with Two Circles of Equilibrium Points: Multistability, Electronic Circuit and FPGA Realization. Electronics. 2019; 8(11):1211. https://doi.org/10.3390/electronics8111211
Chicago/Turabian StyleSambas, Aceng, Sundarapandian Vaidyanathan, Esteban Tlelo-Cuautle, Sen Zhang, Omar Guillen-Fernandez, Sukono, Yuyun Hidayat, and Gugun Gundara. 2019. "A Novel Chaotic System with Two Circles of Equilibrium Points: Multistability, Electronic Circuit and FPGA Realization" Electronics 8, no. 11: 1211. https://doi.org/10.3390/electronics8111211








