Influence of the Shape Factor on the Heating of an Aqueous Solution by Microwave
Abstract
1. Introduction
2. Materials and Methods
2.1. Microwave Reactor
2.2. Container Size and Solution Volume
2.3. Operating Conditions
2.4. Procedure and Calculations
3. Results
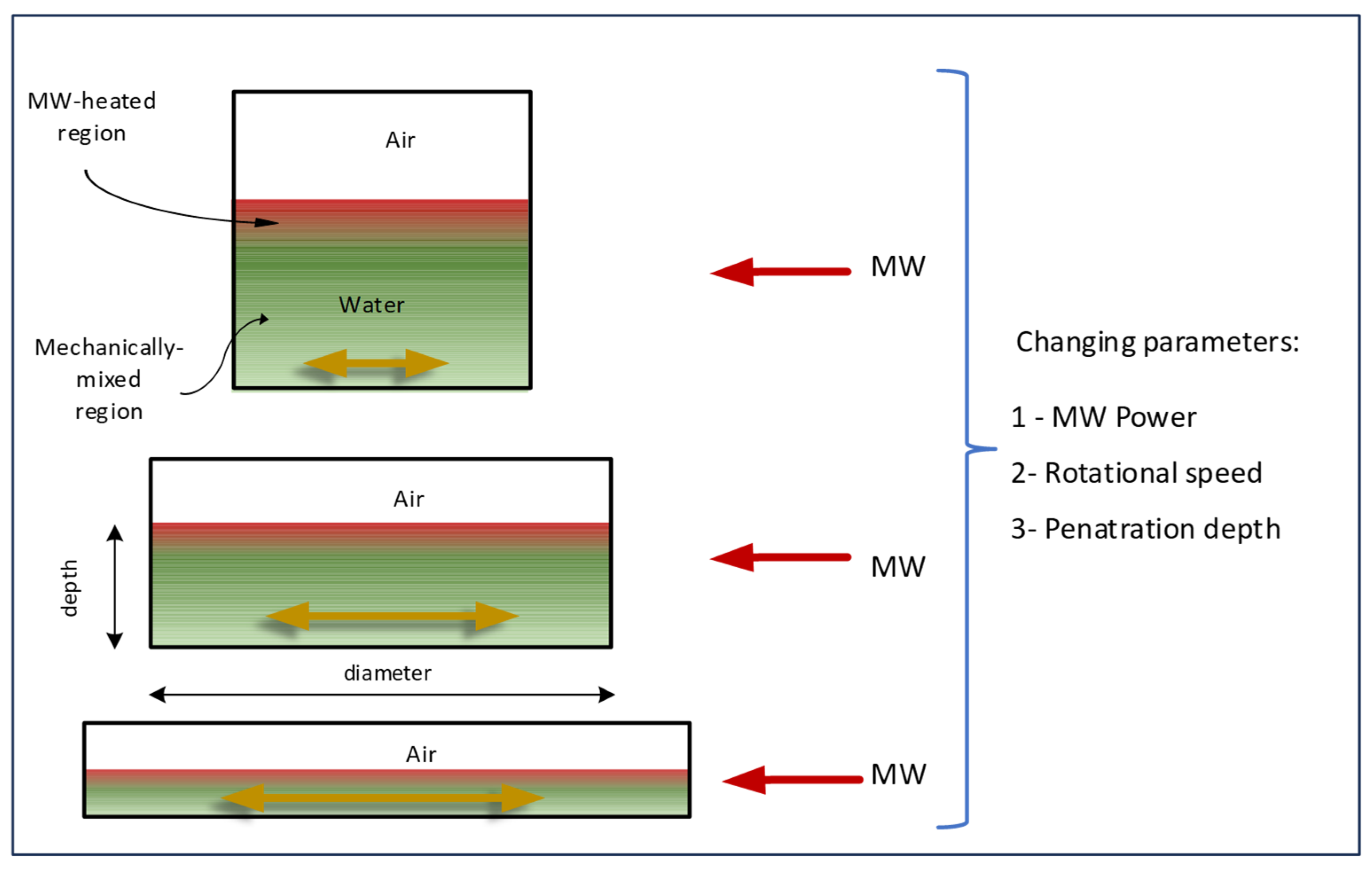
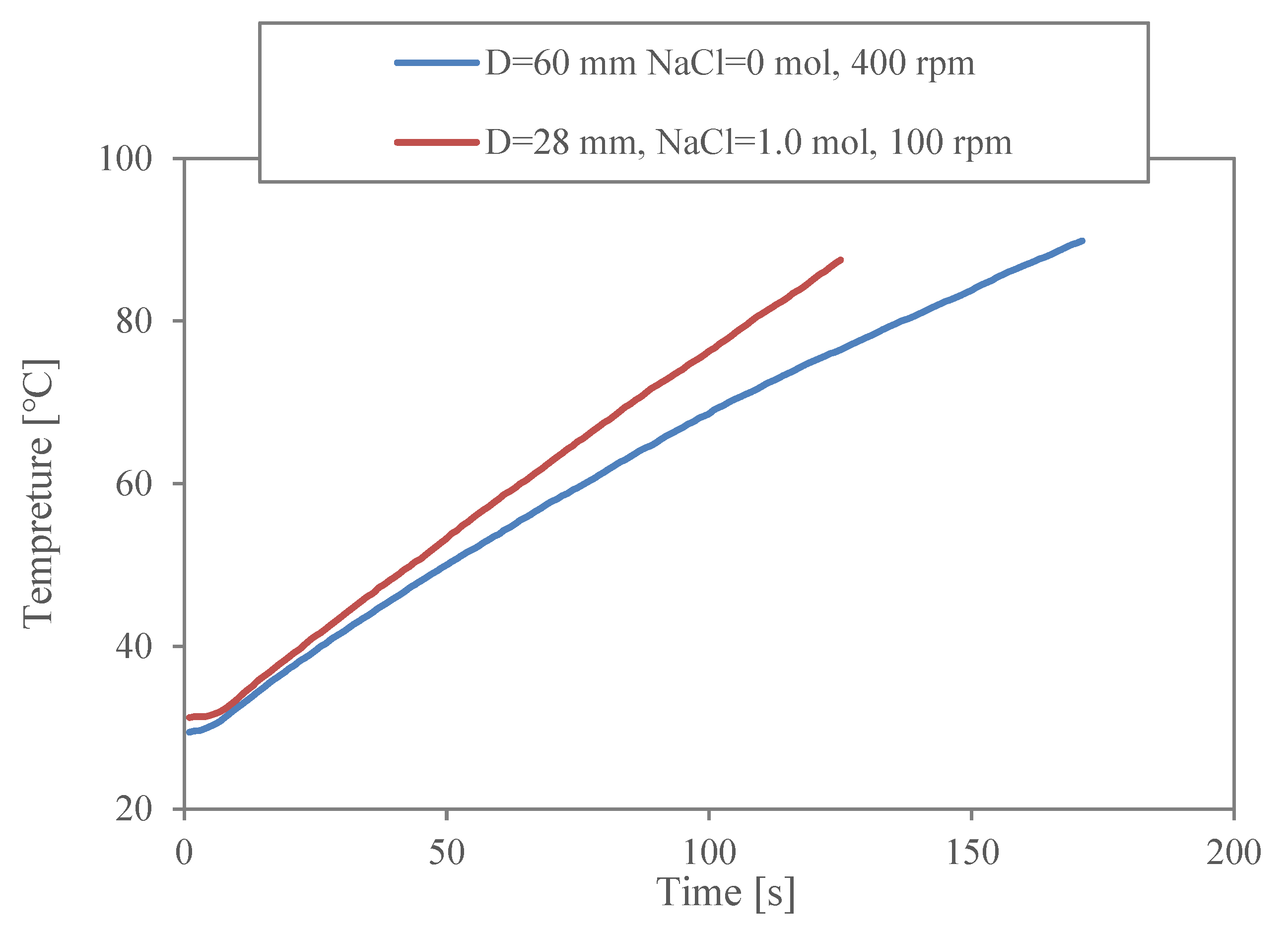
3.1. Characterisation of Heating Conditions
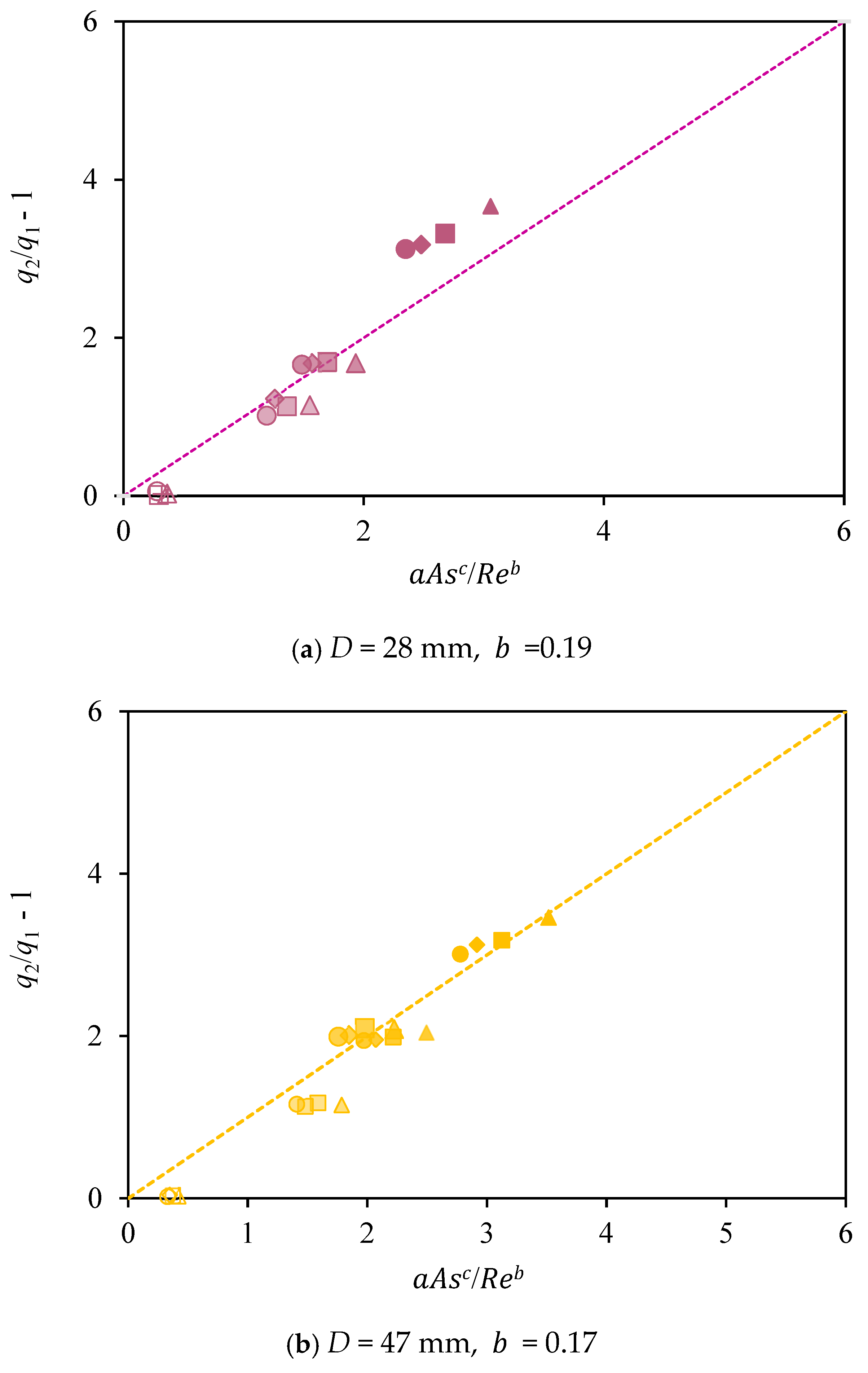
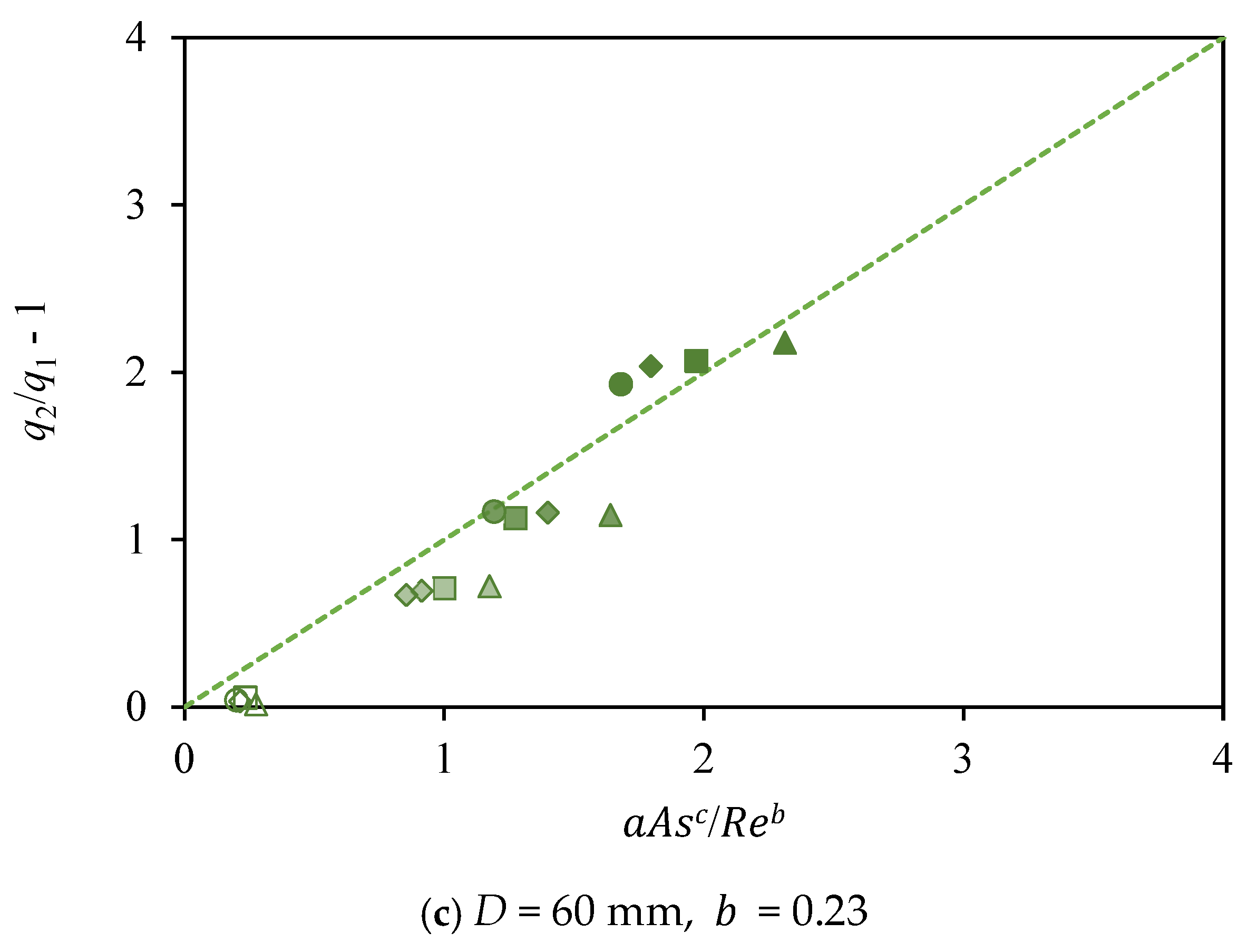
3.2. Influence of the Shape Factor
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Umrigar, V.; Chakraborty, M.; Parikh, P.A. Study of the Reaction Paths for Cleaner Production of Nitrochlorobenzenes Using Microwave Irradiation. Chem. Eng. Res. Des. 2017, 117, 369–375. [Google Scholar] [CrossRef]
- Saifullah, M.; Akanbi, T.O.; McCullum, R.; Van Vuong, Q. Optimization of Commercial Microwave Assisted-Extraction Conditions for Recovery of Phenolics from Lemon-Scented Tee Tree (Leptospermum petersonii) and Comparison with Other Extraction Techniques. Foods 2022, 11, 50. [Google Scholar] [CrossRef]
- Dinçer, C.; Aykın-Dinçer, E.; Kütükçü, Ö. Microwave-Assisted Hot Air Drying of Bone Broth-Based Sauce. J. Microw. Power Electromagn. Energy 2023, 57, 146–160. [Google Scholar] [CrossRef]
- Dinçer, C.; Tongur, T.; Erkaymaz, T. Effect of the Microwave and Thermosonic Vacuum Concentration Methods on Quality Parameters of Hibiscus (Hibiscus sabdariffa L.) Extract and Mathematical Modeling of Concentration. J. Microw. Power Electromagn. Energy 2023, 57, 163–177. [Google Scholar] [CrossRef]
- Tran, T.M.K.; Akanbi, T.O.; Kirkman, T.; Nguyen, M.H.; Vuong, Q. Van Recovery of Phenolic Compounds and Antioxidants from Coffee Pulp (Coffea canephora) Waste Using Ultrasound and Microwave-Assisted Extraction. Processes 2022, 10, 1011. [Google Scholar] [CrossRef]
- Shijarath, T.R.; Madhu, G.; Sahoo, D.K.; Abdullah, S. Microwave Assisted Aqueous Extraction of Phenolic Compounds from Pomegranate and Banana Peels: Process Modelling and Optimization. Food Humanit. 2024, 3, 100456. [Google Scholar] [CrossRef]
- Takai, T.; Shibatani, A.; Asakuma, Y.; Saptoro, A. Microwave-Assisted Nanoparticle Synthesis Enhanced with Addition of Surfactant. Chem. Eng. Res. Des. 2022, 182, 714–718. [Google Scholar] [CrossRef]
- González-Lavín, J.; Arenillas, A.; Rey-Raap, N. Overcoming Scaling Challenges in Sol–Gel Synthesis: A Microwave-Assisted Approach for Iron-Based Energy Materials. Microwave 2025, 1, 6. [Google Scholar] [CrossRef]
- Gao, X.; Li, X.; Zhang, J.; Sun, J.; Li, H. Influence of a Microwave Irradiation Field on Vapor–Liquid Equilibrium. Chem. Eng. Sci. 2013, 90, 213–220. [Google Scholar] [CrossRef]
- Macioszczyk, J.; Słobodzian, P.; Malecha, K.; Golonka, L.J. Microfluidical Microwave Reactor for Accelerating Chemical Reactions. Procedia Eng. 2015, 120, 683–686. [Google Scholar] [CrossRef]
- Zhao, Z.; Tang, X.; Jiang, B.; Li, H.; Li, X.; Gao, X. Structure Effect on Heating Performance of Microwave Inductive Waste Lubricating Oil Pyrolysis. Heat Transf. Eng. 2020, 42, 1381–1389. [Google Scholar] [CrossRef]
- Bogdal, D.; Bednarz, S.; Lukasiewicz, M. Microwave Induced Thermal Gradients in Solventless Reaction Systems. Tetrahedron 2006, 62, 9440–9445. [Google Scholar] [CrossRef]
- Eghbal Sarabi, F.; Ghorbani, M.; Stankiewicz, A.; Nigar, H. Coaxial Traveling-Wave Microwave Reactors: Design Challenges and Solutions. Chem. Eng. Res. Des. 2020, 153, 677–683. [Google Scholar] [CrossRef]
- Tian, W.; Feng, X.; Gao, L.; Chen, K.; Chen, Y.; Shi, J.; Lao, H. Improvement of Microwave Heating Uniformity Using Symmetrical Stirring. Symmetry 2025, 17, 659. [Google Scholar] [CrossRef]
- Tang, J. Unlocking Potentials of Microwaves for Food Safety and Quality. J. Food Sci. 2015, 80, E1776–E1793. [Google Scholar] [CrossRef] [PubMed]
- Sonobe, S.; Shibata, Y.; Asakuma, Y.; Hyde, A.; Phan, C. Characterization of the Microwave-Induced Boiling Behaviour at Oil/Water Interface. Int. J. Heat Mass Transf. 2020, 159, 120107. [Google Scholar] [CrossRef]
- Shibata, Y.; Tanaka, K.; Asakuma, Y.; Nguyen, C.V.; Hoang, S.A.; Phan, C.M. Selective Evaporation of a Butanol/Water Droplet by Microwave Irradiation, a Step toward Economizing Biobutanol Production. Biofuel Res. J. 2020, 7, 1109–1114. [Google Scholar] [CrossRef]
- Eames, I.W.; Marr, N.J.; Sabir, H. The Evaporation Coefficient of Water: A Review. Int. J. Heat Mass Transf. 1997, 40, 2963–2973. [Google Scholar] [CrossRef]
- Nagata, Y.; Usui, K.; Bonn, M. Molecular Mechanism of Water Evaporation. Phys. Rev. Lett. 2015, 115, 236102. [Google Scholar] [CrossRef]
- Vu, H.T.; Scarlett, C.J.; Vuong, Q.V. Maximising Recovery of Phenolic Compounds and Antioxidant Properties from Banana Peel Using Microwave Assisted Extraction and Water. J. Food Sci. Technol. 2019, 56, 1360–1370. [Google Scholar] [CrossRef]
- Hisatake, K.; Tanaka, S.; Aizawa, Y. Evaporation Rate of Water in a Vessel. J. Appl. Phys. 1993, 73, 7395–7401. [Google Scholar] [CrossRef]
- Zhao, P.; Gan, W.; Feng, C.; Qu, Z.; Liu, J.; Wu, Z.; Gong, Y.; Zeng, B. Multiphysics Analysis for Unusual Heat Convection in Microwave Heating Liquid. AIP Adv. 2020, 10, 085201. [Google Scholar] [CrossRef]
- Radoiu, M.; Mello, A. Technical Advances, Barriers, and Solutions in Microwave—Assisted Technology for Industrial Processing. Chem. Eng. Res. Des. 2022, 181, 331–342. [Google Scholar] [CrossRef]
- Yang, B.; Huang, H.; Zhou, L.; Jin, H. Method for Solving the Microwave Heating Temperature Distribution of the TE10 Mode. Processes 2022, 10, 1377. [Google Scholar] [CrossRef]
- Liu, S.; Fukuoka, M.; Sakai, N. A Finite Element Model for Simulating Temperature Distributions in Rotating Food during Microwave Heating. J. Food Eng. 2013, 115, 49–62. [Google Scholar] [CrossRef]
- Yakata, R.; Sonobe, S.; Asakuma, Y.; Hyde, A.; Phan, C. Prediction of Temperature Distribution during Microwave Irradiation Using Dimensionless Numbers. Jpn. Soc. Electromagn. Wave Energy Appl. 2022, 8, 6–12. [Google Scholar] [CrossRef]
- Amiraftabi, M.; Khiadani, M.; Mohammed, H.A. Performance of a Dual Helical Ribbon Impeller in a Two-Phase (Gas-Liquid) Stirred Tank Reactor. Chem. Eng. Process. Process Intensif. 2020, 148, 107811. [Google Scholar] [CrossRef]
- Sonobe, S.; Shibata, Y.; Asakuma, Y.; Hyde, A.; Nguyen, C.; Phan, C. A Dimensionless Number for Microwave Non-Equilibrium Local Heating through Surfactant Desorption. Colloids Surf. A Physicochem. Eng. Asp. 2020, 591, 124560. [Google Scholar] [CrossRef]
- Asakuma, Y.; Maeda, T.; Takai, T.; Hyde, A.; Phan, C.; Ito, S.; Taue, S. Microwaves Reduce Water Refractive Index. Sci. Rep. 2022, 12, 11562. [Google Scholar] [CrossRef]
- Meng, Q.; Lan, J.; Hong, T.; Zhu, H. Effect of the Rotating Metal Patch on Microwave Heating Uniformity. J. Microw. Power Electromagn. Energy 2018, 52, 94–108. [Google Scholar] [CrossRef]
- Lamberti, L.; Grillo, G.; Gallina, L.; Carnaroglio, D.; Chemat, F.; Cravotto, G. Microwave-Assisted Hydrodistillation of Hop (Humulus lupulus L.) Terpenes: A Pilot-Scale Study. Foods 2021, 10, 2726. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zhao, Z.; Li, H.; Gao, X. Microwave-Induced Vapor-Liquid Mass Transfer Separation Technology—Full of Breakthrough Opportunities in Electrified Chemical Processes. Curr. Opin. Chem. Eng. 2023, 39, 100890. [Google Scholar] [CrossRef]
- Gharibshahi, R.; Omidkhah, M.; Jafari, A.; Mehrooz, N. Parametric Optimization of In-Situ Heavy Oil Upgrading Using Simultaneous Microwave Radiation and Magnetic Nanohybrids via Taguchi Approach. Fuel 2022, 325, 124717. [Google Scholar] [CrossRef]
- Rosario Núñez, V.; Hernández, A.; Rodríguez, I.; Fernández-Pacheco Ruiz, I.; Acevedo, L. Artificial Intelligence Applied to Microwave Heating Systems: Prediction of Temperature Profile through Convolutional Neural Networks. Thermo 2024, 4, 346–372. [Google Scholar] [CrossRef]
- Wang, S.; Wang, W.; Zheng, Y. Reconfigurable Multimode Microwave Sensor with Resonance and Transmission Sensing Capabilities for Noninvasive Glucose Monitoring. IEEE Trans. Microw. Theory Tech. 2024, 72, 3102–3117. [Google Scholar] [CrossRef]
- Ano, T.; Kishimoto, F.; Sasaki, R.; Tsubaki, S.; Maitani, M.M.; Suzuki, E.; Wada, Y. In Situ Temperature Measurements of Reaction Spaces under Microwave Irradiation Using Photoluminescent Probes. Phys. Chem. Chem. Phys. 2016, 18, 13173–13179. [Google Scholar] [CrossRef] [PubMed]
- Woo, H.; Lee, H.-J.; Yook, J.-G. Noninvasive Detection of Glucose and NaCl Solutions with Environment Correction Using a Dual IDC-Based Microwave Sensor. IEEE Sens. J. 2024, 24, 19039–19049. [Google Scholar] [CrossRef]

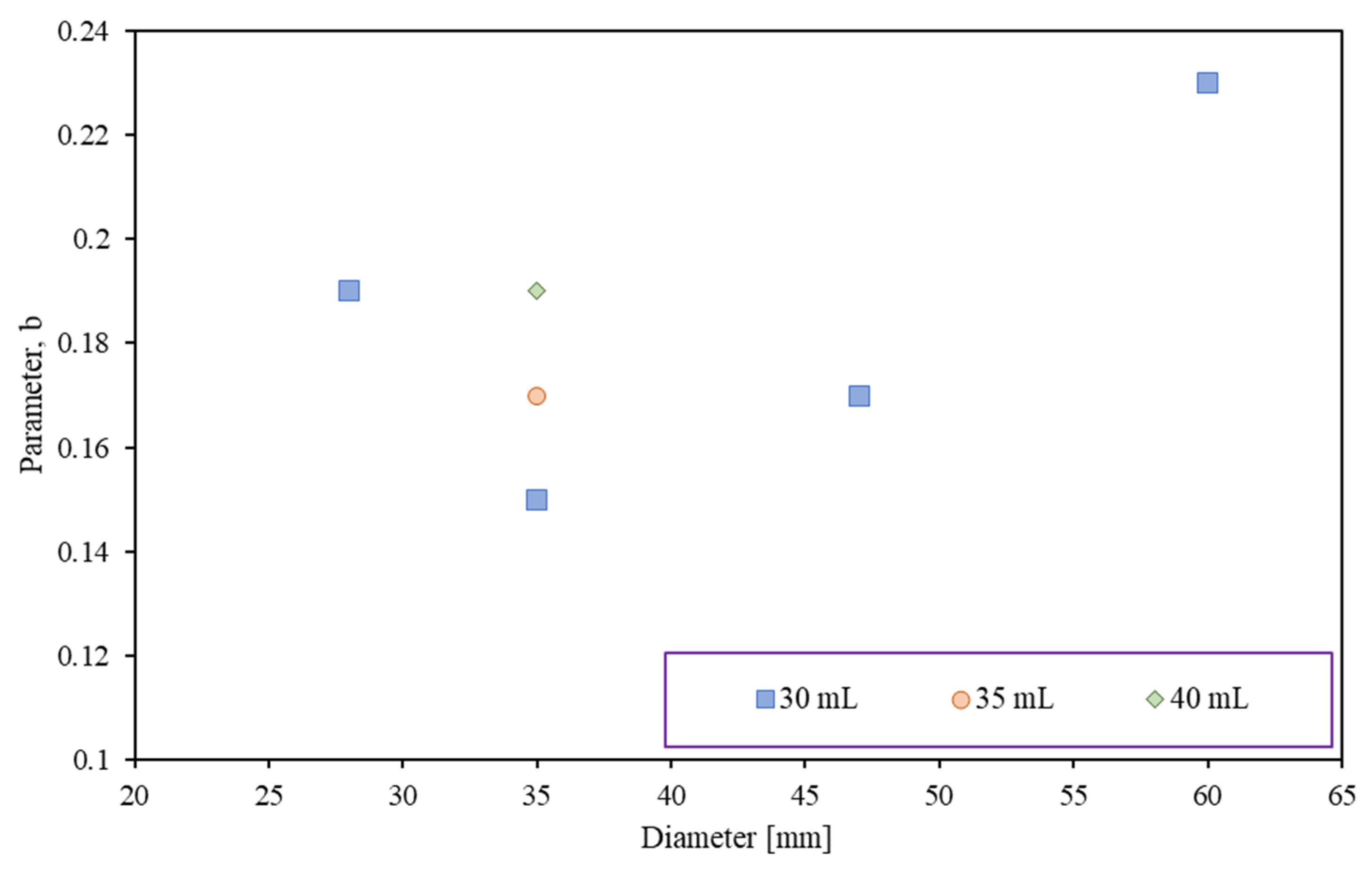
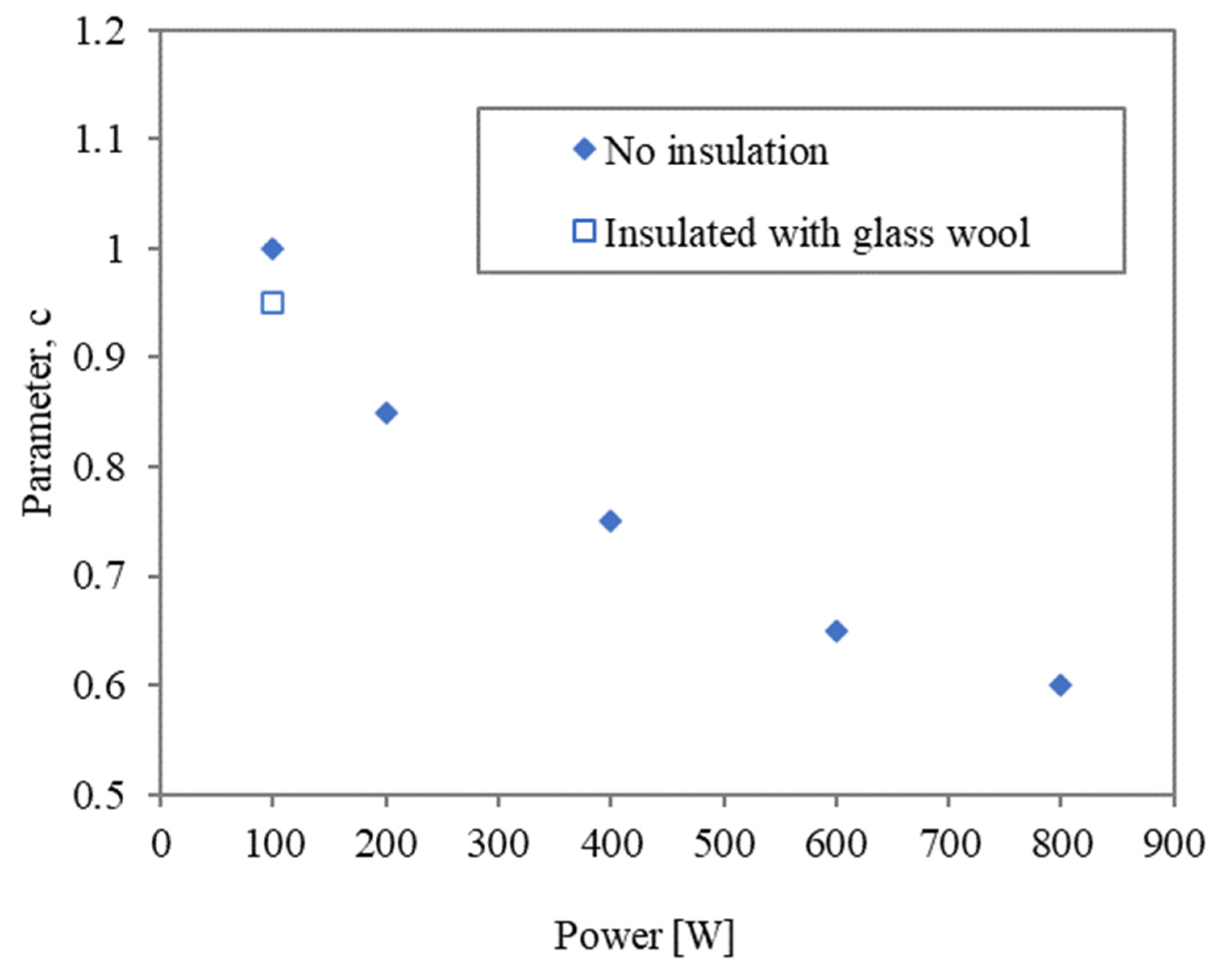
| Power | Diameter, D [mm] | Volume, [mL] | |
|---|---|---|---|
| No. 1 | 100 W | 28, 35, 47, 60 | 30 |
| No. 2 | 100 W | 35 | 35, 40 |
| No. 3 | 200 to 800 W | 35 | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asakuma, Y.; Yakata, R.; Hyde, A.; Phan, C.; Hoang, S.A. Influence of the Shape Factor on the Heating of an Aqueous Solution by Microwave. Microwave 2025, 1, 10. https://doi.org/10.3390/microwave1030010
Asakuma Y, Yakata R, Hyde A, Phan C, Hoang SA. Influence of the Shape Factor on the Heating of an Aqueous Solution by Microwave. Microwave. 2025; 1(3):10. https://doi.org/10.3390/microwave1030010
Chicago/Turabian StyleAsakuma, Yusuke, Ryohei Yakata, Anita Hyde, Chi Phan, and Son A. Hoang. 2025. "Influence of the Shape Factor on the Heating of an Aqueous Solution by Microwave" Microwave 1, no. 3: 10. https://doi.org/10.3390/microwave1030010
APA StyleAsakuma, Y., Yakata, R., Hyde, A., Phan, C., & Hoang, S. A. (2025). Influence of the Shape Factor on the Heating of an Aqueous Solution by Microwave. Microwave, 1(3), 10. https://doi.org/10.3390/microwave1030010








