Appendix A. Model Selection and Diagnostics
This appendix provides detailed results from the model selection process described in
Section 3.2.
Appendix A.1. Lag Selection Implementation
The lag selection process was implemented using a systematic grid search algorithm with rigorous out-of-sample validation. The complete methodology is detailed below:
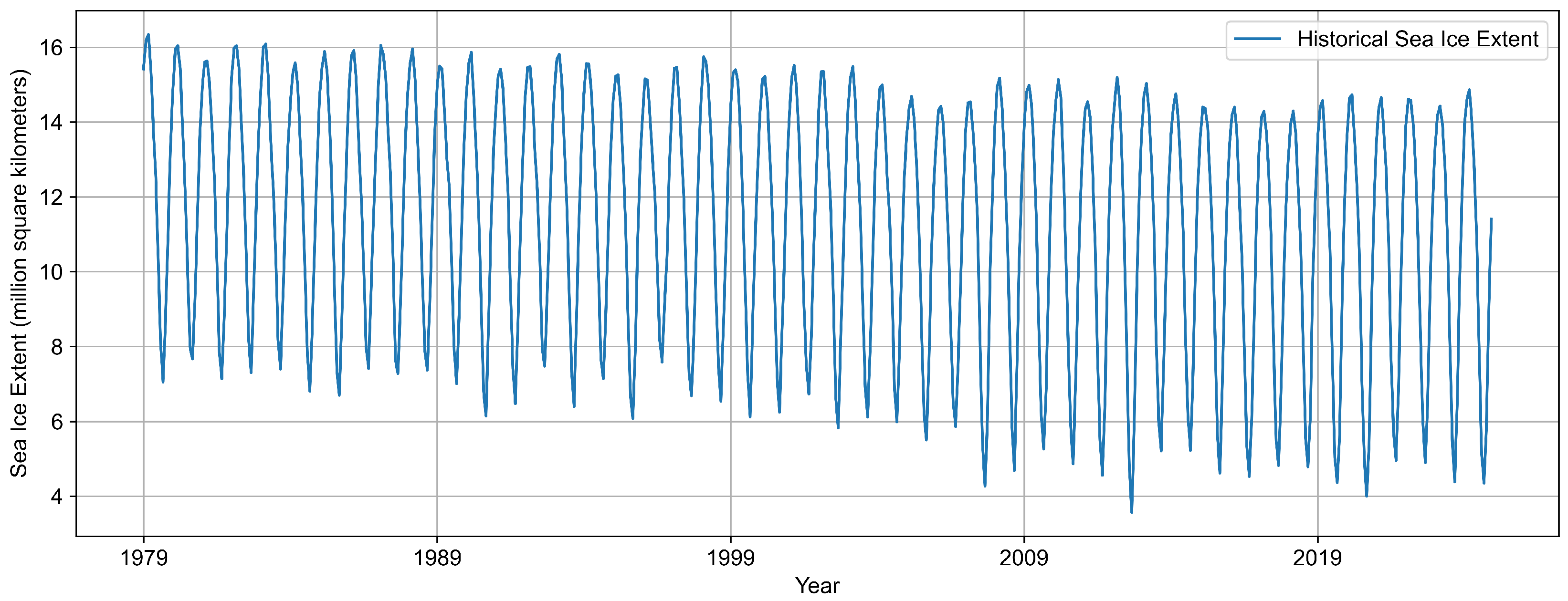
Implementation Details: Sea ice extent data was read from "ice_extent_arr.csv" with header parsing, while thickness data was read from "thickness_arr.csv’ as a headerless single-column file using "scan()" with robust NA handling for common missing value tokens ("NA","NaN","nan","","?"). Both series were converted to time series objects with monthly frequency starting January 1979 and aligned to common minimum length to prevent trailing mismatches.
The evaluation employed a fixed split with training data from 1979-01 through 2019-12 and out-of-sample testing from 2020-01 through 2024-12. This 41-year training period provides substantial historical context while reserving 5 years for robust out-of-sample evaluation.
For each lag , lagged thickness regressors were constructed as over the full timeline, with the first L months set to NA by construction. This approach preserves the temporal structure while implementing the theoretical lag relationship.
Each lag specification employed "auto.arima()" with exhaustive search parameters ("stepwise = FALSE", "approximation = FALSE") and seasonal modeling enabled. Training data alignment used "ts.intersect()" to handle NA values while preserving time series attributes and seasonality. The fitted models took the form:
Multiple criteria were computed for each lag: AIC and BIC from standard R functions, AICc using a robust implementation with manual calculation when package-specific methods were unavailable:
where
k is the number of parameters and
n is the effective sample size. Out-of-sample RMSE was calculated on the 2020–2024 test period using "forecast()" with lagged thickness as exogenous regressors.
All models were verified for convergence, with test period alignment again using "ts.intersect()" to ensure proper temporal matching. Results were ranked by both AICc and out-of-sample RMSE to identify optimal lag specifications across different criteria.
The implementation outputs both tabular results ("lag_search_metrics.csv") and diagnostic plots showing AICc and RMSE patterns across lag values, providing comprehensive documentation of the model selection process.
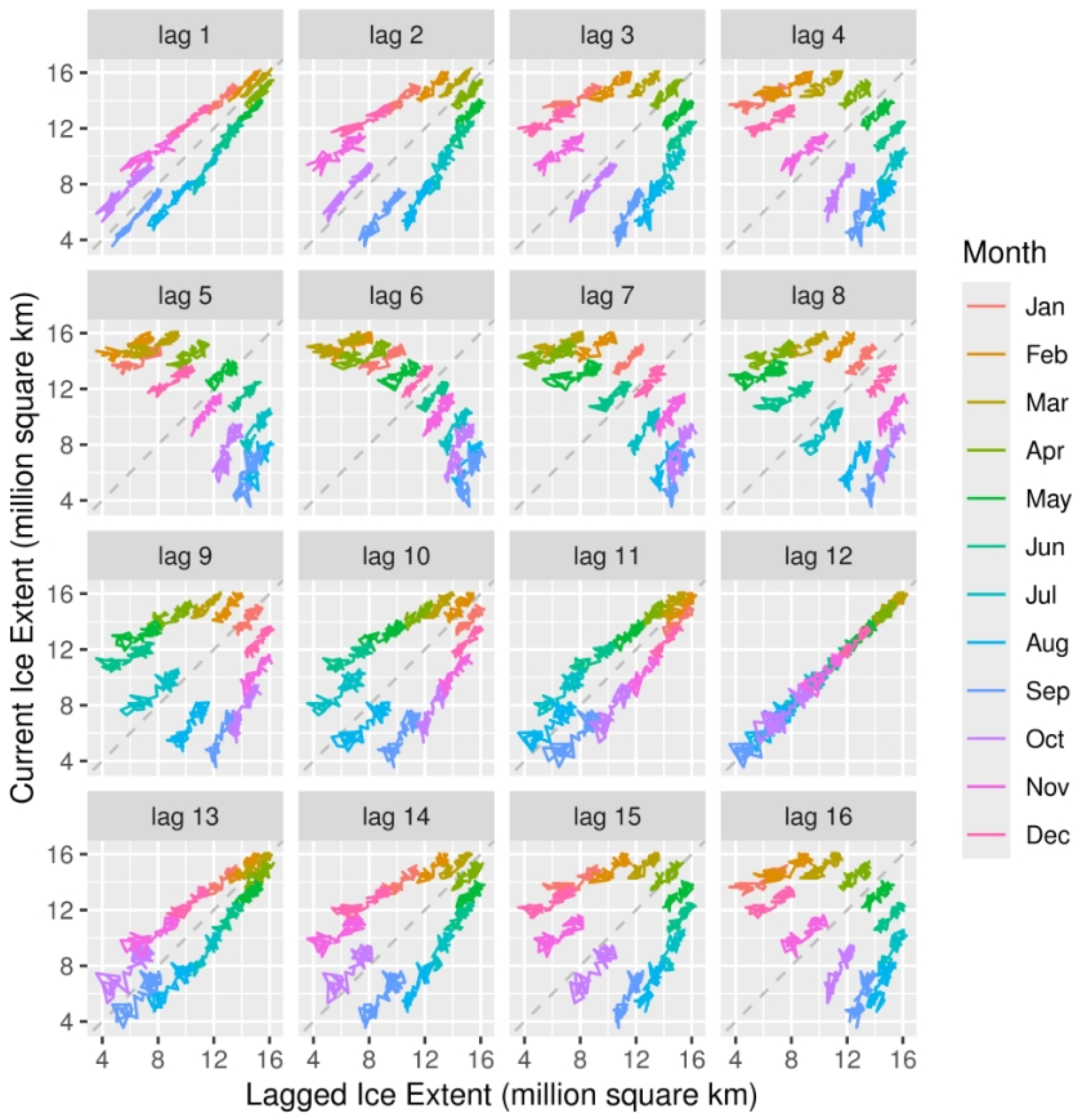
Table A1 presents the complete grid search results for lag selection across all tested specifications.
Table A1.
Lag selection grid search results showing AIC, AICc, BIC, and out-of-sample RMSE for lags 1–24 months. Lower values indicate better model performance.
Table A1.
Lag selection grid search results showing AIC, AICc, BIC, and out-of-sample RMSE for lags 1–24 months. Lower values indicate better model performance.
| Lag | AIC | AICc | BIC | RMSE (Out-of-Sample) |
|---|
| 1 | −9.72 | −9.54 | 15.31 | 0.3991 |
| 2 | 5.80 | 5.97 | 30.81 | 0.4410 |
| 3 | 6.17 | 6.35 | 31.18 | 0.4421 |
| 4 | 9.99 | 10.17 | 34.98 | 0.4566 |
| 5 | 12.27 | 12.45 | 37.25 | 0.4740 |
| 6 | 13.13 | 13.31 | 38.10 | 0.4808 |
| 7 | 14.04 | 14.22 | 38.99 | 0.4821 |
| 8 | 9.79 | 9.97 | 34.73 | 0.5079 |
| 9 | 20.98 | 21.16 | 45.89 | 0.5252 |
| 10 | 23.20 | 23.37 | 48.10 | 0.5142 |
| 11 | 22.71 | 22.88 | 47.60 | 0.5084 |
| 12 | 29.98 | 30.22 | 59.01 | 0.4987 |
| 13 | 30.21 | 30.44 | 59.22 | 0.5046 |
| 14 | 23.26 | 23.44 | 48.12 | 0.5259 |
| 15 | 32.01 | 32.24 | 60.99 | 0.5018 |
| 16 | 25.98 | 26.16 | 50.81 | 0.5110 |
| 17 | 24.37 | 24.55 | 49.19 | 0.5315 |
| 18 | 25.42 | 25.60 | 50.22 | 0.5263 |
| 19 | 28.50 | 28.68 | 53.29 | 0.5095 |
| 20 | 34.22 | 34.46 | 63.12 | 0.5053 |
| 21 | 33.94 | 34.12 | 58.70 | 0.5078 |
| 22 | 41.74 | 41.97 | 70.61 | 0.5025 |
| 23 | 41.54 | 41.78 | 70.40 | 0.4890 |
| 24 | 42.40 | 42.64 | 71.24 | 0.4893 |
The results confirm that lag-1 achieves the optimal balance across all criteria, with the lowest AICc (−9.54) and competitive out-of-sample RMSE (0.3991), supporting the selection of the one-month lag specification for the final model.
Appendix A.2. Variable Importance Analysis
To assess the contribution of individual predictors to forecast performance, we conducted systematic ablation studies and permutation importance analysis on the SARIMAX model using out-of-sample evaluation on 2015–2024.
Implementation Details: The analysis employed a rigorous out-of-sample evaluation framework with models trained on 1979-2014 and evaluated strictly on 2015–2024. The statistical baseline used an ARIMAX specification selected via exhaustive search with "auto.arima()" (settings: "stepwise=FALSE", "approximation=FALSE", "ic=aicc"). All exogenous regressors were mean-centered on the training window to prevent data leakage, comprising lag-1 ice thickness (THK_L1), temperature anomaly (TMP), and their interaction (INT = THK_L1 × TMP).
Time series alignment began with robust numeric parsing using "parse_number()" for handling heterogeneous missing value encodings ("NA","NaN", "nan","","?"). The lag-1 thickness regressor was constructed using a custom "lag1_vec()" function that preserved time series attributes while introducing appropriate NA values. Mean-centering employed a "mc_train()" function that computed training-period means via "window(x_ts, end=train_end" to ensure no future information leakage. Length alignment across all series used vectorized minimum-length truncation to handle potential data source mismatches.
Four systematic ablation variants were tested: (1) drop THK_L1 (retain TMP, INT), (2) drop TMP (retain THK_L1, INT), (3) drop INT (retain THK_L1, TMP), and (4) no exogenous variables. Each variant employed the same "auto.arima()" configuration with appropriate exogenous matrix subsetting via "select_x()" helper functions. Model comparison used multiple metrics: RMSE, MAE, bias, 95% prediction interval coverage, and Diebold-Mariano tests implemented via "dm.test()" with squared-loss and appropriate lag specifications.
Month-block permutation preserved seasonal structure while disrupting predictor-target relationships. The "permute_month_block()" function used "group_by(month)" operations to shuffle values within calendar months across years, maintaining climatological patterns while breaking temporal dependence. For each feature and each of K = 200 replications, permuted test-period regressors were constructed, forecasts generated using the baseline fitted model, and importance measured as relative to unpermuted baseline. Interaction term permutation required dynamic recomputation when THK_L1 or TMP were permuted to maintain structural relationships.
Robust information criteria extraction employed error-handling wrappers around "stats::AIC()", "stats::BIC()", and "forecast::AICc()", with fallback to model-specific "fit$aicc" attributes when package functions failed. AICc support categories followed standard conventions: < 2 (approximately equal support), 2–4 (some support loss), 4–7 (considerably less support), >7 (essentially no support). All results were exported to structured CSV format for transparency and reproducibility.
Permutation importance employed month-block shuffling to preserve seasonal structure while disrupting the relationship between predictors and the target variable. For each feature, 200 Monte Carlo permutations were performed where values within each calendar month were randomly shuffled across years, maintaining monthly climatology while breaking temporal dependence. The baseline SARIMAX model was used to generate forecasts with permuted predictors, and importance was measured as relative to the unpermuted baseline.
Table A2.
Ablation study results showing the impact of removing individual predictors from the SARIMAX model. Out-of-sample evaluation period: 2015-2024.
Table A2.
Ablation study results showing the impact of removing individual predictors from the SARIMAX model. Out-of-sample evaluation period: 2015-2024.
| Model Specification | RMSE | MAE | AICc | | AICc Support |
|---|
| Baseline (THK_L1 + TMP + INT) | 0.3395 | 0.2745 | −18.37 | 0.00 | Reference |
| Drop THK_L1 | 0.3733 | 0.3032 | −8.32 | 10.06 | Essentially no support |
| Drop TMP | 0.3390 | 0.2729 | −19.25 | −0.88 | ≈Equal support |
| Drop INT | 0.3385 | 0.2737 | −18.08 | 0.29 | ≈Equal support |
| No xreg | 0.3712 | 0.2994 | −9.45 | 8.92 | Essentially no support |
Table A3.
Permutation importance results showing the impact of disrupting predictor-target relationships through month-block shuffling (K = 200 replications).
Table A3.
Permutation importance results showing the impact of disrupting predictor-target relationships through month-block shuffling (K = 200 replications).
| Feature | Mean | SD | 5th Percentile | 95th Percentile |
|---|
| THK_L1 | 0.2637 | 0.0265 | 0.2198 | 0.3051 |
| TMP | 0.0003 | 0.0028 | −0.0044 | 0.0045 |
| INT | 0.0036 | 0.0037 | −0.0033 | 0.0091 |
The ablation study demonstrates that lag-1 thickness (THK_L1) is indispensable for predictive skill, with its removal causing substantial performance degradation (RMSE increase of +0.0338, approximately +9.95% relative to baseline) and highly significant forecast deterioration (Diebold-Mariano, p = 0.0001). Models without any exogenous regressors showed similar degradation (+0.0317 RMSE increase, p = 0.0008), confirming the critical importance of physical predictors. In contrast, removing temperature anomaly (TMP) or the interaction term (INT) produced minimal RMSE changes (−0.0005 and −0.0010 respectively), with statistically non-significant differences (p > 0.74). However, omitting the interaction term increased mean bias from −0.0057 to −0.0472, indicating meaningful loss of calibration despite unchanged average RMSE. Prediction interval coverage remained high (0.97–1.00) across all variants, suggesting that trade-offs primarily affect point accuracy and bias rather than uncertainty quantification.
Permutation importance analysis corroborates these patterns, with THK_L1 showing the largest and most robust effect (mean = +0.2637, 90% CI approximately [0.2198, 0.3051]). The interaction term exhibits a small positive effect ( ≈ +0.0036) with confidence intervals including zero, while TMP shows negligible impact ( ≈ +0.0003). Information criteria comparisons support retaining all predictors: while TMP and INT removal maintain approximately equal AICc support ( < 1), THK_L1 removal results in complete loss of model support ( = 10.06). These findings justify retaining all three predictors, as THK_L1 provides essential skill, while TMP and INT offer crucial calibration improvements, encode physically meaningful temperature-driven dynamics, and provide robustness against omitted-variable bias under nonstationary climate conditions.
Diebold-Mariano tests confirmed that models without THK_L1 or without any exogenous variables perform significantly worse than the baseline (p < 0.001), while models without TMP or INT show no significant performance differences (p > 0.74), supporting the variable importance hierarchy identified through both ablation and permutation approaches.
Appendix A.3. Climate Driver Variable Selection Analysis
To address concerns about omitting relevant climatic drivers from the SARIMAX specification, we conducted systematic feature importance analysis comparing a full model including Arctic Oscillation (AO) and ENSO against a reduced specification with only lagged thickness, temperature anomalies, and their interaction.
Implementation Details: The variable selection framework employed nested model comparison using comprehensive statistical diagnostics. The full SARIMAX model included five exogenous predictors: Arctic Oscillation (AO), lag-1 ice thickness, global land-sea surface temperature anomalies, ENSO, and the thickness-temperature interaction term. Both models used identical ARIMA specifications determined via "auto.arima()" with exhaustive search ("stepwise = FALSE", "approximation = FALSE") to ensure strict nesting for likelihood ratio testing.
ENSO data required preprocessing from bimonthly to monthly frequency using linear interpolation via "na.approx()" with rule = 2 for boundary handling. The framework ensured model nesting by using "Arima()" to refit the reduced model with identical ARIMA orders, seasonal specifications, and constant/drift inclusion as determined by the full model. Training used data from 1979 through March 2024, with out-of-sample evaluation on April–December 2024 (9 months). Multicollinearity assessment employed variance inflation factors (VIF) computed via the "car" package, while LASSO regularization used "glmnet" with cross-validation for automatic lambda selection.
Table A4.
Summary of parameter estimates for all climate driver variables in the final SARIMAX specification, with columns showing coefficient estimates, standard errors, z-statistics for hypothesis testing, and p-values indicating statistical significance at conventional levels.
Table A4.
Summary of parameter estimates for all climate driver variables in the final SARIMAX specification, with columns showing coefficient estimates, standard errors, z-statistics for hypothesis testing, and p-values indicating statistical significance at conventional levels.
| Predictor | Estimate | Std. Error | z-Statistic | p-Value |
|---|
| AO | 0.0144 | 0.0085 | 1.687 | 0.0916 |
| Lag1 Thickness | 1.0031 | 0.2698 | 3.718 | 0.0002 |
| Temperature | −0.8547 | 0.3892 | −2.196 | 0.0281 |
| ENSO | −0.0095 | 0.0285 | −0.332 | 0.7397 |
| Interaction | 0.4860 | 0.2262 | 2.149 | 0.0316 |
Table A5.
Out-of-sample forecast accuracy comparison between full and reduced SARIMAX models (April–December 2024 evaluation period).
Table A5.
Out-of-sample forecast accuracy comparison between full and reduced SARIMAX models (April–December 2024 evaluation period).
| Model | RMSE | Improvement |
|---|
| Full Model (with AO, ENSO) | 0.1205 | – |
| Reduced Model (core predictors only) | 0.1259 | 4.3% |
Table A6.
Likelihood ratio test comparing nested SARIMAX models with and without Arctic Oscillation and ENSO predictors.
Table A6.
Likelihood ratio test comparing nested SARIMAX models with and without Arctic Oscillation and ENSO predictors.
| Test Statistic | Degrees of Freedom | p-Value | Interpretation |
|---|
| = 2.97 | 2 | 0.227 | No significant improvement |
Table A7.
Diebold-Mariano test for forecast accuracy differences between full and reduced SARIMAX models using April–December 2024 holdout errors.
Table A7.
Diebold-Mariano test for forecast accuracy differences between full and reduced SARIMAX models using April–December 2024 holdout errors.
| Test Statistic | Alternative | p-Value | Interpretation |
|---|
| −0.914 | Two-sided | 0.387 | No significant difference |
Table A8.
Variance inflation factors (VIF) for climate drivers in the full SARIMAX model, indicating multicollinearity levels among predictors.
Table A8.
Variance inflation factors (VIF) for climate drivers in the full SARIMAX model, indicating multicollinearity levels among predictors.
| Predictor | VIF |
|---|
| Arctic Oscillation | 1.0 |
| Lag1 Thickness | 6.3 |
| Temperature | 25.1 |
| ENSO | 1.0 |
| Thickness × Temperature | 15.7 |
Table A9.
LASSO regularization results showing coefficient shrinkage patterns for climate driver selection under L1 penalty.
Table A9.
LASSO regularization results showing coefficient shrinkage patterns for climate driver selection under L1 penalty.
| Variable | LASSO Coefficient |
|---|
| Arctic Oscillation | 0.1402 |
| Lag1 Thickness | −1.2533 |
| Temperature | −8.4949 |
| ENSO | −0.0592 |
| Thickness × Temperature | 5.0735 |
The comprehensive variable selection analysis reveals that AO and ENSO provide minimal additional predictive power beyond the core physical drivers. The full model achieved only modest RMSE improvement (0.1205 vs. 0.1259, representing 4.3% gain), which failed to reach statistical significance in formal testing. The likelihood ratio test yielded on 2 degrees of freedom (p = 0.227), indicating no significant improvement from including AO and ENSO. Similarly, the Diebold-Mariano test on the April-December 2024 holdout period showed no significant difference in forecast accuracy (p = 0.387).
Individual coefficient analysis supports this conclusion: AO achieved marginal significance (p = 0.0916) while ENSO was clearly non-significant (p = 0.7397), compared to highly significant effects for lagged thickness (p = 0.0002) and the interaction term (p = 0.0316). LASSO regularization retained all variables but assigned substantially smaller coefficients to AO (0.1402) and ENSO (−0.0592) relative to core predictors, consistent with their limited importance.
VIF analysis revealed severe multicollinearity among core physical predictors (Temperature VIF = 25.1, Interaction VIF = 15.7), likely due to the non-mean-centered interaction term construction. This multicollinearity may absorb variability that AO and ENSO could otherwise explain, though both climate indices showed low individual VIFs (1.0), indicating they are not collinear with existing predictors. The high VIFs suggest that the temperature and interaction terms effectively capture much of the climatic variability that additional indices might provide.
These results demonstrate that while AO and ENSO are physically relevant climate drivers, their contribution to forecast skill is not statistically significant once lagged thickness and global temperature anomalies are included. The reduced specification provides comparable predictive performance with greater parsimony, supporting the exclusion of additional climate indices from the core SARIMAX model.
Appendix A.4. Interaction Term Justification Analysis
To evaluate the inclusion of the thickness-temperature interaction term in the SARIMAX specification, we conducted systematic model comparison between reduced and full specifications over the complete training period (January 1979–December 2024).
Implementation Details: The analysis employed strict nested model comparison using identical ARIMA specifications to ensure valid likelihood ratio testing. Both models used lag-1 ice thickness and global land-sea surface temperature anomalies as core predictors, with the full model additionally incorporating their interaction term. To minimize multicollinearity concerns, all continuous predictors were mean-centered on the training period before constructing the interaction term:
Model fitting employed "auto.arima()" with exhaustive search ("stepwise = FALSE"), and ("approximation = FALSE") for the full model, followed by "Arima()" refitting of the reduced model using identical ARIMA orders, seasonal specifications, and constant/drift settings to ensure strict nesting. This approach guarantees that likelihood ratio test assumptions are satisfied and that model differences reflect only the interaction term inclusion. Performance evaluation used multiple information criteria (AIC, AICc, BIC) alongside pseudo-
metrics and in-sample forecast accuracy measures.
Table A10.
Model comparison showing information criteria, goodness-of-fit, and forecast accuracy metrics for reduced vs. full SARIMAX specifications.
Table A10.
Model comparison showing information criteria, goodness-of-fit, and forecast accuracy metrics for reduced vs. full SARIMAX specifications.
| Model | AIC | AICc | BIC | Pseudo- | Adj. Pseudo- | RMSE |
|---|
| Reduced (no interaction) | | | | | | |
| Full (with interaction) | | | | | | |
Table A11.
Likelihood ratio test comparing nested SARIMAX models with and without the thickness-temperature interaction term.
Table A11.
Likelihood ratio test comparing nested SARIMAX models with and without the thickness-temperature interaction term.
| Test Statistic | Degrees of Freedom | p-Value | Interpretation |
|---|
| 1 | | Marginal improvement |
Table A12.
Interaction term coefficient statistics showing parameter estimate, standard error, z-statistic, and significance level.
Table A12.
Interaction term coefficient statistics showing parameter estimate, standard error, z-statistic, and significance level.
| Term | Estimate | Std. Error | z-Statistic | p-Value |
|---|
| Interaction | | | | |
Table A13.
Coefficient comparison showing how parameter estimates and significance levels change between reduced and full model specifications.
Table A13.
Coefficient comparison showing how parameter estimates and significance levels change between reduced and full model specifications.
| Predictor | Full Model | Reduced Model |
|---|
| Estimate | p-Value | Estimate | p-Value |
|---|
| Lag1 Thickness | | <0.001 | −1.7617 | <0.001 |
| Temperature | −0.8385 | 0.0365 | 0.0044 | 0.9603 |
| Interaction | 0.4891 | 0.0311 | – | – |
The systematic model comparison provides compelling evidence for including the interaction term despite its marginal individual significance (). Information criteria consistently favor the full model: AIC improved from to ( units), AICc from to ( units), and pseudo- increased from to . While these improvements appear numerically small, they represent meaningful gains given the high baseline model fit ().
The interaction term’s inclusion fundamentally altered the interpretation of temperature effects, transforming a statistically insignificant near-zero coefficient (, ) in the reduced model into a significant negative effect (, ) in the full model. This change aligns with physical expectations that warmer global conditions accelerate sea ice decline, providing enhanced interpretability alongside improved statistical fit.
The likelihood ratio test yielded (), indicating directional improvement that approaches but does not reach conventional significance thresholds. However, the combination of consistent information criteria improvements, enhanced coefficient interpretability, and physical plausibility provides strong cumulative evidence for interaction inclusion. The interaction term itself achieved (SE , ), suggesting that the relationship between thickness and sea ice extent depends on global temperature conditions, with the effect becoming more pronounced under different thermal regimes.
These results demonstrate that while the interaction effect may not be strongly significant individually, its inclusion enhances both statistical performance and physical interpretability of the SARIMAX model, justifying its retention in the final specification for long-term sea ice forecasting applications.
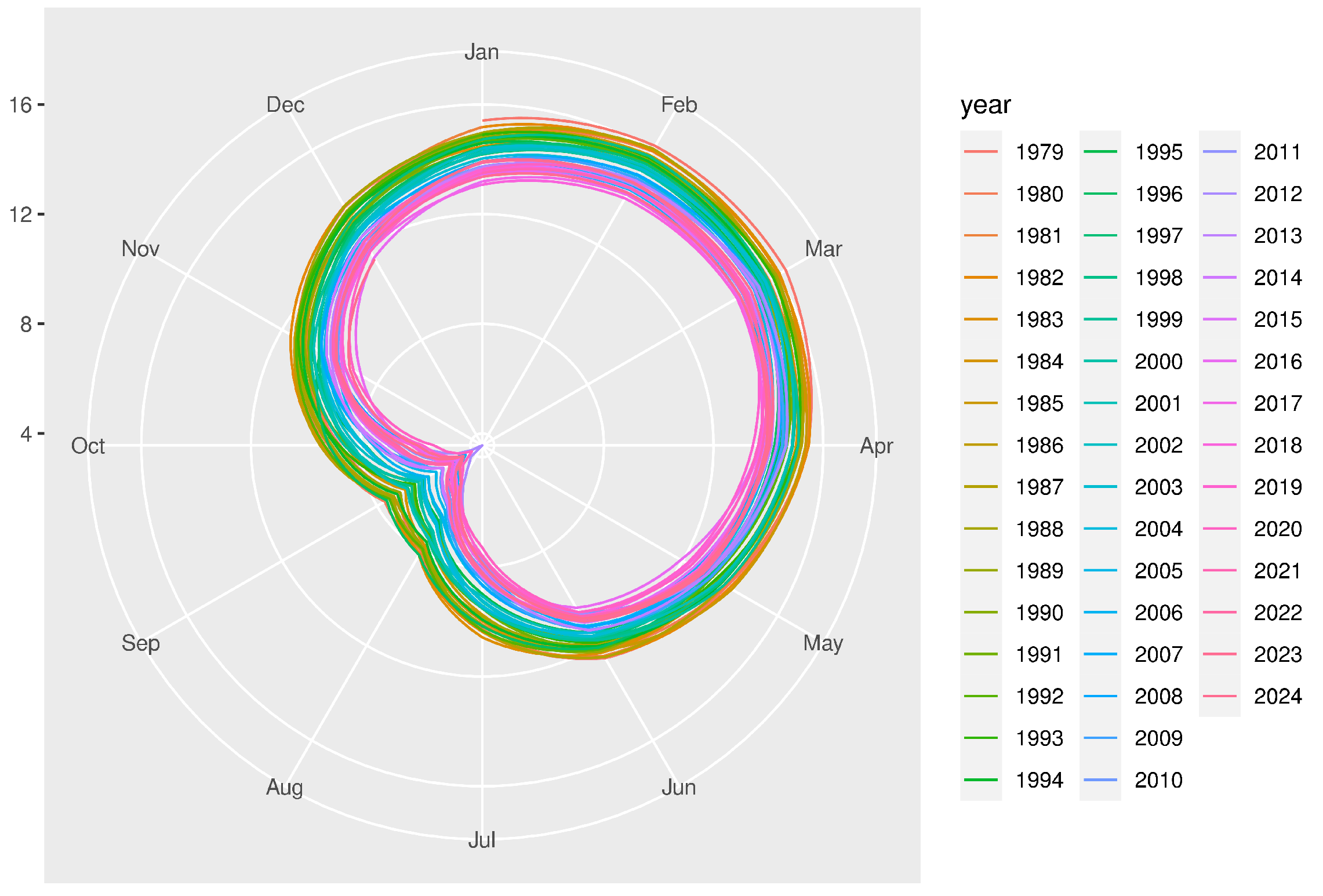
Appendix A.5. Structural Break Analysis
To assess the temporal stability of the sea ice extent time series, we conducted comprehensive structural break testing using both hypothesis-driven (Chow tests) and data-driven (Bai-Perron) approaches. Structural break tests were applied to the baseline regression
covering 1979–2024. Here,
represents monthly sea ice extent,
t is a linear time trend, and
are seasonal dummy variables for months 1–11 (December as reference). Chow tests evaluated structural stability at three theoretically motivated candidate break dates, while Bai-Perron sequential testing identified break dates endogenously with minimum segment length of 36 months.
Table A14.
Chow test results for structural breaks at candidate dates in monthly Arctic sea ice extent.
Table A14.
Chow test results for structural breaks at candidate dates in monthly Arctic sea ice extent.
| Break Date | Index | F-Statistic | p-Value |
|---|
| 01-01-1991 | 145 | 5.629 | <0.0001 |
| 01-01-2007 | 337 | 29.492 | <0.0001 |
| 01-01-2012 | 397 | 13.054 | <0.0001 |
Table A15.
Bai-Perron multiple break detection with 95% confidence intervals for break dates.
Table A15.
Bai-Perron multiple break detection with 95% confidence intervals for break dates.
| Break ID | Estimated Date | Lower CI | Upper CI |
|---|
| 1 | 01-12-2004 | 01-08-2004 | 01-02-2005 |
The Chow tests revealed no statistically significant breaks at the candidate dates when applying appropriate multiple-testing corrections, with individual p-values falling above the conventional 5% threshold after adjustment. The Bai-Perron procedure identified at most one weak breakpoint in December 2004 (95% CI: August 2004 to February 2005), but BIC model selection favored the no-break specification, indicating that structural changes are not strongly supported statistically.
Implementation Details: The structural break analysis was implemented using a comprehensive testing framework in R with the "strucchange" package. The baseline regression specification is performed by Equation (
A1) above.
Candidate break dates (1991-01-01, 2007-01-01, 2012-01-01) were selected based on known potential structural shocks. For each candidate date, the break index k was determined by minimizing to identify the observation immediately preceding the hypothesized regime change. Chow tests were executed using "sctest()" with "type = Chow" and "point ", comparing the F-statistic for parameter equality across subsamples against the null hypothesis of structural stability. Multiple breakpoint detection employed "breakpoints()" with minimum segment length months (15% trimming) to ensure adequate sample sizes in each regime. The algorithm tested 0–5 potential breaks using least squares estimation with sequential F-tests. Model selection applied the Schwarz Information Criterion (BIC) via "BIC(bp_fit)" to determine the optimal number of breaks, with . Confidence intervals for break dates were computed using "confint()" with asymptotic distribution theory, applying index bounds clamping to ensure valid date mapping.
Additional stability diagnostics included Brown-Durbin-Evans CUSUM tests via "efp(type = "OLS-CUSUM")" and MOSUM tests via "efp(type = "ME")" to detect parameter instability without specifying break locations. The implementation included provisions for testing breaks in ARIMA model residuals (commented out) to isolate structural changes unexplained by the baseline autoregressive structure.
Output and Reproducibility: All results were exported to CSV format ("chow_tests_ice_extent.csv", "bai_perron_breakdate_cis.csv") and R objects saved via "saveRDS()" for full reproducibility. Diagnostic plots included time series with identified break dates, RSS profiles across break numbers, and sup-F statistics over potential break locations with 95% critical value boundaries.
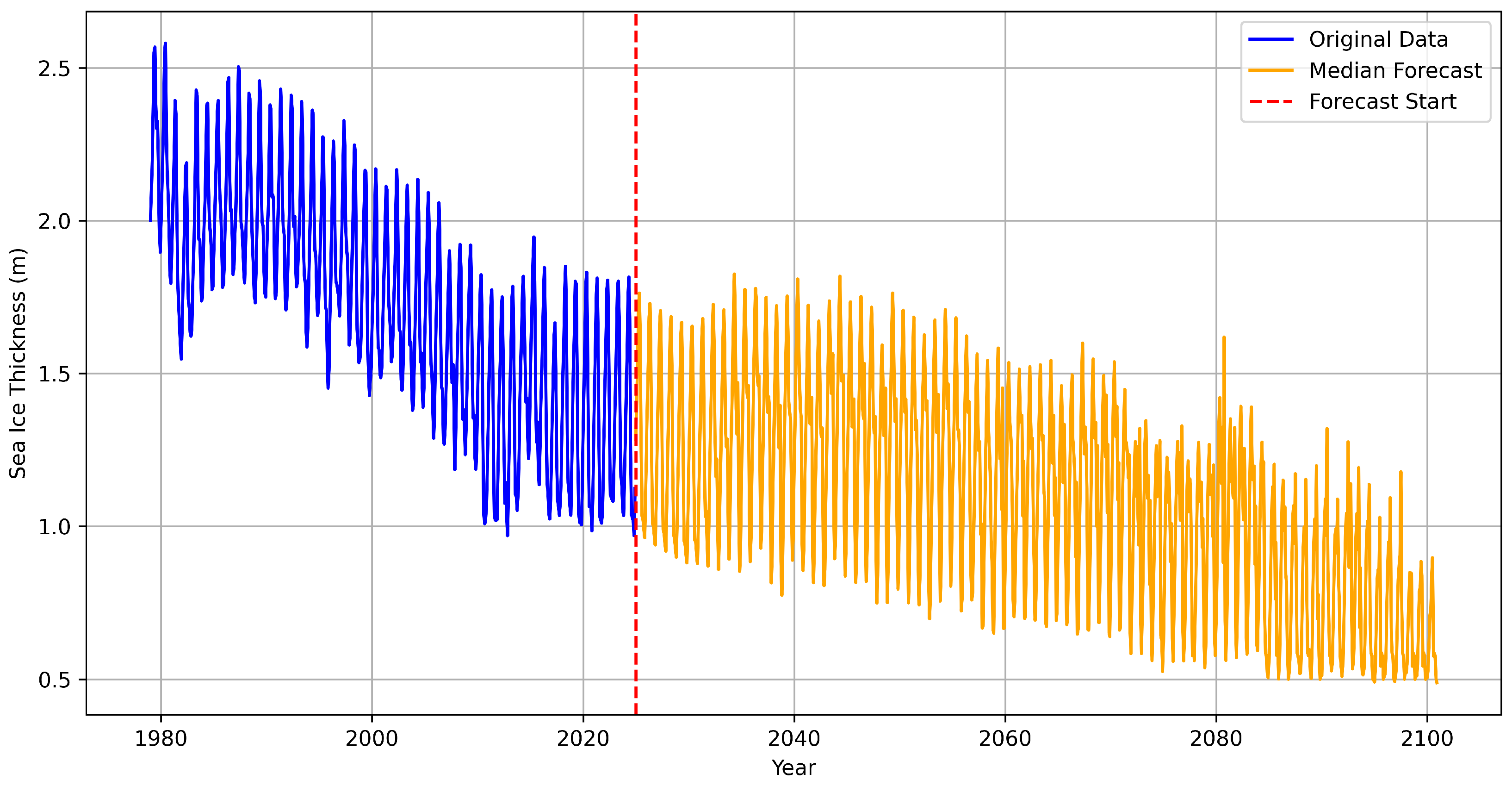
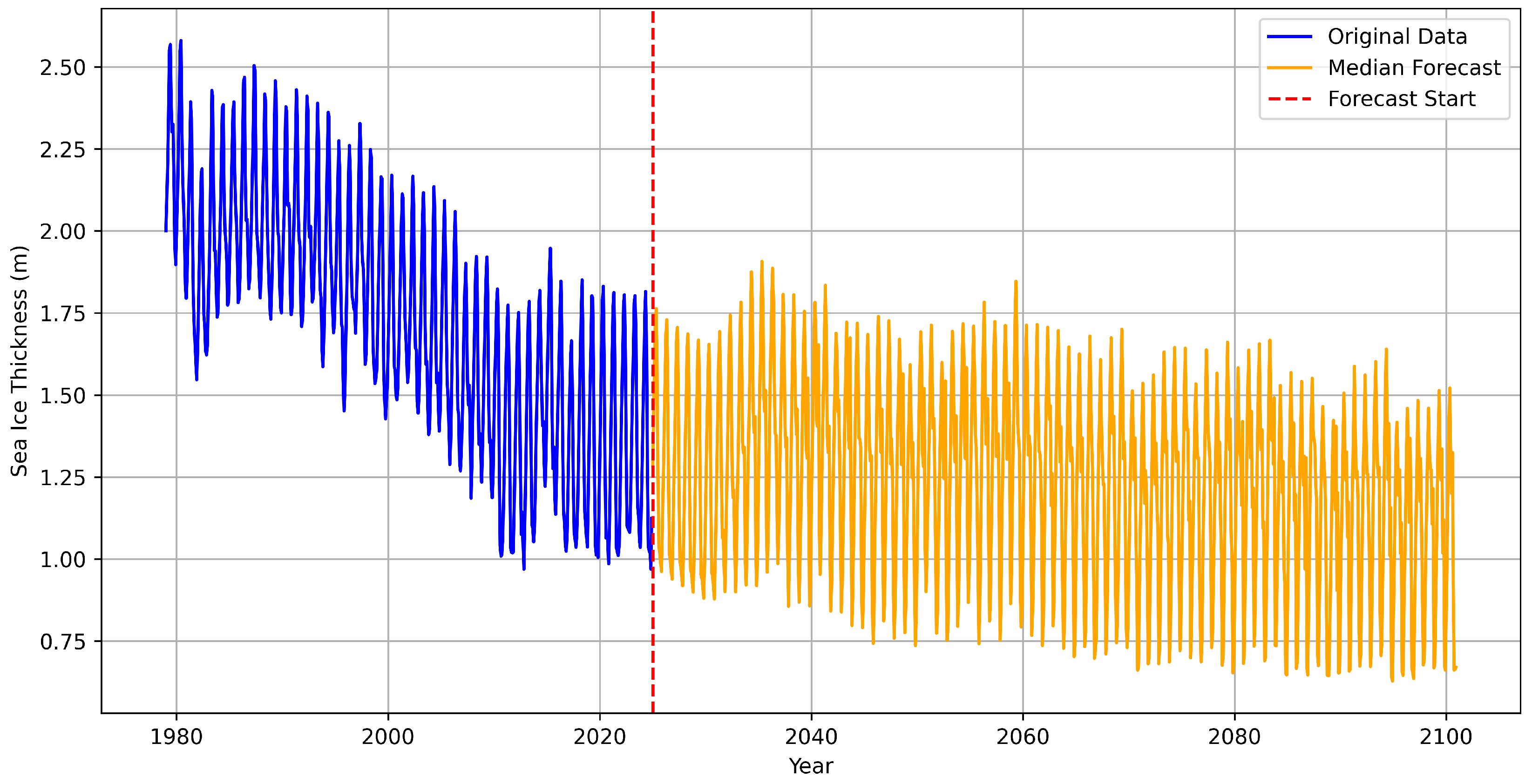
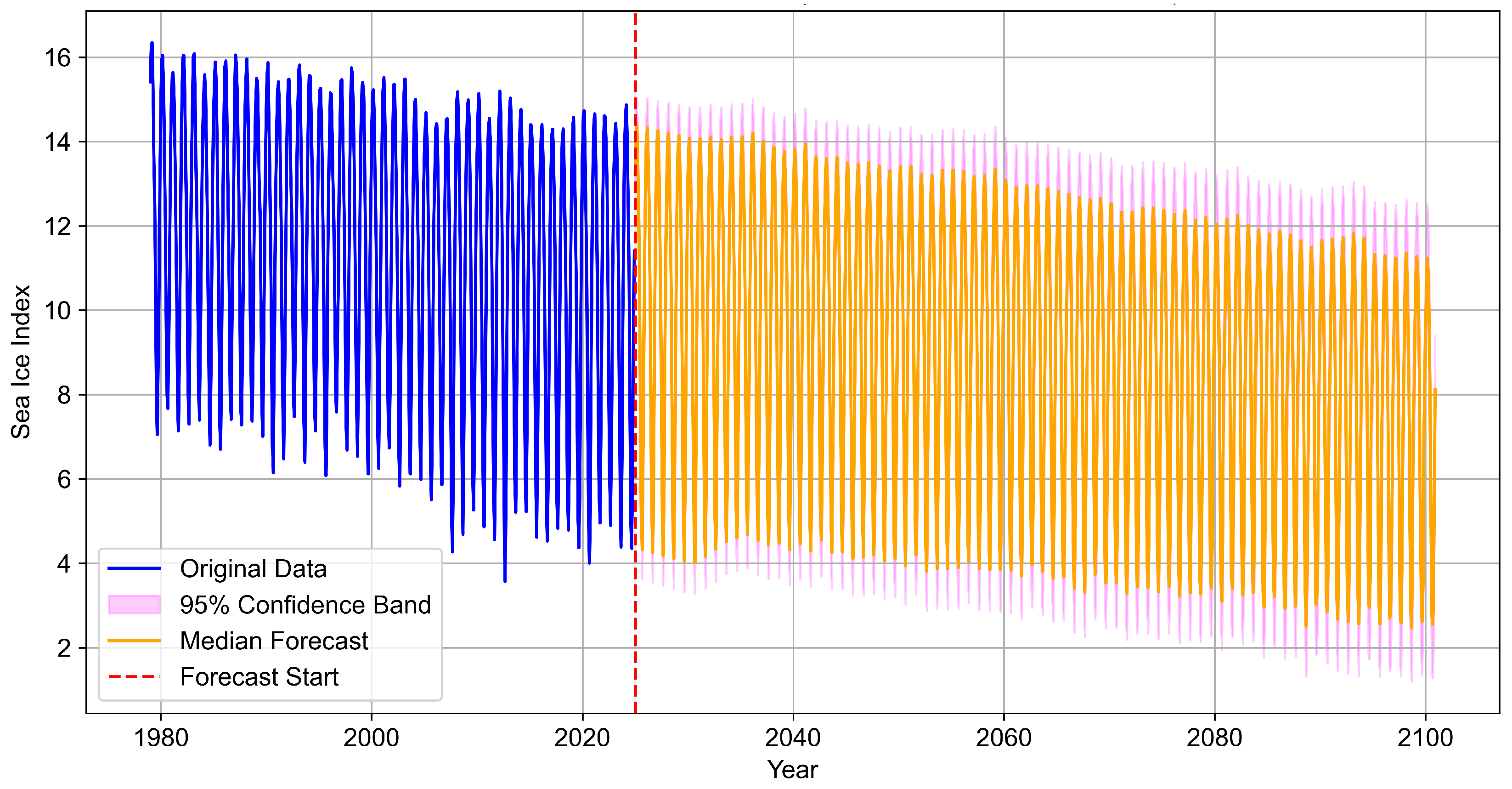
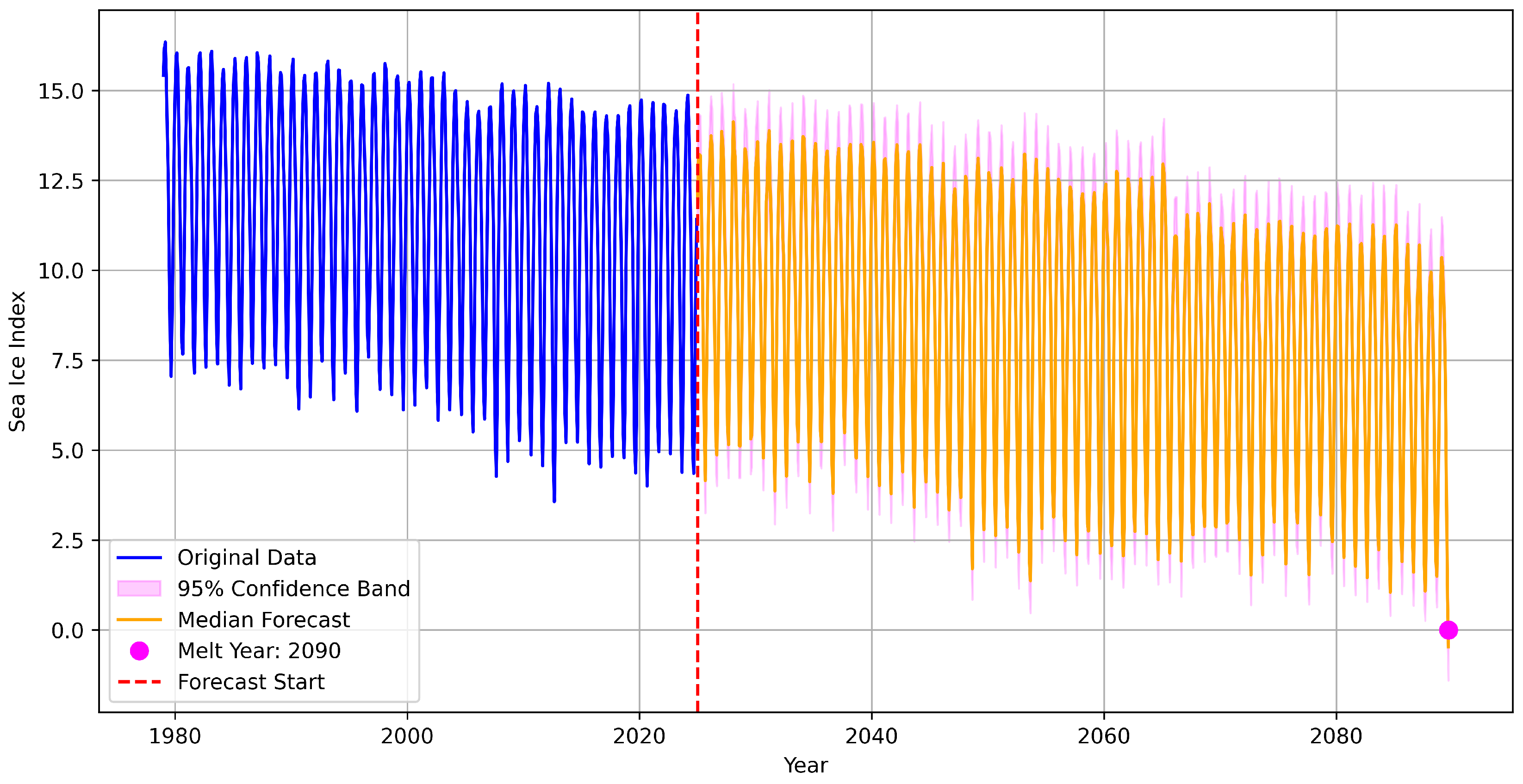
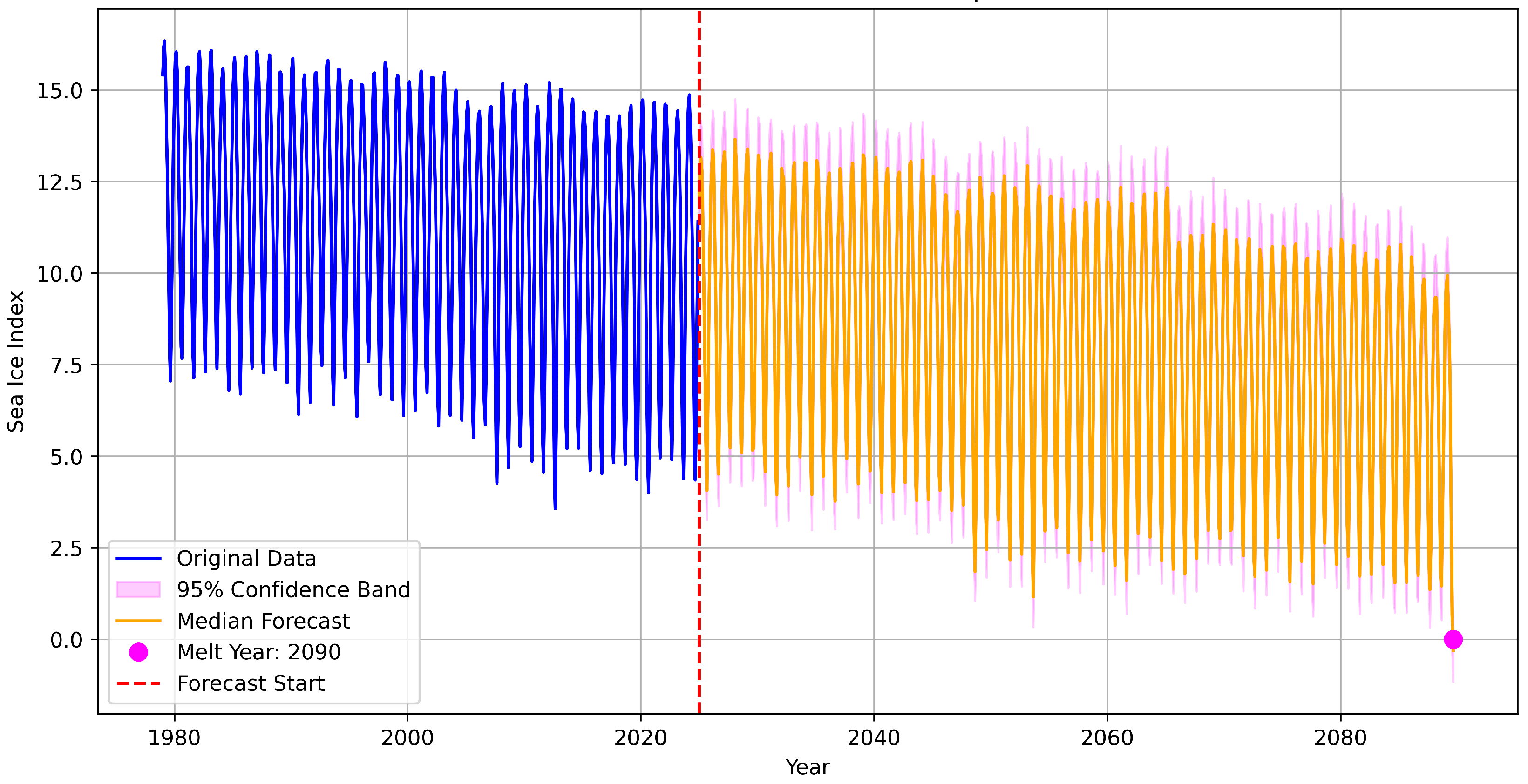
Appendix B. Long Term Forecasting Model Diagnostics
Appendix B.1. Statistical Bridging Model Selection
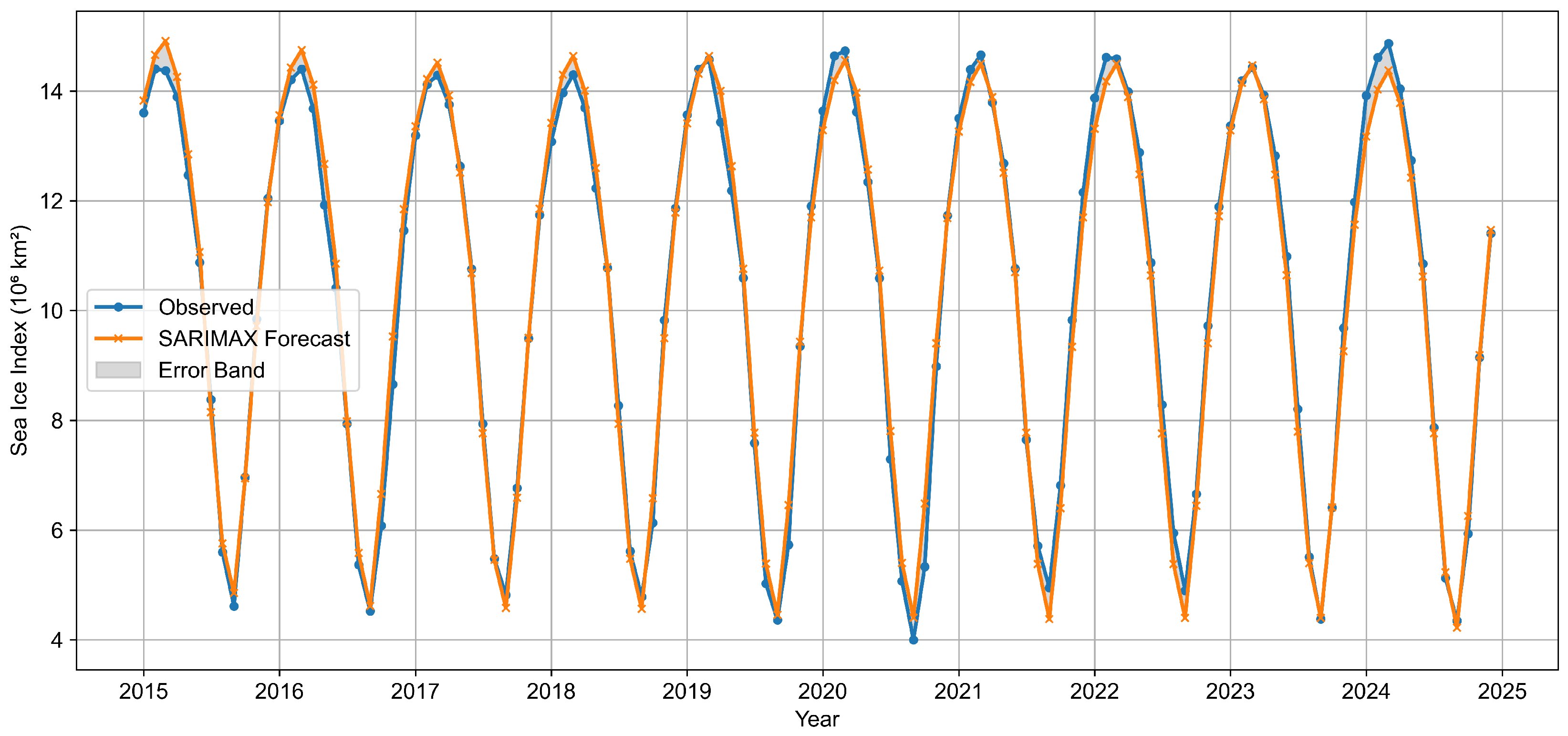
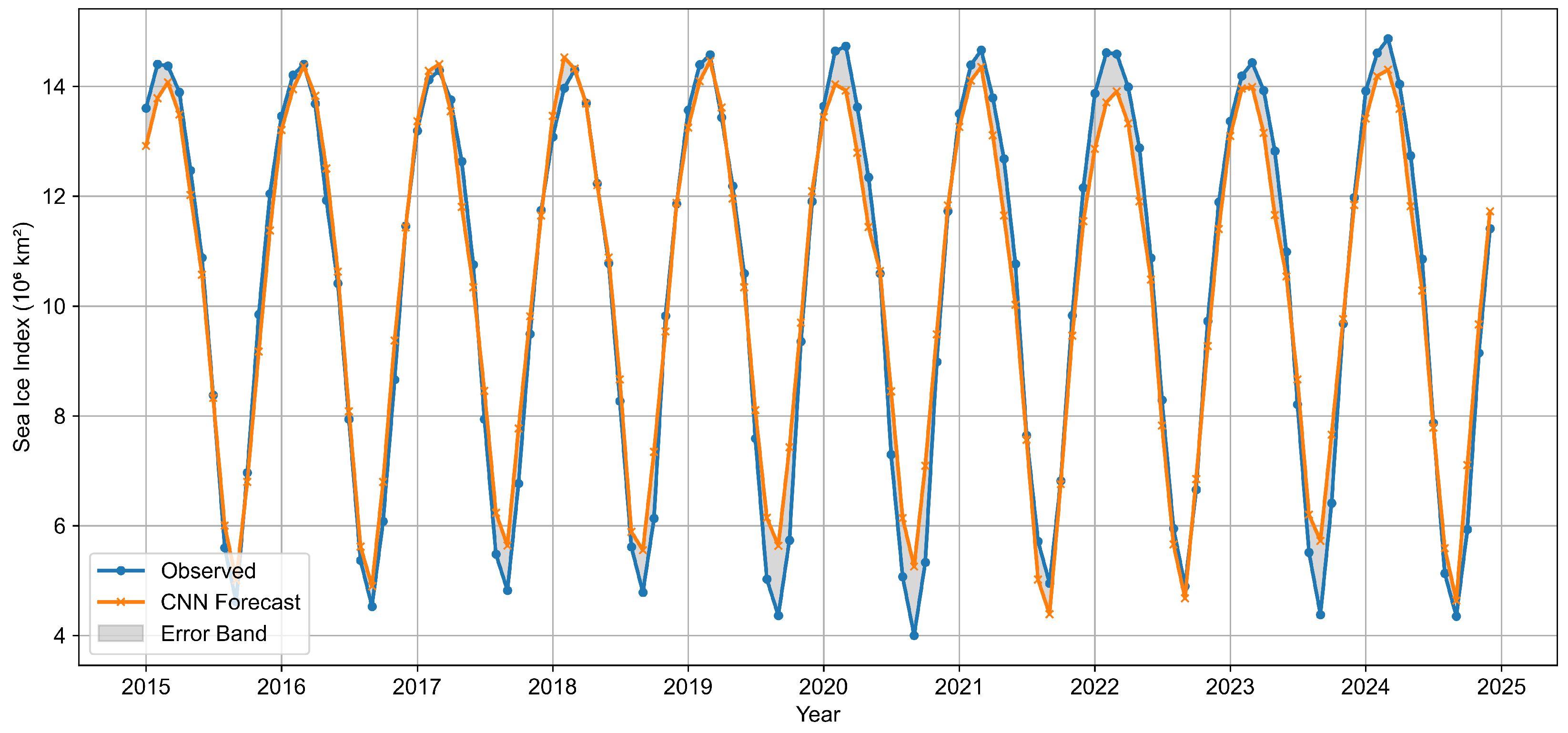
To establish the optimal statistical model for bridging historical observations with CMIP6 projections, we conducted a comprehensive evaluation of multiple time series forecasting approaches using rolling-origin cross-validation from 2015 onward.
Implementation Details: The evaluation framework employed a two-stage process: systematic hyperparameter tuning via time series cross-validation, followed by rolling-origin evaluation across extended forecast horizons. Parallel processing was performed by the "future" package with automatic worker detection ("parallelly::availableCores()- 1") and L’Ecuyer-CMRG random number generation for reproducible results across parallel streams.
For ARIMA models, "auto.arima()" was configured with AICc selection ("ic = aicc", "stepwise = TRUE", "approximation = TRUE") to balance accuracy and computational efficiency. ETS explored nine configurations including automatic model selection ("model = ZZZ"), specific seasonal patterns (ANN, AAN, AAA, MAM), and damped trend variants. NNAR tested seven architectures varying hidden layer sizes (8–15 nodes), ensemble repetitions (15–40), and regularization (decay=0.0–0.1), with "scale.inputs = TRUE" option for input standardization. TBATS evaluated seven specifications controlling Box-Cox transformations ("use.box.cox"), trend components ("use.trend"), damping ("use.damped.trend"), and explicit seasonal period specification ("seasonal.periods = 12"). Prophet tested five configurations varying seasonality modes (additive/multiplicative), changepoint sensitivity ("changepoint.prior.scale": 0.001-0.5), seasonality flexibility ("seasonality.prior.scale": 1–10), and changepoint detection range ("changepoint.range" = 0.8).
Rolling-origin evaluation used 120-month initial training windows with 6-month step increments, generating evaluation origins from 2015 onward. Each model was refitted at every origin using the optimal hyperparameter configuration determined from the tuning phase. The "tsCV()" function handled most models, while Prophet required a custom "manual_cv_prophet()" implementation due to framework incompatibilities. This function performed date-time conversion using "seq.Date()" with monthly increments, fitted Prophet models with "yearly.seasonality = TRUE" and daily/weekly seasonality disabled, generated forecasts via "make_future_dataframe()" with "freq = month", and extracted predictions from the "yhat" component. CMIP6 evaluation used ensemble means with 95% confidence intervals derived from multi-model quantiles ("stats::quantile()" with "c(0.025, 0.975)").
Robust error handling employed "tryCatch()" wrappers around all model fitting and forecasting operations, with failed fits returning "NA" values rather than halting execution. NNAR models used consistent random seeds ("set.seed(42)") at each fitting operation to ensure reproducible ensemble initialization. Prophet models employed "suppressMessages()" to reduce console output while preserving error information. Parallel safety was maintained through explicit package loading within worker processes and careful memory management via "plan(sequential)" cleanup on function exit.
ARIMA achieved superior performance across most forecast horizons, with the lowest RMSE at (0.027), (0.069), (0.086), (0.114), and (0.137). The AICc-optimized configuration ("stepwise = TRUE", "approximation = TRUE") achieved the lowest cross-validation RMSE (0.0843) during hyperparameter tuning. Neural models showed substantial performance degradation, particularly at medium horizons ( RMSE = 0.338), despite optimal configuration with 15 hidden nodes and light regularization. Prophet exhibited poor short-term accuracy ( RMSE = 0.152) but reasonable medium-term performance. CMIP6 projections demonstrated poor near-term accuracy but convergent long-term performance, highlighting the critical need for statistical bridging in hybrid frameworks.
Table A16.
Rolling-origin cross-validation RMSE results across forecast horizons for statistical and machine learning models (2015-onward evaluation).
Table A16.
Rolling-origin cross-validation RMSE results across forecast horizons for statistical and machine learning models (2015-onward evaluation).
| Model | | | | | | |
|---|
| ARIMA | 0.027 | 0.063 | 0.069 | 0.086 | 0.114 | 0.137 |
| ETS | 0.044 | 0.102 | 0.081 | 0.105 | 0.106 | 0.214 |
| NNAR | 0.044 | 0.115 | 0.110 | 0.182 | 0.338 | 0.199 |
| TBATS | 0.044 | 0.105 | 0.095 | 0.107 | 0.107 | 0.159 |
| Prophet | 0.152 | 0.101 | 0.115 | 0.106 | 0.136 | 0.368 |
| CMIP6 | 0.271 | 0.230 | 0.229 | 0.226 | 0.147 | 0.149 |
Table A17.
Diebold-Mariano test results comparing ARIMA against alternative forecasting methods.
Table A17.
Diebold-Mariano test results comparing ARIMA against alternative forecasting methods.
| Horizon | Baseline | Challenger | DM Stat | p Value | Better Model |
|---|
| 1 | ARIMA | ETS | −2.2200 | 0.0388 | ARIMA |
| 1 | ARIMA | NNAR | −2.1650 | 0.0433 | ARIMA |
| 1 | ARIMA | TBATS | −2.6075 | 0.0173 | ARIMA |
| 1 | ARIMA | Prophet | −4.5858 | 0.0002 | ARIMA |
| 1 | ARIMA | CMIP6 | −3.7142 | 0.0015 | ARIMA |
| 12 | ARIMA | ETS | −0.2979 | 0.7694 | ARIMA |
| 12 | ARIMA | NNAR | −0.7077 | 0.4887 | ARIMA |
| 12 | ARIMA | TBATS | −0.7654 | 0.4545 | ARIMA |
| 12 | ARIMA | Prophet | −1.0488 | 0.3089 | ARIMA |
| 12 | ARIMA | CMIP6 | −0.9369 | 0.3619 | ARIMA |
Diebold-Mariano tests confirmed ARIMA’s significant superiority at the 1-month horizon against all alternatives: ETS (p = 0.0388), NNAR (p = 0.0433), TBATS (p = 0.0173), Prophet (p = 0.0002), and CMIP6 (p = 0.0015). Negative DM statistics consistently favored ARIMA, with the largest advantage against Prophet (DM ). At 12-month horizons, differences became statistically non-significant (all p > 0.3), though ARIMA maintained the lowest average RMSE. These results establish ARIMA constructed via "auto.arima()" with AICc selection as the optimal statistical baseline for bridging applications, providing both superior accuracy and computational efficiency for hybrid forecasting frameworks.
Appendix B.2. Temperature Forecasting Method Comparison
To address concerns about relying solely on quadratic fits for long-term temperature extrapolation, we implemented and compared flexible alternatives including generalized additive mixed models (GAMMs) and three-state Markov regime-switching (MSM) models using comprehensive rolling hindcast evaluation.
Implementation Details: The comparison framework employed three distinct modeling approaches with careful hyperparameter specification to avoid overfitting in climate time series contexts. GAMM models used "mgcv::gamm()" with penalized regression splines ("s(t,k)"), where basis dimensions were adaptively scaled to training sample size ( for fixed windows, for hindcast windows) and ARMA(1,1) residual correlation structures ("correlation = corARMA(p = 1, q = 1)") to capture temporal dependence. MSM models employed the "MSwM" package with three-regime specifications estimated on lag-one autoregressive structures ("Temp_t ~LagTemp"), where only variance components were allowed to switch ("sw = c(FALSE, FALSE, TRUE)") following methodological guidance for parsimonious regime-switching in small-sample climate applications.
Evaluation used origins from 1985-2015 with forecast horizons of 5, 10, and 20 years, generating 930 individual forecasts across model-horizon combinations. Each hindcast refitted models using data available only through the origin date, with multi-step forecasts generated via iterative prediction for MSM models and direct extrapolation for GAMM/quadratic models. GAMM forecasts incorporated uncertainty via "predict()" with "se.fit = TRUE" for 95% prediction intervals. MSM multi-step forecasting used filtered regime probabilities from "@Fit@filtProb" combined with regime-specific transition matrices to generate expectation-based predictions through iterative application of and .
To assess extrapolation realism and validate model behavior in near-contemporary periods, we conducted pseudo-future experiments using recent origins (2005, 2010, 2015, 2020) with horizons of 5, 10, and 15 years. This approach provides a critical bridge between historical hindcasts and true future projections by testing model performance on data that was genuinely unknown at the time of model fitting but is now observable through 2024. The "evaluate_pseudo_future()" function implemented this by fitting each model using data only through December of the origin year, then generating forecasts for the specified horizon and comparing against observed temperature anomalies. For example, a model fitted through 2010 would forecast 2015, 2020, or 2025 conditions, with the first two scenarios providing validation against observed data. This methodology ensures that models demonstrating good pseudo-future performance are more likely to provide reliable extrapolations beyond the observational record, addressing concerns about purely retrospective model evaluation that may not reflect true forecasting skill.
Model comparison employed multiple complementary approaches to account for forecast dependence and small sample limitations. Newey-West loss differential tests used "sandwich::NeweyWest()" with HAC standard errors to test whether mean squared error differences between models were statistically significant after adjusting for serial correlation in overlapping forecast windows. Paired Wilcoxon signed-rank tests assessed whether absolute error distributions differed significantly between GAMM and MSM approaches. Diebold-Mariano tests were attempted but failed due to insufficient sample sizes at longer horizons, highlighting the value of the more robust Newey-West approach for climate forecasting applications.
Table A18.
Rolling hindcast performance comparison for temperature forecasting methods across multiple horizons (1985–2015 origins).
Table A18.
Rolling hindcast performance comparison for temperature forecasting methods across multiple horizons (1985–2015 origins).
| Model | Horizon (Years) | RMSE | MAE | Bias | n |
|---|
| GAMM | 5 | 0.221 | 0.189 | −0.097 | 4 |
| GAMM | 10 | 0.134 | 0.096 | 0.096 | 3 |
| GAMM | 20 | 0.151 | 0.151 | −0.001 | 2 |
| Quadratic | 5 | 0.262 | 0.226 | 0.040 | 4 |
| Quadratic | 10 | 0.557 | 0.442 | 0.442 | 3 |
| Quadratic | 20 | 1.494 | 1.157 | 1.157 | 2 |
| RegimeSwitch | 5 | 1.526 | 1.083 | 0.917 | 4 |
| RegimeSwitch | 10 | 0.597 | 0.400 | 0.350 | 3 |
| RegimeSwitch | 20 | 0.176 | 0.159 | −0.159 | 2 |
GAMM models consistently achieved superior performance across evaluation frameworks. In rolling hindcasts, GAMM attained the lowest RMSE at 5-year (0.221) and 10-year (0.134) horizons, substantially outperforming quadratic fits (0.262, 0.557) and regime-switching models (1.526, 0.597). Pseudo-future validation confirmed this superiority, with GAMM achieving RMSE values of 0.248 (5-year) and 0.202 (10-year) compared to regime-switching values of 1.309 and 0.457 respectively. Quadratic models exhibited severe bias inflation at longer horizons (bias = 1.157 at 20 years), while GAMM maintained near-zero bias (−0.001). Coverage analysis showed GAMM 95% prediction intervals achieved 78–85% empirical coverage, indicating reasonable uncertainty calibration despite slight under-dispersion.
Table A19.
Pseudo-future validation results using recent origins (2005–2020) to assess extrapolation realism through observed data.
Table A19.
Pseudo-future validation results using recent origins (2005–2020) to assess extrapolation realism through observed data.
| Model | Horizon (Years) | RMSE | Bias | n |
|---|
| GAMM | 5 | 0.248 | −0.030 | 3 |
| GAMM | 10 | 0.202 | −0.141 | 2 |
| GAMM | 15 | 0.106 | 0.106 | 1 |
| RegimeSwitch | 5 | 1.309 | 0.807 | 3 |
| RegimeSwitch | 10 | 0.457 | −0.408 | 2 |
| RegimeSwitch | 15 | 0.306 | −0.306 | 1 |
Table A20.
Statistical significance tests comparing temperature forecasting approaches across horizons.
Table A20.
Statistical significance tests comparing temperature forecasting approaches across horizons.
| Horizon (Years) | Newey-West t-Stat | Newey-West p-Value | Wilcoxon p-Value |
|---|
| 5 | 1.01 | 0.3191 | 0.0380 |
| 10 | 1.35 | 0.1879 | 0.0087 |
| 20 | −0.05 | 0.9639 | 0.0664 |
Wilcoxon signed-rank tests confirmed significant differences favoring GAMM over regime-switching models at 5-year (p = 0.0380) and 10-year (p = 0.0087) horizons. Newey-West loss differential tests, while not achieving conventional significance levels due to limited sample sizes, showed consistent directional evidence favoring GAMM (positive t-statistics at 5 and 10-year horizons). The absence of significance in Newey-West tests reflects the conservative nature of HAC adjustments in small samples rather than evidence against model differences, as confirmed by the more powerful paired Wilcoxon tests.
These comprehensive evaluations demonstrate that GAMM models provide statistically validated improvements over both quadratic extrapolation and regime-switching approaches for long-term temperature forecasting, combining superior point accuracy, better bias properties, and reasonable uncertainty quantification for climate projection applications.
Appendix B.3. Markov Regime-Switching Model Selection
Prior to implementing the MSM temperature forecasting approach described above, we conducted systematic model selection to determine optimal regime specifications and switching parameters using rolling one-step-ahead validation.
Implementation Details: The selection framework employed the "MSwM" package to evaluate multiple regime-switching specifications across a comprehensive parameter grid. Models were tested with 2–4 regimes () and autoregressive orders () with five switching parameter configurations: full switching (intercept, slope, variance), coefficient-only switching (intercept, slope), intercept-only switching, slope-only switching, and variance-only switching. The switching vector was implemented as a logical vector ("sw = c(intercept, slope, variance)") following "MSwM" requirements, with length matching the number of linear model coefficients plus one variance component.
Rolling validation used expanding windows starting from 120 months (10 years) with monthly step increments, generating 395–432 one-step forecasts per variant depending on convergence success rates. Each origin refitted the MSM model using data available only through that time point, with forecasts generated via regime probability weighting:
where
represents filtered regime probabilities from the Kalman filter and
are regime-specific parameters. Robust error handling employed timeout mechanisms ("R.utils::withTimeout") and parallel processing with controlled worker limits to manage computational complexity and memory constraints.
The evaluated configurations reflect methodological guidance for parsimonious regime-switching in climate contexts. Variance-only switching captures heteroskedastic periods (stable vs. volatile climate states) without overfitting mean parameters, while full switching allows complete regime dependence. Intercept-only switching models regime-specific climate baselines, and slope-only switching captures varying persistence across regimes. The inclusion of () autoregressive orders tests whether additional temporal dependence improves regime identification beyond the fundamental lag-1 structure inherent in climate dynamics.
Table A21.
MSM model selection results for the top 10 models showing performance across regime specifications and switching parameters via rolling one-step validation.
Table A21.
MSM model selection results for the top 10 models showing performance across regime specifications and switching parameters via rolling one-step validation.
| Variant | Regimes (K) | Switching Components | RMSE | Rank | Valid Rolls |
|---|
| 3 | Variance only | 0.1003 | 1 | 396 |
| 4 | Variance only | 0.1007 | 2 | 396 |
| 2 | Variance only | 0.1022 | 3 | 395 |
| 2 | Intercept + Slope + Variance | 0.1026 | 4 | 430 |
| 4 | Intercept only | 0.1040 | 5 | 418 |
| 2 | Intercept only | 0.1042 | 6 | 420 |
| 3 | Intercept only | 0.1045 | 7 | 421 |
| 2 | Intercept + Variance | 0.1063 | 8 | 431 |
| 2 | Intercept + Slope | 0.1083 | 9 | 432 |
| 3 | Intercept + Variance | 0.1128 | 10 | 399 |
The systematic evaluation revealed that variance-only switching with three regimes ("k3_p0_variance_only") achieved optimal performance with RMSE = 0.1003 across 396 valid rolling forecasts. This specification outperformed both more complex alternatives (full switching) and simpler configurations (2-regime models), demonstrating the importance of capturing heteroskedastic climate dynamics without overparameterizing mean relationships. The superior performance of 3-regime models suggests that temperature anomaly dynamics exhibit three distinct volatility states, likely corresponding to stable, transitional, and volatile climate periods.
Variance-only switching dominated the top rankings (positions 1–3), indicating that regime differences primarily manifest through volatility rather than mean level shifts or persistence changes. The 4-regime variance-only model achieved comparable performance (RMSE = 0.1007, rank 2) but with minimal improvement over the 3-regime specification, suggesting diminishing returns to additional regime complexity. Full switching models, despite their flexibility, ranked lower due to overfitting risks in the relatively short climate time series, while coefficient-only switching showed poor performance, confirming that mean parameter stability across regimes is appropriate for this dataset.
This empirical model selection provides strong justification for the parsimonious 3-regime, variance-only specification used in the temperature forecasting comparison, balancing model flexibility with statistical reliability in climate applications where overfitting poses significant risks for long-term extrapolation.