Next Article in Journal
Enhancing Arctic Ice Extent Predictions: Leveraging Time Series Analysis and Deep Learning Architectures
Previous Article in Journal
How Do Climate Change and Deglaciation Affect Runoff Formation Mechanisms in the High-Mountain River Basin of the North Caucasus?
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Glacies
Volume 2
Issue 4
10.3390/glacies2040011
glacies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Reanalyzing and Reinterpreting a Unique Set of Antarctic Acoustic Frazil Data Using River Frazil Results and Self-Validating 2-Frequency Analyses

by
John R. Marko
*,
David R. Topham
and
David B. Fissel
ASL Environmental Sciences Inc., Saanichton, BC V8K 1Z3, Canada
*
Author to whom correspondence should be addressed.
Glacies 2025, 2(4), 11; https://doi.org/10.3390/glacies2040011
Submission received: 4 June 2025 / Revised: 5 September 2025 / Accepted: 28 September 2025 / Published: 7 October 2025
Browse Figures
Versions Notes

Abstract

A previous analysis of Antarctic acoustic data relevant to quantifying frazil contributions to sea ice accretion is reconsidered to address inconsistencies with river frazil results acquired with similar instrumentation but augmented to suppress instrument icing. It was found that sound attenuation by consequent icing limited credible Antarctic acoustic frazil measurements to afternoon and early evening periods, which are shown to encompass daily minimums in frazil production. This reality was masked by use of an unvalidated liquid oblate spheroidal frazil characterization model, which greatly overestimated frazil concentrations. Much lower frazil contents were derived for these periods using a robust 2-frequency characterization algorithm, which incorporated a validated, alternative theory of scattering by elastic solid spheres. Physical arguments based on these results and instrument depth data were strongly suggestive of maximal but, currently, unquantified frazil presences during unanalyzed heavily iced late evening and morning time periods.

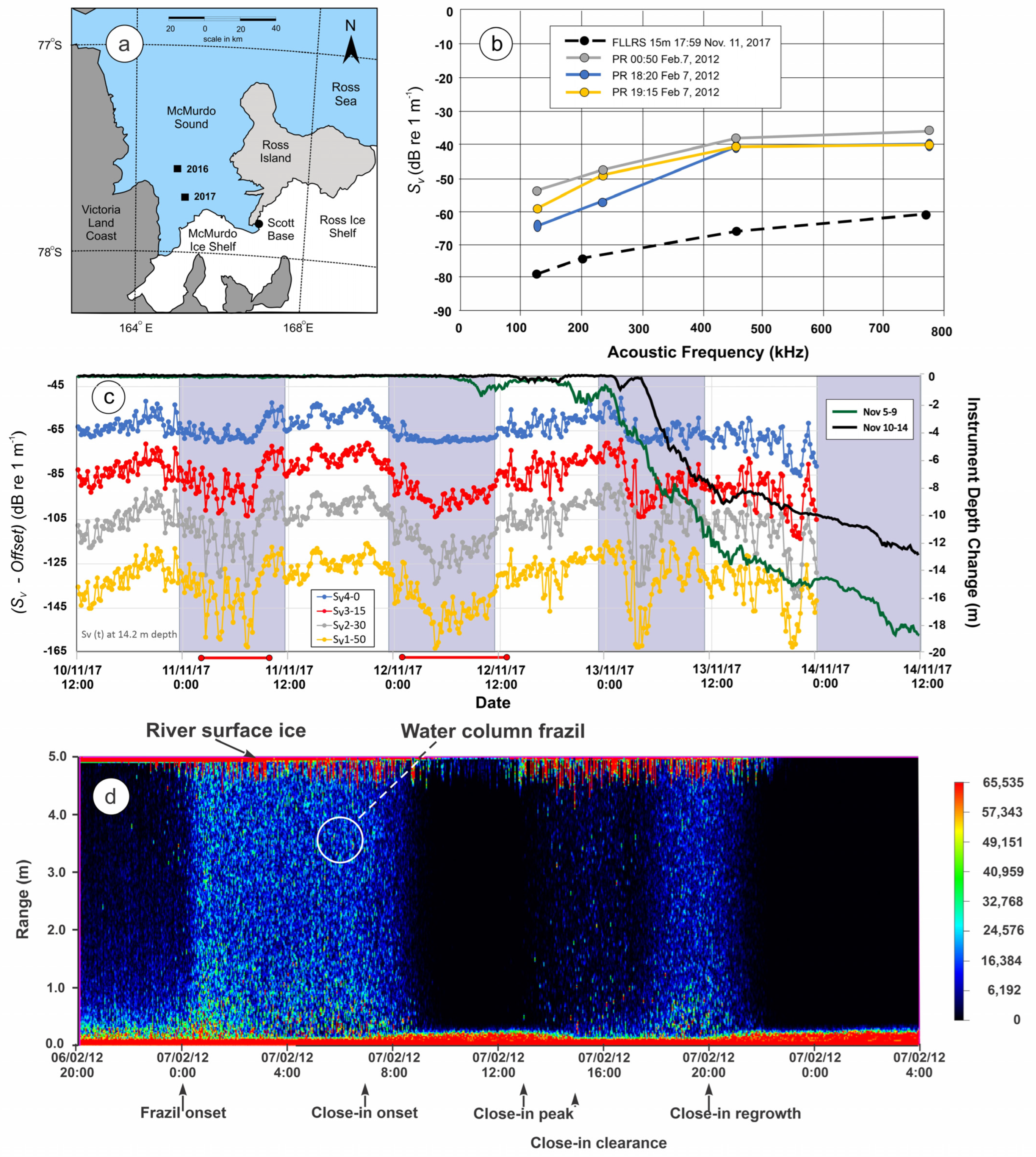
1. Introduction

Frazil ice is a potentially significant contributor to the growth and stability of Antarctic coastal sea ice, which, in turn, is a relevant factor in the erosion of adjacent landfast ice shelves. To date, quantitative data supportive of modelling the underlying suspended frazil populations have been restricted to characterizations derived by Frazer et al. (2020) [1] from acoustic backscattering data. These data were acquired from landfast ice in McMurdo Sound (MS) near the McMurdo Ice Shelf (Figure 1a) using a methodology similar to that applied in river frazil studies [2,3,4,5]. Significantly, however, the MS study did not incorporate critical flows of heated water adjacent to acoustic sensors and employed a new and untested frazil characterization algorithm developed by Kungl et al. (2020) [6]. Heated water flows had previously been found by Marko et al. (2015) [5] to be essential for suppressing in situ ice growth on and near acoustic sensors in the Peace River (PR). Acoustic signal attenuation by such growth precluded accurate estimates of frazil fractional volumes, F, and other parameters descriptive of frazil populations in turbulent river environments.
Concerns regarding the impacts of these methodological differences were first raised by apparent inconsistencies between respective river and Antarctic ratios of measured acoustic volume backscattering coefficients (sV and SV ≡ 10log(sV)) relative to corresponding resulting fractional volume estimates (sV is defined as the fraction of acoustic power incident upon a unit volume of distributed targets that is scattered back toward the source). Unusual correlations between measured SV values and diurnal environmental changes further motivated reviews and evaluations of the utilized measurement and interpretative procedures. In particular, these efforts were directed at assessing and, if possible, enhancing the usefulness of the reported results for quantitatively describing Antarctic frazil processes and increasing the effectiveness of follow-up studies.
Such efforts begin below with an outline of the Frazer et al. [1] acoustic backscattering (AB) study procedures and their relationship to those used in similar river work. Key Antarctic and Peace River study results are used to identify significant anomalies and/or incompatibilities relative to both each other and theoretical expectations. The centrality of the river results in interpreting and understanding the Antarctic marine data necessitated frequent references to AB data collection during typical Peace River frazil events.
The importance of the frazil fractional volume parameter in all interpretations required a critical review of the Kungl et al. (2020) [6] frazil characterization algorithm. This review utilized an expanded version of a 2-frequency characterization approach introduced by Marko and Jasek (2010b) [3] as a general tool for assessing the feasibility of deriving convergent optimal frazil characterizations from given sets of SV data. This, potentially, self-validating approach is applied to the analyzed Frazer et al. (2020) [1] data in conjunction with both the Kungl et al. characterization algorithm and one utilizing a partially validated (Marko and Topham (2015) [7]) analytic theory for backscattering by elastic spheres developed by Faran (1951) [8]. The obtained results provide the principal basis for reassessing and updating MS frazil production estimates during the 12:00 to 00:00 local time periods considered in detail by Frazer et al. (2020) [1]. The temporal bias of the latter analyses prioritized efforts to obtain additional physical understandings over full daily cycles from river data and neglected portions of other MS data sets. These efforts were directed at obtaining rough characterizations and projections capable of characterizing frazil production on daily and shorter time scales. The implications of these results are discussed relative to the role of frazil data in sea ice models and needs for more detailed understandings of frazil growth near an ice shelf.

2. Methods and Data

The data utilized in this work were primarily extracted from compilations of the 2017 Frazer et al. (2020) [1] acoustic environmental field data archived by Robinson et al. (2020) [9]. Additional information essential for new analyses and interpretations of key data features was drawn from similar PR AB studies [5,10]. Focus is given to explication of anomalies in the Frazer et al. results relative to general understandings of marine frazil environments and relevant information from river frazil studies. Key anomalies are noted following a brief summary of basic elements of the Frazer et al. measurements and interpretations, including their distinctions relative to river methodologies. Correlations are identified that link these features to recorded, but otherwise ignored, Frazer et al. (2020) [1] ancillary data as well as to comparable aspects of PR frazil results. The strength and relevance of these correlations were sufficient to justify a brief graphical review of PR AB data acquired during a typical interval of river frazil growth to guide subsequent reinterpretations and reanalyses.

2.1. Basic Elements of the Antarctic Frazil Study

The Frazer et al. field studies [1] were carried out during November in 2016 and 2017 at MS locations 33 and 13 km, respectively, north of the McMurdo ice shelf (Figure 1a). Each field program acquired 2 weeks of data with an upward-looking AZFP (Acoustic Zooplankton Fish Profiler) instrument manufactured by ASL Environmental Sciences Inc. and suspended by rope from the sea ice. For data quality reasons and because of greater proximity to potential ice shelf influences, analyses were confined to the 2017 study results. Measurements utilized AB signal returns from acoustic pulses emitted at 1 Hz at each of four different frequencies (125, 200, 455, and 769 kHz) (referenced as channels 1 through 4, respectively). Instruments were initially positioned 30 m below the sea ice undersurface. SV values were computed from detected signal voltages and instrument and measurement parameters using an ASL MATLAB Toolbox (Version 1.1). Frazil properties were characterized from 11 min-averages of SV(t) values compiled by Robinson et al. [9] after additional averaging over five 0.1 m deep measurement cells. Procedures developed in earlier, suspended sediment- and zooplankton-related AB studies [11,12] were used to quantify lognormal distributions of a representative particle dimension which, in the Frazer et al. work, was a spheroid diameter. Distribution parameters, established by optimal matching of measured SV values to their theoretical counterparts, supported frazil fractional volume estimates. This matching required achieving equalities between measured- and theoretical-backscattering cross-sections, σBS (imaginary areas representing fractions of power intensity incident upon unit fluid volumes scattered directly back toward acoustic sources). The Antarctic work [1] utilized a new, unvalidated, theoretical cross-section relationship [6] that treated frazil particles as liquid oblate spheroids. This choice represented a significant deviation from river frazil characterization procedures [5,10], which utilized theoretical cross-sections applicable to elastic solid ice spheres [8].
Although prior studies [5,10,13] suggested that supercooling sufficient for frazil crystallization supported simultaneous in situ ice growth on stationary submerged surfaces, Frazer et al.’s adjustments for observed apparatus icing were limited to a 9–10 November sequence of instrument-recovery, de-icing, and redeployment. These actions followed sudden decreases in instrument depth, which began to severely degrade SV data roughly 2.5 days after each of the two successive 2017 instrument deployments [1].

2.2. Potential Data Anomalies

Although archived digital data provided the principal basis for our evaluations, possibilities for anomalous backscattering were first raised by the extremely low time-averaged 17:59 NZST (Z +12 h) 11 November 2017 SV values plotted in Frazer et al.’s [1] Figure 1b. The weakness of the detected returns is evident in our Figure 1b, which replots the frequency dependences of the reported MS 15 m SV values alongside estimates made 2.6 m above the riverbed during a typical PR frazil event [5,10]. Given large differences in the respective measurement locations, depths, and, possibly, crystallization mechanisms [14,15,16,17], the 15 to 25 dB depressions of Antarctic SV values relative to Peace River estimates were only recognizably problematic after comparisons of corresponding MS and PR F(t) results. Specifically, peak F value estimates associated with the PR data [5,10] were barely 5 times (7 dB) larger than the 1 × 10−5 15 m Antarctic values indicated in Frazer et al.’s [1] Figure 4e. This result was incompatible with the 400-fold discrepancies anticipated from the rough proportionalities of contemporary F and SV values expected from their common linear theoretical dependences on volumetric particle number density. Such an inconsistency was suggestive of either large differences in the intrinsic scattering strengths of, respectively, MS- and PR-frazil species or major deficiencies in one or both algorithms used to derive F values from SV data.
The latter possibility would have introduced significant problems into Frazer et al.’s analyses since the Kungl et al. (2020) [6] algorithm was used to support an initial “filtering” of raw SV data. This processing step was intended to assure “physically plausible” results by avoiding characterizations of weak returns from extraordinarily high numbers of very small particles. Consequently, all profiles with 200 kHz SV values below −85 dB re 1 m−1 were excluded from frazil fractional volume estimates. Time periods associated with the eliminated data, comprising, roughly, 40% of recorded profiles, are denoted by horizontal red lines in Figure 1c, which plots Frazer et al. (2020) MS SV data as functions of time and frequency. The Figure’s individual SV curves, which avoid overlaps by incorporating the indicated frequency-specific subtractions, represent 10–13 November 2017 data acquired at 14.2 m depths. Background shadings of 00:00–12:00 NZST periods (designated, here, as “prenoon” intervals) show that unprocessed Frazer et al. [1] data were almost completely confined to these portions of the diurnal cycle. Importantly, the prenoon SV data exhibit consistent distinctions relative to corresponding analyzed 12:00–00:00 NZST (postnoon) results. Specifically, prenoon SV(t) values were both lower in magnitude and marked by much greater ranges of variability.
Strong diurnalities were also a feature of river frazil data sets [5,10], albeit with maximal SV and F values occurring during prenoon as opposed to postnoon periods. Moreover, these aspects of river frazil data were only recognized in the presence of active deterrence of instrument icing by sensor warming. In the absence of such warming, it is not unreasonable to consider that the low prenoon SV values excluded from Frazer et al.’s analyses may have been consequences of acoustic signal attenuation by such icing, which, in rivers, was a signature of high frazil content (Marko and Topham (2021) [10]). This possibility was also consistent with the fact that the 2017 oceanographic results in Figure 4g of the Frazer et al. (2020) [1] work showed prenoon periods hosting peak northward inflows of supercooled water from the adjacent ice shelf. Similar flows were previously suggested [14,15,16,17] as potential sources of local Antarctic frazil production initiated by upward movements of buoyant frazil particles.
Figure 1c also includes important ancillary data on changes in instrument depth supportive of occurrences of intensive icing during prenoon intervals similar to those observed in rivers. These data, also drawn from [9], are displayed for both the 10–14 November 2017 period encompassing the SV data in Figure 1c and the immediately preceding 5–9 November 2017 interval omitted from our SV(t) reanalyses. The instrument depth changes during the latter interval, represented by a dark green curve, are plotted relative to the same horizontal time axis used to display all 10–14 November data but with their times increased by, exactly, five days to facilitate direct comparisons with the black curve representing 10–14 November depth changes. This shift highlighted the commonalities of depth change patterns associated with the two different 2017 acoustic measurement periods.
As noted in Section 2.1, each of these intervals included 2.5 days of initial instrument depth stability followed by sudden and continuing depth reductions, which eventually necessitated both the 9 November and, study-ending, 14 November instrument recoveries. Both initial onsets of instability, presumably indicative of accumulated apparatus icing just sufficient for neutral buoyancy, occurred at the beginnings of prenoon intervals. In each case, relative instrument depth stability was only, temporarily, re-established early in the immediately following postnoon period. This pattern was repeated, on reduced spatial scales, during at least the first halves of immediately following diurnal cycles. Such changes suggested that the bulk of icing and, likely, accompanying frazil growth, was accumulated during the prenoon intervals eliminated from Frazer et al. [1] analyses. Similarities between this behavior and diurnal river icing patterns were strong enough to anticipate that interpretations of Figure 1c SV data would be facilitated by the following brief review of the characteristics of acoustic data acquired during river frazil growth intervals.

2.3. Acoustic Backscattering Measurements in Rivers Relevant to Antarctic Frazil Results

Signal attenuation by icing along acoustic trajectories degrades attainable multifrequency frazil characterizations. Information on encountered impacts and available avoidance measures is accessible from measurement results obtained during the typical daily cycle of PR frazil- and in situ-ice growth depicted in the echogram of Figure 1d. These data represent 16-bit 774 kHz digital backscattered signal voltages recorded as functions of time and range to water column targets. Earlier PR analyses [10] showed frazil growth during the represented 7 February, 2012 period began at, roughly, 00:00 MST (Z + 7 h). Coincident in situ growth was initially inferred indirectly through its accompanying releases of latent heat, which partially suppressed measured frazil levels below an initial peak value. Direct evidence of in situ growth appeared seven hours after frazil onset as initial thickening of a ubiquitous red, near-zero range, echogram feature introduced by near-field acoustic measurement effects unrelated to frazil presence. Subsequent thickening of this feature, designated as “close-in” signal returns, represented backscattering by sensor icing, which attenuated both outgoing and incoming sound pulses, thereby weakening water column frazil signals. External sensor warming delayed onsets of signal blockage until upper portions of riverbed ice layers made physical contact with the elevated (by 29 cm) acoustic sensors. Consequent delays in blockage onsets allowed use of the data in Figure 1d to confirm earlier [10,18] 4 cmh−1 estimates of rates of growth for riverbed ice layer thicknesses.
Continued sensor icing and subsequent thinning produced an 11:30 MST peak in close-in thickness coincident with a consequent minimum in river surface signal voltages. Gradual icing clearances, after 14:30 MST, allowed reappearances of weak water column frazil signals, which strengthened into an evening peak, which preceded 20:00 MST reappearances of detectable close-in regrowth. Continuation of this regrowth can be seen to have eventually eliminated detection of all water column signal returns by midnight. The 18:20 and 19:15 MST SV frequency dependence data in Figure 1b corresponded to, respectively, returns at the leading edge and center of a modest early evening peak in echogram signal voltages. The first of these two returns, which was marginally detectable, was almost 15 dB larger than its coplotted Frazer et al. (2020) [1] counterparts, suggesting the latter would have been undetectable in the noisier PR environment.
Applying river frazil understandings to interpret the Antarctic data requires accommodating notable differences in the PR and MS measurement environments. Specifically, the latter environment did not include large natural features, such as riverbeds, capable of supporting in situ ice growth sufficient to suppress suspended frazil contents. Similar growth on sea ice undersurfaces may have been present, but lower water flow speeds and large separations from frazil measurement volumes would have reduced river-like impacts on frazil content (see Section 4). However, without applied warming, signal attenuation by in situ growth on acoustic sensors was an obvious potential source of Frazer et al. [1] frazil content underestimates.
Results in both environments could be expected to be sensitive to prenoon/postnoon differences. In rivers, apart from a short interval following frazil onset, simultaneous frazil and instrument icing growth would have confined uncontaminated unwarmed sensor measurements to time windows associated with early- to mid-postnoon icing clearances. The lengthy periods of potentially uncontaminated postnoon SV data analyzed in the Frazer et al. [1] study could have been taken as evidence for the low icing presences compatible with observed contemporary stabilities in instrument depth. Confirming this inference requires resolving uncertainties in the Frazer et al. characterizations and, hence, in the underlying Kungl et al. (2020) [6] algorithm. More fundamentally, such clarifications are essential for quantifying and assessing the significance of the SV(t) data in Figure 1c with regard to overall MS frazil production.

3. Analyses

3.1. Evaluations of Frazil Content Estimation Algorithms

Our evaluations used observed instrument depth stabilities to tentatively justify ignoring icing-related acoustic attenuation during the postnoon periods associated with all 2017 Frazer et al. (2020) [1] fractional volume estimates. This choice focused attention on differences between algorithms applied to, respectively, PR and MS data in previous work. Both algorithms optimized agreement between theoretical and measured SV values by using squared error minimization techniques and SV(t) data usually acquired at three and four frequencies, respectively, in river studies and in the MS analyses. Ideally, PR optimizations, employing equal numbers of known input and unknown output parameters, were fully determined, allowing exact frazil characterizations. However, data and theory imperfections yielded finite (Marko et al. (2015) [5]) root mean square (rms) errors as rough indicators of F(t) estimate accuracy. No equivalent Frazer et al. error measures were made available for similar evaluations of overdetermined 4-frequency extractions.
In both cases, characterization quality reflected assumed theoretical linkages of backscattering strength to acoustic frequency and parameters defining host fluid and insonified frazil particle properties. PR extractions utilized Faran’s (1951) [8] exact (analytic) formulation of elastic solid ice sphere backscattering cross-sections in terms of water and ice mass densities, a particle dimension, and fluid and target rheologies. These relationships were verified by laboratory measurements [7] on polystyrene sphere- and disk-surrogates treated as “effective spheres” (Ashton (1986) [19]) with “effective radii”, ae, defined to reproduce actual particle volumes. Polystyrene disk results showed small, < 2 dB, errors for frequency and particle size combinations, k1ae, exceeding 0.6 where k1 ≡ 2π/λ with λ denoting sound wavelengths in host fluids. Optimal 3-frequency matching to PR frazil data [5] primarily returned SV(t) values with average rms errors approximating 1 dB in each frequency channel for frazil populations with lognormally distributed ae values and particle number volumetric densities, N. Additional distribution parameters included a mean effective radius, am, and a statistical width parameter, b, representing the standard deviation of ln(ae).
The complexities of 3- and 4-frequency characterizations reflected, in part, efforts to quantify frazil dimension parameters rarely used as fundamental inputs to ice growth models or operational ice assessments. Frazil shape- and size-variations and their temporal instabilities, combined with dearths of independent, non-acoustic verification data, greatly complicated obtaining realistic particle descriptions. Abandoning spherical particle treatments requires poorly documented assumptions to link additional dimension statistics to the particle volumes and cross-sections of principal interest.
Reviews of the largest body of characterizations [5] showed a predominance of zero-width (b = 0) distributions. This tendency was indicative of measurement errors and theoretical imperfections arising, in large part, from shape non-uniformities, which inhibit convergences to finite b value solutions. The resulting frazil population characterizations were closely related to those previously derived by Marko and Jasek (2010b) [3] from data acquired simultaneously with pairs of different frequencies. The latter, 2-frequency, approach characterized frazil in terms of populations of N* identical spheres of radius a* per unit volume. Optimal estimates for a corresponding fractional volume parameter, F*, equated to 4πN*(a*)3/3, were obtainable if differences in SV values measured with a given frequency pair were theoretically calculable from the utilized cross-section relationship, σBS, and the assumption that measured values of sV were equal to N*σBS. In practice, this required that measured pair SV differences had to fall within the ranges of variability depicted by curves representing corresponding pairwise theoretical differences in SV as functions of a*.
While convergences to b = 0 solutions precluded 3-frequency characterizations at finite b values, the obtained 2-frequency results offered coarser, but robust, fractional volume estimates. This capability reflected the fact that 3-frequency convergence methods implicitly included 2-frequency calculations for each of the three possible pairings of the three incorporated frequencies. Nevertheless, apart from requiring a valid cross-section relationship, the obtained individual pair F* estimates are only fully representative of F for frazil populations with narrow distributions of particle dimensions. The consequent degrading of F estimates for realistic non-uniformly sized frazil populations is, however, partially mitigated by averaging over results obtained with multiple frequency pairings. Thus, SV data acquired at 3- and 4-frequencies support 2-frequency F* estimates derived with, respectively, three and six different 2-frequency pairings.
Accuracies of resulting pair-averaged 2-frequency F* estimates were quantified by comparisons with F values characteristic of hypothetical elastic solid ice sphere populations defined by known probability distribution parameters and backscattering cross-sections in full accord with the Faran (1951) [8] cross-section relationship. Such populations were constructed using the latter relationship to calculate SV values at the four acoustic frequencies utilized in the Frazer et al. studies [1], assuming a mean effective radius, am; a width parameter, b, and an arbitrarily selected SV value for an included frequency. The resulting sets of 4-frequency SV data supported exact calculations of F corresponding to the chosen am and b values and a numerical volume density, N, established from these values to be consistent with the arbitrarily selected SV value. The SV data generated for each population allowed 2-frequency F* estimates to be made for each of the six possible frequency pairings. Averaging over these pairings yielded the F*avg/F ratios represented by the solid curve in Figure 2a as a function of b. The resulting sensitivities to frazil size variability suggest that pair-averaged F* values slightly (≈15%) underestimate F for b < 0.2. Broader distributions can be seen to favor overestimates by as much as 50% as b approaches 0.3: a value compatible with the upper limits of reported (McFarlane et al. (2017) [20]) distributions of frazil disk diameters. Such overestimates were comparable in magnitude and opposite in sign to the approximately −2 dB underestimates introduced [7,10] by using elastic sphere cross-sections to represent scattering by frazil disks of identical volume. The fortuitous near-cancellation of these two errors suggests that pair-averaged F* values are roughly representative of corresponding 3-frequency fractional volumes. The low residual errors attained using Faran (1951) [8] cross-sections in b = 0 3-frequency frazil characterizations [10] suggest that the uncertainties in F* introduced by possible additional systematic theoretical cross-section imperfections are unlikely to exceed a factor of two.

3.2. Evaluating the Characterization Algorihm Used in the Antarctic Frazil Study

The Kungl et al. (2020) [6] algorithm used to process the Frazer et al. (2020) [1] acoustic data evolved from an early theory of scattering by penetrable oblate spheroids (Burke (1968) [21]). Importantly, it replaced ice’s elastic rheology with a liquid alternative. The impacts of this difference are illustrated in Figure 2b by plots of normalized, exactly calculable, theoretical backscattering cross-sections as functions of k1ae for ice spheres characterized by, alternatively, elastic solid [8] and liquid (Anderson (1950) [22]) rheologies. These calculations utilized the indicated scattering target parameters, including the saltwater- and ice target-sound speeds employed by the Kungl et al. algorithm in MS acoustic data analyses. The prominent minimum in the elastic solid curve, confirmed in laboratory measurements [7], was introduced by and, roughly, proportional to the strengths of shear stresses, which are not present in liquid targets. This curve feature, consequently, had no analog in either the liquid ice curve or in the additional, third, curve, which depicts the corresponding Kungl et al. [6] relationship with and without conversion of spheroid diameters, D, into effective radii. The latter relationship was constructed from two slightly different power law dependences on k1ae separated by a narrow k1ae “transition” regime. As noted in the Kungl et al. work, these simplifications required additional steps to resolve indeterminacies introduced when matchings of theory and measured data utilized pairs of k1ae values for which corresponding theoretical cross-sections shared a common power law relationship.
Without access to data on rms errors in theory and data matching, tests of Kungl et al. characterization accuracies were carried out in Figure 2c for each of three ((3, 2), (4, 2), (4, 3)) different pairings of frequency channels. This 2-frequency testing was based upon 14.2 m SV data acquired by Frazer et al. [1] during the 12:06 to 19:59 11 November 2017 period. It utilized displays of differences in logarithmic cross-section (ΣBS = 10 log(σBS)) values, i.e., ∆ΣBS(j,i) ≡ 10 log(σBS(j)/σBS(i)), as, respectively, measured and theoretically calculated, for each (j,i) frequency pairing. (Given the above-noted equality between sV and N*σBS, measured logarithmic cross-section differences in 2-frequency calculations are numerically equal to corresponding differences in AB-measured SV parameters.) Figure 2c facilitates judging optimization prospects by establishing whether ∆ΣBS(j,i)meas values (arbitrarily positioned near minima in similarly colored ∆ΣBS(j,i)theo curves) are compatible with theoretical difference relationships for corresponding pairs of frequencies. The latter differences are calculated as functions of both ae and D, using the Kungl et al. (2020) cross-section results (curve C in Figure 2b). Vertical lines and circular markers, respectively, denote the ranges and mean values of pair-wise measured cross-section differences. All such differences can be seen to fall well below all portions of corresponding, pair-specific, Kungl et al. [6] theoretical difference curves. These shortfalls precluded the intersections of difference data with their counterpart theoretical relationships as required for successful matching of data and theory. This matching was essential for estimating the 2-frequency particle dimension parameters a* or D*, the rough equivalents of the mean ae or D parameters associated with 3- and 4-frequency frazil characterizations.
The absence of successful matches reflected qualitative differences between the krae dependences of Kungl et al. [6] cross-sections (curve C in Figure 2b) and the laboratory-verified [7] elastic solid sphere relationship [8] (curve A). Specifically, cross-sections represented by the steadily rising Kungl et al. curve, on average, tend to increase more rapidly as a function of frequency relative to the “flatter” cross-section dependence dictated by the more oscillatory Faran curve. Given laboratory evidence [7] for Faran compatibility with measured disk cross-sections, the larger Kungl et al. cross-section frequency sensitivities would have been expected to consistently elevate pairwise differences above and beyond the ranges of corresponding measured differences as depicted in Figure 2c. The consequent absence of intersections between measured and theoretically expected difference results ruled out possibilities for successful Kungl et al. 2-frequency frazil characterizations based upon the 11 November, 2017 SV data. Given the fundamental role of the 2-frequency approach in multifrequency optimizations, these results suggest that the 4-frequency characterizations reported by Frazer et al. [1] could not have achieved significant convergences and, hence, were spurious. This conclusion reflected either fundamental incompatibilities between the Kungl et al. cross-section relationship and the MS SV data and/or the presence of significant icing-related data contamination.

4. Results

4.1. Recalculated Postnoon Frazil Fractional Volumes

As expected from earlier algorithm verifications [7], similar testing of postnoon Frazer et al. (2020) [1] 2-frequency SV data against the alternative Faran (1951) [8] elastic sphere algorithm confirmed the feasibility of valid elastic solid ice sphere characterizations for each of the 6 possible acoustic frequency pairings. Consequently, fractional volume recalculations were carried out for three different (3,2), (4,2), and (4,3) pairings of 14.2 m SV(t) data constructed from measurements at 200, 455, and 769 kHz and additional 3-point mean data filtering. F*(t) values corresponding to averages over all three pairings are plotted at 33 min intervals along the solid line curve in Figure 3. Additional data markers, denoting maximum and minimum individual pair F*(t) estimates, are included to reflect estimate uncertainties. Limitations of manual calculations to three of the six available frequency pairs may have, according to the broken line, 3-frequency curve in Figure 2a, raised F*avg/F by an additional 10 to 15% for b values above 0.2. However, with allowances for systematic shape-related underestimates (Marko and Topham (2015) [7]), these results suggest that the F* estimates in Figure 3 are still representative of postnoon frazil content variations to within, roughly, a factor of two.
Inspections of initial portions of the recalculated postnoon plots show the dominance of F*(t) values within a relatively narrow “background” range below 2 × 10−7. Data gathered during the first, 10 November, daily period, being recorded immediately following instrument de-icing and redeployment, were most likely to be free of icing contamination. The following, 11 November, postnoon background stability period was briefly interrupted by an early peak in frazil content. All three postnoon periods showed background levels rising sharply at, roughly, 18:00, with F*(t) reaching maximum values of, approximately, 2 × 10−6 shortly before precipitous near-midnight descents to low background levels. Overall, the observed patterns of fluctuating, generally increasing, late afternoon and early evening frazil contents closely resembled the typical river frazil variability depicted in Figure 1d but with fractional volumes reduced by as much as 2 orders of magnitude relative to both river values and as represented in Frazer et al.’s (2020) [1] Figure 4e. Such low values and observed negative correlations between river frazil detectability and in situ icing presence justified our initial neglect of icing impacts during, at least, early and middle portions of postnoon intervals.

4.2. Implications for Daily Frazil Production

In assessing the significance of these results, it is useful to note that corresponding Frazer et al. [1] estimates were interpreted as evidence of “1–9 mm” daily ice accumulations prior to additional in situ growth after frazil attachments on sea ice undersurfaces. These estimates were made with references (McFarlane et al. (2014) [23]) to frazil rise velocities “up to” 9 mms−1 and, presumably, ignored contributions from unanalyzed prenoon intervals. Although suggested (Langhorne et al. (2015) [24]) to be compatible with daily 8–10 mm ice accretions inferred from atmospheric heat flux data, the significance of this conclusion was vitiated by the unquantified allowances made for post-deposition in situ growth on sea ice undersurfaces. Consequently, the quality of the reported frazil production estimates was totally dependent upon atmospheric heat loss estimates and the representativeness of postnoon frazil fractional volumes calculated with a flawed characterization algorithm [6].
The recalculated F* estimates in Figure 3 suggest typical daily postnoon frazil production was equivalent to 4 h presence of 1 × 10−6 fractional volumes. Using the 9 mms−1 upper end of previously utilized frazil rise rate estimates [23], such presences corresponded to daily frazil transports to the sea ice undersurface equivalent to a 0.14 mm thick layer of solid ice. Accretion at such levels would have been insignificant relative to both Frazer et al. [1] estimates and thermodynamic expectations. By default, this result is suggestive of the dominant importance of ice cover contributions from in situ growth and/or prenoon frazil production.
Evidence for the latter possibility is indirect but significant. It draws upon temporal coincidences between prenoon intervals and both icing-driven changes in instrument depth and peaks in flows of supercooled ice shelf water toward the measurement site. To be credible, this possibility requires that the low prenoon SV values in Figure 1c were, as suggested above, consequences of severe acoustic attenuation and multipath scattering endemic to measurements in the presence of in situ icing. Direct insights into these intervals were available, in principle, from effectively zero-range close-in signal returns (see Figure 7 in [10] and Figure 1d above). Unfortunately, this information was not collected in the Frazer et al. [1] studies which restricted acoustic data recording to returns from ice targets located at ranges greater than 2 m.
It was useful to make rough estimates of prenoon frazil contents compatible with physical understandings and postnoon F*(t) results. This effort assumed that the mid-postnoon SV(t) increases in Figure 3 persisted into the following prenoon intervals. Similar continuity in the 7 February, 2012 PR echogram (Figure 1d) was evident in early evening strengthening of frazil signal returns prior to the onset of observable close-in signal growth and gradual water column signal extinctions indicative of progressive sensor icing. This behavior supported expectations that observed late postnoon rises in MS frazil contents were more likely to continue rather than terminate upon approaching a succeeding prenoon period conspicuously associated with icing-driven destabilization and low measured SV values.
Given the impacts of icing on acoustic data collection, it was reasonable to expect that prenoon frazil concentrations considerably exceeded the highest, 2 × 10−6, postnoon F* values plotted in Figure 3. This assumption was also consistent with the timings of maximal coolings inferred from supercooled ice shelf water flows and peak radiative heat losses through the ice cover. Speculative estimates of corresponding frazil content changes were generated by extending the persistence of typical 0.5 × 10−6 h−1 average rates of F*(t) increase during 18:00–22:00 NZST postnoon periods to 06:00 NZST on the following day. This assumption would have raised peak F* values to 6 × 10−6 midway through the following prenoon interval, representing 2.5 mm integrated daily contributions of solid ice to the sea ice undersurface, or about 25% of thermodynamic expectations. Prenoon frazil production in full accord with the Langhorne et al. [24] heat flux loss estimates would have required fractional volumes approaching the 4 × 10−5 levels typical of early prenoon river periods [10].
Definitively quantifying prenoon frazil production requires continuous icing-free access to quantitatively interpretable SV data. In the absence of such capabilities, MS sea ice undersurface ice accretion in the 2017 measurements, currently, can only be validly characterized as unspecified mixtures of in situ growth and water column frazil deposition which occurs shortly prior to and during prenoon time periods.

5. Summary and Discussion

5.1. Summary

The Frazer et al. (2020) [1] estimates of frazil production under Antarctic sea ice were undermined by the absence of precautions against in situ sensor icing. This limited measurements of frazil content to postnoon intervals (starting at 12:00 local time), which, on the basis of variations in atmospheric heat exchanges and influxes of supercooled ice shelf water, might be expected to coincide with minimums in both suspended frazil presence and sensor icing growth. The significance of this restriction was obscured by use of an unvalidated, rheologically incorrect, frazil characterization algorithm (Kungl et al., 2020) [6]. The present work utilized a simplified and validated 2-frequency algorithm to both demonstrate absences of convergence in the Frazer et al. characterizations and offer credible re-estimates of frazil fractional volumes for previously analyzed time periods. Unfortunately, the latter periods coincided with the least productive, postnoon portions of daily ice growth cycles. The low frazil presences characteristic of these periods discouraged acoustic blockages by anchor ice growth: facilitating unambiguous frazil fractional volume estimates during mid-afternoon through early evening hours. Peak fractional volumes at 14.2 m depths during these periods reached 2 × 10−6. Daily contributions to ice cover thickness, less than 0.2 mm, were unlikely to have had major impacts on ice cover stability.
Instead, changes in instrument depth indicative of intensive icings and coincident disappearances of acoustic signals during 0:00–12:00 local time periods suggested that these prenoon intervals, excluded from Frazer et al.’s (2020) [1] characterizations, were likely hosts for the bulk of MS frazil production. Specifically, speculative extrapolations of postnoon SV results into such intervals were indicative of daily accretions of frazil at sea ice undersurfaces amounting to, at least, 25% of thermodynamically based expectations. As well, despite differences in location and, possibly, crystallization mechanisms, frazil production both as estimated in rivers and measured and inferred near an Antarctic ice edge appeared to be confined to evening through mid-morning periods normally associated with peak radiative heat losses.

5.2. Discussion

Apart from a reliance upon an inappropriate frazil characterization algorithm, the problems encountered by Frazer et al. were typical of other past efforts, both in rivers [4,25,26] and in polar and subpolar marine regions [27,28,29], to quantitatively document frazil ice in the presence of in situ ice growth. Marine measurements in the Antarctic have been much more limited than those carried out in the Northern Hemisphere, consisting of only the Frazer et al. [1] studies and the enhanced satellite observations reported by Nakata et al. (2021) [30]. All under-ice acoustic data sets obtained with instruments exposed to frazil ice have encountered the reality that in situ growth rates tend to increase synchronously with rising frazil contents. Consequent failures to obtain detailed frazil characterizations comparable to those associated with key PR studies reflected recognition of AB processing algorithm complexities and the additional efforts and costs required to avoid data contamination by instrument icing. Clearly, use of adjacent warm water flows and retention of backscattering data acquired by acoustic sensors immediately after pulse emissions have to be important elements of effective frazil measurement programs. These additions, respectively, maintain and confirm absences of icing-related contamination of the acoustic data which are the primary inputs to either the user-friendly 2-frequency characterization algorithm or validated alternatives. Additional field program capabilities useful for tracking in situ growth trends could be made available by accommodating real time or recorded retrospective “weighings” of instrument ice accumulation. Obtaining such data to quantify totalities of ice mass adhering to deployed instruments and any attached ballasts could utilize one or more strain gauges incorporated into support ropes. Access to such data could be a first step toward more enlightened understandings of the impacts of in situ processes on frazil variability. The availability of this information would have greatly simplified interpretation of the Frazer et al. SV data sets. Other program design options could include deployments of upward-looking instruments below supercooled ocean layers or use of downward-looking configurations with instruments positioned just below the sea ice undersurface. Primary objectives of detailed frazil characterization studies would include collection of field data as inputs to appropriate models and for calibrations designed to improve the accuracies and information contents of characterization algorithm outputs.
The value of AB measurements has, to date, been most apparent in river studies [2,3,4,5,10,25,26] where site-to-site differences in environmental parameters could both yield data relevant to other river and non-river applications and clarify frazil relationships to other ice forms. Marine frazil ice observations have been previously made in the Arctic Ocean using both satellite data and upward-looking sonar instruments [27,28,29]. The (ULS) instruments used in the latter studies were restricted to measurements made at a single acoustic frequency, greatly limiting potential frazil concentration estimates. Observations of frazil ice in the Antarctic region of the Southern Ocean have been much more restricted. The relevance of the present work to Antarctic and general polar issues is closely tied to frazil’s potentially crucial role in sea ice formation (Roach et al., 2025) [31], which requires realistic representation in coupled climate models (Garuba et al., 2020) [32]). In particular, better field-verified estimates of frazil ice development would support improvements of Antarctic portions of global coupled models (Bailey et al. (2020) [33]), in which coastal frazil ice formation is a significant environmental feature. Possibilities that most coupled climate models may be overestimating rates of new sea ice formation (Mackie et al., (2020) [34]) create a need for field verifications capable of calibrating alternative model representations. The access to frazil ice concentration data offered by multi-frequency acoustic backscattering techniques could also improve Arctic Ocean sea ice models by allowing better characterizations of open water features such as leads and polynyas.

Author Contributions

Conceptualization, J.R.M.; methodology, J.R.M. and D.R.T.; formal analysis, J.R.M. and D.R.T.; data curation, J.R.M., D.R.T. and D.B.F.; writing, J.R.M.; writing—review and editing, J.R.M., D.R.T. and D.B.F.; visualization, J.R.M.; supervision, J.R.M. and D.B.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data from the application example described in this study are available for downloading at the listed Robinson et al. (2020) [9] reference at https://doi.pangaea.de/10.1594/PANGAEA.923761 accessed on 27 September 2025.

Conflicts of Interest

The authors are employees at ASL Environmental Sciences Inc. The authors declare no conflicts of interest.

References

  1. Frazer, E.K.; Langhorne, P.J.; Leonard, G.H.; Robinson, N.J.; Schumayer, D. Observations of the size of frazil ice in an ice shelf waterplume. Geophys. Res. Lett. 2020, 47, e2020GL090498. [Google Scholar] [CrossRef]
  2. Marko, J.R.; Jasek, M. Sonar detection and measurements of ice in a freezing river I: Methods and data characteristics. Cold Reg. Sci. Technol. 2010, 63, 121–134. [Google Scholar] [CrossRef]
  3. Marko, J.R.; Jasek, M. Sonar detection and measurements of ice in a freezing river II: Observations and results on frazil ice. Cold Reg. Sci. Technol. 2010, 63, 135–153. [Google Scholar] [CrossRef]
  4. Ghobrial, T.R.; Loewen, M.R.; Hicks, F.E. Characterizing suspended frazil ice in rivers using upward looking sonars. Cold Reg. Sci Technol. 2012, 86, 113–126. [Google Scholar] [CrossRef]
  5. Marko, J.R.; Jasek, M.; Topham, D.R. (Multifrequency analyses of 2011–2012 Peace River SWIPS frazil backscattering data. Cold Reg. Sci. Technol. 2015, 110, 102–119. [Google Scholar] [CrossRef]
  6. Kungl, A.F.; Schumayer, D.; Frazer, E.K.; Langhorne, P.J.; Leonard, G.H. (An oblate spheroid model for multi-frequency acoustic back-scattering of frazil ice. Cold Reg. Sci. Technol. 2020, 177, 103122. [Google Scholar] [CrossRef]
  7. Marko, J.R.; Topham, D.R. Laboratory measurements of acoustic backscattering from polystyrene pseudo- ice particles as a basis for quantitative frazil characterization. Cold Reg. Sci. Technol. 2015, 112, 66–86. [Google Scholar] [CrossRef]
  8. Faran, J.J., Jr. Sound scattering by solid cylinders and spheres. J. Acoust. Soc. 1951, 23, 405–418. [Google Scholar] [CrossRef]
  9. Robinson, N.J.; Leonard, G.; Frazer, E.; Langhorne, P.; Grant, B.; Stewart, C.; De Joux, P. Temperature, salinity and acoustic backscatter observations and tidal model output in McMurdo Sound, Antarctica in 2016 and 2017—Links to original files [Dataset]. PANGAEA 2020. Available online: https://doi.pangaea.de/10.1594/PANGAEA.923761 (accessed on 27 September 2025).
  10. Marko, J.R.; Topham, D.R. Analyses of Peace River shallow water ice profiling sonar data and their implications for the roles played by frazil ice and in situ ice growth in freezing rivers. Cryosphere 2021, 15, 2473–2489. [Google Scholar] [CrossRef]
  11. Hay, A.E.; Sheng, J. Vertical profiles of suspended sand concentrations and size from multifrequency acoustic backscatter. J. Geophys. Res. 1992, 97, 1566–1567. [Google Scholar] [CrossRef]
  12. Stanton, T.K.; Wiebe, P.H.; Chu, D. Differences between sound scattering by weakly scattering spheres and finite-length cylinders with applications to sound scattering by zooplankton. J. Acoust. Soc. Am. 1998, 103, 254–264. [Google Scholar] [CrossRef]
  13. Piotrovich, V.V. Formation of Depth-Ice; Translated from Priroda; Hope, E.R., Translator; Department of National Defense: Ottawa, ON, Canada, 1956; Volume 9, pp. 1–4. Available online: https://scholar.google.com/scholar_lookup?hl=en&volume=9&publication_year=1956&journal=Priroda&issue=94%E2%80%9395&author=V.+V.+Piotrovich&author=E.+R.+Hope&title=Formation+of+depth+ice (accessed on 27 September 2025).
  14. Lewis, E.L.; Perkin, R.G. The Winter Oceanography of McMurdo Sound in Antarctica. In Oceanography of the Antarctic Continental Shelf; Jacobs, S.S., Translator; American Geophysical Union: Washington, DC, USA, 1985; pp. 145–165. Available online: https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/AR043p0145 (accessed on 27 September 2025).
  15. Lewis, E.L.; Perkin, R.G. Ice pumps and their rates. J. Geophys. Res. 1986, 91, 11756–11762. [Google Scholar] [CrossRef]
  16. Smedsrud, L.H.; Jenkins, A. Frazil ice formation in an ice shelf water plume. J. Geophys. Res. 2004, 109, C03025. [Google Scholar] [CrossRef]
  17. Hughes, K.G.; Langhorne, P.J.; Leonard, G.H.; Stevens, C.L. Extension of an Ice Shelf Water plume model beneath sea ice with application in McMurdo Sound, Antarctica. J. Geophys. Res. Oceans 2014, 119, 8662–8687. [Google Scholar] [CrossRef]
  18. Ghobrial, T.R.; Loewen, M.R. Continuous in situ measurements of anchor ice formation, growth, and release. Cryosphere 2021, 15, 49–67. [Google Scholar] [CrossRef]
  19. Ashton, G.D. Frazil ice. In Theory of Multiphase Flow; Academic Press: Cambridge, MA, USA, 1986; pp. 271–289. [Google Scholar]
  20. McFarlane, V.; Loewen, M.; Hicks, F. Measurements of the size distributions of frazil ice particles in three Alberta rivers. Cold Reg. Sci. Technol. 2017, 142, 100–117. [Google Scholar] [CrossRef]
  21. Burke, J.E. Scattering by penetrable spheroids. J. Acoust. Soc. 1968, 43, 871–875. [Google Scholar] [CrossRef]
  22. Anderson, V.C. Sound scattering from a fluid sphere. J. Acoust. Soc. 1950, 22, 426–431. [Google Scholar] [CrossRef]
  23. McFarlane, V.; Loewen, M.; Hicks, F. Laboratory measurements of the rise velocity of frazil ice particles. Cold Reg. Sci. Technol 2014, 106–107, 120–130. [Google Scholar] [CrossRef]
  24. Langhorne, P.J.; Hughes, K.G.; Gough, A.J.; Smith, I.J.; Williams, M.J.M.; Robinson, N.J.; Haskell, T.G. Observed platelet ice distributions in Antarctic sea ice: An index for ocean-ice shelf heat flux. Geophys. Res. Lett. 2015, 42, 5442–5451. [Google Scholar] [CrossRef]
  25. Richard, M.; Morse, B.; Daly, S.F.; Emond, J. Quantifying suspended frazil ice using multi-frequency underwater acoustic devices. River Res. Appl. 2011, 27, 1106–1117. [Google Scholar] [CrossRef]
  26. Ghobrial, T.R.; Loewen, M.R.; Hicks, F.E. Continuous monitoring of river surface ice during freeze-up using upward looking sonar. Cold Reg. Sci. Technol. 2013, 86, 69–85. [Google Scholar] [CrossRef]
  27. Drucker, R.S.; Martin, S.; Moritz, R.E. Ice thickness and frazil ice behavior in the St. Lawrence Island Polynya as observed with satellite, Upward Looking Sonar and salinity/temperature moorings. J. Geophys. Res. 2003, 108, 18–1–18–11. [Google Scholar] [CrossRef]
  28. Ito, M.; Ohshima, K.I.; Fukamachi, Y.; Simizu, D.; Iwamoto, K.; Matsumura, Y.; Eicken, H. Observations of supercooled water and frazil ice formation in an Arctic coastal polynya from moorings and satellite imagery. Ann. Glaciol. 2015, 56, 307–314. [Google Scholar] [CrossRef]
  29. Ito, M.; Fukamachi, Y.; Ohshima, K.I.; Shirasawa, K. Observational evidence of supercooling and frazil ice formation throughout the water column in a coastal polynya in the Sea of Okhotsk. Cont. Shelf Res. 2020, 196, 104072. [Google Scholar] [CrossRef]
  30. Nakata, K.; Ohshima, K.I.; Nihashi, S. Mapping of active frazil for Antarctic coastal polynyas, with an estimation of sea-ice production. Geophys. Res. Lett. 2021, 48, e2020GL091353. [Google Scholar] [CrossRef]
  31. Roach, L.A.; Smith, M.M.; Herman, A.; Ringeisen, D. Physics of the Seasonal Sea Ice Zone. Annu. Rev. Mar. Sci. 2025, 17, 355–379. Available online: https://www.annualreviews.org/content/journals/10.1146/annurev-marine-121422-015323 (accessed on 11 August 2025).
  32. Garuba, O.A.; Singh, H.A.; Hunke, E.; Rasch, P.J. Disentangling the coupled atmosphere-ocean-ice interactions driving Arctic sea ice response to CO2 increases. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001902. [Google Scholar] [CrossRef]
  33. Bailey, D.A.; Holland, M.M.; DuVivier, A.K.; Hunke, E.C.; Turner, A.K. Impact of a new sea ice thermodynamic formulation in the CESM2 sea ice component. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002154. [Google Scholar] [CrossRef]
  34. Mackie, S.; Langhorne, P.J.; Heorton, H.D.B.S.; Smith, I.J.; Feltham, D.L.; Schroeder, D. Sea ice formation in a coupled climate model including grease ice. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002103. [Google Scholar] [CrossRef]
Glacies 02 00011 g001
Figure 1. Data and additional information relevant to reanalyses. (a) Positions of the 2016 and 2017 MS study sites. (b) Mid-water column PR- and Frazer et al. (2020) [1] (FLLRS)15 m depth-backscattering coefficient, SV, values vs. frequency at indicated times and dates. (c) 10–14 November NZST, 2017 14.2 m SV(t) data plotted for 4 acoustic frequencies with indicated offsets along with changes in instrument depth vs. time during this interval and a preceding 5–9 November 2017 period. The times associated with the 5–9 November depth change data were incremented by 5 days as discussed in the text to facilitate comparisons with 10–14 November depth results. Background shading and red horizontal lines denote, respectively, prenoon periods and unanalyzed data intervals. (d) Echogram display of 774 kHz backscattered signal voltages (in digital counts) vs. range (m) over a 32 h period spanning a 7 February 2012 PR frazil event.
Figure 1. Data and additional information relevant to reanalyses. (a) Positions of the 2016 and 2017 MS study sites. (b) Mid-water column PR- and Frazer et al. (2020) [1] (FLLRS)15 m depth-backscattering coefficient, SV, values vs. frequency at indicated times and dates. (c) 10–14 November NZST, 2017 14.2 m SV(t) data plotted for 4 acoustic frequencies with indicated offsets along with changes in instrument depth vs. time during this interval and a preceding 5–9 November 2017 period. The times associated with the 5–9 November depth change data were incremented by 5 days as discussed in the text to facilitate comparisons with 10–14 November depth results. Background shading and red horizontal lines denote, respectively, prenoon periods and unanalyzed data intervals. (d) Echogram display of 774 kHz backscattered signal voltages (in digital counts) vs. range (m) over a 32 h period spanning a 7 February 2012 PR frazil event.
Glacies 02 00011 g001
Glacies 02 00011 g002
Figure 2. Results relevant to Kungl et al. (2020) [6] and Faran, 1951 [8] algorithm-based comparisons and interpretations of Frazer et al. (2020) [1] data. (a) Plots of F*avg/F vs. b for an exactly characterized frazil population with F*avg representing 2-frequency average F* estimates using data from 6 and 3 different pairs. (b) Normalized backscattering cross-sections vs. k1ae for elastic solid and liquid ice spheres in saltwater. A third curve depicts the Kungl et al. (2020) [6] relationship employed in Frazer et al. (2020) [1]. (c) Comparisons of ranges (vertical lines) and mean values (circular markers) of pairwise differences in measured logarithmic cross-sections during a 12:06 to 19:59 11 November 2017 interval are made relative to expectations based upon the Kungl et al. relationship (curve C in (b)). Curve labelling denotes specific frequency channel pairings (j,i) while curve colors facilitate evaluations of compatibility with corresponding measurement information. Curve variations are referenced to both effective radius, ae, and disk/spheroid diameter, D.
Figure 2. Results relevant to Kungl et al. (2020) [6] and Faran, 1951 [8] algorithm-based comparisons and interpretations of Frazer et al. (2020) [1] data. (a) Plots of F*avg/F vs. b for an exactly characterized frazil population with F*avg representing 2-frequency average F* estimates using data from 6 and 3 different pairs. (b) Normalized backscattering cross-sections vs. k1ae for elastic solid and liquid ice spheres in saltwater. A third curve depicts the Kungl et al. (2020) [6] relationship employed in Frazer et al. (2020) [1]. (c) Comparisons of ranges (vertical lines) and mean values (circular markers) of pairwise differences in measured logarithmic cross-sections during a 12:06 to 19:59 11 November 2017 interval are made relative to expectations based upon the Kungl et al. relationship (curve C in (b)). Curve labelling denotes specific frequency channel pairings (j,i) while curve colors facilitate evaluations of compatibility with corresponding measurement information. Curve variations are referenced to both effective radius, ae, and disk/spheroid diameter, D.
Glacies 02 00011 g002
Glacies 02 00011 g003
Figure 3. Plots of means, maxima and minima corresponding to postnoon 10–13 November 2017 2-frequency F* estimates extracted from different, (3, 2), (4, 2), and 4, 3), frequency pairings using an elastic sphere-based algorithm (Faran, (1951) [8]).
Figure 3. Plots of means, maxima and minima corresponding to postnoon 10–13 November 2017 2-frequency F* estimates extracted from different, (3, 2), (4, 2), and 4, 3), frequency pairings using an elastic sphere-based algorithm (Faran, (1951) [8]).
Glacies 02 00011 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Marko, J.R.; Topham, D.R.; Fissel, D.B. Reanalyzing and Reinterpreting a Unique Set of Antarctic Acoustic Frazil Data Using River Frazil Results and Self-Validating 2-Frequency Analyses. Glacies 2025, 2, 11. https://doi.org/10.3390/glacies2040011

AMA Style

Marko JR, Topham DR, Fissel DB. Reanalyzing and Reinterpreting a Unique Set of Antarctic Acoustic Frazil Data Using River Frazil Results and Self-Validating 2-Frequency Analyses. Glacies. 2025; 2(4):11. https://doi.org/10.3390/glacies2040011

Chicago/Turabian Style

Marko, John R., David R. Topham, and David B. Fissel. 2025. "Reanalyzing and Reinterpreting a Unique Set of Antarctic Acoustic Frazil Data Using River Frazil Results and Self-Validating 2-Frequency Analyses" Glacies 2, no. 4: 11. https://doi.org/10.3390/glacies2040011

APA Style

Marko, J. R., Topham, D. R., & Fissel, D. B. (2025). Reanalyzing and Reinterpreting a Unique Set of Antarctic Acoustic Frazil Data Using River Frazil Results and Self-Validating 2-Frequency Analyses. Glacies, 2(4), 11. https://doi.org/10.3390/glacies2040011

Article Metrics

Back to TopTop