Correlation Methodologies between Land Use and Greenhouse Gas emissions: The Case of Pavia Province (Italy)
Abstract
1. Introduction
Study Area: Pavia Province
2. Materials and Methods
2.1. Environmental Indicator
- CO2eq.: CO2 equivalent emissions in kt/year;
- GWPi: “Global Warming Potential”, coefficient IPCC 2014 equal to 1, 0.025, and 0.298, respectively, for CO2, CH4, and N2O. INEMAR considers a GWP100 (100 years);
- Ei: CO2 emissions (in kt/year), CH4, and N2O etc.
2.2. Socio-Demographic Indicators
- Population: Population growth can significantly impact land use. Increasing population can drive up demand for housing, infrastructure, and industrial and commercial areas, leading to urbanization and land consumption.
- Population density: A dense population can exert pressure on agriculture and natural resources, prompting changes in land use such as converting agricultural land into residential or industrial areas.
- GDP (Gross Domestic Product): The GDP of a region can indicate the level of economic and industrial development, thereby affecting land use. For instance, a high GDP may correlate with increased urbanization, infrastructure expansion, and industrialization, resulting in changes like loss of natural habitats or conversion of rural areas into industrial or urban zones.
2.3. Geographic and Territorial Indicators
- Territorial area (sqm);
- Residential area (sqm): including residential buildings and appliances;
- Gross floor area (sqm);
- Settlements area (sqm): industrial, commercial, and craft settlements, farmhouses, quarries, landfills, cemeteries, campsites, technological system, hospital settlements, degraded or obliterated areas and amusement parks;
- Road lines (m): including road networks;
- Arable land (sqm): including rice fields and agriculture;
- Vegetated land (sqm): including woods, meadows, grasslands, and groves.
2.4. Analytic Correlation Analysis Output
- Nonparametric/rank: Spearman’s rank correlation coefficient;
- Parametric/linear correlation: Pearson’s correlation coefficient.
2.4.1. Spearman’s Rank Correlation Coefficient
- : Spearman’s coefficient;
- di: rank differences;
- n: number of data.
2.4.2. Pearson’ s Correlation Coefficient
- : Pearson’s coefficient;
- : number of data;
- : first variable;
- mean of the first variable;
- : second variable;
- mean of the second variable.
- r = 1 is total positive correlation;
- r = −1 is total negative correlation;
- 0.5 < r < 1 means that the two values are completely or perfectly positively correlated, that is, one variable’s value increases as the other variable’s value increases;
- −1 < r < −0.5 means that the two values are perfectly negatively correlated, that is, one variable’s value decreases as the other variable’s value increases;
- r = 0 means that there is no relationship between two variables and indicates that the two variables are not linearly correlated.
2.5. Spatial Correlation Analysis Output
2.5.1. Moran’s Spatial Autocorrelation Index
- is the number of spatial units (in our case, municipalities);
- and are the values of the variables of interest (e.g., the number of inhabitants or CO2 emissions) for spatial units i and j;
- is the mean of the values of the variables across all spatial units;
- is the weight associated with the pair of spatial units i and j. These weights represent the spatial connection between the units and can be defined based on geographical proximity.
2.5.2. Kernel Density
- : The intensity of the point distribution, measured at point L;
- : i-th event;
- : kernel function;
- : bandwidth defined as the radius of the circle generated by the intersection of the surface within which the density of the point will be evaluated, with the plane containing the study region R.
3. Results
3.1. Analytic Correlation
3.1.1. Spearman Rank Correlation Coefficient
3.1.2. Pearson Correlation Coefficient and Bivariate Map
- y: dependent variable;
- x: independent variable;
- : the coefficient representing the intercept or the amplitude;
- : exponent determining the rate of growth or decay;
- e: the base of the natural logarithm.
3.1.3. Multiple Regression Analysis
- intercept;
- inclination of y with respect to variable holding constant variables ,… ;
- : inclination of y with respect to variable holding constant variables , … .
3.2. Spatial Autocorrelation
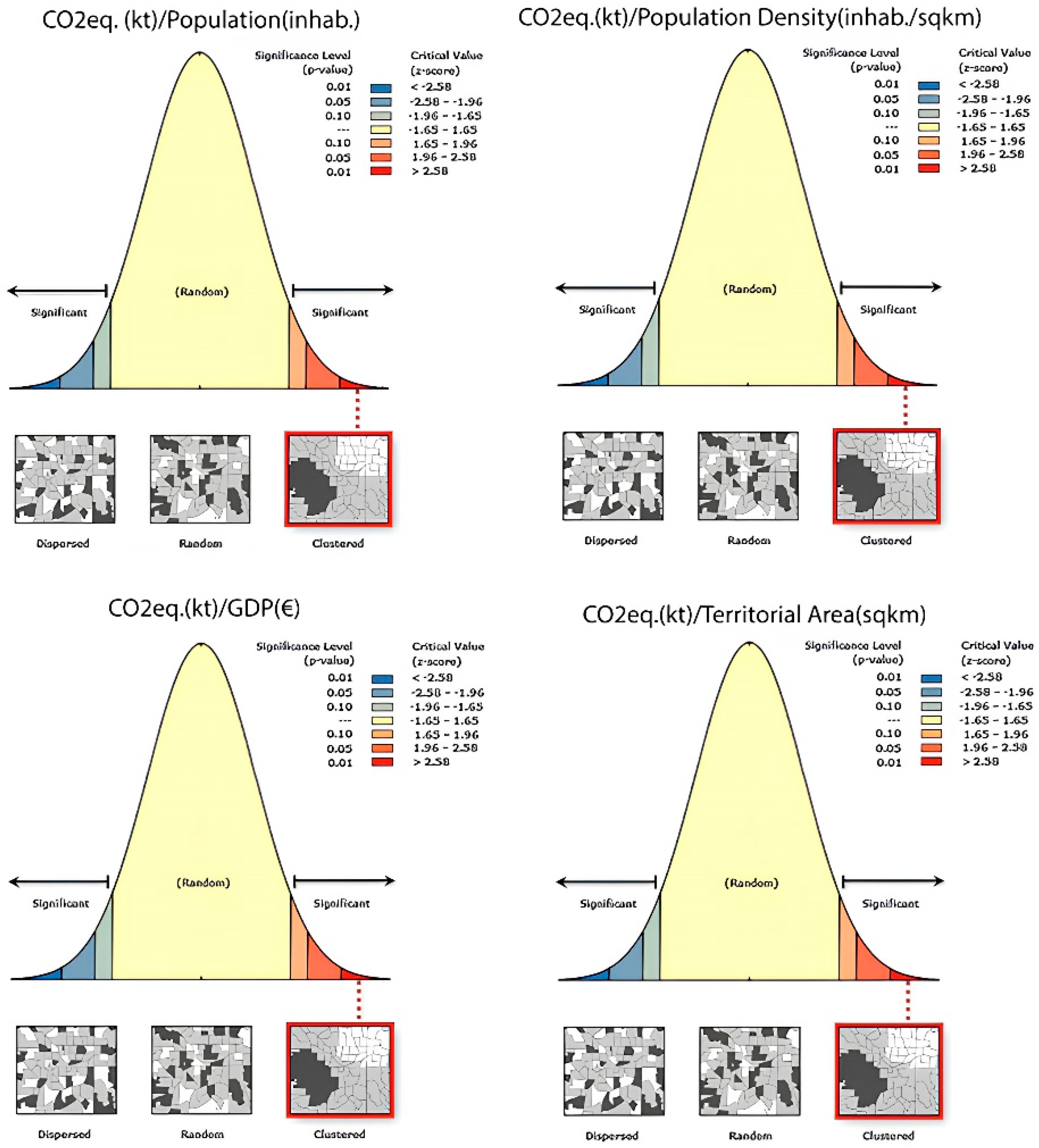
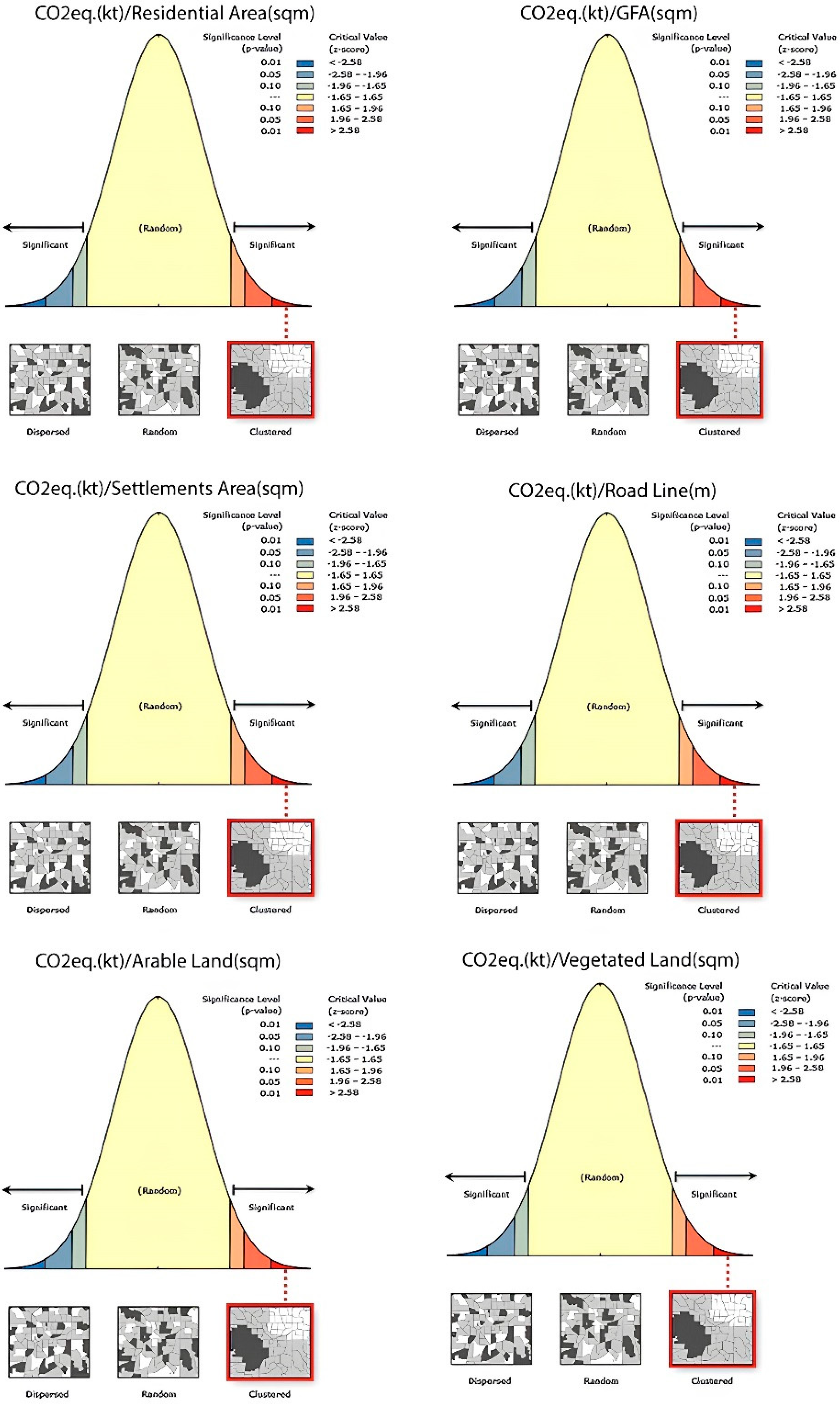
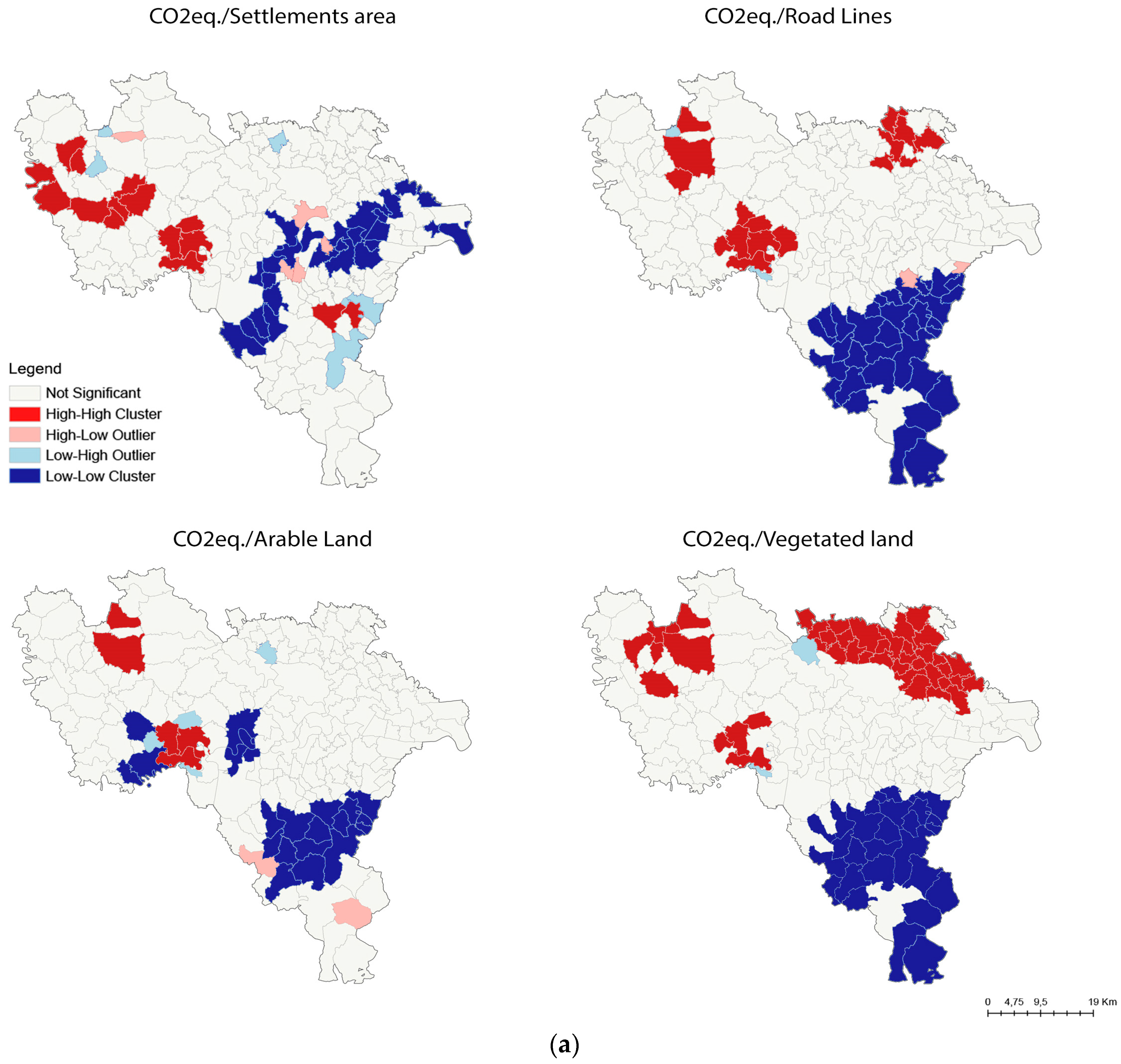
3.2.1. Moran’s I and Cluster Map
- Not Significant: There is no statistical evidence of significant spatial clustering in the data. In other words, there are no obvious spatial patterns that emerge from the analysis.
- High–High Cluster: A cluster of areas with a high CO2 equivalent value and high values of other demographic or territorial indicators. This means that the areas in this cluster have relatively high values for both variables.
- High–Low Outliers: Areas with high CO2 equivalent values but low values of other demographic or territorial indicators.
- Low–High Outliers: Areas with low CO2 equivalent values but high values of other demographic or territorial indicators.
- Low–Low Cluster: A cluster of areas with low CO2 equivalent values and low values of other demographic or territorial indicators. This means that the areas in this cluster have relatively low values for both variables.
3.2.2. Kernel Density
4. Discussion
5. Conclusions
- To forecast emissions based on planning choices, which may concern the distribution of different urban functions within a municipality or the entire province under study.
- To identify areas that require further investigation, especially those elements that represent uniqueness and particular elements (L-L and H-H). This helps to highlight elements of punctual criticality that necessitate further examination.
- With these simplified formulas, it is possible to upscale to the whole national/regional territory. This allows for a first verification to validate the predicted results using the formulas in Table 4 on page 9 and to see if the study can be generalized to other territories outside the Italian context and then to other contexts around the world.
- The simplification of some algorithms that are otherwise very complex and require years of work is important for understanding the order of magnitude of the phenomena observed, particularly the emissions of greenhouse gases. These emissions are important worldwide mainly for macro values and not so much in specific detail, which is measured very precisely by INEMAR, which is the scientific data.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- D’Odorico, P.; Davis, K.F.; Rosa, L.; Carr, J.A.; Chiarelli, D.; Dell’Angelo, J.; Rulli, M.C. The global food-energy-water nexus. Rev. Geophys. 2018, 56, 456–531. [Google Scholar]
- Beall, J.; Fox, S. Cities and Development, 1st ed.; Routledge: London, UK, 2009. [Google Scholar]
- Sathaye, J.; Shukla, P.R.; Ravindranath, N.H. Climate change, sustainable development and India: Global and national concerns. Curr. Sci. 2006, 90, 314–325. [Google Scholar]
- Young, O.R. The Institutional Dimensions of Environmental Change: Fit, Interplay, and Scale; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Treweek, J. Ecological impact assessment. Impact Assess. 1995, 13, 289–315. [Google Scholar] [CrossRef]
- Babiy, A.P.; Kharytonov, M.M.; Gritsan, N.P. Connection between emissions and concentrations of atmospheric pollutants. In Air Pollution Processes in Regional Scale; Springer: Dordrecht, The Netherlands, 2003; pp. 11–19. [Google Scholar]
- Janssen, S.; Dumont, G.; Fierens, F.; Mensink, C. Spatial interpolation of air pollution measurements using CORINE land cover data. Atmos. Environ. 2008, 42, 4884–4903. [Google Scholar] [CrossRef]
- Xu, G.; Jiao, L.; Zhao, S.; Yuan, M.; Li, X.; Han, Y.; Zhang, B.; Dong, T. Examining the impacts of land use on air quality from a spatio-temporal perspective in Wuhan, China. Atmosphere 2016, 7, 62. [Google Scholar] [CrossRef]
- Zheng, S.; Zhou, X.; Singh, R.P.; Wu, Y.; Ye, Y.; Wu, C. The spatiotemporal distribution of air pollutants and their relationship with land-use patterns in Hangzhou city, China. Atmosphere 2017, 8, 110. [Google Scholar] [CrossRef]
- Bashir, M.F.; Jiang, B.; Komal, B.; Bashir, M.A.; Farooq, T.H.; Iqbal, N.; Bashir, M. Correlation between environmental pollution indicators and COVID-19 pandemic: A brief study in Californian context. Environ. Res. 2020, 187, 109652. [Google Scholar] [CrossRef]
- Zimmerman, N.; Li, H.Z.; Ellis, A.; Hauryliuk, A.; Robinson, E.S.; Gu, P.; Shah, R.U.; Ye, G.Q.; Snell, L.; Subramanian, R.; et al. Improving correlations between land use and air pollutant concentrations using wavelet analysis: Insights from a low-cost sensor network. Aerosol Air Qual. Res. 2020, 20, 314–328. [Google Scholar] [CrossRef]
- Hong, J.; Shen, Q. Residential density and transportation emissions: Examining the connection by addressing spatial autocorrelation and self-selection. Transp. Res. Part D Transp. Environ. 2013, 22, 75–79. [Google Scholar] [CrossRef]
- Heres-Del-Valle, D.; Niemeier, D. CO2 emissions: Are land-use changes enough for California to reduce VMT? Specification of a two-part model with instrumental variables. Transp. Res. Part B Methodol. 2011, 45, 150–161. [Google Scholar] [CrossRef]
- Wen, Y.; Wu, R.; Zhou, Z.; Zhang, S.; Yang, S.; Wallington, T.J.; Shen, W.; Tan, Q.; Deng, Y.; Wu, Y. A data-driven method of traffic emissions mapping with land use random forest models. Appl. Energy 2022, 305, 117916. [Google Scholar] [CrossRef]
- Feliciano, D.; Slee, B.; Hunter, C.; Smith, P. Estimating the contribution of rural land uses to greenhouse gas emissions: A case study of North East Scotland. Environ. Sci. Policy 2013, 25, 36–49. [Google Scholar] [CrossRef]
- Pezzagno, M.; Richiedei, A.; Tira, M. Spatial planning policy for sustainability: Analysis connecting land use and GHG emission in rural areas. Sustainability 2020, 12, 947. [Google Scholar] [CrossRef]
- De Lotto, R. Elementi della Città Flessibile; Maggioli Politecnica: Santarcangelo di Romagna, Italy, 2022. [Google Scholar]
- De Lotto, R. Flexibility in urban planning: Rules, opportunities and limits. In Cities and Communities across Europe: Governance Design for a Sustainable Future; Suárez, J.J.R.A., Ed.; ARANZADI/CIVITAS: Pamplona, Spain, 2023; pp. 93–112. [Google Scholar]
- Maranzano, P. Air quality in Lombardy, Italy: An overview of the environmental monitoring system of ARPA Lombardia. Earth 2022, 3, 172–203. [Google Scholar] [CrossRef]
- Caserini, S.; Giani, P.; Cacciamani, C.; Ozgen, S.; Lonati, G. Influence of climate change on the frequency of daytime temperature inversions and stagnation events in the Po Valley: Historical trend and future projections. Atmos. Res. 2017, 184, 15–23. [Google Scholar] [CrossRef]
- ISTAT (National Institute of Statistics). Available online: https://www.istat.it/en/ (accessed on 2 February 2024).
- Emission factors, I.N.E.M.A.R. Available online: https://www.inemar.eu/xwiki/bin/view/InemarDatiWeb/I+fattori+di+emissione (accessed on 2 February 2024).
- INEMAR (INventory of Atmospheric Emissions)—ARPA Lombardia. Available online: https://www.inemar.eu/xwiki/bin/view/Inemar/ (accessed on 2 February 2024).
- Wiggering, H.; Dalchow, C.; Glemnitz, M.; Helming, K.; Müller, K.; Schultz, A.; Zander, P. Indicators for multifunctional land use—Linking socio-economic requirements with landscape potentials. Ecol. Indic. 2006, 6, 238–249. [Google Scholar] [CrossRef]
- Esengulova, N.; Balena, P.; De Lucia, C.; Lopolito, A.; Pazienza, P. Key Drivers of Land Use Changes in the Rural Area of Gargano (South Italy) and Their Implications for the Local Sustainable Development. Land 2024, 13, 166. [Google Scholar] [CrossRef]
- Geoportale Lombardy Region. Available online: https://www.geoportale.regione.lombardia.it/download (accessed on 10 September 2023).
- Gogtay, N.J.; Thatte, U.M. Principles of correlation analysis. J. Assoc. Physicians India 2017, 65, 78–81. [Google Scholar] [PubMed]
- Senthilnathan, S. Usefulness of Correlation Analysis; 2019. SSRN 3416918. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3416918 (accessed on 2 February 2024).
- Myers, L.; Sirois, M.J. Spearman correlation coefficients, differences between. In Encyclopedia of Statistical Sciences; Wiley: Hoboken, NJ, USA, 2004; Volume 12. [Google Scholar]
- De Winter, J.C.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data. Psychol. Methods 2016, 21, 273. [Google Scholar] [CrossRef]
- Bolboaca, S.D.; Jäntschi, L. Pearson versus Spearman, Kendall’s tau correlation analysis on structure-activity relationships of biologic active compounds. Leonardo J. Sci. 2006, 5, 179–200. [Google Scholar]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J. Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Thelwall, M. Interpreting correlations between citation counts and other indicators. Scientometrics 2016, 108, 337–347. [Google Scholar] [CrossRef]
- Anselin, L.; Syabri, I.; Kho, Y. GeoDa: An introduction to spatial data analysis. In Handbook of Applied Spatial Analysis: Software Tools, Methods and Applications; Fischer, M., Getis, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 73–89. [Google Scholar]
- Murgante, B.; Scorza, F. Autocorrelazione Spaziale e Pianificazione del Territorio: Principi ed Applicazioni; Libria: Melfi, Italy, 2023. [Google Scholar]
- Cliff, A.D.; Ord, K. Spatial autocorrelation: A review of existing and new measures with applications. Econ. Geogr. 1970, 46, 269–292. [Google Scholar] [CrossRef]
- Chen, Y. Spatial autocorrelation equation based on Moran’s index. Sci. Rep. 2023, 13, 19296. [Google Scholar] [CrossRef] [PubMed]
- Krisp, J.M.; Špatenková, O. Kernel density estimations for visual analysis of emergency response data. In Geographic Information and Cartography for Risk and Crisis Management: Towards Better Solutions; Springer: Berlin/Heidelberg, Germany, 2010; pp. 395–408. [Google Scholar]
- Shi, X.; Alford-Teaster, J.; Onega, T. Kernel density estimation with geographically masked points. In Proceedings of the 17th International Conference on Geoinformatics, Fairfax, VA, USA, 12–14 August 2009. [Google Scholar]
- Milic, N.; Popovic, B.; Mijalkovic, S.; Marinkovic, D. The influence of data classification methods on predictive accuracy of kernel density estimation hotspot maps. Int. Arab J. Inf. Technol. 2019, 16, 1053–1062. [Google Scholar]
- Lucà, F.; Conforti, M.; Robustelli, G. Comparison of GIS-based gullying susceptibility mapping using bivariate and multivariate statistics: Northern Calabria, South Italy. Geomorphology 2011, 134, 297–308. [Google Scholar] [CrossRef]
- Speich, M.J.; Bernhard, L.; Teuling, A.J.; Zappa, M. Application of bivariate mapping for hydrological classification and analysis of temporal change and scale effects in Switzerland. J. Hydrol. 2015, 523, 804–821. [Google Scholar] [CrossRef]
- Fabrizio, E.; Garnero, G. Analisi di visibilità con tecniche GIS per la valutazione paesistica. In Proceedings of the L’edilizia Rurale Tra Sviluppo Tecnologico e Tutela del Territorio. Convegno della II Sezione AIIA, Florence, Italy, 20–22 September 2012. [Google Scholar]
- Song, Y.; Kang, L.; Lin, F.; Sun, N.; Aizezi, A.; Yang, Z.; Wu, X. Estimating the spatial distribution of soil heavy metals in oil mining area using air quality data. Atmos. Environ. 2022, 287, 119274. [Google Scholar] [CrossRef]
- Kleine Deters, J.; Zalakeviciute, R.; Gonzalez, M.; Rybarczyk, Y. Modeling PM 2.5 urban pollution using machine learning and selected meteorological parameters. J. Electr. Comput. Eng. 2017, 2017, 5106045. [Google Scholar]
- Del Giudice, V. L’analisi di regressione multipla nella stima “per valori tipici” in, C.e.S.E.T. Aspetti evolutivi della scienza estimativa. In Seminario in Onore di Ernesto Marenghi; Firenze University Press: Florence, Italy, 1995; pp. 1–10. [Google Scholar]
- Negri, I. Regressione multipla. In Probabilità e Statistica per L’ingegneria e le Scienze; McGraw Hill: New York, NY, USA, 2006; pp. 420–433. [Google Scholar]
- Berry, W.D.; Feldman, S.; Stanley Feldman, D. Multiple Regression in Practice (No. 50). 1985; Available online: https://www.worldcat.org/title/multiple-regression-in-practice/oclc/12279592 (accessed on 2 February 2024).
- Irwin, J.R.; McClelland, G.H. Misleading heuristics and moderated multiple regression models. J. Mark. Res. 2001, 38, 100–109. [Google Scholar] [CrossRef]
- Nordio, F.; Kloog, I.; Coull, B.A.; Chudnovsky, A.; Grillo, P.; Bertazzi, P.A.; Schwartz, J. Estimating spatio-temporal resolved PM10 aerosol mass concentrations using MODIS satellite data and land use regression over Lombardy, Italy. Atmos. Environ. 2013, 74, 227–236. [Google Scholar] [CrossRef]
- Kumari, M.; Sarma, K.; Sharma, R. Using Moran’s I and GIS to study the spatial pattern of land surface temperature in relation to land use/cover around a thermal power plant in Singrauli district, Madhya Pradesh, India. Remote Sens. Appl. Soc. Environ. 2019, 15, 100239. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Zhao, L.; Zhang, H.; Chen, M.N.; Fang, R.Y.; Yao, Y.; Zhang, Q.P.; Wang, Q. Spatial-temporal characteristics of carbon emissions from land use change in Yellow River Delta region, China. Ecol. Indic. 2022, 136, 108623. [Google Scholar] [CrossRef]
- Ding, H.; Shi, W. Land-use/land-cover change and its influence on surface temperature: A case study in Beijing City. Int. J. Remote Sens. 2013, 34, 5503–5517. [Google Scholar] [CrossRef]
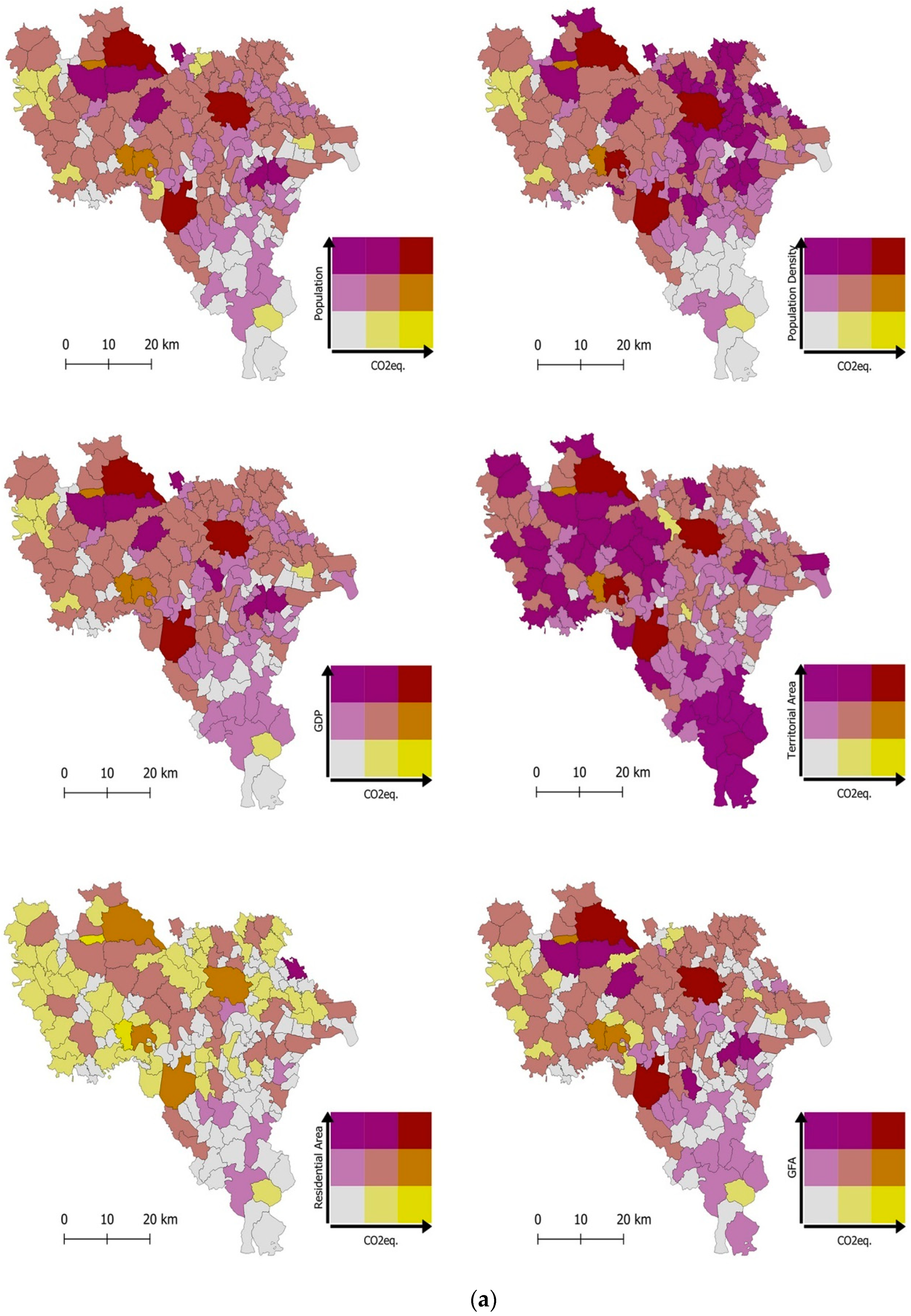
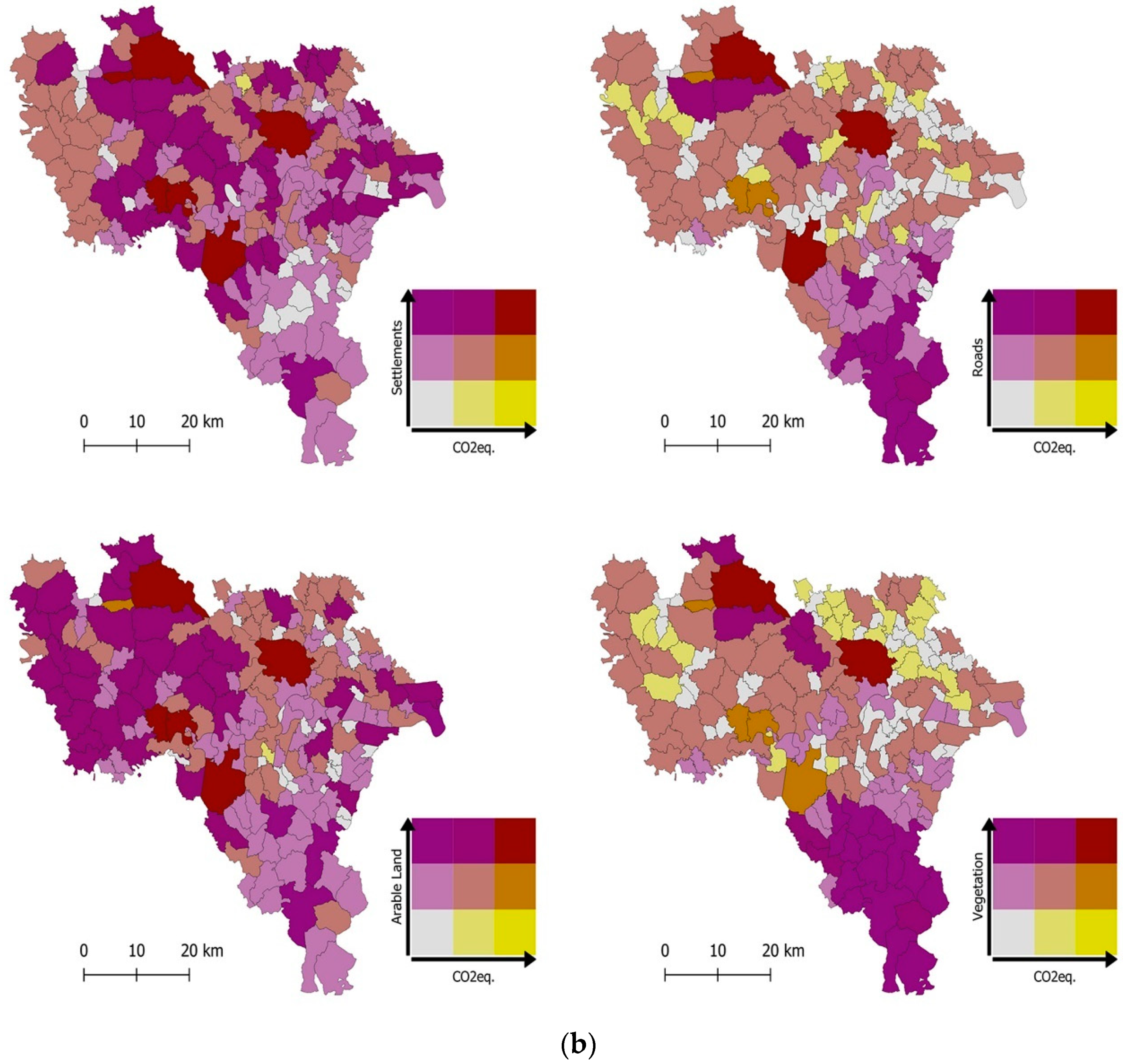



| Municipality | CO2eq. [kt/year] | Population [inhab.] | Population Density [inhab./sqkm] | GDP [EUR] | Territorial Area [sqkm] | Residential Area [sqm] | GFA [mq] | Settlements Area [sqm] | Road Lines [m] | Arable Land [sqm] | Vegetated Area [sqm] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ferrera Erbognone | 2870 | 1171 | 59.9 | 15,442,841.00 | 19.17 | 517,337 | 667,532 | 2,438,116 | 43,778 | 14,728,155 | 1,295,014 |
| Sannazzaro de’ Burgondi | 2245 | 5533 | 237.3 | 77,957,469.00 | 23.33 | 1,385,716 | 1,429,065 | 2,120,149 | 78,233 | 16,561,204 | 1,886,223 |
| Voghera | 886 | 39,356 | 621.9 | 637,341,042.00 | 63.44 | 7,261,991 | 6,785,758 | 3,556,511 | 274,498 | 48,037,718 | 2,467,872 |
| Pavia | 351 | 71,297 | 1134.2 | 1,502,659,302.00 | 63.25 | 8,983,402 | 10,776,269 | 4,734,546 | 346,757 | 38,550,845 | 7,294,540 |
| Vigevano | 287 | 63,268 | 768 | 970,129,252.00 | 81.36 | 10,876,712 | 8,962,370 | 4,413,324 | 434,552 | 43,620,466 | 18,250,505 |
| Verretto | 2 | 402 | 147.3 | 4,957,052.00 | 2.71 | 194,653 | 96,498 | 128,278 | 11,439 | 2,031,408 | 327,641 |
| Golferenzo | 2 | 196 | 45.1 | 2,804,711.00 | 4.42 | 224,208 | 91,058 | 20,452 | 27,638 | 2,992,303 | 1,118,606 |
| Rea | 1.5 | 431 | 145.6 | 5,745,015.00 | 2.16 | 202,116 | 163,207 | 83,606 | 12,558 | 1,313,383 | 234,622 |
| Lirio | 1.56 | 130 | 75.1 | 1,324,318.00 | 1.75 | 130,811 | 59,931 | 22,973 | 11,928 | 1,347,821 | 193,722 |
| Calvignano | 1 | 127 | 18.4 | 1,206,421.00 | 6.98 | 209,447 | 667,532 | 17,173 | 27,830 | 4,600,624 | 1,962,481 |
| Correlation | Population [inhab.] | Population Density [inhab/sqkm] | GDP [EUR] | Territorial Area [sqkm] | Residential Area [sqkm] | GFA [sqm] | Settlements Area [sqm] | Road Lines [m] | Arable Land [sqm] | Vegetated Land [sqm] |
|---|---|---|---|---|---|---|---|---|---|---|
| CO2eq. | 0.750 | 0.383 | 0.727 | 0.631 | 0.713 | 0.779 | 0.790 | 0.488 | 0.760 | 0.241 |
| Correlation | Population [inhabitants] | Population Density [inhab/skmq] | GDP [EUR] | Territorial Area [kmq] | Residential Area [mq] | GFA [mq] | Settlements Area [mq] | Road Lines [m] | Arable Land [mq] | Vegetated Land [mq] |
|---|---|---|---|---|---|---|---|---|---|---|
| CO2eq. | 0.726 | 0.396 | 0.704 | 0.614 | 0.634 | 0.773 | 0.782 | 0.504 | 0.707 | 0.194 |
| Dependent Variable y | Independent Variable x | Equation |
|---|---|---|
| CO2eq. | Population | |
| GDP | ||
| Territorial Area | ||
| Residential Area | ||
| GFA | ||
| Settlements Area | ||
| Road Lines | ||
| Arable Land | ||
| Vegetated land |
| Correlation | CO2eq./Population | CO2eq./Population Density | CO2eq./GDP | CO2eq./Territorial Area | CO2eq./Residential Area | CO2eq./GFA | CO2eq./Settlement Area | CO2eq./Road Lines | CO2eq./Arable Land | Co2eq./Vegetated Land |
|---|---|---|---|---|---|---|---|---|---|---|
| Moran I | 0.726 | 0.396 | 0.704 | 0.614 | 0.634 | 0.773 | 0.782 | 0.504 | 0.707 | 0.194 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Lotto, R.; Bellati, R.; Moretti, M. Correlation Methodologies between Land Use and Greenhouse Gas emissions: The Case of Pavia Province (Italy). Air 2024, 2, 86-108. https://doi.org/10.3390/air2020006
De Lotto R, Bellati R, Moretti M. Correlation Methodologies between Land Use and Greenhouse Gas emissions: The Case of Pavia Province (Italy). Air. 2024; 2(2):86-108. https://doi.org/10.3390/air2020006
Chicago/Turabian StyleDe Lotto, Roberto, Riccardo Bellati, and Marilisa Moretti. 2024. "Correlation Methodologies between Land Use and Greenhouse Gas emissions: The Case of Pavia Province (Italy)" Air 2, no. 2: 86-108. https://doi.org/10.3390/air2020006
APA StyleDe Lotto, R., Bellati, R., & Moretti, M. (2024). Correlation Methodologies between Land Use and Greenhouse Gas emissions: The Case of Pavia Province (Italy). Air, 2(2), 86-108. https://doi.org/10.3390/air2020006







