Identification of Patterns in the Stock Market through Unsupervised Algorithms
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
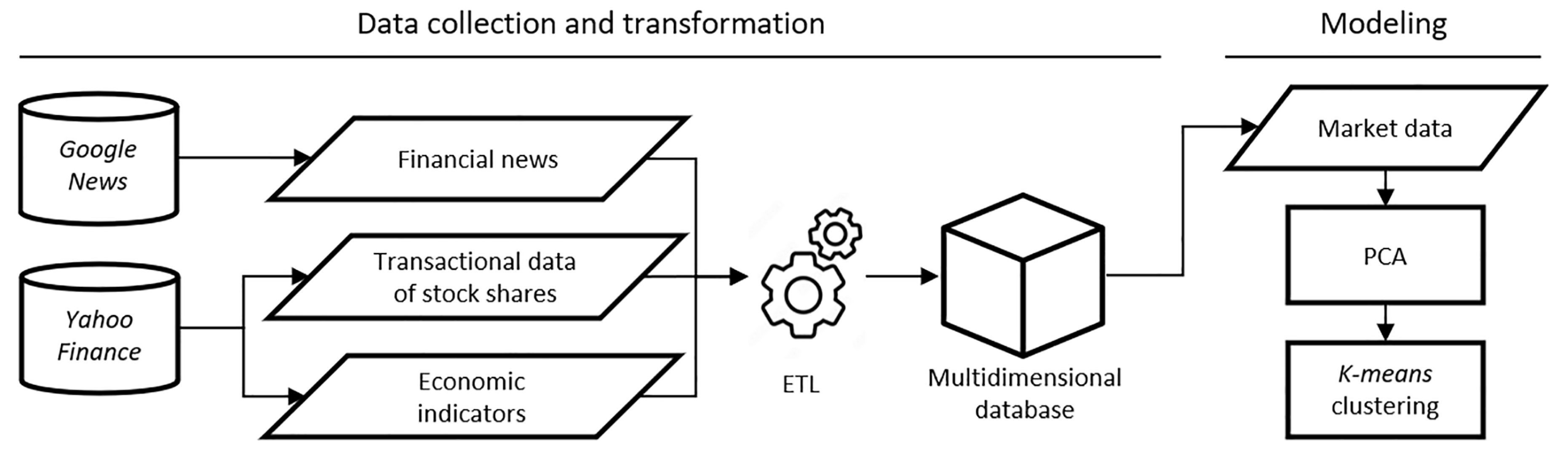
3.1. Data Collection and Transformation
3.2. Modeling
3.3. Principal Component Analysis
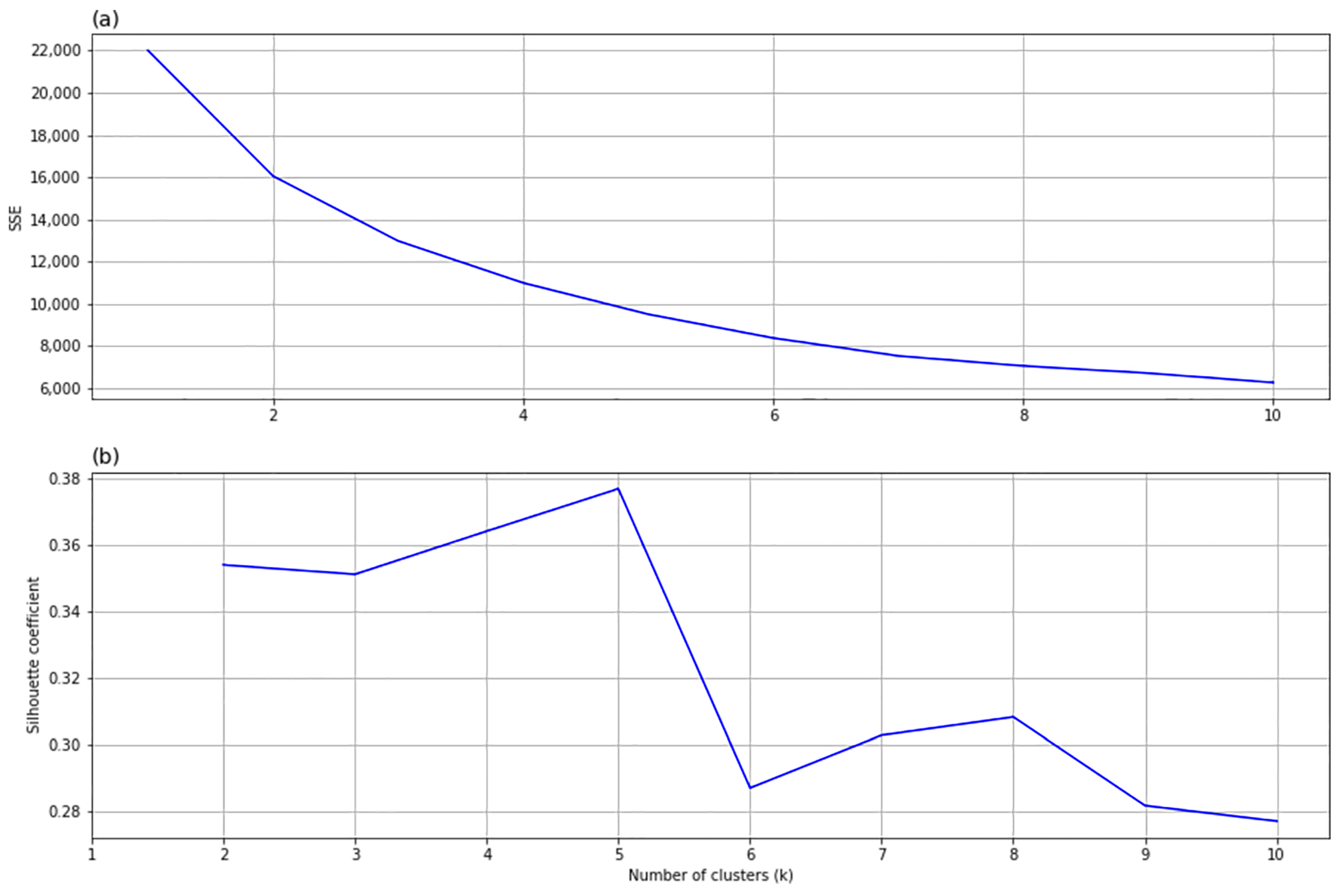
3.4. K-Means Clustering
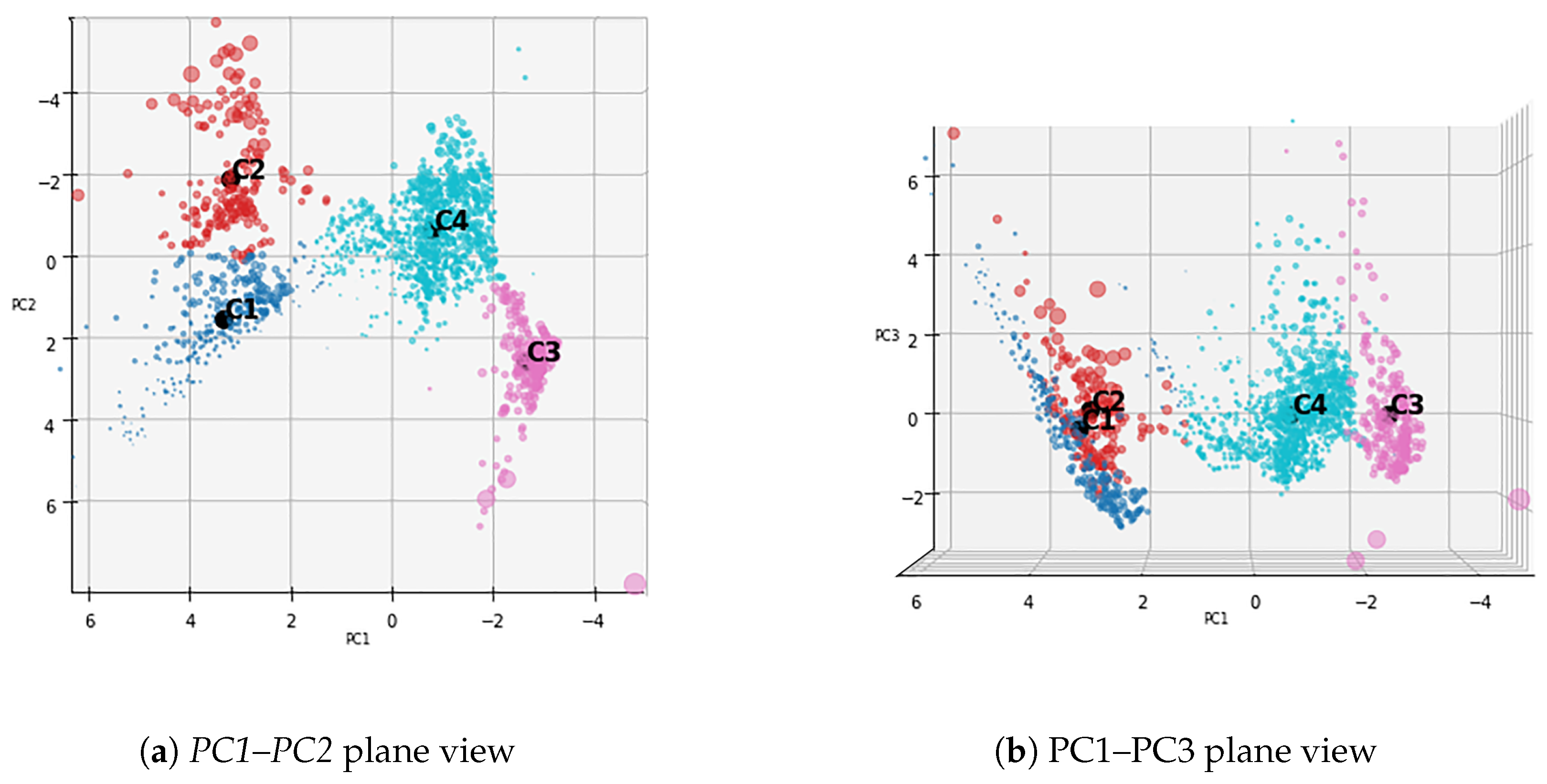
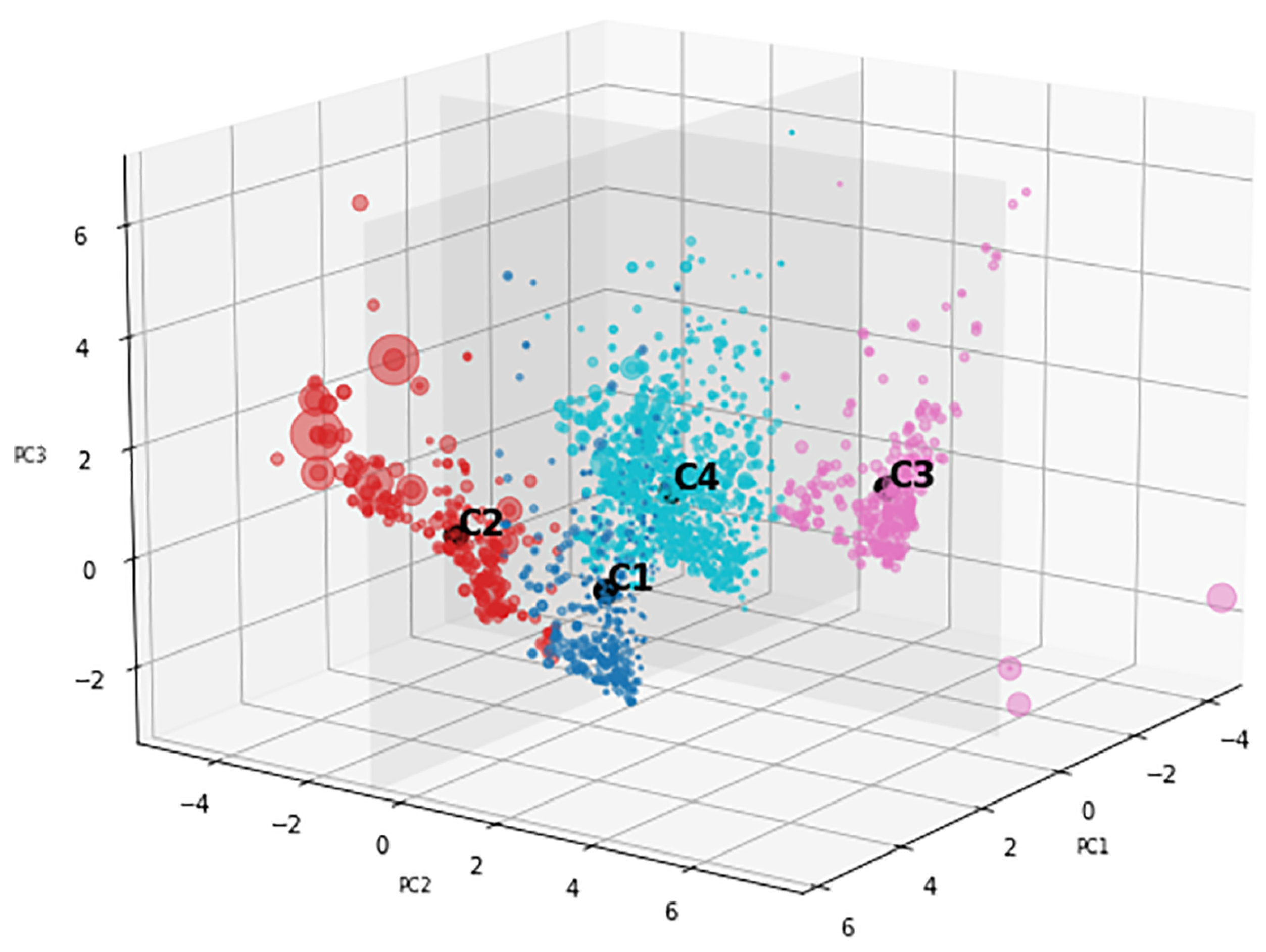
4. Results
4.1. Dimensionality Reduction
- PC1: Gold and S & P500 future expectations.
- PC2: Oil and USD/EUR exchange rate future expectations.
- PC3: Media coverage.
- PC4: Volatility.
- PC5: Financial news sentiment.
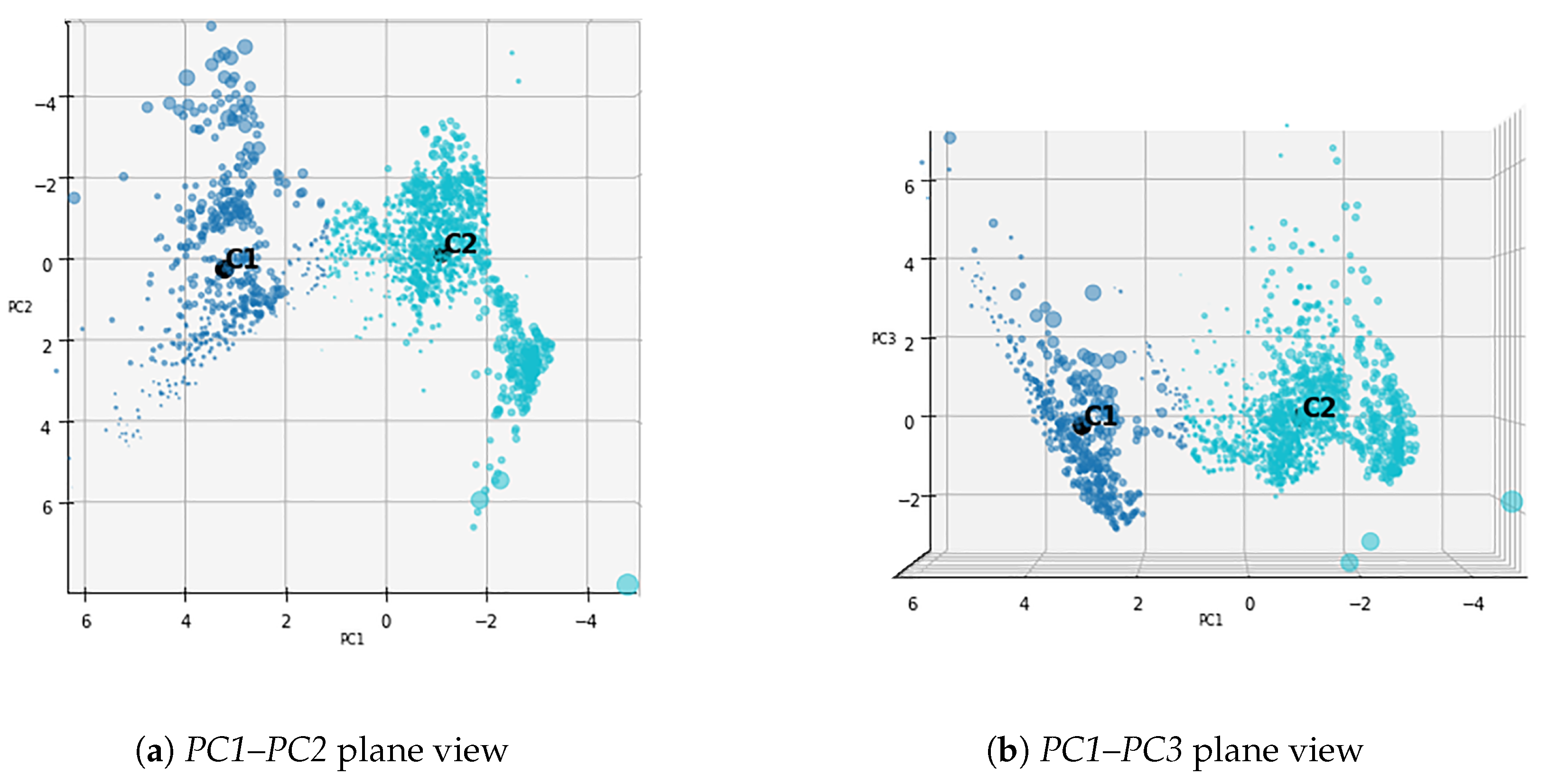
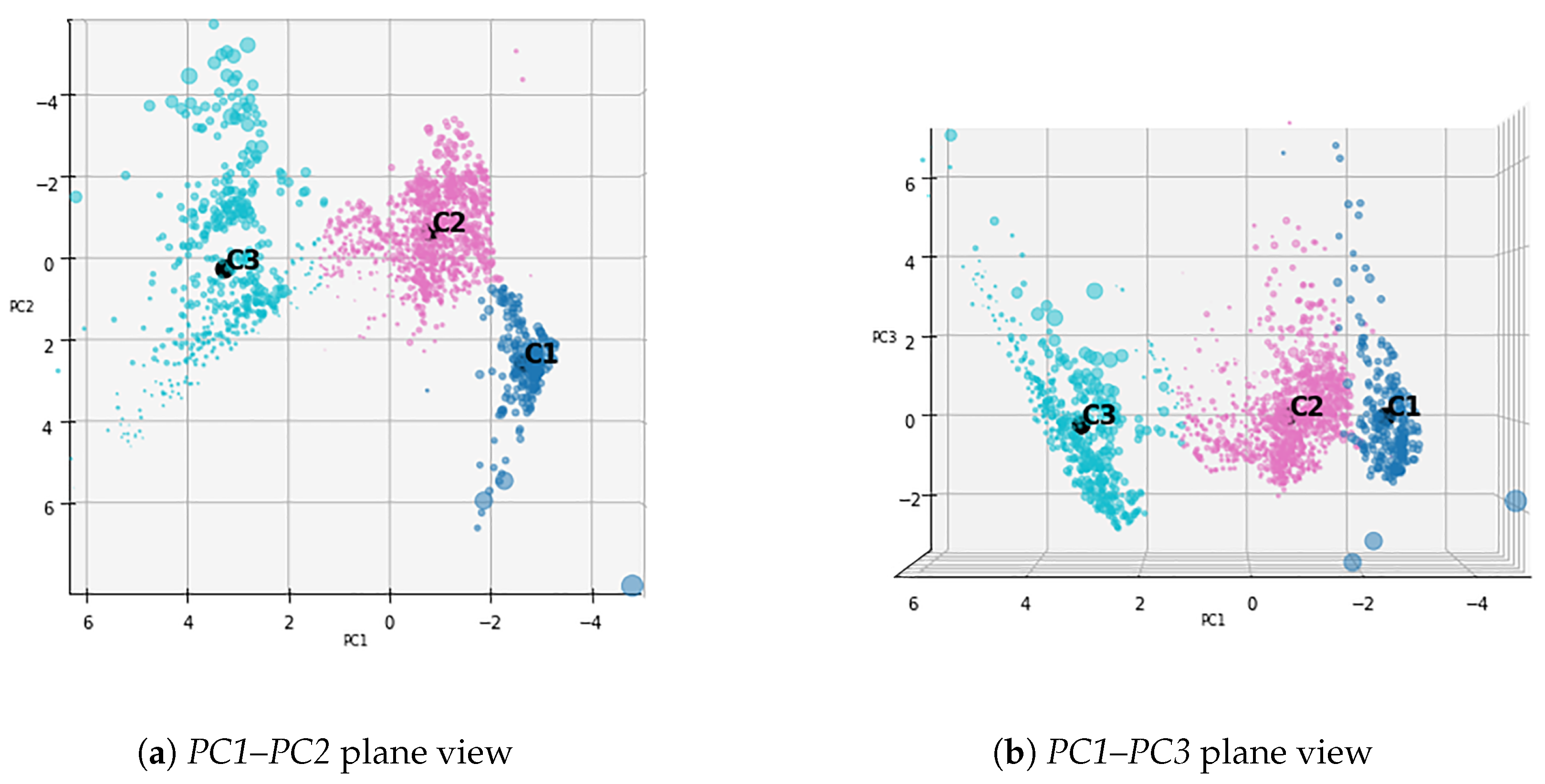
4.2. Clusters Comparison
- C1: Optimistic expectations.
- C2: High volatility.
- C3: Pessimistic expectations.
- C4: Usual steady behavior.
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Date | News | News Sq | Variation | VIX | EEM | TNX | CLF | USD/MXN | USD/EUR | ESF | GCF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 January 2014 | −0.134 | 0.018 | −0.000 | 13.76 | 40.12 | 2.995 | 93.96 | 13.09 | 0.731 | 1825.5 | 1238.4 |
| 6 January 2014 | −1.586 | 2.51 | −0.0028 | 13.55 | 39.74 | 2.961 | 93.43 | 13.06 | 0.735 | 1820.75 | 1237.8 |
| 7 January 2014 | −0.595 | 0.35 | −0.0071 | 12.92 | 39.91 | 2.937 | 93.67 | 13.07 | 0.733 | 1830.75 | 1229.4 |
| 29 December 2021 | 4.332 | 18.76 | 0.0012 | 16.95 | 48.56 | 1.543 | 76.56 | 20.66 | 0.883 | 4784.5 | 1805.1 |
| 30 December 2021 | 1.6 | 2.60 | −0.0027 | 17.33 | 49.09 | 1.515 | 76.99 | 20.55 | 0.880 | 4772.25 | 1812.7 |
| 31 December 2021 | 3.029 | 9.14 | −0.0025 | 17.22 | 48.85 | 1.512 | 75.21 | 20.45 | 0.883 | 4758.5 | 1827.5 |
References
- Peress, J. The Media and the Diffusion of Information in Financial Markets: Evidence from Newspaper Strikes. J. Financ. 2014, 69, 2007–2043. [Google Scholar]
- Rangel, J.G. Macroeconomic News, Announcements, and Stock Market Jump Intensity Dynamics. J. Bank. Financ. 2011, 35, 1263–1276. [Google Scholar] [CrossRef]
- Alanyali, M.; Moat, H.S.; Preis, T. Quantifying the Relationship Between Financial News and the Stock Market. Sci. Rep. 2013, 3, 3578. [Google Scholar] [CrossRef]
- Goonatilake, R.; Herath, S. The Volatility of the Stock Market and News. Int. Res. J. Financ. Econ. 2007, 3, 53–65. [Google Scholar]
- Zhong, X.; Enke, D. Forecasting Daily Stock Market Return Using Dimensionality Reduction. Expert Syst. Appl. 2017, 67, 126–139. [Google Scholar] [CrossRef]
- Chen, T.L.; Chen, F.Y. An Intelligent Pattern Recognition Model for Supporting Investment Decisions in Stock Market. Inf. Sci. 2016, 346–347, 261–274. [Google Scholar] [CrossRef]
- Grouard, M.H.; Lévy, S.; Lubochinsky, C. La volatilité boursière: Des constats empiriques aux difficultés d’interprétation. Banq. Fr. 2003, 61–79. [Google Scholar]
- Atkins, A.; Niranjan, M.; Gerding, E. Financial News Predicts Stock Market Volatility Better than Close Price. J. Financ. Data Sci. 2018, 4, 120–137. [Google Scholar] [CrossRef]
- Kumar, G.; Jain, S.; Singh, U.P. Stock Market Forecasting Using Computational Intelligence: A Survey. Arch. Comput. Methods Eng. 2021, 28, 1069–1101. [Google Scholar] [CrossRef]
- Mystakidis, A.; Tjortjis, C. Big Data Mining for Smart Cities: Predicting Traffic Congestion Using Classification. In Proceedings of the 2020 11th International Conference on Information, Intelligence, Systems and Applications IISA, Piraeus, Greece, 15–17 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Francis, B.K.; Babu, S.S. Predicting Academic Performance of Students Using a Hybrid Data Mining Approach. J. Med. Syst. 2019, 43, 162. [Google Scholar] [CrossRef]
- Ben-David, I.; Franzoni, F.; Moussawi, R. Exchange-Traded Funds. Annu. Rev. Financ. Econ. 2017, 9, 169–189. [Google Scholar] [CrossRef]
- Poterba, J.M.; Shoven, J.B. Exchange-Traded Funds: A New Investment Option for Taxable Investors. Am. Econ. Rev. 2002, 92, 422–427. [Google Scholar] [CrossRef]
- Shah, D.; Isah, H.; Zulkernine, F. Stock Market Analysis: A Review and Taxonomy of Prediction Techniques. Int. J. Financ. Stud. 2019, 7, 26. [Google Scholar] [CrossRef]
- S&P Dow Jones Indices. S&P 500. 2023. Available online: https://www.spglobal.com/spdji/en/indices/equity/sp-500/ (accessed on 29 April 2023).
- Malik, A.; Tuckfield, B. Applied Unsupervised Learning with R; Packt Publishing Ltd.: Birmingham, UK, 2019. [Google Scholar]
- Huang, H.; Ding, C.; Luo, D.; Li, T. Simultaneous Tensor Subspace Selection and Clustering: The Equivalence of High Order Svd and k-Means Clustering. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’08, New York, NY, USA, 24–27 August 2008; pp. 327–335. [Google Scholar] [CrossRef]
- Kumbure, M.M.; Lohrmann, C.; Luukka, P.; Porras, J. Machine Learning Techniques and Data for Stock Market Forecasting: A Literature Review. Expert Syst. Appl. 2022, 197, 116659. [Google Scholar] [CrossRef]
- Vargas, M.R.; de Lima, B.S.L.P.; Evsukoff, A.G. Deep Learning for Stock Market Prediction from Financial News Articles. In Proceedings of the 2017 IEEE International Conference on Computational Intelligence and Virtual Environments for Measurement Systems and Applications (CIVEMSA), Annecy, France, 26–28 June 2017; pp. 60–65. [Google Scholar] [CrossRef]
- Sathya, R.; Abraham, A. Comparison of Supervised and Unsupervised Learning Algorithms for Pattern Classification. Int. J. Adv. Res. Artif. Intell. IJARA 2013, 2, 34–73. [Google Scholar] [CrossRef]
- Pham, D.T.; Dimov, S.S.; Nguyen, C.D. Selection of K in K-means Clustering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2005, 219, 103–119. [Google Scholar] [CrossRef]
- Sharma, M.; Jyoti, Y. A Review of K-mean Algorithm. Int. J. Eng. Trends Technol. IJETT 2013, 4, 2972–2976. [Google Scholar]
- Momeni, M.; Mohseni, M.; Soofi, M. Clustering Stock Market Companies via K-Means Algorithm. Kuwait Chapter Arab. J. Bus. Manag. Rev. 2015, 4, 1–10. [Google Scholar] [CrossRef][Green Version]
- Ghorbani, A.; Yahyazadehfar, M.; Nabavi Chashmi, S.A. Stock Trading Signal Prediction Using a Combination of K-Means Clustering and Colored Petri Nets (Case Study: Tehran Stock Exchange). J. Adv. Comput. Res. 2020, 11, 1–17. [Google Scholar]
- Fang, Z.; Chiao, C. Research on Prediction and Recommendation of Financial Stocks Based on K-means Clustering Algorithm Optimization. J. Comput. Methods Sci. Eng. 2021, 21, 1081–1089. [Google Scholar] [CrossRef]
- Wijesinghe, G.; Rathnayaka, R. ARIMA and ANN Approach for Forecasting Daily Stock Price Fluctuations of Industries in Colombo Stock Exchange, Sri Lanka. In Proceedings of the 2020 5th International Conference on Information Technology Research (ICITR), Moratuwa, Sri Lanka, 2–4 December 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Mulyaningsih, S.; Heikal, J. K-Means Clustering Using Principal Component Analysis (PCA) Indonesia Multi-Finance Industry Performance Before and During Covid-19. APMBA Asia Pac. Manag. Bus. Appl. 2022, 11, 131–142. [Google Scholar]
- Powell, N.; Foo, S.Y.; Weatherspoon, M. Supervised and Unsupervised Methods for Stock Trend Forecasting. In Proceedings of the 2008 40th Southeastern Symposium on System Theory (SSST), New Orleans, LA, USA, 16–18 March 2008; pp. 203–205. [Google Scholar] [CrossRef]
- Jeng, A.M. Using K-Means and PCA in Construction of a Stock Portfolio. 2016. Available online: https://www.diva-portal.org/smash/get/diva2:1079232/FULLTEXT01.pdf (accessed on 13 June 2023).
- Hargreaves, C.A. An Automated Stock Investment System Using Machine Learning Techniques: An Application in Australia. Int. J. Math. Comput. Sci. 2019, 13, 199–202. [Google Scholar]
- Liu, B.; Qiu, H.; Shen, Y. Establishment and Implementation of Securities Company Customer Classification Model Based on Clustering Analysis and PCA. In Proceedings of the 2012 International Conference on Control Engineering and Communication Technology, Shenyang, China, 7–9 December 2012; pp. 325–329. [Google Scholar] [CrossRef]
- State Street Global Advisors. SPY: SPDR S&P 500 ETF Trust. Available online: https://www.ssga.com/us/en/intermediary/etfs/funds/spdr-sp-500-etf-trust-spy (accessed on 17 April 2023).
- Elbagir, S.; Yang, J. Twitter Sentiment Analysis Using Natural Language Toolkit and VADER Sentiment. In Proceedings of the International MultiConference of Engineers and Computer Scientists 2019, Hong Kong, China, 13–15 March 2019. [Google Scholar]
- Agarwal, A. Sentiment Analysis of Financial News. In Proceedings of the 2020 12th International Conference on Computational Intelligence and Communication Networks (CICN), Bhimtal, India, 25–26 September 2020; pp. 312–315. [Google Scholar] [CrossRef]
- Heiden, A.; Parpinelli, R.S. Applying LSTM for Stock Price Prediction with Sentiment Analysis. In Proceedings of the Anais Do 15. Congresso Brasileiro de Inteligência Computacional. SBIC, 2021, Joinville, Santa Catarina, Brazil, 3–6 October 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Hutto, C.; Gilbert, E. VADER: A Parsimonious Rule-Based Model for Sentiment Analysis of Social Media Text. Proc. Int. AAAI Conf. Web Soc. Media 2014, 8, 216–225. [Google Scholar] [CrossRef]
- Bonta, V.; Kumaresh, N.; Janardhan, N. A Comprehensive Study on Lexicon Based Approaches for Sentiment Analysis. Asian J. Comput. Sci. Technol. 2019, 8, 1–6. [Google Scholar] [CrossRef]
- Ghojogh, B.; Samad, M.N.; Mashhadi, S.A.; Kapoor, T.; Ali, W.; Karray, F.; Crowley, M. Feature Selection and Feature Extraction in Pattern Analysis: A Literature Review. arXiv 2019, arXiv:1905.02845. [Google Scholar] [CrossRef]
- Anowar, F.; Sadaoui, S.; Selim, B. Conceptual and Empirical Comparison of Dimensionality Reduction Algorithms (PCA, KPCA, LDA, MDS, SVD, LLE, ISOMAP, LE, ICA, t-SNE). Comput. Sci. Rev. 2021, 40, 100378. [Google Scholar] [CrossRef]
- Scikit-Learn. API Reference. Available online: https://scikit-learn/stable/modules/classes.html (accessed on 29 March 2023).
- Huang, D.; Schlag, C.; Shaliastovich, I.; Thimme, J. Volatility-of-Volatility Risk. J. Financ. Quant. Anal. 2019, 54, 2423–2452. [Google Scholar] [CrossRef]
- Bhowmik, R.; Wang, S. Stock Market Volatility and Return Analysis: A Systematic Literature Review. Entropy 2020, 22, 522. [Google Scholar] [CrossRef]
| Variable | Definition | Source |
|---|---|---|
| news | Weighted average of the sentiment score given to collected financial news related to the ETF (SPY). | Google News |
| news Sq | Squared value of variable news. | Google News |
| variation | Stock price variation with respect to the previous day. | Yahoo Finance |
| VIX | Volatility index. | Yahoo Finance |
| EEM | MSCI emerging markets ETF. | Yahoo Finance |
| TNX | Interest on 10-year treasury bonds. | Yahoo Finance |
| CLF | Crude oil future contracts. | Yahoo Finance |
| Exchange rate between the U.S. dollar and the Mexican peso. | Yahoo Finance | |
| Exchange rate between the U.S. dollar and the euro. | Yahoo Finance | |
| GFC | Gold future contracts. | Yahoo Finance |
| PC | Eigenvalue | Proportion | Cumulative Proportion |
|---|---|---|---|
| PC1 | 4.1470 | 0.379 | 0.379 |
| PC2 | 2.6312 | 0.240 | 0.620 |
| PC3 | 1.5831 | 0.144 | 0.765 |
| PC4 | 1.0038 | 0.091 | 0.857 |
| PC5 | 0.5113 | 0.046 | 0.904 |
| PC6 | 0.4564 | 0.041 | 0.945 |
| PC7 | 0.2762 | 0.025 | 0.971 |
| PC8 | 0.1832 | 0.016 | 0.988 |
| PC9 | 0.0786 | 0.007 | 0.995 |
| PC10 | 0.0522 | 0.004 | 0.999 |
| Variable | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | PC9 | PC10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Cumulative Proportion | 0.379 | 0.620 | 0.765 | 0.857 | 0.904 | 0.945 | 0.971 | 0.988 | 0.995 | 0.999 |
| news | 0.350 | 0.018 | −0.100 | −0.260 | 0.890 | 0.005 | −0.066 | −0.026 | −0.025 | −0.037 |
| news Sq | 0.249 | 0.441 | 0.841 | −0.154 | −0.053 | 0.055 | 0.074 | 0.009 | −0.009 | −0.009 |
| VIX | 0.259 | −0.213 | 0.137 | 0.620 | 0.074 | 0.585 | −0.206 | −0.302 | −0.008 | 0.046 |
| EEM | 0.258 | 0.393 | −0.339 | −0.149 | −0.206 | 0.032 | 0.190 | −0.617 | −0.426 | 0.031 |
| TNX | −0.378 | 0.163 | −0.088 | −0.327 | 0.030 | 0.660 | 0.123 | −0.025 | 0.196 | −0.474 |
| CLF | −0.152 | 0.516 | −0.174 | 0.058 | 0.013 | 0.174 | −0.624 | 0.356 | −0.269 | 0.242 |
| USD/MXN | 0.372 | −0.272 | −0.079 | −0.220 | −0.180 | 0.377 | 0.324 | 0.526 | −0.374 | 0.192 |
| USD/EUR | 0.089 | −0.447 | 0.154 | −0.515 | −0.219 | 0.003 | −0.609 | −0.240 | −0.127 | −0.106 |
| ESF | 0.419 | 0.160 | −0.242 | −0.178 | −0.222 | 0.102 | −0.096 | 0.005 | 0.742 | 0.299 |
| GFC | 0.441 | 0.117 | −0.148 | 0.216 | −0.164 | −0.186 | −0.149 | 0.255 | −0.010 | −0.758 |
| Data | Daily Variation [%] | |||||
|---|---|---|---|---|---|---|
| Qty. | % | Max. | Min. | Variance | Average | |
| C1 | 310 | 15.40% | 2.20 | −2.32 | 0.582 | 0.04650 |
| C2 | 182 | 9.04% | 8.37 | −10.21 | 5.114 | 0.03212 |
| C3 | 237 | 11.77% | 1.79 | −2.14 | 0.400 | −0.00062 |
| C4 | 1284 | 63.79% | 4.64 | −3.96 | 0.631 | −0.01493 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barradas, A.; Canton-Croda, R.-M.; Gibaja-Romero, D.-E. Identification of Patterns in the Stock Market through Unsupervised Algorithms. Analytics 2023, 2, 592-603. https://doi.org/10.3390/analytics2030033
Barradas A, Canton-Croda R-M, Gibaja-Romero D-E. Identification of Patterns in the Stock Market through Unsupervised Algorithms. Analytics. 2023; 2(3):592-603. https://doi.org/10.3390/analytics2030033
Chicago/Turabian StyleBarradas, Adrian, Rosa-Maria Canton-Croda, and Damian-Emilio Gibaja-Romero. 2023. "Identification of Patterns in the Stock Market through Unsupervised Algorithms" Analytics 2, no. 3: 592-603. https://doi.org/10.3390/analytics2030033
APA StyleBarradas, A., Canton-Croda, R.-M., & Gibaja-Romero, D.-E. (2023). Identification of Patterns in the Stock Market through Unsupervised Algorithms. Analytics, 2(3), 592-603. https://doi.org/10.3390/analytics2030033






