Abstract
In this study, the resilience of designed water systems in the face of limited streamflow gauging stations and escalating global warming impacts were investigated. By performing a regression analysis, simulated meteorological data with observed streamflow from 1971 to 2020 across 33 stream gauging stations in the Euphrates-Tigris Basin were correlated. Utilizing the Ordinary Least Squares regression method, streamflow for 2020–2100 using simulated meteorological data under RCP 4.5 and RCP 8.5 scenarios in CORDEX-EURO and CORDEX-MENA domains were also predicted. Streamflow variability was calculated based on meteorological variables and station morphological characteristics, particularly evapotranspiration. Hierarchical clustering analysis identified two clusters among the stream gauging stations, and for each cluster, two streamflow equations were derived. The regression analysis achieved robust streamflow predictions using six representative climate variables, with adj. R2 values of 0.7–0.85 across all models, primarily influenced by evapotranspiration. The use of a global model led to a 10% decrease in prediction capabilities for all CORDEX models based on R2 performance. This study emphasizes the importance of region homogeneity in estimating streamflow, encompassing both geographical and hydro-meteorological characteristics.
1. Introduction
Climate change effects are gaining increasing interest in relation to water management systems, especially for dam structures where the streamflow changes are often studied based on return periods and climate change scenarios [1]. With respect to the pressures on resources provided by climate change and the means to halt them, hydropower energy has emerged as a robust competitor in the field of renewable energy resources in recent years [2,3]. Turkey is a country that is considered rich in hydropower facilities, with growing investments in dams with hydropower facilities. However, the scarcity of gauging stations and their lack of data makes implementing the design and management of systems challenging. As a result, efficient streamflow estimation for future hydropower potential of the facilities is actually detrimental [4]. Alivi et.al. (2021) investigated the climate change effects on annual average streamflow in the Euphrates-Tigris Basin, where a direct proportional relationship between precipitation and streamflow was found [5]. Laimighofer et.al. (2021) provided seasonal results for several statistical learning methods, and they found out that support vector machines perform better in winter while non-linear boosted models perform better in summer [6]. To obtain such results, data from 260 gauging stations in Austria was used. Stagnitta et.al. (2018) correlated baseflow and scaling methods using field measurements. This use of global meteorological data addresses the problem of data scarcity, but still has its own challenges, which need to be overcome. For example, Aich et al. (2014) compared the effects of climate change on streamflow in data scarce African river basins, using bias corrected Earth system models of Coupled Model intercomparison Project Phase 5 (CMIP5) for several concentration pathway scenarios [7]. The scalability of continental data, when properly interpreted, forms a powerful tool for water managers, who are often operating in data scarce settings. The Coordinated Regional Downscaling Experiment (CORDEX) program, which is a new leader in the climate project of the European Union that is sponsored by the World Climate Research Program (WCRP), aims at developing an improved framework for generating regional-scale climate projections for impact assessment, and it has been widely implemented worldwide, especially in the Eastern Mediterranean context for climatological studies where temporal clustering and precipitation trends are commonly analyzed [8,9]. The application of many global and regional climate models in CORDEX has helped to characterize the strength and the weaknesses of several regional climate models in terms of their climate projection capabilities for the selected basins [10,11]. Regression approaches in ungauged regions often rely on empirical data, despite not offering an understanding of the watershed hydrology and characteristics, but their data-driven methodology helps obtain useful correlations between the precipitation and streamflow without the need of intense variable availability that is required for physical models [12,13,14].
Hence, this study aimed to integrate these two existing approaches by estimating the streamflow from meteorological variables in the Euphrates-Tigris river basin through a regression analysis based on empirical data ranging from 1971 to 2020, utilizing it as a proxy for estimating future streamflow using meteorological data provided by CORDEX.
This work introduces an innovative approach by examining the resilience of water resources in the context of limited streamflow gauging stations and escalating global warming impacts. The study employs regression analysis and hierarchical clustering in order to establish correlations between simulated meteorological data and observed streamflow, emphasizing the importance of the homogeneity of a region and the significant role of evapotranspiration in streamflow estimation.
2. Materials and Methods
2.1. Study Area and Dataset Derivation
The Tigris and Euphrates River basin is in southwestern Asia, and it includes the Tigris and Euphrates rivers (Figure 1). With the source starting at Turkey, major hydropower projects are developed through dams. A continental subtropical climate dominates in the basin, where the rivers are mainly snow fed, with annual streamflow reaching the range of 30 billion cubic meters. The methodology of this study starts with acquiring the CORDEX data that is required for regression analysis, employing the simulated multiple meteorological characteristics as independent variables and streamflow as the dependent variable. Quadratic equations and the Ordinary Least Squares technique were formed to estimate streamflow from the meteorological data covering the 1971–2100 period. The 1971–2019 period was used to validate the model, whereas the 2020–2100 period was predicted with the observed equations [3]. To form efficient equations and to obtain relevant data from CORDEX, the domain that needed to be employed as a base was selected. The reason that environments are created in the first place for such climate experiments is that they represent a specific region’s climatology. They have time and space scales which the regional downscaling in CORDEX can handle well, and which are not well resolved in coarser-resolution models [10,15]. Turkey is a complicated country in terms of domain selection, since 4 domain coverages of specific regions could be employed: European (EUR), Central Asian (CAS), the Mediterranean (MED), and Middle Eastern-North African (MNA). However, for the first three domains, Turkey and, specifically, the Euphrates-Tigris Basin, is located on the borders of the selected area [16,17,18], and, thus, the domain may not best represent the climate of Turkey, especially as the Euphrates-Tigris Basin is somewhat left out in the Meditteranean domain, where the Aegean and Mediterranean regions are left out in the Central Asian domain [19]. The Middle Eastern-North African domain is the most suitable choice for Turkey from a climatological point of view.
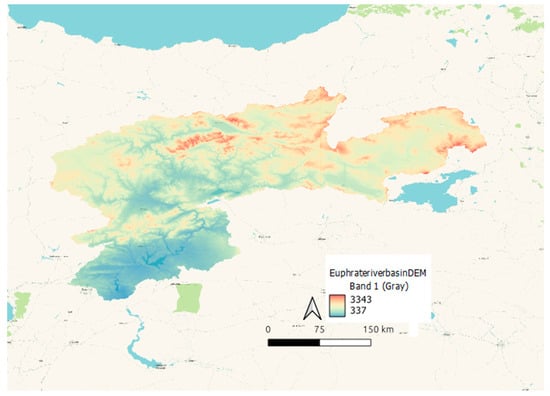
Figure 1.
Digital Elevation model for the studied basin of Tigris and Euphrates with the surrounding countries of Turkey, Iraq, and Syria.
Specific parts of Turkey are located on the borders of the domains, except for the CORDEX-MENA domain. However, being a recent field in the cordex program, not many global climate models with corresponding regional models were employed for this environment. RCA4 and RegCM4 are regional models that are compatible with observed meteorological data in Turkey from previous studies, and they were engaged in the CORDEX-EURO and CORDEX-MENA domains [9,12]. Other regional climatic models (RCM) models were also tested, but the compatibility with the observed meteorological variables (namely, temperature and precipitation) was relatively low compared with these two models [20,21,22]. Another reason these two domains were selected was the 0.11° (~12.5 km) grid for the CORDEX-EURO and 0.22° (~25 km) grid for the CORDEX-MENA domain, which adds value to the meteorological data compared to their coarser-gridded 0.44° (~50 km) counterparts. This selection was made in correspondance with the work conducted by Prein and Goergen (2015), which reached the coarser gridded simulations with the 0.11° grids in the CORDEX-EURO domain, and which then compared pairs of fine and coarse-gridded simulations of eight reanalysis-driven models in the Alps, Germany, Sweden, Norway, France, the Carpathias, and Spain [23], finding that the 0.11° simulations reproduced the mean and extreme precipitation for almost all regions and all seasons, and arguing that the main reason for this robustness in the simulations of finer grids is the improved representation of orography in the 0.11° simulations. Thus, the most significant improvements were found in regions with substantial orographic features [24,25,26]. The 0.11° simulations reduced biases in large areas of the areas investigated, and they had an improved representation of spatial precipitation patterns, as mountainous areas are dominant in the Euphrates-Tigris basin. The employment of finer grids was necessary for the efficiency of this study, too, with a selected set of stream gauging stations (Figure 1). The listed meteorological variables in Table 1 were simulated for the CORDEX-EURO and the CORDEX-MENA domains for the RCA4 and the RegCM4 regional models, respectively. The most refined grid in the relatively new CORDEX-MENA domain was 0.22° (∼25 km), and it was therefore employed for this study. Regional models and the family of the global climate models that they belong to are listed below in Table 2.

Table 1.
Meteorological parameters obtained from the CORDEX program.

Table 2.
Cordex Domains and Regional Models.
The empirical data was downloaded from Copernicus Climate Data Store for the following meteorological stations in the Euphrates-Tigris basin (Figure 2). To compare the efficacy of the simulated data from CORDEX from 1970 to 2019, the temperature, maximum temperature, minimum temperature, and precipitation data were all matched with the observed correspondents [27]. It was observed that all the simulations from both the RCA4 and the RegCM4 models for the EURO and the MENA domains were in line with the observed data for most of the stations. Precipitation and temperature data were most robust for the CORDEX-MENA domain’s RCA4 simulations with a 0.22° grid, since this domain’s climatic features best represent the Euphrates-Tigris basin. However, the CORDEX-EURO domain’s simulations for the RCA4 regional model with the 0.11 grid also yielded almost the same efficacy as the other grids for other fields, especially for the temperature data, even though the stations are located at the eastern borders of the domain. Both RegCM4 and RCA4 overestimated precipitation extremes, especially the eastern part of the Euphrates-Tigris basin. A similarity-dissimilarity analysis was also performed, and the mean values for the four variables that were observed and simulated were compared.
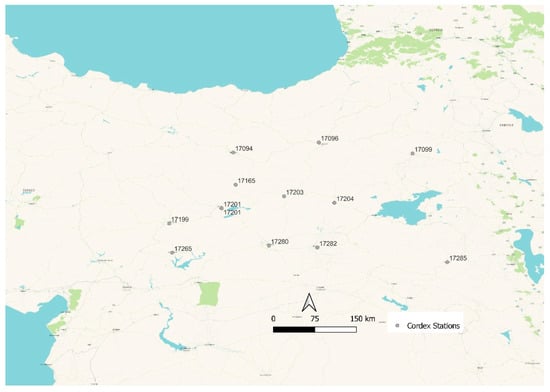
Figure 2.
13 climate stations (with code number) of Cordex where the validated climatic data were downloaded.
In this study, a total of 12 meteorological variables (corresponding to the available Cordex variables in Table 1) with a daily climate series obtained via the regional models in the CORDEX program were considered for 33 stream gauging stations of the General Directorate of Electrical Power Resources Survey and Development: Administration (EIE) as well as the General Directorate of State Hydraulic Works (DSI), and Figure 3 shows the 33 stream gauging stations and their corresponding locations. Hence, the estimation of streamflow will rely on validated global datasets and on national local datasets distributed between two management entities, and Table 3 shows the descriptive statistics of the observed streamflow.
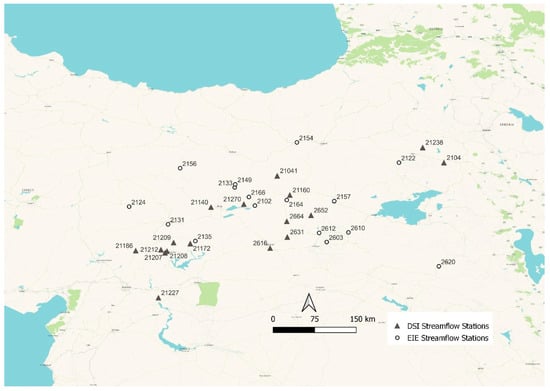
Figure 3.
33 streamflow gauging stations (with code number) with their administrative managing units represented by DSI and EIE.

Table 3.
Descriptive statistics of the average observed streamflows observed the basin.
2.2. Cluster Analysis
Before applying the Ordinary Least Squares method to the simulated meteorological variables via the regional climate models (Table 2), a cluster analysis was performed to group the stations of the Euphrates-Tigris basin in meteorologically homogeneous groups.
The cluster analysis aimed to group the observed data according to their similarities. The cluster sets obtained from the research have homogeneity within the groups, and the stations in different clusters have distinct hydrometeorological properties. Clustering methods are divided into two: hierarchical (staged) and non-hierarchical clustering methods. Hierarchical clustering methods are the methods for determining consecutive sets of units by taking the distance or similarities of the teams in the dataset together in different stages and then considering the distance or the likeness of the units in the dataset and determining at what distance or similarity level the cluster elements are [28]. This method is preferred when the number of subjects is less than 300. The dendrogram is determined by the graphs in which the variables are placed in the hierarchically closest sets, and the most distinct groups are placed furthest away from each other.
Ward’s linkage clustering method, also known as the minimum variance method, takes the average distance (Euclidean distance) of the data corresponding to the median value from all of the other observations within a set and then uses the total deviation squares. This method is therefore affected by extreme values. The Ward linkage clustering method is one of the most used, especially for datasets with limited observations.
If d(x,y) = , then the equation becomes:
Here:
DKL = Euclidean distance between clusters 𝐶𝐾 vs. 𝐶𝐿
= Average vector for Cluster 𝐶𝐾
Nk = Number of variables within the Cluster 𝐶𝐾
In Ward’s method, the distance between the two sets is calculated as the squares of the total deviation between all of the data. In each step, the margin of error within a group is minimized by bringing together the clusters with the minimum variation. The concatenation is terminated if the margin of error of the variable to be concatenated gives a value greater than the previous generation. The evaluation of the influence of climatic variability and human activity on streamflow is one use of Ward’s clustering in streamflow estimates. For instance, Li et al. (2007) employed Ward’s clustering in order to examine how large-scale soil conservation efforts in China have affected the hydrology of the Wuding River basin [29]. They examined the differences in streamflow patterns before and after the application of soil conservation measures by classifying stream gauging stations according to their hydrological parameters. The disaggregation of precipitation data is a further application of Ward’s clustering. To convert coarser-timescale precipitation data into finer resolutions, Li et al. (2018) suggested three resampling techniques based on Ward’s clustering [30]. These methods improve the precision of precipitation disaggregation by considering the inter-site correlation structure. Joo et al. (2020) employed Ward’s clustering and community detection methods to group stream gauging stations in the Yeongsan River basin of South Korea based on their interrelationships [31]. The community detection method showed higher cohesion between stream gauging stations compared to traditional cluster analysis, which indicated its effectiveness in capturing hydrologic similarity, persistence, and connectivity.
2.3. Regression Analysis
Regression analysis is a commonly used application in hydrology that helps form a relationship between watershed characteristics, hydrometeorological variables, and streamflow. From the many studies that were performed in previous years, it is now known that flow and watershed characteristics should be log-transformed to form a near-linear relationship. Many studies have also previously shown the application of the Ordinary Least Squares technique for estimating streamflow by employing stream gauging stations [11,12,13]. However, grouping the stations according to their watershed and meteorological characteristics and then engaging them in a regression analysis, whether linear or non-linear, is a concept yet to be fully explored in different climatic regions of the world. For instance, Immerzeel et al. (2013) used multiple linear regression to predict streamflow at the Bahadurabad station based on historical data, and they downscaled GCM outputs for future temperature and precipitation conditions [32]. Additionally, artificial neural networks and multiple linear regression for streamflow forecasting in ungauged basins have demonstrated the effectiveness and the potential of linear regression models in streamflow estimation [4].
Thus, in this study, before applying the Ordinary Least Squares regression and non-linear regressions to increase the efficacy of the estimated models, the stations were employed in the determined clusters for the purpose of comparison, and a global regression was also performed for all the streamflow data of the domains and the models in this study. The results of the regression analyses for all of the stations versus the regional stations are compared in this chapter of the study. All calculations are performed using the Matlab software.
The linear regression equation that was used in this study in log-space is expressed as follows [33]:
The equation then could be converted to estimate y as:
where:
y is the estimated streamflow at i-th station and j-th data point;
x1, x2, x3, … are the meteorological characteristics listed in table;
βn are the regression coefficients.
The regression analysis will identify the meteorological variables retained from the 12 variables studies for the CORDEX-EURO RegCM4 and the CORDEX MENA for each RCM.
3. Results and Discussion
3.1. Clustering Results
After the application of Ward’s method to 33 stream gauging stations, the cluster sets that are obtained are presented in the following Table 4.

Table 4.
Cluster Sets of Stream Gauging Stations.
Looking at the clusters for the stations in the Euphrates and Tigris-Basin, the stream gauging stations in the east are grouped in Cluster 1 and the stations in the west are grouped in Cluster 2, which is in line with their geographical locations.
3.2. Regression Analysis Results
The Ordinary Least Squares regression was applied on the 12 stream gauging stations’ simulated meteorological data of CORDEX-EURO’s RegCM4 and both CORDEX-MENA’S RCA 4 with the observed streamflow data from 1970–2015. The equations obtained as well as the scatterplots of both the predicted and the observed flows are listed below in Table 5.

Table 5.
Regression equations obtained for each model and each cluster.
In constructing the regression analysis equations, the Stepwise technique of the Ordinary Least Square method was used. The climatic variables that were most effective at influencing the changes in runoff were selected.
For the 0.11 grid, 6 variables have been retained in the model for the 12 stream gauging stations in Cluster 1 [34,35,36]. The six explanatory variables explained 76% of the dependent variable log (adj. runoff). Among the explanatory variables, based on the Type III sum of squares, variable potential evapotranspiration was the most influential. The predicted runoff and the observed runoff are compared in the graph below.
As can be observed from the runoff equations, temperature ( and potential evapotranspiration were the main determinants for explaining the variability in runoff. The main contribution of hierarchical clustering was not only that it decreased the amount of components necessary to estimate the runoff but that the cluster equations overall had more robust estimation strengths than the global equations that contained all of the stream gauging stations. This will further be discussed in the evaluation of data later in this paper.
The comparison of the observed runoff with the estimated runoff from regression analyses for all of the clusters and the regional climate models are as follows in Figure 4.
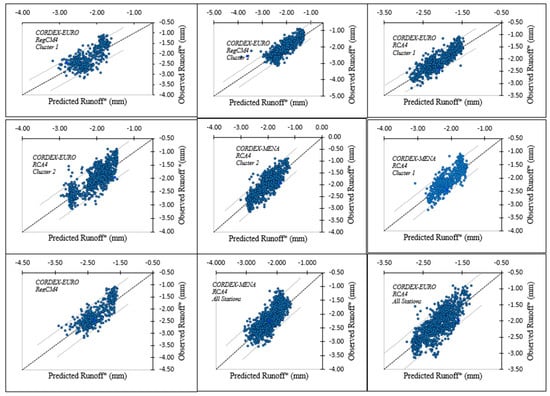
Figure 4.
Plots of Observed vs. Predicted Runoff.
3.2.1. Cluster 2
Ordinary Least Squares regression was applied on 21 stream gauging stations’ simulated meteorological data of RegCM4 with the observed streamflow data from 1970–2015. The equation obtained from the regression analysis is shown as follows:
Using the Stepwise technique of the Ordinary Least Square method, out of the 12 meteorological variables simulated via the CORDEX-EURO Domain’s RegCM4 with the 0.11 grid, six variables have been retained in the model for the 21 stream gauging stations in Cluster 2. A total of 74% of the dependent variable log (adj_runoff) was explained by the 6 explanatory variables. Uneven soil moisture was the most influential among the explanatory variables, based on the Type III sum of squares.
3.2.2. Global Model
Ordinary Least Squares regression was applied on all of the 33 stream gauging stations’ simulated meteorological data of RegCM4 with the observed streamflow data from 1970–2015. The equation obtained from the regression analysis is shown as follows:
Using the Stepwise technique in the Ordinary Least Square method, out of the 12 meteorological variables simulated via the CORDEX-EURO Domain’s RegCM4 with 0.11 grid, six variables have been retained in the model for estimating the streamflow of 33 stream gauging stations. A total of 68% of the dependent variable log (adj_runoff) was explained by the six explanatory variables [25,29]. Among the explanatory variables, based on the Type III sum of squares, variable potential evapotranspiration was the most influential.
3.3. CORDEX-EURO RCA4 Regression Analysis Results
3.3.1. Cluster 1
Ordinary Least Squares regression was applied on 12 stream gauging stations’ simulated meteorological data of RCA4 with the observed streamflow data from 1970–2015. The equation obtained from the regression analysis is shown as follows:
Using the Stepwise technique in the Ordinary Least Square method, out of the 12 meteorological variables simulated via the CORDEX-EURO Domain’s RCA4 with 0.11 grid, six variables have been retained in the model for estimating the streamlow of 12 stream gauging stations in Cluster 1. A total of 79% of the dependent variable log (adj_runoff) was explained by the six explanatory variables [16]. Among the explanatory variables, based on the Type III sum of squares, variable potential evapotranspiration was the most influential.
3.3.2. RCA4 Cluster 2
The Ordinary Least Squares regression method was applied on 21 stream gauging stations’ simulated meteorological data of RCA4 with the observed streamflow data from 1970–2015. The equation obtained from the regression analysis is shown as follows:
Using the Stepwise technique in the Ordinary Least Square method, out of the 12 meteorological variables simulated via the CORDEX-EURO Domain’s RCA4 with 0.11 grid, five variables have been retained in the model for estimating the streamflow of 21 stream gauging stations in Cluster 2. A total of 77% of the dependent variable log (adj_runoff) was explained by the five explanatory variables [16].
Among the explanatory variables, based on the Type III sum of squares, variable potential evapotranspiration was the most influential.
3.3.3. RCA4 Global Model
The Ordinary Least Squares regression method was applied to all 33 stream gauging stations’ simulated meteorological data of RCA4 with the observed streamflow data from 1970–2015. The equation obtained from the regression analysis is shown as follows:
Using the Stepwise technique in the Ordinary Least Square regression method, out of the 12 meteorological variables simulated via the CORDEX-EURO Domain’s RCA4 with 0.11 grid, eight variables have been retained in the model for estimating the streamflow of 33 stream gauging stations, and a total of 67% of the variability of the dependent variable log (adj_runoff) was explained by the eight explanatory variables. Among the explanatory variables, based on the Type III sum of squares, variable potential evapotranspiration was the most influential [25,26].
3.4. CORDEX-MENA RCA 4 Regression Analysis Results
3.4.1. MENA RCA4 Cluster 1
The ordinary least squares regression was applied on 12 stream gauging stations simulated meteorological data of RCA4, with the observed streamflow data from 1970–2015. The equation obtained from the regression analysis is shown as follows:
Using the Stepwise technique of the Ordinary Least Squares method, out of the 12 meteorological variables simulated via the CORDEX-MENA Domain’s RCA4 with 0.22 grid, six variables have been retained in the model for the 12 stream gauging stations in Cluster 1. A total of 86% of the dependent variable log (adj_runoff) was explained by the six explanatory variables [28,29]. Uneven soil moisture was the most influential among the explanatory variables, based on the Type III sum of squares.
The Ordinary Least Square regression was applied on 21 stream gauging stations’ simulated meteorological data of RCA4 with the observed streamflow data from 1970–2015. The equation obtained from the regression analysis is shown as follows:
Using the Stepwise technique in the Ordinary Least Squares method, out of the 12 meteorological variables simulated via the CORDEX-MENA Domain’s RCA4 with 0.22 grid RCA4 regional model, six meteorological variables have been retained in the model for the 21 stream gauging stations of Cluster 2 [24]. A totla of 82% of the dependent variable log (adj_runoff) was explained by the six explanatory variables. Out of these variables, the most influential variable on the dependent variable adjusted runoff was soil moisture [17].
3.4.2. MENA Global Model
Ordinary Least Squares regression was applied on all 33 stream gauging stations’ simulated meteorological data of RCA4 with the observed streamflow data from 1970–2015. The equation obtained from the regression analysis is shown as follows:
Using the Stepwise technique in the Ordinary Least Squares method, out of the 12 were simulated via the CORDEX-MENA Domain’s RCA4 with 0.22 grid, six meteorological variables have been retained in the model for the 33 stream gauging stations. A total of 74% of the dependent variable log (adj_runoff) was explained by the six explanatory variables. Out of these variables, the most influential variable on the dependent variable adjusted runoff was soil moisture [31,32].
The Ordinary Least Squares regression analyses resulted in robust estimation equations for streamflow for the reference period of 1971 to 2020. Below are the comparisons of the and RMSE values for all of the equations.
As observed in Table 6, the most robust equation based on R2 and RMSE values were the CORDEX-MENA domain’s RCA4 simulations for both Cluster 1 and Cluster 2 of the stream gauging stations. The robustness in the regression analysis results from the CORDEX-MENA domain, and was expected because of its best representation of the climate variability of the Euphrates-Tigris basin. Even though the CORDEX-EURO domain’s simulations were conducted in a finer grid (0.11) than the CORDEX-MENA domain (0.22), the location of the Euphrates-Tigris basin on the borders of the EURO domain affected the efficiency of the developed regression models [4]. All of the regression models resulted in relatively robust equations for the clusters, with all explaining 74% to 86% of the variability of the streamflow.

Table 6.
Performance metrics Values for the CORDEX Simulations.
However, the equations for the global models’ streamflow models for all of the 33 stations of the selected basin had significantly lower R2 and higher RMSE values. This study therefore resulted in a cluster analysis that performed at least 10% better than the global models’ results, even for a considerably smaller area.
4. Discussion
The study findings attributed streamflow prediction in the Euphrates-Tigris basin mainly to temperature variables, precipitation, and soil conditions represented by the variables in each regression model. Extending beyond the weather conditions, the soil and the humidity influences obtained from this study complement studies where a regression streamflow simulation model was constructed that accounted for precipitation. In addition, the use of a longer time span and different performance indicators could have resulted in a lesser prediction performance in comparison with other developed models [33]. However, it is worth noting that the use of R2 on a cluster and on a global scale allowed us to investigate the performance of the predictive model and its scalability, since it was observed that the global models lead to lower performance scores. The inclusion of the adj-R2 accounted for the presence of multiple explanatory variables, too. In 2016, Demircan and Gürkan conducted a study in which temperature and precipitation data were manufactured with the RegCM4 model with RCP4.5 and RCP 8.5 scenarios. For the reference period of 1970–2016, they also found that the RegCM4’s simulations were in line with the observed meteorological data—with only extremes being overestimated or underestimated, especially for precipitation data in the Black Sea region, which was compatible with the findings of this study [37]. In addition, we noted that the Q-Q plots showed less dispersion of points and, consequently, a better performance in Cluster 2 obtained. Little difference can be noted concerning variability in catchment characteristics between the two clusters, and reservoir operations are homogeneously present in them. However, such differences in the dispersion of the Q-Q plots could be attributed to the variability of the streamflow patterns where Cluster 2 is dominated by a more natural and agricultural land use with respect to Cluster 1. We also cannot exclude that such difference can occasionally be attributed to data quality and measurement errors, given that two sources of data were used in this study.
Similarly, Kilinc et al. (2022) studied the forecast of streamflow in the Euphrates basin with a focus on the model approach by choosing to assess the performance of several models [38]. The hybrid approach adopted lead to R2 results higher than the values obtained in the study, reaching 0.8667 as an average for all of the regression models tested. This can be attributed to the fact that two gauging stations in the basin were analyzed with a focus on genetic algorithm, while several physical variables were addressed in this study in order to account for the physical nature of the river basin. The regression models presented complimented such a finding while using less computationally intensive data.
The limitations of our study mainly concern two points––verifiability and scale. Improvements to the presented models can look at verifying the obtained coefficients for the variables with regions with similar hydroclimatic and geographical characteristics. This can help in the process of seeing whether a global regression model could be feasible. Recent global models have highlighted the difficulties in accounting for the difference in explanatory variables of streamflow with varying climate and geographical settings. Hence, our regional scale model provides a sound scale of study for application in the ETRB, and could at least be used as a national model for Turkey.
The intrinsic complexity of hydrological processes, restrictions on the availability and quality of data, and assumptions and simplifications built into the modeling approach are only a few of the reasons why there is uncertainty.
The uncertainty of the model’s outputs should be acknowledged and taken into consideration in this investigation. Regression analysis, which implies a linear relationship between the variables, is the foundation of the prediction models created in this study, but it is crucial to understanding, it should be noted, that the actual relationship between the streamflow and the predictor factors (temperature, precipitation, and soil conditions) may not be purely linear. The models might not account for non-linearities, interactions, and other complicated dynamics. Future research could benefit from addressing the limitations of hierarchical clustering, which is susceptible to noise and outliers, and validating the findings with PCA or t-SNE should be considered. Recognizing the potential dependence among ‘y’ values due to spatial proximity or influence between clustered stations is also important. Implementing sophisticated models, such as mixed effects models, can effectively address this inherent correlation [39,40].
5. Conclusions
By evaluating the effectiveness of regional regression analysis in connecting hydrometeorological factors to streamflow, this study concludes by introducing a novel technique. The research is made more original by utilizing the CORDEX-EURO and the CORDEX-MENA domains with various grid resolutions and climate scenarios. We successfully calculated streamflow using observed data as the dependent variable by using two regional climate models, RCA4 and RegCM4, and 12 meteorological variables as independent variables in Ordinary Least Squares regression. With five to six meteorological variables and watershed parameters, such as area and height, accounting for the fluctuation in streamflow, the regression equations had quite good explanatory power. These results are consistent with earlier research [41,42].
The stream gauging stations were subjected to a clustering study prior to the regression technique, which produced two unique groupings. Two streamflow equations were generated for each domain and regional climate model for the corresponding clusters. Notably, almost all of the equations showed that soil moisture or potential evapotranspiration had the greatest influence on calculating streamflow, which is consistent with earlier findings by other researchers. The streamflow explanation improved by at least 10% when the cluster analysis was used before the regression analysis. For authorities and parties operating in the Euphrates-Tigris basin, the regression model established in this study serves as an easily accessible analytical decision tool.
Future explorations can build upon this research by considering additional variables and incorporating advanced modeling techniques. Further investigations should aim to enhance the predictive capabilities of the regression models, particularly in capturing low and high flows. Additionally, the uncertainty associated with the model outputs should be systematically quantified and communicated in order to improve the decision-making process. Overall, this study contributes valuable insights into streamflow prediction, and it presents a promising framework for further studies in the field. The developed regression model has practical applications for decision-makers and stakeholders involved in water resource management within the Euphrates-Tigris basin.
Author Contributions
Conceptualization, G.E.G.; Methodology, G.E.G.; Formal analysis, G.E.G.; Investigation, G.E.G.; Resources, G.E.G.; Writing—original draft, G.E.G.; Writing—review & editing, B.O.; Supervision, B.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable. No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Y.; Li, H.; Reggiani, P. Climate Variability and Climate Change Impacts on Land Surface, Hydrological Processes and Water Management. Water 2019, 11, 1492. [Google Scholar] [CrossRef]
- Bergström, S.; Lindström, G. Interpretation of runoff processes in hydrological modelling-experience from the HBV approach. Hydrol. Process. 2015, 29, 3535–3545. [Google Scholar] [CrossRef]
- Beck, H.; Van Dick, A. Global-Scale Regionalization of Hydrologic Model Parameters. 2016. Available online: https://agupubs.onlinelibrary.wiley.com/doi/epdf/10.1002/2015WR018247 (accessed on 12 March 2022).
- Rezaeianzadeh, M.; Tabari, H.; Yazdi, A.A.; Isik, S.; Kalin, L. Flood flow forecasting using ANN, ANFIS and regression models. Neural Comput. Appl. 2013, 25, 25–37. [Google Scholar] [CrossRef]
- Alivi, A.; Yildiz, O.; Aktürk, G. Investigating the climate change effects on annual average streamflows in the Euphrates-Tigris basin using the climate elasticity method. J. Fac. Eng. Archit. Gazi Univ. 2021, 36, 1449–1465. [Google Scholar] [CrossRef]
- Laimighofer, J.; Melcher, M.; Laaha, G. Parsimonious statistical learning models for low-flow estimation. Hydrol. Earth Syst. Sci. 2022, 26, 129–148. [Google Scholar] [CrossRef]
- Aich, V.; Liersch, S.; Vetter, T.; Huang, S.; Tecklenburg, J.; Hoffmann, P.; Koch, H.; Fournet, S.; Krysanova, V.; Müller, E.N.; et al. Comparing impacts of climate change on streamflow in four large African river basins. Hydrol. Earth Syst. Sci. 2014, 18, 1305–1321. [Google Scholar] [CrossRef]
- Yang, Z.; Villarini, G.; Scoccimarro, E. Evaluation of the capability of regional climate models in reproducing the temporal clustering in heavy precipitation over Europe. Atmospheric Res. 2022, 269, 106027. [Google Scholar] [CrossRef]
- Belvederesi, C.; Zaghloul, M.S.; Achari, G.; Gupta, A.; Hassan, Q.K. Modelling river flow in cold and ungauged regions: A review of the purposes, methods, and challenges. Environ. Rev. 2022, 30, 159–173. [Google Scholar] [CrossRef]
- Liu, X.; Tang, Q.; Voisin, N.; Cui, H. Projected impacts of climate change on hydropower potential in China. Hydrol. Earth Syst. Sci. 2016, 20, 3343–3359. [Google Scholar] [CrossRef]
- Önöz, B.; Ve Bulu, A. Frequency Analysis of Low Flows by the PPCC Test in Turkey; FRIEND-97, 1-4 Ekim; IAHS: Postojna, Slovenia, 1997. [Google Scholar]
- Rossi, G.; Caporali, E. Regional Estimation Method Of Rivers Low Flow from River Basin Characteristics; Department of Civil and Environmental Engineering, University of Firenze: Firenze, Italy, 2017. [Google Scholar]
- Li, H.; Huang, G.; Li, Y.; Sun, J.; Gao, P. A C-Vine Copula-Based Quantile Regression Method for Streamflow Forecasting in Xiangxi River Basin, China. Sustainability 2021, 13, 4627. [Google Scholar] [CrossRef]
- Sengupta, A.; Adams, S.K.; Bledsoe, B.P.; Stein, E.D.; McCune, K.S.; Mazor, R.D. Tools for managing hydrologic alteration on a regional scale: Estimating changes in flow characteristics at ungauged sites. Freshw. Biol. 2018, 63, 769–785. [Google Scholar] [CrossRef]
- Gustard, A.; Marshall, D.C.W.; Sutcliffe, M.F. Low Flow Estimation in Scotland; Report No. 101; Institute of Hydrology: Wallingford, WA, USA, 1987. [Google Scholar]
- Supriya, P.; Krishnaveni, M.; Subbulakshmi, M. Regression Analysis of Annual Maximum Daily Rainfall and Stream Flow for Flood Forecasting in Vellar River Basin. Aquat. Procedia 2015, 4, 957–963. [Google Scholar] [CrossRef]
- Needhidasan, S.; Chenchu Babu, K.; Natrayan, M.; Naveen, D.C.; Vinothkumar, S. Preserving the Environment Due to the Flash Floods in Vellar River at TV Puthur, Virudhachalam Taluk, Tamil Nadu: A Case Study. Int. J. Struct. Civ. Eng. Res. 2013, 2, 104–114. [Google Scholar]
- Roland, M.A.; Stuckey, M.H. Regression Equations for Estimating Flood Flows at Selected Recurrence Intervals for Ungaged Streams in Pennsylvania; U.S. Geological Survey Scientific Investigations Report 2008-5102; U.S. Geological Survey: Reston, VA, USA, 2008; 57p. [Google Scholar]
- Waltemeyer, S.D. Analysis of the Magnitude and Frequency of the 4-Day Annual Low Flow and Regression Equations for Estimating the 4-Day, 3-Year Low-Flow Frequency at Ngagged Sites on Unregulated Streams in New Mexico; U.S. Geological Survey Water-Resources Investigations Report 01–4271; U.S. Geological Survey: Reston, VA, USA, 2002; 22p. [Google Scholar] [CrossRef]
- Shi, P.; Chen, X.; Qu, S.M.; Zhang, Z.C.; Ma, J.L. Regional Frequency Analysis of Low Flow Based On L Moments: Case Study İn Karst Area, Southwest China. J. Hydrol. Eng. 2010, 15, 370–377. [Google Scholar] [CrossRef]
- Evans, J.P.; Smith, R.B.; Oglesby, R.J. Middle East climate simulation and dominant precipitation processes. Int. J. Clim. 2004, 24, 1671–1694. [Google Scholar] [CrossRef]
- Leavesley, G.H. Modeling the effects of climate change on water resources—A review. Clim. Chang. 1994, 28, 159–177. [Google Scholar] [CrossRef]
- Prein, A.F.; Langhans, W.; Fosser, G.; Ferrone, A.; Ban, N.; Goergen, K.; Keller, M.; Tölle, M.; Gutjahr, O.; Feser, F.; et al. A review on regional convection-permitting climate modeling: Demonstrations, prospects, and challenges. Rev. Geophys. 2015, 53, 323–361. [Google Scholar] [CrossRef]
- Lu, W.X.; Zhao, Y.; Chu, H.B.; Yang, L.L. The analysis of groundwater levels influenced by dual factors in western Jilin Province by using time series analysis method. Appl. Water Sci. 2013, 4, 251–260. [Google Scholar] [CrossRef]
- Vicuna, S.; Dracup, J.A. The evolution of climate change impact studies on hydrology and water resources in California. Clim. Chang. 2007, 82, 327–350. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Thomas, W.O. Low-Flow Frequency Estimation Using Base-Flow Measurements; Open-File Report 85-95; U.S. Geological Survey: Reston, VA, USA, 1985; pp. 85–95. [Google Scholar]
- USGS. Estimation Of Minimum 7-Day, 2-Year Discharge for Selected Stream Sites, and Associated Low-Flow Water-Quality Data, Southeast Texas, 1997–1998. 2013. Available online: http://pubs.usgs.gov/fs/fs-122-99/pdf/ (accessed on 12 March 2022).
- Sadik, A.K.; Barghouti, S. The Water Problems of the Arab World: Management of Scarce Water Resources. In Water in the Arab World; Rogers, P., Lydon, P., Eds.; Harvard University Press: Cambridge, MA, USA, 1994; pp. 4–37. [Google Scholar]
- Li, L.-J.; Zhang, L.; Wang, H.; Wang, J.; Yang, J.-W.; Jiang, D.-J.; Li, J.-Y.; Qin, D.-Y. Assessing the impact of climate variability and human activities on streamflow from the Wuding River basin in China. Hydrol. Process. 2007, 21, 3485–3491. [Google Scholar] [CrossRef]
- Li, X.; Meshgi, A.; Wang, X.; Zhang, J.; Tay, S.H.X.; Pijcke, G.; Manocha, N.; Ong, M.; Nguyen, M.T.; Babovic, V. Three resampling approaches based on method of fragments for daily-to-subdaily precipitation disaggregation. Int. J. Clim. 2018, 38, e1119–e1138. [Google Scholar] [CrossRef]
- Joo, H.; Lee, M.; Kim, J.; Jung, J.; Kwak, J.; Kim, H.S. Stream gauge network grouping analysis using community detection. Stoch. Environ. Res. Risk Assess. 2021, 35, 781–795. [Google Scholar] [CrossRef]
- Immerzeel, W.; Pellicciotti, F.; Bierkens, M. Rising river flows throughout the twenty-first century in two Himalayan glacierized watersheds. Nat. Geosci. 2013, 6, 742–745. [Google Scholar] [CrossRef]
- Tangborn, W.V.; Rasmussen, L.A. Hydrology of the North Cascades Region, Washington: 2. A proposed hydrometeorological streamflow prediction method. Water Resour. Res. 1976, 12, 203–216. [Google Scholar] [CrossRef]
- Yıldız, D. Natural Diminishing Trend of the Tigris and Euphrates Streamflows is Alarming for the Middle East Future. World Sci. News 2016, 47, 279–297. [Google Scholar]
- Türkeş, M.; Sümer, U.M.; Kiliç, G. Variations and trends in annual mean air temperatures in Turkey with respect to climatic variability. Int. J. Clim. 1995, 15, 557–569. [Google Scholar] [CrossRef]
- Li, J.; Feng, P.; Wei, Z. Incorporating the data of different watersheds to estimate the effects of land use change on flood peak and volume using multi-linear regression. Mitig. Adapt. Strat. Glob. Chang. 2013, 18, 1183–1196. [Google Scholar] [CrossRef]
- Demircan, M.; Gürkan, H.; Eskioğlu, O.; Arabacı, H.; Coşkun, M. Climate Change Projections for Turkey: Three Models and Two Scenarios. Turk. J. Water Sci. Manag. 2017, 1, 22–43. [Google Scholar] [CrossRef]
- Kilinc, H.C.; Haznedar, B. A Hybrid Model for Streamflow Forecasting in the Basin of Euphrates. Water 2022, 14, 80. [Google Scholar] [CrossRef]
- Lombard, P.J.; Holtschlag, D.J. Estimating Lag to Peak between Rainfall and Peak Streamflow with a Mixed-Effects Model. JAWRA J. Am. Water Resour. Assoc. 2018, 54, 949–961. [Google Scholar] [CrossRef]
- Nielsen, N.M.; Smink, W.A.C.; Fox, J.-P. Small and negative correlations among clustered observations: Limitations of the linear mixed effects model. Behaviormetrika 2021, 48, 51–77. [Google Scholar] [CrossRef]
- Helsel, D.R.; Ve Hirsch, R.M. Studies İn Environmental Science 49. Statistical Methods İn Water Resources; Elsevier: Amsterdam, The Netherlands, 1992; 522p. [Google Scholar]
- Sergienko, O.V.; Bindschadler, R.A.; Vornberger, P.L.; MacAyeal, D.R. Ice stream basal conditions from block-wise surface data inversion and simple regression models of ice stream flow: Application to Bindschadler Ice Stream. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).