Next Article in Journal
Geometric Anatomy Basis for Safe and Effective Focal Ablation of Prostate Cancer by Irreversible Electroporation (IRE)
Next Article in Special Issue
Brain Abscess Secondary to an Apparently Benign Transorbital Injury: An Infrequent Case Report with Literature Review
Previous Article in Journal
Jean Cruveilhier (1791–1874), a Predecessor of Evidence-Based Medicine
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Anatomia
Volume 2
Issue 3
10.3390/anatomia2030020
anatomia-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Hypothesis

Self-Similarity and Spatial Periodicity in Cerebral Cortical Patterning: Structural Design Notes for Neural Tissue Architects

by
Nicolas Rouleau
1,2,* and
Nirosha J. Murugan
1
1
Department of Health Sciences, Wilfrid Laurier University, Waterloo, ON N2L 3C5, Canada
2
Department of Biomedical Engineering, Initiative for Neural Science, Disease, & Engineering, Tufts University, Medford, MA 02155, USA
*
Author to whom correspondence should be addressed.
Anatomia 2023, 2(3), 222-231; https://doi.org/10.3390/anatomia2030020
Submission received: 8 June 2023 / Revised: 6 July 2023 / Accepted: 19 July 2023 / Published: 21 July 2023
(This article belongs to the Special Issue Neuroanatomy, Neuroinflammation and Neurodegeneration)
Browse Figures
Versions Notes

Abstract

:
Tissue engineering is a powerful tool with which to systematically identify the determinants of biological functions. Applied to the design and fabrication of biomimetic brains, tissue engineering serves to disentangle the complex anatomy of neural circuits and pathways by recapitulating structure-function relationships in simplified model systems. The complex neuroanatomy of the cerebral cortex, with its enigmatic columnar and stratified cytoarchitectonic organization, represents a major challenge toward isolating the minimal set of elements that are required to assemble neural tissues with cognitive functions. Whereas considerable efforts have highlighted important genetic and physical correlates of early cortical tissue patterning, no substantive attempt to identify the determinants of how the cortices acquire their relatively conserved, narrow range of numbered layers is evident in the literature. Similarly, it is not yet clear whether cortical columns and laminae are functionally relevant or epiphenomena of embryonic neurodevelopment. Here, we demonstrate that spatial frequencies (m−1) derived from the width-to-height ratios of cerebral cortical columns predict sinusoids with a narrow range of spatial cycles over the average cortical thickness. The resulting periodicities, denoted by theoretical wavenumbers, reflect the number of observed cortical layers among humans and across several other species as revealed by a comparative anatomy approach. We present a hypothesis that cortical columns and their periodic layers are emergent of the intrinsic spatial dimensions of neurons and their nested, self-similar aggregate structures including minicolumns. Finally, we discuss the implications of periodic tissue patterns in the context of neural tissue engineering.

1. Introduction

The anatomy of an organism, including its cellular composition and tissue architecture, serves as a scaffold and the foundational material upon which structural adaptations within the species are built. While the integration of many traits can be attributed to the process of natural selection, others are thought to persist within the species as byproducts of adaptation [1]. Just like the spandrels of an archway, which can be supportive, but are often dispensable or merely decorative, some biological structures may provide supportive materials that bear the marks of adaptation and the patterns of tissue organization but are effectively functionless [2]. This question, of whether or not a particular structure is necessary to an organism’s function, is central to many of the goals of biological engineering. Indeed, as tissue engineers become increasingly capable of designing and building artificial organs in the laboratory, it is worth distinguishing between the structures which must be incorporated to recapitulate the functions of the natural organs and those which can be replaced or omitted without compromising function. Fundamental to bioengineering is the assumption that there should be a minimal set of factors or conditions which, together, are sufficient to generate the desired biological function.
Neural tissue engineering represents one of the most exciting and challenging frontier areas of bioengineering. Investigators are now building brains to model disease [3,4,5,6], accelerate the discovery of life-saving therapies [7] and even display minimal features of cognition [8]; however, the inordinate complexity of brain structure-function continues to bottleneck progress. In particular, recapitulating the functional anatomy of the cerebral cortex—one of the most conspicuous structural neural correlates of cognition—represents a uniquely daunting task. The extreme interconnectedness of its microcircuitry represents as much of a challenge to the anatomist [9] as the problem of how mind emerges from matter represents to the physicist [10]. Ultimately, bioengineers will need to grapple with these and similar challenges to successfully build artificial brains with higher-order cognitive functions, which is to say, brains that can think, behave, and experience [11]. However, before significant progress can be achieved, the dependence or independence of neural function on particular neural structures should be elucidated. Toward engineering a comprehensively biomimetic brain, it may be necessary to identify the essential building blocks of the cerebral cortex and, on the bases of quantifiable patterns therein, to delineate the principles that determine cortical form and function. Further, the same principles could potentially inspire the design of synthetic brains in silico, thus contributing to the development of novel neuromorphic computers, artificial intelligences, and synthetic biological intelligences. What is the minimal set of neuroanatomical features that must be recapitulated in vitro to successfully enable higher-order function?
Unfortunately, it is not yet clear which patterns are functionally relevant. Indeed, sensory processing and mapping functions were largely unaffected by a lack of cortical layering in a mutant reeler mouse model [12,13]. On the other hand, there are examples such as FMR1 knockout mice that display both altered cortical cytoarchitecture and behavioral patterns consistent with Fragile X Syndrome [14]. Is there any indication that lamination is essential to cortical function? Or is laminar organization an anatomical remnant of cell migration and other tissue patterning events associated with embryogenesis? If the latter is true, it may be possible to recapitulate cortical functions in bioengineered models of the central nervous system without laminar cytoarchitecture. Such a demonstration would support the related functionalist concepts of multiple realizability and substrate independence, indicating that cognitive function may be achieved by very different means. In pursuit of an accurate, functional model of the cerebral cortex, it will be necessary to determine its most essential tissue elements or “building blocks”.

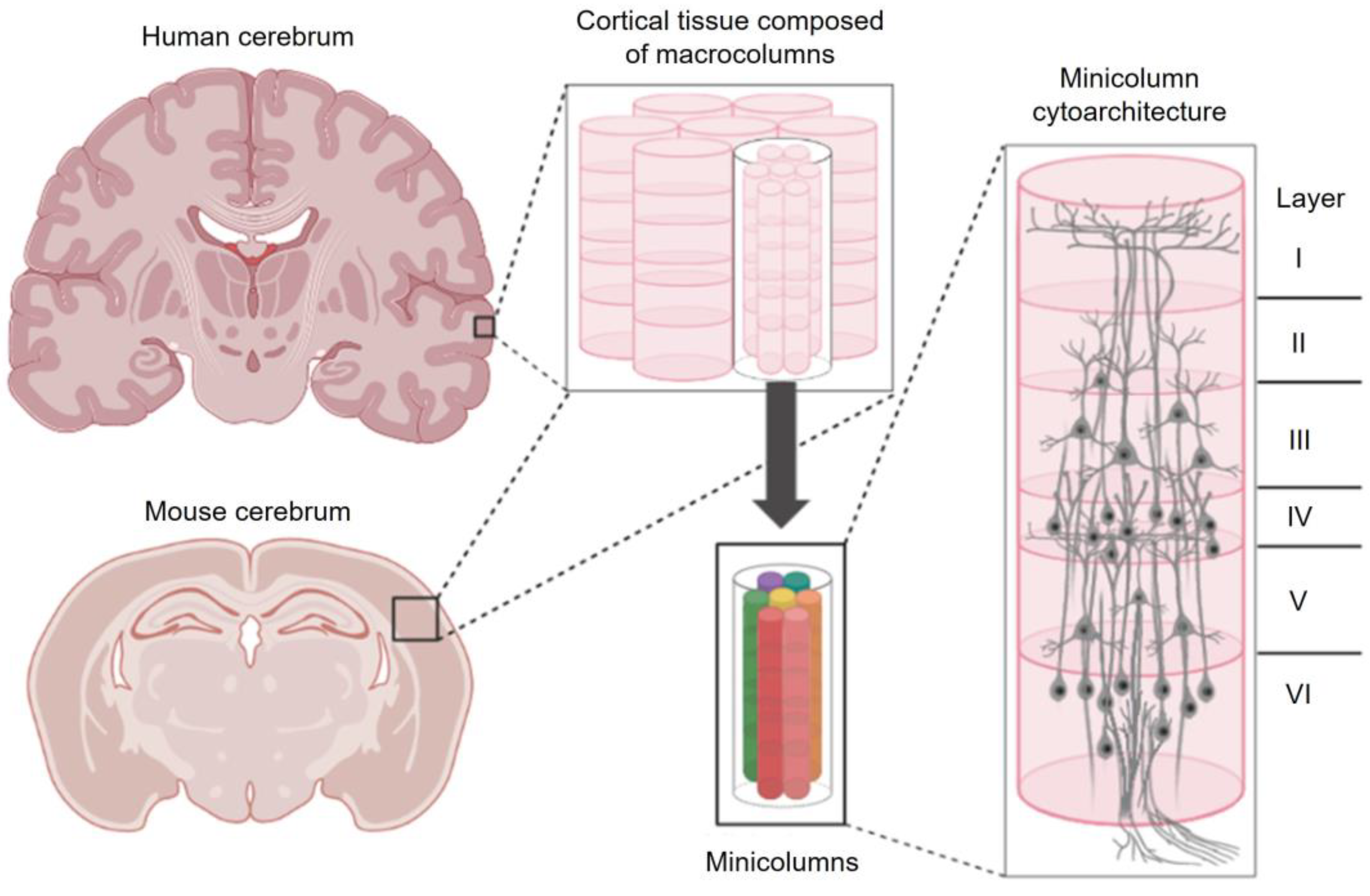
2. The Cortical Column Conundrum

In search of a fundamental unit of the cerebral cortex, investigators have historically focused on the cortical column. Cortical columns, which are also known as “macrocolumns” or “hypercolumns”, are modular subunits of the cerebral cortex (Figure 1). They are comprised of 1000 to 10,000 cells on average [15] organized into highly-interconnected vertical assemblies. Though cells within cortical columns respond to common stimulations within the spatial domains of their shared receptive fields, a review [16] of the famously contradictory literature on cortical columns [17] suggested these microanatomical assemblies could be structures without functions. If columns do play a role in the transmission, integration, coding, or storage of neural information, existing models do not accommodate their functional significance. However, with recent advances in neural biophysics including the possible identification of optical channels in the brain [18], the discovery of ephaptic coupling [19], and a renewed interest in brain biophotons [20], recondite functions may soon be identified.
Columns are organized into inconsistent patches, bands, and blobs that are found within both motor and sensory regions of the cortex [21]. Some clusters are symmetrically patterned across the cerebral hemispheres while others display reliable asymmetry [22]. Some columns are only transiently expressed during brain development while others persist into adulthood [23]. To complicate matters further, cortical columns appear to be macro-scale structures that are formed by many “minicolumns” that are bound together by short horizontal connections [24] (Figure 1). Interestingly, connections within and between cortical columns are not haphazard—they are periodic and display predictable structural features [25]. Disorders including Autism [26,27], Alzheimer’s Disease [28], and Dyslexia [29] have been linked to pathological minicolumnar anatomy. Indeed, the number of columns, spaces between columns, and their internal cytoarchitecture can be significantly distorted in diseased and developmentally disordered brains [26]. However, no clear genetic determinant of columnar organization including periodicity has yet been identified [16,23]. How then are cortical columns formed? How are they related to laminar organization and other periodic features of the cortex? Finally, what is the function of a cortical column?
Here, we present an analysis of the dimensions of cortical columns, their self-similar properties within the cortices, and we discuss their potential role with tissue patterning periodicities. Specifically, we observe a relationship between the width-to-height ratio of cortical columns and the observed range of cytoarchitectonically distinct tissue layers, or laminae, within the cerebral cortices. The quantitative relationships between nested levels of cortical cells, minicolumns, macrocolumns, and laminar tissues suggest a pattern of self-similarity within the cortex. Just as the spatial configuration of atoms within bulk or lattice materials express alternative physical properties despite identical, homogeneous atomic constituents, the morphological properties and resultant functional consequences of the cerebral cortices could be determined by similar organizational principles and constraints. Consistent with many previous observations of the fractal-like organization of brain structure [30,31,32,33], we will present a hypothesis that positions the cortical column as a periodic and self-similar structure that emerges spontaneously from spatial frequencies intrinsic to neural tissue patterning.

3. The Dimensions of Columns

A review of the structure of cortical columns was performed to instruct our analysis. Mountcastle’s (1957) original observations in feline brains suggested the upper limit for the width of a cortical column was approximately 500 µm and the vertical dimension was defined by cortical thickness [34]. However, subsequent measurements would reveal that the dimensions of cortical columns are non-uniform within brains and across species. In Rhesus monkeys (Macaca mulatta), the widths of columns also vary by age, ranging from as low as 230 µm in infants to as high as 1.2 mm in adults [35] and cortical thickness (vertical axis) is approximately 2.37 ± 0.19 mm when averaged across brain regions [36]. However, cortical thickness is also region-dependent, averaging 3.55 mm in the frontal-temporal regions and 1.73 mm in the parieto-occipital regions of M. mulatta [32]. In squirrel monkeys (Saimiri sciureus), widths are less variable, ranging from 330 µm to 830 µm (median of ~550 µm) with vertical dimensions of approximately 1.42 mm ± 0.12 mm on average in the foveal region of the striate cortex [37]. Wistar rat (Mus Musculus) pups display column widths ranging from 170 µm to 435 µm (mean of 310 µm) [38], with vertical dimensions of approximately 735–900 µm (from pia to layer 4/5 boundary) [39]. Unfortunately, methods for measuring the dimensions of columns are inconsistent across the literature, which complicates interpretation. For the purposes of developing the present hypothesis, we have focused on representative averages as reported in the literature.
Birds and fish also display columnar organization within their structural-functional equivalent of the cerebral cortex: the pallium. For example, the weakly electric fish Apteronotus leptorhynchus expresses 104 µm-wide (±31.2 µm) pallial columns which overlap and are less distinct than the barrel columns of rodents, extending vertically for approximately 300 µm across three ~60–100 µm layers of cells [40]. In chicks (Gallus gallus), the caudal mesopallium and three subnuclei of Field L also display columns with a cryptic layered organization (width: 300 µm to 500 µm; length: 1.28 mm ± 322 µm) [41]. Table 1 presents the dimensions of cortical columns of several species.
One of the few constants of columnar organization within cortices and pallia is that the vertical axes are longer than the horizontal axes. For example, human cortical columns are generally 5 to 6 times as long as they are wide [42]. And while cortical surface area can vary by many orders of magnitude across species, thickness is relatively constant where mice, macaques, and humans display vertical axes of approximately 2 to 4 mm on average from pia to white matter [22]. Indeed, there is more variability of cortical thickness within individual animal brains than between the aforementioned species. In the following section, quantifications will be based upon typical values which are characteristic of mammalian cortical dimensions to derive spatial relationships.

4. Spatial Periodicities within Columns Predict Observed Laminar Organization

To better understand the significance of the cortical column’s structure, we performed a quantitative analysis of its intrinsic spatial periodicities. Spatial frequency in cycles per unit of length (1 m−1), analogous to temporal frequency, can be thought of as a measure of periodicity over positions in space. Spatial frequencies, represented by wavenumbers, indicate how frequent the sinusoidal peak-to-peak component of the structure repeats over a length (cycles per meter). The wavenumber is given by the formula
ξ = 1 λ−1
where spatial frequency (ξ) is equivalent to the quotient of 1 over a wavelength (λ) in meters. Inputting wavelengths, wavenumbers can be computed within the spatial boundaries of the cerebral cortices. Assuming an average cortical column width of 500 µm [30], a wavenumber of 2 cycles per mm is achieved. When the average column’s wavenumber is multiplied over the average human neocortical thickness of 2.69 mm [43], the result is 5.38 cycles per average cortical thickness (Figure 2A). This spatial frequency is predictive of the stratification of the neocortex, which expresses 6 layers. It should be noted that layer I does not contain cell bodies and may represent a boundary that is distinct from the other 5 layers (II–VI). In summary, the width of a column tends to repeat over its own length as periodic layers with a spatial frequency that is proportional to the horizontal and vertical dimensions of the macrocolumn.
Concerning spatial frequency as a determinant of cerebral cortical stratification, the precise width and height values of cortical columns are less relevant than is the ratio between them. The width-to-height ratios necessary to generate 1, 2, 3, 4, 5, and 6 layers based upon spatial frequency (m−1) alone are 1, 0.5, 0.33, 0.25, 0.20, and 0.17 respectively. In other words, dividing the length of the cortex into equal spatial increments necessarily requires that the length of each increment must be equal fractions of the total length. For example, dividing an arbitrary length (1 mm) into 6 equal parts yields increments of approximately 0.17 mm. Similarly, dividing the empirically derived average human cortical thickness of 2.69 mm into 6 equal parts yields increments of approximately 0.45 mm or 448 µm to be precise—a value that is typically observed and convergent with empirical reports of average macrocolumn width. In both cases, the ratio between the periodic spatial increment (width) and the total spatial increment (length) is 0.17. Table 1 reports predicted wavenumbers within a conserved range across several species. Based upon the minimum and maximum wavenumbers presented in Table 1, the average periodic range was 1.57–6.24. Figure 2B–D plots cortical column width (W) by height (H) for the aforementioned species, with reported slopes for three column morphologies based upon minima, maxima, and average dimensions: Short and wide (Low H, High W, slope= 1.62), Long and thin (High H, Low W, slope= 6.56), and average (Average H, W, slope= 2.92). This analysis supports the restricted range of lamination that is observed in the cerebrocortical tissues of animals.
The neocortex (6 layers), paleocortex (4–5 layers), and archicortex (3 layers) are accommodated by the possible range of observable values. Similar to neocortical regions, the archicortical regions of the subiculum and hippocampus display columnar organization [44]. While we are not aware of any published width values associated with column structures within the archicortex, it is clear that cortical thickness decreases upon transition from the entorhinal region to the subiculum-CA1 hippocampal region to approximately 1.8 mm [45]. Assuming a standard 500 µm-wide column, the predicted periodicity within the subiculum would be 3.6 (layers) over 1.8 mm, which reflects the transition from the 6-layered parahippocampal cortex to the 3-layered hippocampal cortex.
If cortical columns expressed widths within the range of a single cell (10 µm) or several cells (100 µm), the model would predict tens or hundreds of cortical layers. No such macrocolumn or example of macrocolumnar hyperlamination has yet been identified. However, similar periodicities may be reflected at microscopic scales within the column in sub-laminar space. Indeed, the typical diameter of a minicolumn is within the range of 20 µm to 60 µm [24,46], which across 2.69 mm (the typical length of a minicolumn), would generate wavenumbers between approximately 45 (minimum) and 135 (maximum) cycles per column. It may be relevant to note that there are approximately 60 to 80 periodically spaced minicolumns within each macrocolumn, which converges with the predicted periodicity [47]. Interestingly, each minicolumn contains approximately 100 cells, which is also within the range of units predicted by the spatial periodicity of a single neuron (10–100 µm) over the length of a minicolumn. These repeating and self-similar quantitative patterns suggest a conserved and scale-invariant cytoarchitectonic principle underlying the organization of cortical subunits. It should be noted that self-similarity is observed throughout the nervous system. Indeed, it is a known feature of the dendritic arborization patterns of neurons [48], which define their receptive fields, and in turn, the widths of columns.

5. A Hypothesis of Cytoarchitectonic Self-Similarity and Periodicity

Based upon our calculations, we hypothesize that cortical columns are self-similar subunits of the cerebral cortex that are emergent of the intrinsic spatial dimensions of neurons and their aggregate structures including minicolumns. Our analysis predicts a periodic spatial relationship between the dimensions of cortical columns and macro-scale cortical laminae with a conserved range of approximately 3-to-6 cycles per column on average—a prediction that converges with the observed 3-to-6 layers of cells within cortices and pallia across species. This model, though based upon averages, does not require the assumption of a direct genetic determinant of cortical layering. Whereas strata are proximally determined by neural migration and the antecedent underlying genetic mechanisms, the ultimate explanation for the number of layers expressed within the cortices might be geometrically constrained by the spatial range of cortical columnar width and the widths of neuronal receptive fields, in turn. From this perspective, the cortical column could represent either a spatial determinant of cortical stratification or a byproduct of neuroembryonic tissue patterning.
Tissue-patterning within the cerebral cortices may be guided by geometrical factors and their physical influences. In recent years, it has become evident that the structure of the brain is at least partially determined by non-molecular factors. Most notably, Tallinen et al. (2016) demonstrated that gyri and sulci—the characteristic hills and valleys that constitute the cerebral convolutions—likely emerge as a function of the mechanical interaction between the growing fetal brain and skull [49]. Whereas genes and downstream molecules provide some instruction, it seems that constructing the brain’s shape involves information not found within any individual cell. Rather, the brain’s structure is a product of an interaction between programmed tissue patterning (genetic factors) and cues, forces, or constraints found outside cells, tissues, and organs (non-genetic factors). Scale-invariant relationships between cortical microanatomy and spatial frequency have been reported previously [50]; however, our analysis suggests that the formation of columns and laminae in the cerebral cortex may be related by organizational rules of self-similarity across the dimensions of cells, their receptive fields, and their distributions in brain-space.

6. Implications for Neural Tissue Engineering

From a bioengineering perspective, the identification and quantification of patterns and principles underlying cortical structure-function relationships is more likely to instruct the design of artificial tissues than is the isolation of highly specific, substrate-dependent mechanisms. Designing and building in vitro brain tissues with the capacity to process information such that the signal patterns are indistinguishable from human brain measurements would provide a path to understanding the fundamental neural basis of cognition [11]. Existing neural tissue models of autism [51,52], and Alzheimer’s disease [4,53]—both of which have been linked to columnar abnormalities [26,54]—could benefit from an informed patterning approach that emphasizes the organization of the cytoarchitecture of the cortex.
The hypothesis we have presented may represent one of potentially many structural “rules” or tissue patterning “guides” underlying the cytoarchitecture of the cerebral cortex. This interpretation is consistent with the discovery that models of cortical composition predict scaling laws associated with white-to-gray matter volume ratios and gyrification [55]. If structure dictates function, it may be fruitful to recapitulate the specific microstructures of the cortex in pursuit of artificial, biomimetic brain tissues. With techniques such as bioprinting and biomaterial scaffolding [56,57], the recapitulation of cortical column architecture is now within the realm of possibility. Designing unique neural architectures and examining emergent patterning phenomena as well as their functional correlates could reveal unique relationships. Indeed, in our recent reviews of advances in neural tissue engineering technologies [58] and their application as tools to explore cognition in vitro [11], we predicted that iterative brain tissues with alternative cytoarchitectures could represent toolkits to uncover mechanisms underlying learning, memory, decision-making, and consciousness.
A scientific framework to evaluate the current hypothesis would involve designing tissues with tightly controlled spatial parameters and observing emergent, self-organizing features. According to the hypothesis presented here, we should expect to observe increased laminar subdivisions as columnar widths and lengths decrease or increase respectively—parameters that can now be systematically manipulated using tissue engineering techniques. In other words, long, thin bioengineered columns are expected to self-organize into periodic, multi-layered structures (shorter, wider columns are predicted to be less periodic). By controlling the way neurons aggregate into clustered units or arborize, it should be possible to modify the number of laminae which develop assuming other relevant factors are held constant.

Author Contributions

N.R. and N.J.M. contributed equally to the paper, including conceptualization, methodology, quantitative analysis, writing, review, editing, visualization, and funding acquisition. All authors have read and agreed to the published version of the manuscript.

Funding

The authors acknowledge support from the National Sciences and Engineering Research Council of Canada (NSERC), Discovery Grants RGPIN-2022-04162 (to N.R.) and RGPIN-2021-03783 (to N.J.M.).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data presented are available in the manuscript.

Acknowledgments

The authors would like to thank MAP for inspiration and MB for his motivational feedback and insights.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gould, S.J.; Lewontin, R.C. The spandrels of San Marco and the Panglossian paradigm: A critique of the adaptationist programme. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1979, 205, 581–598. [Google Scholar]
  2. Buss, D.M.; Haselton, M.G.; Shackelford, T.K.; Bleske, A.L.; Wakefield, J.C. Adaptations, exaptations, and spandrels. Am. Psychol. 1998, 53, 533. [Google Scholar] [CrossRef] [PubMed]
  3. Raja, W.K.; Mungenast, A.E.; Lin, Y.T.; Ko, T.; Abdurrob, F.; Seo, J.; Tsai, L.H. Self-organizing 3D human neural tissue derived from induced pluripotent stem cells recapitulate Alzheimer’s disease phenotypes. PLoS ONE 2016, 11, e0161969. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Rouleau, N.; Cantley, W.L.; Liaudanskaya, V.; Berk, A.; Du, C.; Rusk, W.; Peirent, E.; Koester, C.; Nieland, T.J.F.; Kaplan, D.L. A Long-Living Bioengineered Neural Tissue Platform to Study Neurodegeneration. Macromol. Biosci. 2020, 20, 2000004. [Google Scholar] [CrossRef]
  5. Tian, W.; Hou, S.; Ma, J.; Zhang, C.; Xu, Q.; Lee, I.; Li, H.; Spector, M.; Cui, F.; Chung, C.; et al. Hyaluronic acid–poly-D-lysine-based three-dimensional hydrogel for traumatic brain injury. Tissue Eng. 2005, 11, 513–525. [Google Scholar] [CrossRef]
  6. Zhang, T.; Yan, Y.; Wang, X.; Xiong, Z.; Lin, F.; Wu, R.; Zhang, R. Three-dimensional gelatin and gelatin/hyaluronan hydrogel structures for traumatic brain injury. J. Bioact. Compat. Polym. 2007, 22, 19–29. [Google Scholar] [CrossRef]
  7. Chung, B.G.; Kang, L.; Khademhosseini, A. Micro-and nanoscale technologies for tissue engineering and drug discovery applications. Expert Opin. Drug Discov. 2007, 2, 1653–1668. [Google Scholar] [CrossRef]
  8. Rouleau, N.; Cairns, D.M.; Rusk, W.; Levin, M.; Kaplan, D.L. Learning and synaptic plasticity in 3D bioengineered neural tissues. Neurosci. Lett. 2021, 750, 135799. [Google Scholar] [CrossRef] [PubMed]
  9. Sporns, O.; Tononi, G.; Edelman, G.M. Theoretical neuroanatomy and the connectivity of the cerebral cortex. Behav. Brain Res. 2002, 135, 69–74. [Google Scholar] [CrossRef]
  10. Bohm, D. A new theory of the relationship of mind and matter. Philos. Psychol. 1990, 3, 271–286. [Google Scholar] [CrossRef]
  11. Rouleau, N.; Murugan, N.J.; Kaplan, D.L. Toward Studying Cognition in a Dish. Trends Cogn. Sci. 2021, 25, 294–304. [Google Scholar] [CrossRef]
  12. Guy, J.; Wagener, R.J.; Möck, M.; Staiger, J.F. Persistence of functional sensory maps in the absence of cortical layers in the somsatosensory cortex of reeler mice. Cereb. Cortex 2015, 25, 2517–2528. [Google Scholar] [CrossRef] [Green Version]
  13. Guy, J.; Staiger, J.F. The functioning of a cortex without layers. Front. Neuroanat. 2017, 11, 54. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Lee, F.H.; Lai, T.K.; Su, P.; Liu, F. Altered cortical Cytoarchitecture in the Fmr1 knockout mouse. Mol. Brain 2019, 12, 56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  15. Krueger, J.M.; Rector, D.M.; Roy, S.; Van Dongen, H.P.; Belenky, G.; Panksepp, J. Sleep as a fundamental property of neuronal assemblies. Nat. Rev. Neurosci. 2008, 9, 910–919. [Google Scholar] [CrossRef]
  16. Horton, J.C.; Adams, D.L. The cortical column: A structure without a function. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2005, 360, 837–862. [Google Scholar] [CrossRef] [PubMed]
  17. Rakic, P. Confusing cortical columns. Proc. Natl. Acad. Sci. USA 2008, 105, 12099–12100. [Google Scholar] [CrossRef] [PubMed]
  18. Kumar, S.; Boone, K.; Tuszyński, J.; Barclay, P.; Simon, C. Possible existence of optical communication channels in the brain. Sci. Rep. 2016, 6, 36508. [Google Scholar] [CrossRef] [Green Version]
  19. Anastassiou, C.A.; Koch, C. Ephaptic coupling to endogenous electric field activity: Why bother? Curr. Opin. Neurobiol. 2015, 31, 95–103. [Google Scholar] [CrossRef]
  20. Tang, R.; Dai, J. Biophoton signal transmission and processing in the brain. J. Photochem. Photobiol. B Biol. 2014, 139, 71–75. [Google Scholar] [CrossRef]
  21. Adams, D.L.; Horton, J.C. Capricious expression of cortical columns in the primate brain. Nat. Neurosci. 2003, 6, 113–114. [Google Scholar] [CrossRef]
  22. Rakic, P. Evolution of the neocortex: A perspective from developmental biology. Nat. Rev. Neurosci. 2009, 10, 724–735. [Google Scholar] [CrossRef]
  23. Molnár, Z.; Rockland, K.S. Cortical columns. In Neural Circuit and Cognitive Development; Academic Press: Cambridge, MA, USA, 2020; pp. 103–126. [Google Scholar]
  24. Buxhoeveden, D.P.; Casanova, M.F. The minicolumn hypothesis in neuroscience. Brain 2002, 125, 935–951. [Google Scholar] [CrossRef]
  25. Buxhoeveden, D.P.; Casanova, M.F. The minicolumn and evolution of the brain. Brain Behav. Evol. 2002, 60, 125–151. [Google Scholar] [CrossRef]
  26. Casanova, M.F.; Buxhoeveden, D.P.; Switala, A.E.; Roy, E. Minicolumnar pathology in autism. Neurology 2002, 58, 428–432. [Google Scholar] [CrossRef]
  27. Hutsler, J.J.; Casanova, M.F. Cortical construction in autism spectrum disorder: Columns, connectivity and the subplate. Neuropathol. Appl. Neurobiol. 2016, 42, 115–134. [Google Scholar] [CrossRef]
  28. Beker, S.; Kellner, V.; Kerti, L.; Stern, E.A. Interaction between amyloid-β pathology and cortical functional columnar organization. J. Neurosci. 2012, 32, 11241–11249. [Google Scholar] [CrossRef]
  29. Casanova, M.F.; Buxhoeveden, D.P.; Cohen, M.; Switala, A.E.; Roy, E.L. Minicolumnar pathology in dyslexia. Ann. Neurol. Off. J. Am. Neurol. Assoc. Child Neurol. Soc. 2002, 52, 108–110. [Google Scholar] [CrossRef] [PubMed]
  30. Aceves, G.A.G.; López, M.A.C.; Vanegas, M.A.; Meléndez, O.R.M.; Jiménez, S.M.; Cruz, J.C.P.; Peregrino, R.D.; Aguilar, A.G.; González, J.A.H. Fractal anatomy of the hippocampal formation. Surg. Radiol. Anat. 2018, 40, 1209–1215. [Google Scholar] [CrossRef] [PubMed]
  31. Jelinek, H.F.; Elston, G.N. Dendritic branching of pyramidal cells in the visual cortex of the nocturnal owl monkey: A fractal analysis. Fractals 2003, 11, 391–396. [Google Scholar] [CrossRef]
  32. Kiselev, V.G.; Hahn, K.R.; Auer, D.P. Is the brain cortex a fractal? Neuroimage 2003, 20, 1765–1774. [Google Scholar] [CrossRef] [Green Version]
  33. Milošević, N.T.; Ristanović, D.; Stanković, J.B. Fractal analysis of the laminar organization of spinal cord neurons. J. Neurosci. Methods 2005, 146, 198–204. [Google Scholar] [CrossRef]
  34. Mountcastle, V.B. Modality and topographic properties of single neurons of cat’s somatic sensory cortex. J. Neurophysiol. 1957, 20, 408–434. [Google Scholar] [CrossRef] [Green Version]
  35. Bugbee, N.M.; Goldman-Rakic, P.S. Columnar organization of corticocortical projections in squirrel and rhesus monkeys: Similarity of column width in species differing in cortical volume. J. Comp. Neurol. 1983, 220, 355–364. [Google Scholar] [CrossRef]
  36. Koo, B.-B.; Schettler, S.P.; Murray, D.E.; Lee, J.-M.; Killiany, R.J.; Rosene, D.L.; Kim, D.-S.; Ronen, I. Age-related effects on cortical thickness patterns of the Rhesus monkey brain. Neurobiol. Aging 2012, 33, 200.e23–200.e31. [Google Scholar] [CrossRef] [Green Version]
  37. Cowey, A. Projection of the retina on to striate and prestriate cortex in the squirrel monkey, Saimiri sciureus. J. Neurophysiol. 1964, 27, 366–393. [Google Scholar] [CrossRef]
  38. Petersen, C.C.; Sakmann, B. Functionally independent columns of rat somatosensory barrel cortex revealed with voltage-sensitive dye imaging. J. Neurosci. 2001, 21, 8435–8446. [Google Scholar] [CrossRef] [Green Version]
  39. Bureau, I.; Shepherd, G.M.; Svoboda, K. Precise development of functional and anatomical columns in the neocortex. Neuron 2004, 42, 789–801. [Google Scholar] [CrossRef] [Green Version]
  40. Trinh, A.T.; Harvey-Girard, E.; Teixeira, F.; Maler, L. Cryptic laminar and columnar organization in the dorsolateral pallium of a weakly electric fish. J. Comp. Neurol. 2016, 524, 408–428. [Google Scholar] [CrossRef]
  41. Wang, Y.; Brzozowska-Prechtl, A.; Karten, H.J. Laminar and columnar auditory cortex in avian brain. Proc. Natl. Acad. Sci. USA 2010, 107, 12676–12681. [Google Scholar] [CrossRef]
  42. LaBerge, D. Attention, consciousness, and electrical wave activity within the cortical column. Int. J. Psychophysiol. 2001, 43, 5–24. [Google Scholar] [CrossRef]
  43. Pakkenberg, B.; Gundersen, H.J.G. Neocortical neuron number in humans: Effect of sex and age. J. Comp. Neurol. 1997, 384, 312–320. [Google Scholar] [CrossRef]
  44. Goldman-Rakic, P.S.; Selemon, L.D.; Schwartz, M.L. Dual pathways connecting the dorsolateral prefrontal cortex with the hippocampal formation and parahippocampal cortex in the rhesus monkey. Neuroscience 1984, 12, 719–743. [Google Scholar] [CrossRef]
  45. Burggren, A.C.; Siddarth, P.; Mahmood, Z.; London, E.D.; Harrison, T.M.; Merrill, D.A.; Small, G.W.; Bookheimer, S.Y. Subregional hippocampal thickness abnormalities in older adults with a history of heavy cannabis use. Cannabis Cannabinoid Res. 2018, 3, 242–251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  46. Buxhoeveden, D.P. Minicolumn size and human cortex. Prog. Brain Res. 2012, 195, 219–235. [Google Scholar]
  47. Casanova, M.F.; Buxhoeveden, D.; Gomez, J. Disruption in the inhibitory architecture of the cell minicolumn: Implications for autisim. Neuroscientist 2003, 9, 496–507. [Google Scholar] [CrossRef] [PubMed]
  48. Milošević, N.T.; Ristanović, D. Fractality of dendritic arborization of spinal cord neurons. Neurosci. Lett. 2006, 396, 172–176. [Google Scholar] [CrossRef]
  49. Tallinen, T.; Chung, J.Y.; Rousseau, F.; Girard, N.; Lefèvre, J.; Mahadevan, L. On the growth and form of cortical convolutions. Nat. Phys. 2016, 12, 588–593. [Google Scholar] [CrossRef]
  50. Schwartz, E.L. Cortical anatomy, size invariance, and spatial frequency analysis. Perception 1981, 10, 455–468. [Google Scholar] [CrossRef] [PubMed]
  51. Choi, H.; Song, J.; Park, G.; Kim, J. Modeling of autism using organoid technology. Mol. Neurobiol. 2017, 54, 7789–7795. [Google Scholar] [CrossRef] [PubMed]
  52. Ilieva, M.; Svenningsen, Å.F.; Thorsen, M.; Michel, T.M. Psychiatry in a dish: Stem cells and brain organoids modeling autism spectrum disorders. Biol. Psychiatry 2018, 83, 558–568. [Google Scholar] [CrossRef]
  53. Cairns, D.M.; Rouleau, N.; Parker, R.N.; Walsh, K.G.; Gehrke, L.; Kaplan, D.L. A 3D human brain–like tissue model of herpes-induced Alzheimer’s disease. Sci. Adv. 2020, 6, eaay8828. [Google Scholar] [CrossRef]
  54. Lee, P.; Kim, H.R.; Jeong, Y. Detection of gray matter microstructural changes in Alzheimer’s disease continuum using fiber orientation. BMC Neurol. 2020, 20, 362. [Google Scholar] [CrossRef]
  55. de Lussanet, M.H.; Boström, K.J.; Wagner, H. A model of uniform cortical composition predicts the scaling laws of the mammalian cerebrum. bioRxiv 2020. [Google Scholar] [CrossRef]
  56. Chwalek, K.; Tang-Schomer, M.D.; Omenetto, F.G.; Kaplan, D.L. In vitro bioengineered model of cortical brain tissue. Nat. Protoc. 2015, 10, 1362–1373. [Google Scholar] [CrossRef]
  57. Knowlton, S.; Anand, S.; Shah, T.; Tasoglu, S. Bioprinting for neural tissue engineering. Trends Neurosci. 2018, 41, 31–46. [Google Scholar] [CrossRef]
  58. Rouleau, N.; Murugan, N.J.; Kaplan, D.L. Functional bioengineered models of the central nervous system. Nat. Rev. Bioeng. 2023, 1, 252–270. [Google Scholar] [CrossRef]
Anatomia 02 00020 g001 550
Figure 1. The columnar and stratified organization of the cerebral cortex. Cerebral cortical tissues display repeated, column-like patterning with nested, self-similar minicolumns at finer scales. Cells within minicolumns are distributed by cell type into distinct layers (laminae). This figure was created with BioRender.com (accessed on 19 May 2023).
Figure 1. The columnar and stratified organization of the cerebral cortex. Cerebral cortical tissues display repeated, column-like patterning with nested, self-similar minicolumns at finer scales. Cells within minicolumns are distributed by cell type into distinct layers (laminae). This figure was created with BioRender.com (accessed on 19 May 2023).
Anatomia 02 00020 g001
Anatomia 02 00020 g002 550
Figure 2. Spatial frequency of lamination and the dimensions of cortical columns. (A) Width (W), height (H) and spatial frequency (1 m−1) plotted along a macrocolumn. Plotting column dimension values for M. mulatta, S. sciureus, M. Musculus, A. leptorhynchus and G. gallus revealed slope values of (B) 1.62, (C) 6.56, and (D) 2.92 for three types of columns: Short and wide columns (Low H, High W), long and thin columns (High H, Low W), and average columns (Average H, W). R2 values are also reported. This figure was partly created with BioRender.com, accessed on 19 May 2023.
Figure 2. Spatial frequency of lamination and the dimensions of cortical columns. (A) Width (W), height (H) and spatial frequency (1 m−1) plotted along a macrocolumn. Plotting column dimension values for M. mulatta, S. sciureus, M. Musculus, A. leptorhynchus and G. gallus revealed slope values of (B) 1.62, (C) 6.56, and (D) 2.92 for three types of columns: Short and wide columns (Low H, High W), long and thin columns (High H, Low W), and average columns (Average H, W). R2 values are also reported. This figure was partly created with BioRender.com, accessed on 19 May 2023.
Anatomia 02 00020 g002
Table
Table 1. Species-specific ranges of cortical column widths, heights, and wavenumbers predicting spatially periodic laminae.
Table 1. Species-specific ranges of cortical column widths, heights, and wavenumbers predicting spatially periodic laminae.
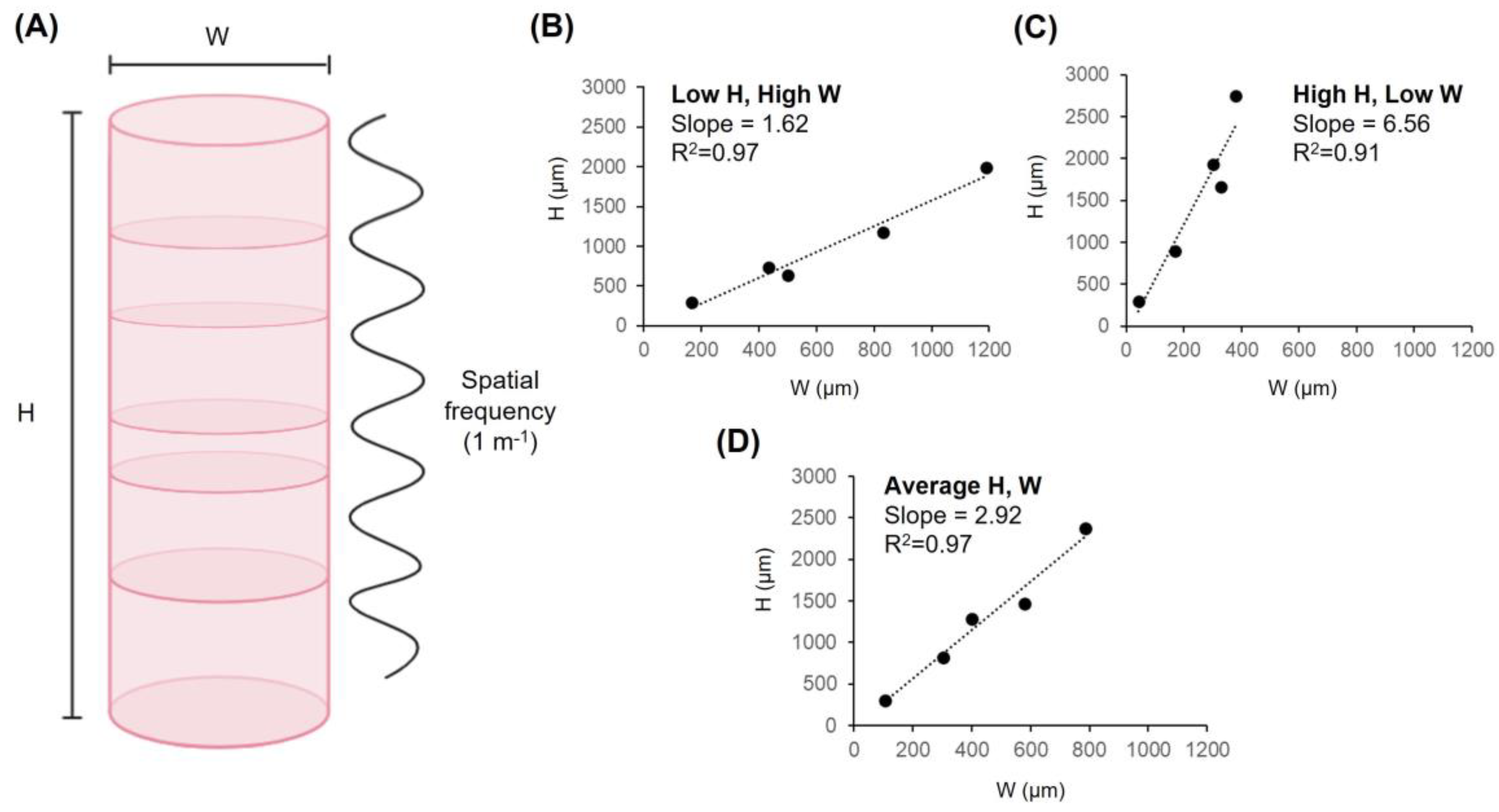
SpeciesColumn Dimensions (µm)Predicted
Wavenumbers		References
WidthHeight
MinMaxMinMax
Rhesus monkey
(M. mulatta)		3801190199027501.67–7.24[35,36]
Squirrel monkey
(S. sciureus)		330830117616641.42–5.04[35]
Wistar rat
(M. musculus)		1704357359001.69–5.29[38,39]
Electric fish
(A. leptorhynchus)		41.6166.43003001.80–7.21[40]
Chick
(G. gallus)		30050064019281.28–6.43[41]
Predicted wavenumbers reflect cycles per species-specific cortical dimensions for representative (averaged) brain regions. Column dimensions reflect reported min-max ranges; if ranges were not reported, means ± 2 standard deviations were used to compute conservative estimates.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Rouleau, N.; Murugan, N.J. Self-Similarity and Spatial Periodicity in Cerebral Cortical Patterning: Structural Design Notes for Neural Tissue Architects. Anatomia 2023, 2, 222-231. https://doi.org/10.3390/anatomia2030020

AMA Style

Rouleau N, Murugan NJ. Self-Similarity and Spatial Periodicity in Cerebral Cortical Patterning: Structural Design Notes for Neural Tissue Architects. Anatomia. 2023; 2(3):222-231. https://doi.org/10.3390/anatomia2030020

Chicago/Turabian Style

Rouleau, Nicolas, and Nirosha J. Murugan. 2023. "Self-Similarity and Spatial Periodicity in Cerebral Cortical Patterning: Structural Design Notes for Neural Tissue Architects" Anatomia 2, no. 3: 222-231. https://doi.org/10.3390/anatomia2030020

APA Style

Rouleau, N., & Murugan, N. J. (2023). Self-Similarity and Spatial Periodicity in Cerebral Cortical Patterning: Structural Design Notes for Neural Tissue Architects. Anatomia, 2(3), 222-231. https://doi.org/10.3390/anatomia2030020

Article Metrics

Back to TopTop