Modelling Crime Data Using the Non-Stationary Bivariate Integer-Valued Autoregressive (BINAR(1)) Models with Poisson-Lindley (PL) Innovations ^†

Abstract

This paper proposes a family of first order bivariate integer-valued autoregressive (BINAR(1)) with Poisson Lindley innovations (BINAR(1)PL). The model parameters are estimated using the conditional maximum likelihood (CML) estimation approach. The proposed models are applied on some real life crime data.

1. Introduction

New first-order autoregressive models (INAR(1)) with various innovation and marginal distributions are constantly being added to the literature on integer-valued time series. Inspired by McKenzie’s work [1] on discrete-valued ARIMA models, a number of INAR(1) models put out that are based on generalized thinning techniques, such as the binomial [2] for overdispersed series counting. Livio et al.’s introduced an INAR(1) with the Poisson–Lindley (PL) innovations (INAR(1)PL) [3] to model overdispersed series because INAR(1)PL produces better AICs than some of their peers, including PLINAR(1) in Mohammadpour et al. [4] and NGINAR(1) in Ristic et al. [5]. As for the bivariate INAR(1) (BINAR(1)) models, we have the work by Mamode Khan et al. [6] which introduce a class of BINAR(1)PL models under different cross-correlation functions and show that their models provide superior model fitness criteria than other competing INAR(1) models. However, all the above models have been developed under stationary assumptions, which is not applicable to real life situations.

The PL distribution is appropriate for unimodality, overdispersion, and infinite divisibility since it is a member of the compound Poisson distribution family (for further information, see Mohammadpour et al. [4]). The superiority of the AICs under the integer-valued bilinear time series model with the PL distribution under the binomial thinning and Pegram operations was recently observed by Mohammadpour et al. [7]. The INAR(1)PL is a promising model for analyzing bivariate integer-valued autoregressive series of order 1 (BINAR(1)) with PL innovations (BINAR(1)PL) because of these characteristics. Hence, this paper proposed a new class of constrained and unconstrained BINAR(1)PL models under non-stationary assumptions. The conditional maximum likelihood (CML) approach is used to estimate the model parameters.

The organisation of the paper is as follows: Section 2 provides the model construction of the proposed class of constrained and unconstrained BINAR(1) PL models. The moments are derived under non-stationary assumptions. In Section 3, the CML method is used to estimate the model parameters. A simulation experiment is presented in Section 4 and the conclusion in Section 5.

2. Model Development

2.1. INAR(1)PL Model

Consider

$$Y_t=\rho \ast Y_{t-1}+{ϵ}_t$$

(1)

where $\rho \in$ [0, 1] and $\rho \ast Y_{t-1}$ indicates the binomial thinning operation [8]. In the above INAR(1) model, ${ϵ}_t\sim \mathrm{PL}\left({\theta }_t\right)$, where $E\left({ϵ}_t\right)={\displaystyle \frac{({\theta }_t+2)}{{\theta }_t(1+{\theta }_t)}}$ and Var$({ϵ}_t)=E\left({ϵ}_t\right)[1+c_t]={\displaystyle \frac{{\theta }_t^3+4{\theta }_t^2+6{\theta }_t+2}{{\theta }_t{({\theta }_t+1)}^2}}$, where $c_t={\displaystyle \frac{{\theta }_t^2+4{\theta }_t+2}{{\theta }_t({\theta }_t+1)({\theta }_t+2)}}$.

Based on the above assumptions, it is proved that

$$\begin{array}{cc}\hfill E\left(Y_t\right)& =\rho E\left(Y_{t-1}\right)+E\left({ϵ}_t\right)\hfill \\ \hfill E\left(Y_t\right)& =\rho E\left(Y_{t-1}\right)+{\displaystyle \frac{({\theta }_t+2)}{{\theta }_t(1+{\theta }_t)}}\hfill \end{array}$$

(2)

For $t=1$, we assume $E\left(Y_0\right)=E\left(Y_1\right)$, we have

$$E\left(Y_1\right)={\displaystyle \frac{({\theta }_1+2)}{{\theta }_1(1+{\theta }_1)(1-\rho )}}$$

(3)

For $t=2,\dots ,T$, $E\left(Y_t\right)$ is computed iteratively using Equation (2).

$$\begin{array}{cc}\hfill Var\left(Y_t\right)& =\rho (1-\rho )E\left(Y_{t-1}\right)+{\rho }^{2}Var\left(Y_{t-1}\right)+Var\left({ϵ}_t\right)\hfill \\ \hfill Var\left(Y_t\right)& =\rho (1-\rho )E\left(Y_{t-1}\right)+{\rho }^{2}Var\left(Y_{t-1}\right)+{\displaystyle \frac{{\theta }_t^3+4{\theta }_t^2+6{\theta }_t+2}{{\theta }_t{({\theta }_t+1)}^2}}\hfill \end{array}$$

(4)

For $t=1$, we assume $Var\left(Y_0\right)=Var\left(Y_1\right)$, we have

$$Var\left(Y_1\right)=E\left(Y_1\right)\left[1+{\displaystyle \frac{{\theta }_1^2+4{\theta }_1+2}{{\theta }_1({\theta }_1+1)({\theta }_1+2)(1+\rho )}}\right]$$

(5)

For $t=2,\dots ,T$, $Var\left(Y_t\right)$ is computed iteratively using Equation (4).

2.2. Constrained BINAR(1)PL Model

The constrained BINAR(1) model is specified as

$$Y_t^{\left[1\right]}={\rho }_1\ast Y_{t-1}^{\left[1\right]}+{ϵ}_t^{\left[1\right]},$$

(6)

$$Y_t^{\left[2\right]}={\rho }_2\ast Y_{t-1}^{\left[2\right]}+{ϵ}_t^{\left[2\right]}$$

(7)

where ${\rho }_k\in$ [0, 1], for k ∈$\{1,2\}$. Once again, ${\rho }_k\ast Y_{t-1}^{\left[k\right]}$ indicates the binomial thinning operation such that $\{{\rho }_k\ast Y_{t-1}^{\left[k\right]}|Y_{t-1}^{\left[k\right]}\}Binomial(Y_{t-1}^{\left[k\right]},{\rho }_k)$ [8,9,10]. The distribution of the innovation terms are as follows: ${ϵ}_t^{\left[k\right]}\sim \mathrm{PL}\left({\theta }_t^{\left[k\right]}\right)$, where $E\left({ϵ}_t^{\left[k\right]}\right)={\displaystyle \frac{({\theta }_t^{\left[k\right]}+2)}{{\theta }_t^{\left[k\right]}(1+{\theta }_t^{\left[k\right]})}}$ and Var$({ϵ}_t^{\left[k\right]})=E\left({ϵ}_t^{\left[k\right]}\right)[1+c_t^{\left[k\right]}]={\displaystyle \frac{{\left({\theta }_t^{\left[k\right]}\right)}^3+4{\left({\theta }_t^{\left[k\right]}\right)}^2+6{\theta }_t^{\left[k\right]}+2}{{\theta }_t^{\left[k\right]}{({\theta }_t^{\left[k\right]}+1)}^2}}$, where $c_t^{\left[k\right]}={\displaystyle \frac{{\left({\theta }_t^{\left[k\right]}\right)}^2+4{\theta }_t^{\left[k\right]}+2}{{\theta }_t^{\left[k\right]}({\theta }_t^{\left[k\right]}+1)({\theta }_t^{\left[k\right]}+2)}}$.

Based on the above conditions, it can be shown that

$$\begin{array}{cc}\hfill E\left(Y_t^{\left[k\right]}\right)& ={\rho }_{k}E\left(Y_{t-1}^{\left[k\right]}\right)+E\left({ϵ}_t^{\left[k\right]}\right)\hfill \\ \hfill E\left(Y_t^{\left[k\right]}\right)& ={\rho }_{k}E\left(Y_{t-1}^{\left[k\right]}\right)+{\displaystyle \frac{({\theta }_t^{\left[k\right]}+2)}{{\theta }_t^{\left[k\right]}(1+{\theta }_t^{\left[k\right]})}}\hfill \end{array}$$

(8)

For $t=1$, we assume $E\left(Y_0^{\left[k\right]}\right)=E\left(Y_1^{\left[k\right]}\right)$, we have

$$E\left(Y_1^{\left[k\right]}\right)={\displaystyle \frac{({\theta }_1^{\left[k\right]}+2)}{{\theta }_1^{\left[k\right]}(1+{\theta }_1^{\left[k\right]})(1-{\rho }_k)}}$$

(9)

For $t=2,\dots ,T$, $E\left(Y_t\right)$ is computed iteratively using Equation (10).

$$\begin{array}{c}\hfill Var\left(Y_t^{\left[k\right]}\right)={\rho }_k(1-{\rho }_k)E\left(Y_{t-1}^{\left[k\right]}\right)+{\rho }_k^{2}Var\left(Y_{t-1}^{\left[k\right]}\right)+Var\left({ϵ}_t^{\left[k\right]}\right)\end{array}$$

(10)

For $t=1$, we assume $Var\left(Y_0\right)=Var\left(Y_1\right)$, we have

$$\begin{array}{cc}\hfill Var\left(Y_1\right)& ={\displaystyle \frac{{\rho }_k(1-{\rho }_k)E\left(Y_1^{\left[k\right]}\right)+Var\left({ϵ}_1^{\left[k\right]}\right)}{(1-{\rho }_k^2)}}\hfill \\ \hfill & ={\displaystyle \frac{\frac{{\rho }_k(1-{\rho }_k)({\theta }_1^{\left[k\right]}+2)}{{\theta }_1^{\left[k\right]}(1+{\theta }_1^{\left[k\right]})(1-{\rho }_k)}+\frac{{\left({\theta }_1^{\left[k\right]}\right)}^3+4{\left({\theta }_1^{\left[k\right]}\right)}^2+6{\theta }_1^{\left[k\right]}+2}{{\theta }_1^{\left[k\right]}{({\theta }_1^{\left[k\right]}+1)}^2}}{1-{\rho }_k^2}}\hfill \end{array}$$

(11)

For $t=2,\dots ,T$, $Var\left(Y_t\right)$ is computed iteratively using Equation (4).

$$\begin{array}{cc}\hfill \mathrm{Cov}(Y_t^{\left[1\right]},Y_t^{\left[2\right]})& ={\rho }_1{\rho }_2\mathrm{Cov}(Y_{t-1}^{\left[1\right]},Y_{t-1}^{\left[2\right]})+\mathrm{Cov}({ϵ}_t^{\left[1\right]},{ϵ}_t^{\left[2\right]})\hfill \end{array}$$

(12)

where $\mathrm{Cov}({ϵ}_t^{\left[1\right]},{ϵ}_t^{\left[2\right]})={\rho }_{12}(R_{t,t}^{\left[1\right]}-{\theta }_t^{\left[1\right]}{R}_t^{\left[1\right]})(R_{t,t}^{\left[2\right]}-{\theta }_t^{\left[2\right]}{R}_t^{\left[2\right]})$, where $R_t^{\left[k\right]}={\displaystyle \frac{{\left({\theta }_t^{\left[k\right]}\right)}^2}{1+{\theta }_t^{\left[k\right]}}}{\displaystyle \frac{{\theta }_t^{\left[k\right]}+2-\exp (-1)}{{({\theta }_t^{\left[k\right]}+1-\exp (-1))}^2}}$ and $R_{t,t}^{\left[k\right]}={\displaystyle \frac{{\left({\theta }_t^{\left[k\right]}\right)}^2}{1+{\theta }_t^{\left[k\right]}}}{\displaystyle \frac{{\theta }_t^{\left[k\right]}\exp (-1)-\exp (-2)+3\exp (-1)}{{({\theta }_t^{\left[k\right]}+1-\exp (-1))}^3}}$. For $t=1$, we assume $\mathrm{Cov}(Y_0^{\left[1\right]},Y_0^{\left[2\right]})=\mathrm{Cov}(Y_1^{\left[1\right]},Y_1^{\left[2\right]})$, we have

$$\mathrm{Cov}(Y_1^{\left[1\right]},Y_1^{\left[2\right]})={\displaystyle \frac{\mathrm{Cov}({ϵ}_1^{\left[1\right]},{ϵ}_1^{\left[2\right]})}{(1-{\rho }_1{\rho }_2)}}$$

(13)

For $t=2,\dots ,T$, $\mathrm{Cov}(Y_t^{\left[1\right]},Y_t^{\left[2\right]})$ is computed iteratively using Equation (13).

The forecasting equation for the constrained BINAR(1)PL model is given by

$$\begin{array}{cc}\hfill E\left(Y_t^{\left[k\right]}\right|Y_{t-1}^{\left[k\right]})& ={\widehat{\rho }}_k{Y}_{t-1}^{\left[k\right]}+{\displaystyle \frac{({\widehat{\theta }}_t^{\left[k\right]}+2)}{{\widehat{\theta }}_t^{\left[k\right]}(1+{\widehat{\theta }}_t^{\left[k\right]})}}\hfill \end{array}$$

(14)

2.3. The Unconstrained BINAR(1)PL Model

Consider the unconstrained BINAR(1)PL Model with full correlation structure:

$$Y_t^{\left[1\right]}={\rho }_{11}\ast Y_{t-1}^{\left[1\right]}+{\rho }_{12}\ast Y_{t-1}^{\left[2\right]}+R_t^{\left[1\right]},$$

(15)

$$Y_t^{\left[2\right]}={\rho }_{21}\ast Y_{t-1}^{\left[1\right]}+{\rho }_{22}\ast Y_{t-1}^{\left[2\right]}+R_t^{\left[2\right]},$$

(16)

with similar assumptions of the model paramters as the constrained BINAR(1)PL model in Section 2.2. ${ϵ}_t^{\left[k\right]}\sim \mathrm{PL}\left({\theta }_t^{\left[k\right]}\right)$, where $E\left({ϵ}_t^{\left[k\right]}\right)={\displaystyle \frac{({\theta }_t^{\left[k\right]}+2)}{{\theta }_t^{\left[k\right]}(1+{\theta }_t^{\left[k\right]})}}$ and Var$({ϵ}_t^{\left[k\right]})=E\left({ϵ}_t^{\left[k\right]}\right)[1+c_t^{\left[k\right]}]={\displaystyle \frac{{\left({\theta }_t^{\left[k\right]}\right)}^3+4{\left({\theta }_t^{\left[k\right]}\right)}^2+6{\theta }_t^{\left[k\right]}+2}{{\theta }_t^{\left[k\right]}{({\theta }_t^{\left[k\right]}+1)}^2}}$, where $c_t^{\left[k\right]}={\displaystyle \frac{{\left({\theta }_t^{\left[k\right]}\right)}^2+4{\theta }_t^{\left[k\right]}+2}{{\theta }_t^{\left[k\right]}({\theta }_t^{\left[k\right]}+1)({\theta }_t^{\left[k\right]}+2)}}$.

Based on the above conditions, the moments are derived as follows:

$$\begin{array}{cc}\hfill E\left(Y_t^{\left[1\right]}\right)& ={\rho }_{11}E\left(Y_{t-1}^{\left[1\right]}\right)+{\rho }_{12}E\left(Y_{t-1}^{\left[2\right]}\right)+E\left(R_t^{\left[1\right]}\right)\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill E\left(Y_t^{\left[2\right]}\right)& ={\rho }_{21}E\left(Y_{t-1}^{\left[1\right]}\right)+{\rho }_{22}E\left(Y_{t-1}^{\left[2\right]}\right)+E\left(R_t^{\left[2\right]}\right)\hfill \end{array}$$

(18)

For $t=1$, we assume $E\left(Y_0^{\left[k\right]}\right)=E\left(Y_1^{\left[k\right]}\right)$, we have

$$E\left(Y_1^{\left[1\right]}\right)={\displaystyle \frac{{\rho }_{12}E\left(Y_1^{\left[2\right]}\right)+\frac{({\theta }_1^{\left[1\right]}+2)}{{\theta }_1^{\left[1\right]}(1+{\theta }_1^{\left[1\right]})}}{1-{\rho }_{11}}}$$

(19)

$$E\left(Y_1^{\left[2\right]}\right)={\displaystyle \frac{{\rho }_{21}E\left(Y_1^{\left[1\right]}\right)+\frac{({\theta }_1^{\left[2\right]}+2)}{{\theta }_1^{\left[2\right]}(1+{\theta }_1^{\left[2\right]})}}{1-{\rho }_{22}}}$$

(20)

By solving Equations (19) and (20), we obtain

$$E\left(Y_1^{\left[1\right]}\right)={\displaystyle \frac{\frac{{\rho }_{12}({\theta }_1^{\left[2\right]}+2)}{{\theta }_1^{\left[2\right]}({\theta }_1^{\left[2\right]}+1)}+\frac{({\theta }_1^{\left[1\right]}+2)(1-{\rho }_{22})}{{\theta }_1^{\left[1\right]}(1+{\theta }_1^{\left[1\right]})}}{(1-{\rho }_{11})(1-{\rho }_{22})-{\rho }_{12}{\rho }_{21}}}$$

(21)

$$E\left(Y_1^{\left[2\right]}\right)={\displaystyle \frac{\frac{{\rho }_{21}({\theta }_1^{\left[1\right]}+2)}{{\theta }_1^{\left[1\right]}({\theta }_1^{\left[1\right]}+1)}+\frac{({\theta }_1^{\left[2\right]}+2)(1-{\rho }_{22})}{{\theta }_1^{\left[2\right]}(1+{\theta }_1^{\left[2\right]})}}{(1-{\rho }_{11})(1-{\rho }_{22})-{\rho }_{12}{\rho }_{21}}}$$

(22)

For $t=2,\dots ,T$, $E\left(Y_t^{\left[k\right]}\right)$ is computed iteratively using Equations (17) and (18).

$$\begin{array}{cc}\hfill Var\left(Y_t^{\left[1\right]}\right)& ={\rho }_{11}(1-{\rho }_{11})E\left(Y_{t-1}^{\left[1\right]}\right)+{\rho }_{11}^{2}Var\left(Y_{t-1}^{\left[1\right]}\right)+{\rho }_{12}(1-{\rho }_{12})E\left(Y_{t-1}^{\left[2\right]}\right)+{\rho }_{12}^{2}Var\left(Y_{t-1}^{\left[2\right]}\right)\hfill \\ \hfill & +Var\left({ϵ}_t^{\left[1\right]}\right)+2{\rho }_{11}{\rho }_{12}Cov(Y_{t-1}^{\left[1\right]},Y_{t-1}^{\left[2\right]})\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill Var\left(Y_t^{\left[2\right]}\right)& ={\rho }_{21}(1-{\rho }_{21})E\left(Y_{t-1}^{\left[1\right]}\right)+{\rho }_{21}^{2}Var\left(Y_{t-1}^{\left[1\right]}\right)+{\rho }_{22}(1-{\rho }_{22})E\left(Y_{t-1}^{\left[2\right]}\right)+{\rho }_{22}^{2}Var\left(Y_{t-1}^{\left[2\right]}\right)\hfill \\ \hfill & +Var\left({ϵ}_t^{\left[2\right]}\right)+2{\rho }_{21}{\rho }_{22}Cov(Y_{t-1}^{\left[1\right]},Y_{t-1}^{\left[2\right]})\hfill \end{array}$$

(24)

For $t=1$, we assume $Var\left(Y_0^{\left[k\right]}\right)=Var\left(Y_1^{\left[k\right]}\right)$, $E\left(Y_0^{\left[k\right]}\right)=E\left(Y_1^{\left[k\right]}\right)$, $Cov(Y_0^{\left[1\right]},Y_0^{\left[2\right]})=Cov(Y_1^{\left[1\right]},Y_1^{\left[2\right]})$ we have

$$\begin{array}{cc}\hfill Var\left(Y_1^{\left[1\right]}\right)& ={\displaystyle \frac{{\rho }_{11}(1-{\rho }_{11})E\left(Y_1^{\left[1\right]}\right)+{\rho }_{12}(1-{\rho }_{12})E\left(Y_1^{\left[2\right]}\right)+{\rho }_{12}^{2}Var\left(Y_1^{\left[2\right]}\right)}{(1-{\rho }_{11}^2)}}\hfill \\ \hfill & +{\displaystyle \frac{Var\left({ϵ}_1^{\left[1\right]}\right)+2{\rho }_{11}{\rho }_{12}Cov(Y_1^{\left[1\right]},Y_1^{\left[2\right]})}{(1-{\rho }_{11}^2)}}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill Var\left(Y_1^{\left[2\right]}\right)& ={\displaystyle \frac{{\rho }_{21}(1-{\rho }_{21})E\left(Y_1^{\left[1\right]}\right)+{\rho }_{21}^{2}Var\left(Y_1^{\left[1\right]}\right)+{\rho }_{22}(1-{\rho }_{22})E\left(Y_1^{\left[2\right]}\right)}{(1-{\rho }_{22}^2)}}\hfill \\ \hfill & +{\displaystyle \frac{Var\left({ϵ}_1^{\left[2\right]}\right)+2{\rho }_{21}{\rho }_{22}Cov(Y_1^{\left[1\right]},Y_1^{\left[2\right]})}{(1-{\rho }_{22}^2)}}\hfill \end{array}$$

(26)

Explicit expressions for $Var\left(Y_1^{\left[1\right]}\right)$ and $Var\left(Y_1^{\left[2\right]}\right)$ are obtained by solving Equations (25) and (26). For $t=2,\dots ,T$, $Var\left(Y_t^{\left[k\right]}\right)$ is computed iteratively using Equations (23) and (24).

$$\begin{array}{cc}\hfill \mathrm{Cov}(Y_t^{\left[1\right]},Y_t^{\left[2\right]})& ={\rho }_{11}{\rho }_{21}Var\left(Y_{t-1}^{\left[1\right]}\right)+{\rho }_{12}{\rho }_{22}Var\left(Y_{t-1}^{\left[2\right]}\right)+({\rho }_{12}{\rho }_{21}+{\rho }_{11}{\rho }_{22})\mathrm{Cov}(Y_{t-1}^{\left[1\right]},Y_{t-1}^{\left[2\right]})\hfill \end{array}$$

(27)

For $t=1$, we assume $\mathrm{Cov}(Y_0^{\left[1\right]},Y_0^{\left[2\right]})=\mathrm{Cov}(Y_1^{\left[1\right]},Y_1^{\left[2\right]})$, $Var\left(Y_0^{\left[k\right]}\right)=Var\left(Y_1^{\left[k\right]}\right)$, we have

$$\mathrm{Cov}(Y_1^{\left[1\right]},Y_1^{\left[2\right]})={\displaystyle \frac{{\rho }_{11}{\rho }_{21}Var\left(Y_1^{\left[1\right]}\right)+{\rho }_{12}{\rho }_{22}Var\left(Y_1^{\left[2\right]}\right)}{(1-{\rho }_{12}{\rho }_{21}-{\rho }_{11}{\rho }_{22})}}$$

(28)

For $t=2,\dots ,T$, $\mathrm{Cov}(Y_t^{\left[1\right]},Y_t^{\left[2\right]})$ is computed iteratively using Equation (27).

The forecasting equations for the unconstrained BINAR(1)PL model are given by

$$E\left(Y_t^{\left[1\right]}\right|Y_{t-1}^{\left[1\right]},Y_{t-1}^{\left[2\right]})={\widehat{\rho }}_{11}{Y}_{t-1}^{\left[1\right]}+{\widehat{\rho }}_{12}{Y}_{t-1}^{\left[2\right]}+{\displaystyle \frac{({\widehat{\theta }}_t^{\left[1\right]}+2)}{{\widehat{\theta }}_t^{\left[1\right]}(1+{\widehat{\theta }}_t^{\left[1\right]})}}$$

(29)

$$E\left(Y_t^{\left[2\right]}\right|Y_{t-1}^{\left[1\right]},Y_{t-1}^{\left[2\right]})={\widehat{\rho }}_{21}{Y}_{t-1}^{\left[1\right]}+{\widehat{\rho }}_{22}{Y}_{t-1}^{\left[2\right]}+{\displaystyle \frac{({\widehat{\theta }}_t^{\left[2\right]}+2)}{{\widehat{\theta }}_t^{\left[2\right]}(1+{\widehat{\theta }}_t^{\left[2\right]})}}$$

(30)

3. Estimation Method

This section proposes the CML approach to estimate the unknown parameters of the model. Using the convolution property [11], the conditional distribution function is given by

$$f\left(y_t^{\left[1\right]}{y}_t^{\left[2\right]}\right|y_{t-1}^{\left[1\right]},y_{t-1}^{\left[2\right]})=\sum _{k=0}^u\sum _{j=0}^v{f}_1\left(k\right)f_2\left(s\right)P(R_t^{\left[1\right]}=y_t^{\left[1\right]}-k)P(R_t^{\left[2\right]}=y_t^{\left[2\right]}-s)$$

(31)

where $u=min\left(Y_t^{\left[1\right]}{Y}_{t-1}^{\left[1\right]}\right)$ and $v=min\left(Y_t^{\left[2\right]}{Y}_{t-1}^{\left[2\right]}\right)$. Here, we define

$$f_1\left(k\right)=\sum _{j_1=0}^k\left(\begin{array}{c}{y}_{t-1}^{\left[1\right]}\\ j_1\end{array}\right)\left(\begin{array}{c}{y}_{t-1}^{\left[2\right]}\\ k-j_1\end{array}\right){\rho }_{11}^{j_1}{(1-{\rho }_{11})}^{y_{t-1}^{\left[1\right]}-j_1}{\rho }_{12}^{k-j_1}{(1-{\rho }_{12})}^{y_{t-1}^{\left[2\right]}-k+j_1}$$

(32)

$$f_2\left(s\right)=\sum _{j_2=0}^s\left(\begin{array}{c}{y}_{t-1}^{\left[2\right]}\\ j_2\end{array}\right)\left(\begin{array}{c}{y}_{t-1}^{\left[1\right]}\\ s-j_2\end{array}\right){\rho }_{22}^{j_2}{(1-{\rho }_{22})}^{y_{t-1}^{\left[2\right]}-j_2}{\rho }_{21}^{s-j_2}{(1-{\rho }_{21})}^{y_{t-1}^{\left[1\right]}-s+j_2}$$

(33)

Then, we can write the conditional likelihood function as $L\left(ϵ\right)={\prod }_{t=2}^{T}f(Y_t^{\left[1\right]},Y_t^{\left[2\right]}|y_{t-1}^{\left[1\right]},$$Y_{t-1}^{\left[2\right]})$. The maximization of $L\left(ϵ\right)$ is done using the standard $optim$ routine in R with quasi-Newton approaches (BFGS).

4. Data Application

In this section, the constrained and unconstrained BINAR(1)PL model is applied on a monthly series of theft and burglary for the period January 1990 to December 2001 (available at https://www.pittsburghpa.gov/Safety/Police/Police-Data-Portal/PBP-Annual-Reports), accessed on 1 February 2024. The count data consists of 144 observations for each type of offence. The descriptive statistics are provided in Table 1 and the time series plots in Figure 1 and Figure 2:

Table 1. Descriptive Statistics for the number of crimes from January 1990 to December 2001.

Crimes	Mean	Variance	Fisher Index	Cross-Correlation
Theft $\left(Y_t^{\left[1\right]}\right)$	13.1035	121.0238	9.2360	0.2182
Burglary $\left(Y_t^{\left[2\right]}\right)$	7.5795	37.6811	4.9714

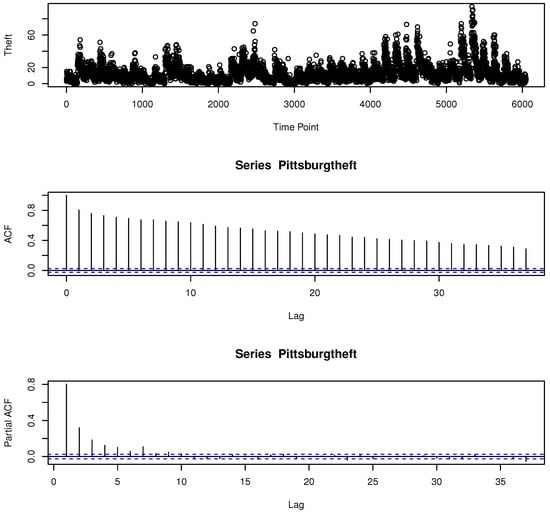
Figure 1. Time series, ACF and PACF plots of the monthly thefts from January 1990 to December 2001.

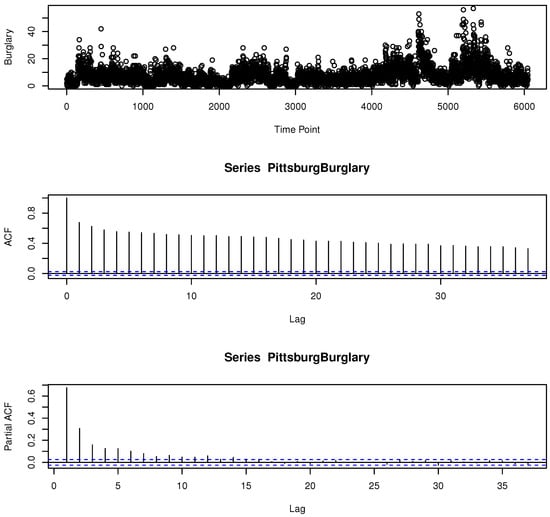
Figure 2. Time series, ACF and PACF plots of the monthly burglary from January 1990 to December 2001.

Table 2 clearly indicates that the bivariate time series data for theft and burglary are over-dispersed and the cross-correlation coefficient confirms the existence of cross-dependence between the two series. Hence, we fit both the constrained and unconstrained BINAR(1)PL models and the estimates are provided in Table 2:

Table 2. Thefts and Robbery: Estimates of the model parameters.

Model	${\widehat{\mathit{\theta }}}_{\mathit{t}}^{\left[1\right]}$	${\widehat{\mathit{\theta }}}_{\mathit{t}}^{\left[2\right]}$	${\widehat{\mathit{\rho }}}_1$	${\widehat{\mathit{\rho }}}_2$	${\widehat{\mathit{\rho }}}_{12}$	${\widehat{\mathit{\rho }}}_{21}$	${\widehat{\mathit{\alpha }}}_{12}$
CBINAR(1)PL	0.4682	0.4212	0.5079	0.0.4128			0.3605
s.e	(0.0539)	(0.0403)	(0.0484)	(0.0565)			(0.0549)
UBINAR(1)PL	0.4798	0.4051	0.4863	0.4397	0.0241	0.312
s.e	(0.0516)	(0.0374)	(0.0375)	(0.0419)	(0.0205)	(0.0306)

Using the forecasting Equations (14), (29) and (30), we compute the one-step ahead forecasts for the number of monthly theft and robbery, with corresponding root mean square errors (RMSEs) as shown in Table 3:

Table 3. RMSE values for number of theft and robbery.

Models	RMSE	RMSE
	${\mathit{Y}}_{\mathit{t}}^{\mathbf{\left[}\mathbf{1}\mathbf{\right]}}$	${\mathit{Y}}_{\mathit{t}}^{\mathbf{\left[}\mathbf{2}\mathbf{\right]}}$
CBINAR(1)	4.174	5.382
UBINAR(1)	3.381	4.428

5. Conclusions

This paper introduces two types of BINAR(1)PL model, namely the constrained and unconstrained BINAR(1)PL. The moments of the proposed models are derived and the CML approach is used to estimate the model parameters. Both models are applied on a real theft and burglary time series data and the two proposed BINAR are commendable models for the bivariate time series modelling.