Classifying Two Banking Cultures: The Pragmatic Structure of Economic Revelations †
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Unconditional Drift: OLS and Fixed Effects Regression of the Original Dataset
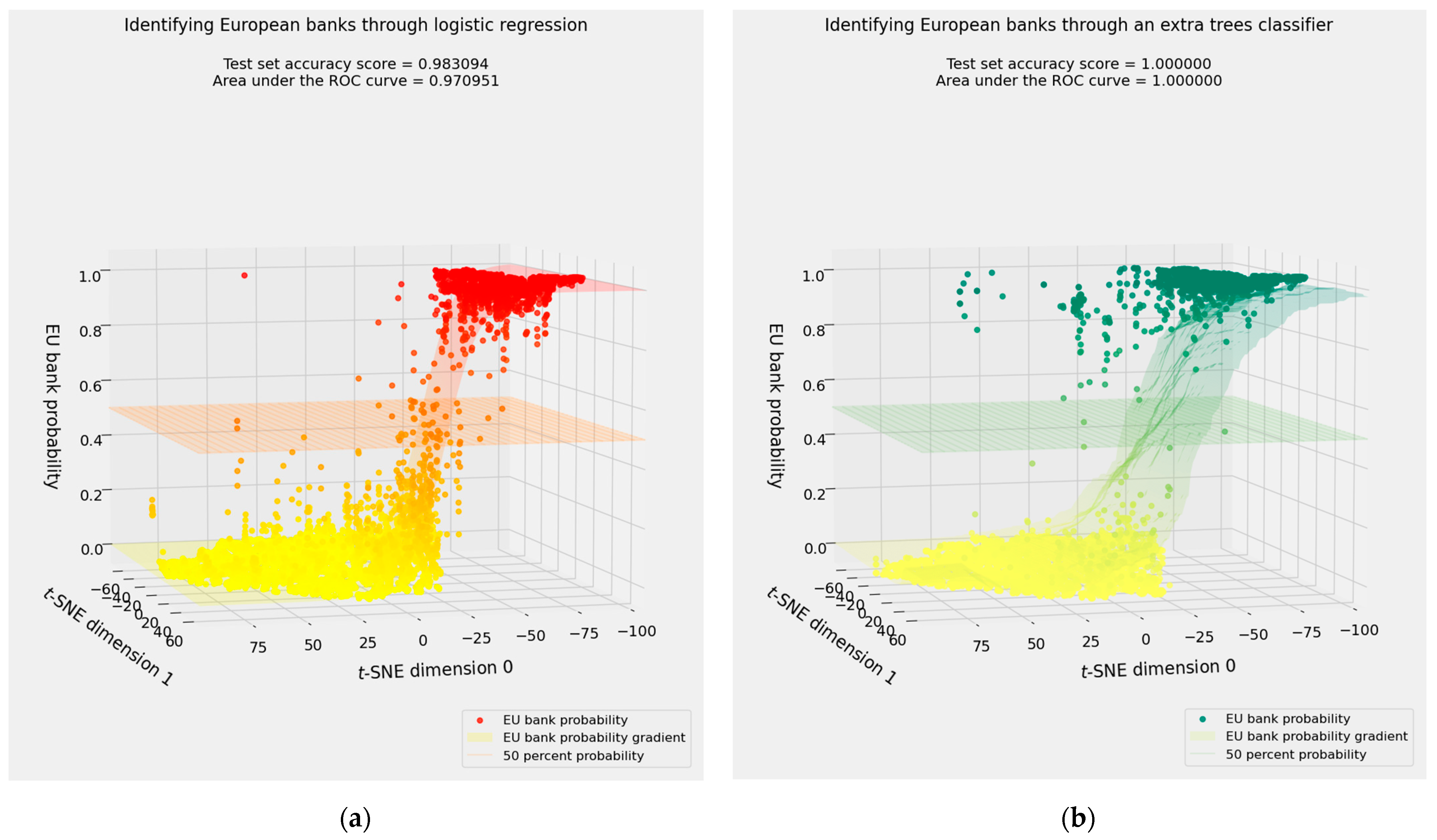
3.2. Binary Classification
3.3. Separate Regression of the European and American Subsets
4. Discussion
4.1. Predictive Accuracy for Different Risk Measures
4.2. Fixed Effects and Categorical Differences as “Natural” Variations on the Theme of Clustering
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LARS | Least angle regression |
| NHST | Null hypothesis significance testing |
| OLS | Ordinary least squares |
| SGD | Stochastic gradient descent |
References
- Chen, J.M.; Chesini, G. The Two Banking Cultures: Risk and Profitability in the European Union and the United States. 20 May 2025; Unpublished manuscript in preparation. [Google Scholar]
- Di Vito, L.; Fuentes, N.M.; Leite, J.M. Understanding the Profitability Gap Between Euro Area and US Global Systemically Important Banks. ECB Occasional Paper Series, N. 327. 2023. Available online: https://op.europa.eu/en/publication-detail/-/publication/b1025886-4228-11ee-8548-01aa75ed71a1/language-en (accessed on 19 May 2025).
- Clair, R.T.; O’Driscoll, G.P., Jr. Learning from one another: The U.S. and European banking experience. J. Multinatl. Fin. Mgmt. 1993, 2, 33–55. [Google Scholar] [CrossRef]
- Hutukka, P. Regulation of banks in the European Union, the United States, and China: Banking law in comparative context. Eur. Bus. Law Rev. 2025, 36, 1–48. [Google Scholar] [CrossRef]
- Majone, G. Cross-national sources of regulatory policymaking in Europe and the United States. J. Pub. Policy 1991, 11, 79–106. Available online: https://www.jstor.org/stable/4007339 (accessed on 20 May 2025). [CrossRef]
- Forbes, K.J. A reassessment of the relationship between inequality and growth. Am. Econ. Rev. 2000, 90, 869–887. [Google Scholar] [CrossRef]
- Chen, J.M. Drift and diffusion in geospatial econometrics: Implications for panel data and time-series. Comput. Sci. Math. Forum, May 2025; under review. [Google Scholar]
- Livieris, I.E.; Stavroyiannis, S.; Pintelas, E.; Pintelas, P. A novel validation framework to enhance deep learning models in time-series forecasting. Neural Comput. Appl. 2020, 32, 17149–17167. [Google Scholar] [CrossRef]
- Wahyuddin, E.P.; Caraka, R.E.; Kurniawan, R.; Caesarendra, W.; Gio, P.U.; Pardamean, B. Improved LSTM hyperparameters alongside sentiment walk-forward validation for time series prediction. J. Open Innov. Technol. Mkt. Complex. 2025, 11, 100458. [Google Scholar] [CrossRef]
- Ferreira, C. Competition and stability in the European Union banking sector. Intl. Adv. Econ. Res. 2023, 29, 207–224. [Google Scholar] [CrossRef]
- Karadayi, N. Determinants of return on assets. Eur. J. Bus. Mgmt. Res. 2023, 8, 37–44. [Google Scholar] [CrossRef]
- Petersen, M.A.; Schoeman, I. Modeling of banking profit via return-on-assets and return-on-equity. In Proceedings of the World Congress on Engineering, London, UK, 2–4 July 2008; Volume 2, pp. 828–833. [Google Scholar]
- Altman, E.I. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. J. Fin. 1968, 23, 589–609. [Google Scholar] [CrossRef]
- Altman, E.I.; Loris, B. A financial early warning system for over-the-counter broker dealers. J. Fin. 1976, 31, 1201–1217. [Google Scholar] [CrossRef]
- Bajaj, N.; Huffman, A.; Plastino, D.T. Solvency shortcuts: The use and misuse of simple tools for predicting financial distress. Am. Bankruptcy Inst. J. 2022, 41, 38–83. Available online: https://www.abi.org/abi-journal/solvency-shortcuts-the-use-and-misuse-of-simple-tools-for-predicting-financial-distress (accessed on 20 May 2025).
- Mare, D.S.; Moreira, F.; Rossi, R. Nonstationary Z-Score measures. Eur. J. Oper. Res. 2017, 260, 348–358. [Google Scholar] [CrossRef]
- Eidleman, G.J. Z scores—A guide to failure prediction. CPA J. 1995, 65, 52–53. [Google Scholar]
- U.S. Court of Federal Claims. Litman v. United States. In Federal Claims Reporter; District Court for the Southern District of Florida: Miami, FL, USA, 2007; pp. 90–146. [Google Scholar]
- U.S. District Court for the Southern District of Florida. Figueroa v. Sharper Image Corp; Federal Supplement, 2d Series; U.S. District Court for the Southern District of Florida: Miami, FL, USA, 2007; Volume 517, pp. 1292–1329.
- U.S. District Court for the Western District of Pennsylvania. In re SoClean, Inc., No. 2:22-cv-542; Westlaw: Pittsburgh, PA, USA, 2025; Document Number 1330539.
- Altman, E.I.; Iwanicz-Drozdowska, M.; Laitinen, E.K.; Suvas, A. Financial distress prediction in an international context: A review and empirical analysis of Altman’s Z-score model. J. Intl. Fin. Mgmt. Account. 2017, 28, 131–171. [Google Scholar] [CrossRef]
- Velliscig, G.; Floreani, J.; Polato, M. Capital and asset quality implications for bank resilience and performance in the light of NPLs’ regulation: A focus on the Texas ratio. J. Bank. Regul. 2023, 24, 66–88. [Google Scholar] [CrossRef]
- Jesswein, K.R. An examination of the “Texas ratio” as a bank failure model. Acad. Bank. Stud. J. 2009, 8, 63–73. [Google Scholar]
- Siems, T.F. The so-called Texas ratio. Fed. Reserve Bank Dallas Fin. Insights 2012, 1, 1–3. [Google Scholar]
- Ferrarin, A.; Polato, M.; Velliscig, G. Disentangling the Texas ratio: The case of the Italian banking sector. Intl. J. Manag. Fin. Account. 2020, 12, 217–241. [Google Scholar] [CrossRef]
- Floreani, J.; Velliscig, G.; Stefano, P.; Polato, M. The effects of capital on bank risk-taking: New evidence for the European banking system. Theor. Econ. Lett. 2023, 13, 597–626. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Tolles, J.; Meurer, W.J. Logistic regression relating patient characteristics to outcomes. JAMA 2016, 316, 533–534. [Google Scholar] [CrossRef]
- Yu, H.-F.; Huang, F.-L.; Lin, C.-J. Dual coordinate descent methods for logistic regression and maximum entropy models. Mach. Learn. 2011, 85, 41–75. [Google Scholar] [CrossRef]
- Tsuruoka, Y.; Tsujii, J.; Ananiadou, S. Stochastic gradient descent training for L1-regularized log-linear models with cumulative penalty. In Proceedings of the 47th Annual Meeting of the ACL and the 4th IJCNLP of the AFNLP, Singapore, 2–7 August 2009; pp. 477–485. Available online: https://aclanthology.org/P09-1054.pdf (accessed on 20 May 2025).
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Wasserstein, R.L.; Schirm, A.L.; Lazar, N.A. Moving to a world beyond “p < 0.05”. Am. Stat. 2019, 73 (Suppl. 1), 1–19. [Google Scholar] [CrossRef]
- Hooper, D.; Whyld, K. The Oxford Companion to Chess, 2nd ed.; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- European Banking Authority. Differences in Provisioning Practices in the United States and the European Union; Thematic Note EBA/REP/2021/13; European Banking Authority: Paris, France, 2021. [Google Scholar]
- Beaver, W.H.; Engel, E.E. Discretionary behavior with respect to allowances for loan losses and the behavior of security prices. J. Account. Econ. 1996, 22, 177–206. [Google Scholar] [CrossRef]
- Goodhart, C. Problems of monetary management: The U.K. experience. In Inflation, Depression, and Economic Policy in the West; Courakis, A.S., Ed.; Rowman and Littlefield: Lanham, MD, USA, 1981; Volume 3, pp. 111–146. [Google Scholar]
- Strathern, M. ‘Improving ratings’: Audit in the British University system. Eur. Rev. 1997, 5, 305–321. [Google Scholar] [CrossRef]
- Sheng, A.; Looi, T.G. Is there a Goodhart’s law in financial regulation? In Monetary History, Exchange Rates and Financial Markets: Essays in Honour of Charles Goodhart; Mizen, P., Ed.; Edward Elgar: Cheltenham, UK, 2003; Volume 2, pp. 234–249. [Google Scholar] [CrossRef]
- Charles Moyer, R. Forecasting Financial Failure: A Re-Examination. Financ. Manag. 1977, 6, 11–17. [Google Scholar] [CrossRef]
- Li, L.; Faff, R. Predicting corporate bankruptcy: What matters? Intl. Rev. Econ. Fin. 2019, 62, 1–19. [Google Scholar] [CrossRef]
- Shumway, T. Forecasting bankruptcy more accurately: A simple hazard model. J. Bus. 2001, 74, 101–124. Available online: https://www.jstor.org/stable/10.1086/209665 (accessed on 20 May 2025). [CrossRef]
- Johnson, C.G. Ratio analysis and the prediction of firm failure. J. Fin. 1970, 25, 1166–1168. Available online: https://www.jstor.org/stable/2325590 (accessed on 20 May 2025). [CrossRef]
- Goodhart, C.A.E. The regulatory response to the financial crisis. J. Fin. Stab. 2008, 4, 351–358. [Google Scholar] [CrossRef]
- Acrey, J.C.; Lee, W.Y.; Yeager, T.J. Can Federal Home Loan Banks effectively self-regulate lending to influential banks? J. Bank. Regul. 2019, 20, 197–210. [Google Scholar] [CrossRef]
- Rhoades, S.A. The relative size of banks and industrial firms in the U.S. and other countries: A note. J. Bank. Fin. 1982, 6, 579–585. [Google Scholar] [CrossRef]
- Chen, J.M.; Poufinas, T.; Pagagopoulou, A. Drift and diffusion in panel data: Extracting geopolitical and temporal effects in a study of passenger rail traffic. Comput. Sci. Math. Forum, September 2025; forthcoming. [Google Scholar]
- Chabal, E. The rise of the Anglo-Saxon: French perceptions of the Anglo-American world in the long twentieth century. Fr. Politics Cult. Soc. 2013, 31, 24–46. [Google Scholar] [CrossRef]
- Brown, R.S. Sampling. In International Encyclopedia of Education, 3rd ed.; Peterson, P., Baker, E., McGaw, B., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2010; pp. 142–146. [Google Scholar] [CrossRef]


| Variables | RoA: OLS | RoA: Lars 1 | Altman: OLS | Altman: Lars | Texas: OLS | Texas: Lars |
|---|---|---|---|---|---|---|
| eu_dummy | −0.024343 * 2 | 0.000000 | 0.039521 | 0.000000 | 0.012592 | 0.010587 |
| annual_net_interest_margin | −0.006112 | 0.000000 | 0.037261 * | 0.000000 | 0.008885 | 0.008412 |
| cash_near_cash_item | 0.035992 ** | 0.000000 | −0.276452 *** | −0.203883 *** | −0.084858 *** | −0.080918 *** |
| disclosed_intangibles | −0.001844 | 0.000000 | 0.073143 *** | 0.029977 | 0.192894 *** | 0.190362 *** |
| tier1_capital_ratio | −0.007557 | 0.000000 | 0.087373 ** | 0.079151 ** | −0.047821 *** | −0.045256 *** |
| total_capital_over_risk_based_capital | 0.005328 | 0.000000 | 0.090190 *** | 0.084811 ** | 0.099128 *** | 0.095523 *** |
| common_equity_over_total_assets | 0.166054 *** | 0.163208 *** | 0.203412 *** | 0.196500 *** | −0.272485 *** | −0.270965 *** |
| efficiency_ratio | −0.037198 *** | −0.029197 *** | 0.025382 * | 0.015931 | 0.042799 *** | 0.042459 *** |
| eps_growth | 0.020005 * | 0.014881 | −0.003541 | 0.000000 | −0.034549 *** | −0.032629 *** |
| growth_in_total_deposits | 0.006270 | 0.000000 | 0.034507 ** | 0.016388 | 0.000519 | 0.000000 |
| growth_in_total_loans | 0.004685 | 0.000000 | −0.042596 ** | −0.014259 | −0.000519 | 0.000000 |
| net_income_growth | 0.009829 | 0.006175 | −0.024967 | −0.019372 | 0.031106 *** | 0.029354 *** |
| nonperforming_loans_over_total_assets | −0.071650 *** | −0.073357 *** | −0.275734 *** | −0.250955 *** | 0.837755 *** | 0.837340 *** |
| return_on_common_equity | 0.779113 *** | 0.777358 *** | 0.298634 *** | 0.291045 *** | 0.007467 | 0.006593 |
| t12_net_interest_margin | 0.086433 *** | 0.075754 *** | −0.127733 *** | −0.094787 *** | 0.066768 *** | 0.065320 *** |
| total_loans_over_total_deposits | −0.013440 * | −0.006152 | 0.049391 *** | 0.037200 ** | 0.025881 *** | 0.025853 *** |
| ℓ1 alpha | N/A | 0.010945 | N/A | 0.007232 | N/A | 0.000349 |
| Variables | Logistic Regression | SGD (with a ℓ1 Penalty) 3 | Random Forest | Extra Trees |
|---|---|---|---|---|
| intercept | −2.378868 *** 4 | −2.474330 *** | N/A | N/A |
| annual_net_interest_margin | −0.492577 *** | −0.084153 *** | 0.088243 | 0.065691 |
| cash_near_cash_item | 1.351696 *** | 1.637565 *** | 0.148800 | 0.262538 |
| disclosed_intangibles | 0.204390 *** | 0.000000 | 0.031807 | 0.078799 |
| tier1_capital_ratio | 0.281099 *** | 0.238743 *** | 0.005840 | 0.011768 |
| total_capital_over_risk_based_capital | 0.022195 *** | 0.000000 | 0.004864 | 0.009598 |
| common_equity_over_total_assets | −1.065244 *** | −0.953667 *** | 0.026012 | 0.131921 |
| efficiency_ratio | −0.107207 *** | 0.000000 | 0.002366 | 0.005198 |
| eps_growth | 0.168614 *** | 0.041315 *** | 0.000829 | 0.001818 |
| growth_in_total_deposits | 0.063693 *** | 0.000000 | 0.001586 | 0.002556 |
| growth_in_total_loans | 0.006979 * | 0.000000 | 0.002355 | 0.004634 |
| net_income_growth | −0.089263 *** | 0.000000 | 0.000990 | 0.001596 |
| nonperforming_loans_over_total_assets | 1.457363 *** | 1.513600 *** | 0.093624 | 0.114464 |
| return_on_common_equity | 0.565925 *** | 0.629780 *** | 0.002358 | 0.007141 |
| t12_net_interest_margin | −1.052515 *** | −1.438182 *** | 0.547773 | 0.239952 |
| total_loans_over_total_deposits | 1.183871 *** | 1.195250 *** | 0.042551 | 0.062325 |
| Variables | RoA: Europe | RoA: USA | Altman: Europe | Altman: USA | Texas: Europe | Texas: USA |
|---|---|---|---|---|---|---|
| annual_net_interest_margin | 0.000000 | −0.019170 * | −0.026492 | 0.000000 | −0.010052 | 0.015696 * |
| cash_near_cash_item | 0.000000 | 0.029691 ** | 0.000000 | −0.366997 *** | 0.033483 * | −0.105701 *** |
| disclosed_intangibles | 0.000000 | 0.012955 | 0.179605 *** | 0.057135 * | 0.142307 *** | 0.175521 *** |
| tier1_capital_ratio | 0.000000 | 0.000000 | 0.000000 | 0.110124*** | −0.034321 + | 0.000000 |
| total_capital_over_risk_based_capital | 0.000000 | 0.006749 | 0.052463 | 0.000000 | −0.028943 | −0.014578 + |
| common_equity_over_total_assets | 0.263023 *** 5 | 0.116345 *** | 0.481305 *** | 0.230170 *** | −0.319784 *** | −0.145884 *** |
| efficiency_ratio | −0.016034 + | −0.075350 *** | 0.030215 * | −0.066502 ** | 0.000000 | 0.043169 *** |
| eps_growth | 0.000000 | 0.020825 * | 0.042796 + | −0.063479 * | −0.015779 + | −0.019164 * |
| growth_in_total_deposits | 0.042873 ** | −0.014543 * | 0.047554 * | 0.021917 | 0.000000 | 0.011883 * |
| growth_in_total_loans | 0.074695 *** | −0.026108 *** | 0.000000 | −0.049490 ** | −0.015144 + | 0.024720 *** |
| net_income_growth | 0.018685 | 0.019369 + | 0.000000 | 0.000000 | 0.000000 | 0.014629 + |
| nonperforming_loans_over_total_assets | −0.107255 *** | −0.059011 *** | −0.451297 *** | −0.027021 | 0.658933 *** | 1.180277 *** |
| return_on_common_equity | 0.644823 *** | 0.866887 *** | 0.136747 *** | 0.417484 *** | 0.034315 *** | 0.038409 *** |
| t12_net_interest_margin | 0.000000 | 0.156754 *** | −0.163328 *** | −0.098905 ** | 0.000000 | 0.068231 *** |
| total_loans_over_total_deposits | 0.000000 | −0.014060 + | 0.024022 | 0.064179 ** | −0.051219 *** | 0.016657 ** |
| ℓ1 alpha | 0.011445 | 0.000075 | 0.011189 | 0.002772 | 0.004883 | 0.000059 |
| Reversals and Negations | RoA | Altman | Texas |
|---|---|---|---|
| Flipped signs | 2 | 1 | 3 |
| Significant for one, sparse in the other | 5 | 3 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.M.; Chesini, G. Classifying Two Banking Cultures: The Pragmatic Structure of Economic Revelations. Comput. Sci. Math. Forum 2025, 11, 33. https://doi.org/10.3390/cmsf2025011033
Chen JM, Chesini G. Classifying Two Banking Cultures: The Pragmatic Structure of Economic Revelations. Computer Sciences & Mathematics Forum. 2025; 11(1):33. https://doi.org/10.3390/cmsf2025011033
Chicago/Turabian StyleChen, James Ming, and Giusy Chesini. 2025. "Classifying Two Banking Cultures: The Pragmatic Structure of Economic Revelations" Computer Sciences & Mathematics Forum 11, no. 1: 33. https://doi.org/10.3390/cmsf2025011033
APA StyleChen, J. M., & Chesini, G. (2025). Classifying Two Banking Cultures: The Pragmatic Structure of Economic Revelations. Computer Sciences & Mathematics Forum, 11(1), 33. https://doi.org/10.3390/cmsf2025011033





