Winner-Take-All and Loser-Take-All Circuits: Architectures, Applications and Analytical Comparison
Abstract
1. Introduction
2. Literature Review
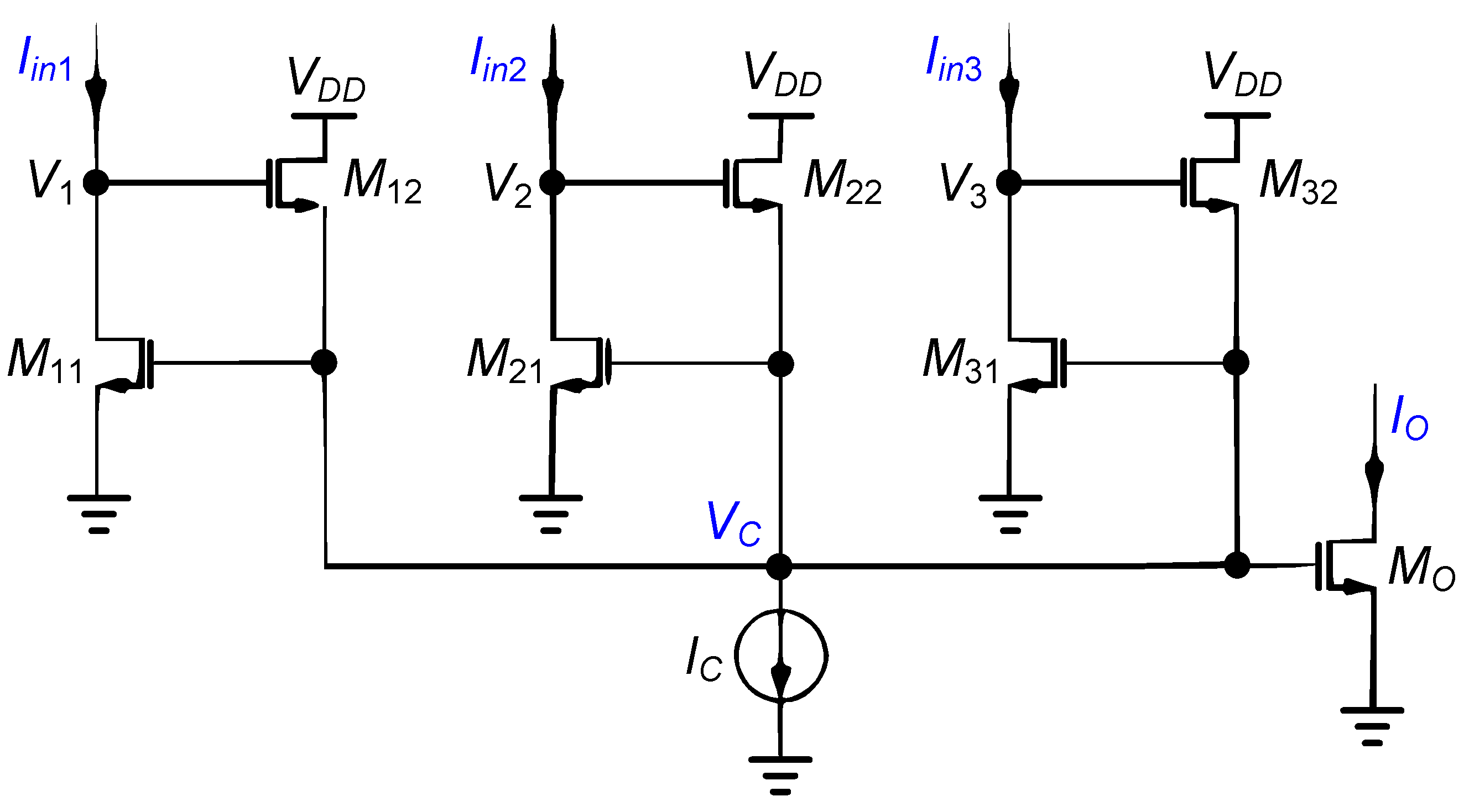
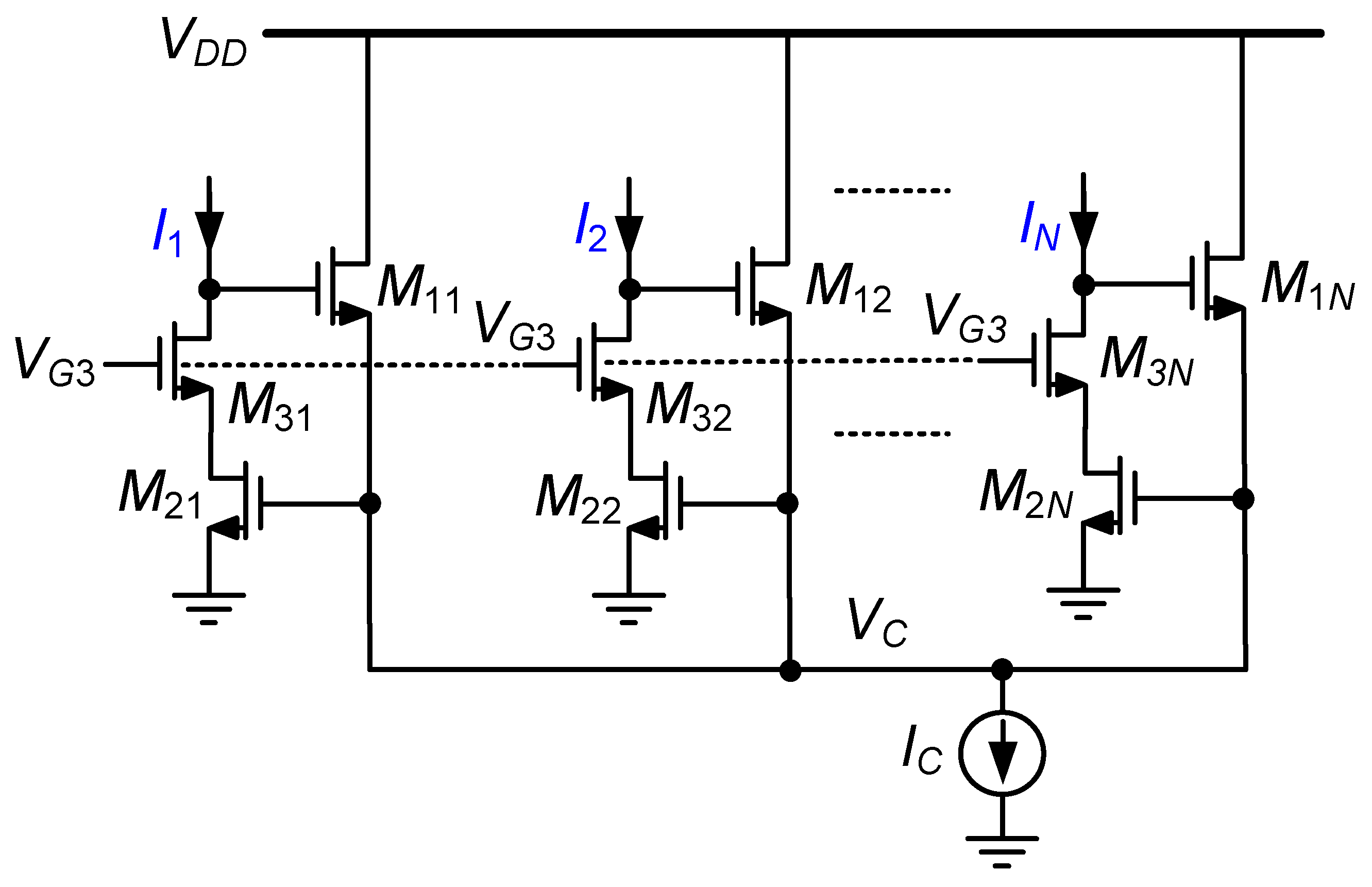
2.1. Current Conveyors
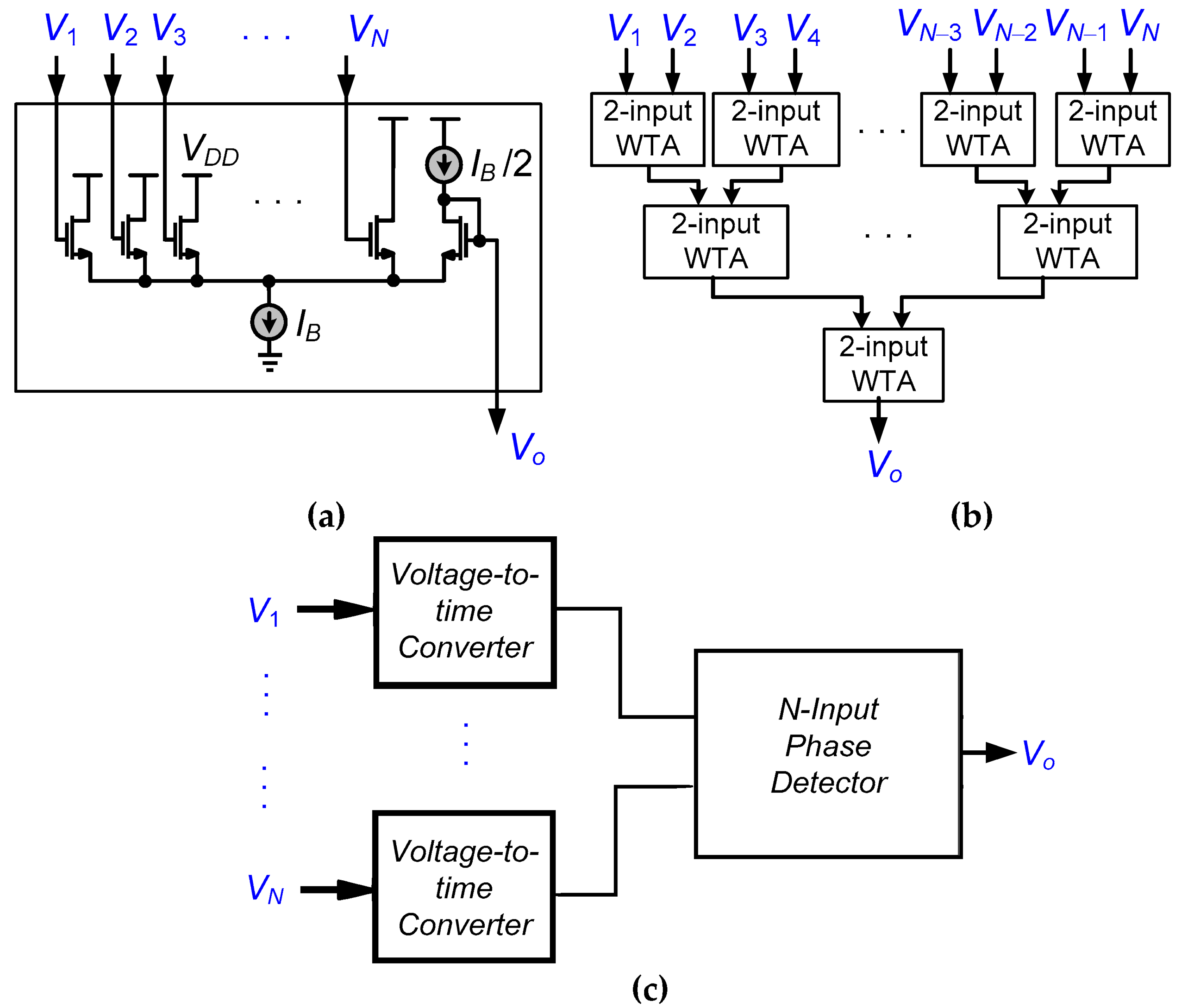
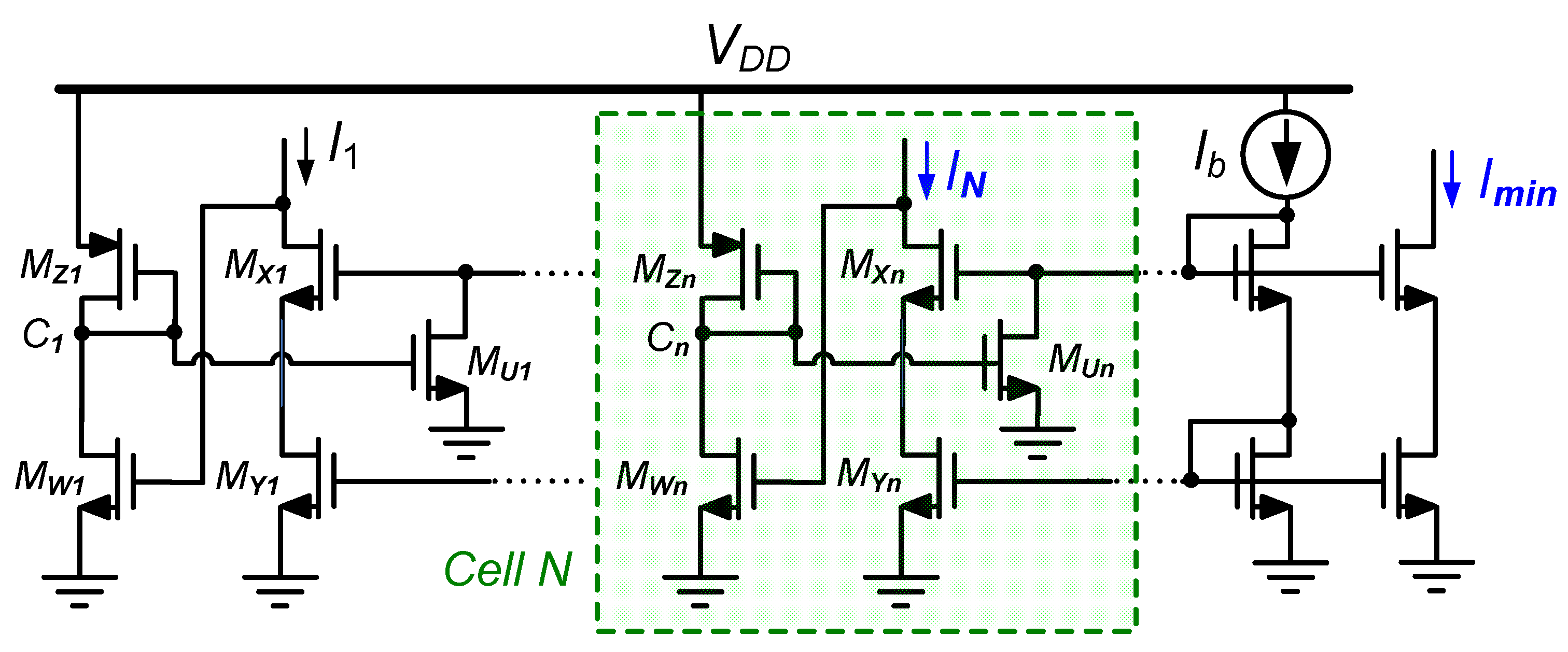
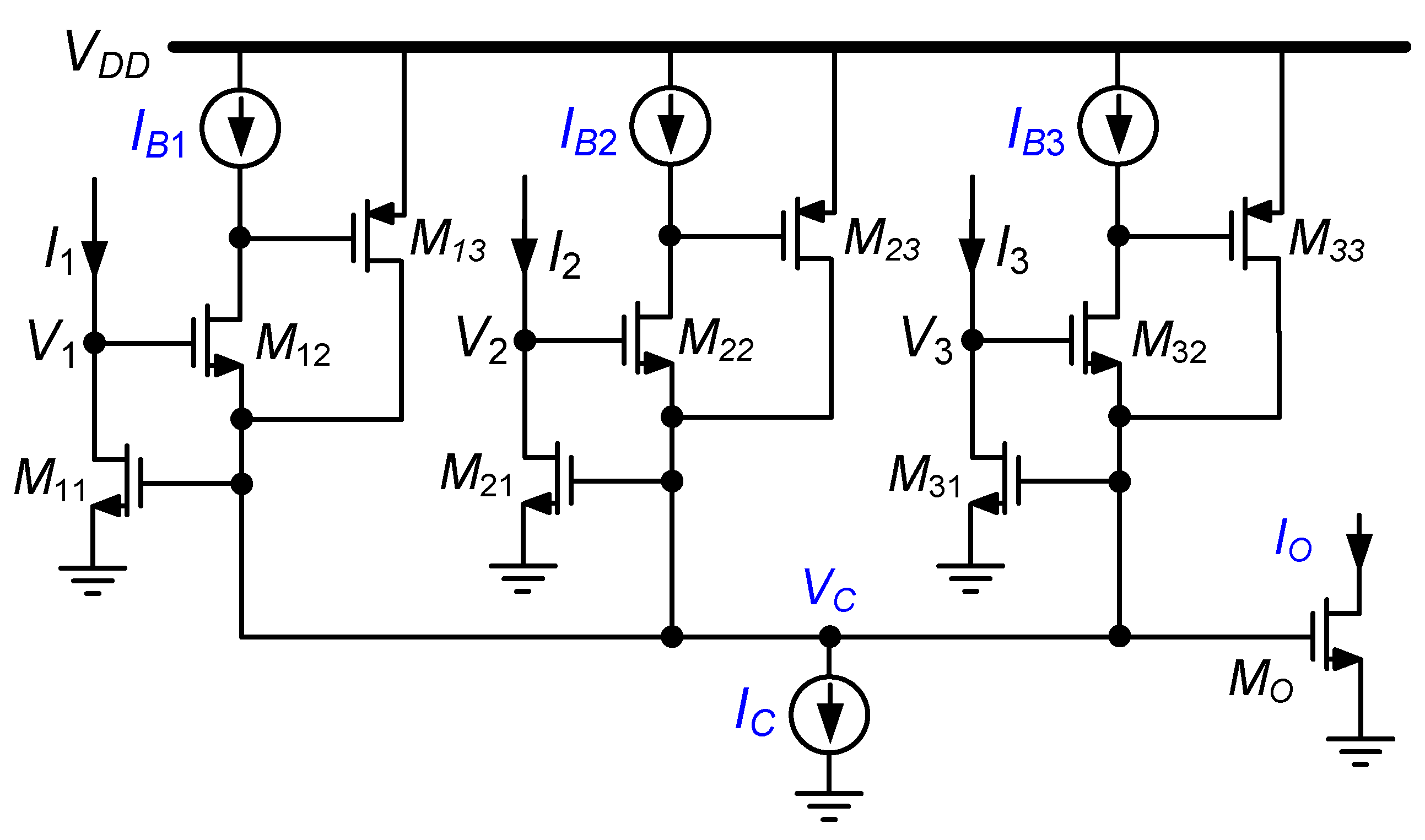
2.2. Binary Tree WTA Circuits
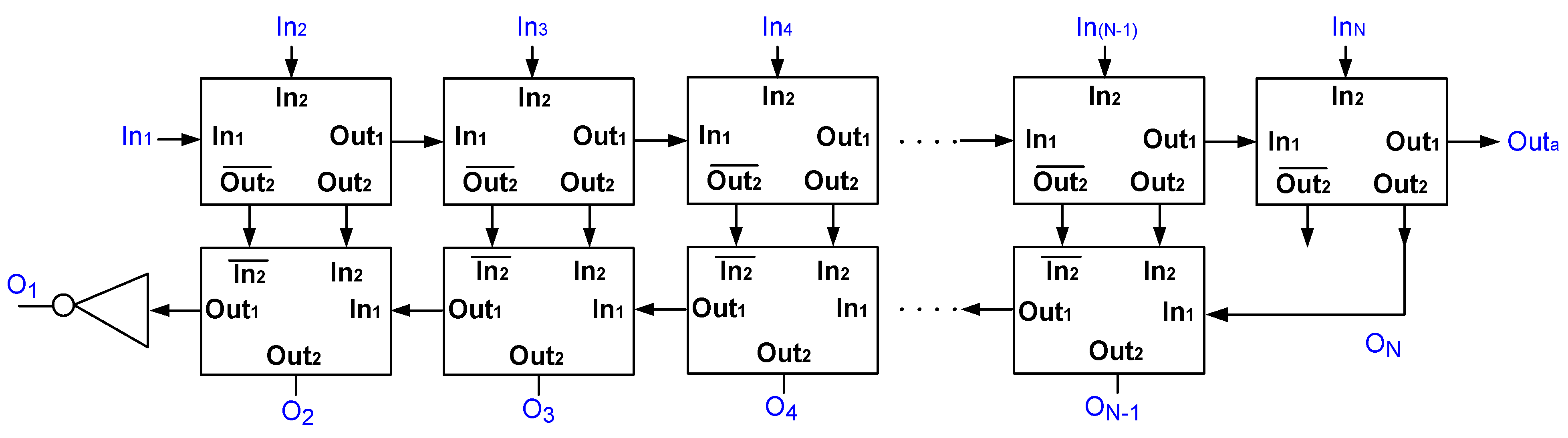
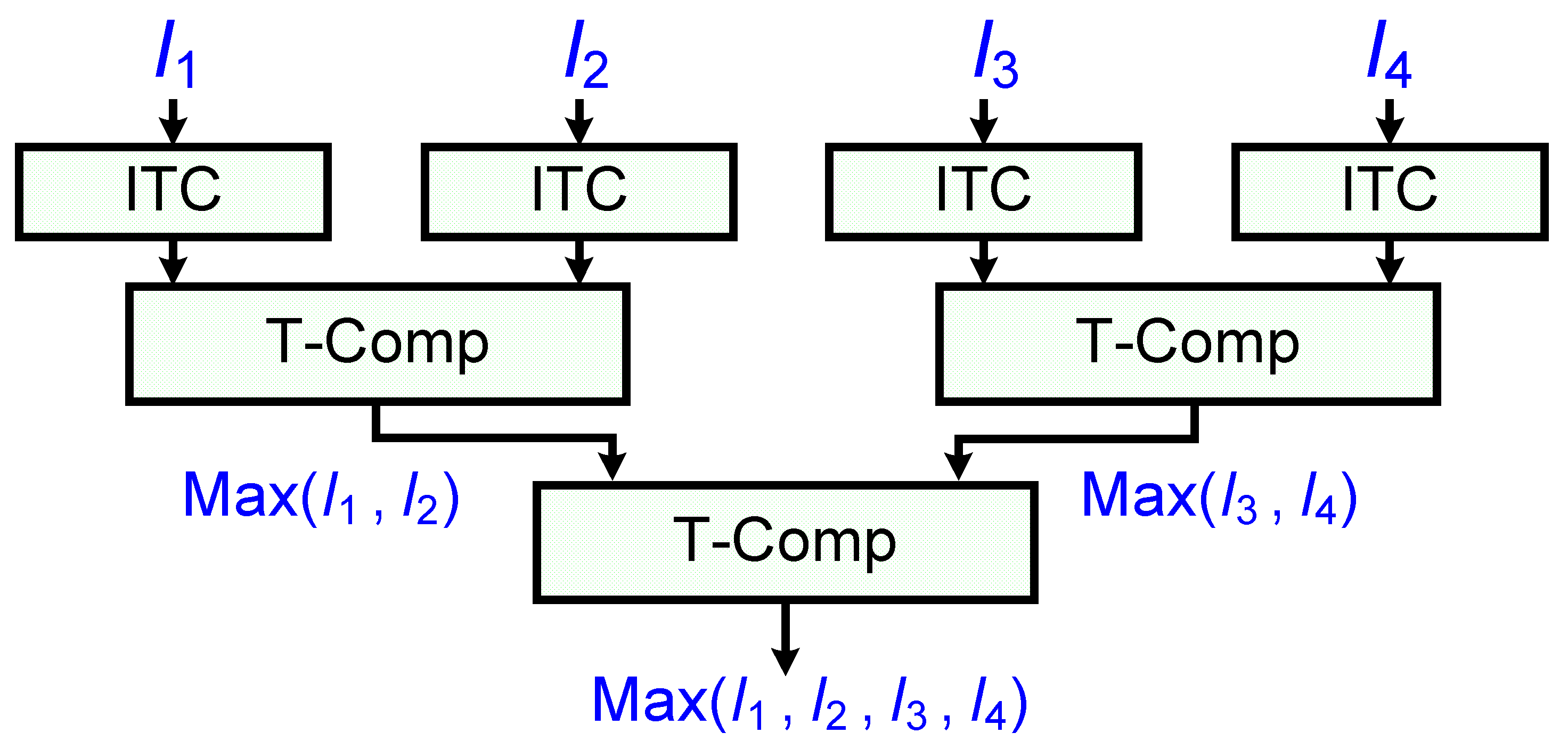
2.3. Time-Domain WTA/LTA Circuits
3. Comparison and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lazzaro, J.; Ryckebusch, S.; Mahowald, M.A.; Mead, C.A. Winner-Take-All Networks of O(N) Complexity; Defense Technical Information Center: Fort Belvoir, VA, USA, 1988. [Google Scholar]
- Sasaki, M.; Inoue, T.; Shirai, Y.; Ueno, F. Fuzzy multiple-input maximum and minimum circuits in current mode and their analyses using bounded-difference equations. IEEE Trans. Comput. 1990, 39, 768–774. [Google Scholar] [CrossRef]
- Choi, J.; Sheu, B.J. A high-precision VLSI winner-take-all circuit for self-organizing neural networks. IEEE J. Solid-State Circuits 1993, 28, 576–584. [Google Scholar] [CrossRef]
- Tuttle, G.T.; Fallahi, S.; Abidi, A.A. An 8 b CMOS vector A/D converter. In Proceedings of the 1993 IEEE International Solid-State Circuits Conference Digest of Technical Papers, San Francisco, CA, USA, 24–26 February 1993. [Google Scholar]
- Le Nguyen, B.; Hock Choong, C. A neural-network contention controller for packet switching networks. IEEE Trans. Neural Netw. 1995, 6, 1402–1410. [Google Scholar] [CrossRef] [PubMed]
- Smedley, S.; Taylor, J.; Wilby, M. A scalable high-speed current-mode winner-take-all network for VLSI neural applications. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1995, 42, 289–291. [Google Scholar] [CrossRef]
- Gunay, Z.S.; Sanchez-Sinencio, E. CMOS winner-take-all circuits: A detailed comparison. In Proceedings of the 1997 IEEE International Symposium on Circuits and Systems (ISCAS), Hong Kong, China, 12 June 1997; pp. 41–44. [Google Scholar]
- Pouliquen, P.O.; Andreou, A.G.; Strohbehn, K. Winner-Takes-All Associative Memory: A Hamming Distance Vector Quantizer. In Neuromorphic Systems Engineering; The Springer International Series in Engineering and Computer Science; Springer: Boston, MA, USA, 1998; pp. 437–456. [Google Scholar] [CrossRef]
- Sekerkiran, B.; Cilingiroglu, U. Improving the resolution of Lazzaro winner-take-all circuit. In Proceedings of the International Conference on Neural Networks (ICNN’97), Houston, TX, USA, 12 June 1997. [Google Scholar]
- Demosthenous, A.; Smedley, S.; Taylor, J. A CMOS analog winner-take-all network for large-scale applications. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1998, 45, 300–304. [Google Scholar] [CrossRef]
- Dobrescu, D.; Comanescu, R.; Dobrescu, L. Neuron MOS technique designed 8 channels Winner Takes it All integrated circuit. In Proceedings of the 1998 International Semiconductor Conference. CAS’98 Proceedings (Cat. No.98TH8351), Sinaia, Romania, 6–10 October 1998. [Google Scholar]
- Opris, I.E. Rail-to-rail multiple-input min/max circuit. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1998, 45, 137–140. [Google Scholar] [CrossRef]
- Serrano-Gotarredona, T.; Linares-Barranco, B. A high-precision current-mode WTA-MAX circuit with multichip capability. IEEE J. Solid-State Circuits 1998, 33, 280–286. [Google Scholar] [CrossRef]
- Vlassis, S.; Siskos, S. High speed and high resolution WTA circuit. In Proceedings of the ISCAS’99. 1999 IEEE International Symposium on Circuits and Systems VLSI (Cat. No.99CH36349), Orlando, FL, USA, 30 May–2 June 1999. [Google Scholar]
- Zhang, Y.; Pheng-Ann, H.; Ping-Fu, F. Winner-take-all discrete recurrent neural networks. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 2000, 47, 1584–1589. [Google Scholar] [CrossRef][Green Version]
- Wawryn, K.; Strzeszewski, B. Current mode AB class WTA circuit. In Proceedings of the ICECS 2001. 8th IEEE International Conference on Electronics, Circuits and Systems (Cat. No.01EX483), Malta, Malta, 2–5 September 2001. [Google Scholar]
- Aksin, D.Y. A high-precision high-resolution WTA-MAX circuit of O(N) complexity. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 2002, 49, 48–53. [Google Scholar] [CrossRef]
- Chien-Cheng, Y.; Yun-Ching, T.; Bin-Da, L. Design of high performance CMOS current-mode winner-take-all circuit. In Proceedings of the 2003 5th International Conference on ASIC Proceedings (IEEE Cat No 03TH8690) ICASIC-03, Beijing, China, 21–24 October 2003. [Google Scholar]
- Abrahamsen, J.P.; Hafliger, P.; Lande, T.S. A time domain winner-take-all network of integrate-and-fire neurons. In Proceedings of the 2004 IEEE International Symposium on Circuits and Systems (IEEE Cat. No.04CH37512), Vancouver, BC, Canada, 23–26 May 2004. [Google Scholar]
- Fish, A.; Milrud, V.; Yadid-Pecht, O. High-speed and high-precision current winner-take-all circuit. IEEE Trans. Circuits Syst. II Express Briefs 2005, 52, 131–135. [Google Scholar] [CrossRef]
- Ramirez-Angulo, J.; Ducoudray-Acevedo, G.; Carvajal, R.G.; Lopez-Martin, A. Low-voltage high-performance voltage-mode and current-mode WTA circuits based on flipped voltage followers. IEEE Trans. Circuits Syst. II Express Briefs 2005, 52, 420–423. [Google Scholar] [CrossRef]
- Tomatsopoulos, B.; Demosthenous, A. Low power, low complexity CMOS multiple-input replicating current comparators and WTA/LTA circuits. In Proceedings of the 2005 European Conference on Circuit Theory and Design, Cork, Ireland, 2 September 2005. [Google Scholar]
- Dlugosz, R.; Talaśka, T.; Wojtyna, R. New binary-tree-based Winner-Takes-All circuit for learning on silicon Kohonen’s networks. In Proceedings of the International Conference On Signals And Electronic Systems (ICSES), Łódź, Poland, 17–20 September 2006; pp. 441–446. [Google Scholar]
- Talaska, T.; Dlugosz, R.; Wojtyna, R. Current Mode Analog Kohonen Neural Network. In Proceedings of the 2007 14th International Conference on Mixed Design of Integrated Circuits and Systems, Ciechocinek, Poland, 21–23 June 2007. [Google Scholar]
- Temel, T. High-performance current-mode multi-input loser-take-all minimum circuit. Electron. Lett. 2008, 44, 718. [Google Scholar] [CrossRef]
- Dlugosz, R.; Talaska, T. A low power current-mode binary-tree WTA/LTA circuit for Kohonen neural networks. In Proceedings of the 2009 MIXDES-16th International Conference Mixed Design of Integrated Circuits & Systems, Lodz, Poland, 25–27 June 2009; pp. 201–204. [Google Scholar]
- Rahman, M.; Baishnab, K.L.; Talukdar, F.A. A high speed and high resolution VLSI Winner-take-all circuit for neural networks and fuzzy systems. In Proceedings of the 2009 International Symposium on Signals, Circuits and Systems, Iasi, Romania, 9–10 July 2009. [Google Scholar]
- Dlugosz, R.; Talaśka, T. Low power current-mode binary-tree asynchronous Min/Max circuit. Microelectron. J. 2010, 41, 64–73. [Google Scholar] [CrossRef]
- Hsieh, H.-Y.; Tang, K.-T.; Tsai, Z.-H.; Chen, H. A low-power, high-resolution WTA utilizing translinear-loop pre-amplifier. In Proceedings of the The 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010. [Google Scholar]
- Hung, Y.-C. CMOS Nonlinear Signal Processing Circuits. In Advances in Solid State Circuit Technologies; InTech: London, UK, 2010. [Google Scholar] [CrossRef]
- Molinar-Solis, J.E.; Garcia-Lozano, R.; Morales-Ramirez, A.; Ramirez-Angulo, J. Simple improvement stage for low voltage WTA and Rank Order circuits. In Proceedings of the 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011. [Google Scholar]
- Prommee, P.; Chattrakun, K. CMOS WTA maximum and minimum circuits with their applications to analog switch and rectifiers. Microelectron. J. 2011, 42, 52–62. [Google Scholar] [CrossRef]
- Soleimani, M.; Nazaraliloo, M. Voltage-mode loser/winner-take-all circuits. In Proceedings of the 2011 IEEE 54th International Midwest Symposium on Circuits and Systems (MWSCAS), Seoul, Republic of Korea, 7–10 August 2011. [Google Scholar]
- Molinar-Solis, J.E.; García-Lozano, R.; Morales-Ramirez, A.; Espinoza-Ortega, O.; Rocha-Perez, M.; Diaz-Sanchez, A.; Ramirez-Angulo, J.; Vazquez-Leal, H. Low Voltage Lazzaro’s WTA with enhanced loop gain. IEICE Electron. Express 2012, 9, 648–653. [Google Scholar] [CrossRef]
- Fernandez-Berni, J.; Carmona-Galan, R.; Rodriquez-Vazquez, A. An ultra-low-power voltage-mode asynchronous WTA-LTA circuit. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS2013), Beijing, China, 19–23 May 2013. [Google Scholar]
- Ramakrishnan, S.; Hasler, J. A compact programmable analog classifier using a VMM + WTA network. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Moro-Frias, D.; Ventura-Arizmendi, C.; Sanz-Pascual, M.-T.; de la Cruz-Blas, C.-A. Current-Mode Winner-Take-All Circuit with Improved Dynamic Response. Circuits Syst. Signal Process. 2014, 34, 625–639. [Google Scholar] [CrossRef]
- Naderi Saatlo, A.; Ozoguz, S. CMOS high-precision loser-take-all circuit. IEEJ Trans. Electr. Electron. Eng. 2014, 9, 695–696. [Google Scholar] [CrossRef]
- Dlugosz, R.; Rydlewski, A.; Talaśka, T. Novel, low power, nonlinear dilatation and erosion filters realized in the CMOS technology. FACTA Univ. Ser. Electron. Energetics 2015, 28, 237–249. [Google Scholar] [CrossRef]
- Pardo, F.; Boluda, J.A.; Vegara, F. Selective Change Driven Vision Sensor With Continuous-Time Logarithmic Photoreceptor and Winner-Take-All Circuit for Pixel Selection. IEEE J. Solid-State Circuits 2015, 50, 786–798. [Google Scholar] [CrossRef]
- Pedroni, V.A. Low-Offset Neural Winner-take-all Network. In Proceedings of the Anaisdo1. Congresso Brasileirode Redes Neurais, Itajuba, Brasil, 17 October 2016. [Google Scholar]
- Hanada, K.; Ueda, S.; Ito, H.; Hikawa, H. Winner-Take-All Neural Network with Distributed Winner Search Circuit. In Proceedings of the 2017 International Symposium on Nonlinear Theory and Its Applications, Cancun, Mexico, 4–7 December 2017; Volume 29. [Google Scholar]
- Wu, C.-H.; Chen, T.-S.; Lee, D.-Y.; Liu, T.-T.; Wu, A.-Y. Low-latency Voltage-Racing Winner-Take-All (VR-WTA) circuit for acceleration of learning engine. In Proceedings of the 2017 International Symposium on VLSI Design, Automation and Test (VLSI-DAT), Hsinchu, Taiwan, 24–27 April 2017. [Google Scholar]
- Doevenspeck, J.; Degraeve, R.; Cosemans, S.; Roussel, P.; Verhoef, B.-E.; Lauwereins, R.; Dehaene, W. Analytic variability study of inference accuracy in RRAM arrays with a binary tree winner-take-all circuit for neuromorphic applications. In Proceedings of the 2018 48th European Solid-State Device Research Conference (ESSDERC), Dresden, Germany, 3–6 September 2018. [Google Scholar]
- Ferré, P.; Mamalet, F.; Thorpe, S.J. Unsupervised Feature Learning with Winner-Takes-All Based STDP. Front. Comput. Neurosci. 2018, 12, 24. [Google Scholar] [CrossRef]
- Pardo, F.; Reig, C.; Boluda, J.A.; Vegara, F. A 4K-Input High-Speed Winner-Take-All (WTA) Circuit with Single-Winner Selection for Change-Driven Vision Sensors. Sensors 2019, 19, 437. [Google Scholar] [CrossRef] [PubMed]
- Rahiminejad, E.; Saberi, M.; Lotfi, R.; Taherzadeh-Sani, M.; Nabki, F. A Low-Voltage High-Precision Time-Domain Winner-Take-All Circuit. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 4–8. [Google Scholar] [CrossRef]
- Akbari, M.; Chou, T.I.; Tang, K.T. An adjustable 0.3 V current winner-take-all circuit for analogue neural networks. Electron. Lett. 2021, 57, 685–687. [Google Scholar] [CrossRef]
- Singh, J.K.; Kapur, G. Design of an adaptive winner takes all circuit explaining features of binocular rivalry in visual brain. Integration 2023, 88, 11–19. [Google Scholar] [CrossRef]
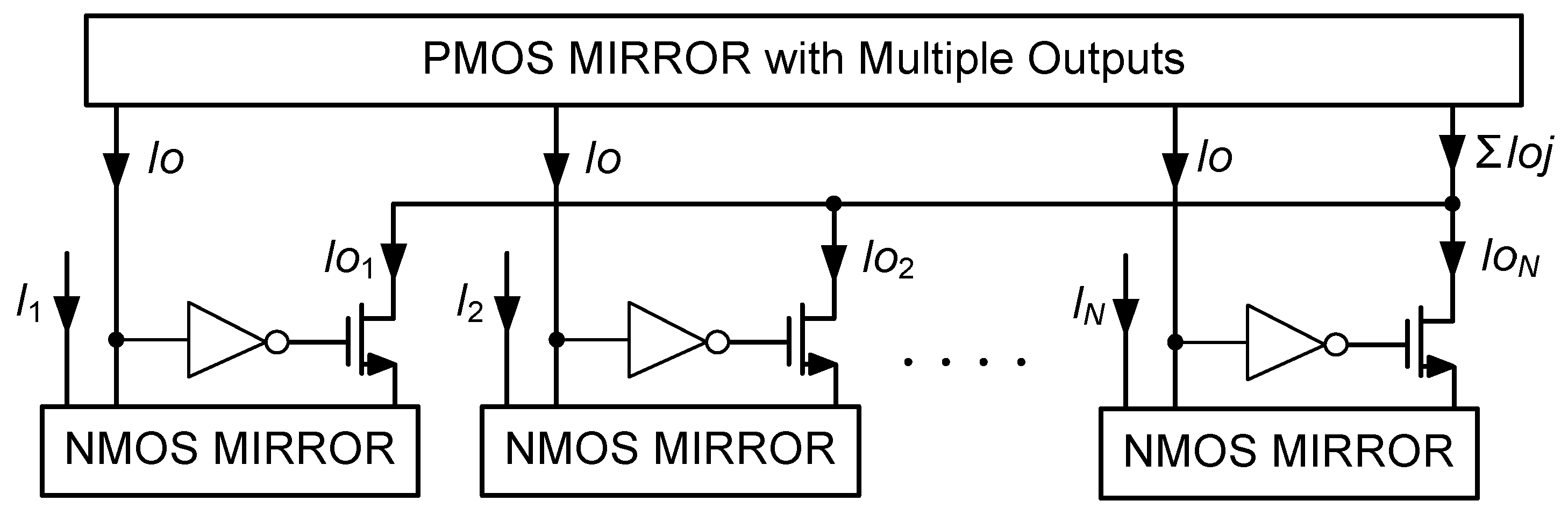

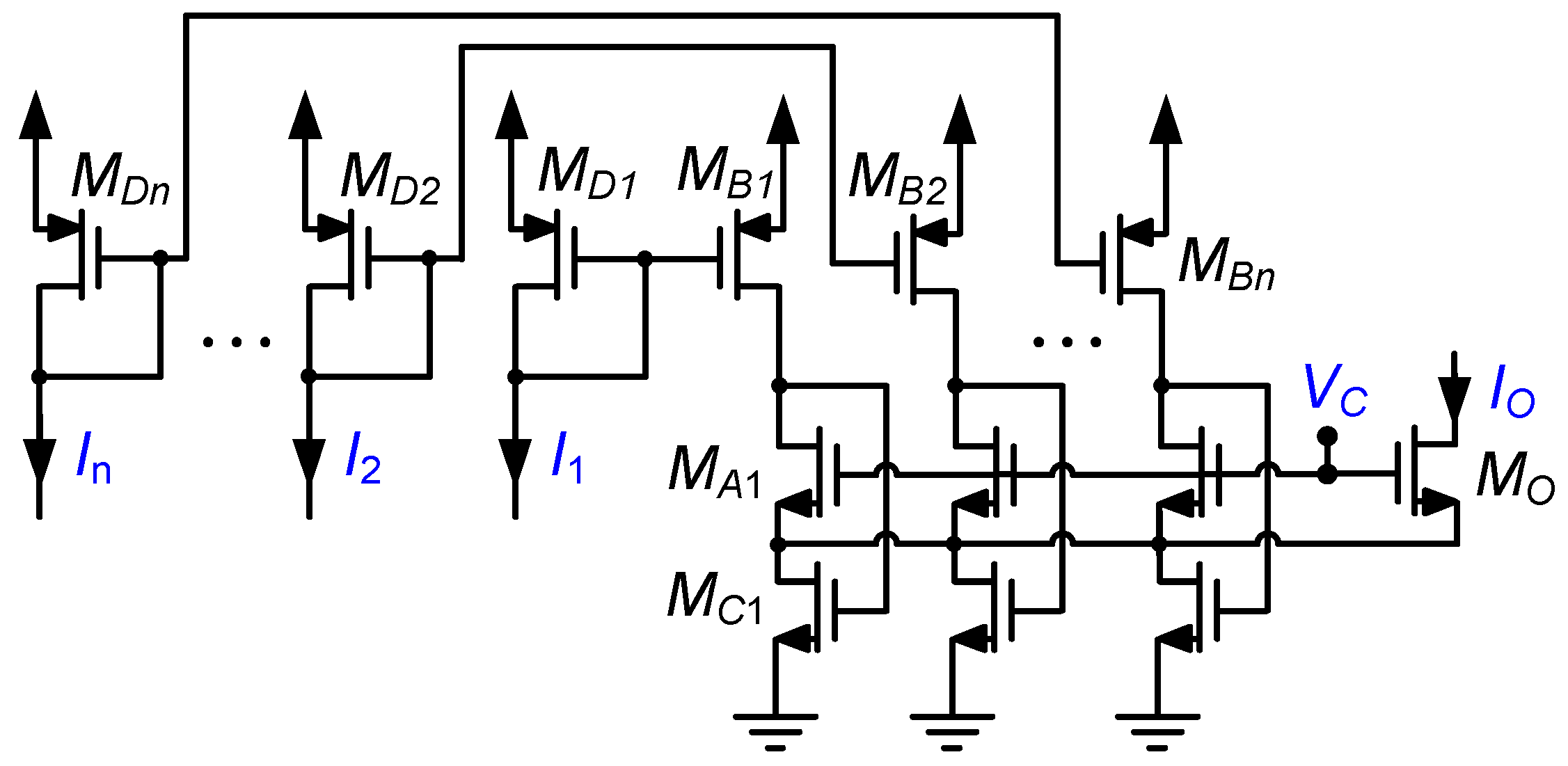
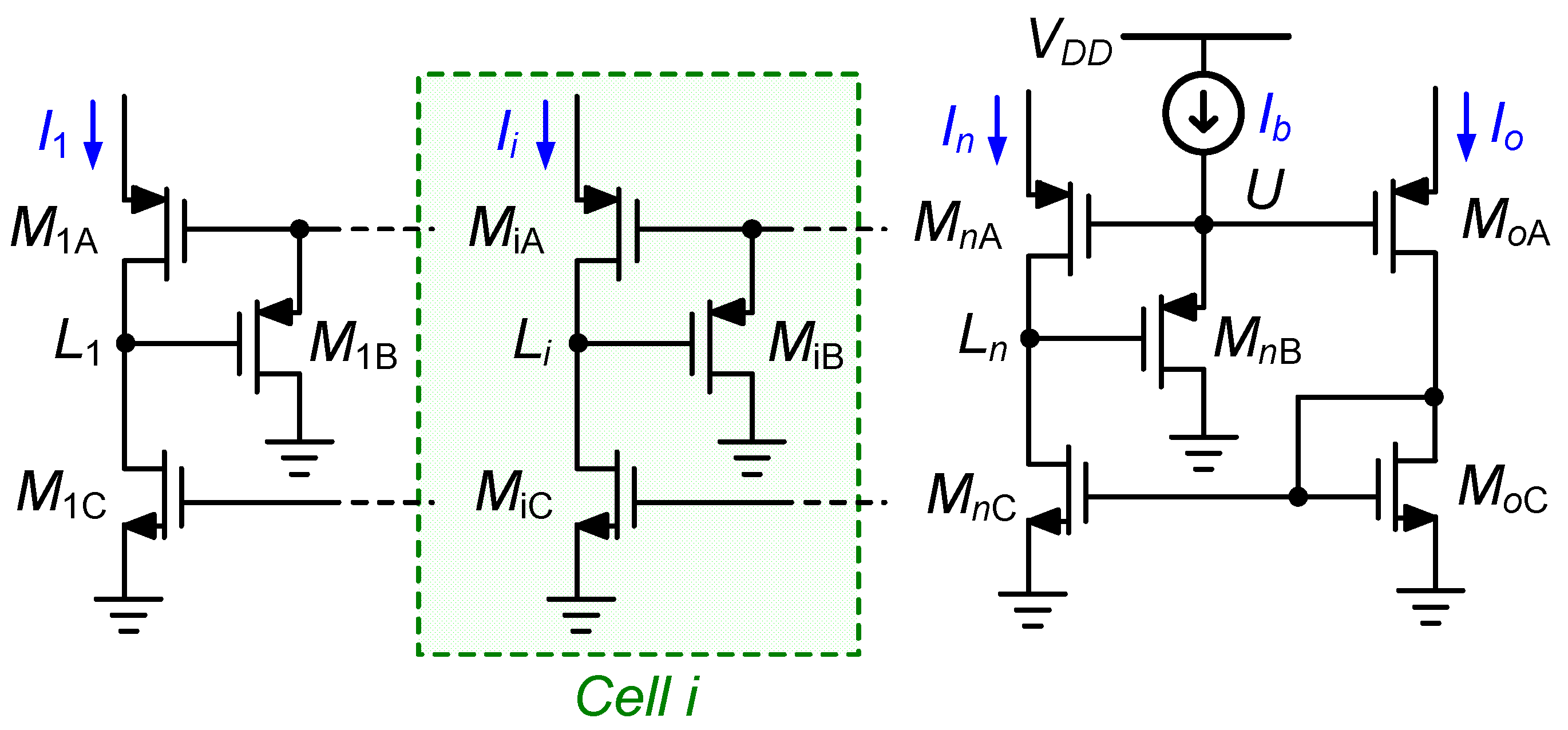
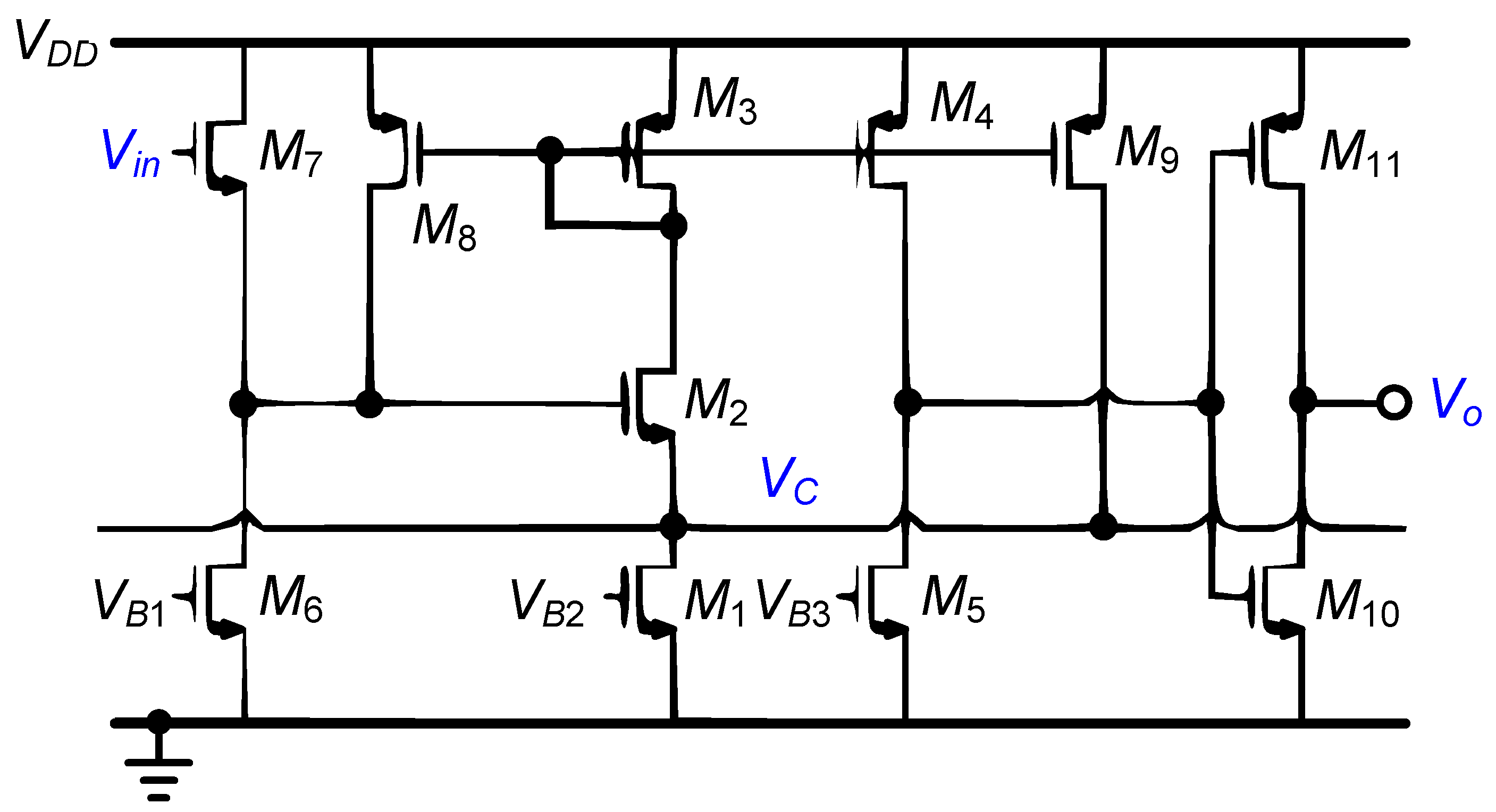
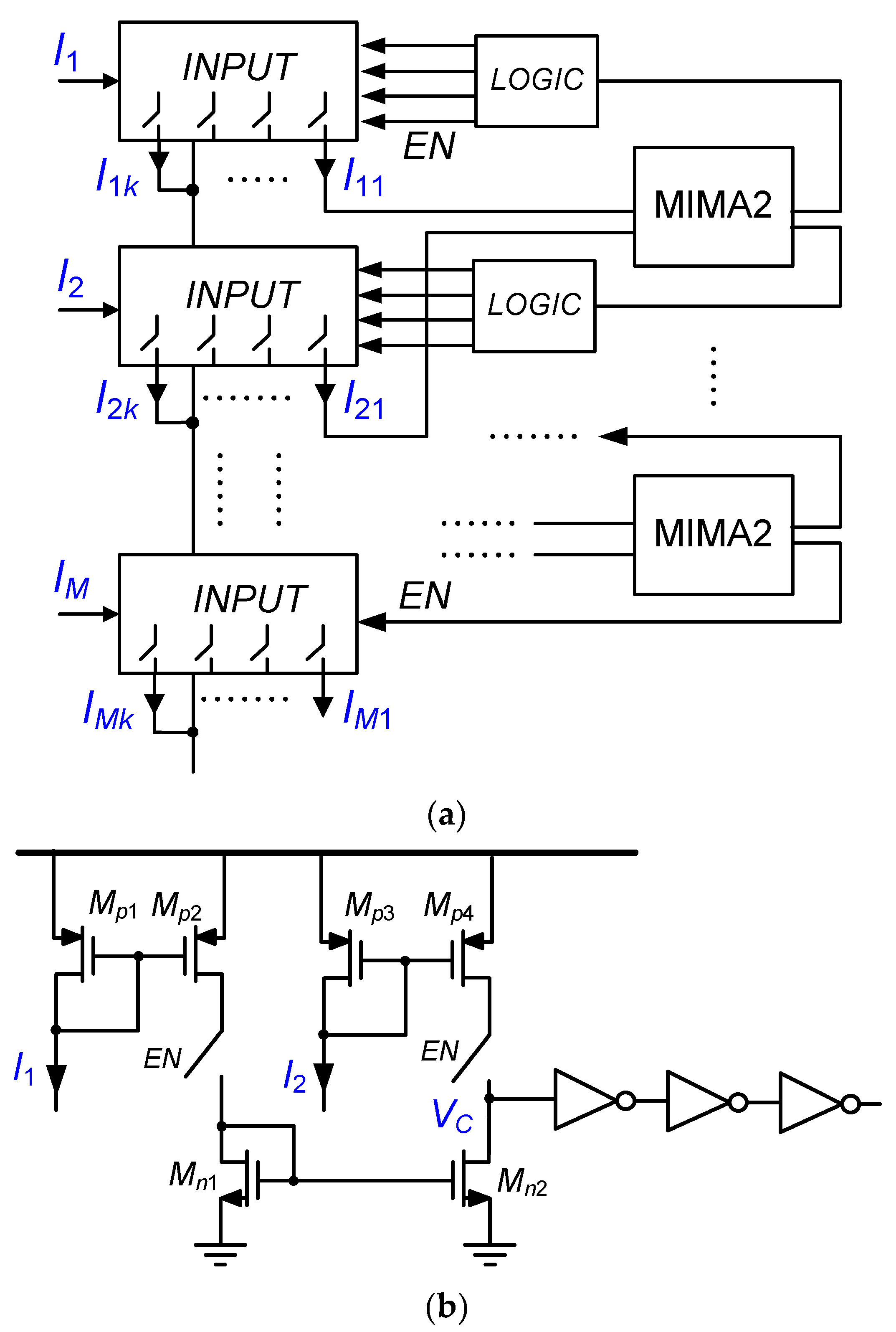
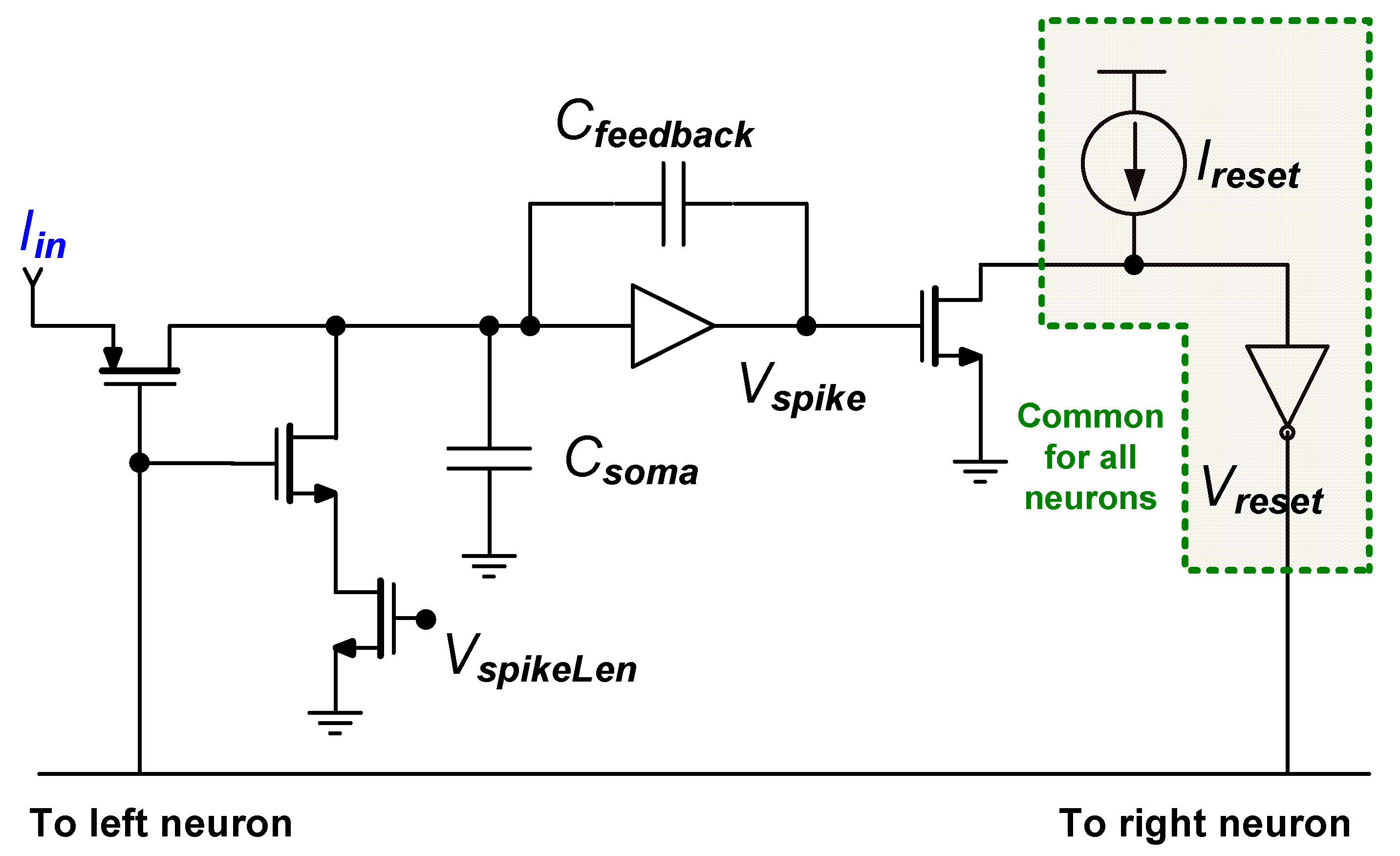
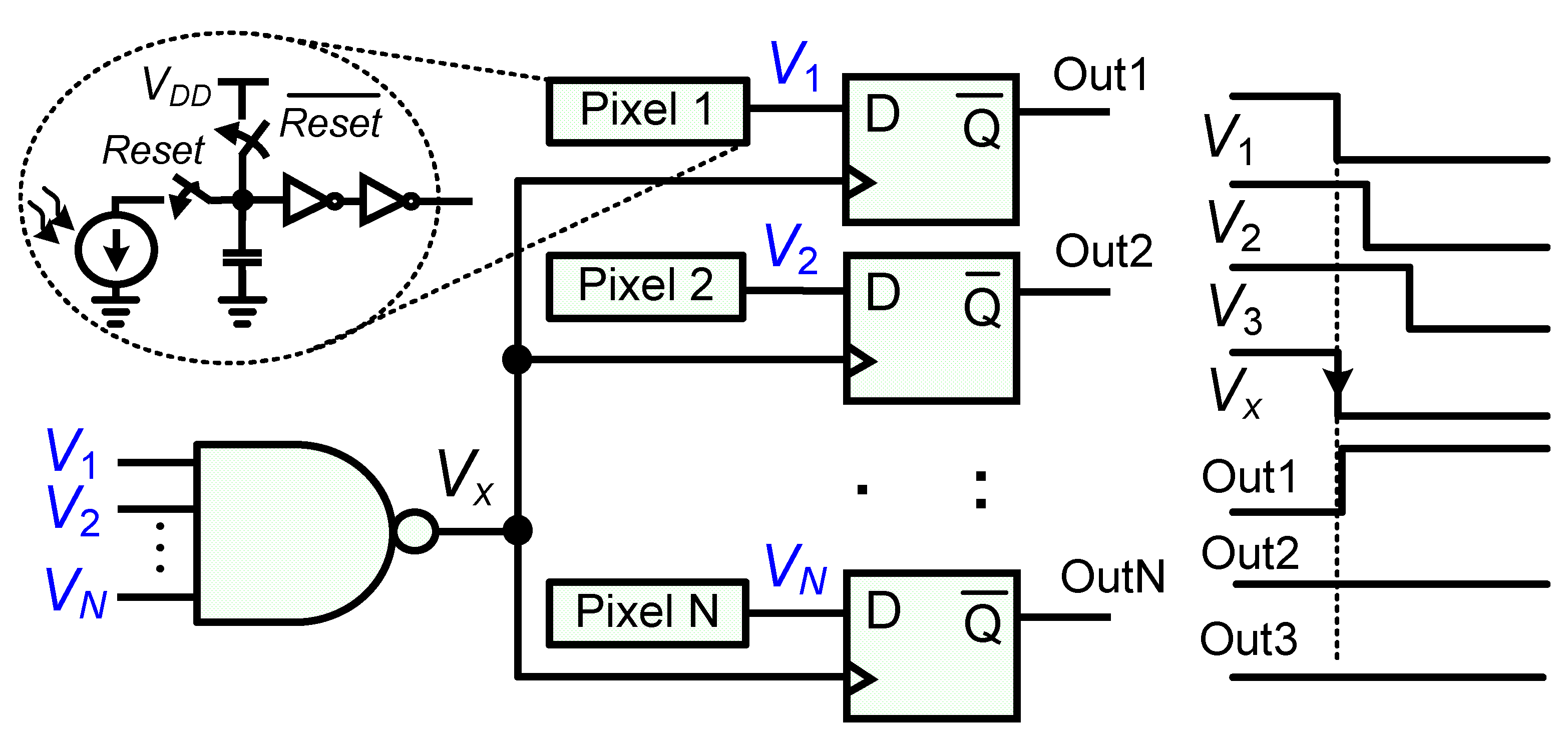
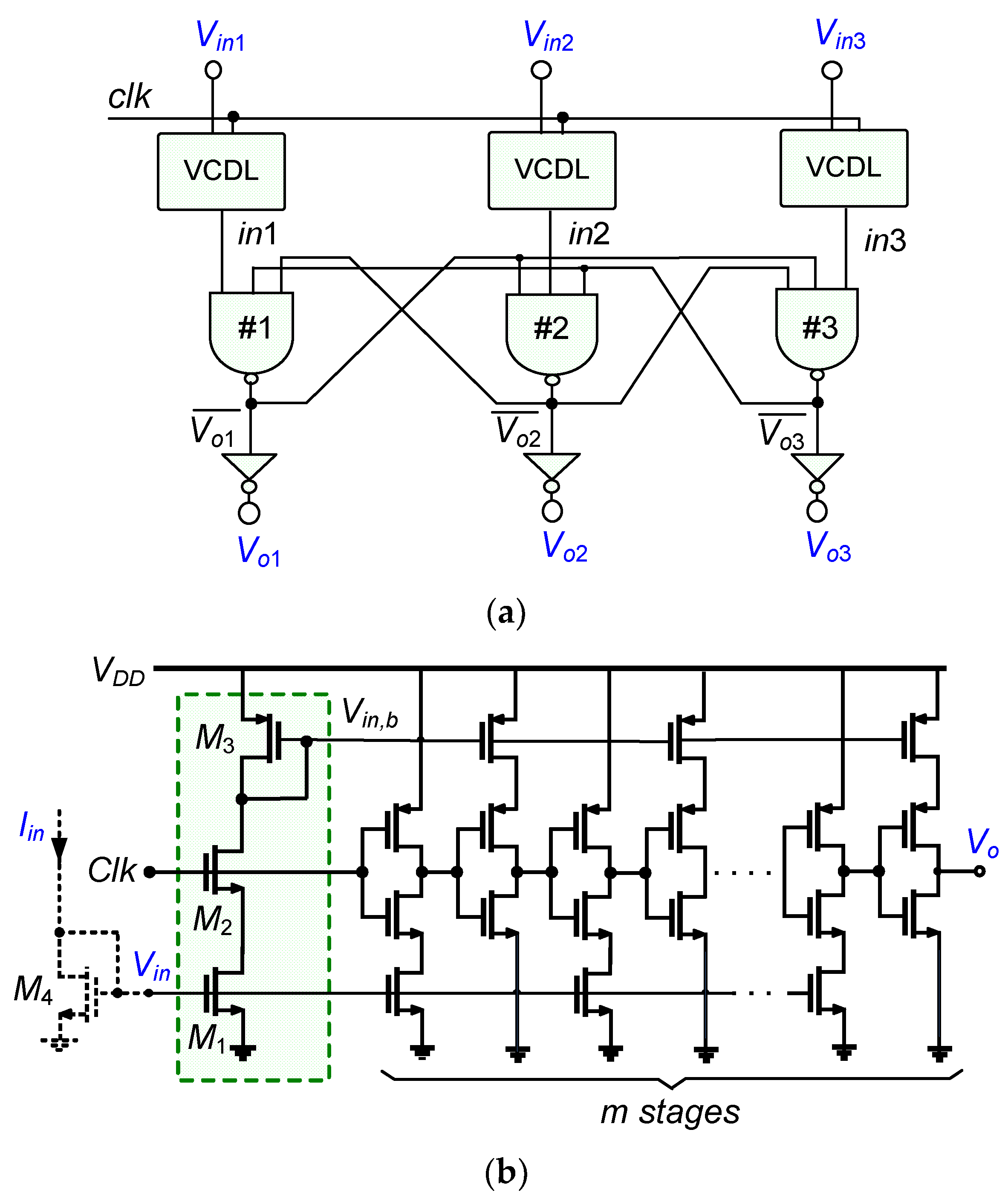

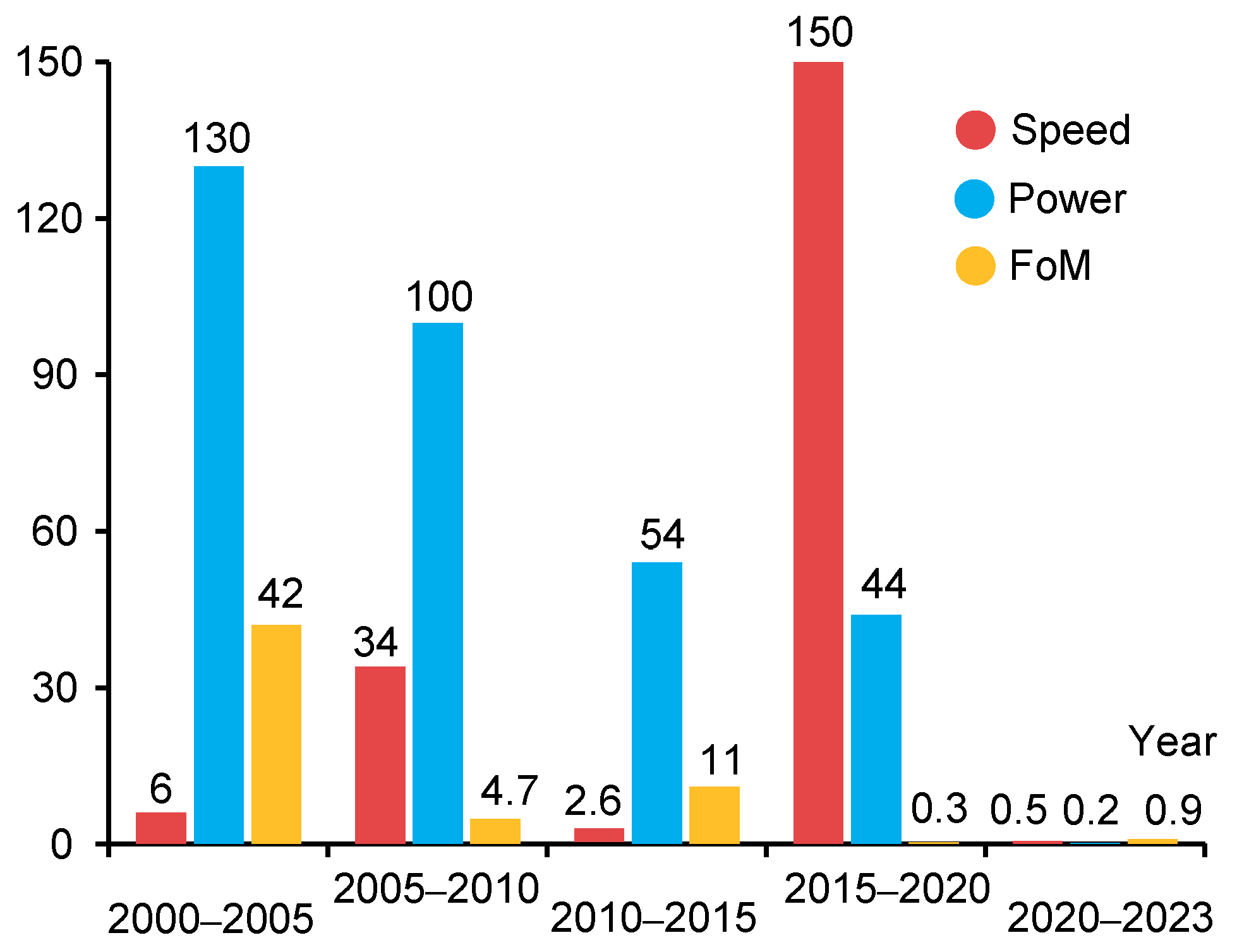
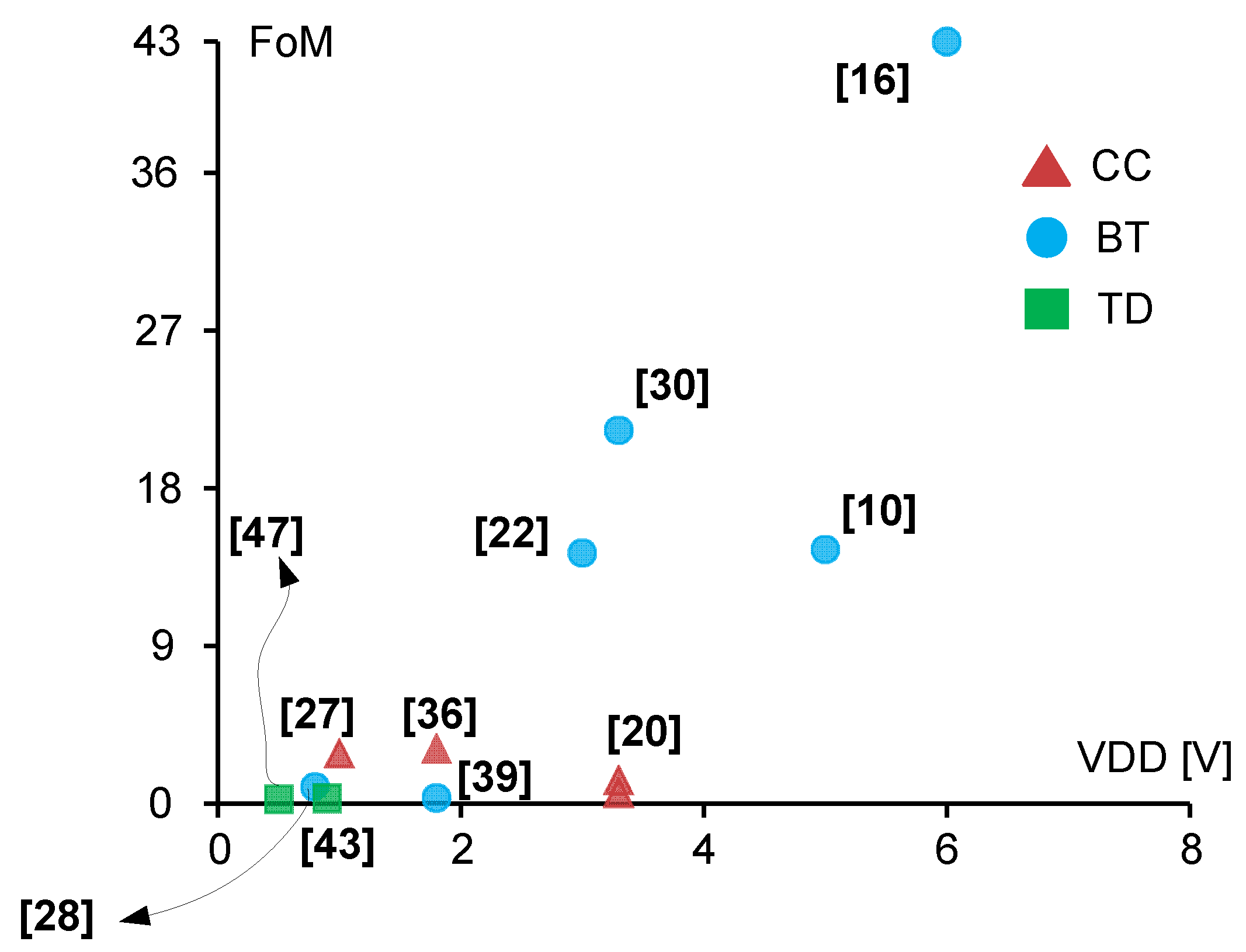
| [20] | [27] | [38] | [33] | [12] | [48] | [49] | [10] | [16] | [22] | [18] | [28] | [30] | [39] | [43] | [47] | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Technology [µm] | 0.35 | 0.35 | 0.18 | 0.35 | 0.35 | 2.00 | 0.18 | 0.045 | 2.40 | 0.80 | 0.60 | 0.35 | 0.18 | 0.50 | 0.18 | 0.04 | 0.13 |
| Supply Voltage [V] | 3.3 | 3.3 | 1.0 | 2.5 | 3.3 | 5.0 | 0.3 | 1.0 | 5.0 | 6.0 | 3.0 | 3.3 | 0.8 | 3.3 | 1.8 | 0.9 | 0.5 |
| No. Inputs | 8 | 8 | 8 | 3 | 5 | 2 | 3 | 2 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 16 | 3 |
| Precision [%] | 96.4 | 99.95 | 99 | 99.6 | 99.8 | - | - | - | 99.0 | - | - | - | 99.5 | - | 99.0 | - | 99.6 |
| Operating Frequency [MHz] | 29 | 83 | 3.5 | 10 | - | - | 0.04 | 0.04 | 13.8 | 2.8 | 20 | 1 | 0.383 | 5 | 50 | 250 | 1 |
| Power per Input [µW] | 22.5 | 87.5 | 10 | - | 22 | 400 | - | 0.062 | 200 | 120 | 284 | 70 | 0.36 | 106 | 15.75 | 72 | 0.25 |
| Area per cell [µm2] | 569 | 569 | - | - | 110 | 32,500 | 217 | 150 | 11,200 | - | - | - | - | 60,000 | - | - | 280 |
| FoM [µW/MHz] | 0.77 | 1.05 | 2.85 | - | - | - | - | 1.55 | 14.5 | 43.5 | 14.3 | 71.5 | 0.93 | 21.30 | 0.31 | 0.29 | 0.25 |
| Architecture | CC | CC | CC | CC | CC | CC | CC | CC | BT | BT | BT | BT | BT | BT | BT | BT-TD | TD |
| Meas./Sim. | Meas. | Sim. | Sim. | Sim. | Meas | Meas | Meas | Meas | Meas | Sim. | Sim. | Meas | Meas | Sim | Sim | Meas. | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahiminejad, E.; Aminzadeh, H. Winner-Take-All and Loser-Take-All Circuits: Architectures, Applications and Analytical Comparison. Chips 2023, 2, 262-278. https://doi.org/10.3390/chips2040016
Rahiminejad E, Aminzadeh H. Winner-Take-All and Loser-Take-All Circuits: Architectures, Applications and Analytical Comparison. Chips. 2023; 2(4):262-278. https://doi.org/10.3390/chips2040016
Chicago/Turabian StyleRahiminejad, Ehsan, and Hamed Aminzadeh. 2023. "Winner-Take-All and Loser-Take-All Circuits: Architectures, Applications and Analytical Comparison" Chips 2, no. 4: 262-278. https://doi.org/10.3390/chips2040016
APA StyleRahiminejad, E., & Aminzadeh, H. (2023). Winner-Take-All and Loser-Take-All Circuits: Architectures, Applications and Analytical Comparison. Chips, 2(4), 262-278. https://doi.org/10.3390/chips2040016