Evaluation of an Hourly Empirical Method Against ASCE PM (2005), for Hyper-Arid to Subhumid Climatic Conditions of the State of California
Abstract
1. Introduction
2. Materials and Methods
2.1. Methods
2.1.1. ASCE PM (2005) Method
2.1.2. Empirical Method
2.2. Statistical and Climatic Indices
2.2.1. Coefficient of Determination
2.2.2. Slope
2.2.3. Intercept
2.2.4. Root Mean Square Error (RMSE)
2.2.5. Index of Agreement (IoA)
2.2.6. The Aridity Index (AI)
2.3. Data
2.3.1. Data Source: CIMIS Network
2.3.2. Quality Control
2.3.3. Meteorological Data
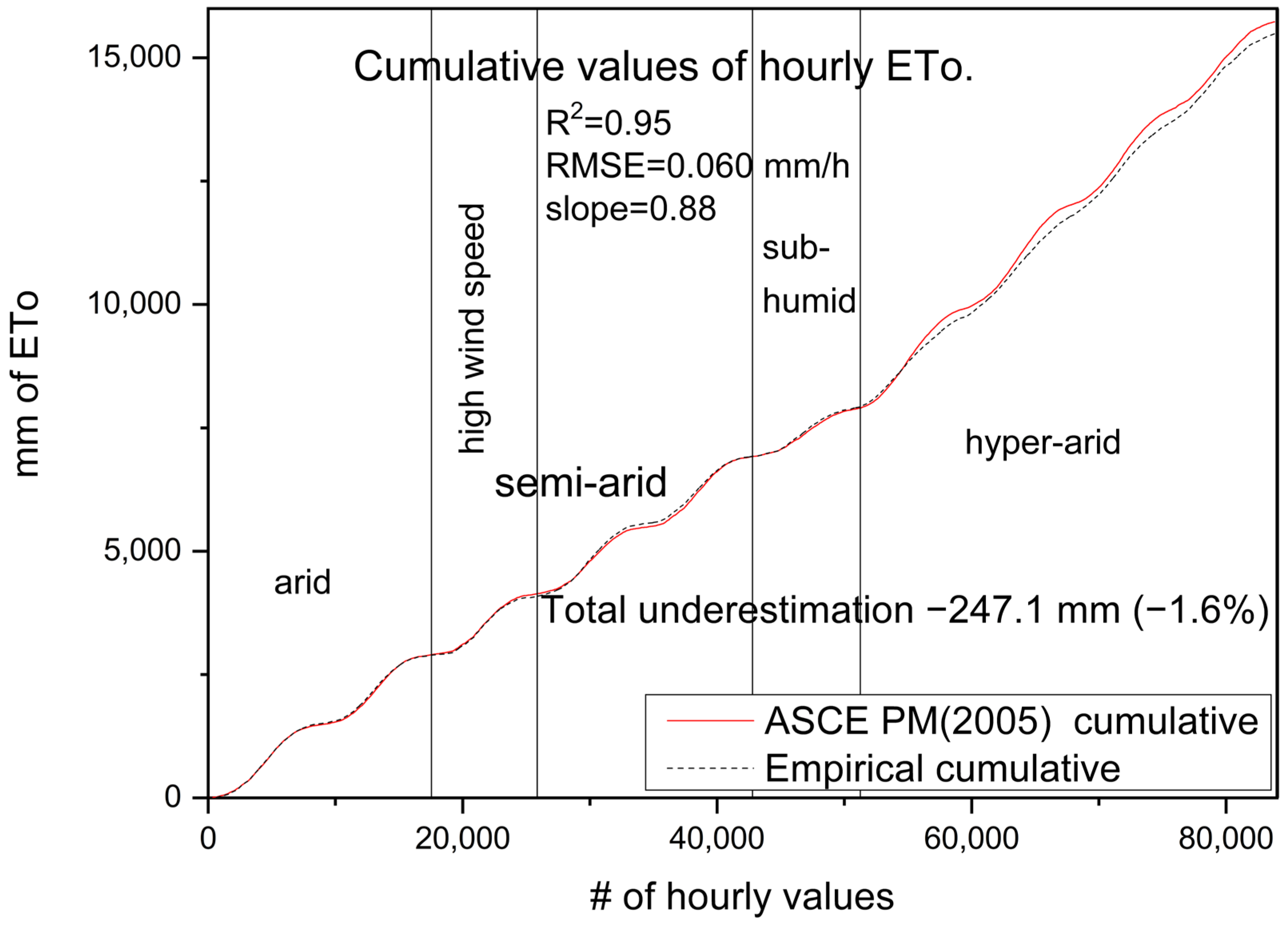
3. Results and Discussion
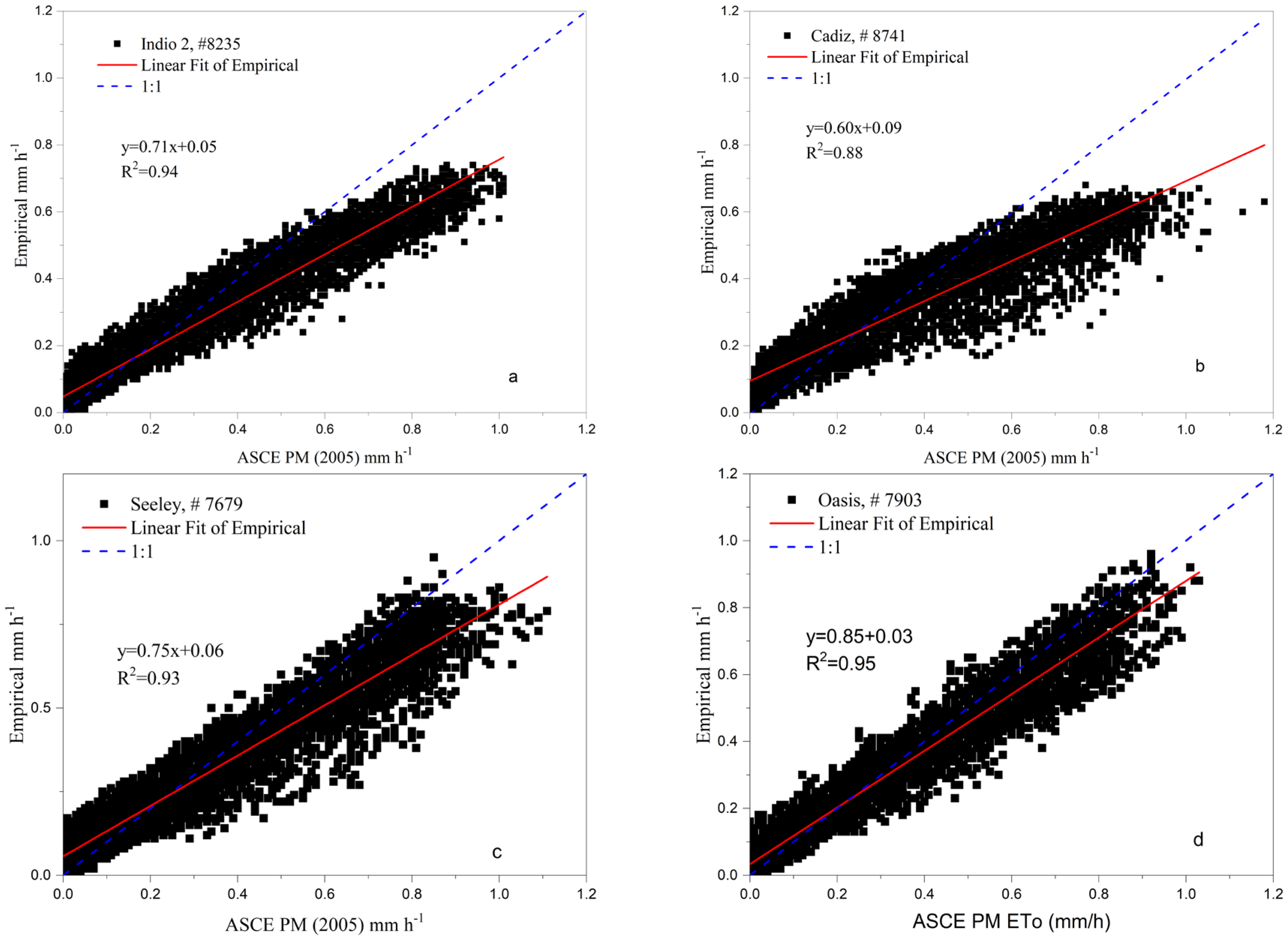
3.1. Stations with Hyper-Arid Climatic Regimes
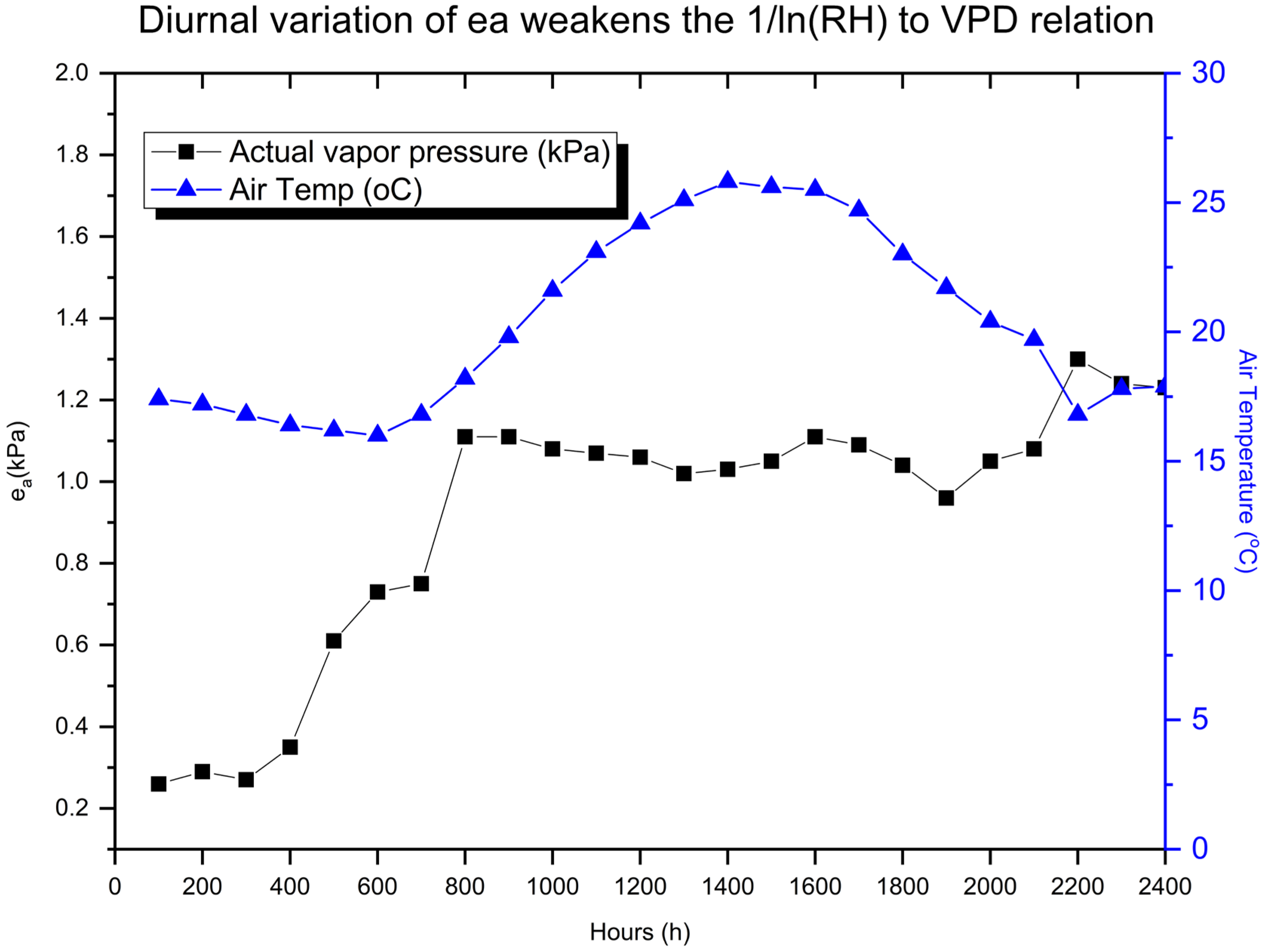
3.2. Investigation of the VPD − 1/ln(RH) Relation
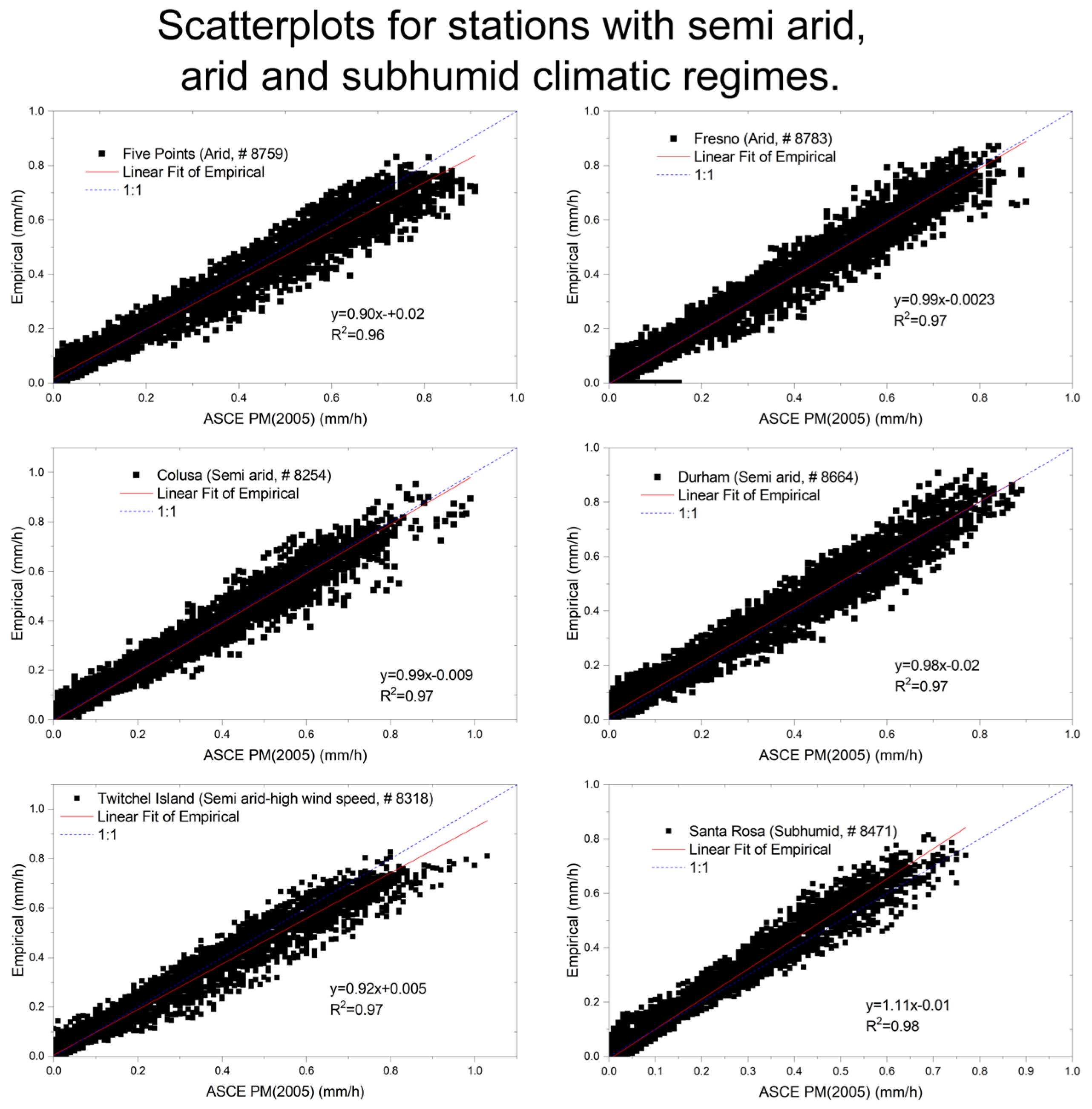
3.3. Stations with Arid, Semi-Arid and Subhumid Climatic Regimes
3.4. Evaluation of the Relation of the Values of u2 and VPD, and the RMSE Values Between the Two Methods, for All the Climatic Regimes
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Monteith, J.L. Evaporation and Environent. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Penman, H.L. Natural Evaporation from Open Water, Bare Soil and Grass. Proc. R. Soc. A Math. Phys. Eng. Sci. 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Walter, I.A.; Allen, R.G.; Elliott, R.L.; Itenfisu, D.; Brown, P.; Jensen, M.E.; Mecham, B.; Howell, T.A.; Snyder, R.L.; Echings, S.; et al. The ASCE Standardized Reference Evapotranspiration Equation; Standardization of Reference Evapotranspiration Task Committee Final Report; ASCE: Reston, VA, USA, 2005. [Google Scholar]
- Jensen, M.; Burman, R.; Allen, R.G. Evapotranspiration and Irrigation Water Requirements; ASCE: Reston, VA, USA, 1990. [Google Scholar]
- Alexandris, S.; Kerkides, P.; Liakatas, A. Daily reference evapotranspiration estimates by the “Copais” approach. Agric. Water Manag. 2006, 82, 371–386. [Google Scholar] [CrossRef]
- Alexandris, S.; Kerkides, P. New empirical formula for hourly estimations of reference evapotranspiration. Agric. Water Manag. 2003, 60, 157–180. [Google Scholar] [CrossRef]
- Blaney, H.F.; Criddle, W.D. Determining Water Requirements in Irrigated Areas from Climatological and Irrigation Data; US Department of Agriculture, Soil Conservation Service: Washington, DC, USA, 1950. [Google Scholar]
- Linacre, E.T. A simple formula for estimating evaporation rates in various climates, using temperature data alone. Agric. Meteorol. 1977, 18, 409–424. [Google Scholar] [CrossRef]
- Makkink, G.F. Testing the Penman formula by means of lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach towards a rational calssification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Tsesmelis, D.E.; Machairas, I.; Skondras, N.; Oikonomou, P.; Barouchas, P.E. GAIA: A New Formula for Reference Evapotranspiration. Atmosphere 2024, 15, 1465. [Google Scholar] [CrossRef]
- Tegos, A.; Malamos, N.; Koutsoyiannis, D. A parsimonious regional parametric evapotranspiration model based on a simplification of the Penman-Monteith formula. J. Hydrol. 2015, 524, 708–717. [Google Scholar] [CrossRef]
- Malamos, N.; Tegos, A.; Bourantas, G.; Chalvantzis, C.; Koutsoyiannis, D. Global reference evapotranspiration clustering and its relation to the Köppen-Geiger climate classification. J. Hydrol. 2025, 660, 133342. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Khabba, S.; Simonneaux, V.; Jarlan, L.; Ouldbba, A.; Rodriguez, J.C.; Allen, R.G. Assessment of reference evapotranspiration methods in semi-arid regions: Can weather forecast data be used as alternate of ground meteorological parameters? J. Arid. Environ. 2010, 74, 1587–1596. [Google Scholar] [CrossRef]
- Huo, Z.; Dai, X.; Feng, S.; Kang, S.; Huang, G. Effect of climate change on reference evapotranspiration and aridity index in arid region of China. J. Hydrol. 2013, 492, 24–34. [Google Scholar] [CrossRef]
- Itenfisu, D.; Elliott, R.L.; Allen, R.G.; Walter, I.A. Comparison of Reference Evapotranspiration Calculations as Part of the ASCE Standardization Effort. J. Irrig. Drain. Eng. 2003, 129, 440–448. [Google Scholar] [CrossRef]
- Raza, A.; Shoaib, M.; Faiz, M.A.; Baig, F.; Khan, M.M.; Ullah, M.K.; Zubair, M. Comparative Assessment of Reference Evapotranspiration Estimation Using Conventional Method and Machine Learning Algorithms in Four Climatic Regions. Pure Appl. Geophys. 2020, 177, 4479–4508. [Google Scholar] [CrossRef]
- Chipula, G.; Moyo, V.; Reuben, T.N.; Fiwa, L.; Nkhata, M.; Phiri, H.; Fandika, I. Development and evaluation of site-specific evapotranspiration models in Malawi through a comparative analysis of existing models. Phys. Chem. Earth Parts A/B/C 2025, 137, 103814. [Google Scholar] [CrossRef]
- Eludire, O.; Faloye, O.; Alatise, M.; Ajayi, A.; Oguntunde, P.; Badmus, T.; Fashina, A.; Adeyeri, O.; Olorunfemi, I.; Ogunrinde, A. Evaluation of Evapotranspiration Prediction for Cassava Crop Using Artificial Neural Network Models and Empirical Models over Cross River Basin in Nigeria. Water 2025, 17, 87. [Google Scholar] [CrossRef]
- Cutting, N.G.; Kaur, S.; Singh, M.C.; Sharma, N.; Mishra, A. Estimating Crop Evapotranspiration in Data-Scare Regions: A Comparative Analysis of Eddy Covariance, Empirical and Remote-Sensing Approaches. Water Conserv. Sci. Eng. 2024, 9, 65. [Google Scholar] [CrossRef]
- Celestin, S.; Qi, F.; Li, R.; Yu, T.; Cheng, W. Evaluation of 32 Simple Equations against the Penman–Monteith Method to Estimate the Reference Evapotranspiration in the Hexi Corridor, Northwest China. Water 2020, 12, 2772. [Google Scholar] [CrossRef]
- Chatzithomas, C. Evaluation of a radiation-based empirical model for estimating hourly reference evapotranspiration for high-altitude climatic conditions: A case study for the state of California. J. Earth Syst. Sci. 2019, 128, 79. [Google Scholar] [CrossRef]
- Gao, G.; Zhang, X.; Yu, T.; Liu, B. Comparison of three evapotranspiration models with eddy covariance measurements for a Populus euphratica Oliv. forest in an arid region of northwestern China. J. Arid. Land 2016, 8, 146–156. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, W. Evapotranspiration of an oasis-desert transition zone in the middle stream of Heihe River, Northwest China. J. Arid. Land 2014, 6, 529–539. [Google Scholar] [CrossRef]
- Ratshiedana, P.E.; Abd Elbasit, M.A.M.; Adam, E.; Chirima, J.G. Evaluation of Micrometeorological Models for Estimating Crop Evapotranspiration Using a Smart Field Weighing Lysimeter. Water 2025, 17, 187. [Google Scholar] [CrossRef]
- Boso, A.C.M.R.; Campos, F.S.; Pai, A.D. Calibrated models to estimate Referensce evapotranspiration, for the city of Botucatu/Sp, in relation to the weighing lysimeter. Model. Earth Syst. Environ. 2024, 10, 6599–6612. [Google Scholar] [CrossRef]
- Lu, Y.; Sun, L.; Li, C.; He, J.; Guo, Z.; Duan, L.; Zhang, J.; Łupikasza, E.; Malik, I.; Wistuba, M.; et al. Spatiotemporal Changes in and Driving Factors of Potential Evapotranspiration in a Hyper-Arid Locale in the Hami Region, China. Atmosphere 2024, 15, 136. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z. Reference crop evapotranspiration from ambient air temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Ghiat, I.; Govindan, R.; Al-Ansari, T. Evaluation of evapotranspiration models for cucumbers grown under CO2 enriched and HVAC driven greenhouses: A step towards precision irrigation in hyper-arid regions. Front. Sustain. Food Syst. 2023, 7, 1155443. [Google Scholar] [CrossRef]
- Alexandris, S.; Proutsos, N. How significant is the effect of the surface characteristics on the Reference Evapotranspiration estimates? Agric. Water Manag. 2020, 237, 106181. [Google Scholar] [CrossRef]
- Faunt, C.C.; Sneed, M.; Traum, J.; Brandt, J.T. Water availability and land subsidence in the Central Valley, California, USA. Hydrogeol. J. 2016, 24, 675–684. [Google Scholar] [CrossRef]
- Temesgen, B.; Eching, S.; Davidoff, B.; Frame, K. Comparison of Some Reference Evapotranspiration Equations for California. J. Irrig. Drain. Eng. 2005, 131, 73–84. [Google Scholar] [CrossRef]
- Snyder, R.L.; Orang, M.; Matyac, S.; Grismer, M.E. Simplified Estimation of Reference Evapotranspiration from Pan Evaporation Data in California. J. Irrig. Drain. Eng. 2005, 131, 249–253. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Allen, R.G. History and Evaluation of Hargreaves Evapotranspiration Equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Djaman, K.; Irmak, S.; Sall, M.; Sow, A.; Kabenge, I. Comparison of sum-of-hourly and daily time step standardized ASCE Penman-Monteith reference evapotranspiration. Theor. Appl. Climatol. 2018, 134, 533–543. [Google Scholar] [CrossRef]
- Chatzithomas, C.D.; Alexandris, S. Solar radiation and relative humidity based, empirical method, to estimate hourly reference evapotranspiration. Agric. Water Manag. 2015, 152, 188–197. [Google Scholar] [CrossRef]
- Blonquist, J.M.; Allen, R.G.; Bugbee, B. An evaluation of the net radiation sub-model in the ASCE standardized reference evapotranspiration equation: Implications for evapotranspiration prediction. Agric. Water Manag. 2010, 97, 1026–1038. [Google Scholar] [CrossRef]
- Ventura, F.; Spano, D.; Duce, P.; Snyder, R.L. An evaluation of common evapotranspiration equations. Irrig. Sci. 1999, 18, 163–170. [Google Scholar] [CrossRef]
- Choi, M.; Kustas, W.P.; Ray, R.L. Evapotranspiration models of different complexity for multiple land cover types. Hydrol. Process. 2012, 26, 2962–2972. [Google Scholar] [CrossRef]
- Willmott, C.J. Some Comments on the Evaluation of Model Performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Kukal, M.; Irmak, S. Long-term patterns of air temperatures, daily temperature range, precipitation, grass-reference evapotranspiration and aridity index in the USA Great Plains: Part I. Spatial trends. J. Hydrol. 2016, 542, 953–977. [Google Scholar] [CrossRef]
- Shan, N.; Shi, Z.; Yang, X.; Zhang, X.; Guo, H.; Zhang, B.; Zhang, Z. Trends in potential evapotranspiration from 1960 to 2013 for a desertification-prone region of China. Int. J. Climatol. 2016, 36, 3434–3445. [Google Scholar] [CrossRef]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. A Comparison of six potential evapotranspiration methods for regional use in the Southeastern United States. J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; ISBN 92-5-104219-5. [Google Scholar]
- Xu, C.; Gong, L.; Jiang, T.; Chen, D.; Singh, V.P. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Saxton, K.E. Sensitivity analysis of the combination evapotranspiration equation. Agric. Meteorol. 1975, 15, 343–353. [Google Scholar] [CrossRef]
- Allen, R.G. Assessing Integrity of Weather Data for Reference Evapotranspiration Estimation. J. Irrig. Drain. Eng. 1996, 122, 97–106. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Hartogensis, O.K.; Allen, R.G.; Kramer, J.W.J.L. Regional Advection Perturbations in an Irrigated Desert (RAPID) experiment. Theor. Appl. Climatol. 2004, 80, 143–152. [Google Scholar] [CrossRef]

| Stn Id | Name | Long. | Lat | Elev (m) | Year | # of Records | AI (P/ETo) | Remarks |
|---|---|---|---|---|---|---|---|---|
| 200 | Indio 2 | 33.75 | −116.25 | 12 | 2008 | 8235 | 0.00 | hyper-arid |
| 190 | Five Points | 36.38 | −120.23 | 82 | 2005 | 8759 | 0.10 | arid |
| 80 | Fresno | 36.82 | −119.74 | 103 | 2000 | 8783 | 0.20 | arid |
| 32 | Colusa | 39.23 | −122.02 | 16 | 2000 | 8254 | 0.34 | semi-arid |
| 12 | Durham | 39.61 | −121.82 | 130 | 2001 | 8664 | 0.45 | semi-arid |
| 83 | Santa Rosa | 38.40 | −122.80 | 24 | 2011 | 8471 | 0.74 | subhumid |
| 221 | Cadiz Valley | 34.51 | −115.51 | 47 | 2011 | 8741 | 0.03 | high VPD (hyper-arid) |
| 140 | Twitchell Island | 38.12 | −121.66 | −1 | 2000 | 8318 | 0.23 | high wind speed (semi-arid) |
| 68 | Seeley | 32.76 | −115.73 | 12 | 2011 | 7679 | 0.04 | high ETo (hyper-arid) |
| 136 | Oasis | 33.52 | −116.16 | 4 | 2005 | 7903 | 0.03 | max temp (hyper-arid) |
| Station | Emp (mm yr−1) | PM (mm yr−1) | Emp-PM | (Emp-PM)% | R2 | RMSE | Slope | ΙοA |
|---|---|---|---|---|---|---|---|---|
| Indio 2 | 1825.8 | 2019.4 | −193.7 | −9.6% | 0.94 | 0.095 | 0.71 | 0.957 |
| Five Points | 1502.2 | 1479.6 | 22.6 | 1.5% | 0.96 | 0.046 | 0.90 | 0.989 |
| Fresno | 1389.4 | 1422.0 | −32.6 | −2.3% | 0.97 | 0.038 | 0.99 | 0.993 |
| Colusa | 1189.2 | 1233.7 | −44.5 | −3.6% | 0.97 | 0.037 | 0.99 | 0.993 |
| Durham | 1477.6 | 1350.9 | 126.8 | 9.4% | 0.97 | 0.040 | 0.98 | 0.991 |
| Santa Rosa | 999.3 | 980.1 | 19.3 | 2.0% | 0.98 | 0.033 | 1.11 | 0.992 |
| Cadiz Valley | 2108.1 | 2141.9 | −33.8 | −1.6% | 0.88 | 0.115 | 0.60 | 0.919 |
| Twitchell Island | 1368.1 | 1434.1 | −66.0 | −4.6% | 0.97 | 0.041 | 0.92 | 0.991 |
| Seeley | 1877.6 | 1916.4 | −38.9 | −2.0% | 0.93 | 0.088 | 0.75 | 0.968 |
| Oasis | 1749.3 | 1755.7 | −6.4 | −0.4% | 0.95 | 0.062 | 0.85 | 0.983 |
| Average | 1548.7 | 1573.4 | ||||||
| Total (83,807 records) | 15,486.6 | 15,733.7 | −247.1 | −1.6% | 0.95 | 0.060 | 0.88 | 0.978 |
| All Hourly Values (1) | Warm Period (2) | Cold Period (3) | Daily Values (4) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slope | Intercept | R2 | Slope | Intercept | R2 | Slope | Intercept | R2 | Slope | Intercept | R2 | |
| Indio 2 | 0.0239 | 0.2343 | 0.61 | 0.0235 | 0.2284 | 0.61 | 0.0327 | 0.2304 | 0.66 | 0.0365 | 0.2192 | 0.93 |
| Cadiz | 0.0256 | 0.2671 | 0.51 | 0.0249 | 0.2654 | 0.46 | 0.0359 | 0.2569 | 0.49 | 0.0471 | 0.2388 | 0.88 |
| Seeley | 0.0175 | 0.2425 | 0.45 | 0.0181 | 0.2337 | 0.56 | 0.0266 | 0.2390 | 0.46 | 0.0290 | 0.2296 | 0.88 |
| Oasis | 0.0248 | 0.2263 | 0.67 | 0.0236 | 0.2263 | 0.61 | 0.0338 | 0.2205 | 0.80 | 0.0325 | 0.2162 | 0.96 |
| All stations | 0.0249 | 0.2395 | 0.52 | 0.0253 | 0.2314 | 0.54 | 0.0339 | 0.2357 | 0.54 | 0.0366 | 0.2262 | 0.91 |
| u2 | |||||
| RMSE (mm h−1) | All hourly records | Hyper-arid | arid | semi-arid | subhumid |
| 0.073 | (5 m s−1) 94% | (2.2 m s−1) 60% | (6 m s−1) 99% | 100% | 100% |
| 0.13 | (8 m s−1) 99% | (5.3 m s−1) 94% | 100% | 100% | 100% |
| VPD | |||||
| RMSE (mm h−1) | All hourly records | Hyper-arid | arid | semi-arid | subhumid |
| 0.073 | (2.5 kPa) 87% | (2.1 kPa) 59% | 4.5 (kPa) 98% | (3 kPa) 97% | 100% |
| 0.13 | (7.5 kPa) 100% | (4.1 kPa) 86% | 100% | 100% | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatzithomas, C.D. Evaluation of an Hourly Empirical Method Against ASCE PM (2005), for Hyper-Arid to Subhumid Climatic Conditions of the State of California. Meteorology 2025, 4, 22. https://doi.org/10.3390/meteorology4030022
Chatzithomas CD. Evaluation of an Hourly Empirical Method Against ASCE PM (2005), for Hyper-Arid to Subhumid Climatic Conditions of the State of California. Meteorology. 2025; 4(3):22. https://doi.org/10.3390/meteorology4030022
Chicago/Turabian StyleChatzithomas, Constantinos Demetrios. 2025. "Evaluation of an Hourly Empirical Method Against ASCE PM (2005), for Hyper-Arid to Subhumid Climatic Conditions of the State of California" Meteorology 4, no. 3: 22. https://doi.org/10.3390/meteorology4030022
APA StyleChatzithomas, C. D. (2025). Evaluation of an Hourly Empirical Method Against ASCE PM (2005), for Hyper-Arid to Subhumid Climatic Conditions of the State of California. Meteorology, 4(3), 22. https://doi.org/10.3390/meteorology4030022







