On the Field Strength of Vacuum Energy and the Emergence of Mass †
Abstract
:1. Introduction
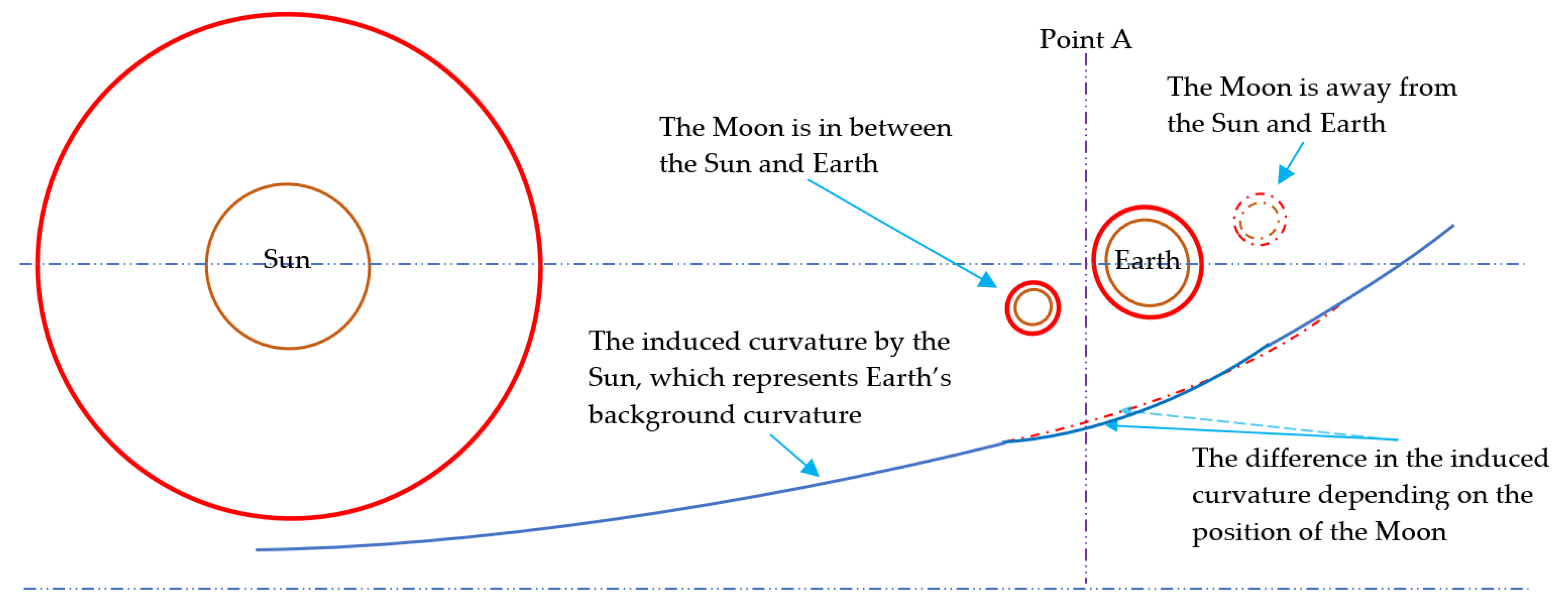
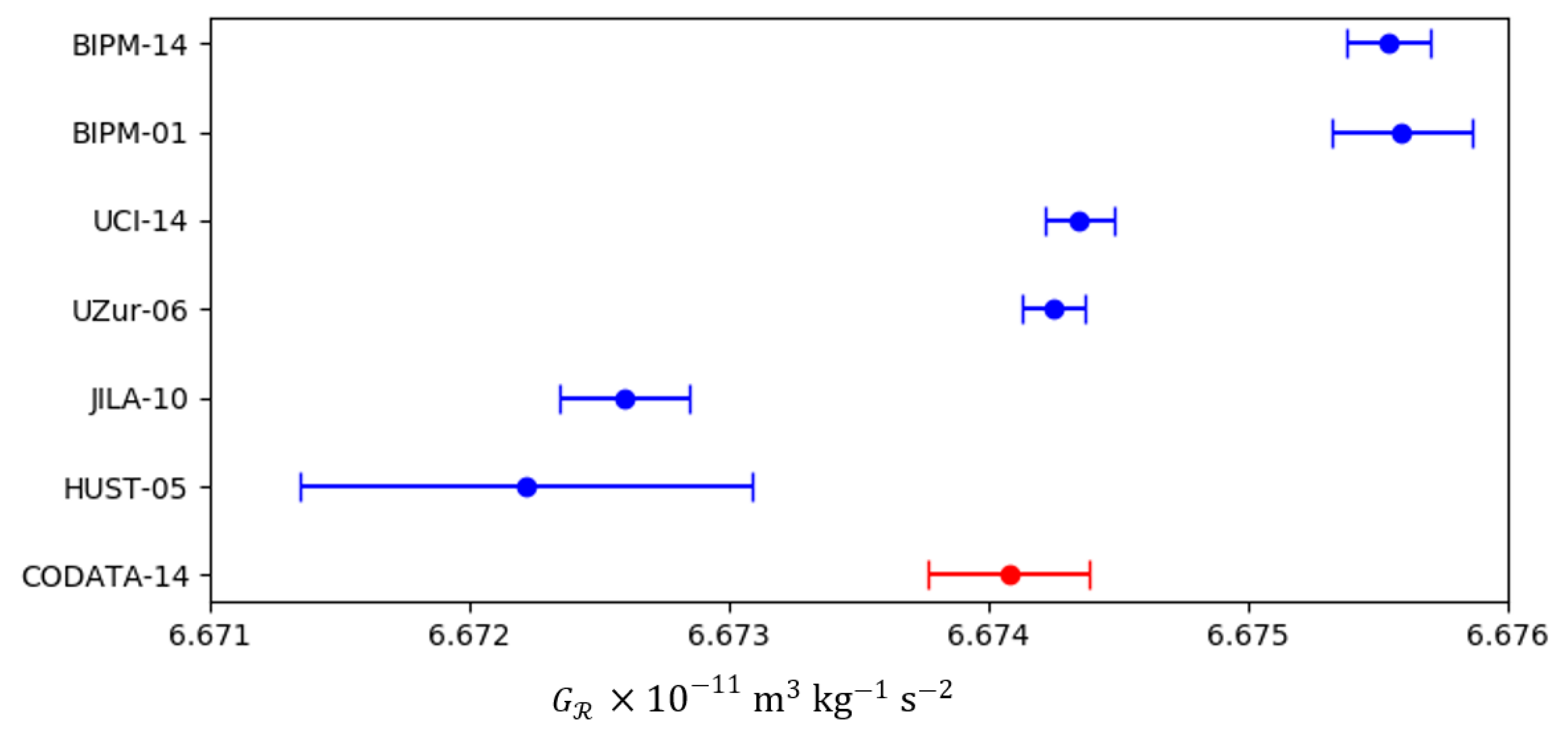
2. Newtonian Gravitational Parameter
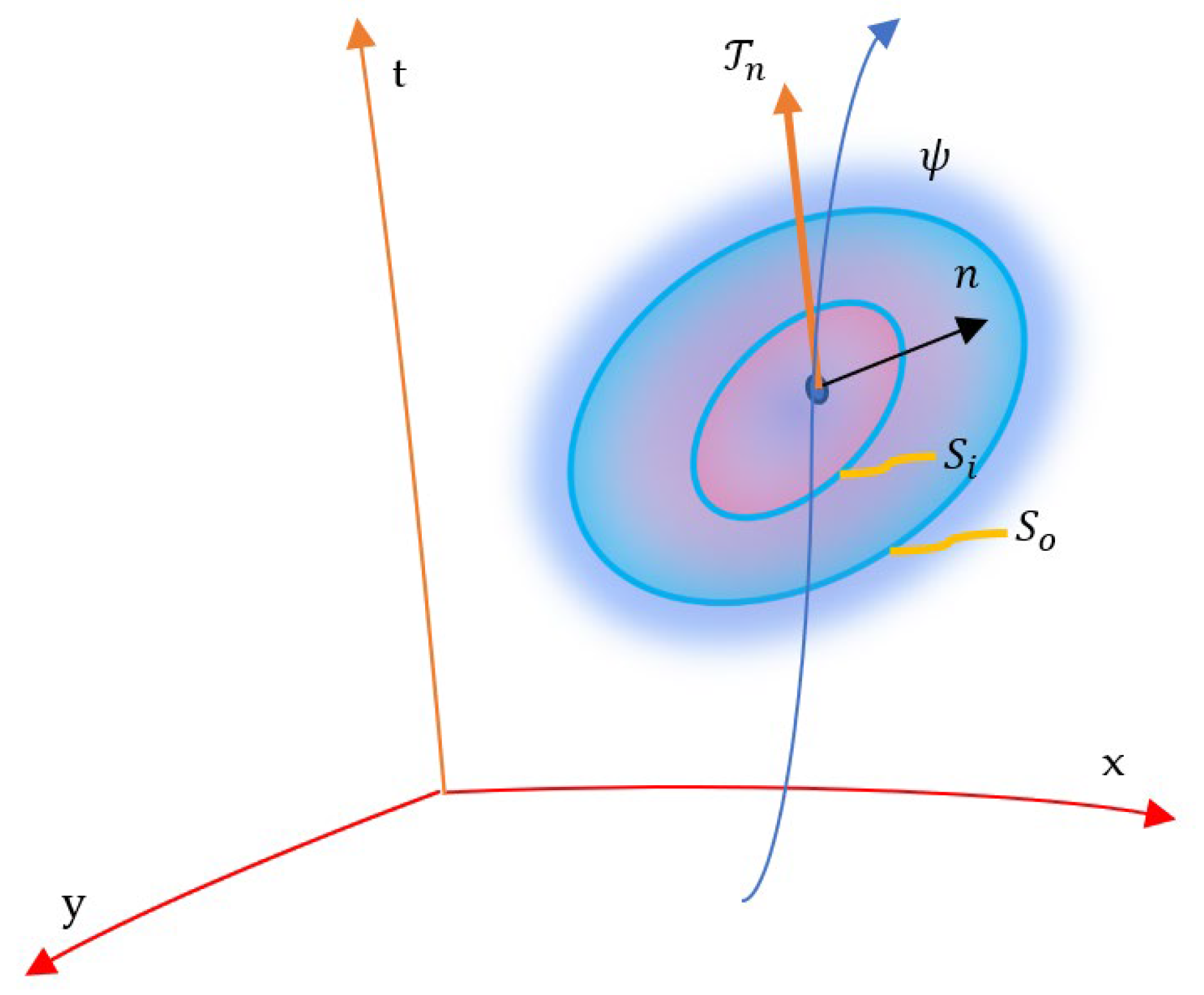
3. Emergence of Mass
4. Conclusions and Future Experiment Recommendations
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xue, C.; Liu, J.-P.; Li, Q.; Wu, J.-F.; Yang, S.-Q.; Liu, Q.; Shao, C.-G.; Tu, L.-C.; Hu, Z.-K.; Luo, J. Precision measurement of the Newtonian gravitational constant. Natl. Sci. Rev. 2020, 7, 1803–1817. [Google Scholar] [CrossRef] [PubMed]
- Rosi, G.; Sorrentino, F.; Cacciapuoti, L.; Prevedelli, M.; Tino, G.M. Precision measurement of the Newtonian gravitational constant using cold atoms. Nature 2014, 510, 518–521. [Google Scholar] [CrossRef] [PubMed]
- Schlamminger, S. Gravity measured with record precision. Nature 2018, 560, 562–563. [Google Scholar] [CrossRef] [PubMed]
- Gibney, E. Rivals join forces to nail down Big G. Metrologists meet to design the ultimate gravitational-constant experiment. Nature 2014, 514, 150–151. [Google Scholar] [CrossRef] [PubMed]
- Schlamminger, S. A cool way to measure big G. Nature 2014, 510, 478–480. [Google Scholar] [CrossRef] [PubMed]
- Al-Fadhli, M.B. Celestial and Quantum Propagation, Spinning, and Interaction as 4D Relativistic Cloud-Worlds Embedded in a 4D Conformal Bulk: From String to Cloud Theory. Preprints 2020, 2020100320. [Google Scholar] [CrossRef]
- Kozameh, C.N.; Newman, E.T.; Tod, K.P. Conformal Einstein spaces. Gen. Relat. Gravit. 1985, 17, 343–352. [Google Scholar] [CrossRef]
- Quinn, T.; Parks, H.; Speake, C.; Davis, R. Improved determination of G using two methods. Phys. Rev. Lett. 2013, 111, 101102. [Google Scholar] [CrossRef] [PubMed]
- Quinn, T.J.; Speake, C.C.; Richman, S.J.; Davis, R.S.; Picard, A. A New Determination of G Using Two Methods. Phys. Rev. Lett. 2001, 87, 111101. [Google Scholar] [CrossRef] [PubMed]
- Newman, R.; Bantel, M.; Berg, E.; Cross, W. A measurement of G with a cryogenic torsion pendulum. Philos. Trans. R. Soc. A 2014, 372, 20140025. [Google Scholar] [CrossRef] [PubMed]
- Schlamminger, S.; Holzschuh, E.; Kündig, W.; Nolting, F.; Pixley, R.E.; Schurr, J.; Straumann, U. Measurement of Newton’s gravitational constant. Phys. Rev. D 2006, 74, 082001. [Google Scholar] [CrossRef]
- Parks, H.V.; Faller, J.E. Simple pendulum determination of the gravitational constant. Phys. Rev. Lett. 2010, 105, 110801. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.-K.; Guo, J.-Q.; Luo, J. Correction of source mass effects in the HUST-99 measurement of G. Phys. Rev. D 2005, 71, 127505. [Google Scholar] [CrossRef]
- Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA recommended values of the fundamental physical constants: 2014. Rev. Mod. Phys. 2016, 88, 035009. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Fadhli, M.B. On the Field Strength of Vacuum Energy and the Emergence of Mass. Phys. Sci. Forum 2023, 7, 50. https://doi.org/10.3390/ECU2023-14104
Al-Fadhli MB. On the Field Strength of Vacuum Energy and the Emergence of Mass. Physical Sciences Forum. 2023; 7(1):50. https://doi.org/10.3390/ECU2023-14104
Chicago/Turabian StyleAl-Fadhli, Mohammed B. 2023. "On the Field Strength of Vacuum Energy and the Emergence of Mass" Physical Sciences Forum 7, no. 1: 50. https://doi.org/10.3390/ECU2023-14104
APA StyleAl-Fadhli, M. B. (2023). On the Field Strength of Vacuum Energy and the Emergence of Mass. Physical Sciences Forum, 7(1), 50. https://doi.org/10.3390/ECU2023-14104





