Heating Kinetics of Gold Nanoparticles in Biological Tissues with a Femtosecond Laser †
Abstract
1. Introduction
2. Theoretical Study
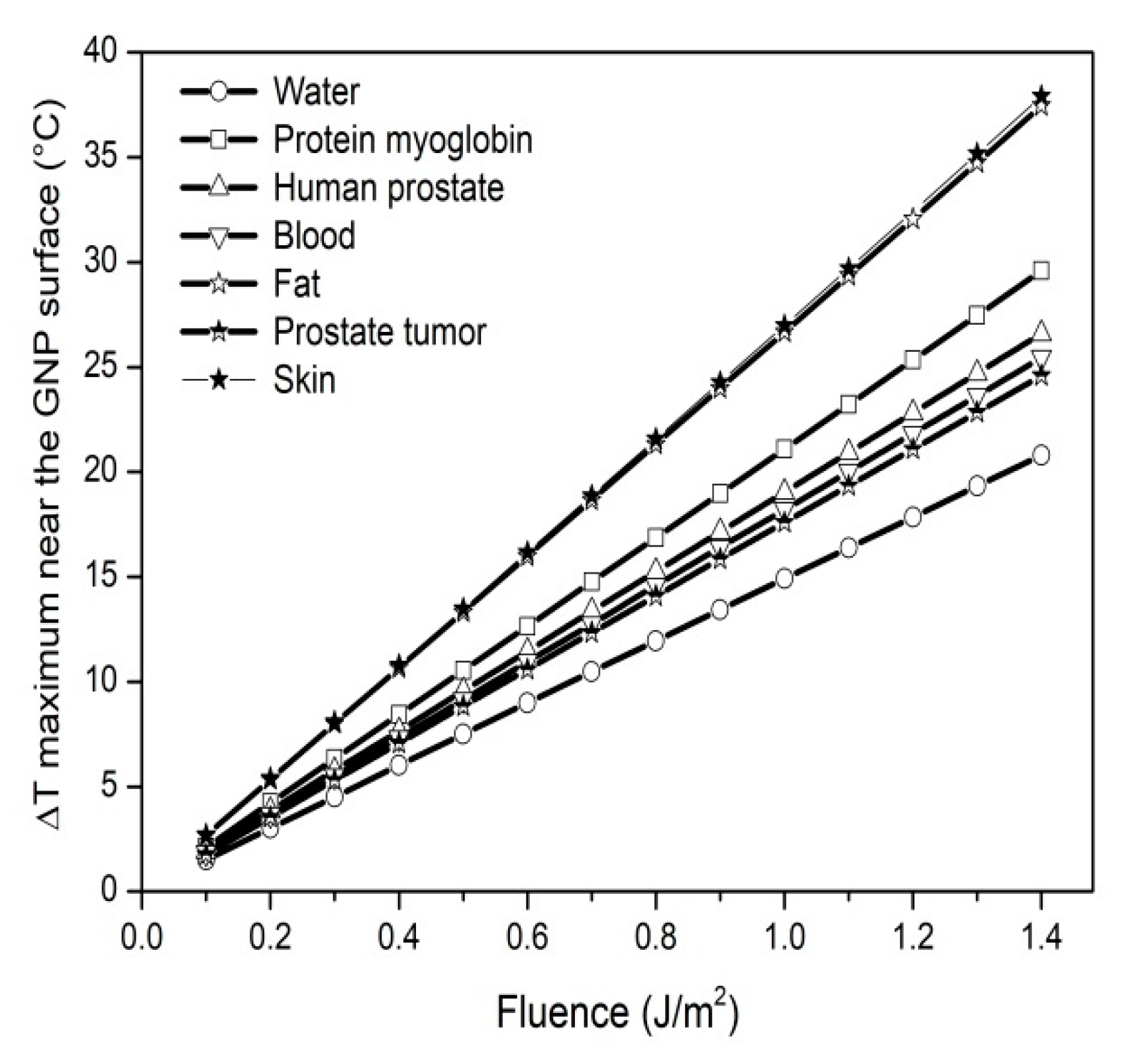
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Letfullin, R.R.; George, T.F.; Duree, G.C.; Bollinger, B.M. Ultrashort Laser Pulse Heating of Nanoparticles: Comparison of Theoretical Approaches. Adv. Opt. Technol. 2008, 2008, 251718. [Google Scholar] [CrossRef]
- Pustovalov, K.V. Theoretical study of heating of spherical nanoparticle in media by short laser pulses. Chem. Phys. 2008, 308, 103–108. [Google Scholar] [CrossRef]
- Fasla, F.; Senoudi, A.R.; Boussaid, A.; Benmouna, M.; Benmouna, R. Heating of Biological Tissues by Gold Nano Particles: Effects of Particle Size and Distribution. J. Biomat. Nanobiotech. 2011, 2, 49–54. [Google Scholar] [CrossRef]
- Guillaume, B.; Herve, R. Femtosecond pulsed optical heating of gold nanoparticles. Phys. Rev. B 2011, 84, 035415. [Google Scholar]
- Wang, X.; Xu, X. Thermo elastic wave in metal induced by ultrafast laser pulses. J. Ther. Stress. 2002, 25, 457–473. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley-Interscience: New York, NY, USA, 1983. [Google Scholar]
- French, P.M.W.; Williams, J.A.R.; Taylor, J.R. Passively mode locked c.w. dye lasers operating from 490 nm to 800 nm. Revue Phys. 1987, 22, 1651–1655. [Google Scholar] [CrossRef]
- Dmitriev, P.A.; Makarov, S.V.; Milichko, V.A.; Mukhin, I.S.; Samusev, A.K.; Krasnok, A.E.; Belov, P.A. Direct femtosecond laser writing of optical Nanoresonators. J. Phys. 2016, 690, 012021. [Google Scholar] [CrossRef]
- Jain, S.; Hirst, D.G.; O’Sullivan, J.M. Gold nanoparticles as novel agents for cancer therapy. Br. J. Radiol. 2012, 85, 101–113. [Google Scholar] [CrossRef]
- Pitsillides, C.M.; Joe, E.K.; Wei, X.; Anderson, R.R.; Charles, P.; Lin, C.P. Selective Cell Targeting with Light-Absorbing Microparticles and Nanoparticles. Biophys. J. 2003, 84, 4023–4032. [Google Scholar] [CrossRef]
- Anisimov, I.S.; Kapeliovich, B.L.; Perel’man, T.L. Electron emission from metal surfaces exposed to ultrashort laser pulses. Soviet Phys. JETP 1974, 39, 375–377. [Google Scholar]
- Hashimoto, S.; Werner, D.; Uwada, T. Studies on the interaction of pulsed lasers with plasmonic gold nanoparticles toward light manipulation, heat management, and nanofabrication. J. Photochem. Photobiol. C Photochem. Rev. 2012, 13, 28–54. [Google Scholar] [CrossRef]
- Jing, H.; Kapil, B.; Chen, J.K.; Zhang, Y. An axisymetric model for solid-liquid-vapor change in thin metal films induced by an ultrashort laser pulse. Front. Heat Mass Transf. 2011, 2, 013005. [Google Scholar]
- Ekici, O.; Harrison, R.K.; Durr, N.J.; Eversole, D.S.; Lee, M.; Ben-Yakar, A. Thermal analysis of gold nanorods heated with femtosecond laser pulses. J. Phys. D Appl. Phys. 2008, 4, 185501. [Google Scholar] [CrossRef]
- Bresson, P.; Bryche, J.F.; Besbes, M.; Moreau, J.; Karsenti, P.L.; Charette, P.G.; Morris, D.; Canva, M. Improved two-temperature modeling of ultrafast thermal and optical phenomena in continuous and nanostructured metal films. Phys. Rev. B 2020, 102, 155127. [Google Scholar] [CrossRef]
- Cesaria, M.; Caricato, A.P.; Beccaria, M.; Perrone, A.; Martino, M.; Taurino, A.; Catalano, M.; Resta, V.; Klini, A.; Gontad, F. Physical insight in the fluence-dependent distributions of Au nanoparticles produced by sub-picosecond UV pulsed laser ablation of a solid target in vacuum environment. Appl. Surf. Sci. 2019, 400, 330–340. [Google Scholar] [CrossRef]
- Gan, R.; Fan, H.; Wei, Z.; Liu, H.; Lan, S.; Dai, Q. Photothermal Response of Hollow Gold Nanorods under Femtosecond Laser Irradiation. Nanomaterials 2019, 9, 711. [Google Scholar] [CrossRef]
- Lombard, J.; Biben, T.; Merabia, S. Nanobubbles around plasmonic nanoparticles: Thermodynamic analysis. Phys. Rev. 2015, E91, 043007. [Google Scholar] [CrossRef]
- Aibusha, A.V.; Astaf’eva, A.A.; Gosteva, F.E.; Denisovb, N.N.; Titova, A.A.; Shelaeva, I.V.; Shakhova, A.M.; Nadtochenko, V.A. Pulse Heating of Water at the Surface of Gold Nanoparticles: Femtosecond Laser Spectroscopy of Energy Relaxation of Aqueous Colloid of Plasmonic Nanoparticles under Strong Excitation Conditions. High Energy Chem. 2015, 49, 336–340. [Google Scholar] [CrossRef]
- Morris, J.; Dobson, J. Small Animal Oncology; Blackwell Science Ltd.: Oxford, UK, 1991. [Google Scholar]
- Draine, B.T.; Flatau, P.J. User guide for the discrete dipole approximation code DDSCAT 7.3. arXiv 2013, arXiv:1002.1505. [Google Scholar]
- Carpenter, M.; Kennedy, C.A. Fourth-Order 2N-Storage Runge-Kutta Schemes; NASA: Washington, DC, USA, 1994; p. 24. [Google Scholar]
- Kurisaki, K.; Tanaka, S.; Mori, I.; Umegaki, T.; Mori, Y.; Tanaka, S. Thermal conductivity and conductance of protein in aqueous solution: Effects of geometrical shape. J. Comput. Chem. 2023, 44, 857–868. [Google Scholar] [CrossRef]
- DeLunaa, F.; Cadenaa, M.; Wang, B.; Sun, L.S.; Yea, J.Y. Cellular Refractive Index Comparison of Various Prostate Cancer and Noncancerous Cell Lines via Photonic-Crystal Biosensor. Proc. SPIE Int. Soc. Opt. Eng. 2019, 10881, 2507505. [Google Scholar]
- Elblbesy, M.M. The refractive index of human blood measured at the visible spectral region by single-fiber reflectance spectroscopy. AIMS Biophys. 2020, 8, 57–65. [Google Scholar] [CrossRef]
- Bacallao, R.; Sohrab, S.; Phillips, C. Guiding Principles of Specimen Preservation for Confocal Fluorescence Microscopy. In Handbook of Biological Confocal Microscopy, 3rd ed.; Pawley, J.B., Ed.; Springer: Boston, MA, USA, 2006; pp. 368–380. [Google Scholar]
- Ding, H.; Lu, J.Q.; Wooden, W.A.; Kragel, P.J.; Hu, X.-H. Refractive indices of human skin tissues at eight wavelengths and estimated dispersion relations between 300 and 1600 nm. Phys. Med. Biol. 2006, 51, 1479–1489. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Varela, O.; Merabia, S.; Santamaria, R. Size-dependent effects of the thermal transport at gold nanoparticle-water interfaces. J. Chem. Phys. 2022, 157, 0096033. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Munjiza, A.; Wen, K.Z.D. Molecular Dynamics Simulation of Heat Transfer from a Gold Nanoparticle to a Water Pool. J. Phys. Chem. C 2014, 118, 1285–1293. [Google Scholar] [CrossRef]
- Anderson, A.M.; Anderson, B.E.; Baker, B.A.; Blotter, J.D.; Bramfitt, B.L.; Brown, R.E.; Bruno, B.A.; Collins, P.; Collins, J.A.; Daniewicz, S.R.; et al. Mechanical Engineers’ Handbook, 4th ed.; Kurz, M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; Volume 1. [Google Scholar]
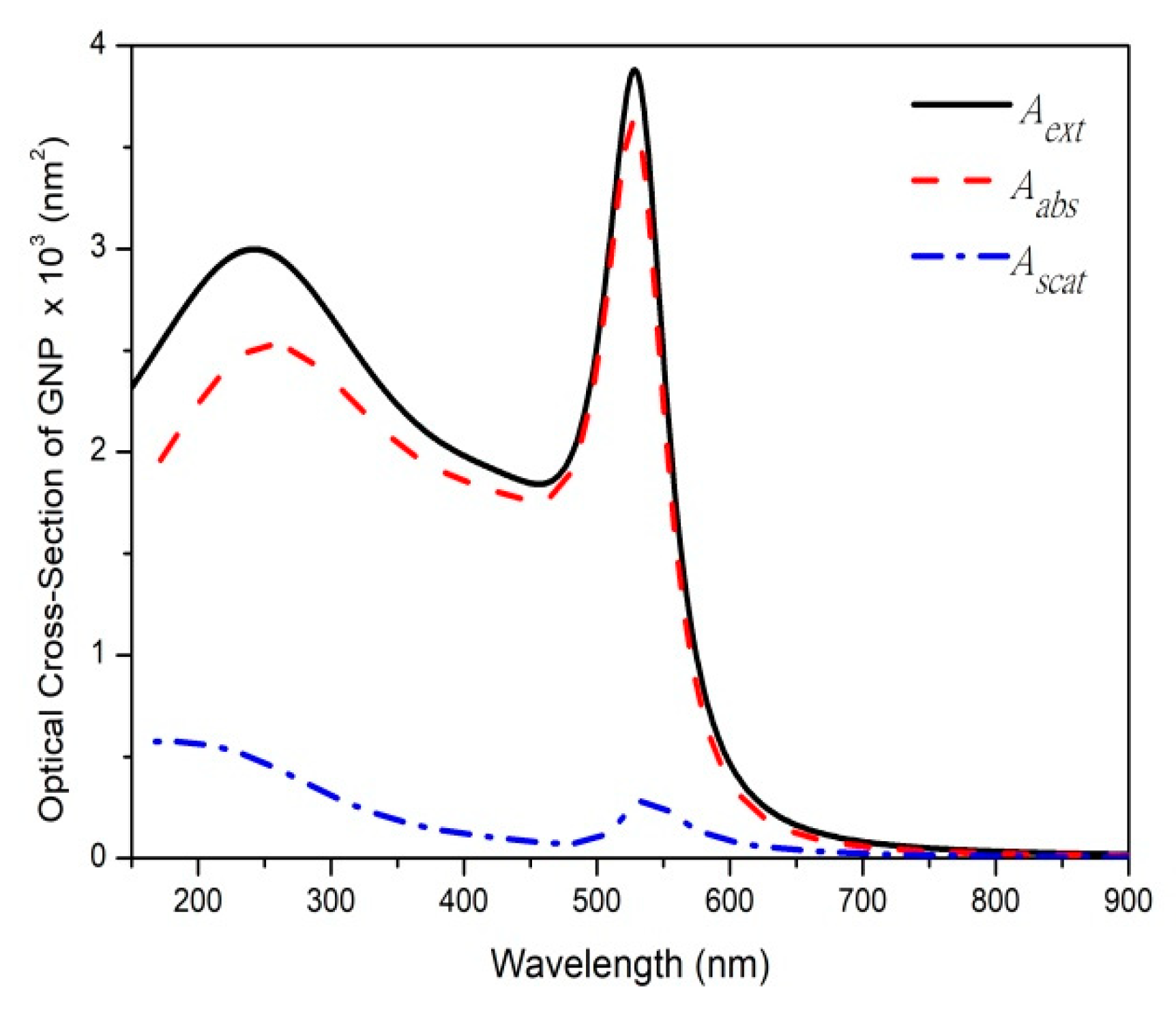
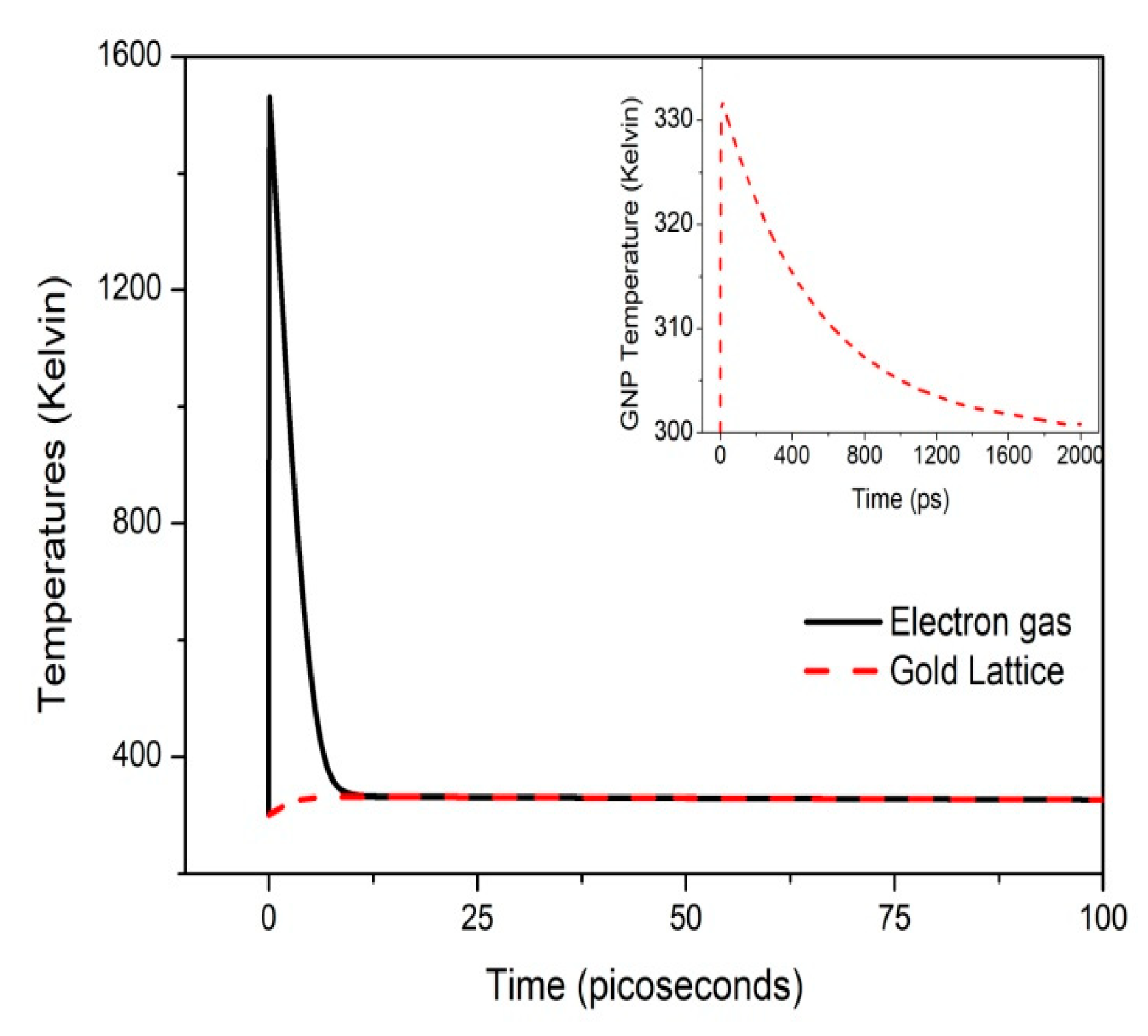
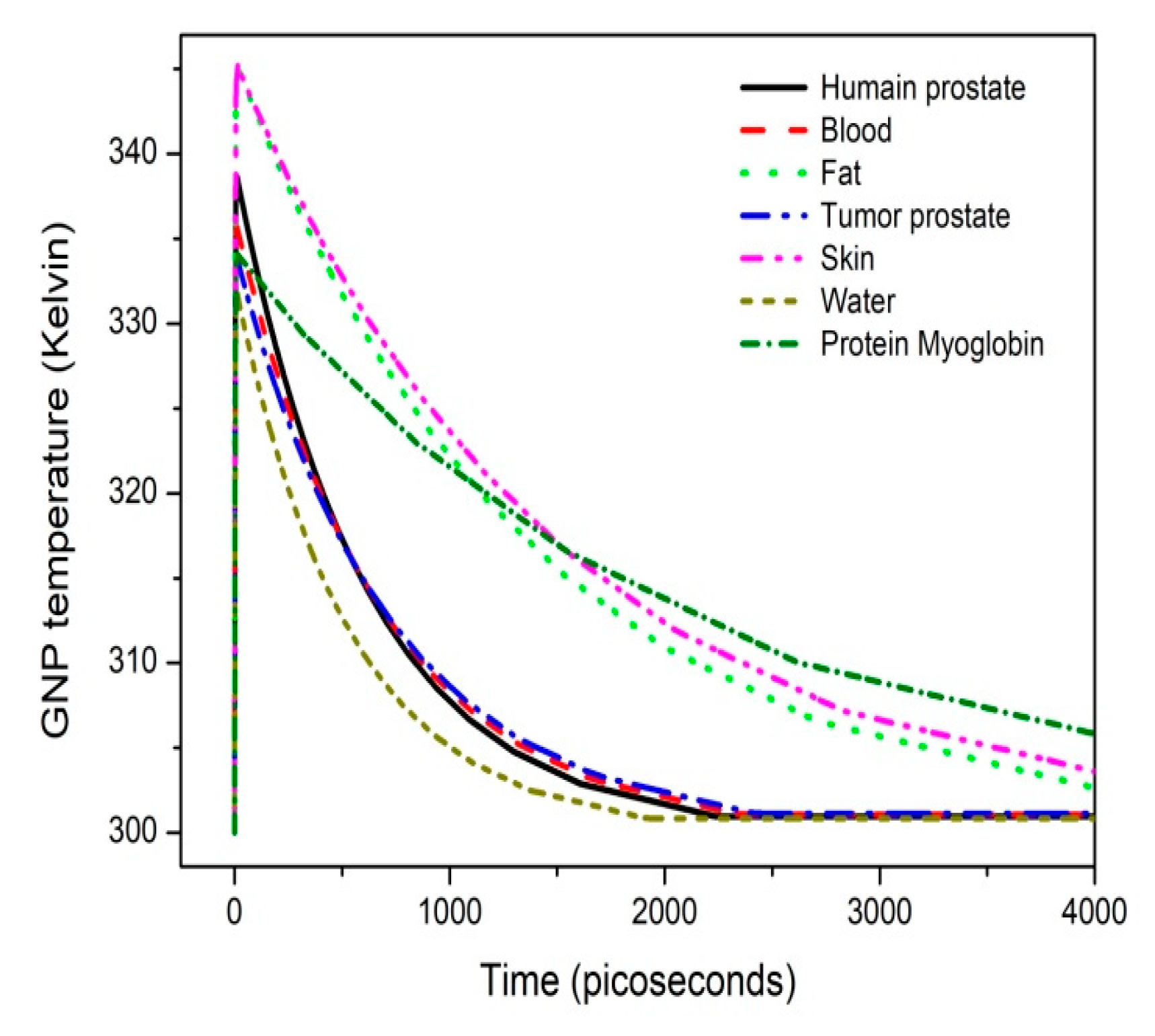
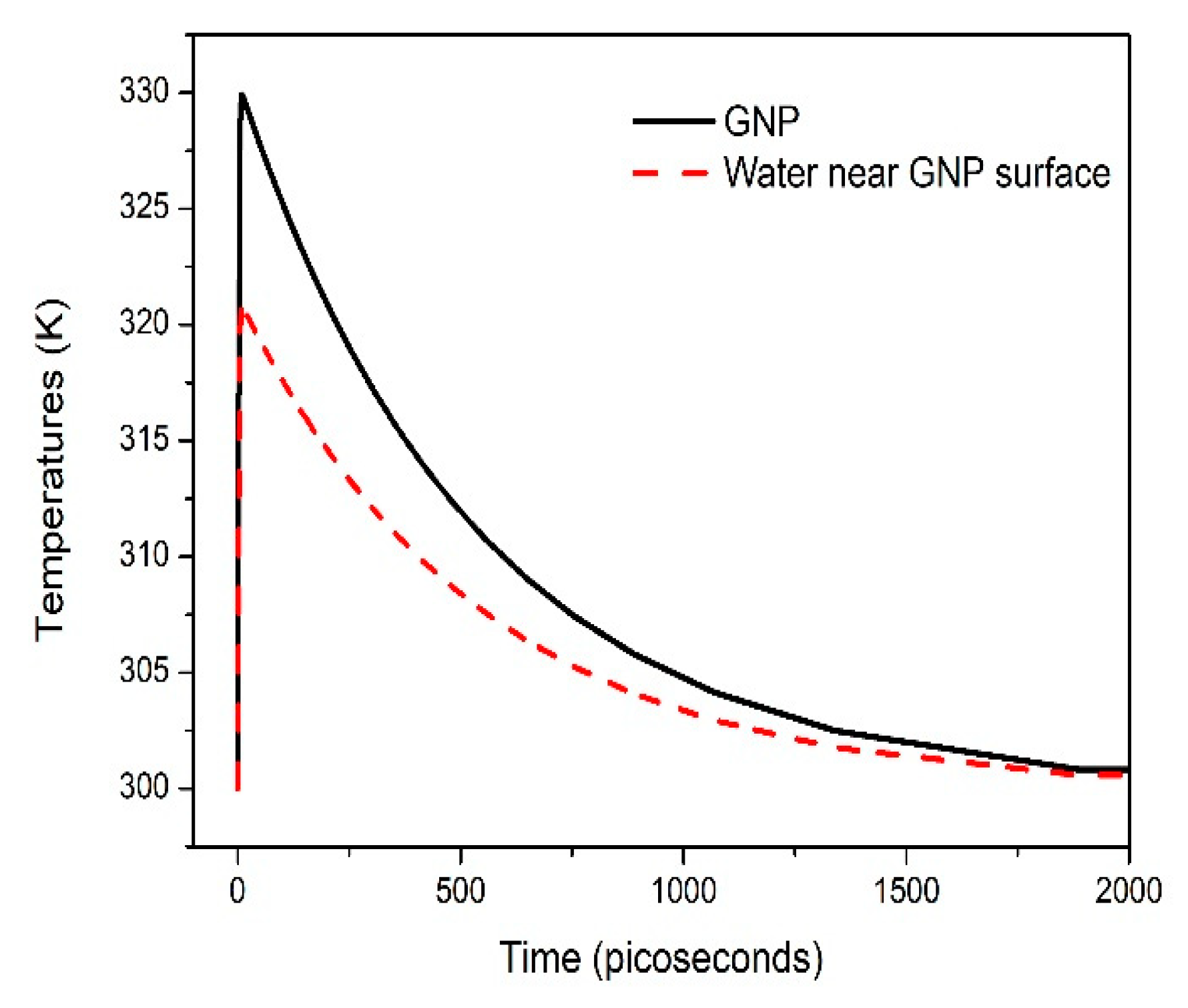
| Parameters | Unit (SI) | Value | Ref. |
|---|---|---|---|
| The electron heat capacity, Ce | J/(Km3) | [17] | |
| The lattice heat capacity, CL | J/(Km3) | [14] | |
| Density, ρgold | Kg/m3 | [17] | |
| Electron–lattice coupling coefficient, | W/(Km3) | [9] | |
| Thermal conductance, G | W/(Km2) | [14] |
| Biological Tissues | Thermal Conductivity k∞ (W/m/K) [8] | Refractive Indexes | References | Computed Optical Absorption Aabs Cross-Section (nm2) |
|---|---|---|---|---|
| Protein myoglobin | 0.15 | 1.35 | [23] Kurisaki | 3831.29 |
| Human prostate | 0.529 | 1.40 | [24] DeLunaa | 4375.18 |
| Blood | 0.48–0.6 | 1.37 | [25] Elblbesy | 4045.33 |
| Fat | 0.23 | 1.47 | [26] Bacallao | 5064.83 |
| Tumor prostate | 0.45 | 1.35 | [24] DeLunaa | 3829.58 |
| Skin | 0.210–0.410 | 1.46 | [27] Ding | 5064.83 |
| Water | 0.61 | 1.33 | [14] Ikici | 3623.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mediene, S.; Senoudi, A.R. Heating Kinetics of Gold Nanoparticles in Biological Tissues with a Femtosecond Laser. Phys. Sci. Forum 2023, 6, 1. https://doi.org/10.3390/psf2023006001
Mediene S, Senoudi AR. Heating Kinetics of Gold Nanoparticles in Biological Tissues with a Femtosecond Laser. Physical Sciences Forum. 2023; 6(1):1. https://doi.org/10.3390/psf2023006001
Chicago/Turabian StyleMediene, Selma, and Assia Rachida Senoudi. 2023. "Heating Kinetics of Gold Nanoparticles in Biological Tissues with a Femtosecond Laser" Physical Sciences Forum 6, no. 1: 1. https://doi.org/10.3390/psf2023006001
APA StyleMediene, S., & Senoudi, A. R. (2023). Heating Kinetics of Gold Nanoparticles in Biological Tissues with a Femtosecond Laser. Physical Sciences Forum, 6(1), 1. https://doi.org/10.3390/psf2023006001






