Nonsingular Bouncing Model in Closed and Open Universe †
Abstract
1. Introduction
2. Einstein Equations in FRW Closed and Open Universe
3. Fixed Point Analysis
3.1. Closed Universe
3.1.1. Case I, with
3.1.2. Case II,
3.2. Open Universe
3.2.1. Case I, with
3.2.2. Case II,
4. Bouncing Scenario
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Finelli, F.; Brandenberger, R. On the generation of a scale-invariant spectrum of adiabatic fluctuations in cosmological models with a contracting phase. Phys. Rev. D 2002, 65, 103522. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Steinhardt, P.J.; Turok, N. The ekpyrotic universe: Colliding branes and the origin of the hot big bang. Phys. Rev. D 2001, 64, 123522. [Google Scholar] [CrossRef]
- Khoury, J.; Ovrut, B.A.; Seiberg, N.; Steinhardt, P.J.; Turok, N. From big crunch to big bang. Phys. Rev. D 2002, 65, 086007. [Google Scholar] [CrossRef]
- Brandenberger, R.H. Alternatives to Cosmological Inflation. arXiv 2009, arXiv:0902.4731. [Google Scholar] [CrossRef]
- Brandenberger, R.H. Cosmology of the Very Early Universe. AIP Conf. Proc. 2010, 1268, 3–70. [Google Scholar]
- Brandenberger, R.H. Introduction to Early Universe Cosmology. arXiv 2010, arXiv:1103.2271. [Google Scholar]
- Brandenberger, R.H. The Matter Bounce Alternative to Inflationary Cosmology. arXiv 2012, arXiv:1206.4196. [Google Scholar]
- Lehners, J.-L. Ekpyrotic and Cyclic Cosmology. Phys. Rept. 2008, 465, 223. [Google Scholar] [CrossRef]
- Panda, S.; Sharma, M. Anisotropic bouncing scenario in F(X)−V(ϕ) model. Astrophys. Space Sci. 2016, 361, 87. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Vikman, A. Enhancing the tensor-to-scalar ratio in simple inflation. JCAP 2006, 0602, 4. [Google Scholar] [CrossRef]
- Panotopoulos, G. Detectable primordial non-gaussianities and gravitational waves in k-inflation. Phys. Rev. D 2007, 76, 127302. [Google Scholar] [CrossRef]
- Unnikrishnan, S.; Sahni, V.; Toporensky, A. Refining inflation using non-canonical scalars. JCAP 2012, 1208, 18. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753. [Google Scholar] [CrossRef]
- Bertacca, D.; Bartolo, N.; Matarrese, S. Unified Dark Matter Scalar Field Models. Adv. Astron. 2010, 2010, 904379. [Google Scholar] [CrossRef]
- Bose, N.; Majumdar, A.S. A k-essence Model Of Inflation, Dark Matter and Dark Energy. Phys. Rev. D 2009, 79, 103517. [Google Scholar] [CrossRef]
- Bose, N.; Majumdar, A.S. Unified Model of k-Inflation, Dark Matter and Dark Energy. Phys. Rev. D 2009, 80, 103508. [Google Scholar] [CrossRef]
- De-Santiago, J.; Cervantes-Cota, J.L. Generalizing a Unified Model of Dark Matter, Dark Energy, and Inflation with Non Canonical Kinetic Term. Phys. Rev. D 2011, 83, 063502. [Google Scholar] [CrossRef]
- Copeland, E.J.; Liddle, A.R.; Wands, D. Exponential potentials and cosmological scaling solutions. Phys. Rev. D 1998, 57, 4686. [Google Scholar] [CrossRef]
- De-Santiago, J.; Cervantes-Cota, J.L.; Wands, D. Cosmological phase space analysis of the F (X) - V (phi) scalar field and bouncing solutions. Phys. Rev. D 2013, 87, 023502. [Google Scholar] [CrossRef]

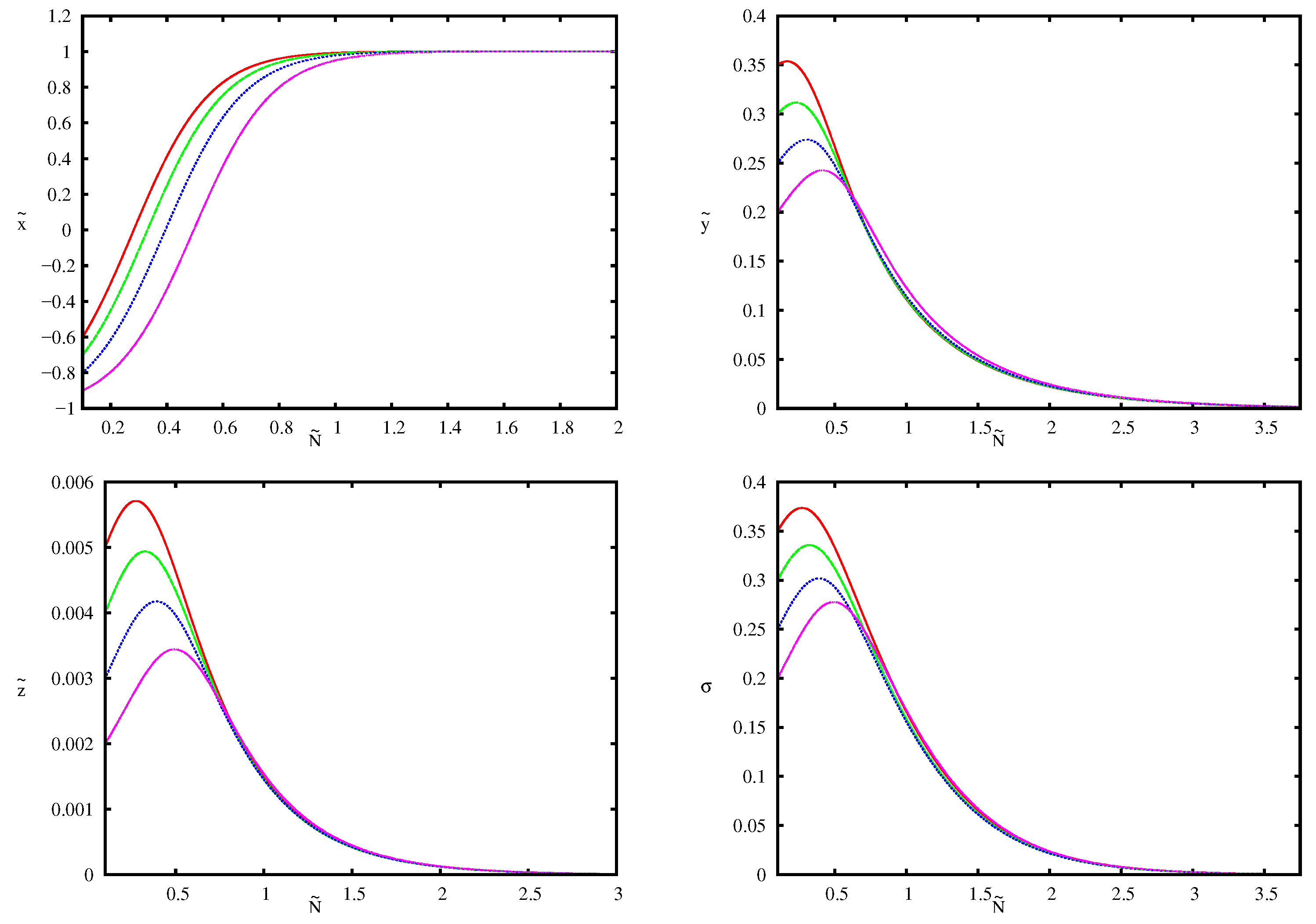



| Fixed Points | Stability Conditions |
|---|---|
| for | Ca not decide |
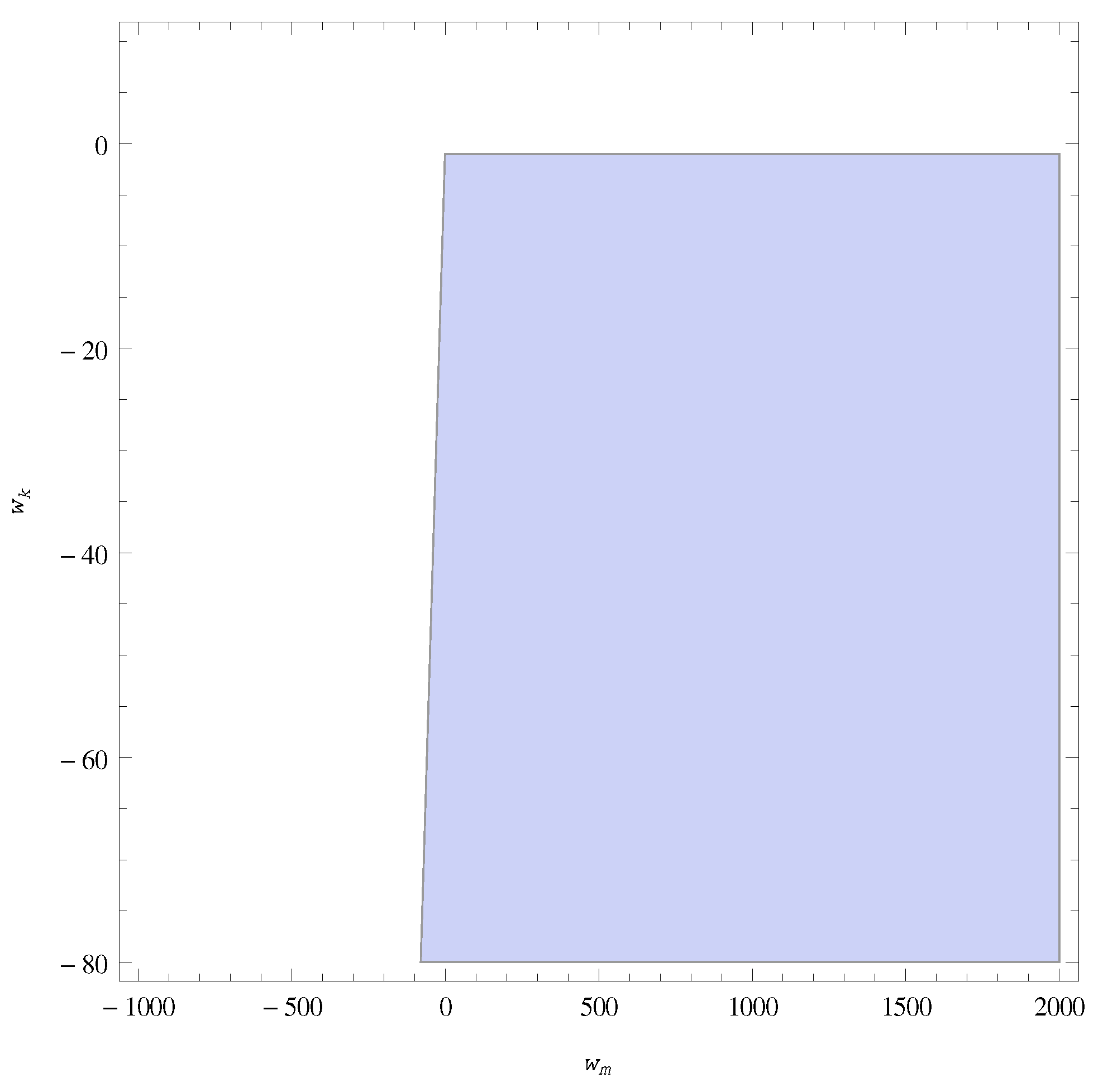
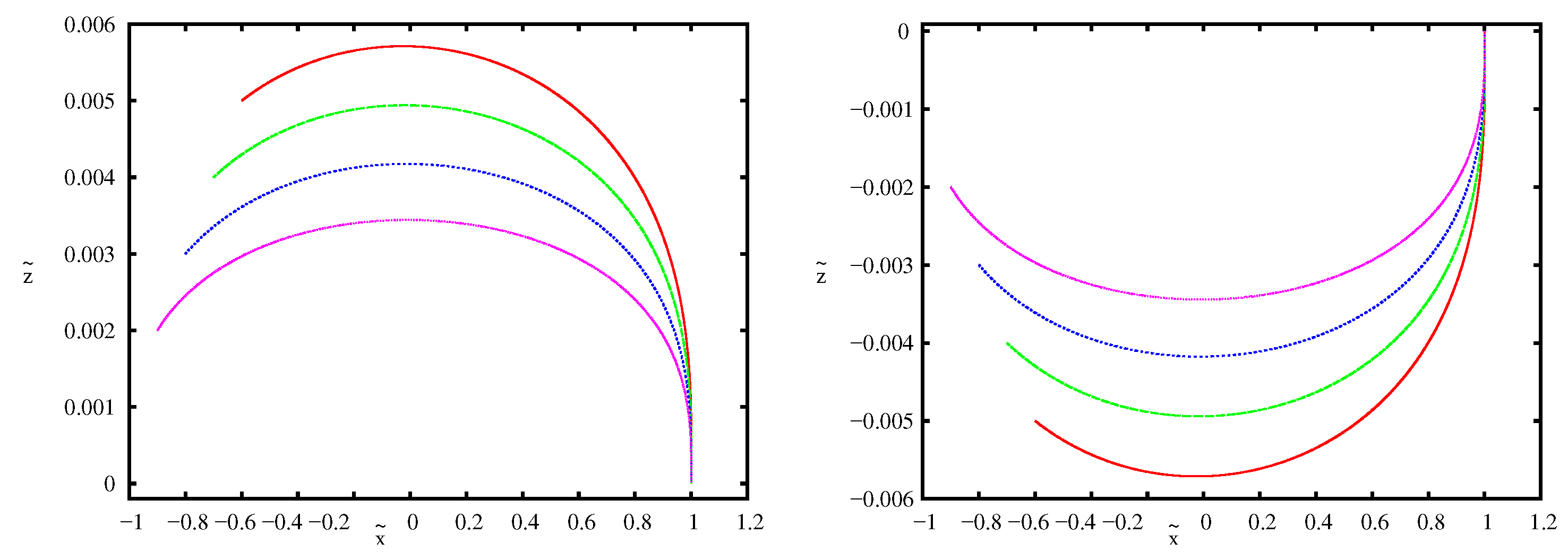
| Stable (see Figure 1) | |
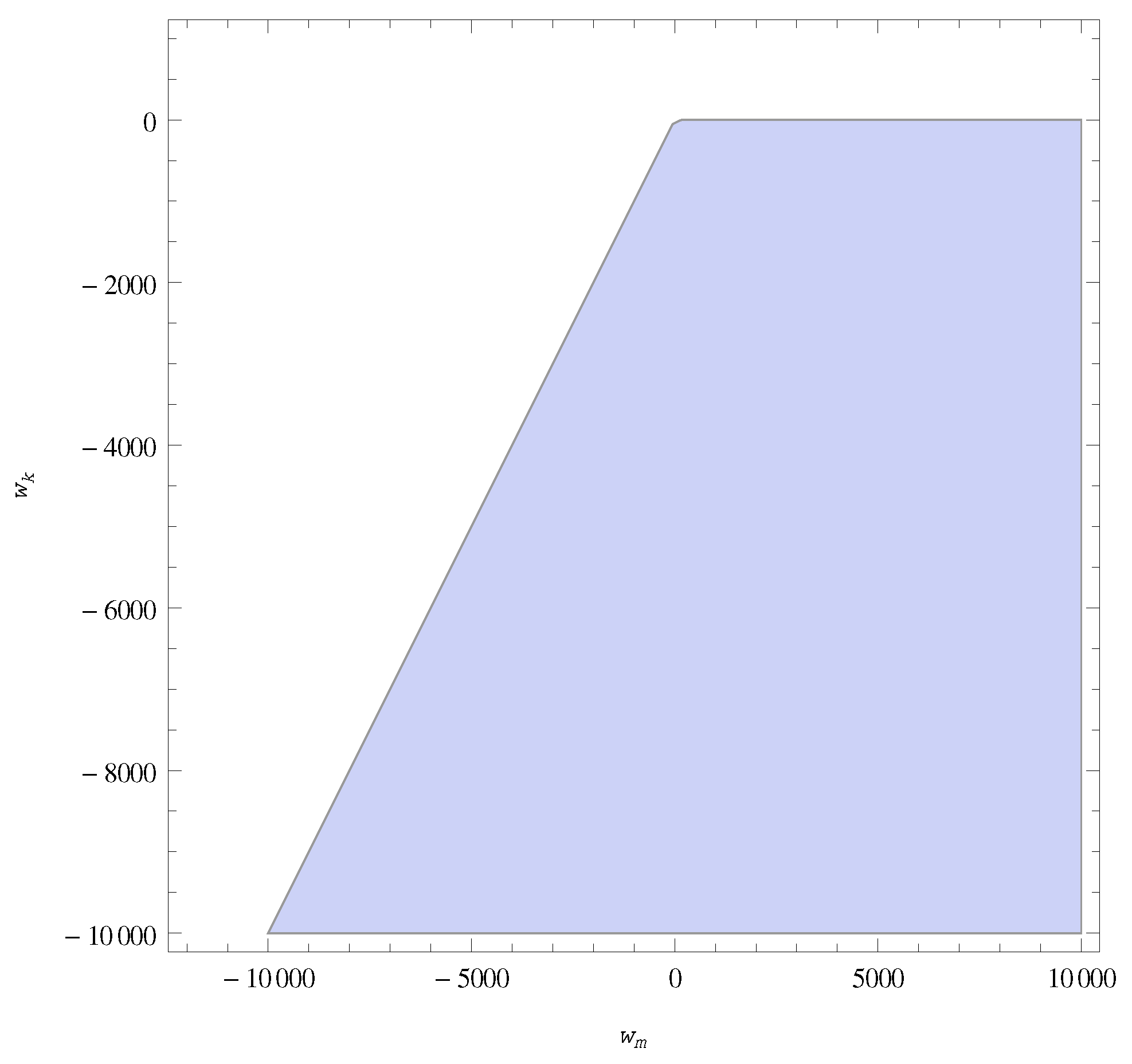
| Stable (see Figure 2) | |
| with and | Ca not decide |
| with and | Ca not decide |
| Fixed Points | Stability Conditions |
|---|---|
| for | Ca not decide |
| Ca not decide | |
| Ca not decide |
| Fixed Points | Stability Conditions |
|---|---|
| for | Ca not decide |
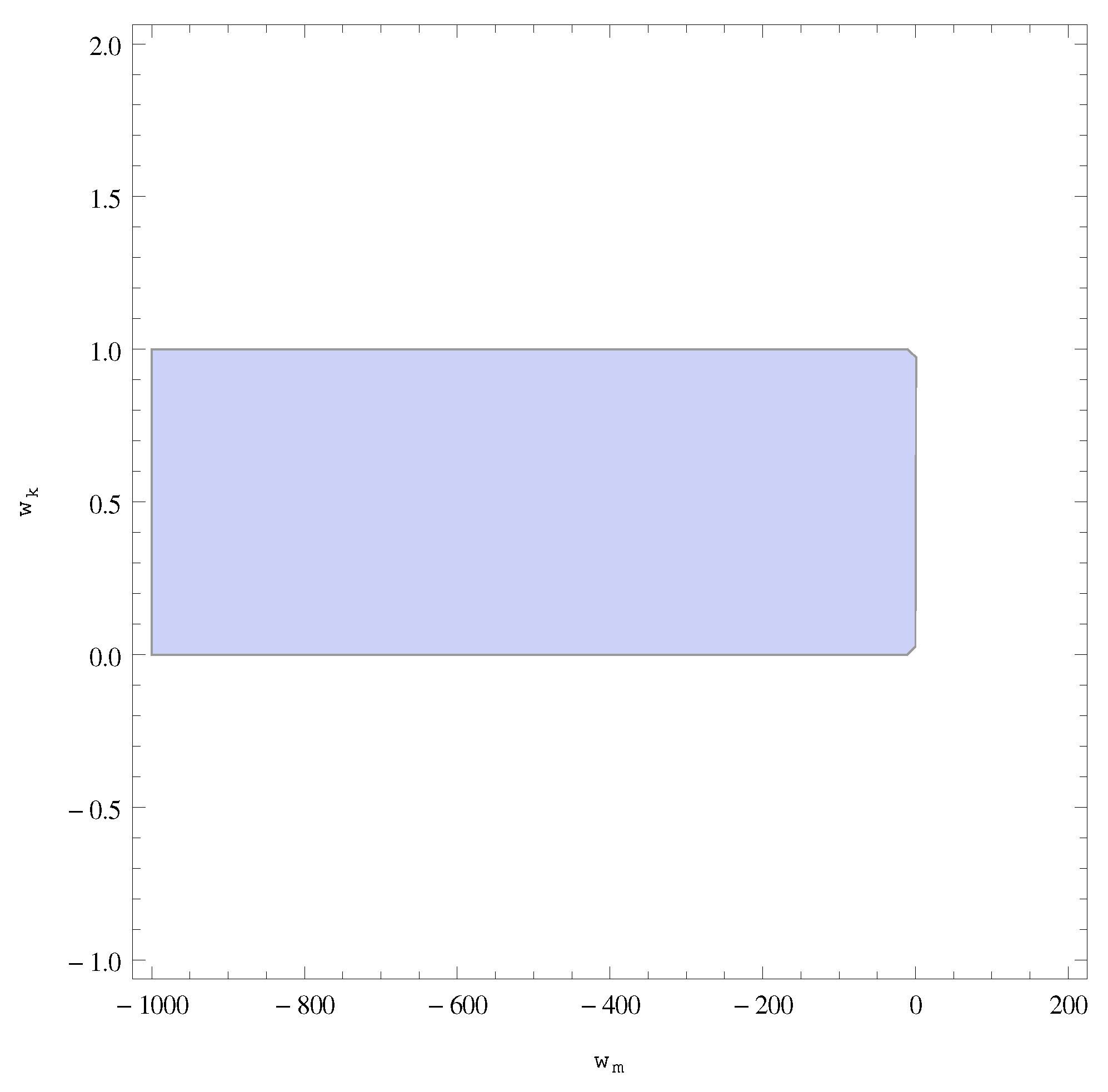
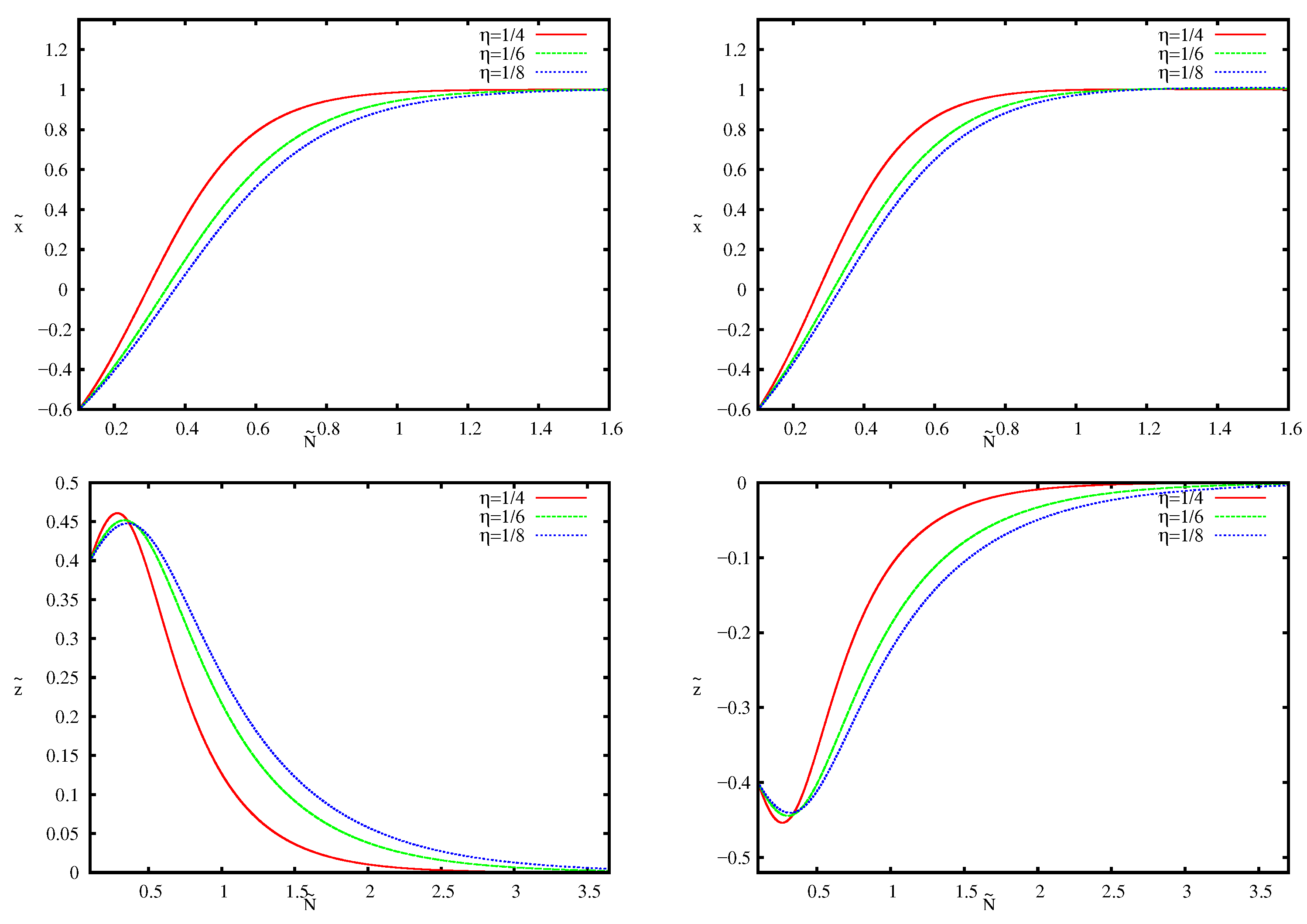
| Stable (see Figure 3) | |
| Stable (see Figure 4) | |
| with and | Ca not decide |
| with and | Ca not decide |
| Fixed Points | Stability Conditions |
|---|---|
| for | Ca not decide |
| with and | Ca not decide |
| with and | Ca not decide |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, M.; Pathak, S.D.; Li, S. Nonsingular Bouncing Model in Closed and Open Universe. Phys. Sci. Forum 2023, 7, 49. https://doi.org/10.3390/ECU2023-14035
Sharma M, Pathak SD, Li S. Nonsingular Bouncing Model in Closed and Open Universe. Physical Sciences Forum. 2023; 7(1):49. https://doi.org/10.3390/ECU2023-14035
Chicago/Turabian StyleSharma, Manabendra, Shankar Dayal Pathak, and Shiyuan Li. 2023. "Nonsingular Bouncing Model in Closed and Open Universe" Physical Sciences Forum 7, no. 1: 49. https://doi.org/10.3390/ECU2023-14035
APA StyleSharma, M., Pathak, S. D., & Li, S. (2023). Nonsingular Bouncing Model in Closed and Open Universe. Physical Sciences Forum, 7(1), 49. https://doi.org/10.3390/ECU2023-14035






