The Shape of Dark Matter Halos as a Strong Cosmological Probe ^†

Abstract

Halo Dark Matter (DM) formation is a complex process, intertwining both gravitational and cosmological nonlinear phenomena. One of the manifestations of this complexity is the shape of the resulting present-day DM halos: simulations and observations show that they are triaxial objects. Interestingly, those shapes carry cosmological information. We prove that cosmology, and particularly the dark energy model, leaves a lasting trace on the present-day halos and their properties: the overall shape of the DM halo exhibits a different behavior when the DE model is varied. We explain how that can be used to literally “read” the fully nonlinear power spectrum within the halos’ shape at $z=0$. To that end, we worked with “Dark Energy Universe Simulations” DM halos: DM halos are grewed in three different dark energy models, whose parameters were chosen in agreement with both CMB and SN Ia data.

1. Introduction

Among the various cosmological probes, galaxy groups and clusters occupy a key position: the dynamics of their collapse is both sensitive to gravity and to cosmology. The study of their properties, such as the distribution of their mass [1], allows observers to tightly constrain the cosmological parameters of the Universe.

One of the most striking features of dark matter halos, even at $z=0$, is the deviation from sphericity that they generally present. This can be stated from N-body simulations [2], but is also observed in particular for the Milky Way halo [3]. A review of related observational methods and theoretical considerations can be found in [4]. It is natural for this to lead to studying the links between the shapes of halos and the underlying cosmological model.

Previously [5,6], we showed that the knowledge of mass and shape profiles of dark matter halos allows the appropriate machine learning device to distinguish between dark energy models. For these proceedings, our task will be to briefly present why and how much cosmological information can be extracted from mass and shape relations. An extended version with more detailed discussions will be available in [7].

2. Methods

2.1. Cosmological Models and Dark Matter Halos

Dark Energy Universe Simulations [8,9,10,11] are high performance N-body simulations based on the adaptive mesh refinement RAMSES code [12]. They probe structure collapse, assuming various dark energy models: the concordance model ΛCDM, the Ratra-Peebles quintessence model RPCDM [13], and a phantom model that we denote wCDM. The last ones are dynamical dark energy models, the first having e.o.s. parameter $w_0>1$ and the last $w_0<-1$. In addition, the parameters of the selected models (${\mathsf{\Omega }}_m,{\mathsf{\sigma }}_8,{\mathrm{w}}_0,{\mathrm{w}}_{\mathrm{a}})$, summarized in

Table 1. Dark Energy Universe simulations parameters and characteristics. $n_s=0.96$ and $h=0.72$.

Model	$\mathbf{\Lambda }\mathbf{CDM}$	$\mathbf{RPCDM}$	$\mathbf{wCDM}$
${\mathsf{\Omega }}_m$	0.2573	0.23	0.275
${\mathsf{\sigma }}_8$	0.83	0.68	0.88
$w_0$	−1	−0.87	−1.2
$w_a$	0	0.08	0
FOF halos	411,909	338,883	441,683

, were chosen in accordance with both SNIa and CMB WMAP7 constraints [14]. As a consequence, the resulting present-day Universes have the interesting feature to be realistic [8], and they are thus very similar to each other.

At both $z=0$, linear $P\left(k\right)$ and nonlinear $\tilde{P}\left(k\right)$ power spectra of the matter density field were also computed. The corresponding variances are given by smoothing the power spectra with a gaussian window $W\left[x\right]=\exp -\frac{x^2}{10}$ so that

$$\left(M\right)=\frac{1}{2{\pi }^2}{{\displaystyle \int }}_0^{+\infty }{k}^{2}P\left(k\right)W^2\left[k\cdot {\left(3M/\left(4\pi {\Omega }_m{\rho }_c\right)\right)}^{1/3}\right]dk$$

and similarly for $\tilde{\sigma }\left(k\right)$ and $\tilde{P}\left(k\right).$

2.2. Dark Matter Halos and Their Shape

We consider the Universes evolved in a $648 \mathrm{MPc}/\mathrm{h}$ simulation box, containing ${2048}^3$ particles. Their halos are identified by the Friends of Friends algorithm, with a linking length $b=0.2$. Finally, only well-resolved halos containing more than 1000 particles are retained, which correspond to those whose FOF mass excesses $2.4\cdot {10}^{12} {\mathrm{M}}_{\mathrm{S}}/\mathrm{h}$. Table 1 features the number of such halos in each cosmological model.

To assess the shape of halos, we compute the $3\times 3$ inertia tensor of each halo:

$${ℳ}_{ij}=\langle {\mathrm{x}}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{j}}\rangle {}_{\mathrm{halo}}-\langle {\mathrm{x}}_{\mathrm{i}}\rangle {}_{\mathrm{halo}}\langle {\mathrm{x}}_{\mathrm{j}}\rangle {}_{\mathrm{halo}}\mathrm{for}1\le i,j\le 3.$$

Diagonalizing this tensor allows to extract the eigenvalues, denoted $\frac{a^2}{\sqrt{5}},\frac{b^2}{\sqrt{5}}\mathrm{and}\frac{c^2}{\sqrt{5}}$ where $a\ge b\ge c$ are the three principal axis semi-lengths of the best-fitting ellipsoid of the full halo. The triaxiality of the halo can be quantified through its prolateness:

$$\mathrm{p}=\left(a-2b+c\right)/2\left(a+b+c\right)$$

Note that this way of extracting the shape of halos necessarily induces resolution sensitiveness. In [7], we explain how to adapt it to get measures that do not depend on the size of simulation box, on the total number of particles it contains, or on the presence of sub-structures inside the halos. We also discuss the imprint of the cosmology on other shape parameters as ellipticity, triaxiality, and eigenvalues ratios.

3. Results and Discussion

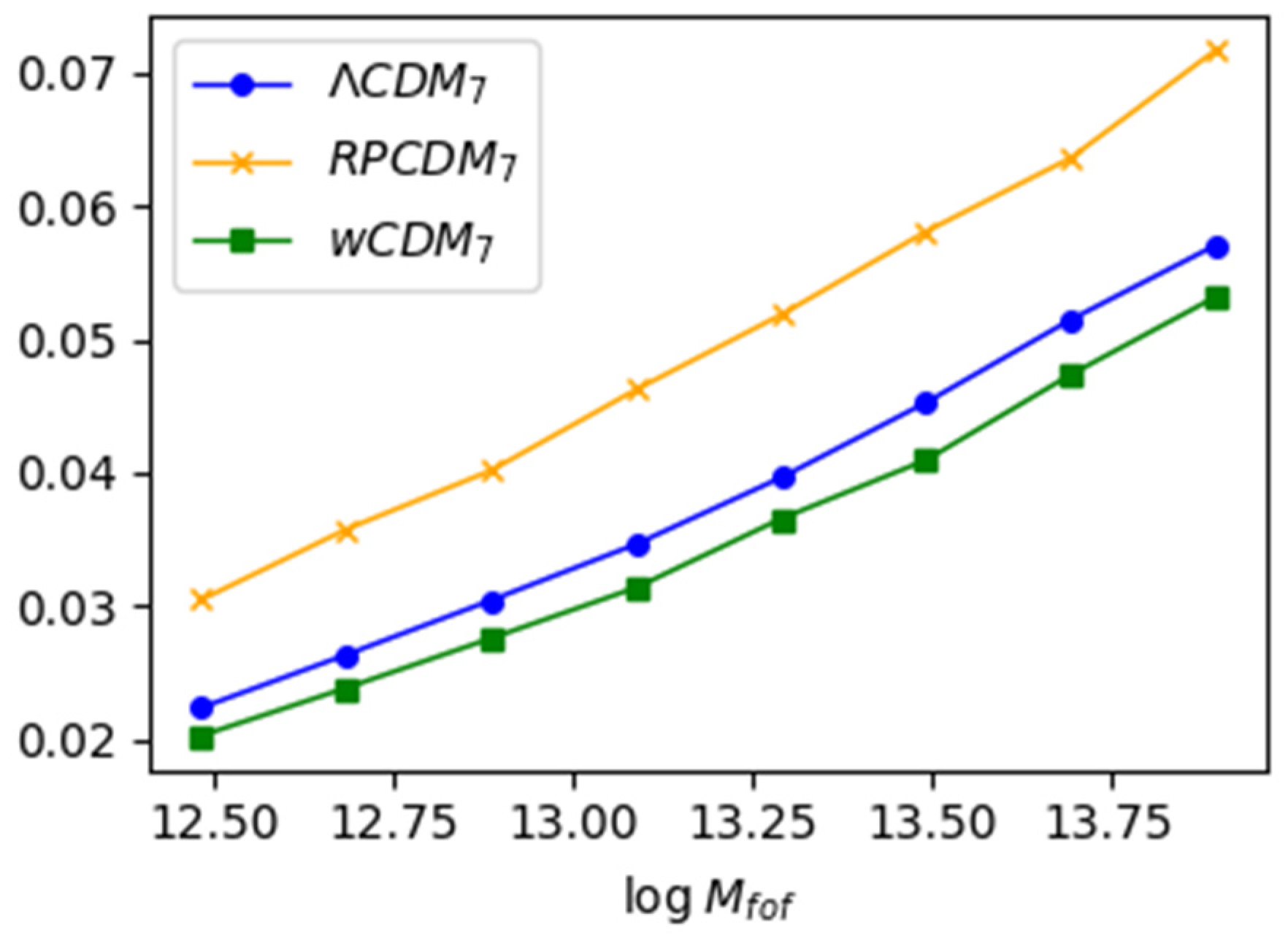
3.1. Mass Dependence

Let us start by plotting the prolateness of halos against their FoF mass. Figure 1 features the median prolateness in each mass bin for each cosmological model. Two observations can be made:

-

First, the heavier the halo, the greater is the p. Indeed, large mass halos are less virialized and, therefore, less spherical [15].

-

Meanwhile, RPCDM halos are about 25% more prolate than LCDM ones. This can be explained by the fact that ${\sigma }_8$ of RPCDM is much lower than the fiducial one. As a result, the halos of RPCDM formed more recently and are, again, less relaxed and more prolate.

In a sense, this extends the results of [16], which tested redshift dependence of mass-shape relations at a fixed cosmology.

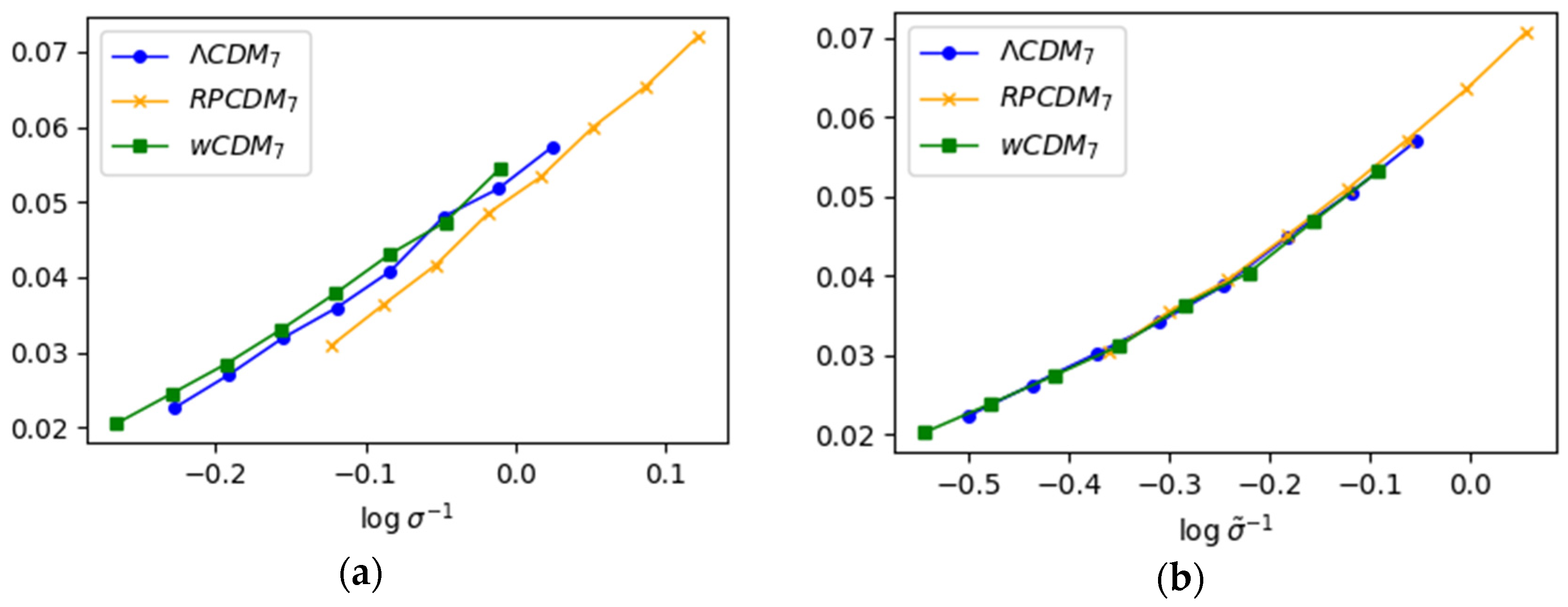
3.2. Towards Universality

To understand exactly how cosmology intervenes in mass shape relations, we aim to find a cosmological dependent function $f_c$ so that $p\left(f_c\left(M\right)\right)$ curves superpose. In the light of the observations in the previous subsections, a first attempt would be $f_c:=\sigma$, as already suggested by [16,17]. The resulting median prolateness curves are plotted in Figure 2a. Surprisingly, they are closer in $\left(\sigma ,p\right)$ space than in $\left(M,p\right)$ space, but very substantial differences subsist both in slope and in intercept. In other words, the linear power spectrum absorbs part of the cosmological dependence of the shape of halos.

We conjecture that the reason for that is the existence of a (cosmologically independent) analogy between halos’ shape (i.e., two points correlations in real space) and the power spectrum (i.e., two points correlations in Fourier space). If true, since the shapes are computed on the fully collapsed halo, one should rather consider the fully nonlinear variance $\tilde{\sigma }$. Indeed, as Figure 2b shows, median prolateness curves superpose almost completely when using $\tilde{\sigma }$ as abscissa. They are about seven times closer than in Figure 2a, so that the common $p\left(\tilde{\sigma }\right)$ relation can be taken to be universal—that is to say, independent of the details of background cosmology. Furthermore, this result holds not only for the median curves (that we plot here) but for the whole of the p distribution (except the most extreme values).

In other words, we have shown that all the cosmological content of a clusters’ shape is embedded in the (nonlinear) power spectrum. Therefore, the only reason that linear information explains part of prolateness cosmological dependence at a fixed mass is the fact that the linear power spectrum is a first order approximation of the nonlinear one.

3.3. Power Spectrum Reconstruction

We have now at hand all the tools to build a new procedure to measure the non-linear power spectrum:

• Measure the p(M) curve in our universe.
• Since we know the universal p($\tilde{\sigma })$ relation, one can deduce the $\tilde{\sigma }\left(M\right)$ function of our Universe.
• The nonlinear power spectrum is finally directly inferred from this $\tilde{\sigma }\left(M\right)$.

In Figure 3a, we reproduce the reconstructed $\tilde{\sigma }\left(M\right)$ functions of the tested cosmological models from the sole measure of p(M), and in Figure 3b, the corresponding nonlinear power spectra. The concordance with the expected $\tilde{\sigma }\left(M\right)$ at $z=0$ is excellent.

We can then also deduce ${\sigma }_8$ at $z=0$ and reconstruct the initial ${\sigma }_8$ of each cosmological model. The agreement with the known results of the numerical simulation is remarkable (see

Table 2. Estimated and expected, linear and nonlinear, variance at 8 Mpc/h. All the estimations are given with only one significant number, with 15% of uncertainty, and a uniform prior on ${\mathsf{\Omega }}_m\in \left[0.2,0.3\right]$.

Model	$\mathbf{\Lambda }\mathit{C}\mathit{D}\mathit{M}$	$\mathit{R}\mathit{P}\mathit{C}\mathit{D}\mathit{M}$	$\mathit{w}\mathit{C}\mathit{D}\mathit{M}$
$\widetilde{{\sigma }_8}$ (estimated with shapes)	0.9	0.7	1
$\widetilde{{\sigma }_8}$ (expected)	0.9	0.8	1
${\sigma }_8$ (estimated with shapes)	0.8	0.6	0.9
${\sigma }_8$ (expected)	0.8	0.7	0.9

).

4. Conclusions

We have shown that if the distribution of the prolateness of halos at a fixed mass heavily depends on cosmology, this dependence is completely explained by the nonlinear power spectrum, and, reciprocally, the nonlinear fluctuations are encoded in the shape distributions of DM halos. Consequently, the fact that there exists a universal relation between the shape of halos and nonlinear variance allows one to reconstruct the power spectrum of a given Universe from the sole mass and shape measures of the halos it contains. A full discussion of the shape determination procedure, including the effects of substructures and simulation resolution, will be in [7].