Escaping the Pair-Instability Mass Gap with the Help of Dark Matter †
Abstract
1. Introduction
2. Method
3. Results and Discussion
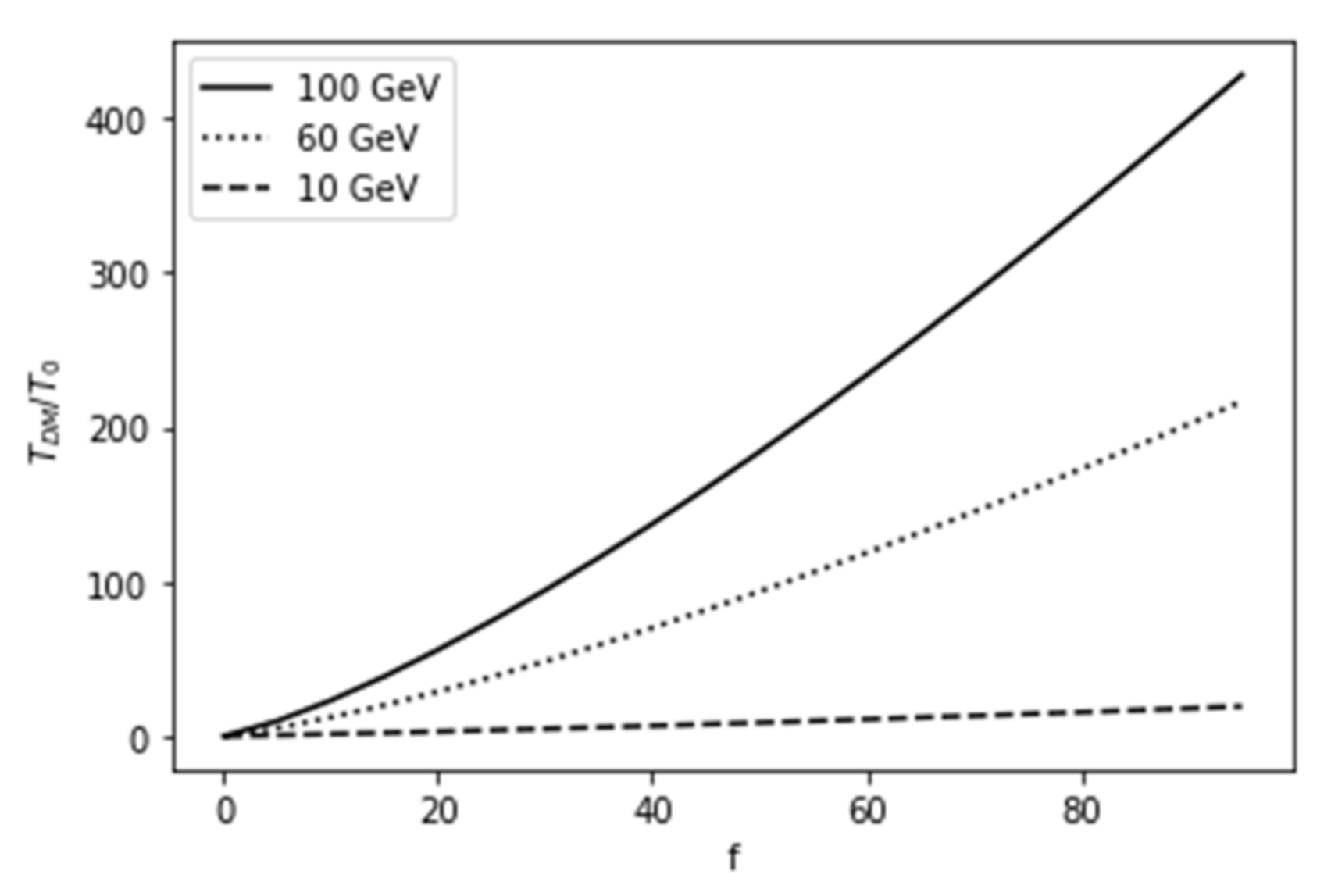
3.1. Effect of Dark Matter on the Temperature of the PISN Progenitors
3.2. Effect of Dark Matter on the Lifetime of the PISN Progenitors
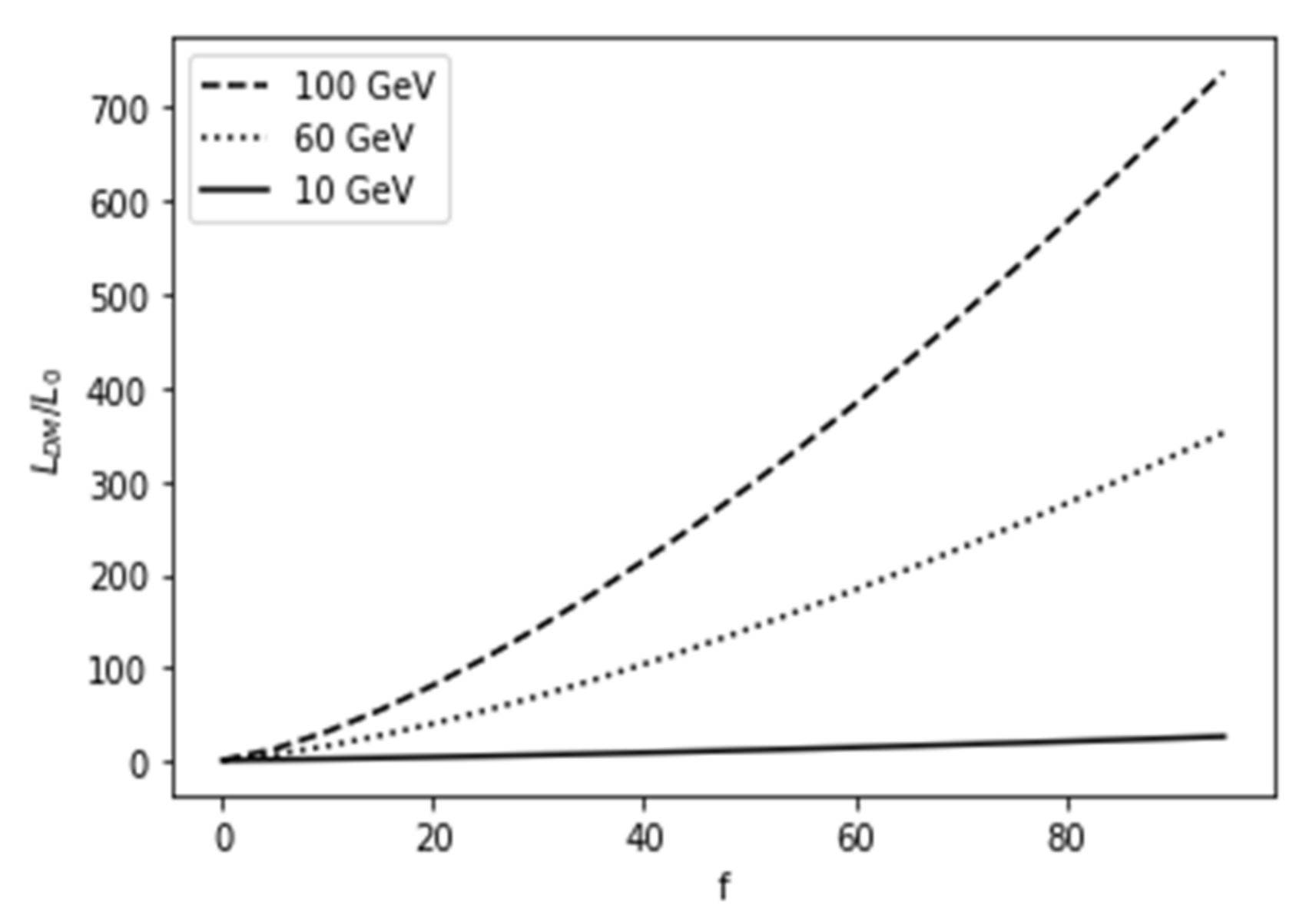
3.3. Effect of Dark Matter on the Luminosity of the PISN Progenitors
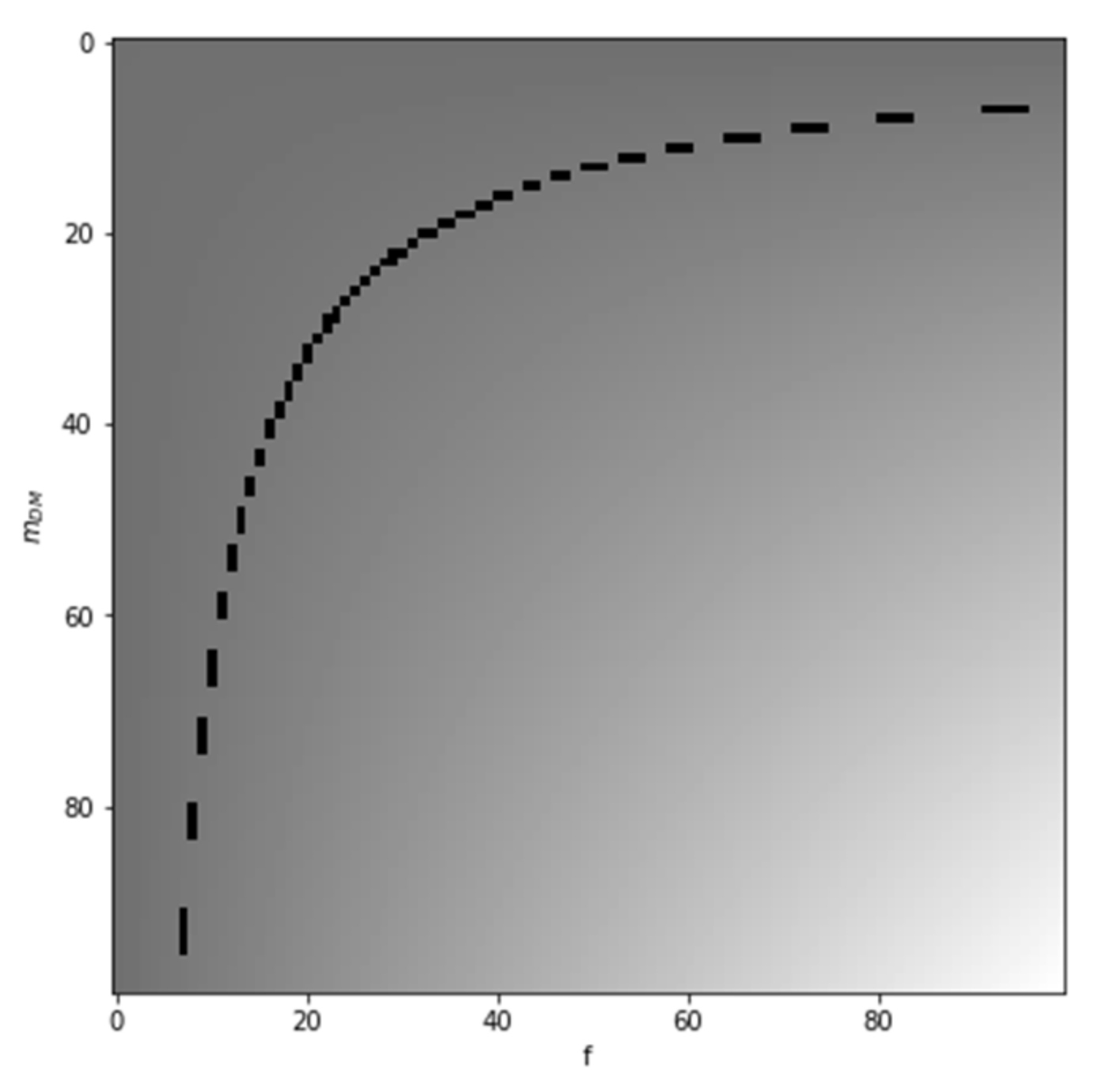
3.4. Overcoming the PISN Stage
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. (LIGO Scientific Collaboration and Virgo Collaboration). A Binary black hole merger with a total mass of 150 M⊙. Phys. Rev. Lett. 2020, 125, 101102. [Google Scholar] [CrossRef] [PubMed]
- Heger, A.; Fryer, C.L.; Woosley, S.E.; Langer, N.; Hartmann, D.H. How Massive Single Stars End Their Life. Astrophys. J. 2003, 591, 288–300. [Google Scholar] [CrossRef]
- Heger, A.; Woosley, S.E. The nucleosynthetic signature of population III. Astrophys. J. 2002, 567, 532–543. [Google Scholar] [CrossRef]
- Chatzopoulos, E.; Wheeler, J.C.; Couch, S.M. Multi-dimensional Simulations of Rotating Pair Instability Supernovae. Astrophys. J. 2013, 776, 129. [Google Scholar] [CrossRef]
- Chen, K.J.; Woosley, S.E.; Heger, A.; Almgren, A.S.; Whalen, D.J. Two Dimentional Simulations of Pulsational Pair Instability Supernovae. Astrophys. J. 2014, 792, 28. [Google Scholar] [CrossRef]
- Mapelli, M.; Spera, M.; Montanari, E.; Limongi, M.; Chieffi, A.; Giacobbo, N.; Bressan, A.; Bouffanais, Y. Impact of the rotation and compactness of progenitors on the mass of black holes. Astrophys. J. 2020, 888, 76. [Google Scholar] [CrossRef]
- Woosley, S.E.; Blinnikov, S.; Heger, A. Pulsational pair instability as an explanation for the most luminous supernovae. Nature 2007, 450, 390–392. [Google Scholar] [CrossRef]
- Barkat, Z.; Rakavy, G.; Sack, N. Dynamics of Supernova Explosion Resulting from Pair Formation. Phys. Rev. Lett. 1967, 18, 379–381. [Google Scholar] [CrossRef]
- Fraley, G.S. Supernovae Explosions Induced by Pair-Production Instability. Astrophys. Space Sci. 1968, 2, 96–114. [Google Scholar] [CrossRef]
- Rakavy, G.; Shaviv, G. Instabilities in Highly Evolved Stellar Models. Astrophys. J. 1967, 148, 803–816. [Google Scholar] [CrossRef]
- Fragione, G.; Loeb, A.; Rasio, F.A. On the origin of GW190521-like events from repeated black hole mergers in star clusters. Astrophys. J. 2020, 902, L26. [Google Scholar] [CrossRef]
- Di Carlo, U.N.; Mapelli, M.; Bouffanais, Y.; Giacobbo, N.; Santoliquido, F.; Bressan, A.; Spera, M.; Haardt, F. Binary black holes in the pair instability mass gap. Mon. Not. R. Astron. Soc. 2020, 497, 1043–1049. [Google Scholar] [CrossRef]
- De Luca, V.; Desjacques, V.; Franciolini, G.; Pani, P.; Riotto, A. GW190521 Mass Gap Event and the Primordial Black Hole Scenario. Phys. Rev. Lett. 2021, 126, 051101. [Google Scholar] [CrossRef] [PubMed]
- Sakstein, J.; Croon, D.; McDermott, S.D.; Straight, M.C.; Baxter, E.J. Beyond the Standard Model Explanations of GW190521. Phys. Rev. Lett. 2020, 125, 261105. [Google Scholar] [CrossRef] [PubMed]
- Natarajan, P. A new channel to form IMBHs throughout cosmic time. Mon. Not. R. Astron. Soc. 2020, 501, 1413–1425. [Google Scholar] [CrossRef]
- Gamba, R.; Breschi, M.; Carullo, G.; Albanesi, S.; Rettegno, P.; Bernuzzi, S.; Nagar, A. GW190521 as a dynamical capture of two nonspinning black holes. Nat. Astron. 2023, 7, 11–17. [Google Scholar] [CrossRef]
- Ziegler, J.; Freese, K. Filling the black hole mass gap: Avoiding pair instability in massive stars through addition of nonnuclear energy. Phys. Rev. D 2021, 104, 043015. [Google Scholar] [CrossRef]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; et al. Planck 2015 results. xiii. cosmological parameters. A&A 2016, 594, A13. [Google Scholar]
- Zwicky, F. On the Masses of Nebulae and of Clusters of Nebulae. Astrophys. J. 1937, 86, 217–246. [Google Scholar] [CrossRef]
- Fu, L.; Kilbinger, M.; Erben, T.; Heymans, C.; Hildebrandt, H.; Hoekstra, H.; Kitching, T.D.; Mellier, Y.; Miller, L.; Semboloni, E.; et al. CFHTLenS: Cosmological constraints from a combination of cosmic shear two-point and three-point correlations. Mon. Not. R. Astron. Soc. 2014, 441, 2725–2743. [Google Scholar] [CrossRef]
- Massey, R.J.; Kitching, T.D.; Richard, J. The dark matter of gravitational lensing. Rep. Prog. Phys. 2010, 73, 086901. [Google Scholar] [CrossRef]
- Clowe, D.; Bradac, M.; Gonzalez, A.H.; Markevitch, M.; Scott, W.; Jones, C.; Zaritsky, D. A direct empirical proof of the existence of dark matter. Astrophys. J. 2006, 648, 109–113. [Google Scholar] [CrossRef]
- Arun, K.; Gudennavar, S.B.; Sivaram, C. Dark matter, dark energy, and alternate models: A review. Adv. Space Res. 2017, 60, 166–186. [Google Scholar] [CrossRef]
- Steigman, G.; Turner, M.S. Cosmological constraints on the properties of weakly Interacting massive particles. Nucl. Phys. B 1985, 253, 375–386. [Google Scholar] [CrossRef]
- Arun, K.; Gudennavar, S.B.; Prasad, A.; Sivaram, C. Effects of dark matter in star formation. Astrophys. Space Sci. 2019, 364, 24. [Google Scholar] [CrossRef]
- Arun, K.; Gudennavar, S.B.; Prasad, A.; Sivaram, C. Alternate models to dark energy. Adv. Space Res. 2018, 61, 567–570. [Google Scholar] [CrossRef]
- Kumar, S.S.; Arun, K.; Sivaram, C. Discrepancy in the upper Bound mass of neutron stars. arXiv 2019, arXiv:1902.08618. [Google Scholar]
- Sunny, C.; Arun, K.; Sivaram, C.; Gudennavar, S.B. Effects of dark matter in red giants. Phys. Dark Univ. 2020, 30, 100727. [Google Scholar]
- Kippenhahn, R.; Weigert, A.; Weiss, A. Stellar Structure and Evolution, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 450–454. [Google Scholar]
- Lamers, H.J.G.L.M.; Levesque, E.M. Understanding Stellar Evolution, 1st ed.; IOP Publishing: Bristol, UK, 2017; pp. 26-1–26-7. [Google Scholar]
- Yusof, N.; Hirschi, R.; Meynet, G.; Crowther, P.A.; Ekström, S.; Frischknecht, U.; Georgy, C.; Kassim, H.A.; Schnurr, O. Evolution and fate of very massive stars. Mon. Not. R. Astron. Soc. 2013, 433, 1114–1132. [Google Scholar] [CrossRef]
- Jose, J. Stellar Explosions: Hydrodynamics and Nucleosynthesis, 1st ed.; CRC Press: Boca Raton, FL, USA, 2015; pp. 108–110. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narasimha, R.; Vincent, D.; Kenath, A.; Sivaram, C. Escaping the Pair-Instability Mass Gap with the Help of Dark Matter. Phys. Sci. Forum 2023, 7, 24. https://doi.org/10.3390/ECU2023-14059
Narasimha R, Vincent D, Kenath A, Sivaram C. Escaping the Pair-Instability Mass Gap with the Help of Dark Matter. Physical Sciences Forum. 2023; 7(1):24. https://doi.org/10.3390/ECU2023-14059
Chicago/Turabian StyleNarasimha, Raghav, Della Vincent, Arun Kenath, and Chandra Sivaram. 2023. "Escaping the Pair-Instability Mass Gap with the Help of Dark Matter" Physical Sciences Forum 7, no. 1: 24. https://doi.org/10.3390/ECU2023-14059
APA StyleNarasimha, R., Vincent, D., Kenath, A., & Sivaram, C. (2023). Escaping the Pair-Instability Mass Gap with the Help of Dark Matter. Physical Sciences Forum, 7(1), 24. https://doi.org/10.3390/ECU2023-14059





