Abstract
At finite isospin chemical potential , the tension between measured decays and partial branching ratios of neutral and charged bosons as functions of dimuon mass squared and the Standard Model (SM) isospin asymmetry can be analyzed in nonperturbative QCD-effective models, for instance, the Polyakov linear sigma-model. With almost first-principle derivation of the explicit isospin symmetry breaking, namely, the isospin sigma field, and the third generator of the matrix of the explicit symmetry breaking . and are decay constants of and , respectively. is the mass of meson. Accordingly, the QCD phase structure could be extended to finite . With the thermal and density dependence of , , and , and are accordingly expressed in dependence on the temperatures and the chemical potentials. We find that the resulting critical chiral temperatures decrease with the increase in and/or . We conclude that the () boundary has almost the same structure as that of the () plane.
PACS:
11.30.Rd; 11.10.Wx; 12.39.Fe; 21.10.Hw
1. Introduction
At finite isospin chemical potential , the lattice Quantum ChromoDynamics (QCD) simulations have real and positive action so that the Monte Carlo (MC) techniques are well applicable [1]. On the other hand, at finite baryon chemical potential , the action becomes complex, i.e., sign problem [2]. Both types of nonperturbative simulations share common features, for example, deconfinement, hadronization, hadron-parton phase transition, Silverblaze phenomenon, and Bose–Einstein condensations. Hence, even qualitative if not quantitative conclusions on nonperturbative QCD, at finite , are of great importance [3]. This might go beyond the current limitations and offer a theoretical framework for the Bose–Einstein condensations and the yet-still-hypothetical superconducting phases [4]. Thereby, the QCD phase diagram is enriched [5]. Characterizing the possible imbalance between the charged pions degrees-of-freedom [6] in dense quark matter, such as the neutron stars [7,8], is an astrophysical example of the chiral isospin asymmetry.
The QCD-like effective models, such as the Ployakov linear-sigma model (PLSM), offer a complementary approach to the nonperturbative QCD [9,10,11,12]. The present script introduces a novel study suggesting first-principle derivations of a new set of PLSM parameters, namely, and the isospin sigma field. As a result of the spontaneous symmetry breaking in the QCD-like effective nonperturbative QCD approach, the PLSM, the mean value of the field , , and that of its conjugate could be related to the quantum numbers of the vacuum [13]. Therefore, while the mean values of vanish, that of the quark condensates remain finite. Concretely, corresponding to the diagonal generators . On the other hand, the isospin symmetry is broken in SU(2) though finite quark condensates [13] and finite in the PLSM Langrangian. Thus, the symmetry generators are conjectured to break the isospin symmetry, as . Therefore, the finite diagonal components of lead to finite condensates corresponding to the three quark flavors. Accordingly, the masses of the three quark flavors are no longer degenerate, i.e., . It is obvious that the nature likely prefers such a configuration. By converting the three quark condensates through the orthogonal basis transformation from the original basis, , and to pure up (), down (), and strange () quark flavor basis, we obtain,
In light of this, the masses of u-, d-, and s-quarks can be expressed as,
In the present calculations, we introduce PLSM calculations for the thermodynamic properties and thereby the chiral QCD phase structure, at finite isospin asymmetry. Firstly, the effects of finite isospin asymmetry on differentiation between the nonstrange (light) condensates of u- and d-quark shall be analyzed. Secondly, as a result of the isospin symmetry breaking, should have a nonzero value because and . To this end, we estimate the pure mesonic potential for quark flavors, Equation (14), as functions of temperatures and chemical potentials.
To the author’s best knowledge, there is so-far no reliable estimation for the generator . Following the assumption of refs. [14,15], we first assume that the violation of the isospin symmetry is negligibly small, i.e., , see Table 1. In this limit, one assumes that the u- and d-quark condensates can be given as and , where is the nonstrange light condensate for non-degenerated masses of the light quarks, Equation (1). The main contribution of the present script is revising such an assumption. Finite , the third generator of the matrix of the explicit symmetry breaking , and , the isospin sigma field, considerably contribute to the isospin symmetry breaking. We are not just assigning finite values to and . We rather introduce a theoretical framework for the thermal and dense dependence of both and .

Table 1.
Various LSM parameters fixed at MeV and [16].
The present script is organized as follows. In Section 2, the formalism is outlined. The effective nonperturbative QCD approach, the SU(3) Polyakov linear-sigma model (PLSM), at vanishing , is introduced in Section 2.1. The isospin symmetry breaking based on suggesting finite is discussed in Section 2.2. In Section 3, we investigate the impacts of the isospin asymmetry on the QCD phase transition(s). Last but not least, Section 4 is devoted to the conclusions.
2. Formalism
The limitation of the MC techniques to vanishing baryon chemical potential in the non-perturbative lattice QCD promotes the utilization of QCD-like effective approaches. In the present study, we focus on the Polyakov linear-sigma model (PLSM). Various QCD quantities, including the thermodynamics of conserved charges and chiral quark-hadron phase transitions, can be estimated at least qualitatively [15,17,18,19,20,21,22,23,24,25].
Here, we aim at analyzing how the finite isospin asymmetry should be integrated in the chiral models, PLSM, especially that the nonperturbative lattice QCD simulations—in contrast to the finite baryon chemical potential—are reliable, at finite isospin chemical potential. Having done this allows the characterization of the thermodynamic properties of the nonperturbative QCD and thereby the mapping out of the QCD phase diagram. With finite isospin asymmetry, the generic chemical potentials of both light quarks are no longer degenerate. The PLSM thermodynamics in thermal and dense medium shall be confronted to the recent lattice QCD simulations. To this end, we aim at presenting a general expression of the chiral limit, at finite isospin asymmetry.
2.1. PLSM at Finite Chemical Potential
In flat Minkowski space, the Lagrangian of the linear-sigma model (LSM) with quark flavors and Polyakov-loop potential would be summarized as
where represent the quarks (fermions), while represents the mesons (bosons), and represents the Polyakov-loop potential contributions. For , the color degrees of freedom, the contributions of the quarks (fermions) read
where are the Dirac spinor fields; are the quark flavors; and and g, respectively, represent the covariant derivative, Lorentz index, chiral spinors, and Yukawa coupling constant. The contributions of the mesons (bosons) are given as,
where is the nonet meson -matrix,
and is a generator operator in U(3) algebra. can be determined from the Gell–Mann matrices with [26].
So far, we have various LSM parameters to be fixed, namely, , , , , , and c. They are strongly dependent on the mass of the sigma meson [16]. In the present calculations, we assumed that MeV. Table 1 summarizes all these parameters [16]. The present script aims at determining another set of parameters, namely, and , the third generator of the matrix of the explicit symmetry breaking H and isospin sigma field, respectively. In this regard, we recall that the same symbol was used in refs. Refer to [27,28] for the dimensionless coupling constant distinguishing between u and d quark flavors.
The third type of contributions to the PLSM Lagrangian, Equation (3), represents the Polyakov-loop potential responsible for the gluonic degrees of freedom and the dynamics of the quark-gluon interactions, . The Polyakov-loop potentials are suggested to characterize the QCD symmetries in pure-gauge theory [18,19,23,29,30]. For example, based on strong coupling simulations and by including higher-order Polyakov-loop variables, we have
In temporal space, the thermal expectation value of the color traced Wilson loop, also known as the Polyakov-loop variable, reads
where are the Polyakov loops.
Then, in the mean-field approximation, the PLSM grand-canonical potential can be expressed as
where are the chemical potentials of the three quark flavors. For the conserved charge baryon B, strangeness S, electric charge Q, and isospin I, the quark chemical potentials are composed as
accordingly, the mesonic contributions to the LSM potential can be determined by substituting Equation (6), the mesonic field, into Equation (5)
where shall be derived in Section 2.2.
The contributions of quarks and antiquarks to the PLSM potential are given as [18,31,32,33]
It is evident that is identical to with a double replacement, namely, by and the order parameter of the Ployakov-loop field by its conjugate or vice versa.
gives the energy-momentum dispersion relation corresponding to the quark and antiquark, where is the mass of fth quark flavor. Equation (10) expresses the grand canonical potential, which in mean-field approximation derives the various physical quantities characterizing the QCD thermodynamics and thereby the QCD phase structure in thermal and dense medium.
2.2. Isospin Asymmetry and Meson Potential
As discussed in the previous section, the isospin asymmetry SU(2) is broken, at finite [13], not only , which breaks the isospin symmetry, but also the potential of pure mesonic contributions in SU(), which can be rewritten as [14],
where the coefficients and are given as [14]
We notice that the explicitly symmetry breaking terms, , and , can be determined by minimizing the potential, Equation (17), on tree level, . Concretely, both and can be determined from the partially conserved axial current (PCAC) relations.
The generator operator in U(3) is obtained from Gell–Mann matrices [26] with the indices running as . From U(3) algebra, we have
where and , respectively, are the standard antisymmetric and symmetric structure constants of SU(3). In this regard, the symmetric structure constant can be defined as
In PCAC relation, the decay constant is related to the symmetric structure constant as
Accordingly, the decay constants of the charged and neutral pion mesons () and the kaon meson () are given as
where the isospin sigma field, , is the difference between the decay constants of neutral and charged kaon mesons as
From the experimental and recent lattice review on physical constants [34,35,36], and . Then, we suggest expressions for both and ,
The explicit symmetry breaking term, , the third generator of the matrix of the explicit symmetry breaking , can be deduced from ,
where the square brackets is the squared mass of the meson, Equation (28). Then, can be expressed as
As discussed in the Introduction, the finite isospin asymmetry leads to degenerate masses of the quark flavors, namely, . At nonvanishing , the PLSM parameters listed in Table 1 are revised, Table 2.

Table 2.
The revised values of the LSM parameters, Equation (5), at MeV [16].
3. Results and Discussion
For a reliable differentiation between u- and d-quark condensates, the influences of the finite isospin asymmetry on the corresponding PLSM chiral condensates and on the deconfinement order parameters should be estimated [37]. It was pointed out that the impacts of finite isospin asymmetry enhances the PLSM thermodynamics, especially with the increase in temperatures. The dependence of the PLSM critical chiral temperatures on the isospin asymmetry obviously maps out the QCD phase structure. The critical chiral temperature decreases as the isospin asymmetry increases. We also conclude that the PLSM results on the critical temperatures reproduce the recent lattice QCD simulations well [38,39], Figure 1 For a reliable comparison, both temperature and isospin chemical potential are normalized to the critical temperature and the pion mass, respectively, as follows. For lattice QCD: MeV and MeV. For PLSM: MeV and MeV.
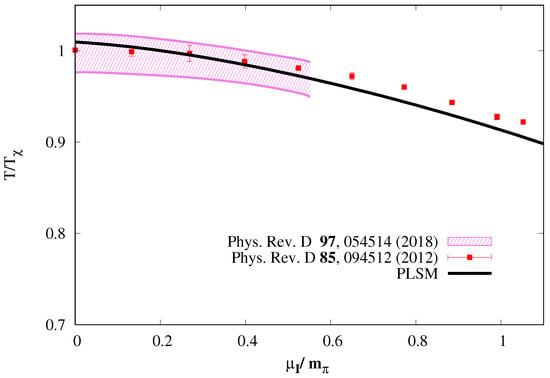
Figure 1.
The QCD phase diagram at vanishing baryon chemical potential but finite isospin chemical potential. The PLSM results (solid curves) are confronted to recent lattice QCD calculations (symbols) [38,39].
At finite , the potential impacts of and are taken into consideration. The procedure to determine the critical chiral temperature goes as follows.
- Both u- and d-quark chiral condensates become distinguishable. As the temperature approaches a critical value, the normalized nonstrange condensates are split into two different curves. At this point, the critical chiral temperatures, , can be at least qualitatively estimated. We notice that the value of the resulting decreases with increasing .
- Both Ployakov-loop variables and also become distinguishable. Increasing decreases but increases . Moreover, both and become more distinguishable with a further increase in .
- Both nonstrange quark susceptibilities become distinguishable as well. The critical chiral temperature is positioned in the middle of the deconfinement phase transition. The resulting decreases with the increase in .
The Figure 1 illustrates that similar to the lattice QCD simulations [38,39], the critical temperature decreases with increasing . Because the PLSM results reproduce the available lattice QCD calculations well, it is possible to predict the tendency at larger . Furthermore, when comparing our results for Figure 1, with the QCD phase structure in (-) plane reported in refs. [10,40,41,42], good similarity can be concluded.
4. Conclusions
We have studied the Ployakov linear-sigma model with three quark flavors and U anomaly, at finite isospin asymmetry. The finite isospin asymmetry emerges nonvanishing diagonal generators of the mean sigma-fields . This means that the SU isospin asymmetry is broken through , i.e., and [14,43,44].
From the thermal and dense dependence of the quark condensates , , and , and the Polyakov-loop variables and , fruitful information, especially about the QCD chiral phase transition, becomes available. All of these quantities can be estimated by minimizing the real part of thermodynamic potential, , Equation (10). We conclude the chiral QCD phase transition, the dependence of the critical chiral temperatures on the isospin chemical potential, looks very similar to the QCD phase transition, the dependence of the critical temperatures on the baryon chemical potential, i.e., the (-) plane looks very similar to the (-) plane. We conclude that the critical chiral temperatures are not universally constant. This apparently depends on the quark flavors and the isospin chemical potentials.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All types of relevant data are included in the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- Son, D.T.; Stephanov, M.A. QCD at finite isospin density. Phys. Rev. Lett. 2001, 86, 592. [Google Scholar] [CrossRef]
- Philipsen, O. Lattice QCD at finite temperature and density. Eur. Phys. J. Spec. Top. 2007, 152, 29. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G.; Schmalzbauer, S. QCD phase diagram for nonzero isospin-asymmetry. EPJ Web Conf. 2018, 175, 07020. [Google Scholar] [CrossRef]
- Detmold, W.; Orginos, K.; Shi, Z. Lattice QCD at non-zero isospin chemical potential. Phys. Rev. 2012, D86, 054507. [Google Scholar]
- Tawfik, A. QCD phase diagram: A Comparison of lattice and hadron resonance gas model calculations. Phys. Rev. D 2005, 71, 054502. [Google Scholar] [CrossRef]
- Li, B.-A.; Ko, C.M.; Bauer, W. Isospin physics in heavy ion collisions at intermediate-energies. Int. J. Mod. Phys. 1998, E7, 147. [Google Scholar] [CrossRef]
- Migdal, A.B.; Saperstein, E.E.; Troitsky, M.A.; Voskresensky, D.N. Pion degrees of freedom in nuclear matter. Phys. Rep. 1990, 192, 179. [Google Scholar] [CrossRef]
- Steiner, A.W.; Prakash, M.; Lattimer, J.M.; Ellis, P.J. Isospin asymmetry in nuclei and neutron stars. Phys. Rep. 2005, 411, 325. [Google Scholar] [CrossRef]
- Abdel Aal Diab, A.M.; Tawfik, A.N. Quark-hadron phase structure of QCD matter from SU(4) Polyakov linear sigma model. EPJ Web Conf. 2018, 177, 09005. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M.; Hussein, M.T. Quark-hadron phase structure, thermodynamics, and magnetization of QCD matter. J. Phys. 2018, G45, 055008. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Magdy, N. SU(3) Polyakov linear-σ model in magnetic fields: Thermodynamics, higher-order moments, chiral phase structure, and meson masses. Phys. Rev. 2015, C91, 015206. [Google Scholar]
- Tawfik, A.N.; Diab, A.M. Polyakov SU(3) extended linear-σ model: Sixteen mesonic states in chiral phase structure. Phys. Rev. 2015, C91, 015204. [Google Scholar]
- Gasiorowicz, S.; Geffen, D.A. Effective Lagrangians and field algebras with chiral symmetry. Rev. Mod. Phys. 1969, 41, 531. [Google Scholar] [CrossRef]
- Lenaghan, J.T.; Rischke, D.H.; Schaffner-Bielich, J. Chiral symmetry restoration at nonzero temperature in the SU(3)(r) x SU(3)(l) linear sigma model. Phys. Rev. 2000, D62, 085008. [Google Scholar]
- Rischke, D.H. The Quark gluon plasma in equilibrium. Prog. Part. Nucl. Phys. 2004, 52, 197. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Wagner, M. The Three-flavor chiral phase structure in hot and dense QCD matter. Phys. Rev. 2009, D79, 014018. [Google Scholar] [CrossRef]
- Asakawa, M.; Yazaki, K. Chiral Restoration at Finite Density and Temperature. Nucl. Phys. 1989, A504, 668. [Google Scholar]
- Fukushima, K. Phase diagrams in the three-flavor Nambu–Jona–Lasinio model with the Polyakov loop. Phys. Rev. 2008, D77, 114028. [Google Scholar] [CrossRef]
- Ratti, C.; Thaler, M.A.; Weise, W. Phases of QCD: Lattice thermodynamics and a field theoretical model. Phys. Rev. 2006, D73, 014019. [Google Scholar] [CrossRef]
- Carignano, S.; Nickel, D.; Buballa, M. Influence of vector interaction and Polyakov loop dynamics on inhomogeneous chiral symmetry breaking phases. Phys. Rev. 2010, D82, 054009. [Google Scholar] [CrossRef]
- Bratovic, N.M.; Hatsuda, T.; Weise, W. Role of Vector Interaction and Axial Anomaly in the PNJL Modeling of the QCD Phase Diagram. Phys. Lett. 2013, B719, 131. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Wambach, J. Susceptibilities near the QCD (tri)critical point. Phys. Rev. 2007, D75, 085015. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Pawlowski, J.M.; Wambach, J. The Phase Structure of the Polyakov-Quark-Meson Model. Phys. Rev. 2007, D76, 074023. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Wagner, M. On the QCD phase structure from effective models. Prog. Part. Nucl. Phys. 2009, 62, 381. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Wagner, M.; Wambach, J. QCD thermodynamics with effective models. PoS 2009, 71, 017. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Parganlija, D.; Kovacs, P.; Wolf, G.; Giacosa, F.; Rischke, D.H. Meson vacuum phenomenology in a three-flavor linear sigma model with (axial-)vector mesons. Phys. Rev. 2013, D87, 014011. [Google Scholar] [CrossRef]
- Kovacs, P.; Wolf, G.; Giacosa, F.; Parganlija, D. Meson vacuum phenomenology in a three-flavor linear sigma model with (axial-)vector mesons. EPJ Web Conf. 2011, 13, 02006. [Google Scholar]
- Roessner, S.; Ratti, C.; Weise, W. Polyakov loop, diquarks and the two-flavour phase diagram. Phys. Rev. 2007, D75, 034007. [Google Scholar]
- Lo, P.M.; Friman, B.; Kaczmarek, O.; Redlich, K.; Sasaki, C. Polyakov loop fluctuations in SU(3) lattice gauge theory and an effective gluon potential. Phys. Rev. 2013, D88, 074502. [Google Scholar] [CrossRef]
- Kapusta, J.I.; Gale, C. Finite-Temperature Field Theory: Principles and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Mao, H.; Jin, J.; Huang, M. Phase diagram and thermodynamics of the Polyakov linear sigma model with three quark flavors. J. Phys. 2010, G37, 035001. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Wagner, M.; Wambach, J. Thermodynamics of (2+1)-flavor QCD: Confronting Models with Lattice Studies. Phys. Rev. 2010, D81, 074013. [Google Scholar] [CrossRef]
- Barnett, R.M.; Carone, C.D.; Groom, D.E.; Trippe, T.G.; Wohl, C.G.; Armstrong, B.; Gee, P.S.; Wagman, G.S.; James, F.; Mangano, M.; et al. Review of Particle Physics. Phys. Rev. D 1996, 54, 1. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Aoki, S.; Aoki, Y.; Bečirević, D.; Bernard, C.; Blum, T.; Colangelo, G.; Della Morte, M.; Dimopoulos, P.; Dürr, S.; Fukaya, H.; et al. Review of lattice results concerning low-energy particle physics. Eur. Phys. J. C 2017, 77, 112. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M.; Ghoneim, M.T.; Anwer, H. SU(3) Polyakov Linear-Sigma Model With Finite Isospin Asymmetry: QCD Phase Diagram. Int. J. Mod. Phys. A 2019, 34, 1950199. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G.; Schmalzbauer, S. QCD phase diagram for nonzero isospin-asymmetry. Phys. Rev. 2018, D97, 054514. [Google Scholar] [CrossRef]
- Cea, P.; Cosmai, L.; D’Elia, M.; Papa, A.; Sanfilippo, F. The critical line of two-flavor QCD at finite isospin or baryon densities from imaginary chemical potentials. Phys. Rev. 2012, D85, 094512. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M.; Hussein, T.M. Chiral phase structure of the sixteen meson states in the SU(3) Polyakov linear-sigma model for finite temperature and chemical potential in a strong magnetic field. Chin.Phys.C 2019, 43, 034103. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M.; Hussein, M.T. SU(3) Polyakov linear-sigma model: Magnetic properties of QCD matter in thermal and dense medium. J. Exp. Theor. Phys. 2018, 126, 620. [Google Scholar] [CrossRef]
- Tawfik, A.; Magdy, N.; Diab, A. Polyakov linear SU(3) σ model: Features of higher-order moments in a dense and thermal hadronic medium. Phys. Rev. 2014, C89, 055210. [Google Scholar]
- Schaffner-Bielich, J.; Stiele, R. The QCD Phase Transition at finite Isospin. In Proceedings of the 10th Conference on Quark Confinement and the Hadron Spectrum (Confinement X), Munich, Germany, 8–12 October 2012. [Google Scholar]
- Beisitzer, T.; Stiele, R.; Schaffner-Bielich, J. Supernova Equation of State with an extended SU(3) Quark-Meson Model. Phys. Rev. 2014, D90, 085001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).