Next Article in Journal
Influence of the Thickness of the Seasonally Thawed Layer of Permafrost in the Eastern Siberia Catchments on the Content of Organic Matter in River Waters
Previous Article in Journal
Holistic Approach for Estimating Water Quality Ecosystem Services of Danube Floodplains: Field Measures, Remote Sensing, and Machine Learning
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Hydrobiology
Volume 1
Issue 2
10.3390/hydrobiology1020017
hydrobiology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Gillnet Selectivity for Three Freshwater Alien Invasive Fish Species in a Long-Term Monitoring Scenario

by
Jorge Rubén Sánchez-González
1,2,* and
Frederic Casals
1,2,3
1
Wildlife Section, Department of Animal Science, University of Lleida, Av. Alcalde Rovira Roure 191, 25198 Lleida, Spain
2
Iberian Society of Ichthyology, Department of Environmental Biology, University of Navarra, C/Irunlarrea 1, 31008 Pamplona, Spain
3
Forest Science and Technology Centre of Catalonia, 25280 Solsona, Spain
*
Author to whom correspondence should be addressed.
Hydrobiology 2022, 1(2), 232-242; https://doi.org/10.3390/hydrobiology1020017
Submission received: 14 March 2022 / Revised: 4 May 2022 / Accepted: 11 May 2022 / Published: 19 May 2022
Browse Figures
Versions Notes

Abstract

:
Gillnet selectivity is poorly understood for most freshwater fish species, particularly for invasive alien species. However, their use to determine mesh selectivity could be essential for establishing management measures, such as the selective removal of exotic invasive species. This study aims to the assess size selectivity of exotic invasive species in a restored lentic freshwater ecosystem. Therefore, we analysed gillnet size selectivity based on experimental fishing trials performed by using multimesh gillnets. Twice a year, for 8 years, multimesh nylon gillnets were set up in the Estany d’Ivars i Vila-sana, a restored shallow lake in Catalonia (NE Iberian Peninsula). We caught 4105 individuals belonging to three widely distributed freshwater fish species—3583 pikeperches (Sander lucioperca (Linnaeus, 1758)), 115 common roaches (Rutilus rutilus (Linnaeus, 1758)) and 407 common carps (Cyprinus carpio, Linnaeus, 1758). The SELECT method was applied to fit six different gillnet selectivity uni- and bimodal models. As a result, bi-lognormal provides the best fit for the three species. This is in line with previous studies that found size–frequency data skewed to the right or to multimodal models when high numbers of fish are captured. These results provide the essential information required for fish community management with the presence of these invasive alien species.

1. Introduction

Fisheries research, stock assessment and management often require the evaluation of ichthyological community composition, as well as the estimation of ichthyologic diversity, spatial distribution and the monitoring and determination of population structure [1]. Abundance estimates are, nevertheless, greatly influenced by gear selectivity and efficiency parameters [1]. According to Santos et al. (2003) [2], gillnets have a strong size selectivity, with a relatively narrow size range being caught (±20% of the optimum length of a particular mesh size). Therefore, knowledge of the size selectivity of fishing gear types is crucial for fish stock assessment and management, and provides essential information (distribution of catches, composition of fish community) to understand the fish community, its evolution and ecology [3,4,5,6]. It can be also used to establish the Minimum Landing Size (MLS) and regulate mesh sizes to respect sexual maturation length in different species [6]. Nonetheless, one of the most important applications is based on its potential to perform management strategies to efficiently and selectively remove exotic species, whose negative impacts on freshwater ecosystems have been widely described [7].
Furthermore, gillnet survey is a widely used method for sampling fish populations in lentic ecosystems [3,6,8,9,10,11], and has been also used to analyse the mortality from spring to late summer, catchability differences due to environmental factors (temperature, visibility…) [12] and it will be proposed as a standardised method for sampling freshwater fish within the context of the European Water Framework Directive [13], in non-wadeable lotic water bodies and lentic ecosystems [14].
Gillnets provide biased estimates of abundance and distribution of species, but, despite their drawbacks [4,15], their use brings about some important advantages: ease of use, low cost and the possibility to be set at any depth and in areas with difficult bottom conditions [16]. Furthermore, gillnet selectivity studies are characterised by the simultaneous use of a defined number of gillnets of differing mesh sizes, called multimesh gillnets, to guarantee similar catchability for different fish sizes [17], decreasing bias problems.
Even though the importance of gillnet selectivity at the European level for freshwater species is increasing, due to its inclusion within Water Framework Directive bioassessment protocols, there is an important lack of knowledge because there are no studies on gillnet selectivity for most of the European and alien species [3]. One of the most common methods for estimating gillnet selectivity was described by Holt (1963) [18]. However, this method is restrictive due to the assumption in its selection model of the normal location curve (the spread is constant for all mesh sizes) [3]. We, therefore, used other methods, based on Baranov’s principle of geometric similarity [19,20], which is, in addition, one of the most widely used assumptions of gillnet selectivity [1,3,5,21,22]. This principle interprets gillnet captures as a mechanical process that depends only on the relative geometry of the mesh and the fish and, consequently, describes selection as a function of the fish length and mesh size ratio. This assumption allows us to compare catches in the same length group taken by different gear, assuming that the fishing power is the same for all mesh sizes.
A widely used approach for estimating length-based gear selectivity is the Share Each Lengthclass’s Catch Total (SELECT) method, first proposed by Millar (1992) [23]. The SELECT method, as a statistical method for estimating gillnet selectivity and their related curves, is being consolidated on freshwater species in Europe [3,4,5,9,10,11,12,15,24], in spite of the limitations it shows [24]. According to Brenden and Zhao (2012) [24], the SELECT method has been used to estimate length-based selectivity for a variety of gear types, in both marine and freshwater organisms (see, for example, [3,25,26,27,28,29]. Indirect estimates of gillnet selectivity are obtained by comparing the observed catch length frequencies across several meshes with known distributions [17]. Gillnet selectivity has been extensively studied in marine and estuarine systems, (e.g., [4,16,26]); until recent times, a reduced number of gillnet selectivity studies have focussed on European freshwater fish, but this is intensively changing [3,4,6,9,10,11,12,15,30,31,32].
The aim of this study consists of modelling gillnet selectivity for three exotic species introduced in a shallow lake by using the SELECT method, within the context of a long-term monitoring study. The main objectives are to evaluate the size selectivity of three alien invasive species, providing essential information for inland fisheries management to remove those species from restored shallow lakes.

2. Materials and Methods

2.1. Sampling Methods and Data Collection

We obtained our sample from the Estany d’Ivars i Vila-sana shallow lake in Lleida (Catalonia, NE Spain) restored in 2005 (Figure 1) over an 8-year period. It is a shallow lake with an area of 131.3 ha, a mean depth of 1.9 m, a maximum depth of 3.8 m and a total volume of 2.4 hm3. Conductivity varies between 0.5 and 3.0 mS/cm and the water temperature ranges from 3–5 °C in winter to 26–28 °C in summer [33].
Three to six multimesh nylon gillnets were set up in the lake in two different sampling seasons (early summer and autumn) over 8 years (from 2008 to 2015). They were placed separated from 200 to 1500 m in such a way that they represent the habitat variability of the lake (pelagic and littoral habitats with helophyte vegetation dominated by Thypha sp. and Phragmites australis). All nets were set up simultaneously in the late afternoon at 0–2 m depth and lifted the next morning, averaging a soak time of 12 h. Gillnets were always far from saturation and its effects. Each gillnet consisted of a series of 14 panels (2.5 m width and 1.5 m height) of different mesh sizes, ranging from 6.25 to 75.00 mm bar length (see Figure 2 for mesh sizes). Each panel, with a specific mesh size, was randomly interspersed within the net to avoid different capturability associated with environmental gradients and followed a geometric progression to optimise efficiency [34]. The nets were made of monofilament twine (ranging from 0.10 to 0.20 mm depending on the panel) and the hanging ratio oscillated between 0.493 and 0.5 depending on the panel mesh size. All captured fish specimens were weighed, identified to species level, sorted by mesh size, and their fork length (hereinafter, FL) was measured to the nearest mm.

2.2. Estimation of Gillnet Selectivity

The gillnet selectivity for each species was estimated by using the function gillnetfit from gillnetfunctions.R, for unimodal models, and function NetFit from NextGeneration.R for bimodal models from SELECT method [31], a generalised linear model that estimates gillnet selection curves (i.e., retention probabilities) from comparative gillnet catch data, thereby providing a cohesive approach to selectivity analyses [17,35]. In addition to its statistical accuracy and availability of several models, the SELECT method analyses the data of all meshes within a single model, thus, increasing the statistical precision and power [3]. SELECT is a maximum likelihood estimation approach that conditions the catch from a particular gear variant or mesh size on the combined catches of all gear variants or mesh sizes [24]. In this work, SELECT method was used to estimate retention curves under six different models: normal location, normal scale, gamma and log-normal, binormal scale and bi-lognormal. All of them are available in the R [36] scripts of SELECT developed by Russell B. Millar (2009) [37] downloaded from the University of Auckland website [38]. The four first models are unimodal and consist of two parameters describing the location and dispersion of the curves. The normal location and normal scale models are based on the normal distribution, while the other two (gamma and log-normal) are skewed curves with positive asymmetry. Finally, the last two models are bimodal models whose goodness of fit has been estimated. Binormal scale is a binomial distribution based on the normal distribution and bi-lognormal is based on lognormal distribution.
All models were fitted under the assumption of equal efficiency and effort for all mesh sizes. The bin width of the frequency distribution was optimised for each species, given the sample size and length range. The goodness of fit was evaluated by comparing model deviances, so that the lowest deviance value corresponded to the best fitting model. Chi-squared distribution was used to assess the lack of fit, therefore, p-value < 0.05 denotes lack of fit [39]. The analysis of residual plots was performed following [17]. See Data Availability Statement.
Deviance residual plots for a given mesh were performed to show length residuals for each species [17].
By using the selectivity model with best fit, modal lengths and range for each species were estimated for each mesh size in concordance with the Millar and Holst (1997) [17] selection curve models. Moreover, the observed mean fork length (FL) and range were also calculated (See Data Availability Statement).

3. Results

During monitoring, 4176 fish from 9 different fish species were caught by using multimesh nylon gillnets: 6 exotic species (Alburnus alburnus (Linnaeus, 1758), Carassius auratus (Linnaeus, 1758), Cyprinus carpio (Linnaeus, 1758), Rutilus rutilus (Linnaeus, 1758), Sander lucioperca (Linnaeus, 1758) and Scardinius erythrophthalmus (Linnaeus, 1758)), 2 native species (Luciobarbus graellsii (Steindachner, 1866) and Squalius laietanus Doadrio, Kottelat and de Sostoa, 2007)) and 1 translocated species from another neighbouring watershed (Gobio lozanoi Doadrio and Madeira, 2004). Only three species were present in all the surveys and all of them are exotic invasive species: pikeperch, Sander lucioperca (N = 3583), common roach, Rutilus rutilus (N = 115) and common carp, Cyprinus carpio (N = 407). Total captures of three fish species (Cyprinus carpio, Rutilus rutilus and Sander lucioperca) over the 8-year sampling period for different gillnet mesh sizes are shown in Figure 2.
The results, after fitting uni- and bimodal models by using the SELECT method, are shown in Table 1. In general terms, the results obtained show a lack of fit (p < 0.01) for many cases. Goodness-of-fit analyses tested deviations in the observed catch from the model predictions for each species. In the case of unimodal models, the exception is the common roach, whose results show a good fit to gamma, log-normal and normal-scale distributions (Table 1). However, the results for common roach might be treated with caution because we caught only 115 individuals, which could be considered a small sample size. For the common carp and pikeperch, normal location, normal scale, gamma and log-normal models obtained negative results due to the lack of fit (Table 1). However, for these two species, the log-normal model had the lowest deviance value, indicating a better fit. On the contrary, for the common roach, the best fit model was the gamma model. The normal location model for pikeperch was the worse fit (Table 1).
In contrast to the results of fitting to unimodal models, in general terms, the results obtained from using the bimodal model show a fair fit (p > 0.05) in all cases. For the three species, the bi-lognormal had the lowest deviance value, indicating an optimal fit. In all cases, our captures fit to the binomial models (p > 0.05), and the bi-lognormal model provides the best results (lower deviance) (Table 1).
After analysing species-specific selectivity curves, a general trend for increased length of captured fish with greater mesh size for the three studied fish species was observed (Figure 2). However, there were a few larger-than-expected fish in the smallest mesh sizes (e.g., in Sander lucioperca, individuals between 50 and 420 mm were captured in a 6.25 mm mesh), due to the fact that some fish were captured by tangling; conversely, it was uncommon (Figure 2) to catch smaller-than-expected fish. In fact, most fish were captured with the smallest mesh sizes, in accordance with the observed range and the expected modal length of most fish species (Table 2). An increase in size variability was detected when increasing mesh size (Figure 2). Thanks to the graphical representation of length–frequency distributions by gillnet size, it can be observed, as was expected, that a huge amount of 0+ individuals were captured and most of them were caught by the smallest mesh sizes.
Deviance residual plots for each species are shown in Figure 3.

4. Discussion

In general terms, our results match most of the previous studies that showed skewed distribution [3]. In line with previous studies, we found a huge amount of 0+ captured individuals [40]. Within the unimodal models, the gamma model had a good fit for the common roach, while the log-normal model had the best results for the pikeperch and common carp, but without fitting. Contrarily, the results obtained after using bimodal models were better and the bi-lognormal model obtained the best results and an adequate fit.
Theoretically, gillnet selectivity curves might fit or approach normal curves when most fish are gilled [22]. However, as previous studies have already demonstrated, when many fish are captured, data are skewed to the right, implying a better fit into gamma, log-normal or multimodal models [2,3,22]. In our study, the best unimodal models are, indeed, log-normal and gamma and bi-lognormal (Table 1), in the case of bimodal models (lowest deviance).
Firstly, we tested how our captures fit to unimodal models, in the case of the common roach, whose model fits gamma (p = 0.974), which is the model with the lowest deviance. This is because a relatively large number of juveniles (0+ and 1+) were captured. In fact, rates decreased progressively with an increasing mesh size. On the other hand, we have the case of pikeperch, whose distribution almost fits log-normal (lowest deviation) but, due to the huge number of juveniles that were captured, its model does not perfectly fit gamma nor log-normal models (Table 1). Nevertheless, we did not obtain an accurate fit due to the huge catch of 0+ individuals. The common carp’s case is not so extreme but similar to pikeperch, i.e., the log-normal model shows the best results (lowest deviance) but it does not fit (p < 0.0001) (Table 1). Our results for the common roach and common carp are not similar to those reported in previous, similar studies [3,5] (Table 1), in which most of the models showed a proper fit, probably because, in our case, there is subjacent binomial distribution (Figure 2) and, moreover, we captured a significant number of young-of-year (Y-O-Y) fish over 8 years that could generate a skewness towards log-normal and gamma models (Figure 2). In the case of pikeperch, our results are similar to those obtained in previous studies because we registered the huge presence of 0+ individuals [3,40], causing skewness towards log-normal and gamma models (Figure 2). Obviously, those results are not exclusively explained by biological traits but by ecological specific processes from the Estany d’Ivars i Vila-sana shallow lake, whose temperatures rise to around 30 °C and occasionally above and oxygen saturation decreases under 50% (manuscript under preparation), leading to a high mortality rate for juveniles. Probably, there is an overestimation of pikeperch and common roach juveniles due to their higher catch and behavioural patterns (especially in the case of pikeperch whose juveniles move in schools of fish), but the sudden and strong decrease in bigger sizes of pikeperch likely indicates a problem within the ichthyological community, where the alien fish species are evolving to readjust their densities (manuscript under preparation) and/or the above-mentioned lake conditions.
Log-normal and gamma models achieved the best fit, but the normal scale model is the most common in most studies, which implies a unimodal form selectivity curve. Nevertheless, as mentioned by Carol and García-Berthou (2007) [3], recent studies in several fish species have shown that bimodal distributions (binormal) and, consequently, bimodal curves, may yield better fits [2,3,41,42]. Consequently, a potential explanation for this lack of fit could be substantiated in bimodal curves (binormal) that may have better yields [2,24,28,41,42]. Apparently, bimodality was not evident in our study (Figure 2), except in the common roach case, where bimodality could only residually appear (Figure 2). In consequence, and due to the unsatisfactory results of unimodal models, we also tested binormal scale and bi-lognormal models, the latter being the model with the lowest deviation for the three species. Bimodal distribution is due to the presence of two maximus of captures and he mentioned skewness. One of these peaks is explained by the relatively large number of juveniles (0+ and 1+), as previously mentioned. The second maximum corresponds to 3+ and 4+-year-old individuals and the first cohorts that settled in the lake.
Of course, fish are caught by gillnets by different mechanisms (gilling, wedging, tangling, etc.) that are reflected in the size distributions. The majority are caught by gilling and wedging but those captured by tangling can explain part of the bimodal pattern [5].
Deviance residual plots (Figure 3) for a given mesh showed that length residuals had more or less uniform and symmetric residuals for common roach and common carp (see Millar and Holst 1997 [17]. The variability decreased by increasing mesh size in the common carp. A similar pattern was found in the common roach, whose variability decreased at high mesh sizes, but it had high catchability for medium-sized individuals at large mesh sizes. On the other hand, pikeperch showed a different pattern because some juveniles were captured by larger mesh sizes in their jaws and, mostly, their operculum and spiny fins.
Baranov (1914, 1948) [19,20] explained gillnet capture as a mechanical process that depends only on the relative geometry of the fish and the mesh size. He based the principle on the idea that all meshes are geometrically similar and all fish of the same species (within a reasonable size range) are also geometrically similar. However, in most cases, the principle of geometrical similarity, assumed in the models, is an unreal simplification and, of course, essentially wrong due to allometric processes [22] that are very common in fish species whose body shape may change as they grow older. These allometric processes might, thus, have implications for catchability.
Brenden and Zhao (2012) [24] mentioned how difficult it can be to generalise the results of specific research, as they used a limited number of intensity patterns and gillnet configurations. In fact, methods used to evaluate gillnet selectivity are not fully optimised and remain contested [24]. Fortunately, since this type of fishing gear is widely recommended to be used for the monitoring of fish populations in lakes and reservoirs, this situation will likely be resolved soon.
Despite these limitations, and thanks to the results, this study offers a significant contribution to the analysis of size selectivity of three species that are exotic, within the context of a restored shallow lake where they have become dominant. This knowledge, along with the evaluation of the biological and ecological traits of these species, will allow stakeholders and managers to design a plan for the management of exotic invasive species populations by catching the size classes that mainly contribute to population recruitment [30] and reduce their abundance, limiting their impact on other fish species and aiming for future eradication. In the case of the Estany d’Ivars i Vila-sana, high mortality of Y-O-Y were detected (unpublished data). In consequence, in spite of the high catchability of small sizes, especially Y-O-Y fish, and considering our objective is removing alien invasive species, efforts and resources might focus on mature or reproductive individuals by using 30–33 mm mesh sizes. These mesh sizes provide the highest captures for the three species, ranging from 150 to 250 fork length in the case of the common roach, from 350 to 450 mm for pike perch and, finally, from 200 to 350 mm for common carp.

Author Contributions

Conceptualization, F.C. and J.R.S.-G.; methodology, F.C. and J.R.S.-G.; validation, F.C. and J.R.S.-G.; formal analysis, J.R.S.-G.; investigation, F.C. and J.R.S.-G.; resources, F.C.; data curation, J.R.S.-G.; writing—original draft preparation, J.R.S.-G.; writing—review and editing, F.C.; visualization, F.C. and J.R.S.-G.; supervision, F.C.; project administration, F.C.; funding acquisition, F.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by the Consorci de l’Estany d’Ivars i Vila-sana and the Fundació Catalunya La Pedrera and supported by the Government of Catalonia (CERCA Programme).

Institutional Review Board Statement

The study did not require ethical approval according to Spanish legislation.

Informed Consent Statement

Not applicable.

Data Availability Statement

Dataset deposited in Figshare and Github https://doi.org/10.6084/m9.figshare.19786276, accessed on 13 March 2022.

Acknowledgments

We thank Carles Alcaraz for his essential helpful assistance and comments on the use of the R scripts, Emili Garcia-Berthou, Lluis Benejam, Alfredo G. Nicieza and Ivan Torres for their comments and essential assistance and Pablo Manzano and Sergio Velasco Ayuso for their comments and English revision. We also wish to thank Amadeo Arbonés, Nuno Caiola, Claudi Gallardo, David Margalejo, Eduardo Montejano, Anna Ñaco, Daniel Roque and David Sebastià for field assistance.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Askey, P.J.; Post, J.R.; Parkinson, E.A.; Rivot, E.; Paul, A.J.; Biro, P.A. Estimation of Gillnet Efficiency and Selectivity across Multiple Sampling Units: A Hierarchical Bayesian Analysis Using Mark-Recapture Data. Fish. Res. 2007, 83, 162–174. [Google Scholar] [CrossRef]
  2. Dos Santos, M.N.; Gaspar, M.; Monteiro, C.C.; Erzini, K. Gillnet Selectivity for European Hake Merluccius Merluccius from Southern Portugal: Implications for Fishery Management. Fish. Sci. 2003, 69, 873–882. [Google Scholar] [CrossRef] [Green Version]
  3. Carol, J.; García-Berthou, E. Gillnet Selectivity and Its Relationship with Body Shape for Eight Freshwater Fish Species. J. Appl. Ichthyol. 2007, 23, 654–660. [Google Scholar] [CrossRef]
  4. Olin, M.; Malinen, T.; Ruuhijärvi, J. Gillnet Catch in Estimating the Density and Structure of Fish Community-Comparison of Gillnet and Trawl Samples in a Eutrophic Lake. Fish. Res. 2009, 96, 88–94. [Google Scholar] [CrossRef]
  5. Petriki, O.; Erzini, K.; Moutopoulos, D.K.; Bobori, D.C. Gillnet Selectivity for Freshwater Fish Species in Three Lentic Systems of Greece. J. Appl. Ichthyol. 2014, 30, 1016–1027. [Google Scholar] [CrossRef]
  6. Rodríguez-Climent, S.; Alcaraz, C.; Caiola, N.; Ibáñez, C.; Nebra, A.; Muñoz-Camarillo, G.; Casals, F.; Vinyoles, D.; de Sostoa, A. Gillnet Selectivity in the Ebro Delta Coastal Lagoons and Its Implication for the Fishery Management of the Sand Smelt, Atherina boyeri (Actinopterygii: Atherinidae). Estuar. Coast. Shelf Sci. 2012, 114, 41–49. [Google Scholar] [CrossRef] [Green Version]
  7. Cucherousset, J.; Olden, J.D. Ecological Impacts of Non-Native Freshwater Fishes. Fisheries 2011, 36, 215–230. [Google Scholar] [CrossRef]
  8. Boy, V.; Crivelli, A.J. Simultaneous Determination of Gillnet Selectivity and Population Age-Class Distribution for Two Cyprinids. Fish. Res. 1988, 6, 337–345. [Google Scholar] [CrossRef]
  9. Prchalová, M.; Kubečka, J.; Říha, M.; Mrkvička, T.; Vašek, M.; Jůza, T.; Kratochvíl, M.; Peterka, J.; Draštík, V.; Křížek, J. Size Selectivity of Standardized Multimesh Gillnets in Sampling Coarse European Species. Fish Stock Assess. Methods Lakes Reserv. Towar. True Pict. Fish Stock. Conf. 2009, 96, 51–57. [Google Scholar] [CrossRef]
  10. Prchalová, M.; Kubečka, J.; Říha, M.; Litvín, R.; Čech, M.; Frouzová, J.; Hladík, M.; Hohausová, E.; Peterka, J.; Vašek, M. Overestimation of Percid Fishes (Percidae) in Gillnet Sampling. Fish. Res. 2008, 91, 79–87. [Google Scholar] [CrossRef]
  11. Prchalová, M.; Mrkvička, T.; Peterka, J.; Čech, M.; Berec, L.; Kubečka, J. A Model of Gillnet Catch in Relation to the Catchable Biomass, Saturation, Soak Time and Sampling Period. Fish. Res. 2011, 107, 201–209. [Google Scholar] [CrossRef]
  12. Olin, M.; Tiainen, J.; Kurkilahti, M.; Rask, M.; Lehtonen, H. An Evaluation of Gillnet CPUE as an Index of Perch Density in Small Forest Lakes. Ecol. Fish Lakes Reserv. 2016, 173 Pt 1, 20–25. [Google Scholar] [CrossRef] [Green Version]
  13. WFD Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 Establishing a Framework for the Community Action in the Field of Water Policy. 2000. Available online: https://www.eea.europa.eu/policy-documents/water-framework-directive-wfd-2000 (accessed on 13 March 2022).
  14. CEN European Standard EN 14 757; Water Quality—Sampling of Fish with Multimesh Gillnets. CEN European Standard: 2005; pp. 1–34. Available online: https://standards.globalspec.com/std/9929986/EN%2014757 (accessed on 13 March 2022).
  15. Deceliere-Vergès, C.; Argillier, C.; Lanoiselée, C.; De Bortoli, J.; Guillard, J. Stability and Precision of the Fish Metrics Obtained Using CEN Multi-Mesh Gillnets in Natural and Artificial Lakes in France. Fish. Res. 2009, 99, 17–25. [Google Scholar] [CrossRef]
  16. Hovgård, H.; Lassen, H. Manual on Estimation of Selectivity for Gillnet and Longline Gears in Abundance Surveys; FAO: Rome, Italy, 2000. [Google Scholar]
  17. Millar, R.B.; Holst, R. Estimation of Gillnet and Hook Selectivity Using Log-Linear Models. ICES J. Mar. Sci. 1997, 54, 471–477. [Google Scholar] [CrossRef] [Green Version]
  18. Holt, S.J. A Method for Determining Gear Selectivity and Its Application. ICNAF Spec. Publ. 1963, 5, 106–115. [Google Scholar]
  19. Baranov, F.I. Theory and Assessment of Fishing Gear; English Version Issued as Theory of Fishing with Gill Nets; Pishchepromizdat: Moscow, Russia, 1948; p. 45. [Google Scholar]
  20. Baranov, F.I. The Capture of Fish by Gillnets. Mater. Pozn. Russ. Rybolov. 1914, 3, 56–99. [Google Scholar]
  21. Kurkilahti, M.; Appelberg, M.; Hesthagen, T.; Rask, M. Effect of Fish Shape on Gillnet Selectivity: A Study with Fulton’s Condition Factor. Fish. Res. 2002, 54, 153–170. [Google Scholar] [CrossRef]
  22. Hamley, J. Review of Gillnet Selectivity. J. Fish. Res. Board Canada 1975, 32, 1943–1969. [Google Scholar] [CrossRef]
  23. Millar, R.B. Estimating the Size-Selectivity of Fishing Gear by Conditioning on the Total Catch. J. Am. Stat. Assoc. 1992, 87, 962–968. [Google Scholar] [CrossRef]
  24. Brenden, T.O.; Zhao, Y. Simulation-Based Evaluation of the Accuracy in Indirectly Estimating Gillnet Selectivity. Fish. Res. 2012, 134–136, 64–72. [Google Scholar] [CrossRef]
  25. Vandergoot, C.S.; Kocovsky, P.M.; Brenden, T.O.; Liu, W. Selectivity Evaluation for Two Experimental Gill-Net Configurations Used to Sample Lake Erie Walleyes. N. Am. J. Fish. Manag. 2011, 31, 832–842. [Google Scholar] [CrossRef]
  26. Treble, R.J.; Millar, R.B.; Walker, T.I. Size-Selectivity of Lobster Pots with Escapegaps: Application of the SELECT Method to the Southern Rock Lobster (Jasus edwardsii) Fishery in Victoria, Australia. Fish. Res. 1998, 34, 289–305. [Google Scholar] [CrossRef]
  27. Xu, X.; Millar, R.B. Estimation of Trap Selectivity for Male Snow Crab (Chionoecetes opilio) Using the SELECT Modeling Approach with Unequal Sampling Effort. Can. J. Fish. Aquat. Sci. 1993, 50, 2485–2490. [Google Scholar] [CrossRef]
  28. Poulsen, S.; Nielsen, J.R.; Holst, R.; Stæhr, K.-J. An Atlantic Herring (Clupea harengus) Size Selection Model for Experimental Gill Nets Used in the Sound (ICES Subdivision 23). Can. J. Fish. Aquat. Sci. 2000, 57. [Google Scholar] [CrossRef]
  29. Baremore, I.E.; Bethea, D.M.; Andrews, K.I. Gillnet Selectivity for Juvenile Blacktip Sharks (Carcharhinus limbatus). Fish. Bull. 2012, 110, 230–241. [Google Scholar]
  30. Giannetto, D.; Carosi, A.; Ghetti, L.; Pompei, L.; Viali, P.; Lorenzoni, M. Size Selectivity of Gill-Nets and Growth of Roach Rutilus rutilus (Linnaeus, 1758) an Alien Species in Piediluco Lake (Italy). Knowl. Manag. Aquat. Ecosyst. 2014, 413, 1–13. [Google Scholar] [CrossRef] [Green Version]
  31. Borgström, R. Direct Estimation of Gill-Net Selectivity for Roach (Rutilus rutilus (L.)) in a Small Lake. Fish. Res. 1989, 7, 289–298. [Google Scholar] [CrossRef]
  32. Jensen, J.W. Evaluating Catches of Salmonids Taken by Gillnets. J. Fish Biol. 1995, 46, 862–871. [Google Scholar] [CrossRef]
  33. Alonso, M.; Palau, A.; Pedrocchi, V.; Pau, R.; Palau-Nadal, A. Islas de Agua en Tierras de Sed: Lagos Esteparios. Medio Ambiente Iberia-Biodiversidad, I+D+i Ambiental y Recursos Hídricos. 2015. Available online: https://www.scribd.com/document/375114869/Islas-de-Agua-en-Tierras-de-Sed-Lagos-Esteparios-pdf (accessed on 13 March 2022).
  34. Kurkilahti, M.; Appelberg, M.; Bergstrand, E.; Enderlein, O. An Indirect Estimate of Bimodal Gillnet Selectivity of Smelt. J. Fish Biol. 1998, 52, 243–254. [Google Scholar] [CrossRef]
  35. Millar, R.B. Untangling the Confusion Surrounding the Estimation of Gillnet Selectivity. Can. J. Fish. Aquat. Sci. 2000, 57, 507–511. [Google Scholar] [CrossRef]
  36. R Development Core Team. R: A Language and Environment for Statistical Computing; R Version 4.0.2—“Taking Off Again”; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
  37. Millar, R.B. SELECT. R Code for Fitting Models to Gillnet Data. Available online: https://www.stat.auckland.ac.nz/~millar/selectware/code.html (accessed on 12 April 2019).
  38. Millar, R.B. Selectivity Software and Documentation. Available online: www.stat.auckland.ac.nz/~millar/selectware/code.html (accessed on 2 June 2017).
  39. Crawley, M.J. The R Book, 2nd ed.; John Wiley & Sons, Ltd.: Sussex, UK, 2013; ISBN 9780470973929. [Google Scholar]
  40. Lappalainen, J.; Dörner, H.; Wysujack, K. Reproduction of Pikeperch (Sander lucioperca (L.)): A Review. Ecol. Freshw. Fish 2003, 12, 95–106. [Google Scholar] [CrossRef]
  41. Erzini, K.; Gonçalves, J.M.S.; Bentes, L.; Lino, P.G.; Ribeiro, J.; Stergiou, K.I. Quantifying the Roles of Competing Static Gears: Comparative Selectivity of Longlines and Monofilament Gill Nets in a Multi-Species Fishery of the Algarve (Southern Portugal). Sci. Mar. 2003, 67, 341–352. [Google Scholar] [CrossRef]
  42. Fujimori, Y.; Tokai, T. Estimation of Gillnet Selectivity Curve by Maximum Likelihood Method. Fish. Sci. 2001, 67, 644–654. [Google Scholar] [CrossRef] [Green Version]
Hydrobiology 01 00017 g001 550
Figure 1. Estany d’Ivars I Vila-sana shallow lake in Catalonia (NE Spain), located in the middle of the plain of Urgell. Numbers 1–6 indicate gillnets positions.
Figure 1. Estany d’Ivars I Vila-sana shallow lake in Catalonia (NE Spain), located in the middle of the plain of Urgell. Numbers 1–6 indicate gillnets positions.
Hydrobiology 01 00017 g001
Hydrobiology 01 00017 g002 550
Figure 2. Number of captured fish per length class of three fish species in the Estany d’Ivars I Vila-sana shallow lake for different gillnet mesh sizes (lines are stretched mesh in mm). Number of captured fish per length class are log10 transformed for Sander lucioperca. Counts are given as pooled over the 8-year sampling period.
Figure 2. Number of captured fish per length class of three fish species in the Estany d’Ivars I Vila-sana shallow lake for different gillnet mesh sizes (lines are stretched mesh in mm). Number of captured fish per length class are log10 transformed for Sander lucioperca. Counts are given as pooled over the 8-year sampling period.
Hydrobiology 01 00017 g002
Hydrobiology 01 00017 g003 550
Figure 3. Fitted gillnet selectivity curves for three exotic invasive fish species from the Estany d’Ivars I Vila-sana shallow lake. Model shown with best fit for each species (see Table 1). The first curve is for 6.25 mm mesh (stretched), the second for 8 mm mesh, and so on consecutively (see legend of Figure 2 for mesh sizes). In deviance residual plots, solid circles represent positive residuals and open circles negative ones. The area of the circles is proportional to the square of the residual.
Figure 3. Fitted gillnet selectivity curves for three exotic invasive fish species from the Estany d’Ivars I Vila-sana shallow lake. Model shown with best fit for each species (see Table 1). The first curve is for 6.25 mm mesh (stretched), the second for 8 mm mesh, and so on consecutively (see legend of Figure 2 for mesh sizes). In deviance residual plots, solid circles represent positive residuals and open circles negative ones. The area of the circles is proportional to the square of the residual.
Hydrobiology 01 00017 g003
Table
Table 1. Fitting results of different models (normal location, normal scale, Gamma, log-normal, binormal and bi-lognormal models) of gillnet selectivity with the SELECT method for 3 exotic invasive species from the Estany d’Ivars I Vila-sana shallow lake.
Table 1. Fitting results of different models (normal location, normal scale, Gamma, log-normal, binormal and bi-lognormal models) of gillnet selectivity with the SELECT method for 3 exotic invasive species from the Estany d’Ivars I Vila-sana shallow lake.
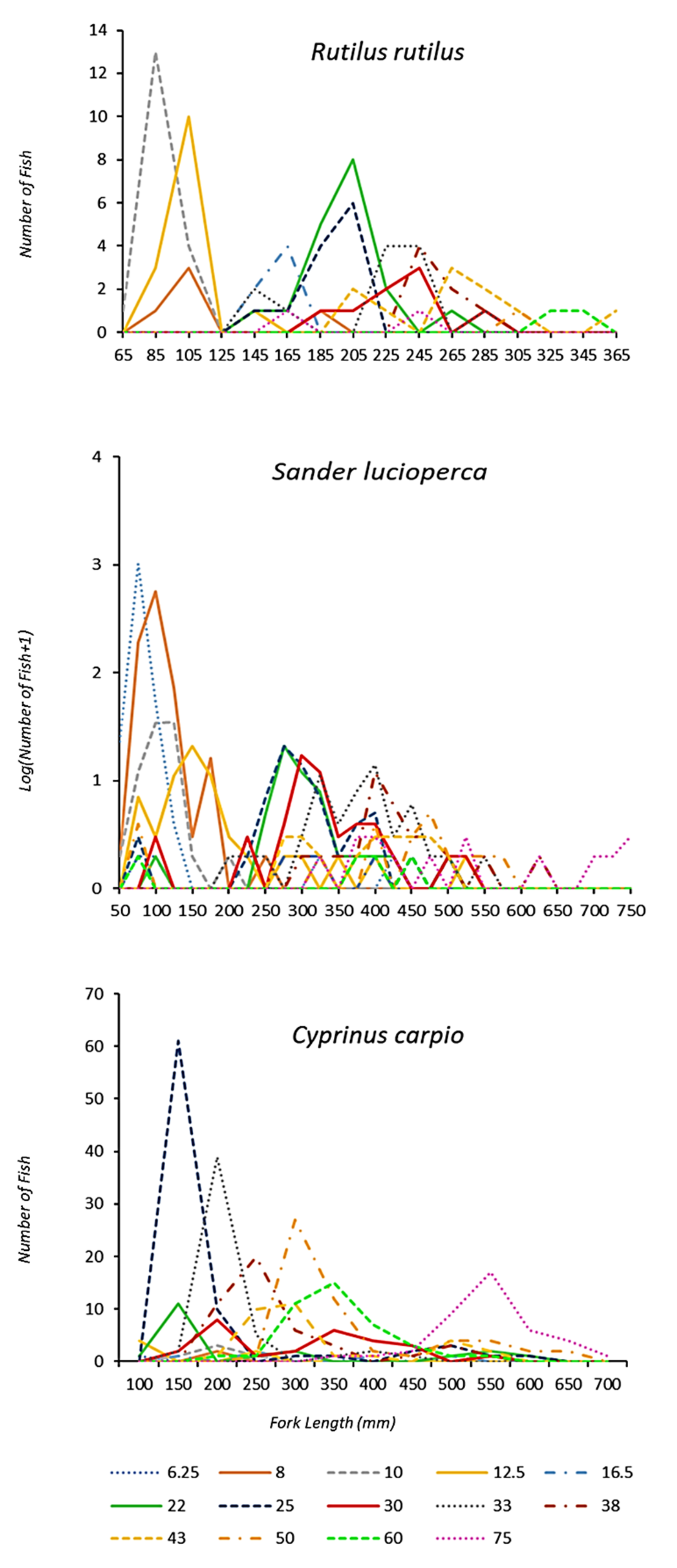
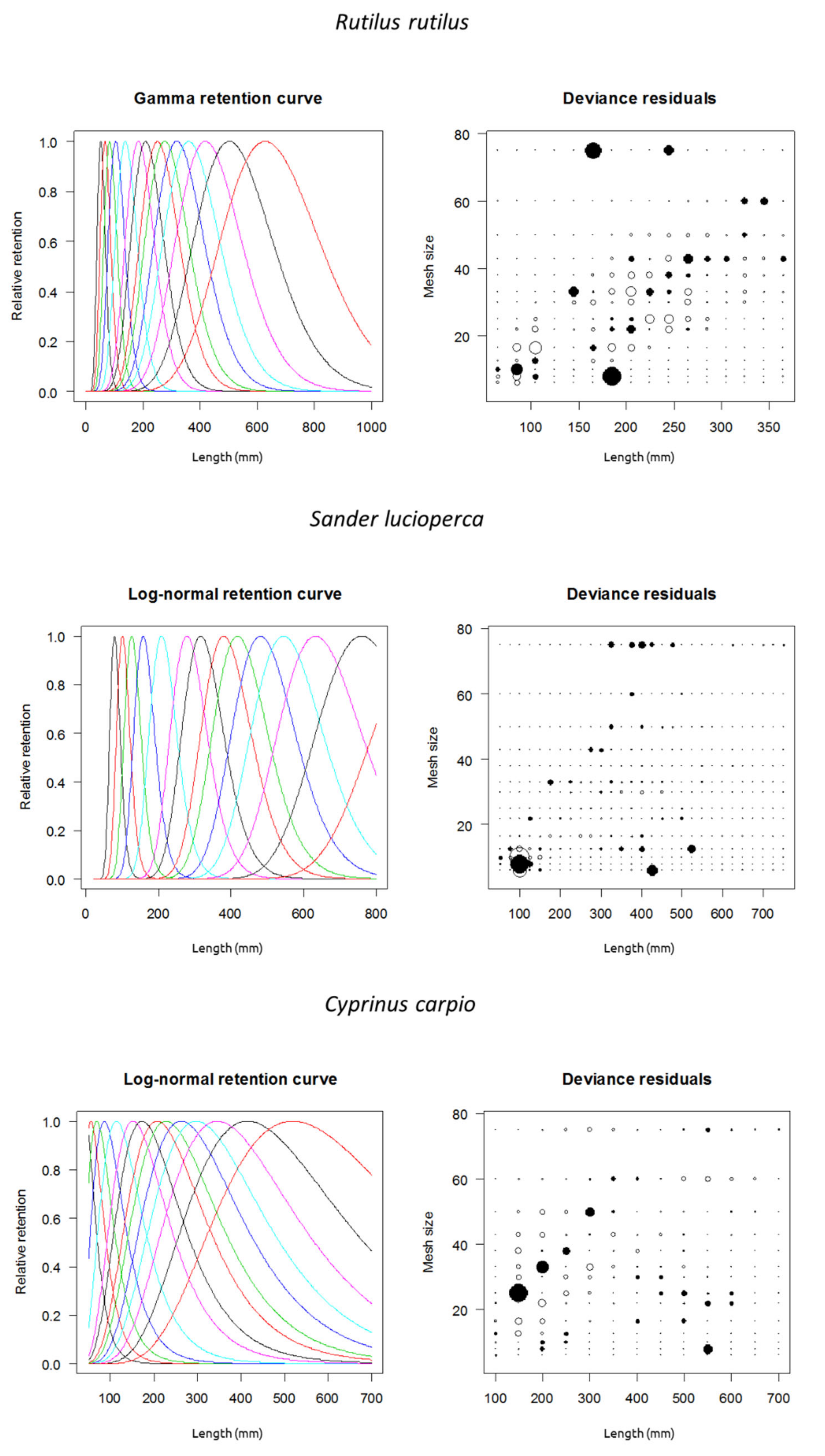
Fish SpeciesCommon NamenModelMode 1Std_Dev 1Mode 2Std_Dev 2Deviance 3d.f.p 4
Rutilus rutilusCommon roach115Normal Location43.10 ± 1.4163.19 ± 4.97NANA233.902060.089
Normal scale56.52 ± 1.5114.34 ± 0.97NANA185.502060.844
Gamma52.37 ± 1.4314.88 ± 1.20NANA168.492060.974
Log-normal50.53 ± 1.4216.55 ± 1.63NANA170.902060.964
Binormal scale54.01 ± 1.2311.68 ± 0.81144.53 ± 0.260.16 ± 0.31141.451900.848
Bi-lognormal50.99 ± 1.118.80 ± 1.7347.46 ± 7.4446.60 ± 29.10141.331900.925
Sander luciopercaPikeperch3583Normal Location78.14 ± 0.5948.57 ± 0.99NANA4945.11375<0.0001
Normal scale84.06 ± 0.4214.63 ± 0.21NANA1417.08375<0.0001
Gamma80.31 ± 0.3814.41 ± 0.25NANA1234.17375<0.0001
Log-normal79.08 ± 0.3815.08 ± 0.30NANA1229.54375<0.0001
Binormal scale79.47 ± 0.3011.11 ± 0.16187.44 ± 13.2251.84 ± 4.49867.533330.952
Bi-lognormal76.91 ± 0.3211.62 ± 0.27117.48 ± 11.3390.69 ± 24.26865.973330.959
Cyprinus carpioCommon carp407Normal Location41.73 ± 1.20116.23 ± 4.63NANA665.62167<0.0001
Normal scale−177.68 ± 216.12121.24 ± 49.81NANA769.79167<0.0001
Gamma45.04 ± 1.7527.88 ± 1.68NANA673.16167<0.0001
Log-normal43.21 ± 1.1624.94 ± 1.68NANA584.79167<0.0001
Binormal scale39.72 ± 0.384.92 ± 0.2991.45 ± 16.5279.18 ± 14.34314.571640.946
Bi-lognormal38.70 ± 0.354.84 ± 0.3368.87 ± 6.2664.25 ± 12.22265.501640.926
1 Mode and standard deviation for the retention curve of the first mesh. 2 Second mode and standard deviation for the retention curve of the first mesh Only available for bimodal models. 3 Deviance statistic measures goodness of fit (lowest deviance, in bold, indicates a better fit) and is distributed as a Chi-square statistic. 4 If the model fits (p > 0.05) in bold. Note: When it is required: Value ± Standard Error. NA: Not Applicable.
Table
Table 2. Predicted modal fork length (mm) of 3 fish species for different gillnet mesh sizes (stretched) in the Estany d’Ivars I Vila-sana shallow lake. Selectivity model with best fit was used to estimate modal lengths (NS = normal scale; NL = normal location; GM = Gamma; LG = log-normal; BN = binormal; BL = bi-lognormal). Only modal lengths less than approx. known maximum length of species given. Mean and range of observed FL for each species also given.
Table 2. Predicted modal fork length (mm) of 3 fish species for different gillnet mesh sizes (stretched) in the Estany d’Ivars I Vila-sana shallow lake. Selectivity model with best fit was used to estimate modal lengths (NS = normal scale; NL = normal location; GM = Gamma; LG = log-normal; BN = binormal; BL = bi-lognormal). Only modal lengths less than approx. known maximum length of species given. Mean and range of observed FL for each species also given.
Fish SpeciesBest Fit ModelMesh Size (mm)Mean FL (mm)Range (mm)
281012.516.5222530333843506075
Rutilus rutilusBL55.070.488.0110.0145.2193.6220.0264.0290.4334.4378.4440.0528.0660.0170.9665–354
Sander luciopercaBL72.693.0116.2145.3191.7255.6290.5348.6383.5441. 6499.7581.0697.2871.593.1347–738
Cyrpinus carpioBL30.338.748.460.579.9106.5121.0145.2159.7183.9208.1242.0290.4363.0279.7165–664
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Sánchez-González, J.R.; Casals, F. Gillnet Selectivity for Three Freshwater Alien Invasive Fish Species in a Long-Term Monitoring Scenario. Hydrobiology 2022, 1, 232-242. https://doi.org/10.3390/hydrobiology1020017

AMA Style

Sánchez-González JR, Casals F. Gillnet Selectivity for Three Freshwater Alien Invasive Fish Species in a Long-Term Monitoring Scenario. Hydrobiology. 2022; 1(2):232-242. https://doi.org/10.3390/hydrobiology1020017

Chicago/Turabian Style

Sánchez-González, Jorge Rubén, and Frederic Casals. 2022. "Gillnet Selectivity for Three Freshwater Alien Invasive Fish Species in a Long-Term Monitoring Scenario" Hydrobiology 1, no. 2: 232-242. https://doi.org/10.3390/hydrobiology1020017

APA Style

Sánchez-González, J. R., & Casals, F. (2022). Gillnet Selectivity for Three Freshwater Alien Invasive Fish Species in a Long-Term Monitoring Scenario. Hydrobiology, 1(2), 232-242. https://doi.org/10.3390/hydrobiology1020017

Article Metrics

Back to TopTop