A Two-Stage Numerical Algorithm for the Simultaneous Extraction of All Zeros of Meromorphic Functions

Abstract

In this paper, we present an effective two-stage numerical algorithm for the simultaneous finding of all roots of meromorphic functions in a region within the complex plane. At the first stage, we construct a polynomial with the same roots as the ones of the considered function; at the next step, we apply some method for the simultaneous approximation of its roots. To show the efficiency and applicability of our algorithm together with its advantages over the classical Newton, Halley and Chebyshev’s iterative methods, we conduct three numerical examples, where we apply it to two test functions and to an important engineering problem.

1. Introduction

Suppose that $f:\mathbb{C}\to \mathbb{C}$ is an arbitrary function. Solving the equation

$$f\left(x\right)=0$$

(1)

is one of the main tasks that arises from the real world problems. It is well known that iteration methods are among the most efficient tools for solving (1). Undoubtedly, the most famous among them are Newton’s method, Halley’s method [1] and Chebyshev’s method [2]. Convergence analysis and some historical notes about these methods applied to simple and multiple zeros of analytic functions can be found in [3,4,5]. However, it could be a very difficult task to find all the roots of (1), or even detect their number, within a given finite region applying iterative methods that involve derivatives of f. A simple example is the function $f\left(x\right)=\sqrt{x}$ which root is zero but the mentioned methods might not find it because its first derivative has singularity at $x=0$.

The polynomials are quite a different case. The iteration methods for polynomial zeros have drawn a great interest among the mathematicians in the last 70 years (see, e.g., [6,7,8] and the references therein). In particular, detailed convergence analysis of Newton, Halley and Chebyshev’s methods for simple and multiple polynomial zeros has been conducted in the recent papers [9,10,11,12]. Let $P\left(x\right)=a_0{x}^n+a_1{x}^{n-1}+\cdots +a_n$ be a complex polynomial of degree $n\ge 1$. In 1891, Weierstrass [13] offered a different approach for finding the zeros of P, namely to compute all of them at once, i.e., simultaneously. He established and studied the first simultaneous method which can be defined as follows:

$$x^{(k+1)}=x^{\left(k\right)}-W\left(x^{\left(k\right)}\right),k=0,1,2,\dots ,$$

(2)

where the Weierstrass iteration function $W:\mathcal{D}\subset {\mathbb{C}}^n\to {\mathbb{C}}^n$ is given by $W\left(x\right)=(W_1\left(x\right),\dots ,$$W_n\left(x\right))$ with

$$W_i\left(x\right)={\displaystyle \frac{P\left(x_i\right)}{a_0{\prod }_{j\ne i}(x_i-x_j)}}(i=1,\dots ,n),$$

(3)

where $\mathcal{D}$ denotes the set of all vectors in ${\mathbb{C}}^n$ with pairwise distinct components. The second simultaneous method in the literature is due to Bulgarian mathematicians Dochev and Byrnev [14], and the third one is due to Ehrlich [15] in 1967 and was rediscovered by Börsch-Supan [16] in 1970.

The approximation of analytic functions by polynomials has a very long history associated with the works of Taylor, Euler, Lagrange and Newton since the early 18th century. However, a great disadvantage of such an approach is that the zeros of f may bear no relation with those of its approximation P. An obvious example is

$$f\left(x\right)=e^x\mathrm{with}P\left(x\right)=\sum _{i=0}^n{\displaystyle \frac{x^i}{i!}}.$$

Therefore, to reduce the solving of (1) to the solving of some polynomial equation, many authors have attempted to find a polynomial that has exactly the same zeros as f in some domain within the complex plane (see, e.g., [17,18,19]). In 1995, Tovmasyan and Kosheleva summarized the results in this direction in the following theorem:

Theorem 1

([20] Theorem 1). Let $D\subset \mathbb{C}$ be an $(n+1)$-connected domain with closure Γ, the function $f:\mathbb{C}\to \mathbb{C}$ be analytic in D, and let P be a monic polynomial of degree $n\ge 1$ with coefficients

$$a_l=-{\displaystyle \frac{1}{l}}\sum _{j=0}^{l-1}{a}_j{c}_{l-j},l=1,\dots ,n,$$

(4)

where

$$c_0=n\mathit{and}{c}_k={\displaystyle \frac{1}{2\pi \mathrm{i}}}{\int }_{\mathrm{\Gamma }}{\displaystyle \frac{z^k{f}^{\prime }\left(z\right)}{f\left(z\right)}}dz,k=1,2,\dots .$$

Then, the zeros of f in D coincide with the zeros of P.

In order to avoid using the derivatives of f, we reformulate this theorem in the following equivalent form (see also [21]):

Theorem 2.

Let the assumptions of Theorem 1 be fulfilled with

$$c_k={\displaystyle \frac{1}{2\pi i}}\left(i{z}^{k}Argf\left(z\right){|}_{\mathrm{\Gamma }}-k{\int }_{\mathrm{\Gamma }}{z}^{k-1}lnf\left(z\right)dz\right),k=1,2,\dots .$$

Then, the zeros of f in D coincide with the ones of P.

Proof. 

The proof follows immediately from Theorem 1 because of the identity

$${\int }_{\mathrm{\Gamma }}{\displaystyle \frac{z^k{f}^{\prime }\left(z\right)}{f\left(z\right)}}dz=z^k(ln|f\left(z\right)|+iArgf\left(z\right)){|}_{\mathrm{\Gamma }}-k{\int }_{\mathrm{\Gamma }}{z}^{k-1}lnf\left(z\right)dz=i{z}^{k}Argf\left(z\right){|}_{\mathrm{\Gamma }}-k{\int }_{\mathrm{\Gamma }}{z}^{k-1}lnf\left(z\right)dz.$$

   □

Obviously, the main drawback of Theorem 2 is that it only pertains to analytic functions but not to meromorphic functions, which, as a larger class of functions, have many more applications in natural sciences, engineering and others. The problem of locating the zeros and poles of meromorphic functions also has a long history. Since 1932, many authors proposed different numerical techniques to solve this problem; however, most of them are either ill-conditioned or computationally high-cost because of generating orthogonal polynomials for certain bilinear forms, deal with Vandermonde or Hankel matrices, embedding additional refinement mechanisms, etc. (see, e.g., [22,23,24] and references therein).

In this paper, we propose a new two-stage numerical algorithm for the simultaneous determination of all roots of Equation (1) in a region $D^{\ast }\subset \mathbb{C}$ whenever f is meromorphic in $D^{\ast }$. Our algorithm unites and refines several well-known techniques in an effective and easy implementable procedure. More precisely, at the first stage, only by tracking the phase of f ($Argf$), we find a domain $D\subset D^{\ast }$, where f is analytic. Then, using Theorem 2, we compute the coefficients of a polynomial P, which has the same zeros as f in D. At the second stage, we implement a method for the simultaneous approximation of all the zeros of P. In summary, the main novelties and advantages of our study are as follows:

(i)

We use a new effective empirical method for locating the poles of f only by tracking its phase;

(ii)

Our algorithm may not require the computation of any derivatives, depending on the choice of the method at the second stage;

(iii)

We compute all the zeros of f at once with high accuracy.

2. Description of the Algorithm

In this section, we first provide a general description of our algorithm. Then, we implement it using some particular approaches at certain steps.

2.1. The General Algorithm

Let the function $f:\mathbb{C}\to \mathbb{C}$ be meromorphic in a closed region $D^{\ast }\subset \mathbb{C}$ with closure ${\mathrm{\Gamma }}^{\ast }$.

• Stage 1. Take a rectangle containing the domain $D^{\ast }$ and compute $ln\left|f\right(z\left)\right|$ in any node of a mesh of $p\times q$ points. Identifying the points where $ln\left|f\right(z\left)\right|>K$, for a preselected real number K (a suitable choice is $K>1$), cover the rectangle with squares or circles with side (radius) r, which is preselected depending on the function f, namely, the closer the poles or the poles and roots of f are to each other, a smaller r should be chosen. To sift out the false poles, we track the changing of $Argf\left(z\right)$ on these squares (circles). Note that, $Argf\left(z\right)$ decreases around a pole. If more than one pole or pole with roots are detected in some of the squares, we chose a smaller r and track the changing of $Argf\left(z\right)$ on the newly taken squares (circles). This procedure is repeated until we isolate all the poles of f. Then, by setting $D_1,\dots ,D_s$ to be the domains containing the poles of f, we obtain a domain

  $$D=D^{\ast }\setminus (D_1\cup \cdots \cup D_s)$$

  in which the function f is analytic. Finally, setting Γ to be the closure of D and applying Theorem 2, we obtain the coefficients $a_1\dots a_n$ of the corresponding polynomial P.

• Stage 2.  Choose an initial vector $x^{\left(0\right)}\in {\mathbb{C}}^n$ and a simultaneous method to apply it for computing all the zeros of P.

2.2. Our Implementation

• Stage 1. In our implementation, we consider $D^{\ast }$ as a square with side R meshed by $8000\times 8000$ points and cover it with circles with radius r which is different in the different examples. Identifying the nodes with $ln\left|f\right(z\left)\right|>1.1$, on any of the circles we apply Cauchy’s argument principle and track the continuity of $Argf\left(z\right)$ by the function unwrap(angle(f)) of MATLAB in order to detect the number of poles in it. Thus, we extract the domain D in which the function f is analytic. Then, computing the integrals in Theorem 2 by the vectorized adaptive quadrature ([25]), we get the coefficients of the polynomial P.

• Stage 2.  Using the second coefficient $a_1$ and the degree n of the polynomial P, we generate Aberth’s initial approximation (see [26]) $x^{\left(0\right)}\in {\mathbb{C}}^n$, which is given as follows:

  $$x_{\nu }^{\left(0\right)}=-{\displaystyle \frac{a_1}{n}}+r_{0}exp\left(i{\theta }_{\nu }\right),{\theta }_{\nu }={\displaystyle \frac{\pi }{n}}\left(2\nu -{\displaystyle \frac{3}{2}}\right),\nu =1,\dots ,n,$$

  (5)

  where $r_0=R/2$. Then, in order to avoid any usage of derivatives, we use the following family of cubically convergent simultaneous methods that has been constructed and studied in [27,28]:

  $$x^{(k+1)}=T_{\alpha }\left(x^{\left(k\right)}\right),k=0,1,2,\dots$$

  (6)

  with the iteration function $T_{\alpha }$ being defined by

  $$T_{\alpha }\left(x\right)=(T_1\left(x\right),\dots ,T_n\left(x\right))\mathit{with}{T}_i\left(x\right)=x_i-W_i\left(x\right){\displaystyle \frac{{\displaystyle 1+(\alpha -1)\sum _{j\ne i}\frac{W_j\left(x\right)}{x_i-x_j}}}{{\displaystyle 1+\alpha \sum _{j\ne i}\frac{W_j\left(x\right)}{x_i-x_j}}}},$$

  (7)

  where $\alpha \in \mathbb{C}$, while W is the above-defined Weierstrass correction.

Remark 1.

At the second step, different ways for choosing the initial guess can be used, e.g., to take its coordinates randomly from D (see, for example, [29] and the references therein).

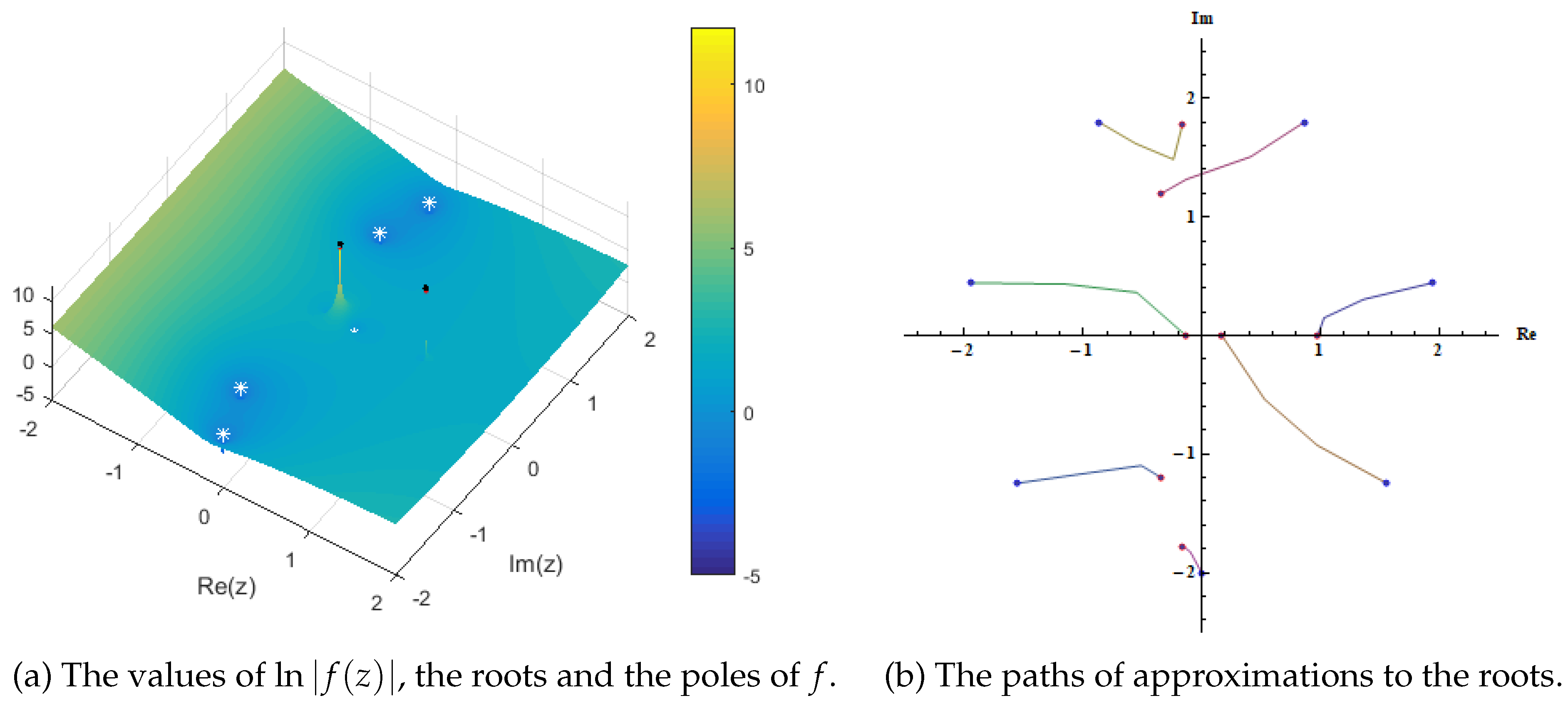
3. Numerical Examples

In this section, we apply our algorithm to some functions that cause problems for the classical iteration methods, such as Newton, Halley and Chebyshev’s ones. In order to obtain higher precision in extracting the poles and the roots of the considered functions, we use a mesh of $8000\times 8000$ points and origin-centered squares with sides 4 and $2.6$ for Example 1 and Example 2, respectively, while a square with side $0.6$ centered in $0.9$ is used in Example 3. At the second stage, we apply the family (6) with $\alpha =1$, which, in fact, is the famous Ehrlich’s method [15] that is also known as Börsch-Supan’s one [16], and we implement the following a posteriori error estimate ([29], Corollary 4.2):

• A posteriori error estimate.  Let P be a complex polynomial of degree $n\ge 2$ and let ${\left(x^{\left(k\right)}\right)}_{k=0}^{\infty }$ be a sequence of vectors in ${\mathbb{C}}^n$ with pairwise distinct coordinates. Then, for every $k\ge 0$, there is a vector $\xi \in {\mathbb{C}}^n$ of the roots of f such that

  $$E\left(x^{\left(k\right)}\right)={∥{\displaystyle \frac{W\left(x^{\left(k\right)}\right)}{d\left(x^{\left(k\right)}\right)}}∥}_{\infty }<\tau \Rightarrow \parallel x^{\left(k\right)}{-\xi \parallel }_{\infty }\le {\epsilon }_k=\mathrm{\Phi }\left(E\left(x^{\left(k\right)}\right)\right){\parallel W\left(x^{\left(k\right)}\right)\parallel }_{\infty },$$

  where the number τ and the function $\mathrm{\Phi }:[0,\tau ]\to {\mathbb{R}}_{+}$ are defined by

  $$\tau ={\displaystyle \frac{1}{{(1+\sqrt{n-1})}^2}}\mathit{and}\mathrm{\Phi }\left(t\right)={\displaystyle \frac{2}{1-(n-2)t+\sqrt{{(1-(n-2)t)}^2-4t}}}.$$

Using this error estimate, we apply the following stopping criterion:

$$E\left(x^{\left(k\right)}\right)<\tau \mathrm{and}{\epsilon }_k<{10}^{-10}.$$

(8)

Moreover, to show the convergence behavior of Newton, Halley and Chebyshev’s methods, when applied to the chosen functions, we define the quantity ${ϵ}_k=|z_k-z_{k+1}|$ for all $k\ge 0$ and we use the stopping criterion ${ϵ}_k<{10}^{-10}$ (see

Table 1. Convergence of Newton, Halley and Chebyshev’s methods for Examples 1–3.

Function	Method	Initial Guess	Root	k	${\mathit{ϵ}}_{\mathit{k}}$
	Newton	$0.999990+0.044504i$	$-0.349178+1.194062i$	14	$3.852\times {10}^{-13}$
$f_1$	Halley	$0.000669-0.445041i$	$-1.413711-3.573154i$	6	$1.872\times {10}^{-20}$
	Chebyshev	$0.999990+0.044504i$	The method diverges
	Newton	$0.000001-0.001136i$	$-0.001$	5	$1.643\times {10}^{-14}$
$f_2$	Halley	$0.000001-0.001136i$	$-0.001$	4	$1.135\times {10}^{-12}$
	Chebyshev	$0.000001-0.001136i$	$-0.001$	4	$4.644\times {10}^{-14}$
	Newton	$0.703493+0.042135i$	The method diverges
$f_3$	Halley	$0.703493+0.042135i$	$0.757396$	3	$1.323\times {10}^{-22}$
	Chebyshev	$0.703493+0.042135i$	The method diverges

).

In the tables below, for any of the examples, we give the values of k, $E\left(x^{\left(k\right)}\right)$, $\tau$, ${\epsilon }_k$, ${ϵ}_k$ and ${\epsilon }_{k+1}$. All numbers in the remainder are given with at least six decimal digits.

In our first example, we take a function from [30] that causes many problems for the famous Newton, Halley and Chebyshev’s methods.

Example 1

([30] Example 3). Consider the following function:

$$f_1\left(z\right)={\displaystyle \frac{1}{z^2(z-1)(z^2+9)}}+zsinz+e^{-3z}+4$$

with poles 0 and 1 and with roots $-0.163231\pm 1.778842i,-0.349178\pm 1.194062i,0.978436,0.169748,$$-0.133271$ in the circle $\left|z\right|\le 2$.

At the first stage, we obtain the corresponding polynomial of $f_1$ as follows:

$$P_1\left(x\right)=x^7+0.009906x^6+3.939586x^5-2.271493x^4+2.251773x^3-4.866621x^2+0.125048x+0.109315$$

(9)

and we use Aberth’s initial vector (5) with $n=7$, $a_1=0.009906$ and $r_0=2$.

No matter the rough initial guess, one can see from

Table 2. Numerical data for Examples 1–3.

Polynomial	k	${\mathit{E}}_{\mathit{f}}\left({\mathit{x}}^{\left(\mathit{k}\right)}\right)$	$\mathit{\tau }$	${\mathit{\epsilon }}_{\mathit{k}}$	${\mathit{\epsilon }}_{\mathit{k}+1}$
$P_1$	6	$8.77\times {10}^{-12}$	$0.084040$	$5.384\times {10}^{-12}$	$2.875\times {10}^{-34}$
$P_2$	10	$1.037\times {10}^{-11}$	$0.171573$	$1.036\times {10}^{-14}$	$1.116\times {10}^{-36}$
$P_3$	4	$1.481\times {10}^{-25}$	$0.25$	$5.060\times {10}^{-26}$	$1.110\times {10}^{-75}$

that the stopping criterion (8) is satisfied at the sixth iteration with an error estimation that is less than ${10}^{-11}$. At the next iteration, the roots are found with an accuracy of ${10}^{-34}$.

We have to note that trying to find the zeros of $f_1$ Chebyshev’s method diverges when starting from the initial point $0.999990+0.044504i$ (see Table 1) while starting from $1.948440+0.445041i$ it converges to the root outside the circle. What for Newton and Halley’s methods, it is seen by Table 1 that Halley’s method ‘jumps out of the circle’ starting from the initial guess $0.000669-0.445041i$ no matter its closeness to the roots inside and Newton’s method finds the root $-0.349178+1.194062i$ instead of someone closer to the initial guess. In fact, all three methods encounter difficulties to find the root $0.978436$ maybe because of its closeness to a pole.

In Figure 1a,b, the values of $ln|f_1\left(z\right)|$ and the trajectories of approximations to the roots are shown. On the left, the white stars depict the zeros, while the black ones are the poles of f. On the right, blue points depict the initial guess, and the red ones are the roots.

To show the high precision of our algorithm, for the next example, we constructed a function with very close poles and zeros.

Example 2.

We consider the function

$$f_2\left(z\right)={\displaystyle \frac{(z+0.001)(z-1.001-0.2i)sinz}{e^z-e^{0.0005}}}$$

in the circle $\left|z\right|\le 1.3$.

We obtain its corresponding polynomial as

$$P_2\left(x\right)=x^3-(1+0.2i)x^2-(0.001+0.0002i)x+5.991\times {10}^{-11}-3.765\times {10}^{-10}i$$

(10)

and we use Aberth’s initial approximation (5) with $r_0=1.3$.

One can see from Table 2 that the stopping criterion (8) is satisfied at the tenth iteration with an error estimation less than ${10}^{-13}$, and at the eleventh step all the roots are found with an accuracy of ${10}^{-36}$. On the other hand, both Halley and Chebyshev’s methods run into great difficulties to find the root 0 of $f_2$. One can see from Table 1, that regardless of how close the initial guess is to 0 the three methods converge to another root.

As in the previous example, in Figure 2a,b, we plot the values of $ln|f_2\left(z\right)|$ and the trajectories of approximations to the roots.

In the last example, we consider a function that models an important chemical engineering problem which has been studied in ([31], Problem 7). It is worth noting that the mentioned authors, being unable to solve the problem directly due to its singularities, have transformed it into a much suitable transcendental function. In our example, a solution of the basic problem is given.

Example 3

(Fractional conversion in a reactor [5,31]). The fractional chemical conversion in a reactor is described by the following function:

$$f_3\left(z\right)={\displaystyle \frac{z}{1-z}}-5ln\left({\displaystyle \frac{0.4(1-z)}{0.4-0.5z}}\right)+4.45977,$$

where z is the fractional conversion of the limiting reactant. We consider $f_3$ in the circle with center $0.9$ and radius $0.3$ which contains its zeros $0.757396$ and $1.098983$.

At the first step, we get the following corresponding polynomial:

$$P_3\left(x\right)=x^2-1.856380x-0.832366$$

(11)

and then we use Aberth’s initial approximation (5) with $r_0=0.3$.

One can see from Table 2 that the stopping criterion (8) is satisfied at the fourth iteration with an error estimation less than ${10}^{-24}$ and at the next step all the roots are found with an accuracy of ${10}^{-75}$. For Chebyshev’s method or even for Newton’s one there are infinitely many divergent points in the considered region. An example is the point $0.703493+0.042135i$ no matter its closeness to one of the roots (see Table 1).

The values of $ln|f_3\left(z\right)|$ and the trajectories of approximations to the roots are plotted in Figure 3a and Figure 3b, respectively.

4. Conclusions

We have united and refined several previous approaches into a new effective and easy implementable two-step numerical algorithm for the simultaneous extraction of all the zeros of a meromorphic function f in a certain domain within the complex plane. Our method involves some simple techniques for excluding the poles and finding the roots of f without a need of computing any of its derivatives. To show the advantages and applicability of our method, we have conducted three examples, where we apply it to two test functions and to a chemical engineering problem for which the famous Newton, Halley and Chebyshev’s iterative methods fail or run into great difficulties in finding some of the roots. Our method face no difficulties to extract all the roots of ill-conditioned functions with high precision but the manual adjustment of the parameters at the first stage cause a bit of inconvenience. Our approach could be further extended for finding the roots of multivariate functions and system of linear equations.