Advanced ILC Analysis of Switched Systems Subject to Non-Instantaneous Impulses Using Composite Fractional Derivatives
Abstract
1. Introduction
2. System Description
3. P-Type ILC
3.1. Open-Loop Case
- Case (i).
- Case (ii).
- Case (iii).
3.2. Closed-Loop Case
- Case (i).
- Case (ii).
- Case (iii).
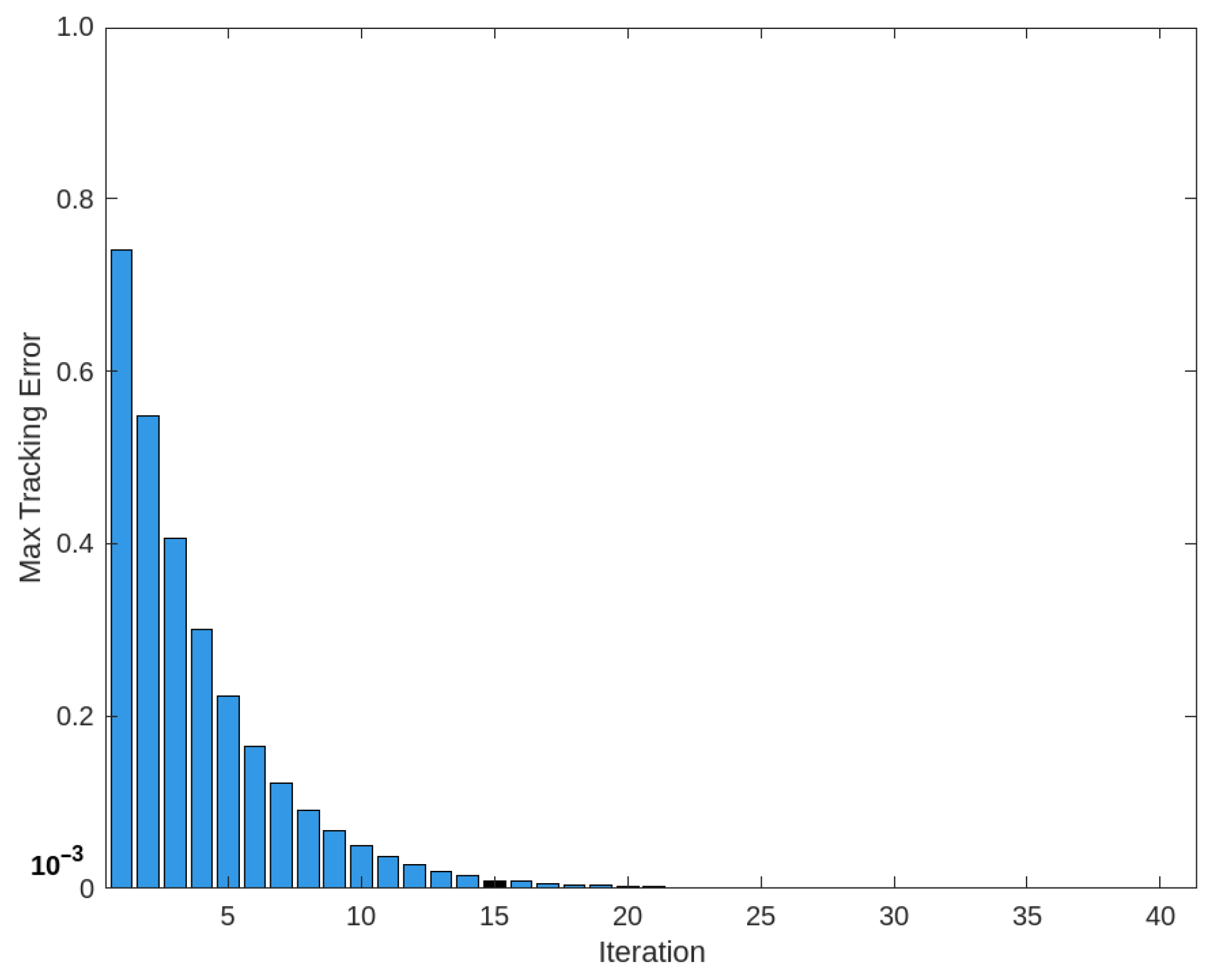
4. An Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Technical University of Kosice: Kosice, Slovak Republic, 1999. [Google Scholar]
- Zhou, Z.; Gong, W. Finite element approximation of optimal control problems governed by time fractional diffusion equation. Comput. Math. Appl. 2016, 71, 301–318. [Google Scholar] [CrossRef]
- Karthikeyan, K.; Karthikeyan, P.; Chalishajar, D.N.; Raja, D.S. Analysis on ψ-Hilfer fractional impulsive differential equations. Symmetry 2021, 13, 1895. [Google Scholar] [CrossRef]
- Johnson, M.; Kavitha, K.; Chalishajar, D.; Malik, M.; Vijayakumar, V.; Shukla, A. An analysis of approximate controllability for Hilfer fractional delay differential equations of Sobolev type without uniqueness. Nonlinear Anal. Model. Control 2023, 45, 1086–1107. [Google Scholar] [CrossRef]
- Hussain, S.; Sarwar, M.; Malaiki, N.; Azmi, F. Existence and controllability of fractional semilinear mixed Volterra-Fredholm integro-differential equation. Alex. Eng. J. 2023, 73, 259–267. [Google Scholar] [CrossRef]
- Khan, A.; Shah, K.; Abdeljawad, T.; Alqudah, M.A. Existence of results and computational analysis of a fractional order two strain epidemic model. Results Phys. 2022, 39, 1–11. [Google Scholar] [CrossRef]
- Kusnezov, D.; Bulgac, A.; Dang, G.D. Quantum Levy processes and fractional kinetics. Phys. Rev. Lett. 1999, 82, 1136–1139. [Google Scholar] [CrossRef]
- Baleanu, D.; Hasanabadi, M.; Vaziri, A.M.; Jajarmi, A. A new intervention strategy for an HIV/AIDS transmission by a general fractional modeling and an optimal control approach. Chaos Solitons Fractals 2023, 167, 113078. [Google Scholar] [CrossRef]
- Hussain, S.; Sarwar, M.; Nisar, K.S.; Shah, K. Controllability of fractional differential evolution equation of order γ∈(1, 2) with nonlocal conditions. AIMS Math. 2023, 8, 14188–14206. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional Thermoelasticity; Springer: New York, NY, USA, 2015. [Google Scholar]
- Ge, Z.M.; Jhuang, W.R. Chaos, control and synchronization of a fractional order rotational mechanical system with a centrifugal governor. Chaos Solitons Fractals 2007, 33, 270–289. [Google Scholar] [CrossRef]
- Hilfer, R. Application of Fractional Calculus in Physics; World Science Publishing: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. In North-Holland Mathematics Studies; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Goedegebure, N.; Marynets, K. A numerical Bernstein splines approach for nonlinear initial value problems with Hilfer fractional derivative. arXiv 2025, arXiv:2503.22335. [Google Scholar] [CrossRef]
- Subashini, R.; Ravichandran, C.; Jothimani, K.; Baskonus, H.M. Existence results of Hilfer integro-differential equations with fractional order. Discr. Contin. Dynam. Syst. S 2020, 13, 911–923. [Google Scholar] [CrossRef]
- Kavitha, K.; Vijayakumar, V. Discussion on controllability of non-densely defined Hilfer fractional neutral differential equations with finite delay. Int. J. Nonlinear Sci. Numer. Simul. 2022, 24, 1751–1767. [Google Scholar] [CrossRef]
- Kavitha, K.; Vijayakumar, V.; Shukla, A.; Nisar, K.S.; Udhayakumar, R. Results on approximate controllability of Sobolev-type fractional neutral differential inclusions of Clarke’s subdifferential type. Chaos Solitons Fractals 2021, 151, 111264. [Google Scholar] [CrossRef]
- Gu, H.; Trujillo, J.J. Existence of integral solution for evolution equation with Hilfer fractional derivative. Appl. Math. Comput. 2015, 257, 344–354. [Google Scholar]
- Wang, J.R.; Zhang, Y.R. Nonlocal initial value problems for differential equations with Hilfer fractional derivative. Appl. Math. Comput. 2015, 266, 850–859. [Google Scholar] [CrossRef]
- Pierri, M.; O’Regan, D.; Rolnik, V. Existence of solutions for semi-linear abstract differential equations with not instantaneous impulses. Appl. Math. Comput. 2013, 219, 6743–6749. [Google Scholar] [CrossRef]
- Hernandez, E.; O’Regan, D. On a new class of abstract impulsive differential equations. Proc. Amer. Math. Soc. 2013, 141, 1641–1649. [Google Scholar] [CrossRef]
- Liu, K.; Feckan, M.; O’Regan, D. (ω, c)-periodic solutions for time-varying non-instantaneous impulsive differential systems. Appl. Anal. 2021, 101, 5469–5489. [Google Scholar]
- Chen, P.; Zhang, X.; Li, Y. Existence of mild solutions to partial differential equations with noninstantaneous impulses. Electron. J. Differ. Equ. 2016, 241, 1–11. [Google Scholar]
- Agarwal, R.; O’Regan, D.; Hristova, S.; Cicek, M. Practical stability with respect to initial time difference for Caputo fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 2017, 42, 106–120. [Google Scholar] [CrossRef]
- Benchohra, M.; Seba, D. Impulsive fractional differential equations in Banach Spaces. Electron. J. Qual. Theory Differ. Equ. 2009, 8, 1–14. [Google Scholar] [CrossRef]
- Cicek, M.; Yakar, C.; Gücen, M.B. Practical stability in terms of two measures for fractional order dynamic systems in Caputo’s sense with initial time difference. J. Frankl. Inst. 2014, 351, 732–742. [Google Scholar] [CrossRef]
- Gautama, G.R.; Dabas, J. Mild solution for fractional functional integro-differential equation with not instantaneous impulse. Malaya J. Mat. 2014, 2, 428–437. [Google Scholar] [CrossRef]
- Sankaranarayanan, V.; Mahindrakar, A.D. Switched control of a nonholonomic mobile robot. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2319–2327. [Google Scholar] [CrossRef]
- Cristiano, R.; Carvalho, T.; Tonon, D.J.; Pagano, D.J. Hopf and Homoclinic bifurcations on the sliding vector field of switching systems in ℝn: A case study in power electronics. Phys. D Nonlinear Phenom. 2017, 347, 12–20. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, K.; Li, H.; Cao, Q.; Jin, L.; Li, P. Porous graphitic carbon microtubes derived from willow catkins as a substrate of MnO2 for supercapacitors. J. Power Sources 2017, 344, 176–184. [Google Scholar] [CrossRef]
- Liu, R.; Chang, X.H.; Chen, Z.; Li, Z.; Huang, W.; Xiong, J. Dissipative control for switched nonlinear singular systems with dynamic quantization. Commun. Nonlinear Sci. Numer. Simul. 2023, 127, 107551. [Google Scholar] [CrossRef]
- Li, X.; Zeng, Z.; Shen, J.; Zhang, C.; Zhao, Y. Rectification of depth measurement using pulsed thermography with logarithmic peak second derivative method. Infrared Phys. Technol. 2018, 89, 1–7. [Google Scholar] [CrossRef]
- Wang, J.R.; Ibrahim, A.G.; O’Regan, D. Hilfer-type fractional differential switched inclusions with noninstantaneous impulsive and nonlocal conditions. Nonlinear Anal. Model. Control 2018, 23, 921–941. [Google Scholar] [CrossRef]
- Kumar, V.; Malik, M.; Baleanu, D. Results on Hilfer fractional switched dynamics system with non-instantaneous impulses. J. Phys. 2022, 172, 1–15. [Google Scholar]
- Durgaa, N.; Nageshwari, S.; Chalishajar, D.N. Total controllability of stochastic non-instantaneous impulsive Hilfer fractional switched dynamic systems with deviated arguments. Stoch. Anal. Appl. 2025, 43, 273–302. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, K.S. Iterative learning control applied to batch processes: An overview. Control. Eng. Pract. 2007, 15, 1306–1318. [Google Scholar] [CrossRef]
- Pierallini, M.; Angelini, F.; Mengacci, R.; Palleschi, A.; Bicchi, A.; Garabini, M. Iterative learning control for compliant underactuated arms. IEEE Trans. Syst. Man. Cybern. Syst. 2023, 53, 3810–3822. [Google Scholar] [CrossRef]
- Pei, S.; Zhao, Z.; Liu, F.; Miao, M.; Jin, S.; Sun, F. Iterative learning control for tricalcium neutralization process with initial disturbance. Chem. Eng. Technol 2023, 46, 1028–1038. [Google Scholar] [CrossRef]
- Wang, H.; Han, Z.; Wu, Y.; Liu, Z. Rapid adaptation for active pantograph control in high-speed railway via deep meta reinforcement learning. IEEE Trans. Cybern. 2024, 54, 2783–2796. [Google Scholar] [CrossRef]
- Wei, Y.; Bao, X.J.; Shang, W.; Liao, J.Z. Iterative learning control for non-linear discrete-time systems with iterative varying reference trajectory and varying trail lengths under random initial state shifts. J. Intell. Robot. Syst. 2025, 111, 58. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Chen, X.; Wang, Y.; Chang, Z. An improved deep deterministic policy gradient pantograph active control strategy for high-speed railways. Electronics 2024, 13, 3545. [Google Scholar] [CrossRef]
- Wang, H.; Han, Z.; Wang, X.; Wu, Y.; Liu, Z. Contrastive learning-based Bayes-adaptive meta-reinforcement learning for active pantograph control in high-speed railways. IEEE Trans. Cybern. 2025; 1–15, early access. [Google Scholar] [CrossRef]
- Bhangale, N.; Kachhia, K.B.; Aguilar, J.G. Fractional viscoelastic models with Caputo generalized fractional derivative. Math. Methods. Appl. Sci. 2023, 46, 7835–7846. [Google Scholar] [CrossRef]
- Wang, F.Z.; Shi, L.; Wu, H.; Helian, N.; Chua, L.O. Fractional memristor. Appl. Phys. Lett. 2017, 1114, 243502. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.; Ye, W.; Wu, J.; Shen, Z.; Menshov, I. Mathematical modeling of transport phenomena in compressible multicomponent flows. J. Comput. Phys. 2023, 472, 111628. [Google Scholar] [CrossRef]
- Vivek, D.; Sunmitha, S.; Elsayed, E.M. P-type iterative learning control for impulsive pantograph equations with Hilfer fractional derivative. Math. Found. Comput. 2025; 1–17, early access. [Google Scholar] [CrossRef]
- Lan, Y.H.; Zhou, Y. Dα-Type iterative learning control for fractional-order linear time-delay systems. Asian J. Control 2013, 15, 669–677. [Google Scholar] [CrossRef]
- Yu, X.; Debbouche, A.; Wang, J.R. On the iterative learning control of fractional impulsive evolution equations in Banach spaces. Math. Meth. Appl. Sci. 2015, 40, 6061–6069. [Google Scholar] [CrossRef]
- Cao, X.; Feckan, M.; Shen, D.; Wang, J. Iterative learning control for impulsive multi-agent systems with varying trial lengths. Nonlinear Anal. Model. Control. 2022, 27, 445–465. [Google Scholar] [CrossRef]
- Liu, S.; Wang, J.; Shen, D.; O’Regan, D. Iterative learning control for noninstantaneous impulsive fractional-order systems with varying trial lengths. Int. J. Robust Nonlinear Control. 2018, 28, 6202–6238. [Google Scholar] [CrossRef]
- Liu, S.; Debbouche, A.; Wang, J. ILC method for solving controllability of fractional differential equations with noninstantaneous impulses. J. Comput. Appl. Math. 2018, 339, 343–355. [Google Scholar] [CrossRef]
- Vivek, D.; Sunmitha, S.; Sivasundaram, S. Iterative learning control for Hilfer-type fractional-order quaternion-valued impulsive systems. Math. Eng. Sci. Aerosp. 2025, 16, 1–17. [Google Scholar]
- Vivek, D.; Sunmitha, S.; Sivasundaram, S. Analysis of convergence in ILC for nonlinear pantograph equations with impulses using Hilfer fractional derivative. MESA 2025, 16, 579–591. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-leffler functions and their applications. J. Appl. Math. 2011, 2011, 51. [Google Scholar] [CrossRef]
- Ye, H.; Gao, J.; Ding, Y. A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 2007, 328, 1075–1081. [Google Scholar] [CrossRef]
- Lan, Y.H. Iterative learning control with initial state learning for fractional order nonlinear systems. Comput. Math. Appl. 2012, 64, 3210–3216. [Google Scholar] [CrossRef]
- Luo, Z.J.; Wang, J.R. Study on iterative learning control for Riemann-Liouville fractional order systems. Diff. Equ. Appl. 2017, 9, 123–139. [Google Scholar] [CrossRef]


| Feature’s | R-L Derivative (Ref. [13], Chapter 2, Page 69) | L-C Derivative (Ref. [13], Page 97) | CFD (Ref. [19], Page 852) |
|---|---|---|---|
| Definition | |||
| Initial Conditions | Fractional integral-based | Integer-order derivative-based | Interpolates between R-L and Caputo |
| Used Case | Theoretical modelling | Physical simulations | Generalized modelling with memory interpolation |
| Memory Effect | Strong | Moderate | Tunable via |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunmitha, S.; Vivek, D.; Abdelfattah, W.M.; Elsayed, E.M. Advanced ILC Analysis of Switched Systems Subject to Non-Instantaneous Impulses Using Composite Fractional Derivatives. AppliedMath 2025, 5, 115. https://doi.org/10.3390/appliedmath5030115
Sunmitha S, Vivek D, Abdelfattah WM, Elsayed EM. Advanced ILC Analysis of Switched Systems Subject to Non-Instantaneous Impulses Using Composite Fractional Derivatives. AppliedMath. 2025; 5(3):115. https://doi.org/10.3390/appliedmath5030115
Chicago/Turabian StyleSunmitha, S., D. Vivek, Waleed Mohammed Abdelfattah, and E. M. Elsayed. 2025. "Advanced ILC Analysis of Switched Systems Subject to Non-Instantaneous Impulses Using Composite Fractional Derivatives" AppliedMath 5, no. 3: 115. https://doi.org/10.3390/appliedmath5030115
APA StyleSunmitha, S., Vivek, D., Abdelfattah, W. M., & Elsayed, E. M. (2025). Advanced ILC Analysis of Switched Systems Subject to Non-Instantaneous Impulses Using Composite Fractional Derivatives. AppliedMath, 5(3), 115. https://doi.org/10.3390/appliedmath5030115







