Group Classification and Symmetry Reduction of a (1+1)-Dimensional Porous Medium Equation
Abstract
1. Introduction
2. Group Classification of Equation (4)
3. Optimal System of One-Dimensional Subalgebras of Equation (4)
3.1. Optimal System of Equation (4) for m and d Arbitrary
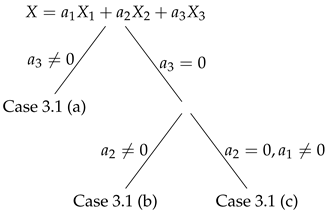
3.2. Optimal System of Equation (4) for and
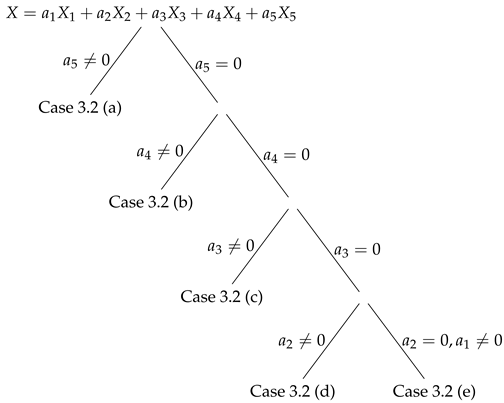
4. Group-Invariant Solutions for Equation (4)
4.1. Solutions of (4) for Arbitrary m and d
4.2. Solutions of (4) for ,
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arrigo, D.J.; Hill, J.M.; Broadbridge, P. Nonclassical symmetry reductions of the linear diffusion equation with a nonlinear source. IMA J. Appl. Math. 1994, 52, 1–24. [Google Scholar] [CrossRef]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: New York, NY, USA, 2013. [Google Scholar]
- Hydon, P.E. Symmetry Methods for Differential Equations: A Beginner’s Guide; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations, 2nd ed.; Springer-Verlag: New York, NY, USA, 1993. [Google Scholar]
- Bluman, G.W.; Cheviakov, A.F.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations; Springer: New York, NY, USA, 2010. [Google Scholar]
- Cantwell, B.J. Introduction to Symmetry Analysis; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Oliveri, F. Lie symmetries of differential equations: Classical results and recent contributions. Symmetry 2010, 2, 658–706. [Google Scholar] [CrossRef]
- Hussain, A.; Usman, M.; Zaman, F.D.; Ibrahim, T.F.; Dawood, A.A. Symmetry analysis, closed-form invariant solutions and dynamical wave structures of the Benney–Luke equation using optimal system of Lie subalgebras. Chin. J. Phys. 2023, 84, 66–88. [Google Scholar] [CrossRef]
- Hussain, A. Invariant analysis and equivalence transformations for the non-linear wave equation in elasticity. Partial Differ. Equ. Appl. Math. 2025, 13, 101123. [Google Scholar] [CrossRef]
- Hussain, A.; Usman, M. On the classification of group invariant solutions of the Barenblatt–Gilman model by a one-dimensional system of subalgebras. Partial Differ. Equ. Appl. Math. 2025, 9, 101176. [Google Scholar] [CrossRef]
- Sophocleous, C.; Tracinà, R. Lie group classification for a reduced Burgers system. Symmetry 2025, 17, 763. [Google Scholar] [CrossRef]
- Charalambous, K.; Sophocleous, C. Lie group classification for a class of compound KdV–Burgers equations with time-dependent coefficients. Int. J. Appl. Comput. Math. 2020, 6, 176. [Google Scholar] [CrossRef]
- Sinkala, W. Revisiting the group classification of the general nonlinear heat equation ut=(k(u)ux)x. Mathematics 2025, 13, 911. [Google Scholar] [CrossRef]
- Aronson, D.G.; Graveleau, J. A selfsimilar solution to the focusing problem for the porous medium equation. Eur. J. Appl. Math. 1993, 4, 65–81. [Google Scholar] [CrossRef]
- Barenblatt, G.I. On self-similar motions of a compressible fluid in a porous medium. Akad. Nauk SSSR Prikl. Mat. Mekh. 1952, 16, 79–86. [Google Scholar]
- Vázquez, J.L. The Porous Medium Equation: Mathematical Theory; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Avdonina, E.D.; Ibragimov, N.H. Conservation laws and exact solutions for nonlinear diffusion in anisotropic media. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2595–2603. [Google Scholar] [CrossRef]
- Antontsev, S.N.; Shmarev, S.I. A model porous medium equation with variable exponent of nonlinearity: Existence, uniqueness and localization properties of solutions. Nonlinear Anal. 2005, 60, 515–545. [Google Scholar] [CrossRef]
- Mbusi, S.O.; Muatjetjeja, B.; Adem, A.R. Exact solutions and conservation laws of a generalized (1+1) dimensional system of equations via symbolic computation. Mathematics 2021, 9, 2916. [Google Scholar] [CrossRef]
- Popovych, R.O.; Ivanova, N.M. Hierarchy of conservation laws of diffusion–convection equations. J. Math. Phys. 2005, 46, 043502. [Google Scholar] [CrossRef]
- Nadjafikhah, M. Classification of similarity solutions for inviscid Burgers’ equation. Adv. Appl. Clifford Algebr. 2010, 20, 71–77. [Google Scholar] [CrossRef]
- Amata, L.; Oliveri, F.; Sgroi, E. Optimal systems of Lie subalgebras: A computational approach. J. Geom. Phys. 2024, 204, 105290. [Google Scholar] [CrossRef]
- Khalique, C.M.; Adeyemo, O.D.; Simbanefayi, I. On optimal system, exact solutions and conservation laws of the modified equal-width equation. Appl. Math. Nonlinear Sci. 2018, 3, 409. [Google Scholar] [CrossRef]
- Agnus, S.; Halder, A.K.; Seshadri, R.; Leach, P.G.L. Analysis of the Calogero–Degasperis equation through point symmetries. J. Anal. 2023, 31, 705–718. [Google Scholar] [CrossRef]
| 0 | |||
| 0 | 0 | ||
| 0 | 0 |
| Ad | |||
|---|---|---|---|
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
| Ad | |||||
|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makibelo, P.C.; Sinkala, W.; Rundora, L. Group Classification and Symmetry Reduction of a (1+1)-Dimensional Porous Medium Equation. AppliedMath 2025, 5, 116. https://doi.org/10.3390/appliedmath5030116
Makibelo PC, Sinkala W, Rundora L. Group Classification and Symmetry Reduction of a (1+1)-Dimensional Porous Medium Equation. AppliedMath. 2025; 5(3):116. https://doi.org/10.3390/appliedmath5030116
Chicago/Turabian StyleMakibelo, Polokwane Charles, Winter Sinkala, and Lazarus Rundora. 2025. "Group Classification and Symmetry Reduction of a (1+1)-Dimensional Porous Medium Equation" AppliedMath 5, no. 3: 116. https://doi.org/10.3390/appliedmath5030116
APA StyleMakibelo, P. C., Sinkala, W., & Rundora, L. (2025). Group Classification and Symmetry Reduction of a (1+1)-Dimensional Porous Medium Equation. AppliedMath, 5(3), 116. https://doi.org/10.3390/appliedmath5030116





