How Babies Learn to Move: An Applied Riemannian Geometry Theory of the Development of Visually-Guided Movement Synergies
Abstract
1. Introduction
2. Preliminaries and Definitions
2.1. Classical Mechanics vs. Riemannian Geometry
2.2. The Configuration Manifold
2.3. A Metric for the Configuration Manifold
2.4. Posture, Place and Orientation
2.5. State Space for Body Movement
2.6. Submanifolds and Controlled Degrees of Freedom
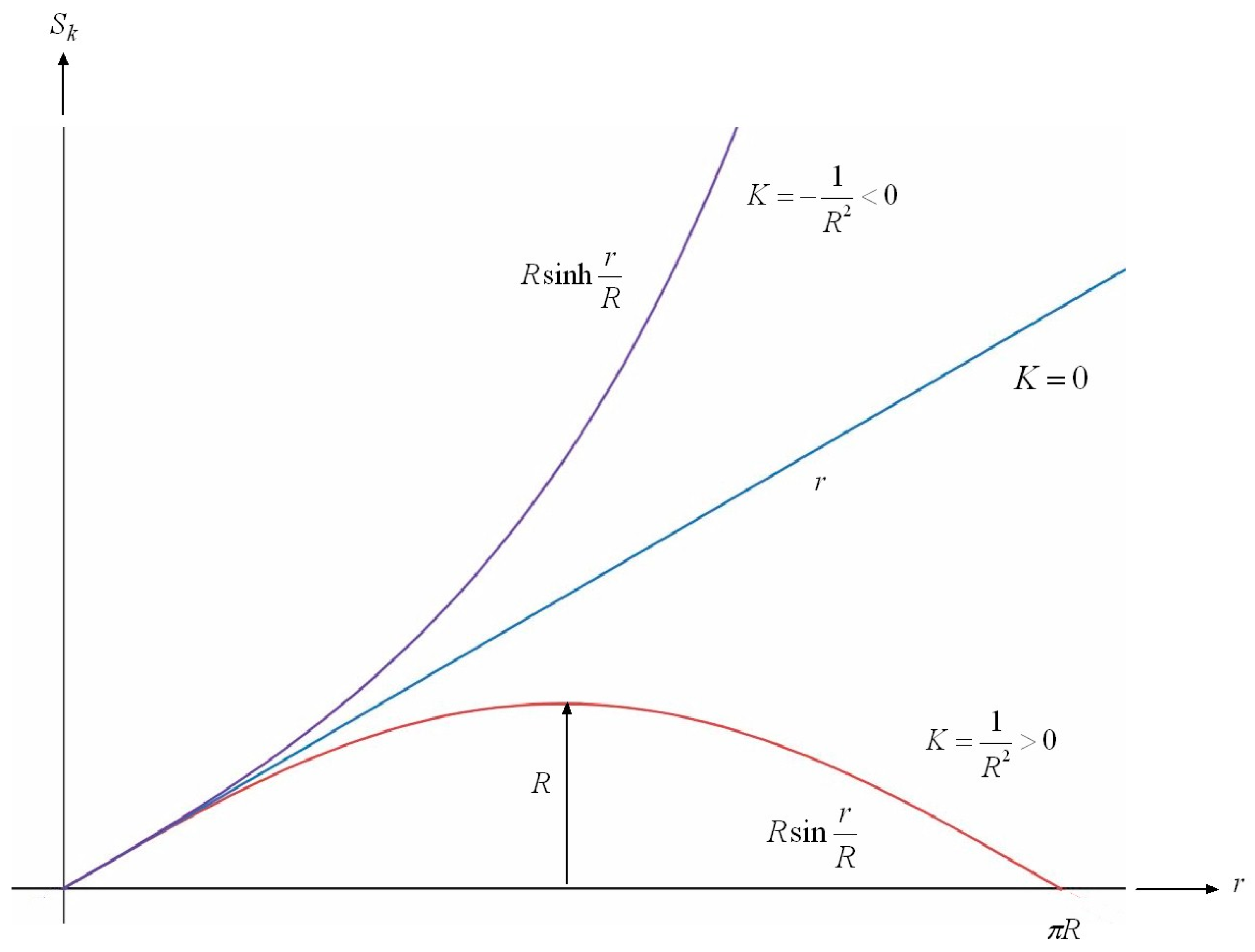
2.7. Curvature of the Configuration Manifold
2.8. Geodesics
3. Motor Development
3.1. Fetal Movements Bootstrap Motor Development
3.2. Movement–Muscle Relations and Mass–Inertia Loads
3.3. Modeling Movement–Muscle Relations
3.4. Modeling Mass–Inertia Loads
3.5. The Connection
3.6. The Covariant Derivative
3.7. Geodesic Trajectory Generator (GTG)
3.8. Geodesic Coordinate Axes
3.9. Synergy Selection Code
4. Visual Development
4.1. The Intrinsic Geometry of Visual Space
4.2. Gaze and Focus Control
4.3. Early Processing in the Primary Visual Cortex
4.4. Image-Point Vectors
4.5. Place-and-Posture Encoding of Visual Images
4.6. A Vector Bundle Model of Visuospatial Memory
4.7. Vector Bundle Morphisms
5. Visuomotor Integration
5.1. Accessing Visual and Motor Memory Simultaneously
5.2. Visual Task Spaces
5.3. Transforming Visual Task Spaces into Synergy Selection Codes
5.4. Error-Reducing Association Memory Network
5.5. Temporal Difference Learning
6. Geodesic Trajectories
6.1. Complications in Generating a Geodesic Trajectory
6.2. Compensating for Gravitational Forces
6.3. Compensating for External Force Fields
6.4. Combining Compensation for Changing Mass–Inertia Loads, Gravitational Forces and External Force Fields
7. The Geometry of Submanifolds
7.1. Minimum-Effort Submanifolds
7.1.1. Radial Geodesic Coordinate Grid Lines
7.1.2. Transverse Coordinate Grid Lines
7.2. Geometry of Submanifolds
7.2.1. Curvature of Submanifolds
7.2.2. Jacobi Vector Fields
7.2.3. The Jacobi Equation
7.2.4. Shape of Submanifolds
7.2.5. Upper and Lower Bounds on the Shape of Submanifolds
8. Concluding Remarks
8.1. The Necessity of Visual and Motor Memory Networks
8.2. Spatial vs. Temporal Response Planning
8.3. A Speculation
8.4. Depth Perception
8.5. Other Geometries
8.6. Coda
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMT | Adaptive model theory |
| CDOFs | Controlled degrees of freedom |
| GTG | Geodesic trajectory generator |
| LGN | Lateral geniculate nucleus |
| LMS | Least mean square |
| SVD | Singular value decomposition |
| VOR | Vestibulo-ocular reflex |
Appendix A. Transition from Pattern-Generator Movements to Purposive Goal-Directed Movements
Appendix A.1. Neural Adaptive Filters
Appendix A.2. Pattern Generators, Synergy Codes and Skill Acquisition
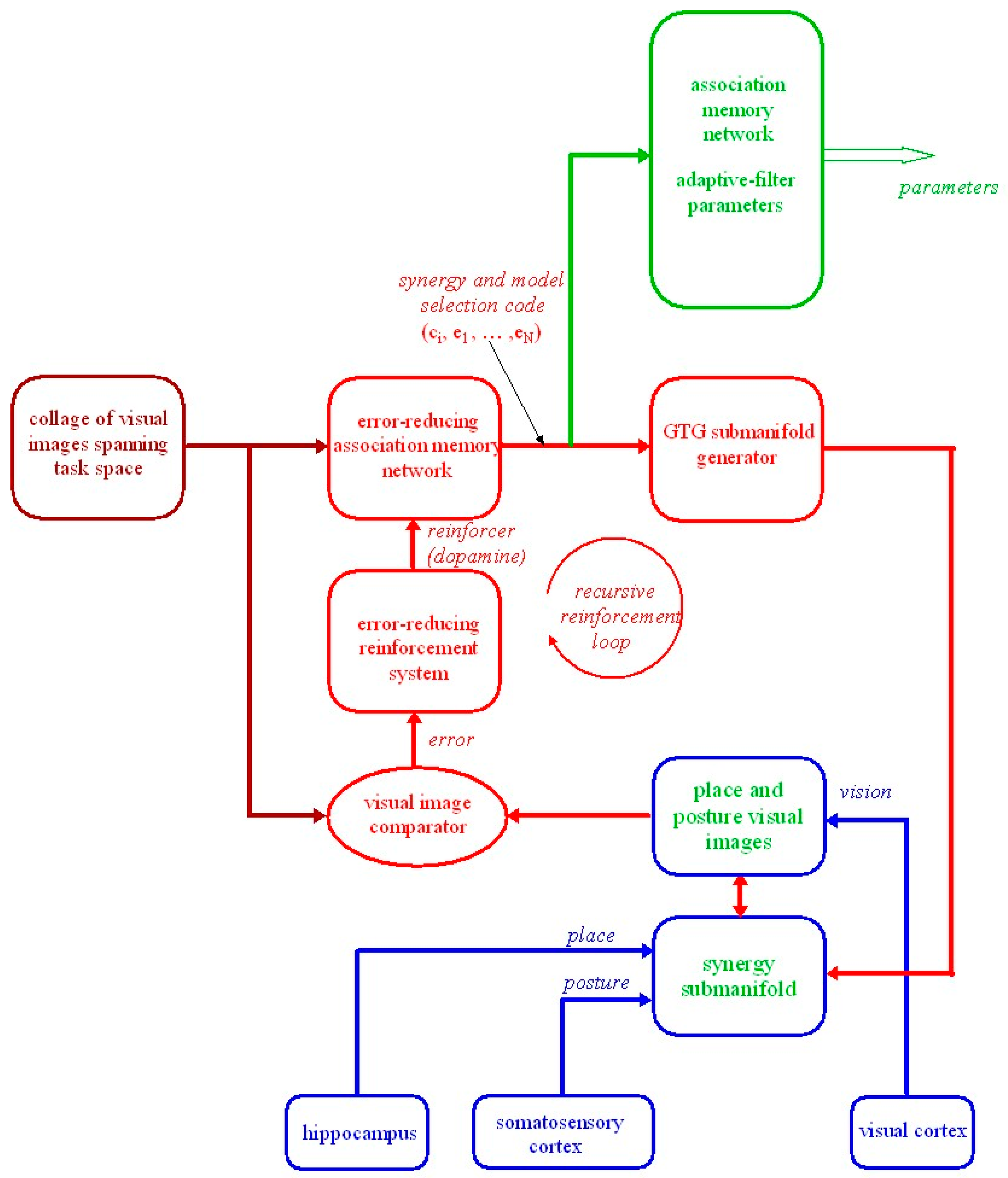
 circuit shows random selection of a pattern-generator selection code that activates one of the many pattern-generator circuits developed within the brain during the first two trimesters of pregnancy. The pattern-generator selection code is connected to a motor association memory network shown in crimson. When activated, the pattern generators send a coordinated trajectory of motor commands m to the
circuit shows random selection of a pattern-generator selection code that activates one of the many pattern-generator circuits developed within the brain during the first two trimesters of pregnancy. The pattern-generator selection code is connected to a motor association memory network shown in crimson. When activated, the pattern generators send a coordinated trajectory of motor commands m to the  functional muscles of the musculo-skeletal-reflex and external systems. These spontaneous fetal and neonatal pattern-generator movements produce motor and sensory afferent signals that tune sensory pathways, leading to the formation of cortical sensory maps illustrated here for only efference copy and vision. Somewhere during the third month after birth, green
functional muscles of the musculo-skeletal-reflex and external systems. These spontaneous fetal and neonatal pattern-generator movements produce motor and sensory afferent signals that tune sensory pathways, leading to the formation of cortical sensory maps illustrated here for only efference copy and vision. Somewhere during the third month after birth, green  neural adaptive filter circuits in cortical–cerebellar–cortical and cortical–basal ganglia-cortical loops come into play. Nonlinear Gram–Schmidt orthogonalizing networks of neural adaptive filters MFE and VFE extract the small number of orthogonalized first-differenced (differentiated) motor M and visual V feature signals associated with the activated pattern generator. Other neural adaptive filters in the cerebellum and basal ganglia tune adaptively to form nonlinear dynamic forward and inverse models of the relationships between the orthogonalized feature signals M and V. The forward models allow afferent signals to be separated into reafference and exafference. Descending neural signals that modulate cerebellar circuits via the inferior olive and basal ganglia circuits via the substantia nigra pars compacta correspond to parameter signals retrieved from the parameter association memory network that tune the cerebellar and basal ganglia neural adaptive filters. The parameter signals are stored in the motor association memory network in association with the pattern-generator selection code. Thus, the fetal and neonatal pattern-generator movements bootstrap, in a piecemeal fashion, the development of forward and inverse models for all the pattern-generator movements. At this stage, the red
neural adaptive filter circuits in cortical–cerebellar–cortical and cortical–basal ganglia-cortical loops come into play. Nonlinear Gram–Schmidt orthogonalizing networks of neural adaptive filters MFE and VFE extract the small number of orthogonalized first-differenced (differentiated) motor M and visual V feature signals associated with the activated pattern generator. Other neural adaptive filters in the cerebellum and basal ganglia tune adaptively to form nonlinear dynamic forward and inverse models of the relationships between the orthogonalized feature signals M and V. The forward models allow afferent signals to be separated into reafference and exafference. Descending neural signals that modulate cerebellar circuits via the inferior olive and basal ganglia circuits via the substantia nigra pars compacta correspond to parameter signals retrieved from the parameter association memory network that tune the cerebellar and basal ganglia neural adaptive filters. The parameter signals are stored in the motor association memory network in association with the pattern-generator selection code. Thus, the fetal and neonatal pattern-generator movements bootstrap, in a piecemeal fashion, the development of forward and inverse models for all the pattern-generator movements. At this stage, the red  pattern-generator circuit is switched off and the crimson
pattern-generator circuit is switched off and the crimson  reinforcement learning system is brought into play. Desired visual task spaces can now be specified to generate an appropriate synergy selection code to replace the pattern-generator selection code. The synergy selection code associated with the specified visual task space retrieves from the association memory network the appropriate set of parameters to tune all the neural adaptive filters in readiness to adaptively model and perform the required goal-directed synergistic movement. The blue
reinforcement learning system is brought into play. Desired visual task spaces can now be specified to generate an appropriate synergy selection code to replace the pattern-generator selection code. The synergy selection code associated with the specified visual task space retrieves from the association memory network the appropriate set of parameters to tune all the neural adaptive filters in readiness to adaptively model and perform the required goal-directed synergistic movement. The blue  response-planning system RP can now plan required visual response trajectories confined to the selected movement synergy using only the small number of orthogonalized signals, V, Va and V*, appropriate for the selected synergy. denotes the first-differenced orthogonalized desired visual response and denotes the first-differenced required orthogonalized motor commands. By this stage of development the pattern generator has been replaced by the yellow
response-planning system RP can now plan required visual response trajectories confined to the selected movement synergy using only the small number of orthogonalized signals, V, Va and V*, appropriate for the selected synergy. denotes the first-differenced orthogonalized desired visual response and denotes the first-differenced required orthogonalized motor commands. By this stage of development the pattern generator has been replaced by the yellow  feedforward, adaptively-tuned inverse models and synergy generator within basal ganglia and cerebellar corticocortical loops. Over the next two years and on into adulthood, driven by imitation, trial and error and coaching, the nervous system acquires, in a piecemeal fashion, a repertoire of visual goal-directed multi-joint coordinated movements, each associated with a visual task space and its own associated synergy selection code.
feedforward, adaptively-tuned inverse models and synergy generator within basal ganglia and cerebellar corticocortical loops. Over the next two years and on into adulthood, driven by imitation, trial and error and coaching, the nervous system acquires, in a piecemeal fashion, a repertoire of visual goal-directed multi-joint coordinated movements, each associated with a visual task space and its own associated synergy selection code.
 circuit shows random selection of a pattern-generator selection code that activates one of the many pattern-generator circuits developed within the brain during the first two trimesters of pregnancy. The pattern-generator selection code is connected to a motor association memory network shown in crimson. When activated, the pattern generators send a coordinated trajectory of motor commands m to the
circuit shows random selection of a pattern-generator selection code that activates one of the many pattern-generator circuits developed within the brain during the first two trimesters of pregnancy. The pattern-generator selection code is connected to a motor association memory network shown in crimson. When activated, the pattern generators send a coordinated trajectory of motor commands m to the  functional muscles of the musculo-skeletal-reflex and external systems. These spontaneous fetal and neonatal pattern-generator movements produce motor and sensory afferent signals that tune sensory pathways, leading to the formation of cortical sensory maps illustrated here for only efference copy and vision. Somewhere during the third month after birth, green
functional muscles of the musculo-skeletal-reflex and external systems. These spontaneous fetal and neonatal pattern-generator movements produce motor and sensory afferent signals that tune sensory pathways, leading to the formation of cortical sensory maps illustrated here for only efference copy and vision. Somewhere during the third month after birth, green  neural adaptive filter circuits in cortical–cerebellar–cortical and cortical–basal ganglia-cortical loops come into play. Nonlinear Gram–Schmidt orthogonalizing networks of neural adaptive filters MFE and VFE extract the small number of orthogonalized first-differenced (differentiated) motor M and visual V feature signals associated with the activated pattern generator. Other neural adaptive filters in the cerebellum and basal ganglia tune adaptively to form nonlinear dynamic forward and inverse models of the relationships between the orthogonalized feature signals M and V. The forward models allow afferent signals to be separated into reafference and exafference. Descending neural signals that modulate cerebellar circuits via the inferior olive and basal ganglia circuits via the substantia nigra pars compacta correspond to parameter signals retrieved from the parameter association memory network that tune the cerebellar and basal ganglia neural adaptive filters. The parameter signals are stored in the motor association memory network in association with the pattern-generator selection code. Thus, the fetal and neonatal pattern-generator movements bootstrap, in a piecemeal fashion, the development of forward and inverse models for all the pattern-generator movements. At this stage, the red
neural adaptive filter circuits in cortical–cerebellar–cortical and cortical–basal ganglia-cortical loops come into play. Nonlinear Gram–Schmidt orthogonalizing networks of neural adaptive filters MFE and VFE extract the small number of orthogonalized first-differenced (differentiated) motor M and visual V feature signals associated with the activated pattern generator. Other neural adaptive filters in the cerebellum and basal ganglia tune adaptively to form nonlinear dynamic forward and inverse models of the relationships between the orthogonalized feature signals M and V. The forward models allow afferent signals to be separated into reafference and exafference. Descending neural signals that modulate cerebellar circuits via the inferior olive and basal ganglia circuits via the substantia nigra pars compacta correspond to parameter signals retrieved from the parameter association memory network that tune the cerebellar and basal ganglia neural adaptive filters. The parameter signals are stored in the motor association memory network in association with the pattern-generator selection code. Thus, the fetal and neonatal pattern-generator movements bootstrap, in a piecemeal fashion, the development of forward and inverse models for all the pattern-generator movements. At this stage, the red  pattern-generator circuit is switched off and the crimson
pattern-generator circuit is switched off and the crimson  reinforcement learning system is brought into play. Desired visual task spaces can now be specified to generate an appropriate synergy selection code to replace the pattern-generator selection code. The synergy selection code associated with the specified visual task space retrieves from the association memory network the appropriate set of parameters to tune all the neural adaptive filters in readiness to adaptively model and perform the required goal-directed synergistic movement. The blue
reinforcement learning system is brought into play. Desired visual task spaces can now be specified to generate an appropriate synergy selection code to replace the pattern-generator selection code. The synergy selection code associated with the specified visual task space retrieves from the association memory network the appropriate set of parameters to tune all the neural adaptive filters in readiness to adaptively model and perform the required goal-directed synergistic movement. The blue  response-planning system RP can now plan required visual response trajectories confined to the selected movement synergy using only the small number of orthogonalized signals, V, Va and V*, appropriate for the selected synergy. denotes the first-differenced orthogonalized desired visual response and denotes the first-differenced required orthogonalized motor commands. By this stage of development the pattern generator has been replaced by the yellow
response-planning system RP can now plan required visual response trajectories confined to the selected movement synergy using only the small number of orthogonalized signals, V, Va and V*, appropriate for the selected synergy. denotes the first-differenced orthogonalized desired visual response and denotes the first-differenced required orthogonalized motor commands. By this stage of development the pattern generator has been replaced by the yellow  feedforward, adaptively-tuned inverse models and synergy generator within basal ganglia and cerebellar corticocortical loops. Over the next two years and on into adulthood, driven by imitation, trial and error and coaching, the nervous system acquires, in a piecemeal fashion, a repertoire of visual goal-directed multi-joint coordinated movements, each associated with a visual task space and its own associated synergy selection code.
feedforward, adaptively-tuned inverse models and synergy generator within basal ganglia and cerebellar corticocortical loops. Over the next two years and on into adulthood, driven by imitation, trial and error and coaching, the nervous system acquires, in a piecemeal fashion, a repertoire of visual goal-directed multi-joint coordinated movements, each associated with a visual task space and its own associated synergy selection code.
References
- Bernstein, N.A. The Co-Ordination and Regulation of Movements; Pergamon Press: Oxford, UK, 1967. [Google Scholar]
- Neilson, P.D.; Neilson, M.D.; O’Dwyer, N.J. Internal models and intermittency: A theoretical account of human tracking behavior. Biol. Cybern. 1988, 58, 101–112. [Google Scholar] [CrossRef] [PubMed]
- Jordan, M.I.; Wolpert, D.M. Computational motor control. In The New Cognitive Neurosciences; Gazzaniga, M., Ed.; MIT Press: Cambridge, MA, USA, 1999; pp. 601–620. [Google Scholar]
- Neilson, P.D.; Neilson, M.D. A neuroengineering solution to the optimal tracking problem. Hum. Mov. Sci. 1999, 18, 155–183. [Google Scholar] [CrossRef]
- Todorov, E.; Jordan, M.I. Optimal feedback control as a theory of motor coordination. Nat. Neurosci. 2002, 5, 1226–1235. [Google Scholar] [CrossRef] [PubMed]
- Neilson, P.D.; Neilson, M.D.; Bye, R.T. A Riemannian geometry theory of synergy selection for visually-guided movement. Vision 2021, 5, 26. [Google Scholar] [CrossRef]
- Neilson, P.D.; Neilson, M.D.; Bye, R.T. A Riemannian geometry theory of human movement: The geodesic synergy hypothesis. Hum. Mov. Sci. 2015, 44, 42–72. [Google Scholar] [CrossRef]
- Bullo, F.; Lewis, A.D. Geometric Control of Mechanical Systems: Modeling, Analysis, and Design for Simple Mechanical Control Systems; Texts in Applied Mathematics; Springer: New York, NY, USA, 2005; ISBN 978-0-387-22195-3. [Google Scholar]
- Neilson, P.D.; Neilson, M.D.; Bye, R.T. A Riemannian geometry theory of three-dimensional binocular visual perception. Vision 2018, 2, e43. [Google Scholar] [CrossRef]
- O’Keefe, J.; Dostrovsky, J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 1971, 34, 171–175. [Google Scholar] [CrossRef] [PubMed]
- O’Keefe, J. Place units in the hippocampus of the freely moving rat. Exp. Neurol. 1976, 51, 78–109. [Google Scholar] [CrossRef]
- Fyhn, M.; Molden, S.; Witter, M.P.; Moser, E.I.; Moser, M.-B. Spatial representation in the entorhinal cortex. Science 2004, 305, 1258–1264. [Google Scholar] [CrossRef]
- Hafting, T.; Fyhn, M.; Molden, S.; Moser, M.-B.; Moser, E.I. Microstructure of a spatial map in the entorhinal cortex. Nature 2005, 436, 801–806. [Google Scholar] [CrossRef]
- Klein, H.; Jaquier, N.; Meixner, A.; Asfour, T. On the design of region-avoiding metrics for collision-safe motion generation on Riemannian manifolds. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2023), Detroit, MI, USA, 1–5 October 2023. [Google Scholar]
- Neilson, P.D.; Neilson, M.D. An overview of adaptive model theory: Solving the problems of redundancy, resources, and nonlinear interactions in human movement control. J. Neural Eng. 2005, 2, S279–S312. [Google Scholar] [CrossRef] [PubMed]
- de Vries, J.I.P.; Visser, G.H.A.; Prechtl, H.F.R. The emergence of fetal behaviour. I. Qualitative aspects. Early Hum. Dev. 1982, 7, 301–322. [Google Scholar] [CrossRef]
- de Vries, J.I.P.; Visser, G.H.A.; Prechtl, H.F.R. The emergence of fetal behaviour. II. Quantitative aspects. Early Hum. Dev. 1985, 12, 99–120. [Google Scholar] [CrossRef] [PubMed]
- Prechtl, H.F.R. The importance of fetal movements. In Neurophysiology and Neuropsychology of Motor Development; Connolly, K.J., Forssberg, H., Eds.; Clinics in Developmental Medicine; Mac Keith Press: London, UK, 1997; pp. 42–53. ISBN 978-1-898683-10-0. [Google Scholar]
- Prechtl, H.F.R. Continuity of Neural Functions from Prenatal to Postnatal Life; Prechtl, H.F.R., Ed.; Clinics in Developmental Medicine; Blackwell Scientific Publications: Oxford, UK, 1984; ISBN 978-0-521-41214-8. [Google Scholar]
- Prechtl, H.F.R. New perspectives in early human development. Eur. J. Obstet. Gynecol. Reprod. Biol. 1986, 21, 347–355. [Google Scholar] [CrossRef]
- Prechtl, H.F.R.; Hopkins, B. Developmental transformations of spontaneous movements in early infancy. Early Hum. Dev. 1986, 14, 233–238. [Google Scholar] [CrossRef] [PubMed]
- Barlow, H.B. The coding of sensory messages. In Current Problems in Animal Behaviour; Thorpe, W.H., Zangwill, O.L., Eds.; Cambridge University Press: Cambridge, UK, 1961; pp. 331–360. [Google Scholar]
- Gandevia, S.C. Roles for perceived voluntary motor commands in motor control. Trends Neurosci. 1987, 10, 81–85. [Google Scholar] [CrossRef]
- Grotheer, M.; Rosenke, M.; Wu, H.; Kular, H.; Querdasi, F.R.; Natu, V.S.; Yeatman, J.D.; Grill-Spector, K. White matter myelination during early infancy is linked to spatial gradients and myelin content at birth. Nat. Commun. 2022, 13, 997. [Google Scholar] [CrossRef]
- Neilson, P.D.; Neilson, M.D. Motor maps and synergies. Hum. Mov. Sci. 2005, 24, 774–797. [Google Scholar] [CrossRef]
- Bye, R.T.; Neilson, P.D. The BUMP model of response planning: Intermittent predictive control accounts for 10Hz physiological tremor. Hum. Mov. Sci. 2010, 29, 713–736. [Google Scholar] [CrossRef]
- Marsden, J.E.; Ratiu, T.S. Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems, 2nd ed.; Texts in Applied Mathematics; Springer: New York, NY, USA, 1999; ISBN 978-0-387-98643-2. [Google Scholar]
- Lang, S. Fundamentals of Differential Geometry; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1999; Volume 191, ISBN 978-1-4612-6810-9. [Google Scholar]
- Handzel, A.A.; Flash, T. Geometric methods in the study of human motor control. Cogn. Stud. 1999, 6, 309–321. [Google Scholar] [CrossRef]
- Ghosh, B.K.; Meegaskumbura, R.; Ekanayake, M.P.B. Human eye movement with and without the Listings constraint. In Proceedings of the 2009 American Control Conference, St Louis, MO, USA, 10–12 June 2009; pp. 1015–1020. [Google Scholar]
- Sekimoto, M.; Arimoto, S.; Prilutsky, B.I.; Isaka, T.; Kawamura, S. Observation of human multi-joint arm movement from the viewpoint of a Riemannian distance. In Proceedings of the ICCAS-SICE 2009-ICROS-SICE International Joint Conference 2009, Proceedings, Fukuoka, Japan, 18–21 August 2009; pp. 2664–2669. [Google Scholar]
- Biess, A. Shaping of arm configuration space by prescription of non-Euclidean metrics with applications to human motor control. Phys. Rev. E 2013, 87, 012729. [Google Scholar] [CrossRef] [PubMed]
- Klein, H.; Jaquier, N.; Meixner, A.; Asfour, T. A Riemannian take on human motion analysis and retargeting. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 5210–5217. [Google Scholar]
- Frisby, J.P.; Stone, J.V. Seeing: The Computational Approach to Biological Vision, 2nd ed.; MIT Press: Cambridge, MA, USA, 2010; ISBN 978-0-262-51427-9. [Google Scholar]
- Neilson, P.D.; Neilson, M.D.; Bye, R.T. The Riemannian geometry theory of visually-guided movement accounts for afterimage illusions and size constancy. Vision 2022, 6, 37. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control, 2nd ed.; Cambridge University Press: Cambridge, UK, 2022; ISBN 978-1-009-09848-9. [Google Scholar]
- Daugman, J.G. Entropy reduction and decorrelation in visual coding by oriented neural receptive fields. IEEE Trans. Biomed. Eng. 1989, 36, 107–114. [Google Scholar] [CrossRef]
- Simoncelli, E.P.; Olshausen, B.A. Natural image statistics and neural representation. Annu. Rev. Neurosci. 2001, 24, 1193–1216. [Google Scholar] [CrossRef] [PubMed]
- Bendat, J.S. Nonlinear System Analysis and Identification from Random Data; Wiley: New York, NY, USA, 1990; ISBN 978-0-471-60623-9. [Google Scholar]
- Bendat, J.S. Nonlinear System Techniques and Applications; Wiley: New York, NY, USA, 1998; ISBN 978-0-471-16576-7. [Google Scholar]
- Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; originally published 1982; The MIT Press: Cambridge, MA, USA, 2010; ISBN 978-0-262-51462-0. [Google Scholar]
- Marr, D.; Poggio, T. Cooperative computation of stereo disparity. Science 1976, 194, 283–287. [Google Scholar] [CrossRef]
- Sprague, N.; Ballard, D.; Robinson, A. Modeling embodied visual behaviors. ACM Trans. Appl. Percept. 2007, 4, 11. [Google Scholar] [CrossRef]
- Graziano, M.S.A. The movement repertoire of monkeys, Chapter 9. In The Intelligent Movement Machine: An Ethological Perspective on the Primate Motor System; Oxford University Press: Oxford, UK, 2009; ISBN 978-0-19-986486-7. [Google Scholar]
- Hayhoe, M.M. Vision and action. Annu. Rev. Vis. Sci. 2017, 3, 389–413. [Google Scholar] [CrossRef]
- Schultz, W.; Dickinson, A. Neuronal coding of prediction errors. Annu. Rev. Neurosci. 2000, 23, 473–500. [Google Scholar] [CrossRef]
- Niv, Y. Reinforcement learning in the brain. J. Math. Psychol. 2009, 53, 139–154. [Google Scholar] [CrossRef]
- Wilson, R.C.; Takahashi, Y.K.; Schoenbaum, G.; Niv, Y. Orbitofrontal cortex as a cognitive map of task space. Neuron 2014, 81, 267–279. [Google Scholar] [CrossRef] [PubMed]
- Rescorla, R.A.; Wagner, A.R. A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In Classical Conditioning II: Current Research and Theory; Black, A.H., Prokasy, W.F., Eds.; Appleton-Century-Crofts: New York, NY, USA, 1972; pp. 64–99. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; Adaptive computation and machine learning series; MIT Press: Cambridge, MA, USA, 2018; ISBN 978-0-262-03924-6. [Google Scholar]
- Lee, J.M. Introduction to Riemannian Manifolds, 2nd ed.; Graduate Texts in Mathematics; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-91754-2. [Google Scholar]
- Craik, K.J.W. Theory of the human operator in control systems I. The operator as an engineering system. Br. J. Psychol. 1947, 38, 56–61. [Google Scholar] [CrossRef]
- Craik, K.J.W. Theory of the human operator in control systems II. Man as an element in a control system. Br. J. Psychol. 1948, 38, 142–148. [Google Scholar] [CrossRef]
- Young, L.R. On adaptive manual control. Ergonomics 1969, 12, 635–674. [Google Scholar] [CrossRef] [PubMed]
- Poulton, E.C. Tracking Skill and Manual Control; Academic Press: New York, NY, USA, 1974; ISBN 0-12-563550-8. [Google Scholar]
- O’Dwyer, N.; Rattanaprasert, U.; Smith, R. Quantification of coordination in human walking. In From Basic Motor Control to Functional Recovery II; Gantchev, N., Ed.; Academic Publishing House: Sofia, Bulgaria, 2001; pp. 107–119. ISBN 954-430-813-X. [Google Scholar]
- Goodale, M.; Milner, D. One brain—Two visual systems. Psychologist 2006, 19, 660–663. [Google Scholar]
- Goodale, M.A.; Milner, D. Sight Unseen: An Exploration of Conscious and Unconscious Vision; Oxford University Press: Oxford, UK, 2013; ISBN 978-0-19-175300-8. [Google Scholar]
- Króliczak, G.; Heard, P.; Goodale, M.A.; Gregory, R.L. Dissociation of perception and action unmasked by the hollow-face illusion. Brain Res. 2006, 1080, 9–16. [Google Scholar] [CrossRef]
- Whitwell, R.L.; Buckingham, G.; Enns, J.T.; Chouinard, P.A.; Goodale, M.A. Rapid decrement in the effects of the Ponzo display dissociates action and perception. Psychon. Bull. Rev. 2016, 23, 1157–1163. [Google Scholar] [CrossRef]
- Whitwell, R.L.; Goodale, M.A.; Merritt, K.E.; Enns, J.T. The Sander parallelogram illusion dissociates action and perception despite control for the litany of past confounds. Cortex 2018, 98, 163–176. [Google Scholar] [CrossRef] [PubMed]
- Luneburg, R.K. Mathematical Analysis of Binocular Vision; Princeton University Press: Princeton, NJ, USA, 1947. [Google Scholar]
- Battro, A.M.; di Pierro Netto, S.; Rozestraten, R.J.A. Riemannian geometries of variable curvature in visual space: Visual alleys, horopters, and triangles in big open fields. Perception 1976, 5, 9–23. [Google Scholar] [CrossRef]
- Battro, A.M. Visual Riemannian space versus cognitive Euclidean space. Synthese 1977, 35, 423–429. [Google Scholar] [CrossRef]
- Hoffman, W.C. Subjective geometry and geometric psychology. Math. Model. 1980, 1, 349–367. [Google Scholar] [CrossRef]
- Koenderink, J.J.; van Doorn, A.J. Geometry of binocular vision and a model for stereopsis. Biol. Cybern. 1976, 21, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Koenderink, J.J.; van Doorn, A.J. Exocentric pointing. In Vision and Action; Harris, L.R., Jenkin, M., Eds.; Cambridge University Press: Cambridge, UK, 1998; pp. 295–313. ISBN 978-0-521-63162-4. [Google Scholar]
- Koenderink, J.J.; van Doorn, A.J.; Lappin, J.S. Direct measurement of the curvature of visual space. Perception 2000, 29, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Cuijpers, R.H.; Kappers, A.M.L.; Koenderink, J.J. Investigation of visual space using an exocentric pointing task. Percept. Psychophys. 2000, 62, 1556–1571. [Google Scholar] [CrossRef] [PubMed]
- Cuijpers, R.H.; Kappers, A.M.L.; Koenderink, J.J. Visual perception of collinearity. Percept. Psychophys. 2002, 64, 392–404. [Google Scholar] [CrossRef]
- Cuijpers, R.H.; Kappers, A.M.L.; Koenderink, J.J. The metrics of visual and haptic space based on parallelity judgements. J. Math. Psychol. 2003, 47, 278–291. [Google Scholar] [CrossRef]
- Cuijpers, R.H.; Kappers, A.M.L.; Koenderink, J.J. On the role of external reference frames on visual judgements of parallelity. Acta Psychol. 2001, 108, 283–302. [Google Scholar] [CrossRef]
- Schoumans, N.; Kappers, A.M.L.; Koenderink, J.J. Scale invariance in near space: Pointing under influence of context. Acta Psychol. 2002, 110, 63–81. [Google Scholar] [CrossRef]
- Koenderink, J.J.; van Doorn, A.J.; Lappin, J.S. Exocentric pointing to opposite targets. Acta Psychol. 2003, 112, 71–87. [Google Scholar] [CrossRef]
- Doumen, M.J.A.; Kappers, A.M.L.; Koenderink, J.J. Visual space under free viewing conditions. Percept. Psychophys. 2005, 67, 1177–1189. [Google Scholar] [CrossRef]
- Doumen, M.J.A.; Kappers, A.M.L.; Koenderink, J.J. Horizontal–vertical anisotropy in visual space. Acta Psychol. 2006, 123, 219–239. [Google Scholar] [CrossRef]
- Doumen, M.J.A.; Kappers, A.M.L.; Koenderink, J.J. Effects of context on a visual 3-D pointing task. Perception 2007, 36, 75–90. [Google Scholar] [CrossRef]
- Koenderink, J.; van Doorn, A. The structure of visual spaces. J. Math. Imaging Vis. 2008, 31, 171–187. [Google Scholar] [CrossRef]
- Koenderink, J.J.; van Doorn, A.J.; Kappers, A.M.L.; Doumen, M.J.A.; Todd, J.T. Exocentric pointing in depth. Vision Res. 2008, 48, 716–723. [Google Scholar] [CrossRef] [PubMed]
- Koenderink, J.; van Doorn, A.; de Ridder, H.; Oomes, S. Visual rays are parallel. Perception 2010, 39, 1163–1171. [Google Scholar] [CrossRef] [PubMed]
- Koenderink, J.; van Doorn, A. The shape of space. In Shape Perception in Human and Computer Vision; Dickinson, S., Pizlo, Z., Eds.; Advances in Computer Vision and Pattern Recognition; Springer: London, UK, 2013; pp. 145–156. ISBN 978-1-4471-5194-4. [Google Scholar]
- van Doorn, A.; Koenderink, J.; Wagemans, J. Exocentric pointing in the visual field. i-Perception 2013, 4, 532–542. [Google Scholar] [CrossRef] [PubMed]
- Wagner, M.; Gambino, A.J. Variations in the anisotropy and affine structure of visual space: A geometry of visibles with a third dimension. Topoi Int. Rev. Philos. 2016, 35, 583–598. [Google Scholar] [CrossRef]
- Wagner, M.; Hatfield, G.; Cassese, K.; Makwinski, A.N. Differentiating between affine and perspective-based models for the geometry of visual space based on judgments of the interior angles of squares. Vision 2018, 2, 22. [Google Scholar] [CrossRef]
- Wagner, M. Sensory and cognitive explanations for a century of size constancy research. In Visual Experience: Sensation, Cognition, and Constancy; Hatfield, G., Allred, S., Eds.; Oxford University Press: Oxford, UK, 2012; pp. 63–86. ISBN 978-0-19-174188-3. [Google Scholar]
- Smeets, J.B.J.; Sousa, R.; Brenner, E. Illusions can warp visual space. Perception 2009, 38, 1467–1480. [Google Scholar] [CrossRef]
- Gogel, W.C. A theory of phenomenal geometry and its applications. Percept. Psychophys. 1990, 48, 105–123. [Google Scholar] [CrossRef]
- Predebon, J. Relative distance judgments of familiar and unfamiliar objects viewed under representatively natural conditions. Percept. Psychophys. 1990, 47, 342–348. [Google Scholar] [CrossRef]
- Predebon, J. The influence of object familiarity on magnitude estimates of apparent size. Perception 1992, 21, 77–90. [Google Scholar] [CrossRef] [PubMed]
- Gogel, W.C. An analysis of perceptions from changes in optical size. Percept. Psychophys. 1998, 60, 805–820. [Google Scholar] [CrossRef] [PubMed]
- Hatfield, G. Representation and constraints: The inverse problem and the structure of visual space. Acta Psychol. 2003, 114, 355–378. [Google Scholar] [CrossRef]
- Granrud, C.E. Development of size constancy in children: A test of the metacognitive theory. Atten. Percept. Psychophys. 2009, 71, 644–654. [Google Scholar] [CrossRef] [PubMed]
- Hatfield, G. Phenomenal and cognitive factors in spatial perception. In Visual Experience: Sensation, Cognition, and Constancy; Hatfield, G., Allred, S., Eds.; Oxford University Press: Oxford, UK, 2012; pp. 35–62. ISBN 978-0-19-174188-3. [Google Scholar]
- Widrow, B.; Stearns, S.D. Adaptive Signal Processing; Prentice Hall: Englewood Cliffs, NJ, USA, 1985; ISBN 978-0-13-004029-9. [Google Scholar]
- Haykin, S. Adaptive Filter Theory; Prentice Hall: Englewood Cliffs, NJ, USA, 1986; ISBN 978-0-13-004052-7. [Google Scholar]
- Widrow, B.; Walach, E. Adaptive Inverse Control; Prentice Hall: Upper Saddle River, NJ, USA, 1996; ISBN 978-0-13-005968-0. [Google Scholar]
- Ito, M. The Cerebellum and Neural Control; Raven Press: New York, NY, USA, 1984; ISBN 978-0-89004-106-2. [Google Scholar]
- Barlow, J.S. The Cerebellum and Adaptive Control; Cambridge University Press: Cambridge, UK, 2002; ISBN 978-0-521-80842-2. [Google Scholar]
- Llinás, R.R. The noncontinuous nature of movement execution. In Motor Control: Concepts and Issues; Humphrey, D.R., Freund, H.-J., Eds.; John Wiley: Chichester, UK, 1991; pp. 223–242. [Google Scholar]
- Llinás, R.R. Electrophysiology of the cerebellar networks. In Comprehensive Physiology; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 831–876. ISBN 978-0-470-65071-4. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neilson, P.D.; Neilson, M.D. How Babies Learn to Move: An Applied Riemannian Geometry Theory of the Development of Visually-Guided Movement Synergies. AppliedMath 2025, 5, 52. https://doi.org/10.3390/appliedmath5020052
Neilson PD, Neilson MD. How Babies Learn to Move: An Applied Riemannian Geometry Theory of the Development of Visually-Guided Movement Synergies. AppliedMath. 2025; 5(2):52. https://doi.org/10.3390/appliedmath5020052
Chicago/Turabian StyleNeilson, Peter D., and Megan D. Neilson. 2025. "How Babies Learn to Move: An Applied Riemannian Geometry Theory of the Development of Visually-Guided Movement Synergies" AppliedMath 5, no. 2: 52. https://doi.org/10.3390/appliedmath5020052
APA StyleNeilson, P. D., & Neilson, M. D. (2025). How Babies Learn to Move: An Applied Riemannian Geometry Theory of the Development of Visually-Guided Movement Synergies. AppliedMath, 5(2), 52. https://doi.org/10.3390/appliedmath5020052





