Next-Gen Video Watermarking with Augmented Payload: Integrating KAZE and DWT for Superior Robustness and High Transparency

Abstract

Background: The issue of digital piracy is increasingly prevalent, with its proliferation further fueled by the widespread use of social media outlets such as WhatsApp, Snapchat, Instagram, Pinterest, and X. These platforms have become hotspots for the unauthorized sharing of copyrighted materials without due recognition to the original creators. Current techniques for digital watermarking are inadequate; they frequently choose less-than-ideal locations for embedding watermarks. This often results in a compromise on maintaining critical relationships within the data. Purpose: This research aims to tackle the growing problem of digital piracy, which represents a major risk to rights holders in various sectors, most notably those involved in entertainment. The goal is to devise a robust watermarking approach that effectively safeguards intellectual property rights and guarantees rightful earnings for those who create content. Approach: To address the issues at hand, this study presents an innovative technique for digital video watermarking. Utilizing the 2D-DWT along with the KAZE feature detection algorithm, which incorporates the Accelerated Segment Test with Zero Eigenvalue, scrutinize and pinpoint data points that exhibit circular symmetry. The KAZE algorithm pinpoints a quintet of stable features within the brightness aspect of video frames to act as central embedding sites. This research selects the chief embedding site by identifying the point of greatest intensity on a specific arc segment on a circle’s edge, while three other sites are chosen based on principles of circular symmetry. Following these procedures, the proposed method subjects videos to several robustness tests to simulate potential disturbances. The efficacy of the proposed approach is quantified using established objective metrics that confirm strong correlation and outstanding visual fidelity in watermarked videos. Moreover, statistical validation through t-tests corroborates the effectiveness of the watermarking strategy in maintaining integrity under various types of assaults. This fortifies the team’s confidence in its practical deployment.

1. Introduction

The proliferation of multimedia content in virtual learning environments, platforms for social media entertainment, and the online distribution of celebrated TV shows and movies without proper recognition or authorization has led to significant economic detriment for the original proprietors of these digital works. Such acts of unauthorized copying, modifying, reproducing, and spreading multimedia materials are encompassed by the term ‘digital piracy’, a legal infraction that can result in penalties, including fines and incarceration, as defined by law. In response to this challenge and in defense of creators’ intellectual property rights, the practice of digital watermarking has become an essential tool over recent years. Digital watermarking offers a reliable solution for embedding distinctive marks like logos or designs into digital media, which can then be retrieved later to affirm ownership rights and pursue legal action against illicit alterations or distributions.

A multitude of digital watermarking techniques have been developed, as referenced in comprehensive reviews [1,2]. These techniques are generally divided into two primary categories based on their method of embedding additional data (the watermark) within digital media, namely, spatial domain methods [3,4] and transform domain methods [5,6]. Spatial domain approaches alter the actual pixel values of an image directly; a prevalent technique is to substitute the least significant bit (LSB) with watermark data [7]. Such methods are relatively simple to implement; however, if not applied correctly, they can lead to watermarks that cannot be detected or extracted without error. Therefore, it’s crucial to maintain synchronization information accurately.

On the other hand, transform domain strategies involve converting the digital content into various frequency components before embedding the watermark within selected frequencies. Commonly used transform-based algorithms include Discrete Cosine Transform (DCT) [8], Discrete Wavelet Transform (DWT) [9], Lifting Wavelet Transform (LWT) [10], and Fast Fourier Transform (FFT) [11]. These strategies offer robust protection against illegal manipulations of signal processing because they spread out the watermark throughout different frequency components—a feature not shared by spatial domain approaches. Recent advancements in image processing have focused on enhancing image quality through spatial filtering methods such as Gaussian filters to improve degraded and unreadable images. The processed images were then fused using Discrete Wavelet Transform (DWT), resulting in significant improvements in accuracy while preserving anatomical details [12]. Similarly, weighted wavelet fusion strategies have shown the potential to preserve perceptual cues by selectively combining high-frequency components [13]. These studies underline the effectiveness of wavelet domain processing for preserving structural and spectral integrity, which motivates the selection of the DWT for watermark embedding in video signals.

Opponents in the digital realm seek to manipulate content bearing watermarks by employing a range of signal-processing methods commonly classified as forms of attack. These include tactics that induce geometric distortions, specialized video-targeted aggressions, strategies that compress content aggressively, and schemes involving the insertion of noise. It is lamentable that numerous watermarking techniques—highlighted in both the survey [14] and preceding discussions—have not succeeded in maintaining the vital spatial and temporal linkages between video frame data and its corresponding metadata. This shortcoming is largely attributed to less-than-ideal choices made when determining where to embed watermarks within the content. Such deficiencies not only bolster the capabilities of these opponents but also lead to economic detriments for creators, accentuating an urgent need for developing a sophisticated approach that safeguards key information embedded within host data while still preserving its visual integrity.

1.1. Research Rationale

The triumph of contemporary computing technologies, such as machine learning and pattern matching, is intricately tied to the analysis, extraction, and processing of discernible patterns and features. In the pursuit of maximal resistance against the adversarial offense, utilizing data attributes in watermarking involves subtly adjusting them or employing their reference orientations for the embedding of watermarks. Digital watermarking, in the broader context, stands as a cornerstone in information security, serving to establish the identity of content owners and enabling legal recourse against unwarranted alterations and dispersion of intellectual property. In the wake of the global upheaval caused by the COVID-19 pandemic, the world has witnessed a rapid and unmitigated surge in online education and the Widespread utilization of online platforms, including the interconnected realm of the internet and social platforms, for the circulation and re-circulation of esteemed TV series and cinematic productions, often bereft of due credit or owner permission. Unquestionably, this has inflicted severe financial losses upon the rightful content owners, necessitating an immediate and comprehensive solution to tackle this issue.

Within the academic landscape, researchers have proffered several solutions with the aim of attaining a commendable degree of resilience against watermarking attacks, all the while safeguarding the imperceptibility of the watermark. However, these solutions falter in maintaining synchronization between crucial information. This is attributed to the inadequate choice of embedding sites, which renders them susceptible to a range of assaults. It is noteworthy that most watermarking solutions are tailored for images, with video-specific strategies largely overlooked. Contrary to this oversight, the architecture of videos fundamentally differs from images, making watermarked videos susceptible to video-specific attacks. These attacks involve frame swapping, averaging, frame insertion (e.g., commercial advertisements), and video compression using lossy techniques. A few authors [15,16] have ventured into video watermarking considering video-specific attacks, but their schemes yield suboptimal results when subjected to frame insertion, video format conversion, and frame rate adjustments.

Video tampering, typically executed with cutting-edge editing tools, conceals the nature of attacks while retaining the commercial value of the video. Consequently, there arises a pressing need for a video watermarking technique that exhibits substantial resilience against video-specific attacks while addressing diverse compression and noise insertion challenges. In light of these challenges, this proposed work introduces a watermarking methodology for videos that effectively tenacities the issues stemming from the unbridled expansion and advancement of digital technologies.

1.2. Prominent Findings and Paper’s Significance

This paper introduces an advanced video watermarking approach that enhances payload capacity through the utilization of circular symmetry, primarily based on the KAZE algorithm and the 2D-DWT. Notably, the choice of 2D-DWT is motivated by its capabilities in multi-resolution analysis, energy compaction, and robustness against certain signal processing attacks and transformations, surpassing alternatives such as DCT and FFT. Stable interest points detected by KAZE serve as reference points to establish circular neighborhoods for precise watermark embedding locations.

The key contributions of this paper include the following:

• Leveraging 2D-DWT: The adoption of 2D-DWT enables the simultaneous capture of time and frequency information, making it well-suited for tasks such as signal denoising and video compression in signal processing applications.
• Robust feature-driven watermark embedding using KAZE: To enhance watermark robustness, the method employs KAZE, a multi-scale 2D feature detection technique known for its repeatability and distinctiveness, resilient in the face of diverse image transformations.
• Payload Augmentation Using Radial Symmetry: Utilizing the notion of radial symmetry of the circle quadruples the watermark capacity while reducing computational demands.
• Impressive Robustness and Ensuring High Transparency: Evaluation metrics reveal the potency of the suggested approach, showcasing a robust Correlation Coefficient (CC) and high Structural Similarity Index Measure (SSIM) near unity. The Peak Signal to Noise Ratio (PSNR) approaches 60 decibels (dB) across various attacks. The use of a deep learning-based LPIPS metric with a score that varies between 0.06 and 0.01 further ensures a near-invisible impact on the perceptual similarity between two video frames.

The subsequent sections are structured as follows: Section 2 provides the related work on recent developments in digital watermarking. Section 3 offers the foundation for research by giving a concise introduction to 2D-DWT, KAZE, and circular symmetry for a better understanding of the proposed method. Section 4 outlines the details of the proposed watermarking procedure. Section 5 presents the empirical setup and outcomes. Finally, Section 6 gives the inference from the study and provides the prospects for future work.

2. Related Work

In the wake of the global proliferation of the coronavirus, the globe has embarked on a novel digital epoch characterized by unprecedented growth and technological advancements in the digital sphere. During this transformation, the generation, manipulation, and dissemination, often with minimal distinction between the original and modified versions, have become seemingly effortless for inexperienced users with limited familiarity with tools that edit images and videos. Regrettably, the methods devised by authors over the last two decades to safeguard content ownership are gradually entering obsolescence due to their inability to maintain synchronization among crucial information in the face of intricate assaults.

Notably, Agarwal et al. [17] and Singh et al. [18] endeavored to develop hybrid techniques that harnessed the advantages of multiple mathematical aspects, achieving a degree of success. However, even their approaches faltered when confronted with attacks that disrupt the temporal relationships within multimedia content. In light of these limitations, a discerning observation of the early research in the domain of what is often referred to as the “first generation” digital watermarking led Kutter et al. [19] to introduce a novel methodology grounded in semantically meaningful data features capable of preserving content integrity even when subjected to intentional attacks. Their method, rooted in these semantically meaningful features, was aptly termed “second-generation watermarking”. This new approach represents a pivotal advancement in the pursuit of content protection, providing resilience against an array of attacks and offering a robust safeguard for the ownership of digital assets in this evolving digital landscape. Kutter et al. [19] initiated their work in the realm of watermark embedding by focusing image point features and employing 2D continuous wavelet transform. While their approach demonstrated a level of effectiveness in countering basic geometric attacks, it fell short when subjected to attacks altering the data’s spatial location. In pursuit of excellence, Jiang et al. [20] introduced a scheme with enhanced efficiency that utilizes regional features acquired through the watershed transformation. This strategy exhibited increased robustness against geometric attacks and JPEG compression compared to Kutter et al.’s method [19]. However, it proved inadequate in safeguarding synchronization information when confronted with diverse filter types.

Over time, several endeavors were made to devise a proficient hybrid watermarking methodology that effectively leverages the advantages of the intrinsic features of the data integration with the transform domain. The method proposed by Lee et al. [21] proposed a technique considering compressed domain watermarking for HD videos. They extract low-frequency coefficients of frames using DCT and apply a quantization index modulation method to embed and extract the watermark. They tested their scheme against three major types of attacks. The result of the simulation shows fair resilience against down-sampling, format conversion and frame rate change attacks, but they fail to test their scheme against most other video-specific attacks. Boris et al. [22] devised a perceptual strategy for image watermarking, incorporating a brightness model and the Hermite Transform. This approach provided an exhaustive examination of regional orientation and leveraged the Gaussian derivatives model to enhance early visual processing. By capitalizing on the masking characteristics of the HVS, they achieved a level of robustness sufficient to withstand rudimentary signal-processing attacks. Nevertheless, the scheme exhibited limitations when subjected to significant compression ratios and specific forms of added noise.

Table 1. Comprehensive Analysis of Various Watermarking Techniques.

Ref. No.	Technique Used	Transparency and Robustness Evaluation (Type of Attacks)
		Frame Swapping	Frame Averaging	Frame Cropping	Salt and Pepper Noise	Frame Insertion	Frame Rate Change	Lossy Compression Motion JPEG 2000	AVI to MP4 Conversion
[17]	A hybrid method using shapes the singular values of LL sub-band Video frame on the singular values of the watermark image using 2D-DWT and Singular value Decomposition (SVD).	√	√	√	√	X	X	X	X
[21]	The authors proposed a technique considering compressed domain watermarking for HD videos. They extract low-frequency coefficients of frames using DCT and apply a quantization index modulation method to embed and extract the watermark.	X	X	X	X	X	√	X	√
[23]	An algorithm for video watermarking that uses the green channel of the RGB frame for the embedding process using the DCT.	X	X	√	√	X	X	X	X
[24]	This technique uses the MPEG-2 standard in which DCT coefficients are adjusted from selected I-frames for watermarking purposes.	X	X	√	√	√	X	X	X
[25]	The method proposed video watermarking for copyright protection using two different algorithms: one is based on a detailed subband, and the other uses an approximate subband of the cover video. The authors embed the watermark in the frames where scene changes were detected.	√	√	X	√	X	X	X	X
[26]	The proposed technique is based on Contourlet Transform (CT) and SVD with the condition of insertion into low-frequency subbands of different SD-quality videos.	√	√	√	√	√	X	√	X
[27]	The technique to embed the watermark on a given video is based on the Harris corner detection method. The technique used the detected corner points for watermark embedding purposes.	√	√	√	√	√	X	X	X

offers a succinct overview of the evaluation of transparency and robustness across various types of attacks, employing a diverse range of methodologies.

Al-Gindy et al. [23] propose an adaptive algorithm for watermarking digital videos using discrete cosine transform in the frequency domain, emphasizing protection in the era of high-speed internet access. The algorithm uses the green channel of the RGB frame for the embedding process using the DCT algorithm and demonstrates robustness against various attacks, but it is filed when frames are inserted or when the video is exposed to a frame rate conversion attack. To fortify resilience and visibility against adversarial incursions, Rakesh and Sarabjeet [24] introduce a video watermark embedding paradigm hinged upon differential pulse code modulation (DPCM) and candidate I-frames. Their method harnessed the contours of the MPEG-2 standard and DCT coefficients, showcasing a measure of efficacy against diverse assaults but revealing susceptibility to incursions involving frame insertion. Notably, their strategy overlooked the nuances of video format and frame rate conversion attacks, integral facets in the realm of adept watermarking methodologies. In a parallel pursuit, Shukla and Sharma [25] devised a watermark embedding stratagem grounded in detecting scene changes in videos utilizing sub-bands of Discrete Wavelet Transform and the nuanced alpha blending technique. Despite exhibiting commendable performance in thwarting the infusion of sundry disturbances and geometric onslaughts, it exhibited vulnerability when confronted with temporal synchronization incursions. Moreover, it remained remiss in addressing the challenges posed by motion JPEG and MPEG-like compression, which are commonplace in the intricate tapestry of video processing and distribution networks.

Recently, a work that explores the intersection of Biology Information Technology and computer security presenting a novel algorithm for digital video watermarking was presented by Farri and Ayubi [26]. The approach combines chaotic systems, Cellular Automata, and DNA sequences, ensuring blind watermarking with robust copyright protection against diverse attacks, as evidenced by statistical criteria evaluation. Embarking on a distinctive trajectory, Agarwal et al. [27] undertook a meticulous exploration into the realm of perceptually consequential attributes in the video watermarking milieu, aspiring to formulate schemes impervious to both noise and affine transformations. Their methodology entailed the identification of the robust corner points in the frame of video via the method of detecting the corner using the approach suggested by Harris, standing as anchor points for the incorporation of watermarks. Although their approach demonstrated a degree of toughness in opposition to conventional image processing and onslaughts that disturb temporal synchronization, it fell short of achieving a discernible perceptibility under most circumstances. Notably, the scheme omitted considerations for prevalent video compression techniques, a pivotal consideration in the intricate landscape of video processing.

Regrettably, the quest for a watermarking solution that seamlessly combines robustness and imperceptibility against digital piracy remains unfulfilled. Industries engaged in the creation and distribution of digital content continue to grapple with revenue losses stemming from illicit changes and dissemination of their assets. Hence, a pressing need exists to devise a way out that not only associates the watermark to its respective cover data but also preserves synchronization among crucial information within watermark bits. In response to the aforementioned challenges, this paper introduces a robust watermarking method that significantly enhances payload capacity. This innovative approach leverages the notion of radial symmetry of a circle in conjunction with 2D-DWT and employs feature points detected through KAZE for watermark embedding.

3. Research Foundation

Within this section, we shall delve into the fundamental concepts and mathematical underpinnings essential for the forthcoming video watermarking scheme. This discussion will encompass key elements, including the 2D-DWT, the KAZE Method, and the acquisition of symmetry points through the application of circular symmetry principles.

3.1. 2D-Discrete Wavelet Transform (2D-DWT)

The Discrete Wavelet Transform (DWT) stands as a pivotal instrument for the multi-resolution dissection of video frames, affording the capacity to introduce watermarks at various scales. This unique attribute ensures that the embedded watermark signal remains imperceptible to the discerning eye, all the while safeguarding its integrity. DWT’s remarkable prowess lies in its simultaneous scrutiny of signals in both the temporal and frequency domains, maintaining a steadfast form. It is this characteristic that renders DWT superior to sinusoidal-based transformations, particularly in the realm of video processing [28]. The 2D-DWT further distinguishes itself as a formidable weapon against compression, courtesy of its adeptness at dispersing the watermark across diverse frequencies. Within a video frame, we find graceful undulations and intricate intricacies, each eloquently expressed through the low-frequency components. These components bear the weight of more energy and play a more pivotal role when a watermark graces the frame. A preeminent advantage of DWT lies in its adroitness in segregating low-frequency constituents from high-frequency counterparts, a feat achieved through an ensemble of discerning filters. In our pursuit, we have employed the discerning Haar filter to accomplish this endeavor.

In the realm of 2D discrete wavelet transformation, an image or video frame unfurls into four distinct components:

(1)

The Approximation Coefficients are often deemed the bedrock image, emblematic of the low-frequency essence.

(2)

The Horizontal Coefficients are a testament to the high-frequency nuances along the horizontal axis.

(3)

The Vertical Coefficients capture the vertical high-frequency elements.

(4)

The Diagonal Coefficients encapsulate the diagonal high-frequency details.

If we consider ‘f’ as the paragon of a video frame, graced by the waves of wavelet transformation, the ensuing outcome of the inaugural level of dissection assumes the form:

$$f=f_{LL}+f_{LH}+f_{HL}+f_{HH}$$

(1)

In this Equation (1), ‘f_LL’ embodies the approximation component of the frame, while ‘f_LH’, ‘f_HL’, and ‘f_HH’ stand as the sentinels of vertical, horizontal, and diagonal intricacies, respectively. It is within the bosom of the LL sub-band that we discover an abundance of energy, rendering it the most judicious candidate for the embrace of a watermark.

3.2. KAZE Feature Points

Feature detection and description constitute a vigorously pursued avenue within the realms of artificial intelligence and computer vision, engendering fervent research endeavors. The acquisition of features characterized by pronounced repeatability and distinctiveness, resilient in the face of diverse image transformations—be they perturbations of viewpoint, blurring, or the introduction of noise—emerges as a matter of paramount significance in the realm of next-generation digital watermarking.

A distinguished luminary in this expansive domain is the KAZE methodology, an example of nonlinear scale space feature point detection and description. It stands as a testament to meticulous refinement, eschewing the propensity for blurring edges and the unfortunate loss of intricate details inherent in linear scale-spaces engendered by the deployment of Gaussian filters. KAZE, an evolutionary stride beyond the Scale Invariant Feature Transform method (SIFT) and Speeded-Up Robust Features (SURF), demonstrate prowess in the identification of key points of heightened stability, eclipsing the capabilities of its precursor [29]. Contrasting prevalent algorithms reliant upon Gaussian scale-spaces and arrays of Gaussian derivatives as their smoothing kernels for scale-space analysis, KAZE diverges significantly. It boldly acknowledges the inherent limitations of the Gaussian scale space, which, in its uniform treatment, tends to efface the nuanced boundaries of natural objects while indiscriminately attenuating both details and noise across all strata of scale. The KAZE method, cognizant of these limitations, architects nonlinear scale spaces through the adroit employment of Additive Operator Splitting (AOS) techniques [30] and variable conductance diffusion [31]. In the crucible of these techniques, KAZE forges feature resilient to the vicissitudes of diverse image transformations, characterized by a superlative blend of repeatability and distinctiveness. The process unfolds as follows: the nonlinear scale space is meticulously constructed for a given input image, evolving up to a predetermined temporal threshold through the judicious application of AOS techniques and variable conductance diffusion. KAZE is founded upon the widely employed nonlinear diffusion equations, notably the Perona-Malik Equations (2) and (3), characterized by the following structure.

$${\displaystyle \frac{\partial I}{\partial t}}=divergence\left(c\left(\left|\left|\nabla I\right|\right|\right)\nabla I\right)$$

(2)

$$c\left(\left|\left|\nabla I\right|\right|\right)=e^{-{\left({\displaystyle \frac{\left|\left|\nabla I\right|\right|}{K}}\right)}^2}$$

(3)

In this context, ‘I’ denotes the image intensity across time ‘t,’ ∇I signifies the gradient of I, ||∇I|| represents the magnitude of the gradient, ‘c’ functions to ascertain the diffusivity, designed to be heightened in zones exhibiting brisk intensity changes (edges) and diminished in comparatively uniform areas. This design ensures that smoothing is accentuated in flat regions, thereby preserving edges. Additionally, ‘K’ stands as a positive constant governing the extent of smoothing, with larger values of ‘K’ yielding more pronounced smoothing effects.

Once the nonlinear scale space is established, KAZE proceeds to discern 2D features of particular interest. The Hessian matrix is a crucial component in the KAZE algorithm for feature detection. The matrix equivalent to its Hessian approximation at a given point G in the x, y, and xy directions is expressed as per Equation (4) as follows:

$$H{s}_{Approx}\left(G,\sigma \right)=\left[\begin{array}{cc}C{o}_{xx}\left(G,\sigma \right)& C{o}_{xy}\left(G,\sigma \right)\\ C{o}_{xy}\left(G,\sigma \right)& C{o}_{yy}\left(G,\sigma \right)\end{array}\right]$$

(4)

In this context, Co_xx(G, σ), Co_yy(G, σ) and Co_xy(G, σ) refer to the convolution of the image with standard deviation σ = 1.2 in x, y and xy direction [32].

• The determinant of Hs_Approx is calculated as,

$$\left|H{s}_{Approx}\right|=C{o}_{xx}\left(G, \sigma \right) C{o}_{yy}\left(G, \sigma \right)-{\left(\omega C{o}_{xy}\left(G, \sigma \right)\right)}^2$$

(5)

where ω serves as a weighting coefficient for the filter response, employed to harmonize the expression for the Hessian determinant. It is approximated to have a value of around 0.9 [32].

As the Hessian matrix signifies local curvature, the magnitude of Hessian approximation, denoted as |Hs_Approx|, signifies the blob indication at position G in the image/frame. The peaks of |Hs_Approx|, as stipulated by the formulation in Equation (5), are subsequently interpolated using the methodology elucidated by Brown and Lowe [32], identifying our point of interest. Culminating these salient features, KAZE proceeds to ascertain the main orientation of the key point. In this intricate tapestry of computational artistry, KAZE emerges as a vanguard, unfurling new vistas in the pursuit of feature detection and description within the realms of AI and computer vision.

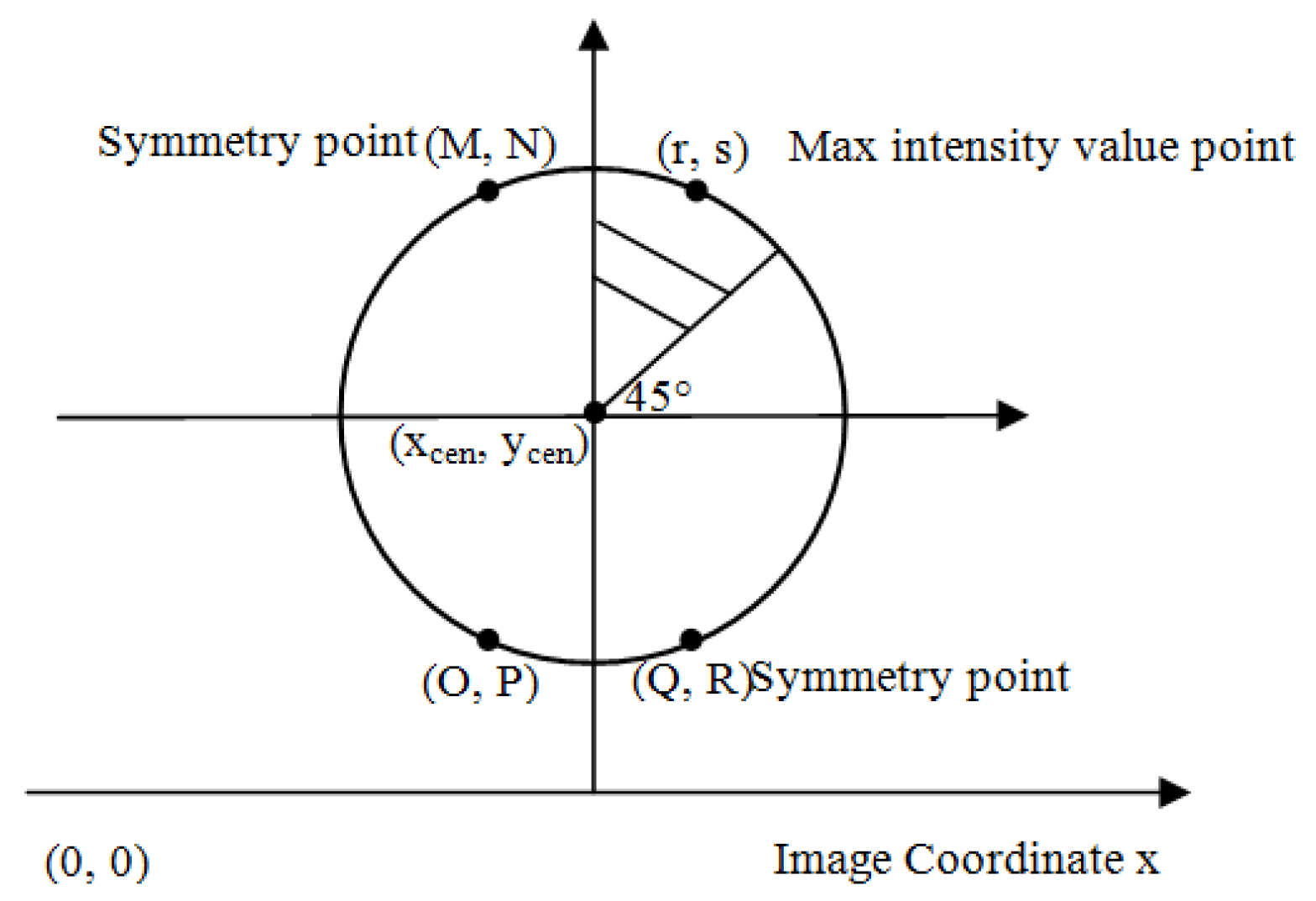
3.3. Symmetry Point Determination via Circular Symmetry Notion

A circle can be delineated as the ensemble of all points positioned at a designated distance ‘rad’ from a central point. (x_c, y_c). To represent this distance relationship in Cartesian coordinates, we can utilize the Pythagorean theorem, as delineated in Equation (6) as follows:

$${\left(\mathrm{x}-{\mathrm{x}}_{\mathrm{c}}\right)}^2+{\left(\mathrm{y}-{\mathrm{y}}_{\mathrm{c}}\right)}^2={ \mathrm{rad}}^2$$

(6)

However, Equation (6) necessitates substantial computational effort involving subtraction and square root calculations. To alleviate this computational burden, we leverage the intrinsic symmetry inherent in the circular shape. It is well-established that the circular form exhibits similarity in every quadrant. Consequently, we can efficiently calculate a point within one quadrant and readily derive three additional points by capitalizing on the symmetry properties mirrored across the horizontal and vertical axes [33], as shown in Figure 1.

Our method calculates point (r, s) as the point where the intensity is maximum on the circular perimeter traced from an angle of 45° to 90°. We can obtain the coordinate locations of other symmetrical points as follows:

M = x_c − (r − x_c) = 2x_c − r

N = x_c − (r − x_c) = s

O = x_c − (r − x_c) = 2x_c − r

P = y_c − (r − y_c) = 2y_c − r

Q = x_c − (r − x_c) = r

R = y_c − (r − y_c) = 2y_c − r

4. Proposed Video Watermarking Method

This section is dedicated to the elucidation of the watermark embedding process at designated locations and the subsequent watermark extraction stages within the proposed methodology. A grayscale image assumes the role of the watermark, owing to its capacity to encapsulate a substantial volume of watermark information, rendering grayscale images exceptionally appropriate for pragmatic application [34]. Notably, the scheme in question harnesses the luminosity elements within the video composition, a strategic choice enhancing its resilience against highly lossy compression [35]. The meticulous procedure guiding the choice of positions for watermark insertion within the video frames is expounded in Section 4.1. Section 4.2 explains the detailed procedure for determining embedding sites and the watermark integration and extraction using Algorithms 1, 2 and 3.

4.1. Determination of Embedding Sites

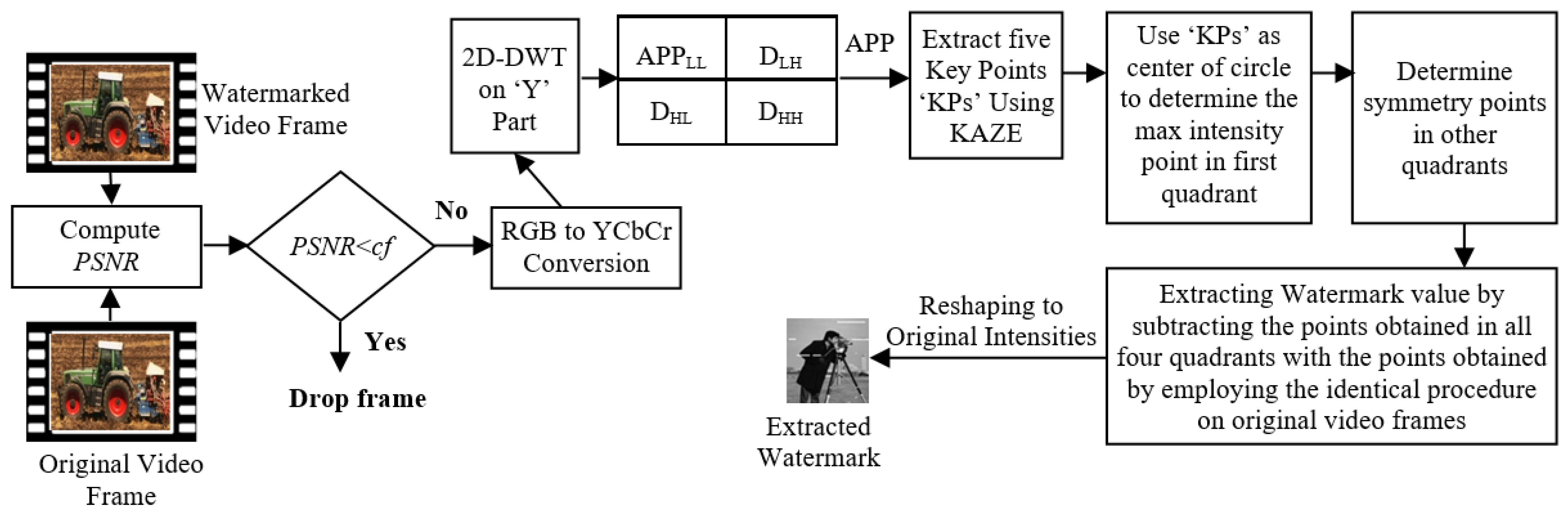
This section delves into the intricate modus operandi governing the meticulous determination of watermark embedding sites, meticulously outlined in Algorithm 1. The process commences by orchestrating a transformation wherein every video frame is transposed into the YCbCr color space, following which the brightness part ‘Y’ is systematically subjected to an extensive decomposition, generating a spectrum of frequency coefficients through the instrumentality of 2D-DWT. Elaborated within the algorithmic framework, Algorithm 1 elucidates the underpinning methodology: the proposed scheme orchestrates the calculation of five invariant feature points, diligently employing the KAZE technique upon the approximation segment of the transformed frame.

Central to the watermark embedding process is the establishment of a circle with a specified radius, ‘rad = 20’ pixels, wherein the previously computed key points act as pivotal centers. In a bid to expedite computational efficiency, the scheme judiciously calculates only the 1/8 segment of this circle, spanning from 45° to 90°. The local maxima residing within this delineated sector are discerningly identified as the primary embedding locations. Complementing this computational optimization strategy, the notion of circular symmetry emerges as a pivotal asset governing the acquisition of additional embedding locations along the circular periphery, as comprehensively addressed in Section 3.3. The strategic deployment of a reduced number of calculated points per frame augments the watermark’s perceptual transparency, while the astute utilization of circular symmetry not only economizes computational resources but also engenders a remarkable fourfold amplification of the payload capacity. In each frame, exactly 20 feature points are selected—five from KAZE and their symmetric counterparts—to serve as embedding locations. This number is fixed and not adaptive.

Algorithm 1. Determination of Watermark Embedding Sites
Input: Primary Video (PV) Output: Watermarking Sites (WS) Commence:    1. For each frame, denoted as j ranging from 1 to the total frame count:
	a. Transform frame Fj into the YCbCr color space and disassemble constituent components in luminance part FjY and the chrominance parts. b. Engage the 2D-Discrete Wavelet Transform (2D-DWT) on FjY to effectuate the disintegration of the frame into its approximation component APP, in conjunction with the detailed components DH, DV, and DD, in accordance with the process elaborated in Section 3.1:   [APP, DH, DV, DD] ← 2D-DWT(FjY) c. Employ the KAZE method to identify five stable key points (KPs) on APP.   KPs ← KAZE_KPs [APP, 5] d. For each of the five feature points, denoted by k ranging from 1 to 5: i. Determine the primary embedding site PES(r, s) by identifying the utmost level of intensity within the one-eight segment of circular vicinity (cir_vic) with a radius of ‘rad’ pixels, spanning from 45° to 90°, originating from the first feature point KPj among the five KPs:   PES(r,s) = max[cir_vic(KPj, rad, 45–90°)] ii. Acquire the remaining three embedding locations (second embedding site SES, third embedding site TES, and fourth embedding site FES) by harnessing the principles of circular symmetry, as elucidated in Section 3.3:   SES(M, N) = (2xc − r, s)   TES(O, P) = (2xc − r, 2yc − r)   FES(Q, R) = (r, 2yc − r) iii. Construct the watermarking sites array WSk:   WSk = [PES(a, b), SES(M, N), TES(O, P), FES(Q, R)] e. Conclude the loop pertaining to feature points.
End of Algorithm

4.2. The Elegance of Watermark Integration and Retrieval Procedure

In Algorithm 2, we elegantly outline the procedure for artistically molding the watermark within the luminance component positions of the video frame. The act of watermark extraction unfolds as a near-mirrored rendition of the watermark embedding process, which we shall elucidate in Algorithm 3. Figure 2 and Figure 3 portray the block diagrams illustrating the processes of watermark embedding and extraction, respectively. The watermark extraction method relies on the same procedure employed during watermark embedding to identify the regions within each frame. Watermark values are subsequently extracted through the subtraction of intensity values derived from the mined locations and the corresponding intensity values acquired by subjecting the identical methodology to the original video. This symmetrical methodology ensures the accurate retrieval of watermark information.

Algorithm 2 delineates the process of perceptually shaping the watermark at the luma locations of the video frame, as ascertained via Algorithm 1, where each feature point yields four distinct embedding sites. Initially, the algorithm introduces the variable ‘tally’, initialized to the value of 1. It is noteworthy that, in MATLAB, numbering commences at 1, in contrast to most other programming languages that typically initiate numbering from 0. Steps 1 through 3 elucidate how Algorithm 2 initially extracts four watermark sites for each KAZE point and visually molds their values onto the positions acquired using Algorithm 1. In order to strike an equilibrium between invisibility and resilience, the watermark value undergoes scaling by a factor denoted as ‘α’ before being shaped onto the acquired sites. To ensure the sequential extraction of fresh pixel locations on each occasion, the algorithm employs the variable ‘tally,’ initially set to 1, increased after each iteration, and a novel and consecutive pixel location is secured. When the value of the ‘tally’ surpasses the dimensions of the watermark (W) represented by m x n, this signals that no further new embed locations remain. Consequently, the ‘tally’ variable is reset to 1 to resume the process anew.

Algorithm 2. Watermark integration process
Input: Watermarking Sites (WS), Watermark Image (W) with dimensions mxn, Visibility factor (α) Output: Watermarked Frame Y component (FjY) Commence:
	1. Read Watermark (W) 2. Set tally = 1 3. Iterate through the luminance component of video frames (FjY), as detailed in Algorithm 1, for each frame denoted by j ranging from 1 to the total number of frames.
		a. For each of the five feature points detected by KAZE, denoted by k ranging from 1 to 5: b. For each of the four embedding sites per key point, denoted by i ranging from 1 to 4: aa. Determine the coordinates (x, y) to select the intensity values from the watermark based on the current location, considering: x = floor((tally − 1)/n) + 1 y = abs(tally % n) if (y == 0), then set y = n Increment tally by 1. bb. If the tally exceeds the watermark dimensions (m × n), reset the tally to 1. cc. Scale the watermark value by a visibility factor α: value(j, k) = W(x, y) × α dd. Embed the watermark value into the locations (WS) acquired through Algorithm 1.
	4. Complete the loops.
End of Algorithm

The extraction of a watermark entails a process nearly antithetical to the embedding of watermark information, as elucidated in the subsequent Algorithm 3.

Algorithm 3. Watermark Extraction Process
Input: Watermarked Video, Original Video, PSNR cutoff (cf), Visibility Factor (α) Output: Extracted Watermark Commence:
	1. Initialize the frame index (frame_index) to 1. 2. Initialize an empty list to store the extracted watermark (extracted_watermark). 3. Repeat the following steps for each frame in the watermarked and original video:
		a. Derive the frame from both the watermarked and the authentic video. b. Compute PSNR for the watermarked video frame in comparison to the corresponding frame in the authentic video. c. If the computed value falls below the designated PSNR cutoff (cf), proceed to the subsequent frame. d. Transform the watermarked frame into YCbCr color space. e. Apply 2D-DWT to the ‘Y’part and decompose it into APP and detailed components. f. Identify five key points within the APP section of the frame employing the KAZE technique. i. Stable_Points = KAZE_Key_Points(Ym) ii. Key_Points = Strongest(Stable_Points, 05) g. For each key point: i. Compute one-eighth of the circular neighborhoods spanning from 45° to 90° around the key point, treating it as the center point of the circle with a radius of ‘rad = 20’ pixels. ii. Acquire the maximum value point among the computed points along with their matching symmetry counterparts using the method described in Section 3.3. h. Retrieve the watermark values by deducing the intensity values of the identified sites from the intensity values identified by employing an identical procedure on the original video. i. Divide the extracted watermark values by the visibility factor ‘α’ to obtain the original intensity values of the watermark. j. Append the extracted watermark values to the extracted_watermark list. k. Increment the frame_index by 1. l. If there are more frames in the video, return to step 3.
	4. Return the extracted_watermark as the output.
End of Algorithm

5. Empirical Setup and Outcomes

The envisioned system is emulated on a personal computer equipped with 12 GB RAM and a 10th-gen i7 processor, employing MATLAB R2022b. The evaluation of the proposed approach was conducted using a set of eight high-definition (HD) color videos sourced from the Xiph dataset, which served as the test content. Each of the eight videos possesses dimensions of 1920 × 1080 pixels, encompassing a sample of 52 frames. In order to subject these videos to a range of potential attacks, the initial step involved the conversion of all videos into an uncompressed AVI format. The video frames corresponding to each of the eight videos can be observed in Figure 4, providing a visual representation of the content under examination.

To substantiate the effectiveness of the suggested approach, each of the eight videos underwent watermarking independently with the utilization of a grayscale image named ‘cameraman.tiff’. This grayscale image, characterized by a wide range of gray shades, was employed as the watermark. The measure of a watermarking system’s embedding capacity is quantified by the volume of watermark bits that can be incorporated into the original data while preserving its invisibility. The proposed method advocates for the incorporation of merely twenty locations designated for watermark embedding in each frame, translating to the insertion of 1040 watermark bits within a video consisting of only 52 frames, all without compromising its imperceptibility. This corresponds to a payload ratio of approximately 0.00052 bits/pixel (for 1920 × 1080 resolution). This capacity can be further expanded by augmenting the number of frames within the video, thereby increasing the size of the watermark. Furthermore, the application of the radial symmetry of a circle can be harnessed to enhance the watermark embedding capacity to even greater extents. By integrating circular symmetry and KAZE into the proposed methodology, we streamline the computational process to determine a singular maximum intensity point. The additional three points are discerned through symmetry. Consequently, the computed watermark embedding time is notably efficient, measured at 2.12 fps, in stark contrast to the 8.41 fps reported by Farri and Peyman [26].

Figure 5 presents a visual comparison between the original frame and the associated watermarked frame derived from ‘tractor.avi’ utilizing the suggested approach, providing a clear illustration of the watermarking process’s effect on the content.

5.1. Assessing Visual Transparency

Evaluating the visual transparency of the watermarked video stands as a paramount parameter and represents a formidable task when gauging the impact of the watermark on the video’s quality. To ensure the utmost reliability, the suggested approach incorporates two widely acknowledged and previously validated objective metrics: the Peak Signal Noise Ratio (PSNR) and the Structural Similarity Index Measure (SSIM) and a deep learning-based metric, Learned Perceptual Image Patch Similarity (LPIPS). These metrics are employed to comprehensively evaluate the perceptual quality of the watermarked videos. In our proposed system, the PSNR, SSIM and LPIPS are calculated on RGB video frames, frame-by-frame, and their average values are reported over the entire video.

5.1.1. PSNR

PSNR serves as a prevalent metric for evaluating the efficiency of watermarking schemes and assessing the visual superiority of watermarked videos. The integration of a watermark typically leads to a reduction in the visual quality of the video. A low PSNR value suggests a significant alteration in the video, whereas an elevated PSNR value indicates that the video has not been significantly distorted. The PSNR is obtained using Equation (7) as,

$$PSNR=10lo{g}_{10}{\displaystyle \frac{{(Max\_In)}^2}{MSE}}$$

(7)

The Mean Square Error (MSE) between the watermarked frame (FW) and the original frame (FO), each having dimensions of hi and wd, can be calculated as per Equation (8).

$$MSE={\displaystyle \frac{{\sum }_{p=1}^{hi}{\sum }_{q=1}^{wd}{\left[FO\left(p,q\right)-FW\left(p,q\right)\right]}^2}{hi x wd}}$$

(8)

Here, Max_In, which equals 255, represents the frame under evaluation’s maximum intensity value.

5.1.2. SSIM

SSIM is a well-established metric utilized in the film and video sector to evaluate the influence of processing on video quality on the basis of perceptual distortion in relation to the difference in brightness values and to measure the similarity of two frames. The SSIM values range between −1 and +1, with +1 signifying that the compared video frames are indistinguishable. This criterion encompasses three functions for comparing luminance (C_L), contrast (C_C), and structure (C_S), respectively. SSIM is defined using Equation (9) as follows:

$$SSIM\left(FO,FW\right)=\left[{\mathrm{C}}_{\mathrm{L}}{\left(FO,FW\right)}^{\delta }.{\mathrm{C}}_{\mathrm{C}}{\left(FO,FW\right)}^{\eta }.{\mathrm{C}}_{\mathrm{S}}{\left(FO,FW\right)}^{\xi }\right]$$

(9)

To calibrate the relative significance of luminance, contrast, or structural components, one consistently considers positive values for the parameters δ, η, and ξ [36].

5.1.3. Subjective Measurement of Imperceptibility

The optimal approach for assessing the quality of a watermarked video lies in conducting a subjective evaluation grounded in the Human Visual System (HVS). The Percent Mean Opinion Score (PMOS) method, advocated by Agarwal and Husain [10], proves to be particularly valuable. This method entails rating videos based on a three-grade impairment scale, a set of scores established by a panel of human observers. The assessment scale spans from 0 to 10, where 0 signifies visible, 5 indicates intermediacy, and 10 represents the transparency of the watermark.

The outcomes of applying the PMOS method to diverse High-Definition watermarked videos within the proposed scheme are delineated in

Table 2. Average PSNR, SSIM and PMOS for untouched Watermarked Videos.

Type of Attack	PSNR	SSIM	PMOS
No Attack	75.02	1	1

. The PMOS, derived from scores assigned by human observers, is calculated using Equation (10), wherein:

$$\mathrm{Percent} \mathrm{Mean} \mathrm{Opinion} \mathrm{Score} ={\displaystyle \frac{\mathrm{Sum} \mathrm{of} \mathrm{Assigned} \mathrm{Score}}{\mathrm{Sum} \mathrm{of} \mathrm{Maximum} \mathrm{Possible} \mathrm{Score}}}\times 100$$

(10)

Table 2 provides a comprehensive overview of video quality and similarity assessment prior to the application of any attacks. This evaluation is based on the four symmetrical points on the circle boundary and is expressed in terms of the average values of PSNR, SSIM and PMOS across all eight videos. Setiadi [37] suggested that to ensure optimal visual quality, it is essential that PSNR remains at a minimum of 30 dB, while SSIM should approach a value of 1. The PSNR, SSIM and PMOS values were computed by comparing the original video with its corresponding watermarked video. For a video considered transparent, the value PMOS should be greater than 8 [10]; in our case, a value equal to 10 is assigned by all the human observers, which shows the effectiveness of the suggested scheme. Impressively, the results reveal exceptionally high PSNR, SSIM and PMOS values for the videos under consideration, underscoring the suggested approach’s capacity to maintain superior visual fidelity even after watermarking.

5.1.4. LPIPS

LPIPS is a deep learning-based metric used to measure the perceptual similarity between two frames/images. The LPIPS uses features from deep neural networks trained on large image datasets, which differentiate it from other popular metrics like PSNR or SSIM that measure the pixel-wise differences. To assess the perceptual similarity between the original and watermarked videos, we employed the LPIPS metric using a pre-trained AlexNet model. The algorithm extracts frame pairs from both videos, processes them through a transformation pipeline, and computes LPIPS scores using learned deep features. The resulting scores reflect the visual similarity as perceived by human observers, with lower values indicating better imperceptibility. The final LPIPS score was computed as the average across all tested frame pairs. Lower values indicate stronger visual similarity and better watermark transparency. Algorithm 4 gives step-by-step measurements of LPIPS score computations. The average LPIPS score computed between the original and watermark videos before the attack and also in case of frame insertion and frame rate change attacks is 0.0003, while its value varies between 0.06 and 0.01 for all other attacks, indicating high imperceptibility (near-invisible impact) aligned with human visual perception.

Algorithm 4. LPIPS Computation

Input: Original video OV1, Watermarked video WV2, Frame count N, Pretrained LPIPS model (AlexNet) Output: Average LPIPS score Commence: 1. Load the Pretrained LPIPS model:    loss_fn ← LPIPS(net = ‘alex’) 2. Create directories to store extracted frames:    original_frames_dir ← “frames/original”    watermarked_frames_dir ← “frames/watermarked” 3. For each input video (OV₁ and WV₂), extract the first N frames:   For i = 0 to N − 1 do:     a. Read frame_i from OV1 and save as original_frame_i.png     b. Read frame_i from WV2 and save as watermarked_frame_i.png 4. Initialize LPIPS scores list:    lpips_scores ← [] 5. Define image transformation pipeline:    transform ← Resize(256 × 256) → ToTensor() → Normalize([0.5], [0.5]) 6. For i = 0 to N − 1 do:   a. Load and transform original_frame_i and watermarked_frame_i:       img1 ← transform(original_frame_i)       img2 ← transform(watermarked_frame_i)   b. Compute LPIPS distance: score ← loss_fn(img1, img2) c. Append score to lpips_scores 7. Compute average LPIPS:    avg_lpips ← mean(lpips_scores) 8. Return: avg_lpips End of Algorithm

5.2. Assessing Robustness

Robustness, a pivotal aspect of watermarking, measures the watermark’s resistance against different attacks. In the investigation given, we evaluate the resilience of the watermark through a series of attacks on the watermarked video followed by the employment of the process of retrieving the watermark outlined in the suggested approach. The robustness property of the proposed scheme is measured by using the parameters Correlation Coefficient (CC). If CC > γ, it is alleged that the watermark is detected in the watermarked video; otherwise, it signals the failure of the scheme to retain the watermark in the video. For optimal robustness and to affirm the video’s copyright integrity, a minimum value of γ = 0.7 is set as the criterion, aligning with the recommendation of Jordi and Ricciardi [14]. The CC value is computed according to Equation (11).

$$CC={\displaystyle \frac{{\sum }_m{\sum }_n\left(W{O}_{mn}-\mu O\right)\left(W{E}_{mn}-\mu E\right)}{\sqrt{\left({\sum }_m{\sum }_n{\left(W{O}_{mn}-\mu O\right)}^2\right)\left({\sum }_m{\sum }_n{\left(W{E}_{mn}-\mu E\right)}^2\right)}}}$$

(11)

Here, WO and WE represent watermark matrices of identical dimensions (m × n), while µO and µE respectively denote the mean values of the original and extracted watermark. For a practical illustration of this process, refer to Figure 6, which provides a visual depiction of the original watermark and the corresponding extracted watermark from the watermarked video ‘tractor’ subjected to a 5% averaging of frames attack.

The watermark’s resilience across all watermarked videos, under the influence of diverse adversarial actions, is quantified by calculating the average CC value. The CC, PSNR and SSIM values are conveniently summarized in

Table 3. Average Value of Robustness and Imperceptibility Metrics Under Various Attacks.

Type of Attack		PSNR	SSIM	CC
No Attack		75.02	1	0.93
Frame Swapping	5%	70.12	0.89	0.77
	10%	67.78	0.84	0.71
Frame Averaging	5%	74.06	0.99	0.90
	10%	74.02	0.99	0.88
Frame Cropping	5%	19.35	0.90	0.81
	10%	16.06	0.81	0.79
Salt and Pepper Noise	Density 0.001	35.09	0.98	0.70
	Density 0.0005	38.09	0.99	0.80
	Density 0.0003	40.32	0.99	0.81
Frame Insertion (In Any Number)		75.02	1	0.93
Frame Rate Change	30 to 15 fps	75.02	1	0.93
	30 to 45 fps	75.02	1	0.93
Lossy Compression Motion JPEG 2000	CR = 5	50.04	1	0.93
	CR = 10	45.08	0.99	0.77
	CR =15	42.52	0.99	0.74
MPEG-4 AVC (.avi to .mp4 conversion)		34.41	0.98	0.53
.avi to .mov conversion		41.92	0.97	0.86

, thereby providing a comprehensive assessment. Remarkably, in almost all scenarios, the CC values exceeded the threshold, affirming the substantial robustness afforded by the proposed method in the face of various attacks.

Table 3 elucidates the efficacy of the proposed technique concerning its robustness and the concurrent preservation of watermark imperceptibility. It delineates the outcomes before and after the videos underwent a group of adversarial measures, encompassing temporal desynchronization, geometric distortion, the introduction of diverse noise profiles, and distinct forms of lossy video compression. The ensuing analysis underscores the technique’s proficiency in maintaining watermark integrity and transparency under these multifaceted assault scenarios. The deviation of the CC value from perfect unity under no attack is primarily attributed to minor quantization errors and rounding artifacts introduced during color space conversions (YCbCr to RGB and back) and DWT transformations, especially due to floating-point operations. In contrast, embedding the watermark in the Y (luminance) channel proves more robust due to its perceptual significance and better retention under standard transformations. This observation aligns with prior studies and is supported by our experimental results.

5.2.1. Assessing the Impact of Frame Swapping and Averaging

The deliberate interchange and blending of video frames introduce disruptions in their temporal alignment, thereby affecting the watermark’s resilience. To gauge the watermark’s robustness, we subjected the watermarked videos to separate frame-swapping attacks, encompassing 5% and 10% random frame exchanges. Notably, the simulation results revealed commendable performance with a correlation coefficient exceeding 0.7 and a PSNR value surpassing 67 dB across all scenarios. These outcomes underscore the scheme’s capability to maintain robust watermark integrity and uphold superior video quality. The notion of frame averaging, wherein each frame’s values are amalgamated with those of its immediate predecessors and successors, was further scrutinized. This temporal collision challenge was applied to the videos by averaging 5% and 10% of frames individually. In both cases, the computed correlation coefficients exceeded 0.88, reaffirming the method’s commendable resistance against assaults that disrupt temporal synchronization between video frames.

5.2.2. Exploring Geometric Synchronization: The Impact of Frame Cropping

In addition to the quantitative assessments of watermark robustness and imperceptibility for swapping and averaging, we delve into one of the most prevalent geometric synchronization attacks, cropping. Our analysis encompasses uniform cropping of video frames at rates of 5% and 10%. To showcase the efficacy of our proposed method, we provide a comprehensive overview in Table 3. The discerning insights gleaned from Table 3 unambiguously highlight the exemplary imperceptibility and remarkable robustness exhibited by the proposed approach across both the cropping scenarios. These findings underscore the method’s capacity to endure cropping attacks with some loss of visual integrity of the watermarked video content.

5.2.3. Resilience Against Noise Intrusion: A Comprehensive Evaluation

In a quest to assess the watermark’s mettle against external perturbations, our method systematically confronts the challenge posed by additive Salt and Pepper noise. The examination covers an array of noise densities, spanning from 0.001 down to 0.0003 and further down to 0.0005. The compelling findings unveil a direct correlation between robustness and noise density, with a pronounced increase in resilience as the noise density diminishes. Across all tested densities, the Correlation Coefficient (CC) values consistently hover around or exceed the 0.70 threshold. This steadfast performance across varying noise intensities underscores the method’s commendable effectiveness in countering both additive and multiplicative noise intrusions. Moreover, the metric of Peak Signal-to-Noise Ratio (PSNR) maintains an optimal standard, with Structural Similarity Index Measure (SSIM) values consistently surpassing the 0.98 benchmark. These outcomes accentuate the method’s unwavering capability to preserve watermark integrity and video quality in the face of diverse noise challenges.

5.2.4. Preserving Integrity in Frame Insertion and Frame Rate Manipulation

In the realm of video editing, the insertion of disparate frames into the ongoing video sequence is not uncommon. Often, this occurrence arises inadvertently during the integration of commercial advertisements. The impact of such unintentional alterations becomes particularly pronounced when assessing the correlation between the embedded watermark and its subsequent extraction. Our method, as elaborated in Section 4.2, employs a selective extraction approach, exclusively recovering the watermark from frames that closely resemble the original, as defined by a predefined cutoff ‘cf’. Non-conforming frames are discreetly omitted from the process. This strategic filtration preserves the queue’s compositional integrity, ensuring an unobtrusive visual quality for the video. Simultaneously, the method consistently regains an undistorted watermark, maintaining its integrity. Furthermore, the method exhibits remarkable resilience even when faced with variations in frame rates, whether by augmentation or reduction. As depicted in Table 3, the visual quality and embedded watermark robustness remain largely unaffected. The Correlation Coefficient (CC) values sustain their proximity to unity by our method. This enduring fidelity underlines the robustness and consistency of our proposed approach.

5.2.5. Balancing Compression and Integrity

In the context of video processing, compression techniques play a pivotal role in reducing storage requirements and expediting file transfers. The application of such methods can significantly affect the integrity and robustness of the embedded watermark. Our simulation results, as presented in Table 3, underscore this relationship. In the case of lossy Motion JPEG 2000 compression, the values of CC, PSNR, and SSIM remain notably high. These metrics exhibit a gradual decline as the videos are subjected to varying compression ratios, including 5, 10, and 15. The watermark detection success rate is, as anticipated, reduced when employing MPEG-4 AVC compression, given its inter-frame compression coding that significantly diminishes video size. In this scenario, the CC value hovers around 0.53, while PSNR and SSIM values remain above the threshold and close to unity, signaling a non-satisfactory watermark detection capability and reasonable visual quality as expected. As shown in Table 3, the average PSNR remained above 42 dB, SSIM above 0.94, and the correlation coefficient of 0.86 was observed after AVI to MOV conversion, which verifies that transparency of the watermarked video and shows that the extracted watermark is clearly correlated with the original which further confirms the reliability of our watermark detection even under common format conversion workflows used in video distribution.

To summarize our findings, the simulation results of our proposed scheme bear witness to a remarkable level of imperceptibility, signified by the high values of PSNR and SSIM. This holds true even in the face of the various video attacks that have been meticulously examined. Our method’s adoption of 2D-Discrete Wavelet Transform and the KAZE technique empowers it to consistently identify the same feature points, thereby effectively thwarting the impact of these assaults. The correlation coefficient values, nearing unity in all instances, serve as further affirmation of the efficacy of our proposed approach. Moreover, harnessing the radial symmetry of the circle not only bolsters payload capacity but also concurrently curtails computational overhead, reinforcing the proposal’s standing as a fitting contender for a multitude of video processing applications.

5.3. Statistical Assessment of Scheme Effectiveness via T-Test Hypothesis Analysis

The security of a watermark hinges upon its transparency and resilience in the face of adversarial attacks. It is imperative that watermarking algorithms demonstrate robustness against a spectrum of potential threats and distortions. In the context of this paper, the efficacy of the proposed algorithm is subjected to rigorous evaluation employing a statistical assessment involving the acceptance or rejection of hypotheses through a t-test. The subsequent sections expound upon the outcomes derived from these comprehensive analyses. In the realm of scientific inquiry, hypothesis testing emerges as a refined mechanism for deducing conclusions, a formal practice that involves discerning between two conjectures predicated on measurements extracted from a judiciously chosen sample. Within the confines of our study, we scrutinize the robustness of the proposed algorithm against an established optimal value. This rigorous assessment entails the juxtaposition of our algorithm’s performance against this optimal benchmark. Employing a meticulously selected hypothesis test, leveraging the t-test and grounded in the t-distribution, we seek to appraise the efficacy of the proposed watermarking scheme through a statistical lens. The formulation of null and alternative hypotheses becomes the linchpin of this endeavor, affording us the means to delve into the watermarking scheme’s resilience against diverse attacks, thus augmenting its ability to extract the watermark even in the wake of exposure to various adversarial scenarios.

The Null and the Alternative Hypotheses in our case are,

Null Hypothesis H₀: μ ≤ 0.7, i.e., the mean value of robustness is less than or equal to 0.7.

Alternative Hypothesis H₁: μ > 0.7, i.e., the mean value of robustness obtained through sample videos is greater than 0.7.

In the intricate realm of hypothesis testing, a judicious selection of the appropriate hypothesis test becomes paramount. This process entails the meticulous evaluation of a test statistic denoted as “t,” derived from the measurements within the sample under consideration. Should the calculated value of “t” prove to be sufficiently improbable under the null hypothesis (H₀), we find ourselves compelled to entertain the alternative hypothesis, denoted as H₁. The decision between H₀ and H₁ hinges on the comparison of the test statistic against a predetermined threshold. In the event that the test statistic surpasses this predefined threshold, H₀ is deemed acceptable; otherwise, H₁ takes precedence. The establishment of this threshold involves a nuanced consideration, carefully navigating the trade-off between two distinct types of error probabilities. The methodology for calculating the test statistic, along with its associated t-values, is contingent upon the specific hypothesis test chosen for the analysis. In instances where the sample size is modest, the venerable t-test assumes prominence for evaluating the significance of the mean difference between two related samples [38]. The relevant test statistic, denoted as “t”, is calculated as:

$$\mathrm{t}={\displaystyle \frac{\overline{X}-{\mathsf{\mu }}_{{\mathrm{H}}_0}}{\frac{{\mathsf{\sigma }}_{\mathrm{S}}}{\sqrt{\mathrm{n}}}}}$$

(12)

where $\overline{X}$ is the mean value of the robustness metric obtained through n sample videos, and the standard deviation of the differences σ_s is calculated as per Equation (13),

$${\mathsf{\sigma }}_{\mathrm{S}}=\sqrt{{\displaystyle \frac{\sum {({\mathrm{X}}_{\mathrm{i}}-\overline{X})}^2}{\mathrm{n}-1}}}$$

(13)

The derived t-values, as determined by the formula represented in Eq. (12), are meticulously presented in

Table 4. Statistical Evaluation of t-values Across Various Attacks.

S. No.	Name of Attack	Mean Value of CC	σs	t-Value
1	5%Frame Swapping	0.77	0.0043	45.08
2	5%Frame Averaging	0.90	0.0026	209.57
3	5%UniformFrame Cropping	0.81	0.0065	47.76
4	Salt and Pepper Noise d = 0.0005	0.80	0.0064	44.09
5	Frame Insertion	0.93	0.0050	129.0
6	Frame Rate Change	0.93	0.0050	129.0
7	Motion JPEG 2000Compression with CR = 5	0.93	0.0050	129.0
8	.AVI to .MP4 conversion	0.53	0.00239	−201.14

. These values assume a pivotal role in the process of either accepting or refuting the proposed hypothesis. A nuanced assessment follows, wherein the computed t-value is juxtaposed against critical values extracted from the t-distribution table. The degrees of freedom (DOF) for this analysis are contingent upon the sample size, denoted as ‘n’, and are defined as n − 1. In our case, where eight sample videos are considered, the degrees of freedom amount to 7. The chosen level of significance, designated as 0.05, further informs our analysis. Should the computed t-value attain statistical significance at this predetermined level, such as 0.05, the rejection of the null hypothesis becomes imperative, ushering in a paradigm where the proposed hypothesis holds sway.

The computed t-values, as delineated in Table 4 through the application of Equation (12), play a pivotal role in the assessment and adjudication of the hypothesis under consideration. A meticulous examination ensues, involving a comparison between the calculated t-value and critical values derived from the t-distribution table, where the degrees of freedom (DOF) are defined as n − 1, with ‘n’ representing the sample size, in our specific scenario involving eight sample videos, the corresponding DOF is established as 7, alongside a predetermined level of significance fixed at 0.05. Upon scrutiny of the observed t-values for attacks from serial numbers 1 to 7, as indicated in Table 4, a noteworthy observation surfaces—the computed t-values exceed the critical value of 1.895, as per the t-distribution. This outcome leads to the affirmative conclusion that the actual robustness results signify an attack-bearing ability for the proposed scheme surpassing the optimal robustness value. Consequently, the proposed scheme exhibits a pronounced effectiveness against these attacks. Conversely, for the attack corresponding to serial number 8, a nuanced analysis is warranted. In this instance, the null hypothesis finds support from the calculated t-value aligning with the corresponding critical value. This divergence implies that the algorithm, when subjected to highly compressed video through .mp4 conversion, does not effectively defend the embedded watermark.

5.4. Comparative Analysis: Our Method Versus State-of-the-Art Approaches

In order to substantiate the efficacy of our proposed approach concerning the robustness of the watermark against various forms of attacks, we conducted a comprehensive comparative analysis. Our results were systematically comparable to the outcomes of recently released state-of-the-art methodologies under diverse attack scenarios. For fairness, we only included state-of-the-art methods that provide full metric reports under similar conditions.

Table 5. Comparison of Evaluation Metrics: Proposed Method Versus State-of-the-Art Approaches.

Evaluation Metric	Reference No. and Method	Frame Swapping (5%)	Frame Averaging (5%)	Uniform Frame Cropping (5%)	Salt and Pepper Noise (d = 0.001)	Frame Insertion (Any Number)	Frame Rate Change (30 to 15 and 45 fps)	Lossy Compression Motion JPEG 2000	AVI to MP4 Conversion
PSNR	[10], A video watermarking utilizing 2D-Lifting Wavelet Transform and SURF with CircularSymmetry	71.33	69.54	18.26	38.73	73.12	73.12	50.44	33.86
SSIM		0.99	0.98	0.89	0.97	1	1	0.99	0.97
CC		0.91	0.81	0.98	0.84	0.95	0.95	0.93	0.74
PSNR	[17], A hybrid method based on 2D-DWT and SVD for ownership protection	32.76	32.91	19.28	(d = 0.01) 29.84	24.10	NR	NR	NR
SSIM		NR	NR	NR	NR	NR	NR	NR	NR
CC		0.85	0.85	0.92	0.69	0.91	NR	NR	NR
PSNR	[23], An algorithm for video watermarking that uses the green channel of the RGB frame for the embedding process using the DCT.	NR	NR	(25% Horizontal only) 52.7624	(d = 0.02) 37.76	NR	NR	NR	NR
SSIM		NR	NR	0.71	0.55	NR	NR	NR	NR
CC		NR	NR	1	0.73	NR	NR	NR	NR
PSNR	[24], Video Watermarking scheme based on candidates I-Frames for copyright protection	NR	NR	NR	NR	NR	NR	NR	NR
SSIM		NR	NR	NR	NR	NR	NR	NR	NR
CC		NR	NR	(20% Horizontal only) 0.86	NR	(13 Frames Inserted) 0.69	NR	NR	NR
PSNR	[25], Scene-based video watermarking scheme for copyright protection	NR	NR	NR	NR	NR	NR	NR	NR
SSIM		0.71	0.66	NR	(d = 0.05) 0.72	NR	NR	NR	NR
CC		0.45	0.49	NR	0.73	NR	NR	NR	NR
PSNR	[27], A method based on Contourlet Transform (CT) and SVD that inserts insertion of the watermark into low-frequency sub-bands of different SD-quality videos	39.86	38.91	30.28	35.84	(10 Frames Inserted) 34.10	NR	NR	NR
SSIM		NR	NR	NR	NR	NR	NR	NR	NR
CC		0.87	0.89	0.96	0.79	0.91	NR	NR	NR
PSNR	Proposed	67.78	74.06	19.35	35.09	75.02	75.02	50.47	34.41
SSIM		0.84	0.99	0.90	0.98	1	1	1	0.98
CC		0.71	0.90	0.81	0.70	0.93	0.93	0.93	0.53

provides a revealing overview of the comparative assessment, indicating a superior performance by our proposed approach when contrasted with established state-of-the-art schemes. Moreover, we observed some authors have introduced an exceedingly high degree of noise into their videos, which had the adverse effect of significantly devaluing the visual appeal and commercial utility of the content. This highlights the importance of a judicious selection of distortion intensities during testing, a criterion that was meticulously considered in the development of our proposed method. The devised methodology exhibits superior efficacy when juxtaposed against the majority of contemporaneously published works. Remarkably elevated levels of transparency are achieved across a spectrum of diverse attacks, thereby substantiating the preeminence of our scheme. This assertion is further underscored by the consistently satisfactory values of the correlation coefficient and very high values of PSNR and SSIM, establishing the supremacy of our approach in comparison to extant methodologies. Notably, certain entries in the comparison provided in Table 5 have been intentionally marked with a “NR”. This symbol serves to denote that the authors of those particular schemes did not report their methodologies to test under the aforementioned attack scenarios, and, therefore, their performance remains unverified in these contexts.

6. Inferences and Prospects for the Future Work

This project introduces a cutting-edge method that advocates for the rights of content creators, ensuring they receive the safeguarding and equitable remuneration they are entitled to. The work began by analyzing the key tenets responsible for successes in modern computer science fields. With these insights at hand, we developed a subtle yet powerful video watermarking solution with precision, aiming to set a new standard in technological advancements. The essence of our strategy is the incorporation of the KAZE algorithm, an impressive means for identifying stable key points. It harnessed the sophisticated principle of radial symmetry within circles to refine our approach to selecting watermark insertion points computationally. This enhancement not only boosts the efficiency of our technique but also increases its capacity to carry more information steps forward that could transform digital watermarking practices significantly. To ensure remarkable resistance against compression-related degradation, we strategically place watermarks into the luminance component of video frames—an act reflecting both creativity and technical acumen in fortifying digital assets.

The tactical decision to utilize a carefully chosen number of twenty embedding points in each video frame guarantees the watermark remains undetectable. By harnessing the combined strengths of DWT and KAZE, we enhance the durability of our watermark, equipping it with an unyielding shield against potential challenges. It is essential to note that our creation has been put through stringent testing, facing a wide spectrum of attacks head-on. The result is a watermarking technique that stands as an example of tenacity and diligently preserves the visual integrity of the protected videos. As we stand at this juncture, we introduce a groundbreaking watermarking innovation ready to make its mark while looking ahead to exciting possibilities on the horizon. This work anticipates the opportunity to delve into the integration of diverse attacks, including collaborative schemes—new frontiers awaiting the development of advanced extraction techniques. As it continues on this path of innovation, dedication lies in forging increasingly sophisticated approaches to navigate a complex array of geometric, temporal, and hybrid distortions that may emerge within the digital realm.