Introducing a Parallel Genetic Algorithm for Global Optimization Problems
Abstract
1. Introduction
2. Method Description
2.1. The Genetic Algorithm
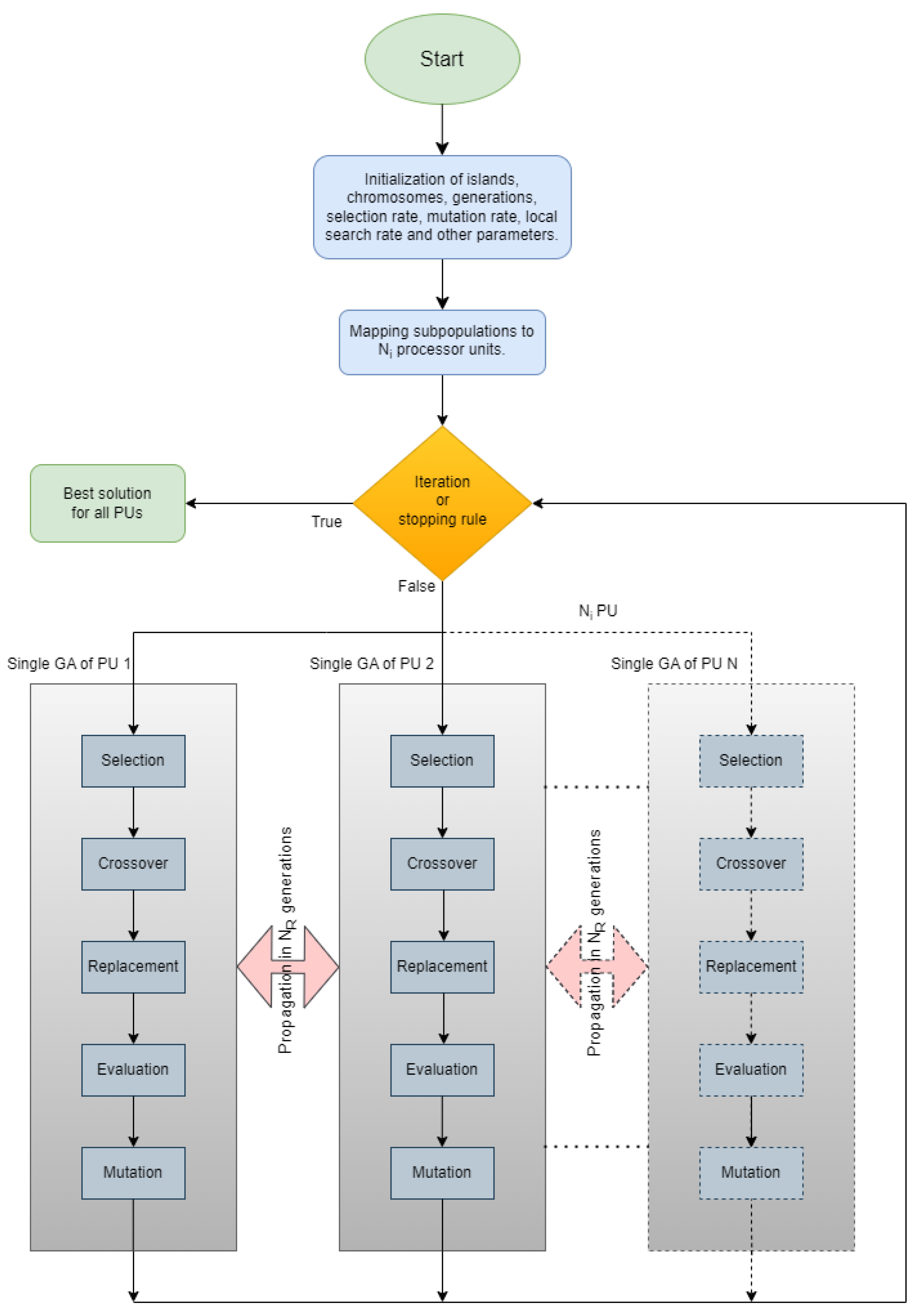
2.2. Parallelization of Genetic Algorithm and Propagation Techniques
| Algorithm 1 The steps of the genetic algorithm. |
|
| Algorithm 2 The overall algorithm. |
|
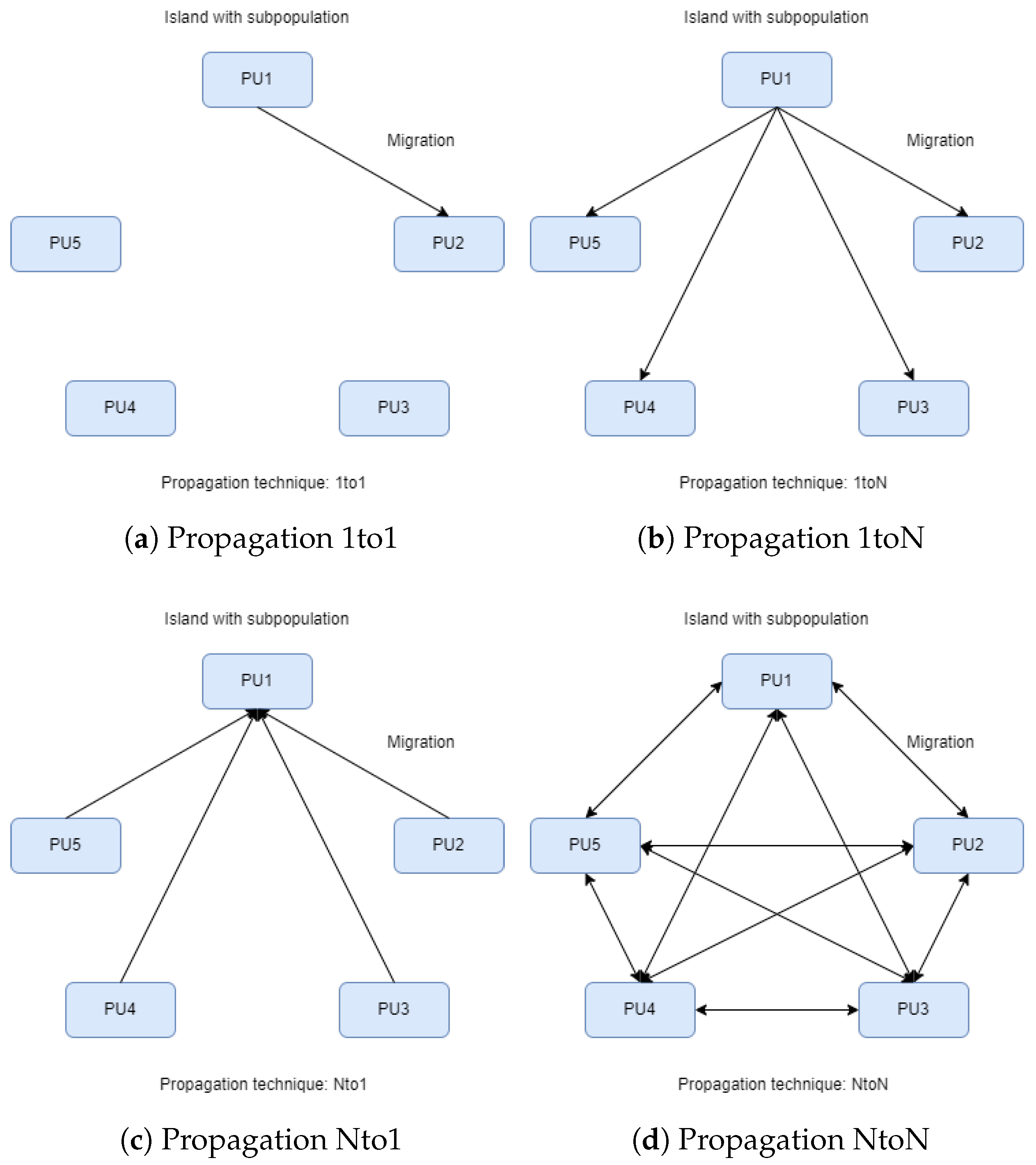
- 1to1: Optimal solutions migrate from a random island to another random one, replacing the worst solutions (see Figure 2a).
- 1toN: Optimal solutions migrate from a random island to all others, replacing the worst solutions (see Figure 2b).
- Nto1: All islands send their optimal solutions to a random island, replacing the worst solutions (see Figure 2c).
- NtoN: All islands send their optimal solutions to all other islands, replacing the worst solutions (see Figure 2d).
2.3. Termination Rule
- In each generation k, the chromosome with the best functional value is retrieved from the population. If this value does not change for a number of generations, then the algorithm should probably terminate.
- Consider as the associated variance of the quantity at generation k. The algorithm terminates whenwhere is the last generation where a lower value of is discovered.
3. Experiments
3.1. Test Functions
- The Bent cigar function is defined as follows:with the global minimum . For the conducted experiments, the value was used.
- The Bf1 function (Bohachevsky 1) is defined as follows:with .
- The Bf2 function (Bohachevsky 2) is defined as follows:with .
- The Branin function is given by with and with .
- The CM function. The cosine mixture function is given by the following:with . The value was used in the conducted experiments.
- Discus function. The function is defined as follows:with global minimum For the conducted experiments, the value was used.
- The Easom function. The function is given by the following equation:with .
- The exponential function. The function is given by the following:The global minimum is situated at , with a value of . In our experiments, we applied this function for , and referred to the respective instances as EXP4, EXP16, EXP64, and EXP100.
- Griewank2 function. The function is given by the following:
- Gkls function. is a function with w local minima, described in [68] with , and n is a positive integer between 2 and 100. The value of the global minimum is −1, and in our experiments, we used and .
- Hansen function. , . The global minimum of the function is −176.541793.
- Hartman 3 function. The function is given by the following:with and andThe value of the global minimum is −3.862782.
- Hartman 6 function.with and andthe value of the global minimum is −3.322368.
- The high-conditioned elliptic function is defined as follows:Featuring a global minimum at , the experiments were conducted using the value .
- Potential function. As a test case, the molecular conformation corresponding to the global minimum of the energy of N atoms interacting via the Lennard–Jones potential [69] is utilized. The function to be minimized is defined as follows:In the current experiments, two different cases were studied: .
- Rastrigin function. This function is given by the following:
- Shekel 7 function.with and .
- Shekel 5 function.with and .
- Shekel 10 function.with and .
- Sinusoidal function. The function is given by the following:The global minimum is situated at with a value of . In the performed experiments, we examined scenarios with and . The parameter (z) is employed to offset the position of the global minimum [70].
- Test2N function. This function is given by the following equation:The function has in the specified range; in our experiments, we used .
- Test30N function. This function is given by the following:with . This function has local minima in the specified range, and we used in the conducted experiments.
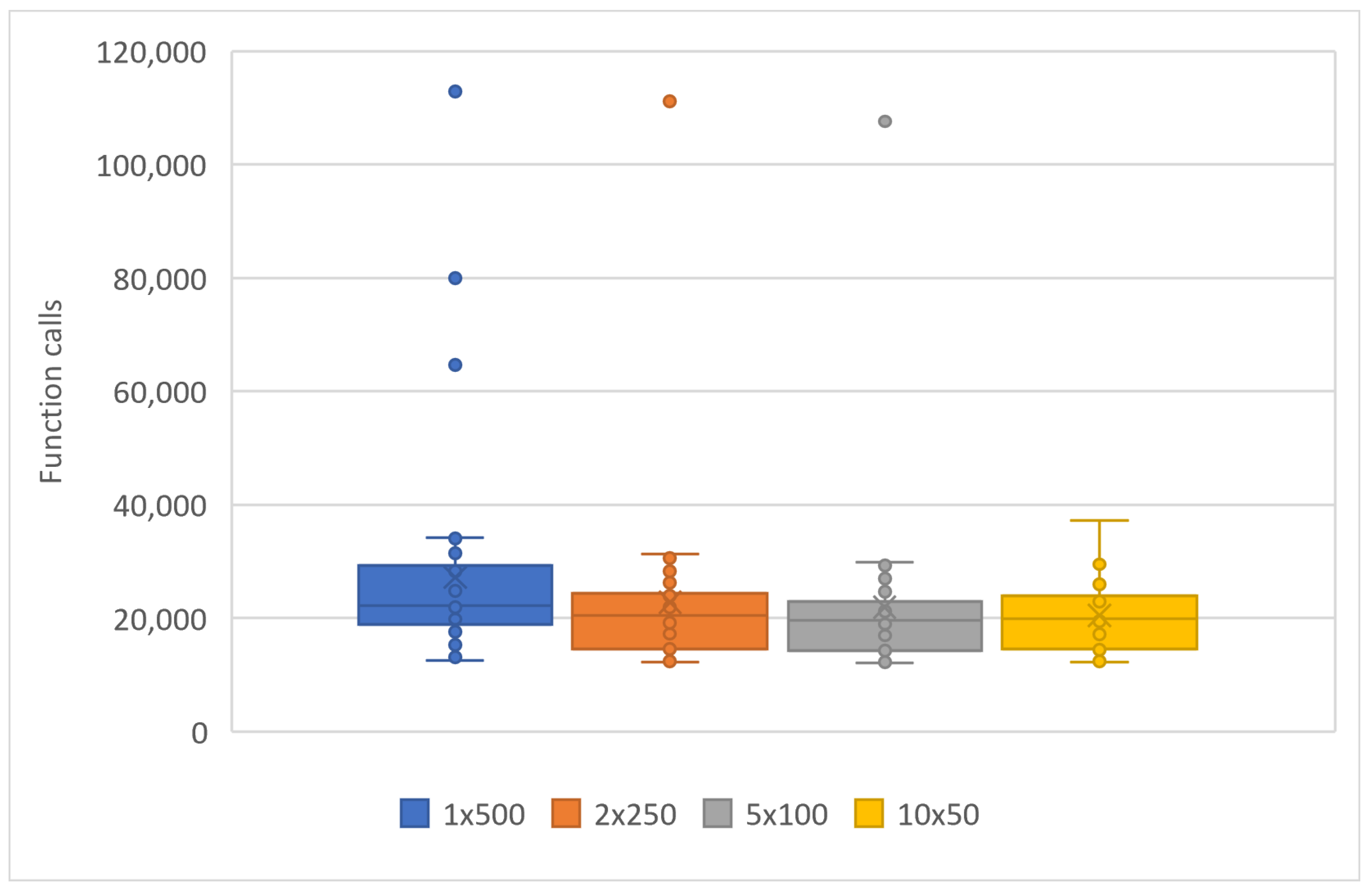
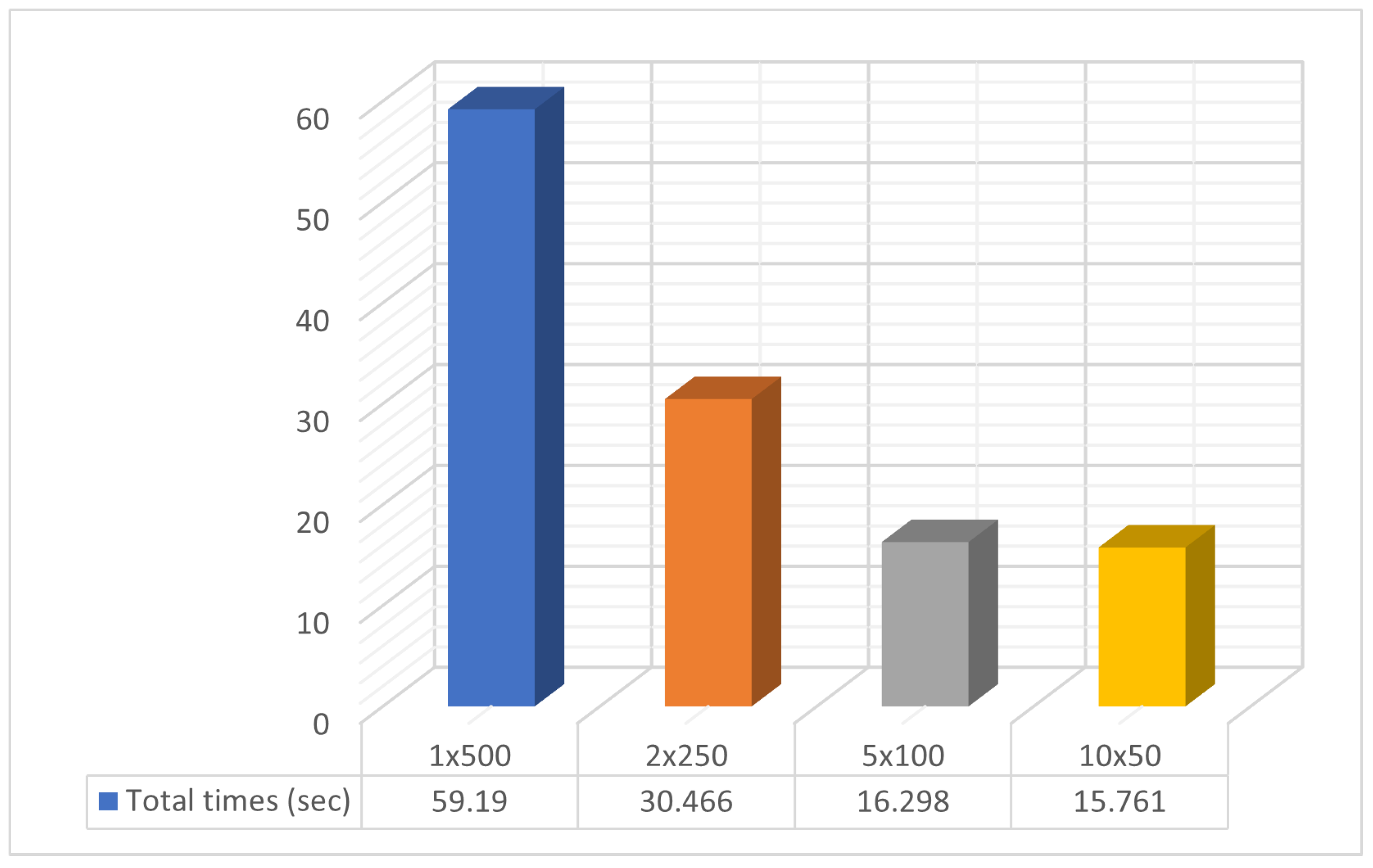
3.2. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Törn, A.; Žilinskas, A. Global Optimization; Springer: Berlin/Heidelberg, Germany, 1989; Volume 350, pp. 1–255. [Google Scholar]
- Fouskakis, D.; Draper, D. Stochastic optimization: A review. Int. Stat. Rev. 2002, 70, 315–349. [Google Scholar] [CrossRef]
- Cherruault, Y. Global optimization in biology and medicine. Math. Comput. Model. 1994, 20, 119–132. [Google Scholar] [CrossRef]
- Lee, E.K. Large-Scale Optimization-Based Classification Models in Medicine and Biology. Ann. Biomed. Eng. 2007, 35, 1095–1109. [Google Scholar] [CrossRef]
- Liwo, A.; Lee, J.; Ripoll, D.R.; Pillardy, J.; Scheraga, H.A. Protein structure prediction by global optimization of a potential energy function. Biophysics 1999, 96, 5482–5485. [Google Scholar] [CrossRef] [PubMed]
- Shin, W.H.; Kim, J.K.; Kim, D.S.; Seok, C. GalaxyDock2: Protein-ligand docking using beta-complex and global optimization. J. Comput. Chem. 2013, 34, 2647–2656. [Google Scholar] [CrossRef] [PubMed]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Yang, L.; Robin, D.; Sannibale, F.; Steier, C.; Wan, W. Global optimization of an accelerator lattice using multiobjective genetic algorithms, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers. Detect. Assoc. Equip. 2009, 609, 50–57. [Google Scholar] [CrossRef]
- Iuliano, E. Global optimization of benchmark aerodynamic cases using physics-based surrogate models. Aerosp. Sci. Technol. 2017, 67, 273–286. [Google Scholar] [CrossRef]
- Maranas, C.D.; Androulakis, I.P.; Floudas, C.A.; Berger, A.J.; Mulvey, J.M. Solving long-term financial planning problems via global optimization. J. Econ. Dyn. Control 1997, 21, 1405–1425. [Google Scholar] [CrossRef]
- Gaing, Z. Particle swarm optimization to solving the economic dispatch considering the generator constraints. IEEE Trans. Power Syst. 2003, 18, 1187–1195. [Google Scholar] [CrossRef]
- Liberti, L.; Kucherenko, S. Comparison of deterministic and stochastic approaches to global optimization. Int. Trans. Oper. Res. 2005, 12, 263–285. [Google Scholar] [CrossRef]
- Wolfe, M.A. Interval methods for global optimization. Appl. Math. Comput. 1996, 75, 179–206. [Google Scholar] [CrossRef]
- Csendes, T.; Ratz, D. Subdivision Direction Selection in Interval Methods for Global Optimization. SIAM J. Numer. Anal. 1997, 34, 922–938. [Google Scholar] [CrossRef]
- Maranas, C.D.; Floudas, C.A. A deterministic global optimization approach for molecular structure determination. J. Chem. Phys. 1994, 100, 1247. [Google Scholar] [CrossRef]
- Barhen, J.; Protopopescu, V.; Reister, D. TRUST: A Deterministic Algorithm for Global Optimization. Science 1997, 276, 1094–1097. [Google Scholar] [CrossRef]
- Evtushenko, Y.; Posypkin, M.A. Deterministic approach to global box-constrained optimization. Optim. Lett. 2013, 7, 819–829. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Price, W.L. Global optimization by controlled random search. J. Optim. Theory Appl. 1983, 40, 333–348. [Google Scholar] [CrossRef]
- Křivý, I.; Tvrdík, J. The controlled random search algorithm in optimizing regression models. Comput. Stat. Data Anal. 1995, 20, 229–234. [Google Scholar] [CrossRef]
- Ali, M.M.; Törn, A.; Viitanen, S. A Numerical Comparison of Some Modified Controlled Random Search Algorithms. J. Glob. Optim. 1997, 11, 377–385. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization An Overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Ingber, L. Very fast simulated re-annealing. Math. Comput. Model. 1989, 12, 967–973. [Google Scholar] [CrossRef]
- Eglese, R.W. Simulated annealing: A tool for operational research. Eur. J. Oper. Res. 1990, 46, 271–281. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Liu, J.; Lampinen, J. A Fuzzy Adaptive Differential Evolution Algorithm. Soft Comput. 2005, 9, 448–462. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Publishing Company: Reading, MA, USA, 1989. [Google Scholar]
- Michaelewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Grady, S.A.; Hussaini, M.Y.; Abdullah, M.M. Placement of wind turbines using genetic algorithms. Renew. Energy 2005, 30, 259–270. [Google Scholar] [CrossRef]
- Lepagnot, I.B.J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A survey on new generation metaheuristic algorithms. Comput. Ind. Eng. 2019, 137, 106040. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Stender, J. Parallel Genetic Algorithms: Theory & Applications; IOS Press: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Santana, Y.H.; Alonso, R.M.; Nieto, G.G.; Martens, L.; Joseph, W.; Plets, D. Indoor genetic algorithm-based 5G network planning using a machine learning model for path loss estimation. Appl. Sci. 2022, 12, 3923. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, D.; Tao, B.; Jiang, G.; Sun, Y.; Kong, J.; Chen, B. Genetic algorithm-based trajectory optimization for digital twin robots. Front. Bioeng. Biotechnol. 2022, 9, 793782. [Google Scholar] [CrossRef] [PubMed]
- Nonoyama, K.; Liu, Z.; Fujiwara, T.; Alam, M.M.; Nishi, T. Energy-efficient robot configuration and motion planning using genetic algorithm and particle swarm optimization. Energies 2022, 15, 2074. [Google Scholar] [CrossRef]
- Liu, K.; Deng, B.; Shen, Q.; Yang, J.; Li, Y. Optimization based on genetic algorithms on energy conservation potential of a high speed SI engine fueled with butanol–Gasoline blends. Energy Rep. 2022, 8, 69–80. [Google Scholar] [CrossRef]
- Zhou, G.; Zhu, Z.; Luo, S. Location optimization of electric vehicle charging stations: Based on cost model and genetic algorithm. Energy 2022, 247, 123437. [Google Scholar] [CrossRef]
- Min, D.; Song, Z.; Chen, H.; Wang, T.; Zhang, T. Genetic algorithm optimized neural network based fuel cell hybrid electric vehicle energy management strategy under start-stop condition. Appl. Energy 2022, 306, 118036. [Google Scholar] [CrossRef]
- Doewes, R.I.; Nair, R.; Sharma, T. Diagnosis of COVID-19 through blood sample using ensemble genetic algorithms and machine learning classifier. World J. Eng. 2022, 19, 175–182. [Google Scholar] [CrossRef]
- Choudhury, S.; Rana, M.; Chakraborty, A.; Majumder, S.; Roy, S.; RoyChowdhury, A.; Datta, S. Design of patient specific basal dental implant using Finite Element method and Artificial Neural Network technique. J. Eng. Med. 2022, 236, 1375–1387. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Hu, X. Design of intelligent control system for agricultural greenhouses based on adaptive improved genetic algorithm for multi-energy supply system. Energy Rep. 2022, 8, 12126–12138. [Google Scholar] [CrossRef]
- Graham, R.L.; Woodall, T.S.; Squyres, J.M. Open MPI: A flexible high performance MPI. In Proceedings of the Parallel Processing and Applied Mathematics: 6th International Conference (PPAM 2005), Poznań, Poland, 11–14 September 2005; Revised Selected Papers 6. Springer: Berlin/Heidelberg, Germany, 2006; pp. 228–239. [Google Scholar]
- Ayguadé, E.; Copty, N.; Duran, A.; Hoeflinger, J.; Lin, Y.; Massaioli, F.; Zhang, G. The design of OpenMP tasks. IEEE Trans. Parallel Distrib. Syst. 2008, 20, 404–418. [Google Scholar] [CrossRef]
- Onbaşoğlu, E.; Özdamar, L. Parallel simulated annealing algorithms in global optimization. J. Glob. Optim. 2001, 19, 27–50. [Google Scholar] [CrossRef]
- Schutte, J.F.; Reinbolt, J.A.; Fregly, B.J.; Haftka, R.T.; George, A.D. Parallel global optimization with the particle swarm algorithm. Int. J. Numer. Methods Eng. 2004, 61, 2296–2315. [Google Scholar] [CrossRef] [PubMed]
- Regis, R.G.; Shoemaker, C.A. Parallel stochastic global optimization using radial basis functions. J. Comput. 2009, 21, 411–426. [Google Scholar] [CrossRef]
- Harada, T.; Alba, E. Parallel Genetic Algorithms: A Useful Survey. ACM Comput. Surv. 2020, 53, 86. [Google Scholar] [CrossRef]
- Anbarasu, L.A.; Narayanasamy, P.; Sundararajan, V. Multiple molecular sequence alignment by island parallel genetic algorithm. Curr. Sci. 2000, 78, 858–863. [Google Scholar]
- Tosun, U.; Dokeroglu, T.; Cosar, C. A robust island parallel genetic algorithm for the quadratic assignment problem. Int. Prod. Res. 2013, 51, 4117–4133. [Google Scholar] [CrossRef]
- Nandy, A.; Chakraborty, D.; Shah, M.S. Optimal sensors/actuators placement in smart structure using island model parallel genetic algorithm. Int. J. Comput. 2019, 16, 1840018. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Tzallas, A.; Tsalikakis, D. PDoublePop: An implementation of parallel genetic algorithm for function optimization. Comput. Phys. Commun. 2016, 209, 183–189. [Google Scholar] [CrossRef]
- Shonkwiler, R. Parallel genetic algorithms. In ICGA; Morgan Kaufmann Publishers Inc: San Francisco, CA, USA, 1993; pp. 199–205. [Google Scholar]
- Cantú-Paz, E. A survey of parallel genetic algorithms. Calc. Paralleles Reseaux Syst. Repartis 1998, 10, 141–171. [Google Scholar]
- Mühlenbein, H. Parallel genetic algorithms in combinatorial optimization. In Computer Science and Operations Research; Elsevier: Amsterdam, The Netherlands, 1992; pp. 441–453. [Google Scholar]
- Lawrence, D. Handbook of Genetic Algorithms; Thomson Publishing Group: London, UK, 1991. [Google Scholar]
- Yu, X.; Gen, M. Introduction to Evolutionary Algorithms; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-1-84996-128-8. e-ISBN 978-1-84996-129-5. [Google Scholar] [CrossRef]
- Kaelo, P.; Ali, M.M. Integrated crossover rules in real coded genetic algorithms. Eur. J. Oper. Res. 2007, 176, 60–76. [Google Scholar] [CrossRef]
- Tsoulos, I.G. Modifications of real code genetic algorithm for global optimization. Appl. Math. Comput. 2008, 203, 598–607. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Program. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Floudas, C.A.; Pardalos, P.M.; Adjiman, C.; Esposoto, W.; Gümüs, Z.; Harding, S.; Klepeis, J.; Meyer, C.; Schweiger, C. Handbook of Test Problems in Local and Global Optimization; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Ali, M.M.; Khompatraporn, C.; Zabinsky, Z.B. A Numerical Evaluation of Several Stochastic Algorithms on Selected Continuous Global Optimization Test Problems. J. Glob. Optim. 2005, 31, 635–672. [Google Scholar] [CrossRef]
- Gaviano, M.; Ksasov, D.E.; Lera, D.; Sergeyev, Y.D. Software for generation of classes of test functions with known local and global minima for global optimization. ACM Trans. Math. Softw. 2003, 29, 469–480. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. On the Determination of Molecular Fields. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar]
- Zabinsky, Z.B.; Graesser, D.L.; Tuttle, M.E.; Kim, G.I. Global optimization of composite laminates using improving hit and run. In Recent Advances in Global Optimization; Princeton University Press: Princeton, NJ, USA, 1992; pp. 343–368. [Google Scholar]
- Charilogis, V.; Tsoulos, I. Toward an Ideal Particle Swarm Optimizer for Multidimensional Functions. Information 2022, 13, 217. [Google Scholar] [CrossRef]
- Charilogis, V.; Tsoulos, I.; Tzallas, A.; Karvounis, E. Modifications for the Differential Evolution Algorithm. Symmetry 2022, 14, 447. [Google Scholar] [CrossRef]
- Wall, M. GAlib: A C++ Library of Genetic Algorithm Components; Mechanical Engineering Department, Massachusetts Institute of Technology: Cambridge, MA, USA, 1996; p. 54. [Google Scholar]
- Charilogis, V.; Tsoulos, I.G. A Parallel Implementation of the Differential Evolution Method. Analytics 2023, 2, 17–30. [Google Scholar] [CrossRef]
- Charilogis, V.; Tsoulos, I.G.; Tzallas, A. An Improved Parallel Particle Swarm Optimization. Comput. Sci. 2023, 4, 766. [Google Scholar] [CrossRef]




| Parameter | Value | Explanation |
|---|---|---|
| 500 × 1, 250 × 2, 100 × 5, 50 × 10 | Chromosomes | |
| 200 | Max generations | |
| 1, 2, 5, 10 | Processing units or islands | |
| no propagation in Table 2, 1: in every generation in Table 3 | Rate of propagation | |
| 0 in Table 2, 10: in Table 3 | Chromosomes for migration | |
| no in Table 2, 1to1 Figure 2a, 1toN Figure 2b, Nto1 Figure 2c, NtoN Figure 2d | Propagation technique | |
| 10% | Selection rate | |
| 5% | Mutation rate | |
| 0.1% in Table 2, 0.5% in Table 3 | Local search rate |
| Problems | Calls | Time | Calls | Time | Calls | Time | Calls | Time |
|---|---|---|---|---|---|---|---|---|
| BF1 | 10,578 | 0.557 | 10,555 | 0.193 | 10,533 | 0.126 | 10,511 | 0.121 |
| BF2 | 10,568 | 0.554 | 10,545 | 0.192 | 10,523 | 0.127 | 10,533 | 0.119 |
| BRANIN | 46,793 | 2.308 | 31,231 | 0.562 | 11,125 | 0.134 | 10,533 | 0.169 |
| CAMEL | 26,537 | 1.338 | 15,875 | 0.29 | 15,833 | 0.188 | 10,861 | 0.123 |
| CIGAR10 | 10,502 | 1.089 | 10,577 | 0.383 | 10,583 | 0.222 | 10,541 | 0.206 |
| CM4 | 10,614 | 1.054 | 10,583 | 0.249 | 10,581 | 0.151 | 10,556 | 0.139 |
| DISCUS10 | 10,548 | 1.09 | 10,532 | 0.382 | 10,500 | 0.222 | 10,502 | 0.205 |
| EASOM | 100,762 | 4.504 | 100,610 | 1.66 | 94,541 | 1.089 | 22,845 | 0.248 |
| ELP10 | 10,601 | 1.15 | 10,590 | 0.436 | 10,574 | 0.26 | 10,557 | 0.242 |
| EXP4 | 16,621 | 1.092 | 10,587 | 0.249 | 10,560 | 0.15 | 10,544 | 0.143 |
| EXP16 | 10,680 | 1.336 | 10,654 | 0.53 | 10,643 | 0.287 | 10,626 | 0.258 |
| EXP64 | 10,857 | 2.333 | 10,829 | 1.235 | 10,814 | 0.825 | 10,830 | 0.728 |
| EXP100 | 10,855 | 3.517 | 10,901 | 1.763 | 10,868 | 1.25 | 10,887 | 1.052 |
| GKLS250 | 50,804 | 2.825 | 25,832 | 0.607 | 11,711 | 0.194 | 10,870 (93) | 0.198 |
| GKLS350 | 40,707 | 2.327 | 23,720 | 0.522 | 17,646 | 0.26 | 14,130 | 0.202 |
| GRIEWANK2 | 10555 | 0.565 | 10532 | 0.197 | 10,517 | 0.126 | 10,492 | 0.118 |
| GRIEWANK10 | 10,679 | 1.079 | 10,629 | 0.407 | 10,613 | 0.239 | 10,609 | 0.22 |
| POTENTIAL3 | 39,607 | 2.057 | 34,327 | 0.881 | 18,313 | 0.34 | 15,471 | 0.279 |
| PONTENTIAL5 | 33,542 | 1.653 | 33737 | 1.074 | 12,040 | 0.34 | 11,082 | 0.291 |
| PONTENTIAL6 | 28,901 (3) | 1.56 | 26,419 (16) | 1.018 | 14,265 (3) | 0.478 | 11,109 (10) | 0.356 |
| PONTENTIAL10 | 42,644 (13) | 3.316 | 37,897 (23) | 2.538 | 14,080 (10) | 0.937 | 11,319 (6) | 0.66 |
| HANSEN | 46,894 (90) | 2.494 | 28,191 (80) | 0.575 | 11,085 (56) | 0.153 | 11,065 | 0.158 |
| HARTMAN3 | 22,235 | 1.525 | 19,030 | 0.379 | 16,463 | 0.212 | 12,048 | 0.146 |
| HARTMAN6 | 18,352 | 1.505 | 15,902 | 0.429 | 16,726 | 0.279 | 12,243 | 0.196 |
| RASTRIGIN | 16,567 | 0.855 | 10,543 | 0.193 | 10,521 | 0.125 | 10,506 | 0.116 |
| ROSENBROCK8 | 10,863 | 0.916 | 10,700 | 0.333 | 10,698 | 0.199 | 10,772 | 0.196 |
| POSENBROCK16 | 10,918 | 1.371 | 10946 | 0.516 | 10,867 | 0.304 | 10,886 | 0.271 |
| SHEKEL5 | 32,319 (50) | 2.069 | 17,913 (50) | 0.412 | 11,185 (36) | 0.159 | 11,010 (40) | 0.15 |
| SHEKEL7 | 51,183 (73) | 3.277 | 14,981 (53) | 0.342 | 11,457 (60) | 0.163 | 11,035 (50) | 0.154 |
| SHEKEL10 | 47,337 (70) | 2.977 | 46,927 (76) | 1.113 | 16,310 (56) | 0.23 | 11,329 (70) | 0.152 |
| SINU4 | 66,625 (83) | 4.344 | 31,511 (86) | 0.77 | 13,979 (73) | 0.211 | 11,004 (43) | 0.161 |
| SINU8 | 29,705 | 2.57 | 27,613 | 0.987 | 24,592 | 0.549 | 11,422 | 0.236 |
| TEST2N4 | 25,553 | 1.558 | 17,701 | 0.397 | 24,763 | 0.359 | 13,217 | 0.178 |
| TEST2N5 | 20,297 | 1.327 | 18,440 | 0.457 | 16,759 | 0.265 | 11,483 | 0.168 |
| TEST2N6 | 20,450 | 1.311 | 20,837 | 0.566 | 18,123 | 0.315 | 11,988 | 0.194 |
| TEST2N7 | 26,113 | 1.924 | 23,940 | 0.723 | 20,825 | 0.384 | 11,339 | 0.196 |
| TEST2N8 | 18,846 | 1.454 | 18,549 | 0.585 | 16,700 | 0.329 | 11,658 | 0.218 |
| TEST2N9 | 18,154 | 1.582 | 18,803 | 0.649 | 17,100 | 0.368 | 13,299 | 0.262 |
| TEST30N3 | 49,235 | 2.46 | 24,129 | 0.458 | 14,743 | 0.188 | 12,345 | 0.152 |
| TEST30N4 | 29,667 | 1.553 | 17,501 | 0.358 | 13,367 | 0.186 | 11,778 | 0.151 |
| SUM | 1,105,268 | 74.376 | 851,319 | 25.61 | 633,126 | 12.923 | 465,835 | 9.532 |
| MINIMUM | 10,502 | 0.554 | 10,532 | 0.192 | 10,500 | 0.125 | 10492 | 0.116 |
| MAXIMUM | 100,762 | 4.504 | 100,610 | 2.538 | 94,541 | 1.25 | 22,845 | 1.052 |
| AVERAGE | 27,631.7 | 1.859 | 21,282.975 | 0.640 | 15,828.15 | 0.323 | 11,645.875 | 0.238 |
| STDEV | 19,305.784 | 0.972 | 15,829.020 | 0.482 | 13,335.509 | 0.260 | 2109.230 | 0.180 |
| Problems | No Propagation Calls | No Propagation Time | 1to1 Calls | 1to1 Time | 1toN Calls | 1toN Time | Nto1 Calls | Nto1 Time | NtoN Calls | NtoN Time |
|---|---|---|---|---|---|---|---|---|---|---|
| BF1 | 10,809 | 0.123 | 10,741 | 0.127 | 10,770 | 0.126 | 10,746 | 0.127 | 10,808 | 0.136 |
| BF2 | 10,725 | 0.124 | 10,773 | 0.126 | 10,764 | 0.13 | 10,783 | 0.126 | 10,731 | 0.136 |
| BRANIN | 48,364 | 0.56 | 31,470 | 0.397 | 18,776 | 0.251 | 35,367 | 0.448 | 19,224 | 0.284 |
| CAMEL | 29,087 | 0.337 | 18,597 | 0.23 | 14,429 | 0.185 | 24,977 | 0.313 | 19,341 | 0.286 |
| CIGAR10 | 10,854 | 0.233 | 10,880 | 0.216 | 10,915 | 0.222 | 10,890 | 0.22 | 10,869 | 0.235 |
| CM4 | 10,911 | 0.147 | 10,923 | 0.15 | 10,941 | 0.15 | 10,918 | 0.15 | 10,915 | 0.163 |
| DISCUS10 | 10,651 | 0.222 | 10,632 | 0.213 | 10,651 | 0.217 | 10,641 | 0.22 | 10,606 | 0.231 |
| EASOM | 99,569 | 1.094 | 100,163 | 1.106 | 100,160 | 1.121 | 100,155 | 1.139 | 98,336 | 1.156 |
| ELP10 | 10,832 | 0.276 | 10,902 | 0.261 | 10,829 | 0.266 | 10,811 | 0.26 | 10,952 | 0.278 |
| EXP4 | 10,803 | 0.151 | 12,037 | 0.167 | 12,695 | 0.183 | 11,416 | 0.164 | 10,819 | 0.158 |
| EXP16 | 11,228 | 0.272 | 11,259 | 0.276 | 11,262 | 0.285 | 11253 | 0.28 | 11,260 | 0.294 |
| EXP64 | 12,127 | 0.837 | 12,204 | 0.848 | 12,184 | 0.85 | 12,151 | 0.849 | 12,199 | 0.877 |
| EXP100 | 12,396 | 1.397 | 12,376 | 1.4 | 12,372 | 1.36 | 12,460 | 1.387 | 12,414 | 1.42 |
| GKLS250 | 48,672 | 0.813 | 55,586 | 0.949 | 31,493 | 0.564 | 58,638 | 1.007 | 27,840 | 0.532 |
| GKLS350 | 55,231 | 0.815 | 42,100 | 0.636 | 28,609 | 0.459 | 46,923 | 0.72 | 25,341 | 0.428 |
| GRIEWANK2 | 10,682 | 0.127 | 10,670 | 0.125 | 10,697 | 0.126 | 10,683 | 0.127 | 10,684 | 0.134 |
| GRIEWANK10 | 11,144 | 0.239 | 11,102 | 0.232 | 11,123 | 0.239 | 11,171 | 0.229 | 11,153 | 0.254 |
| POTENTIAL3 | 45,748 | 0.832 | 33,598 | 0.643 | 17,276 | 0.347 | 32,603 | 0.631 | 16,870 | 0.358 |
| PONTENTIAL5 | 41,946 | 1.156 | 41,112 | 1.179 | 19,912 | 0.597 | 37,687 | 1.089 | 19,622 | 0.614 |
| PONTENTIAL6 | 46,507 | 1.639 | 40,518 | 1.449 | 21,941 | 0.817 | 36,138 | 1.315 | 21,528 | 0.844 |
| PONTENTIAL10 | 47,031 | 3.4 | 45,166 | 3.361 | 40,212 | 3.239 | 42,057 | 3.183 | 34,750 | 2.883 |
| HANSEN | 63,130 | 0.85 | 65,414 | 0.918 | 39,649 | 0.595 | 67,369 | 0.947 | 31,149 | 0.507 |
| HARTMAN3 | 19,170 | 0.248 | 20,339 | 0.274 | 16,280 | 0.226 | 20,001 | 0.265 | 14,587 | 0.219 |
| HARTMAN6 | 23,725 | 0.423 | 16,856 | 0.285 | 14,141 | 0.233 | 16,955 | 0.288 | 13,964 | 0.239 |
| RASTRIGIN | 11,264 | 0.147 | 11,256 | 0.132 | 10,652 | 0.126 | 10,668 | 0.128 | 11,290 | 0.145 |
| ROSENBROCK8 | 11,727 | 0.204 | 11,892 | 0.2 | 11,681 | 0.203 | 11,708 | 0.199 | 11,882 | 0.217 |
| POSENBROCK16 | 12372 | 0.42 | 12,187 | 0.304 | 12,394 | 0.313 | 12,438 | 0.324 | 12,455 | 0.324 |
| SHEKEL5 | 44,893 | 0.645 | 54,184 | 0.751 | 34,937 | 0.491 | 53,277 | 0.755 | 40,859 | 0.621 |
| SHEKEL7 | 45,722 | 0.638 | 55,109 | 0.778 | 33,440 | 0.472 | 49,029 | 0.702 | 46,066 | 0.696 |
| SHEKEL10 | 58,361 | 0.854 | 49,400 | 0.721 | 32,691 | 0.471 | 52,798 | 0.783 | 38,305 | 0.608 |
| SINU4 | 64,584 | 0.972 | 59,414 | 0.922 | 36,052 | 0.591 | 62,924 | 0.972 | 52,937 | 0.857 |
| SINU8 | 32,572 | 0.793 | 25,552 | 0.63 | 19,461 | 0.462 | 28,744 | 0.716 | 18,173 | 0.445 |
| TEST2N4 | 23,430 | 0.339 | 20,474 | 0.3 | 17,001 | 0.261 | 21,468 | 0.316 | 18,436 | 0.294 |
| TEST2N5 | 22,662 | 0.358 | 20,614 | 0.33 | 16,171 | 0.262 | 19,697 | 0.316 | 16,421 | 0.282 |
| TEST2N6 | 21,663 | 0.365 | 18,721 | 0.323 | 16,600 | 0.289 | 19,556 | 0.339 | 14,633 | 0.299 |
| TEST2N7 | 24,401 | 0.456 | 18,990 | 0.354 | 15,792 | 0.3 | 20,967 | 0.405 | 13,995 | 0.28 |
| TEST2N8 | 21,017 | 0.418 | 18,532 | 0.369 | 16,644 | 0.339 | 20,139 | 0.413 | 13,980 | 0.298 |
| TEST2N9 | 22,684 | 0.488 | 18,538 | 0.407 | 16302 | 0.353 | 18,929 | 0.421 | 14,620 | 0.344 |
| TEST30N3 | 24,524 | 0.318 | 22,799 | 0.296 | 20,436 | 0.297 | 23,186 | 0.311 | 19,968 | 0.316 |
| TEST30N4 | 21,090 | 0.28 | 25,160 | 0.358 | 21,216 | 0.319 | 19,444 | 0.276 | 16,711 | 0.267 |
| Total | 1,164,308 | 24.01 | 1,088,240 | 22.74 | 829,551 | 18.33 | 1,097,765 | 22.86 | 836,693 | 18.95 |
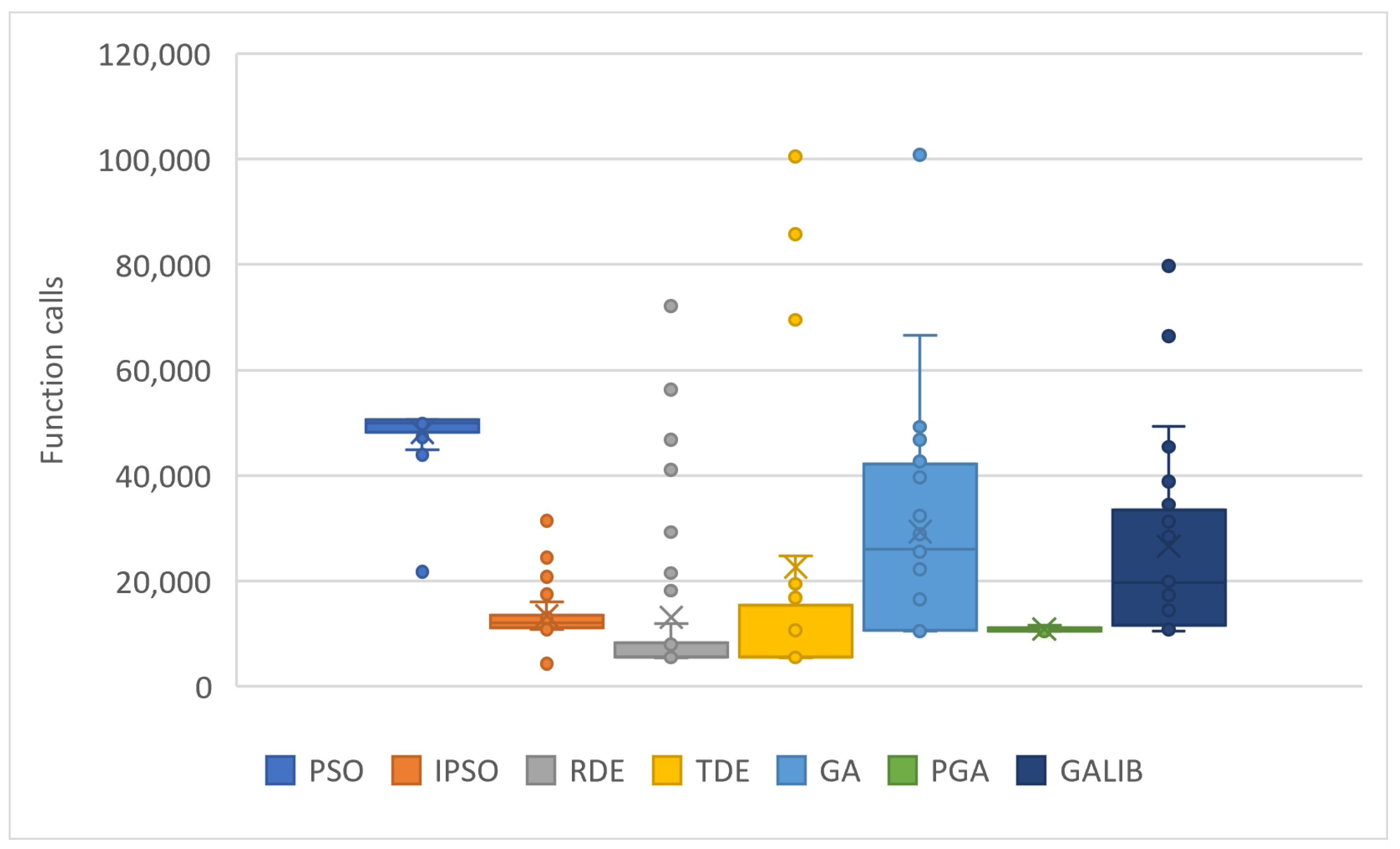
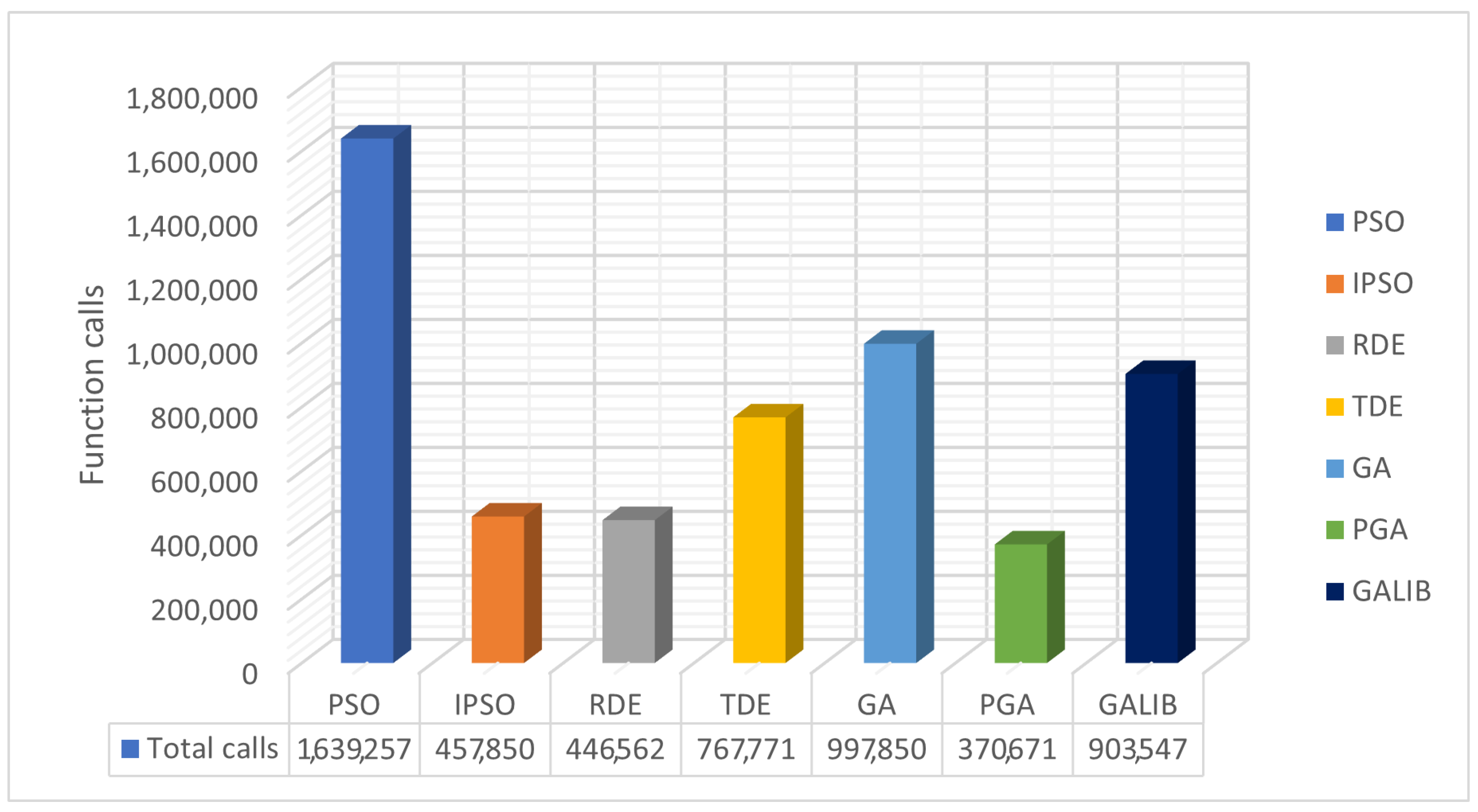
| PROBLEMS | PSO | IPSO | RDE | TDE | GA | GAlib | PGA |
|---|---|---|---|---|---|---|---|
| BF1 | 50,398 | 11,478 | 7943 (86) | 5535 | 10,578 | 11,641 | 10,501 |
| BF2 | 50,397 | 11,292 | 8472 (76) | 5539 | 10,568 | 11,321 | 10,510 |
| BRANIN | 44,800 | 10,849 | 5513 | 5514 | 46,793 | 34,487 | 10,838 |
| CAMEL | 48,242 | 11,051 | 5555 | 5514 | 26,537 | 17,321 | 11,087 |
| CIGAR10 | 50,581 | 12,331 | 5586 | 100,573 | 10,502 | 11,567 (50) | 10,566 |
| CM4 | 48,559 | 11,767 | 5550 | 5538 | 10,614 | 11,118 (70) | 10,548 |
| DISCUS10 | 50,523 | 14,328 | 18,187 | 100,518 | 10,548 | 10,988 | 10,503 |
| EASOM | 21,786 | 10,938 | 29,256 | 24,691 | 100,762 | 79,689 | 10,797 |
| ELP10 | 49,837 | 4323 | 11,933 | 100,584 | 10,601 | 11,673 | 10,559 |
| EXP4 | 48,523 | 11,041 | 46,752 | 19,467 | 16,621 | 16,045 | 10,503 |
| EXP16 | 50,518 | 10,973 | 5537 | 69,494 | 10,680 | 10,500 | 10,595 |
| GKLS250 | 43,925 | 10,869 | 41,016 | 11,430 | 50,804 | 31,298 | 10,893 (76) |
| GKLS350 | 48,202 | 10,750 | 56,220 | 16,831 | 40,707 | 29,897 (96) | 11,555 (96) |
| GRIEWANK2 | 44,021 | 13,514 | 5538 | 5533 | 10,555 | 14,419 (67) | 10,498 |
| GRIEWANK10 | 50,557 (3) | 12,258 (86) | 5612 (13) | 85,742 (3) | 10,679 | 10,800 | 10,576 |
| POTENTIAL3 | 49,213 | 12,124 | 5530 | 5523 | 39,607 | 33,452 | 11,039 |
| PONTENTIAL5 | 50,548 | 16,027 | 5587 | 5569 | 33,542 | 31,285 | 11,134 |
| PONTENTIAL6 | 50,558 (3) | 24,414 (66) | 5607 (6) | 5588 (3) | 28,901 (3) | 28,444 (10) | 11,143 (10) |
| PONTENTIAL10 | 50,641 (6) | 31,434 | 5670 (3) | 5661 (6) | 42,644 (13) | 38,883 (20) | 11,290 (20) |
| HANSEN | 47,296 | 13,131 | 5522 | 5521 | 46,894 (90) | 45,440 | 11,055 |
| HARTMAN3 | 47,778 | 10,961 | 5525 | 5522 | 22,235 | 19,434 | 11,097 |
| HARTMAN6 | 50,088 (33) | 11,085 (86) | 5536 (83) | 5536 | 18,352 | 18,444 (60) | 11,273 |
| RASTRIGIN | 47,433 | 11,594 | 5542 | 5524 | 16,567 | 16,286 (96) | 10,506 |
| ROSENBROCK8 | 50,549 | 13,487 | 72,088 | 100,503 | 10,863 | 11,419 | 10,645 |
| POSENBROCK16 | 50,584 | 12,659 | 21,517 | 10,645 | 10,918 | 11,681 | 10,957 |
| SHEKEL5 | 49,944 (33) | 13,058 (93) | 5532 (86) | 5524 (93) | 32,319 (50) | 29,287 | 10,883 (43) |
| SHEKEL7 | 50,062 (53) | 12,134 (96) | 5533 (96) | 5523 | 51183 (73) | 47,245 (77) | 10,926 (53) |
| SHEKEL10 | 50,124 (63) | 14,176 | 5535 (90) | 5523 | 47,337 (70) | 45,911 (77) | 11,207 (80) |
| SINU4 | 49,239 | 11,349 | 5527 | 5510 | 66,625 (83) | 66,383 | 11,063 (76) |
| SINU8 | 50,224 | 11,295 | 5537 (80) | 5520 | 29,705 | 29,234 | 11,378 |
| TEST2N4 | 50,112 (93) | 13,173 | 5529 | 5519 | 25,553 | 19,913 | 11049 |
| TEST2N9 | 50,517 (13) | 17,510 (60) | 5546 (6) | 5535 (56) | 18,154 | 15,376 | 11,145 |
| TEST30N3 | 44,301 | 19,638 | 5515 | 5511 | 49,235 | 49,234 | 11,051 |
| TEST30N4 | 49,177 | 20,839 | 5514 | 5511 | 29,667 | 33,428 | 11,301 |
| TOTAL | 1,639,257 | 457,850 | 446,562 | 767,771 | 997,850 | 903,547 | 370,671 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charilogis, V.; Tsoulos, I.G. Introducing a Parallel Genetic Algorithm for Global Optimization Problems. AppliedMath 2024, 4, 709-730. https://doi.org/10.3390/appliedmath4020038
Charilogis V, Tsoulos IG. Introducing a Parallel Genetic Algorithm for Global Optimization Problems. AppliedMath. 2024; 4(2):709-730. https://doi.org/10.3390/appliedmath4020038
Chicago/Turabian StyleCharilogis, Vasileios, and Ioannis G. Tsoulos. 2024. "Introducing a Parallel Genetic Algorithm for Global Optimization Problems" AppliedMath 4, no. 2: 709-730. https://doi.org/10.3390/appliedmath4020038
APA StyleCharilogis, V., & Tsoulos, I. G. (2024). Introducing a Parallel Genetic Algorithm for Global Optimization Problems. AppliedMath, 4(2), 709-730. https://doi.org/10.3390/appliedmath4020038







