An Efficient Bi-Parametric With-Memory Iterative Method for Solving Nonlinear Equations
Abstract
:1. Introduction
2. Analysis of Convergence for With-Memory Methods
2.1. The Uni-Parametric With-Memory Method and Its Convergence Analysis
- (1)
- All nodes are sufficiently near to the root ξ.
- (2)
- The condition holds. Then,andwhere .
2.2. The Bi-Parametric With-Memory Method and Its Convergence Analysis
- (1)
- All nodes are sufficiently near to the root ξ.
- (2)
- The condition holds. Then,andwhere = ( − + + + − − + + − ).
3. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Traub, J.F. Iterative Methods for the Solution of Equations; American Mathematical Society: Providence, RI, USA, 1982. [Google Scholar]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. ACM 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Ostrowski, A.M. Solution of Equations in Euclidean and Banach Spaces; Academic Press Inc.: Cambridge, MA, USA, 1973. [Google Scholar]
- Khan, W.A. Numerical simulation of Chun-Hui He’s iteration method with applications in engineering. Int. J. Numer. Methods Heat Fluid Flow 2022, 32, 944–955. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, T. Some Newton-type iterative methods with and without memory for solving nonlinear equations. Int. J. Comput. Methods 2014, 11, 1350078. [Google Scholar] [CrossRef]
- Sharma, J.R.; Arora, H. An efficient family of weighted-Newton methods with optimal eighth order convergence. Appl. Math. Lett. 2014, 29, 1–6. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1970. [Google Scholar]
- Alefeld, G.; Herzberger, J. Introduction to Interval Computation; Academic Press: New York, NY, USA, 2012. [Google Scholar]
- Babajee, D.K.R.; Cordero, A.; Soleymani, F.; Torregrosa, J.R. On improved three-step schemes with high efficiency index and their dynamics. Numer. Algorithms 2014, 65, 153–169. [Google Scholar] [CrossRef]
- Choubey, N.; Cordero, A.; Jaiswal, J.P.; Torregrosa, J.R. Dynamical techniques for analyzing iterative schemes with memory. Complexity 2018, 2018, 1232341. [Google Scholar]
- Choubey, N.; Jaiswal, J.P. Two-and three-point with memory methods for solving nonlinear equations. Numer. Anal. Appl. 2017, 10, 74–89. [Google Scholar] [CrossRef]
- Bradie, B. A Friendly Introduction to Numerical Analysis; Pearson Education Inc.: New Delhi, India, 2006. [Google Scholar]
- Weerakoon, S.; Fernando, T. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
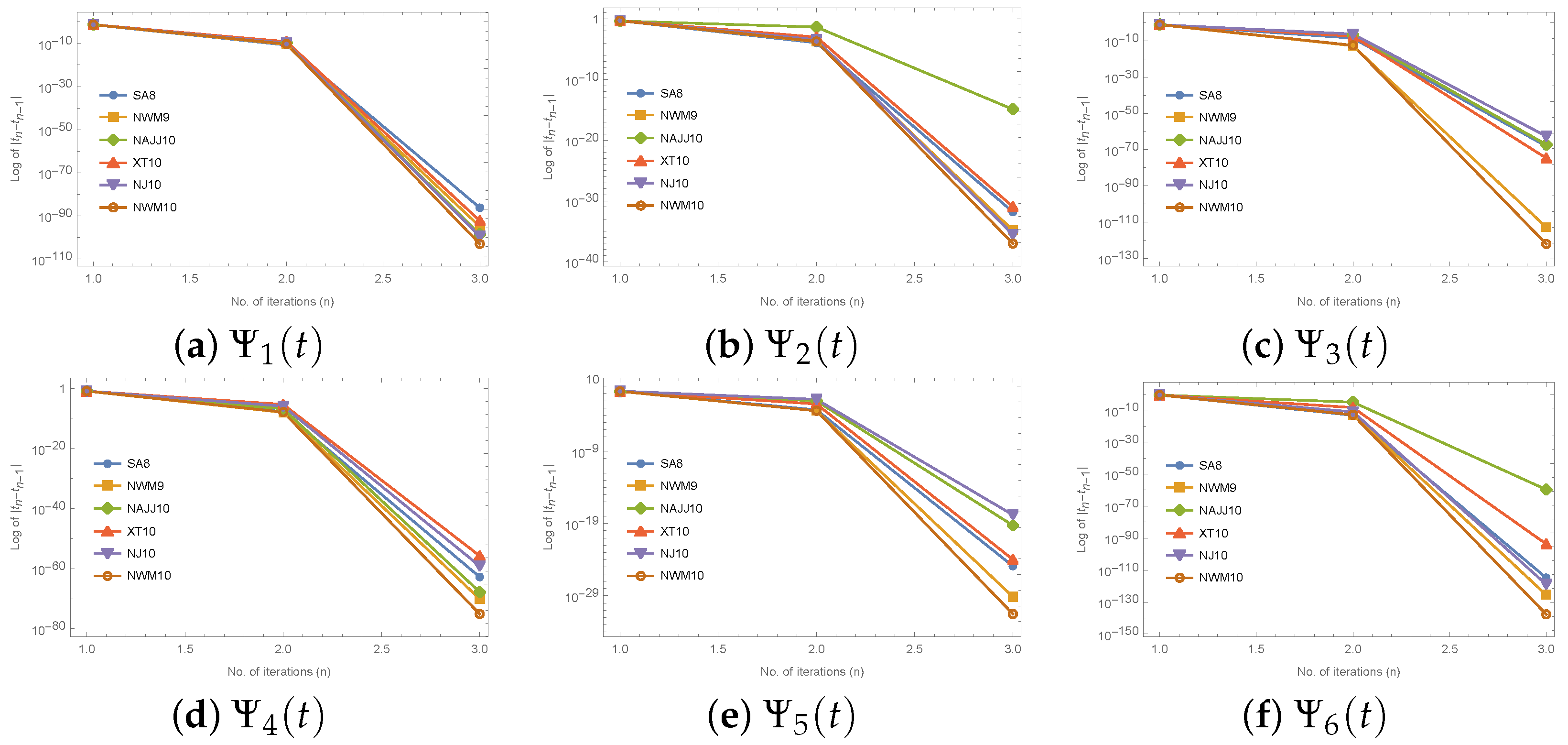
| Test Function | Root () | Initial Approx. () |
|---|---|---|
| 1.4 | ||
| 2.5 | ||
| −1.3 | ||
| 0.5 | ||
| 2.2 |
| Method | COC | |||||
|---|---|---|---|---|---|---|
| SA8 | 1.8816 × 10 | 6.0796 × 10 | 2.6750 × 10 | |||
| NWM9 | 3.7554 × 10 | 1.2228 × 10 | 1.8634 × 10 | |||
| NAJJ10 | 1.7028 × 10 | 2.8001 × 10 | 1.4992 × 10 | |||
| XT10 | 6.9169 × 10 | 5.7293 × 10 | 3.2266 × 10 | |||
| NJ10 | 1.4825 × 10 | 3.6951 × 10 | 1.2667 × 10 | |||
| NWM10 | 5.4649 × 10 | 9.9261 × 10 | 1.4371 × 10 | |||
| SA8 | 1.1417 × 10 | 1.4980 × 10 | 3.9438 × 10 | |||
| NWM9 | 1.7331 × 10 | 1.3929 × 10 | 1.9497 × 10 | |||
| NAJJ10 | 4.5088 × 10 | 1.2500 × 10 | 1.3803 × 10 | |||
| XT10 | 9.9027 × 10 | 1.1220 × 10 | 1.1714 × 10 | |||
| NJ10 | 3.7910 × 10 | 3.0109 × 10 | 9.0709 × 10 | |||
| NWM10 | 1.9492 × 10 | 9.1392 × 10 | 1.4053 × 10 | |||
| SA8 | 3.3415 × 10 | 7.0947 × 10 | 5.9503 × 10 | |||
| NWM9 | 2.0992 × 10 | 1.3500 × 10 | 5.1492 × 10 | |||
| NAJJ10 | 2.1365 × 10 | 5.7705 × 10 | 6.2041 × 10 | |||
| XT10 | 4.0647 × 10 | 2.0381 × 10 | 1.5813 × 10 | |||
| NJ10 | 6.0884 × 10 | 2.3054 × 10 | 5.5259 × 10 | |||
| NWM10 | 3.6090 × 10 | 8.1902 × 10 | 1.7585 × 10 | |||
| SA8 | 1.5156 × 10 | 1.7097 × 10 | 1.6721 × 10 | |||
| NWM9 | 9.0694 × 10 | 8.1008 × 10 | 2.5001 × 10 | |||
| NAJJ10 | 1.3769 × 10 | 1.6706 × 10 | 2.2752 × 10 | |||
| XT10 | 4.2295 × 10 | 1.7971 × 10 | 8.4556 × 10 | |||
| NJ10 | 1.0998 × 10 | 7.3656 × 10 | 1.2708 × 10 | |||
| NWM10 | 1.2105 × 10 | 8.4012 × 10 | 1.2490 × 10 | |||
| SA8 | 5.4711 × 10 | 1.2977 × 10 | 1.7276 × 10 | |||
| NWM9 | 3.9880 × 10 | 7.3134 × 10 | 2.2584 × 10 | |||
| NAJJ10 | 9.4828 × 10 | 5.4826 × 10 | 4.7445 × 10 | |||
| XT10 | 3.5515 × 10 | 1.0600 × 10 | 2.1623 × 10 | |||
| NJ10 | 1.5421 × 10 | 1.6064 × 10 | 1.4753 × 10 | |||
| NWM10 | 4.0057 × 10 | 3.0366 × 10 | 1.3881 × 10 | |||
| SA8 | 5.7168 × 10 | 1.4599 × 10 | 5.0965 × 10 | |||
| NWM9 | 1.1062 × 10 | 3.0900 × 10 | 1.0209 × 10 | |||
| NAJJ10 | 9.5231 × 10 | 2.0821 × 10 | 1.0163 × 10 | |||
| XT10 | 3.9258 × 10 | 1.9159 × 10 | 1.6477 × 10 | |||
| NJ10 | 7.7470 × 10 | 1.2437 × 10 | 2.3307 × 10 | |||
| NWM10 | 1.1664 × 10 | 2.1891 × 10 | 7.6955 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, E.; Mittal, S.K.; Jaiswal, J.P.; Panday, S. An Efficient Bi-Parametric With-Memory Iterative Method for Solving Nonlinear Equations. AppliedMath 2023, 3, 1019-1033. https://doi.org/10.3390/appliedmath3040051
Sharma E, Mittal SK, Jaiswal JP, Panday S. An Efficient Bi-Parametric With-Memory Iterative Method for Solving Nonlinear Equations. AppliedMath. 2023; 3(4):1019-1033. https://doi.org/10.3390/appliedmath3040051
Chicago/Turabian StyleSharma, Ekta, Shubham Kumar Mittal, J. P. Jaiswal, and Sunil Panday. 2023. "An Efficient Bi-Parametric With-Memory Iterative Method for Solving Nonlinear Equations" AppliedMath 3, no. 4: 1019-1033. https://doi.org/10.3390/appliedmath3040051
APA StyleSharma, E., Mittal, S. K., Jaiswal, J. P., & Panday, S. (2023). An Efficient Bi-Parametric With-Memory Iterative Method for Solving Nonlinear Equations. AppliedMath, 3(4), 1019-1033. https://doi.org/10.3390/appliedmath3040051






