Abstract
For linear optimization problems with a parametric objective, so-called parametric linear programs (PLP), we show that the optimal decision values are, under few technical restrictions, unimodal functions of the parameter, at least in the two-degrees-of-freedom case. Assuming that the parameter is random and follows a known probability distribution, this allows for an efficient algorithm to determe the quantiles of linear combinations of the optimal decisions. The novel results are demonstrated with probabilistic economic dispatch. For an example setup with uncertain fuel costs, quantiles of the resulting inter-regional power flows are computed. The approach is compared against Monte Carlo and piecewise computation techniques, proving significantly reduced computation times for the novel procedure. This holds especially when the feasible set is complex and/or extreme quantiles are desired. This work is limited to problems with two effective degrees of freedom and a one-dimensional uncertainty. Future extensions to higher dimensions could yield a key tool for the analysis of probabilistic PLPs and, specifically, risk management in energy systems.
1. Introduction
Economic Dispatch (ED) is a fundamental optimization problem in power system operations. The target is to cost-optimally schedule the power generation required to meet given demands, while taking into account generation and transmission constraints [1,2]. It is often formulated as a linear program. This classic problem has recently received much new interest due to the growing share of variable renewable energies in many power systems around the world, requiring more flexible scheduling, dealing with many more units than before as well as error-prone renewable energy forecasts, and also considering demand side elements and storage units [3]. Economic dispatch is also at the heart of energy markets [4].
If some parameters of the economic dispatch problem are uncertain, e.g., the available power of renewable energies or the specific costs of different energy sources, the scheduling results will also be uncertain. Estimating the quantiles of the resulting distributions of the scheduling decision variables, given a known distribution over the parameters, is a key step for many risk quantification applications.
1.1. Related Literature
The predominant techniques employed for quantile estimation in this context are Monte Carlo Sampling (MCS) and PieceWise Computation (PWC) methods.
To determine the quantiles using MCS [5,6,7], the optimization problem needs to be solved a large number of times, the number being on the order of the squared inverse of the desired quantile accuracy [8]. This is computationally costly, especially for large-scale problems or when extreme target quantiles close to zero or one are to be determined, the number of required samples is especially high in this case [8]. Different variance reduction techniques can be employed to reduce the number of required samples [9]. Latin hypercube sampling as an instance of correlation-induction methods can perform very well for quantile estimation [10,11], with the largest benefits in high dimensions. Importance sampling is another effective approach for non-extreme quantiles [9].
PWC approaches [12,13,14], on the other hand, rely on an analytical characterization of the solution to the optimization problem as the parameters vary. It has been shown that the solutions of Parametric Linear Programs (PLP) exhibit piecewise constant or linear behavior with respect to the parameters [15,16]. However, computing the function values for all or a significant fraction of these pieces—a requisite step for quantile computation—often becomes computationally infeasible due to the substantial growth in the number of pieces when dealing with complex feasibility sets or a high number of constraints [17].
Many works on ED under uncertainty [18] develop decision-making strategies that perform well on average for all instances of the uncertain parameter. These approaches often employ two-stage stochastic programming [19]. By utilizing the Sample Average Approximation (SAA) stochastic programs for linear ED, problems can be reformulated into larger linear programs [19]. Robust versions, which incorporate quantiles or the so-called conditional value at risk, are also commonplace [20,21]. In stochastic programming, the precise characterization of the distribution of second-stage decisions is not of paramount importance as long as it does not alter the optimal first-stage decision. Consequently, it is often feasible to work with relatively coarse approximations of the second-stage decision distribution, relying on a limited number of samples in the SAA. In our research, we aspire to attain more precise distribution results for risk quantification purposes, but not to optimize the distribution.
A last line of related research uses polynomial chaos expansions to characterize power flows under uncertainty [22,23]. This approach can offer exact probabilistic characterizations of power flow problems under uncertainty, i.e., for the solutions of linear or non-linear equations, and the parameters of the resulting probability distributions can be optimized using chance constraints. The outcomes of the optimal power flow problem, which is an instance of an ED optimization problem, are, however, not treated as uncertain.
1.2. Contributions
In this work, we propose a novel, efficient approach to quantile estimation for ED with uncertain cost parameters and two degrees of freedom. Consequently, the number of required ED optimization runs is independent of the ED problem structure or the quantile level to be computed. Instead, it scales with the logarithm of the desired accuracy of the quantile estimate. For various probabilistic ED instances, the approach can thus lead to more overall computational efficiency.
Core to our work are the following two abstract, technical contributions. First, we provide a novel characterization of the solution of a PLP with varying objective function parameters. It was previously known that the optimal objective value is piecewise linear and concave in the varied parameters, and that the optimal decisions are piecewise constant [15,16]. No global characterization was available for the decision values as function of the parameters. For the two-degrees-of-freedom case, we can now show that the decision value function is unimodal, i.e., has only a single bump or valley over the parameter domain. This limits the up-down variability of the decision values as a function of the varied parameter and, in turn, allows for the efficient computation of (upper) quantiles of a random variable mapped through this function. A second general contribution of this work is then to provide a novel algorithm for the latter task.
These novel abstract results can be used to attack the aforementioned ED problem. For an example ED setup, we show how to estimate quantiles of the optimal power transmission flows given uncertain fuel costs. We compare the accuracy and computational performance of the new approach to that of MCS and PWC techniques.
In this work, the analytic results and the algorithms are limited to problems with two effective degrees of freedom and a one dimensional uncertain parameter. Future extensions to higher dimensions would yield a key tool for the analysis of probabilistic PLPs and risk management in energy systems, specifically.
The rest of the paper is structured as follows: in Section 2, we present a novel theorem for PLP, which serves as the basis for a newly proposed quantile estimation algorithm for the optimization outcomes, as described in Section 3. Section 4 illustrates how these theoretical insights can be applied to tackle probabilistic economic dispatch, specifically focusing on estimating the quantiles of economic dispatch decisions under uncertain fuel costs. This section also includes a comparative analysis with commonly employed alternatives. Lastly, in Section 5, we provide a summary of our findings and suggest potential avenues for future research.
2. Novel Characterization of Optimal PLP Decisions
Consider a two-degree-of-freedom Parametric Linear Program (PLP), where the objective depends on a one-dimensional parameter , i.e.,
Here, represents a vector containing coefficients in the objective function, which vary with the uncertain parameter . The matrix corresponds to the coefficient matrix of the constraints and is a vector containing constant values associated with these constraints. We generally denoted matrices with capital bold letters and vectors with small bold letters in this paper.
We first define the direction of a vector via its angle to the first basis vector, according to the standard atan2 definition (https://en.wikipedia.org/wiki/Atan2 (accessed on 1 November 2022)).
Definition 1.
The direction of vector is defined as
Since the directions represent circular variables in standard parameterization, we identify and , . Next, we define unimodality.
Definition 2.
A map is called unimodal with a bump if there exists such that is monotonically increasing for and is monotonically decreasing for .
Definition 3.
A map is called unimodal with a valley if there exists such that is monotonically decreasing for and is monotonically increasing for .
Definition 4.
A map is called unimodal if it is unimodal with either a bump or a valley.
Now, we can introduce the fundamental idea of this study, namely the unimodality of any linear combination of the optimal solutions of the PLP.
Theorem 1.
For the two-degree of freedom PLP presented in Equation (1), let defined as be increasing and its range be contained in an interval of length less than π. Then, the map defined by is unimodal for any . The maximal value of is attained for a θ with , if this equation has a solution.
The proof of the Theorem 1 is described in Appendix A. If jumps by for due to circularity of the angles, it is sufficient that each segment of the curve is increasing. Alternatively, one could choose an equivalent representer , , of the angle such that the curve is continuous.
The theorem provides an important, global characterization of : it limits the up-down variations when changing . As a result, the set is either one or two intervals, but it cannot consist of a multitude of disconnected regions that would be possible without this theorem.
3. Algorithm for Quantile Estimation
The previous characterization of the solution of a PLP can be employed to efficiently determine quantiles of the decision values of a PLP subject to a probabilistic model for . Using the notation introduced in the previous section and assuming that follows distribution , we want to find the smallest value , , which would not exceed with probability , i.e.,
Without loss of generality, we assume from now on that is unimodal with a bump. If was unimodal with a valley, would be unimodal with a bump and we could compute the -quantile of instead of Equation (3).
If is unimodal with a bump, we know that the quantile is determined by one interval containing all for which exceeds , i.e.
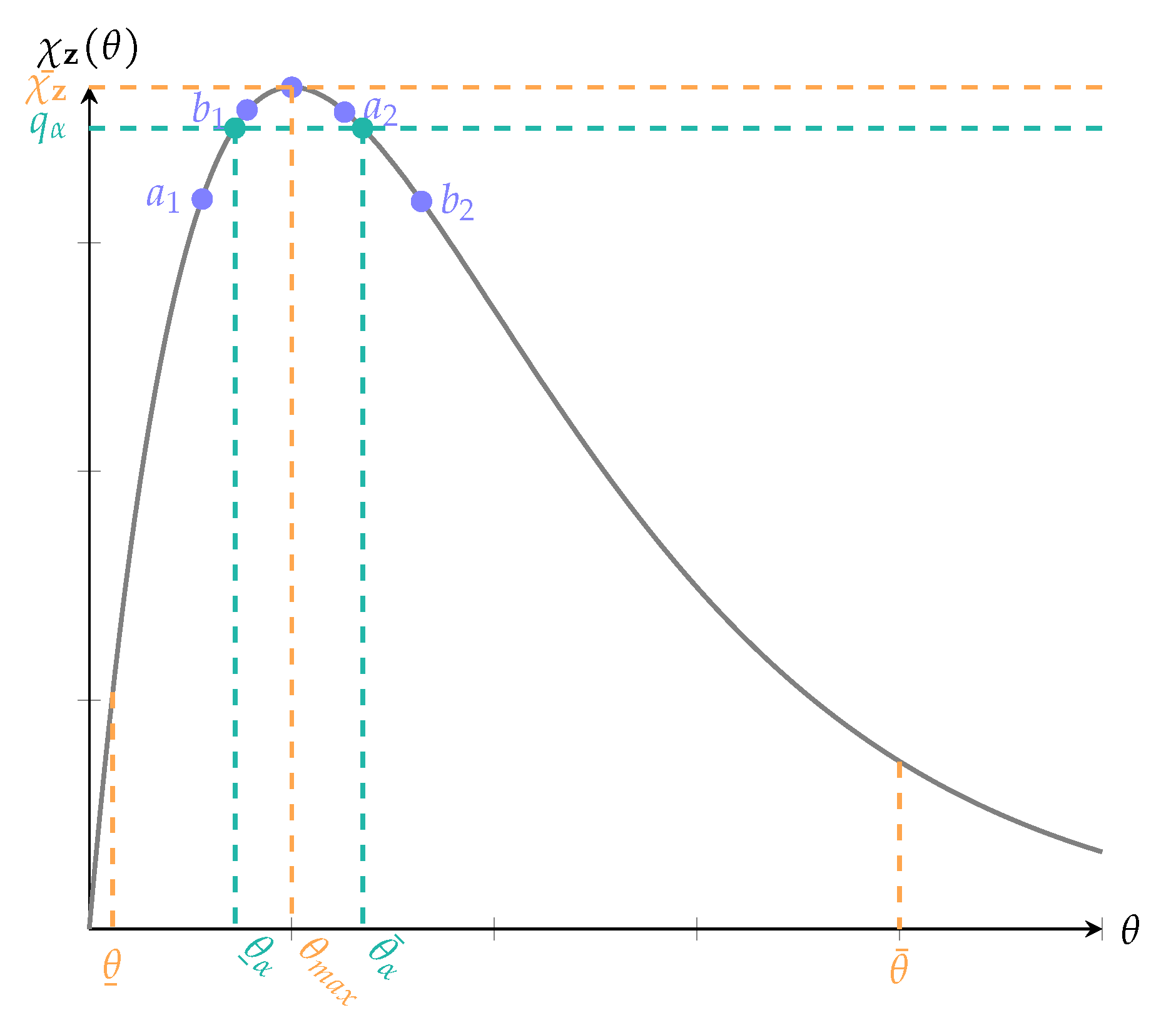
Our proposed algorithm to compute and thereby is described in Algorithm 1 and graphically depicted in Figure 1. It is designed to minimize the number of required optimization runs of Equation (1).
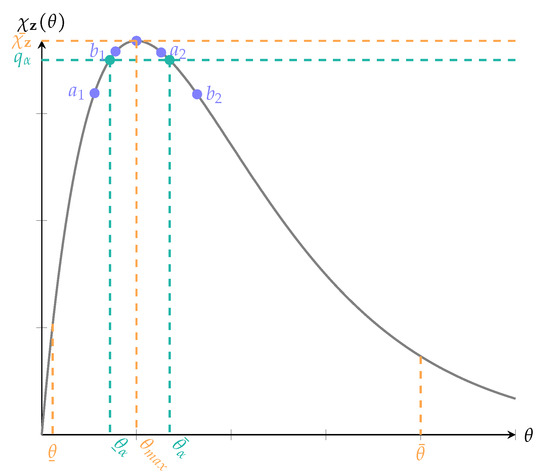
Figure 1.
Two iterations of Algorithm 1 to find the quantile for the unimodal function : in the first iteration, correspond to , , in the second iteration to , . The probability for or is in both cases.
- We first determine . According to Theorem 1, this can be achieved by identifying the value of such that . No optimization run is required for this step (Alternatively, the maximum of the unimodal function could be determined using the Golden Section Search (GSS) algorithm [24,25]. However, this would require some optimization runs).
- The algorithm then proceeds by iteratively searching for two points, the left boundary and the right boundary , where , such that and .In each iteration we first fix the left boundary and then search for right boundary such that . This does not require any optimization runs. It can be achieved via a bisection routine using the Cumulative Distribution Function (CDF) of , which is assumed to be known analytically, i.e.,The stopping accuracy is .
- The left boundary is adapted in an outer loop again via a bisection-like approach. If , then has to be adapted in rightward direction, and vice versa. The procedure is repeated until a range is found in which the left and the right boundary have equal function values with accuracy . One optimization run is required to determine a new or in each step.
| Algorithm 1 Quantile Estimation |
|
To analyze the total number of optimization runs required by the algorithm, note that is only evaluated once for each proposed . Moreover, for the bisection approach the number of visited is bounded above by . The method is thus highly efficient in the number of optimization runs. These could become computationally expensive when the problem size of Equation (1) increases.
4. Simulative Validation with Economic Dispatch
We now evaluate the computational performance and the accuracy of the proposed algorithm for an example economic dispatch problem with uncertain generation costs, as outlined in Section 4.1. This particular problem serves as an illustrative case for the parametric linear program that we introduced earlier in Equation (1). Our goal is then to estimate the magnitudes of the line power flows that are surpassed merely 1% of the time. This problem is an instance of Equation (3) and can be solved using the algorithm from Section 3. We compare the performance of the proposed algorithm with two baselines: Monte Carlo Sampling (MCS) and PieceWise Computation techniques (PWC) as described in Section 4.2. The numerical results are presented in Section 4.3.
4.1. Problem Setup
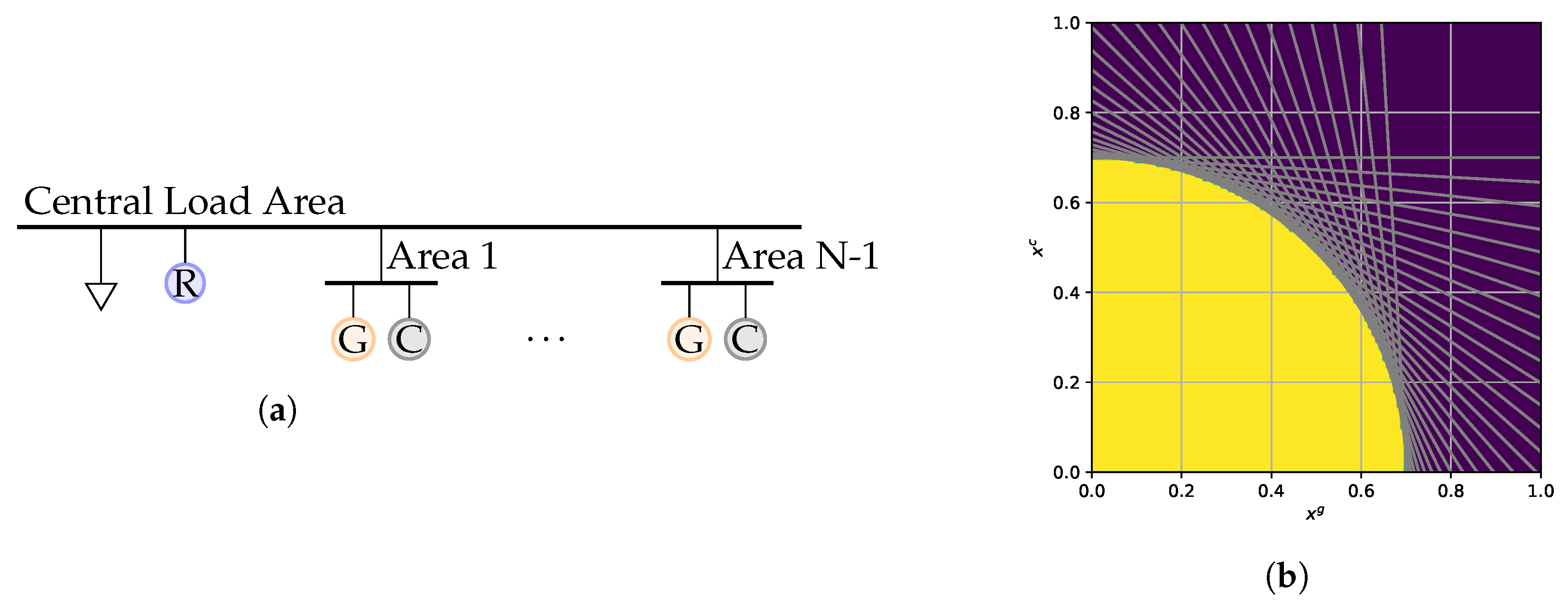
Consider an N-bus radial power system where three types of generators, gas, coal, and reserve power plants, cover a known demand, see Figure 2a. All power plants of the same type are assumed to have the same activation levels relative to the installed capacity.
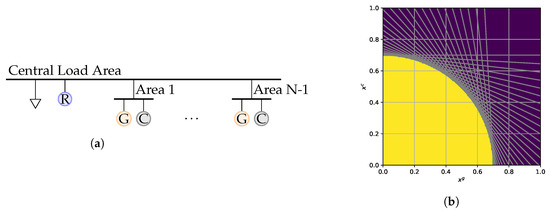
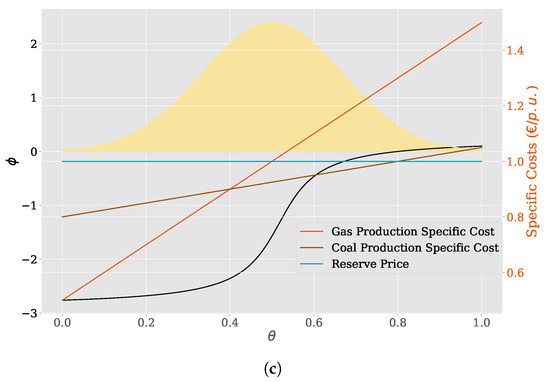
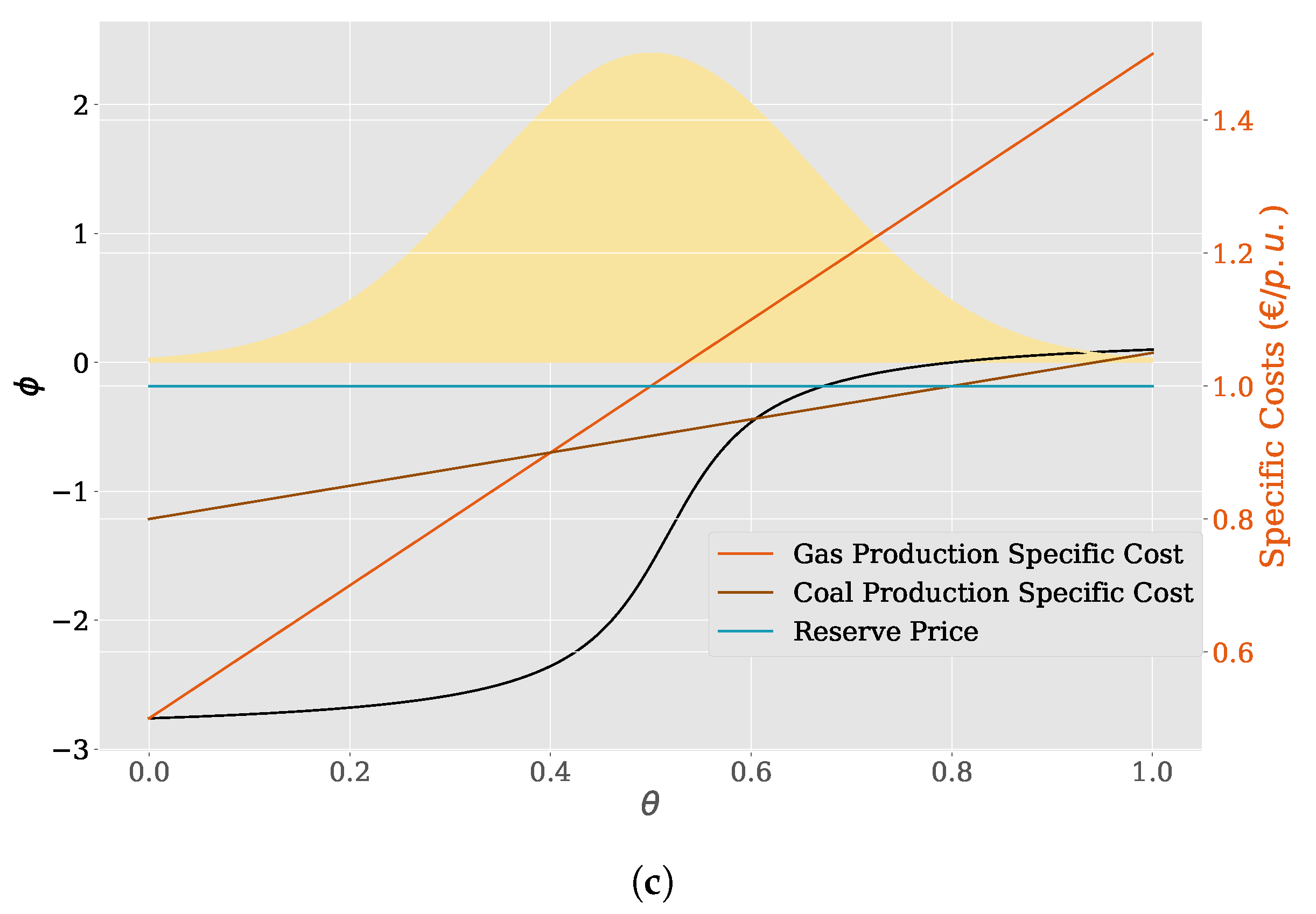
Figure 2.
Setup of the example economic dispatch problem: (a) The radial grid contains a load (triangle) and a reserve generator (R) at the first bus. further buses contain a coal (C) and a gas (G) generator each. (b) The feasible region (yellow) of the dispatch problem depending on the fraction of coal and gas generation in covering the load (using buses). (c) Specific production costs and the direction of the objective function. The assumed probability distribution is depicted via its density function (yellow shaded area).
The problem is formally defined as follows. Variables and parameters associated with each generation type have superscripts: g for gas power plants, c for coal power plants, and r for reserve providers. Matrices and vectors are written in bold letters. We then solve
The objective function in Equation (6) is to minimize the total costs of electricity production. Here, denotes the specific operation costs of power plants of type ▪. is a decision variable and represents the fraction of the installed capacity of type ▪ to be dispatched. is the vector of installed capacities of the power plants of type ▪, where is the number of power plants of type ▪. Thus, denotes the summed capacity of each type. Equation (7) describes the energy balance at each bus. Here, denotes the vector of transmission line flows with maximal absolute value , and is the number of transmission lines. Matrix encodes whether or not the power plants of type ▪ are connected to each of the buses. is the line to bus directed incidence matrix. is the vector of demands at each bus.
There are three variables for power generation fractions , and variables representing the line flows of the radial network. Thus, the total number of decision variables equals . On the other hand, we have N equality constraints regarding the power balance at each bus. Therefore, the optimization problem has only two effective degrees of freedom as is the requirement for the PLP introduced in Equation (1). As a result, all decision variables can be expressed in terms of and .
We parameterize our networks as follows. All parameters are chosen to yield instances with a feasible set of varying complexity. As shown in Figure 2a, one bus (), contains all of the network load, which is set to and the single reserve generator. The gas and coal generators are placed at the other nodes. Each type of generators can together supply all of the load, i.e., . The generation capacities at nodes are chosen as
where represents the base apparent power. The transmission lines all have the capacity of . These parameter values generate a feasible region with a number of vertices that matches the number of buses; for the resulting feasible region is shown in Figure 2b. By modifying the number of buses, we can then analyze the computational performance of different methods depending on the complexity of the feasible set.
The specific production costs are chosen as , , and for , see Figure 2c. The rationale behind this assumption is that in many applications it might be possible to choose two extreme cost configurations, while linear combinations thereof are also possible with some probability.
Since , the objective of the optimization problem can be reduced to two degrees of freedom, namely and . It then reads and thus, is monotonically increasing, as is also shown in Figure c. The uncertain parameter is assumed to have a normal distribution, i.e., with a mean , standard deviation , and the normal distribution being clipped to the interval .
With these settings, the problem formulation meets all the requirements outlined in Theorem 1. As a result, our proposed algorithm can be applied to efficiently estimate quantiles of the decision variables and , or linear combinations thereof, such as the power flows over the transmission lines.
4.2. Baselines
We evaluate the performance of the proposed quantile estimation method by comparing its accuracy and computational performance to that of the two common quantile estimation techniques in probabilistic linear programming, i.e., MCS and PWC.
To implement PWC we proceed as follows. We start with and run one optimization of the PLP presented in Equation (1) to compute an optimal basis for this parameter. It is known that for increasing , the primal solution of the PLP remains constant until the current basis is not optimal anymore, as the non-zero dual variables are linear functions of . When one of these dual variables becomes zero, i.e., the corresponding row of is orthogonal to , another basis becomes optimal. We determine it by re-running the optimization algorithm. We iterate until is reached. The exact quantile of our problem is computed by piecewise analysis of the probability distribution.
Concerning the MCS baseline, statistical analysis shows that the number of samples required to obtain a given quantile accuracy is in expectation proportional to . The scaling factor is large if we search for extreme quantiles, i.e., the -value is close to 0 or 1 [8]. Empirically, we proceed as follows: we first solve the PLP in Equation (1) for a large number K of random samples of the uncertain parameter ( in this case). For a given sample size we determine the average accuracy of the quantile estimate by taking 20 random subsamples of size k and determining the mean absolute error, taking the PWC result as the reference. The minimum numbers k yielding an average quantile estimation error of less than or , respectively, are reported below as the number of required samples / optimization runs. The reported timings are for computing one sample of size k. The minimum sample size required to determine the -quantile is approximated as .
All computations are carried out on a machine with a quad core 1.6 GHz CPU and 8 GBs of RAM.
4.3. Results
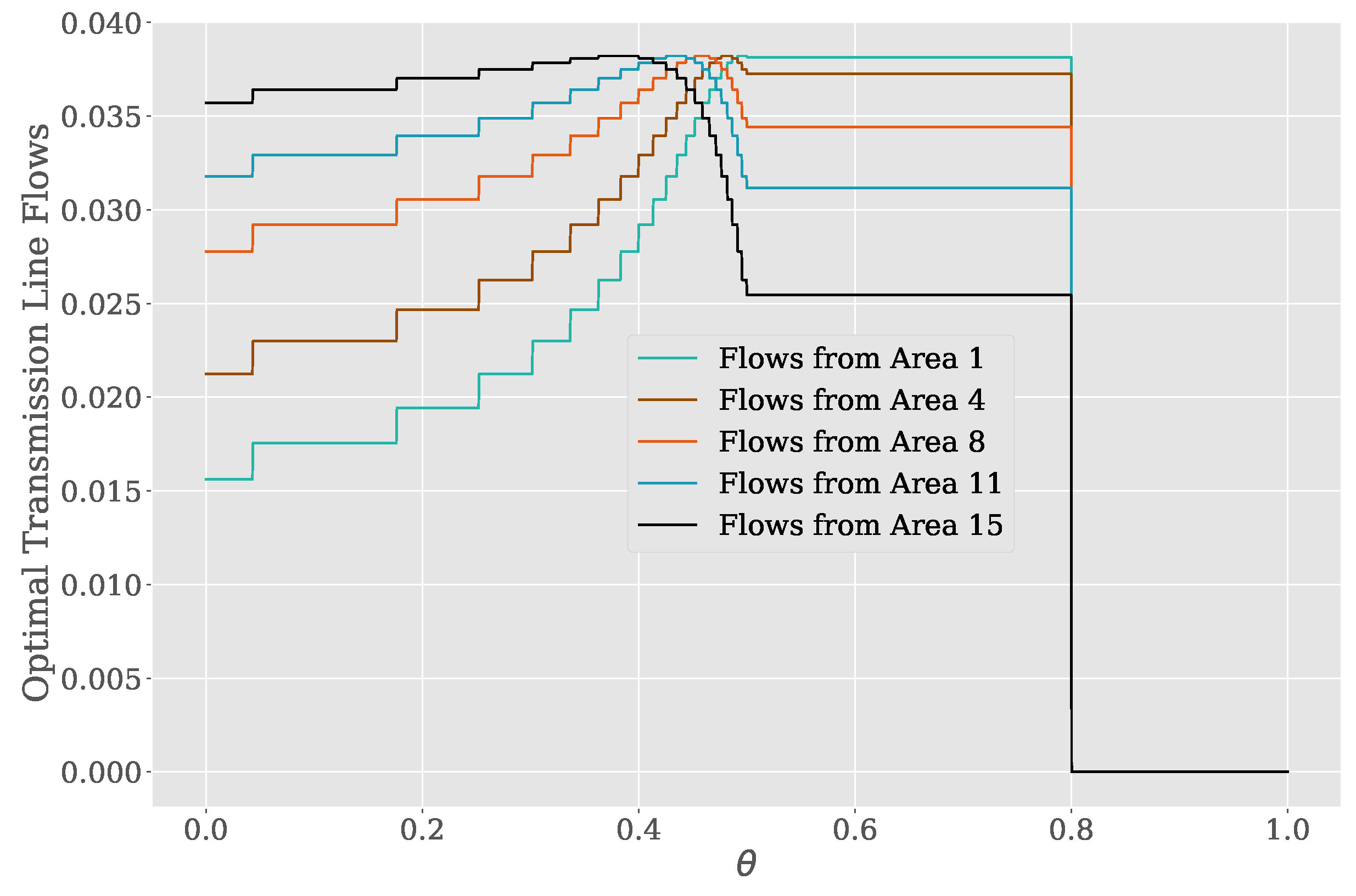
Figure 3 presents the optimal transmission line flows for several interconnections as a function of the parameter . We observe that the curves are surprisingly complex in shape, even though the specific costs of the PLP in Equation (1) vary only linearly in . This proves that the linear optimization represents a highly nonlinear transformation of that, at least in our setting, cannot easily be linearized. Despite the curves’ complexity, we observe that all curves are unimodal, as predicted by our theoretical derivation.
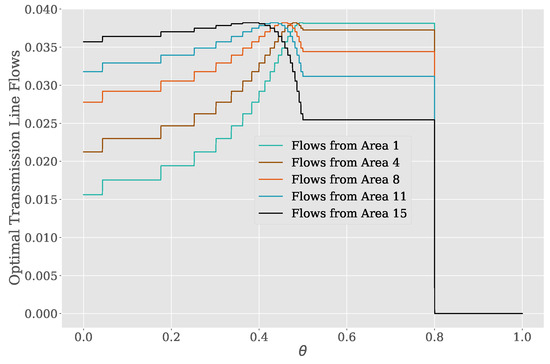
Figure 3.
Optimal power flows from different areas to the central load, cf. Figure 2, as a function of the uncertain parameter .
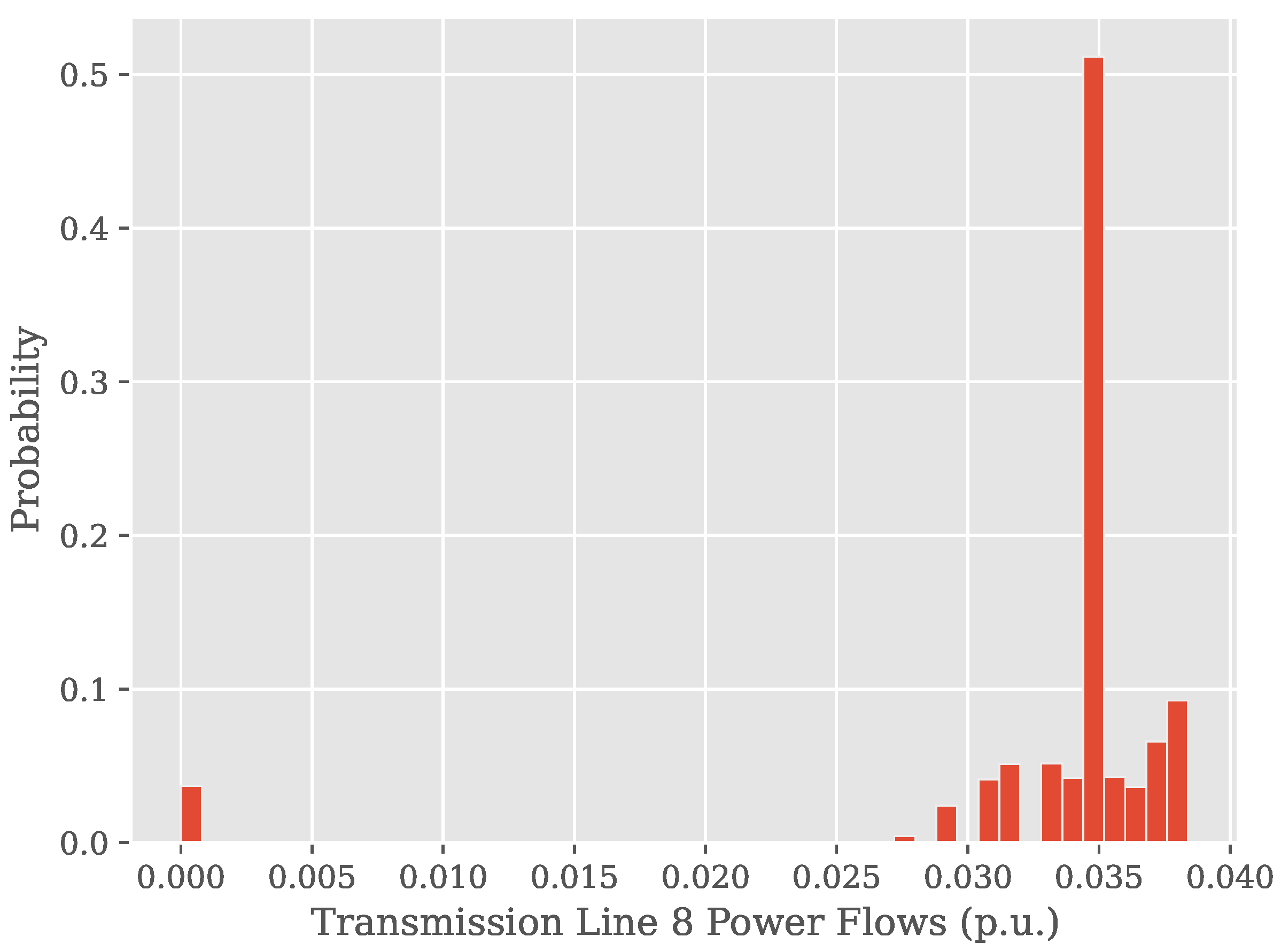
Figure 4 shows the resulting probability distribution , where is a selected transmission line flow (here: connection from the central area to area 8). Although is a simple normal distribution, is not. Thus, approximating it with a normal distribution would not yield reliable quantile estimates.
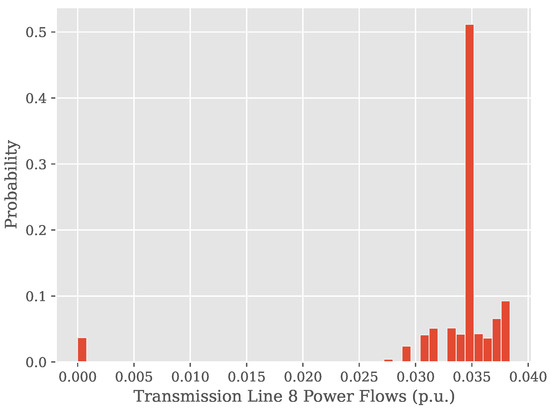
Figure 4.
Probability distribution of optimal power transfers from area 8 to the central load, as implied by the distribution of the uncertain parameter , cf. Figure 2.
Timings for computing the quantiles to different accuracy levels are presented in Table 1, Table 2 and Table 3 for the proposed method as well as for the two baselines. The three tables represent problem setups with different complexity of the feasible set, i.e., we use 30, 100, and 200-bus networks to compare the performance of the three methods as the problem dimension increases.

Table 1.
Timings and accuracy for quantile estimation of one transmission line flow, buses.

Table 2.
Timings and accuracy for quantile estimation of one transmission line flow, buses.

Table 3.
Timings and accuracy for quantile estimation of one transmission line flow, buses.
It can be observed that, even for very high accuracy requirements, the proposed method needs significantly less time and fewer optimization runs compared to the other two methods. As the problem size increases, the relative performance gain of the proposed method increases even more. These two observations prove experimentally that the novel characterization of the PLP solution function can be exploited to develop more efficient algorithms.
The proposed method even reaches an exact solution in many cases. This is because is a distribution with point masses only, due to the piecewise constant nature of . When the binary search of and in our algorithm finds the right segment, the quantile result is precise. Similarly, MCS also benefits from the piecewise constant nature of optimal decisions, which offsets its inherent randomness.
5. Conclusions
With the existence of uncertainties in different input parameters of the economic dispatch problem in power systems, such as renewable production and fuel price, the optimal dispatch solutions are also uncertain. Estimating the quantiles of the optimal decisions is necessary for risk quantification purposes. Formally, this problem is an instance of quantile estimation for the solutions of probabilistic PLPs.
Two methods are often used for this purpose: Monte Carlo Sampling (MCS) and PieceWise Computation techniques (PWC). When using MCS, the sampling rate should be large enough to obtain an acceptable accuracy, leading to a large number of required optimizations to be solved and high computation time. On the other hand, the number of required optimizations in PWC depends on the number of constraints of the optimization problem, which can be both an advantage and a disadvantage.
This paper introduces a new algorithm for computing the quantiles of optimal decisions for setups with two degrees of freedom using a novel theorem outlined in Section 2, resulting in reduced computation time. Results show that the required number of optimizations in the proposed approach is independent of the problem structure and the quantiles to be estimated, making it significantly more efficient than common quantile estimation algorithms as discussed in Section 4.3.
It is important to note that this study is limited to linear optimization problems with two degrees of freedom and a one-dimensional uncertain parameter. A straight-forward extension of the underlying theorem to higher dimensions is not possible since counter-examples for the core unimodality claim can be constructed, if all possible PLPs and all decision variables are considered. However, future research may explore in more detail the question of which subclass of PLPs or which subset of the optimal decision variables unimodality characteristics can still be proved.
Author Contributions
Conceptualization, S.M. and F.S.; methodology, S.M. and F.S.; software, S.M.; validation, S.M, A.S. and F.S.; formal analysis, S.M. and F.S.; investigation, S.M. and F.S.; resources, S.M.; data curation, S.M.; writing—original draft preparation, S.M. and F.S.; writing—review and editing, S.M., A.S. and F.S.; visualization, S.M.; supervision, F.S.; project administration, F.S.; funding acquisition, F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Federal Ministry of Transport and Digital Infrastructure in project CO2030 (grant number 19OS22005D). It was performed in the context of the LOEWE center emergenCITY.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
| Symbols of abstract framework | |
| Coefficient matrix of the PLP constraints | |
| Right-hand side vector of PLP constraints | |
| Uncertain parameter of PLP with domain | |
| Vector of PLP objective function coefficients as a function of | |
| Direction of the vector | |
| Direction of the vector | |
| -quantile of -values induced by distribution | |
| left, right boundary of interval containing -quantile of | |
| , | Left, right boundary of currently selected range of |
| , | Tolerances of bisection search |
| Symbols of specific validation setup | |
| N | Number of buses (index i) |
| Number of power plants of type ▪ | |
| Production of power plants of type ▪ relative to installed capacity | |
| Installed capacity of type ▪ at bus i | |
| Power plant of type ▪ to bus incidence matrix | |
| Specific operation costs of power plants of type ▪ as a function of | |
| Number of transmission lines | |
| Vector of transmission line flows | |
| Vector of transmission line capacities | |
| Line to bus directed incidence matrix | |
| Vector of demands | |
| The base apparent power | |
| Mean and standard deviation of the uncertain parameter | |
| Accepted tolerance of the estimation error in MCS method | |
Appendix A. Proof of the Theorem
To prove Theorem 1 presented in Section 2, we first establish that the optimal solution vector can be characterized as a function of only the direction of the objective vector . We can thus write instead of . Then, we show that has at most one extremum point in any range of with length smaller than . Lastly, we use rotation arguments to prove the theorem for arbitrary result directions .
Lemma A1.
The optimal decision of the linear program presented in Equation (1) only depends on the direction of the objective vector , not its magnitude.
Proof.
Rescaling the objective function does not change the optimum decision variables. □
Next, we characterize the first dimension of the optimal decision vector as a function of .
Theorem A1.
The map is increasing for and decreasing for . Therefore, in any range of ϕ with length less than π, there is at most one extremum point of .
The theorem is proven for one quadrant in the following. The other quadrants can be dealt with analogously.
Lemma A2.
is monotonically increasing.
Proof.
Suppose we have two objective vectors: and with respective directions and where . Furthermore, we represent the optimal solution to the problem with and when the objective vectors are and , respectively.
For any objective vector, the objective function for the optimal decision vector is greater than or equal to the objective function value for any other point in the feasible set. Since both and are feasible solutions, when the objective vector is , we can write:
Similarly, when the objective vector is , we have:
since , dividing both sides of the inequality Equation (A1) by we have
In the same way, dividing both sides of the inequality Equation (A2) by (which is negative) we obtain
Adding Equations (A3) and (A4) we can derive
and by definition of the angles
Since tan is strictly monotonically increasing in the range and by assumption , we have that
Consequently, it must hold that
□
Since is a function of , we can use Theorem A1 and Equation (2) to determine the interval of in which has at most one maximum or minimum point (Having an interval for , as the inverse of the tangent function is monotonic, we can use the boundaries of this interval to find the limits for and thus for , solving the resulting equations).
Now, we generalize the finding of Theorem A1 to obtain Theorem 1. Consequently, the proof of Theorem 1 is as follows.
Proof.
Given , we define new coordinates,
where is perpendicular to . The problem that is presented in Equations (6)–(9) then is equivalent to
This coordinate rotation ensures that the new first axis aligns with , i.e., the direction of the linear combination for which we seek to determine quantiles. Given the redefined coordinates, we can then apply Theorem A1 to in this transformed space. This yields the desired unimodality statement. □
References
- Chowdhury, B.H.; Rahman, S. A review of recent advances in economic dispatch. IEEE Trans. Power Syst. 1990, 5, 1248–1259. [Google Scholar] [CrossRef]
- Wood, A.J.; Wollenberg, B.F.; Sheble, G.B. Power Generation, Operation, and Control, 3rd ed.; Wiley-Blackwell: Chichester, UK, 2013. [Google Scholar]
- Kunya, A.B.; Abubakar, A.S.; Yusuf, S.S. Review of economic dispatch in multi-area power system: State-of-the-art and future prospective. Electr. Power Syst. Res. 2023, 217, 109089. [Google Scholar] [CrossRef]
- Lin, J.; Magnago, F.H. Electricity Markets: Theories and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- González-Fernández, R.A.; da Silva, A.M.L.; Resende, L.C.; Schilling, M.T. Composite systems reliability evaluation based on Monte Carlo simulation and cross-entropy methods. IEEE Trans. Power Syst. 2013, 28, 4598–4606. [Google Scholar] [CrossRef]
- Kim, S.; Hur, J. A probabilistic modeling based on Monte Carlo simulation of wind powered EV charging stations for steady-states security analysis. Energies 2020, 13, 5260. [Google Scholar] [CrossRef]
- Kim, G.; Hur, J. Probabilistic modeling of wind energy potential for power grid expansion planning. Energy 2021, 230, 120831. [Google Scholar] [CrossRef]
- Beard, R.E.; Pentikainen, T.; Pesonen, E. Risk Theory: The Stochastic Basis of Insurance, 3rd ed.; Chapman And Hall: London, UK, 1984. [Google Scholar] [CrossRef]
- Dong, H.; Nakayama, M.K. A Tutorial on Quantile Estimation via Monte Carlo. In Proceedings of the Monte Carlo and Quasi-Monte Carlo Methods: MCQMC 2018, Rennes, France, 1–6 July 2018; pp. 3–30. [Google Scholar]
- Avramidis, A.N.; Wilson, J.R. Correlation-induction techniques for estimating quantiles in simulation experiments. In Proceedings of the Winter Simulation Conference Proceedings, Arlington, VA, USA, 3–6 December 1995; pp. 268–277. [Google Scholar]
- Dong, H.; Nakayama, M.K. Quantile Estimation with Latin Hypercube Sampling. Oper. Res. 2017, 65, 1678–1695. [Google Scholar] [CrossRef]
- Ji, Y.; Thomas, R.J.; Tong, L. Probabilistic Forecasting of Real-Time LMP and Network Congestion. IEEE Trans. Power Syst. 2017, 32, 831–841. [Google Scholar] [CrossRef]
- Yong, P.; Zhang, N.; Kang, C.; Xia, Q.; Lu, D. MPLP-based fast power system reliability evaluation using transmission line status dictionary. IEEE Trans. Power Syst. 2018, 34, 1630–1640. [Google Scholar] [CrossRef]
- Sindt, J.; Santos, A.; Pfetsch, M.E.; Steinke, F. Evaluation of Multiparametric Linear Programming for Economic Dispatch under Uncertainty. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Europe: Smart Grids: Toward a Carbon-Free Future, ISGT Europe 2021, Espoo, Finland, 18–21 October 2021. [Google Scholar] [CrossRef]
- Gal, T.; Nedoma, J. Multiparametric linear programming. Manag. Sci. 1972, 18, 406–422. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J.N. Introduction to Linear Optimization; Athena Scientific: Belmont, MA, USA, 1997; pp. 217–221. [Google Scholar]
- Murty, K.G. Computational complexity of parametric linear programming. Math. Program. 1980, 19, 213–219. [Google Scholar] [CrossRef]
- Roald, L.A.; Pozo, D.; Papavasiliou, A.; Molzahn, D.K.; Kazempour, J.; Conejo, A. Power systems optimization under uncertainty: A review of methods and applications. Electr. Power Syst. Res. 2023, 214, 108725. [Google Scholar] [CrossRef]
- Dantzig, G. Linear Programming Under Uncertainty. Manag. Sci. 1955, 1, 197–206. [Google Scholar] [CrossRef]
- Jabr, R.A. Robust self-scheduling under price uncertainty using conditional value-at-risk. IEEE Trans. Power Syst. 2005, 20, 1852–1858. [Google Scholar] [CrossRef]
- Ackermann, S.; Szabo, A.; Bamberger, J.; Steinke, F. Design and optimization of performance guarantees for hybrid power plants. Energy 2022, 239, 121742. [Google Scholar] [CrossRef]
- Mühlpfordt, T.; Faulwasser, T.; Hagenmeyer, V. A generalized framework for chance-constrained optimal power flow. Sustain. Energy, Grids Netw. 2018, 16, 231–242. [Google Scholar] [CrossRef]
- Mühlpfordt, T.; Roald, L.; Hagenmeyer, V.; Faulwasser, T.; Misra, S. Chance-constrained AC optimal power flow: A polynomial chaos approach. IEEE Trans. Power Syst. 2019, 34, 4806–4816. [Google Scholar] [CrossRef]
- Kiefer, J. Sequential minimax search for a maximum. Proc. Am. Math. Soc. 1953, 4, 502–506. [Google Scholar] [CrossRef]
- Chong, E.K.P.; Zak, S.H. An Introduction to Optimization, 4th ed.; Wiley Series in Discrete Mathematics and Optimization; John Wiley & Sons: Nashville, TN, USA, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).