Measurement and Modelling of Beach Response to Storm Waves: A Case Study of Brandon Bay, Ireland
Abstract
1. Introduction
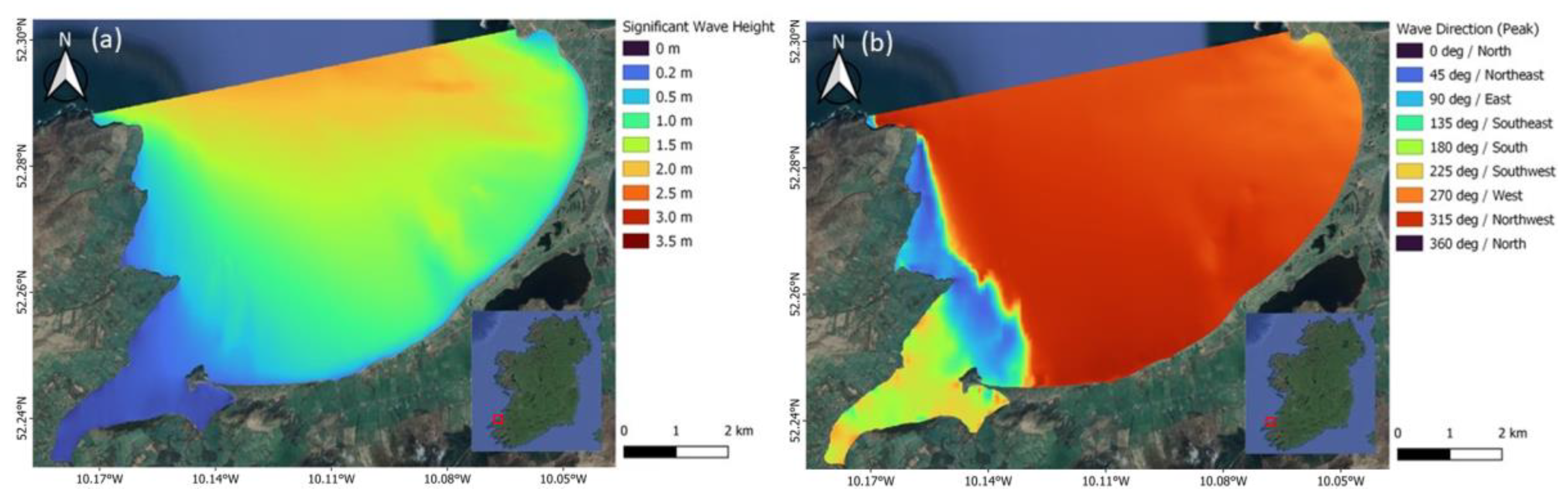
2. Description of Study Area
3. Methodology
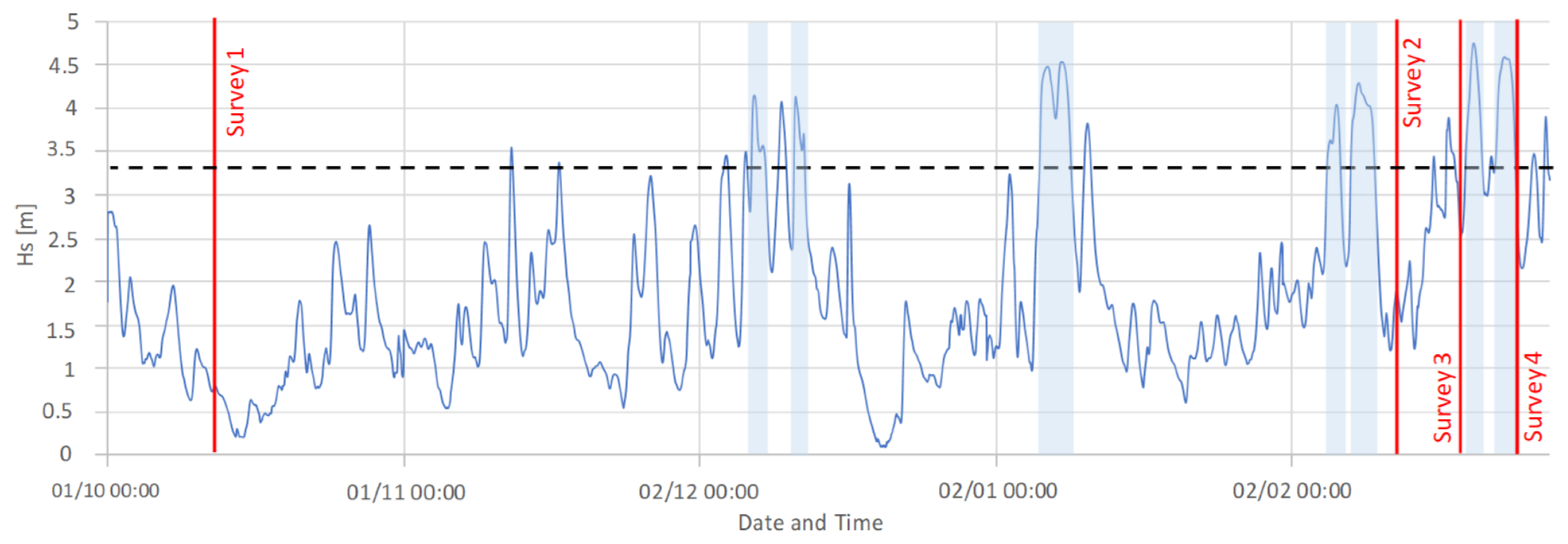
3.1. Collection of Cross-Section Profile Data
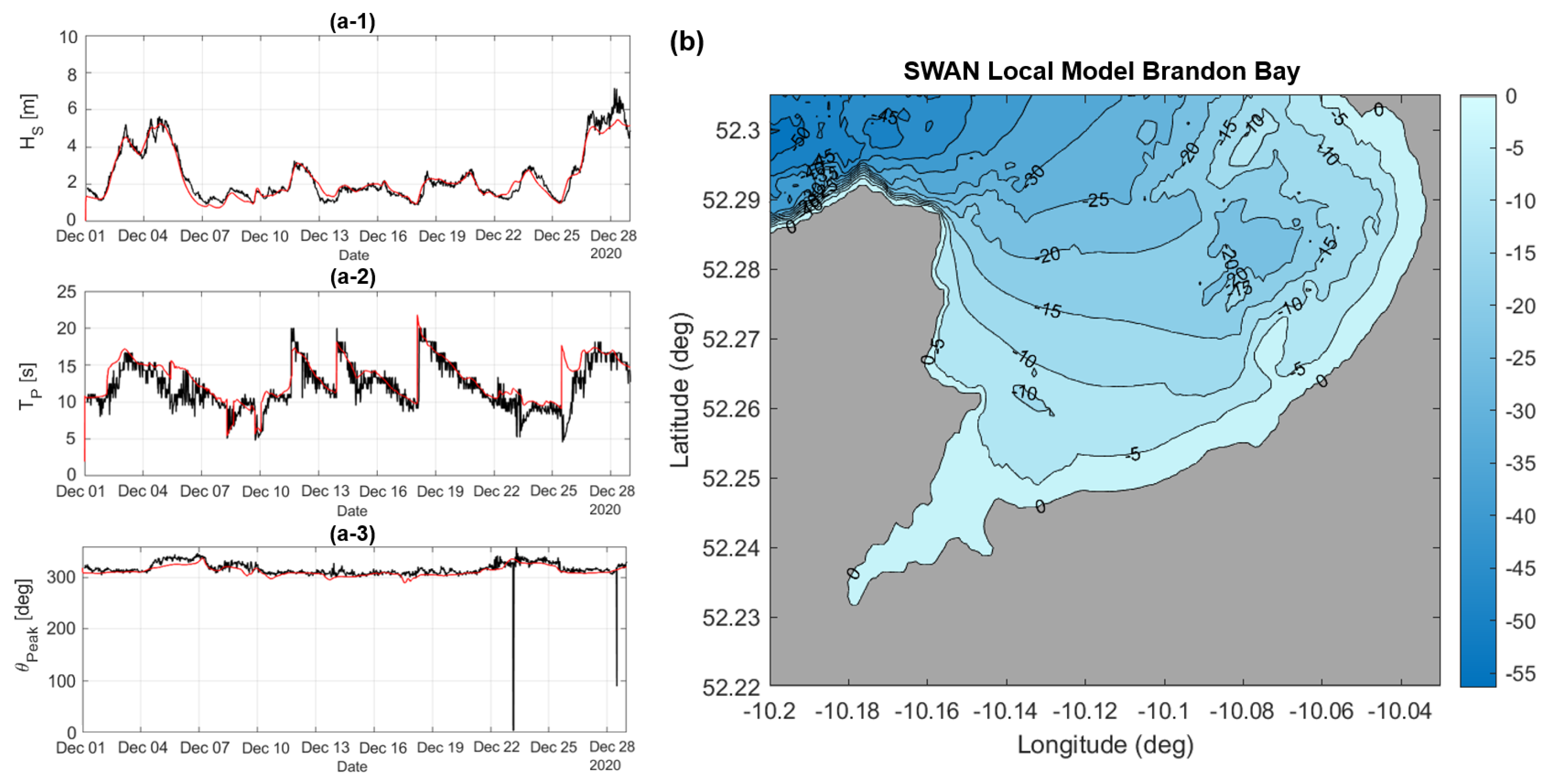
3.2. Numerical Modelling
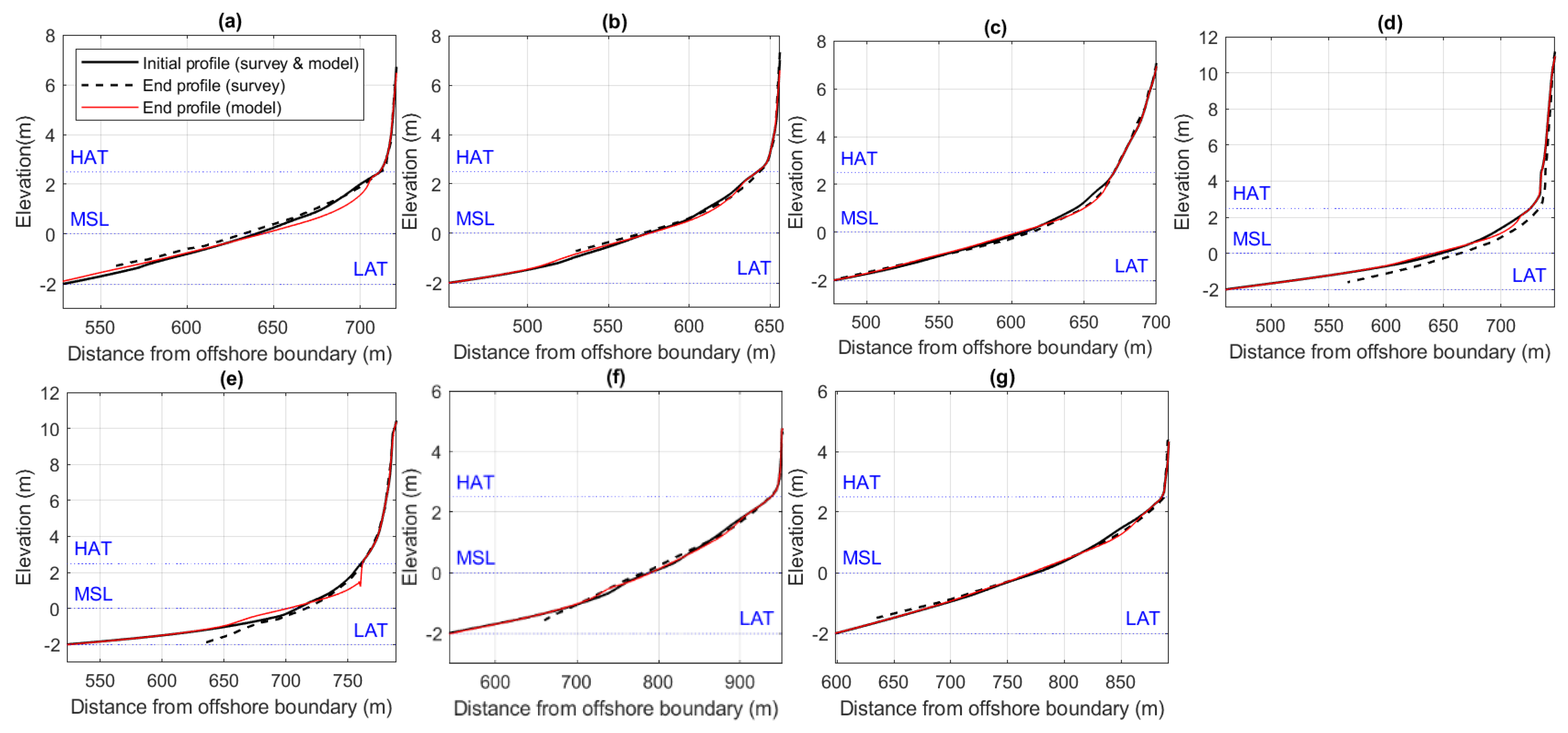
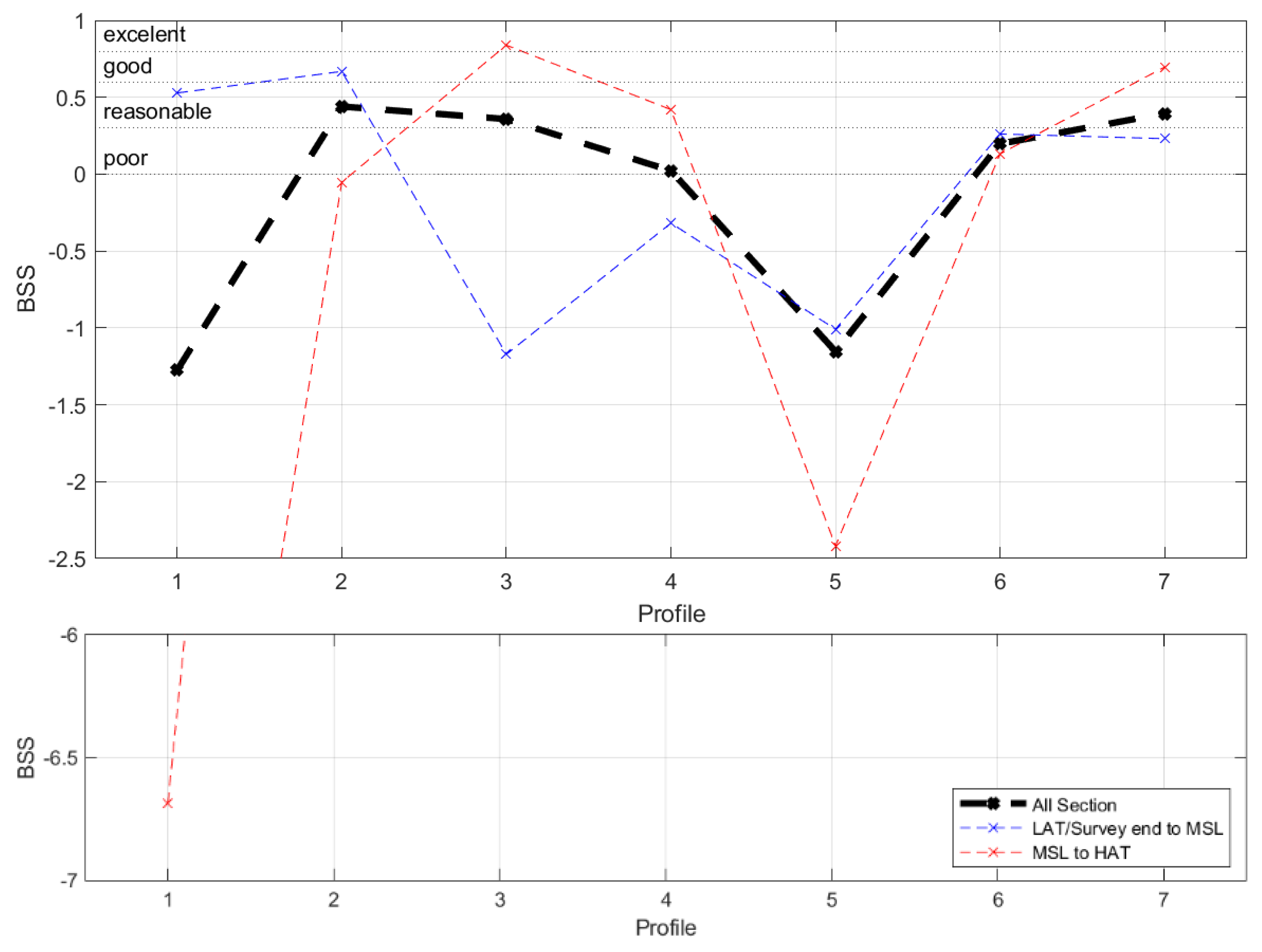
3.3. Model Validation
- Linear regression and correlation coefficient (r) between the measured shoreline elevations (xm) and the predicted elevations from the model simulation (xp);
- The root mean square error (RMSE) between the survey data (xm) and the model predictions (xp) is calculated as:
3.4. Model Simulations
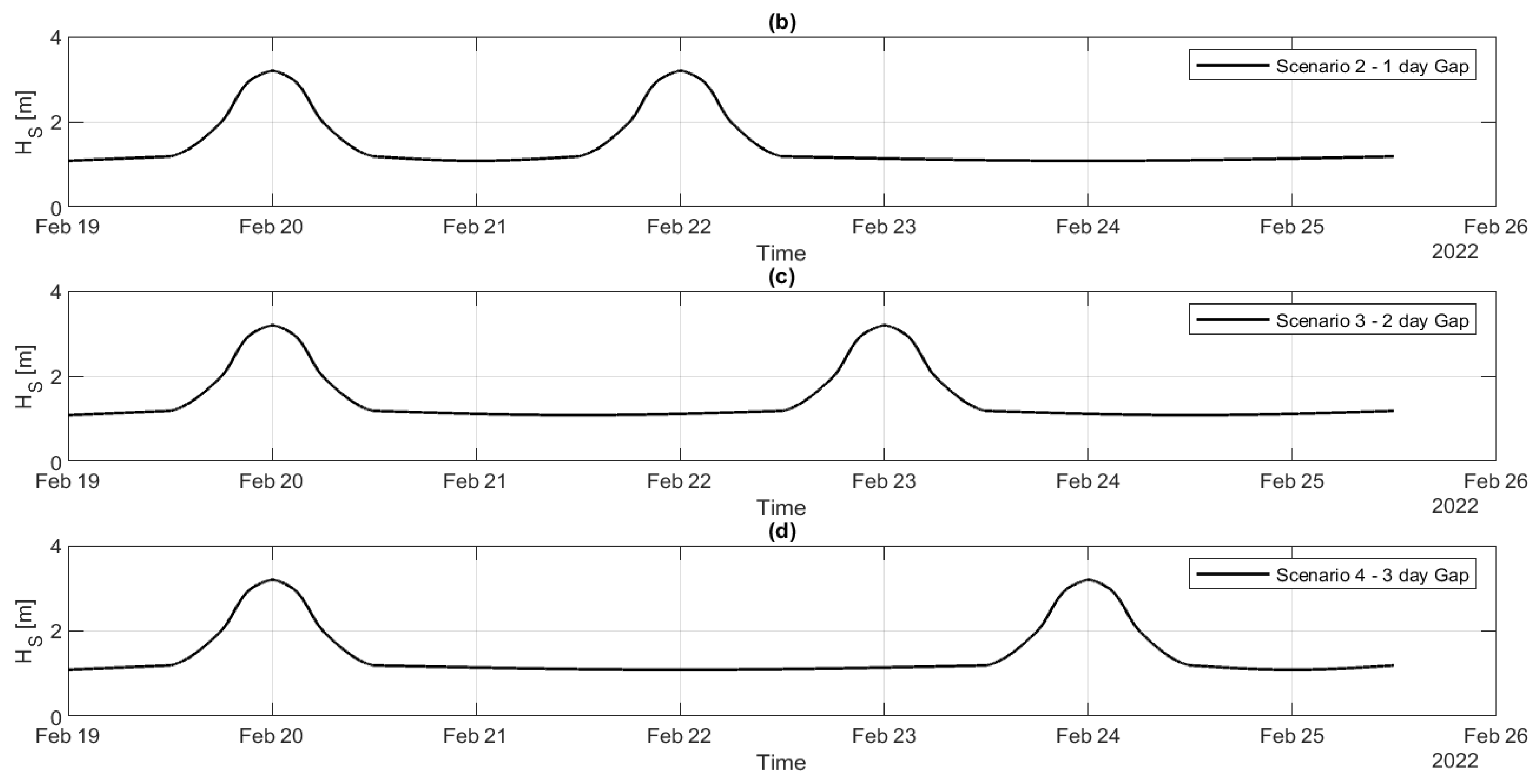
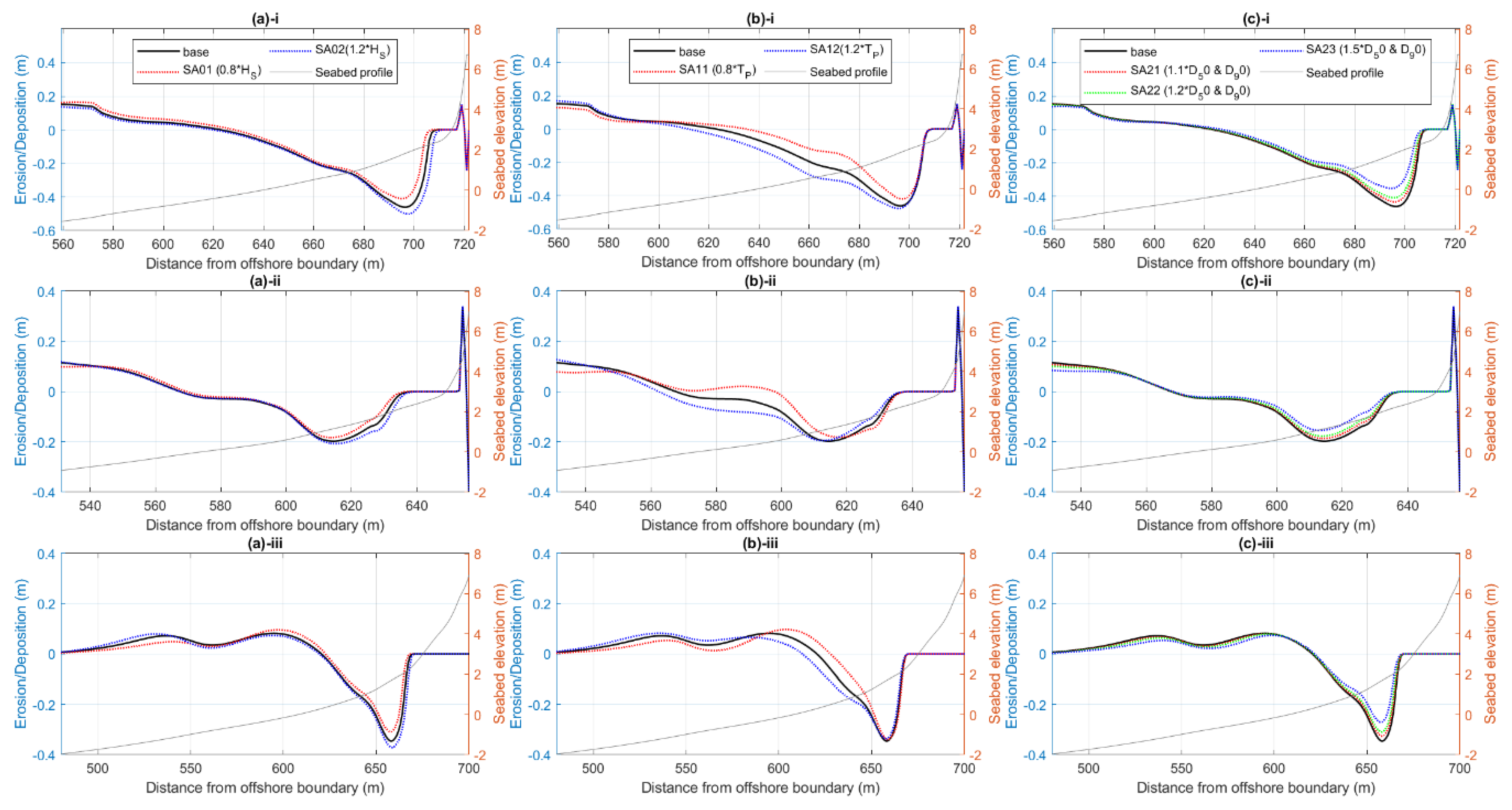
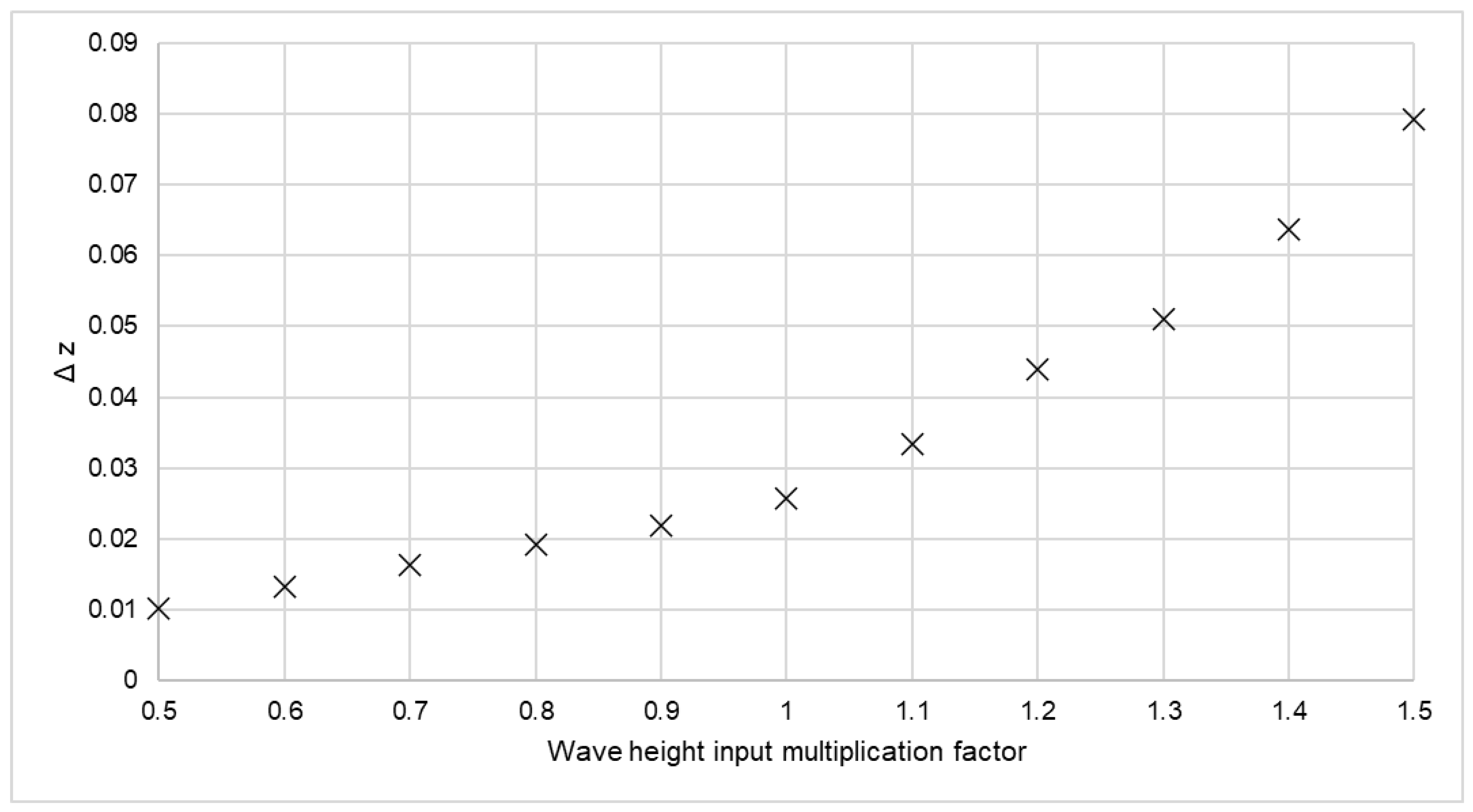
3.4.1. Model Sensitivity Simulations
- The location of the sediment grab samples used to determine sediment characteristics were obtained from a previous survey and so the locations of the sample data did not exactly match the profile location;
- The 1D XBeach model only allows uniform D50 and D90 input across the profiles, while in reality the sediment characteristic might vary across the coastal profile.
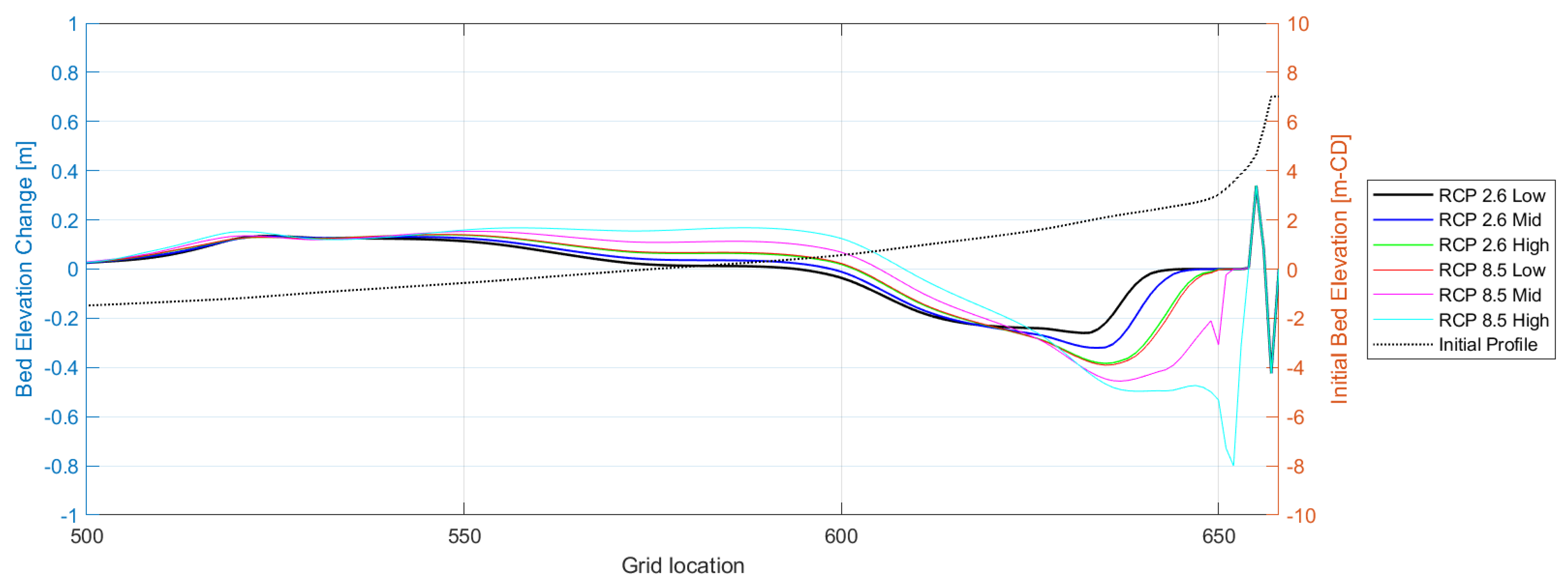
3.4.2. Future Climate Simulations
4. Results and Analysis
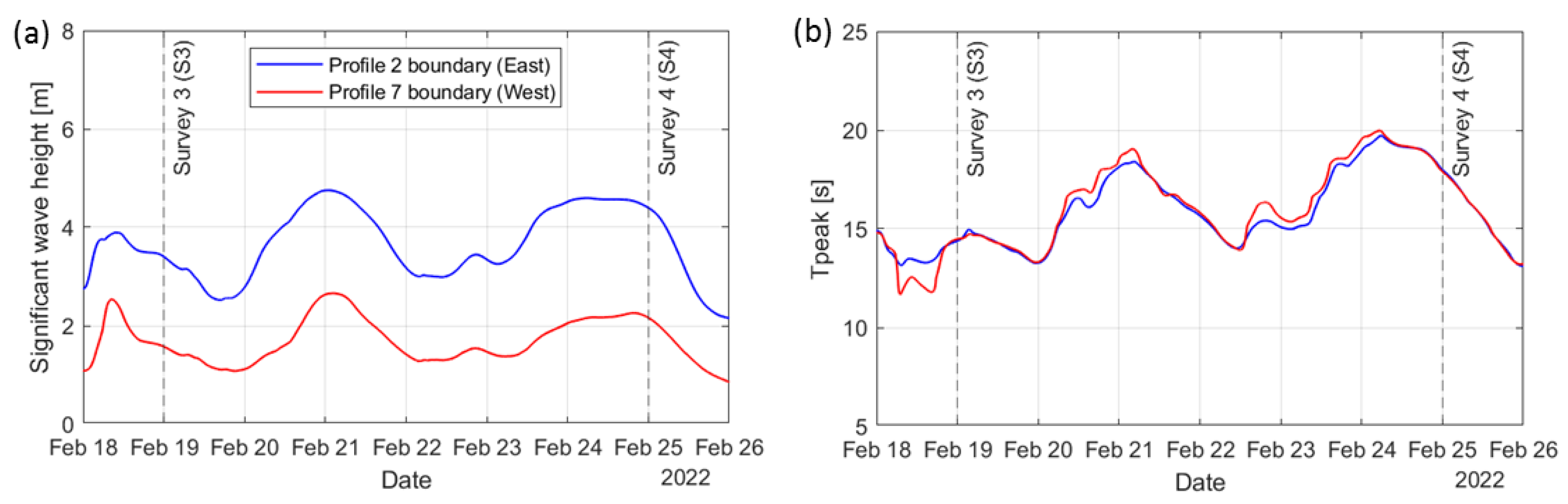
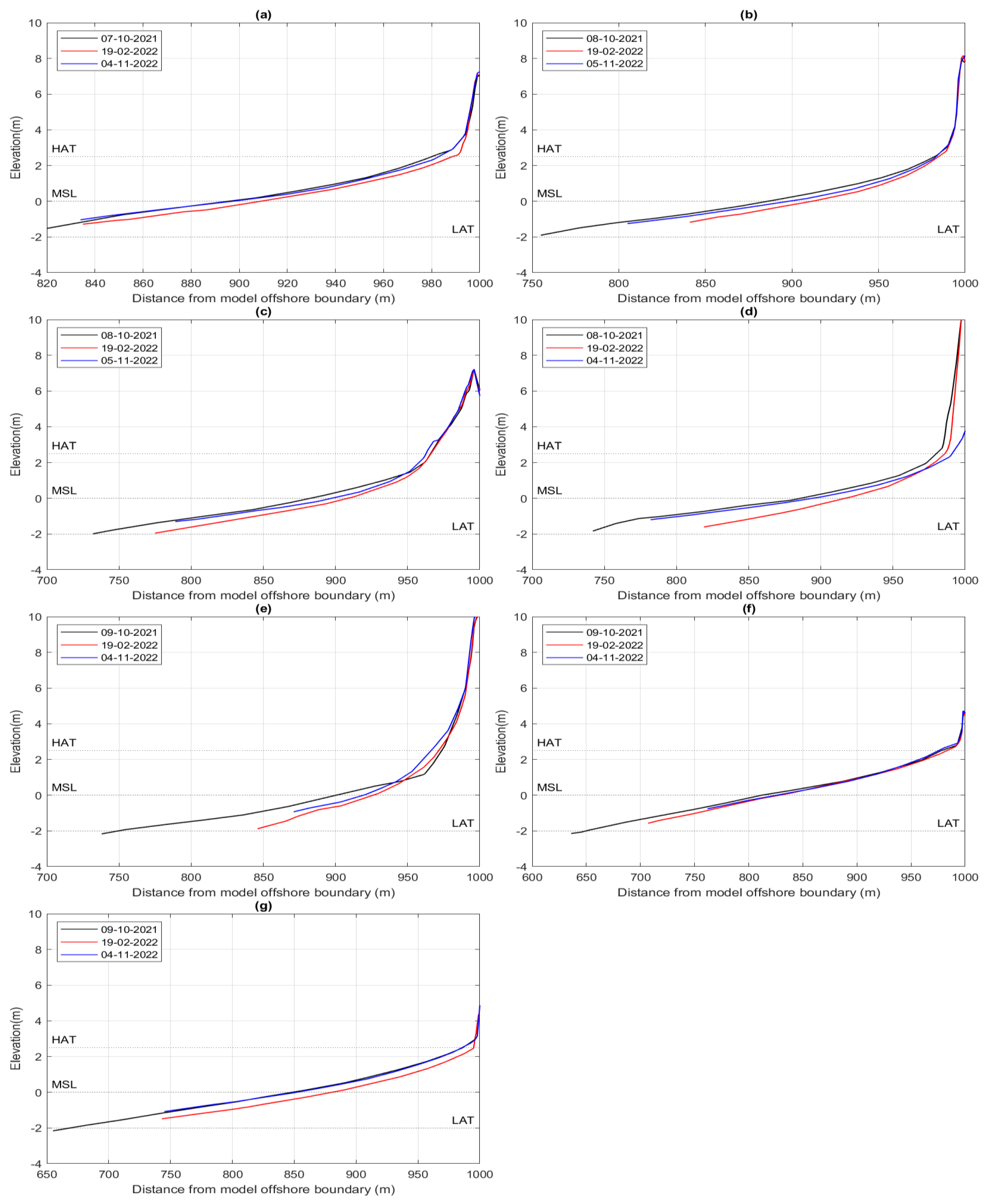
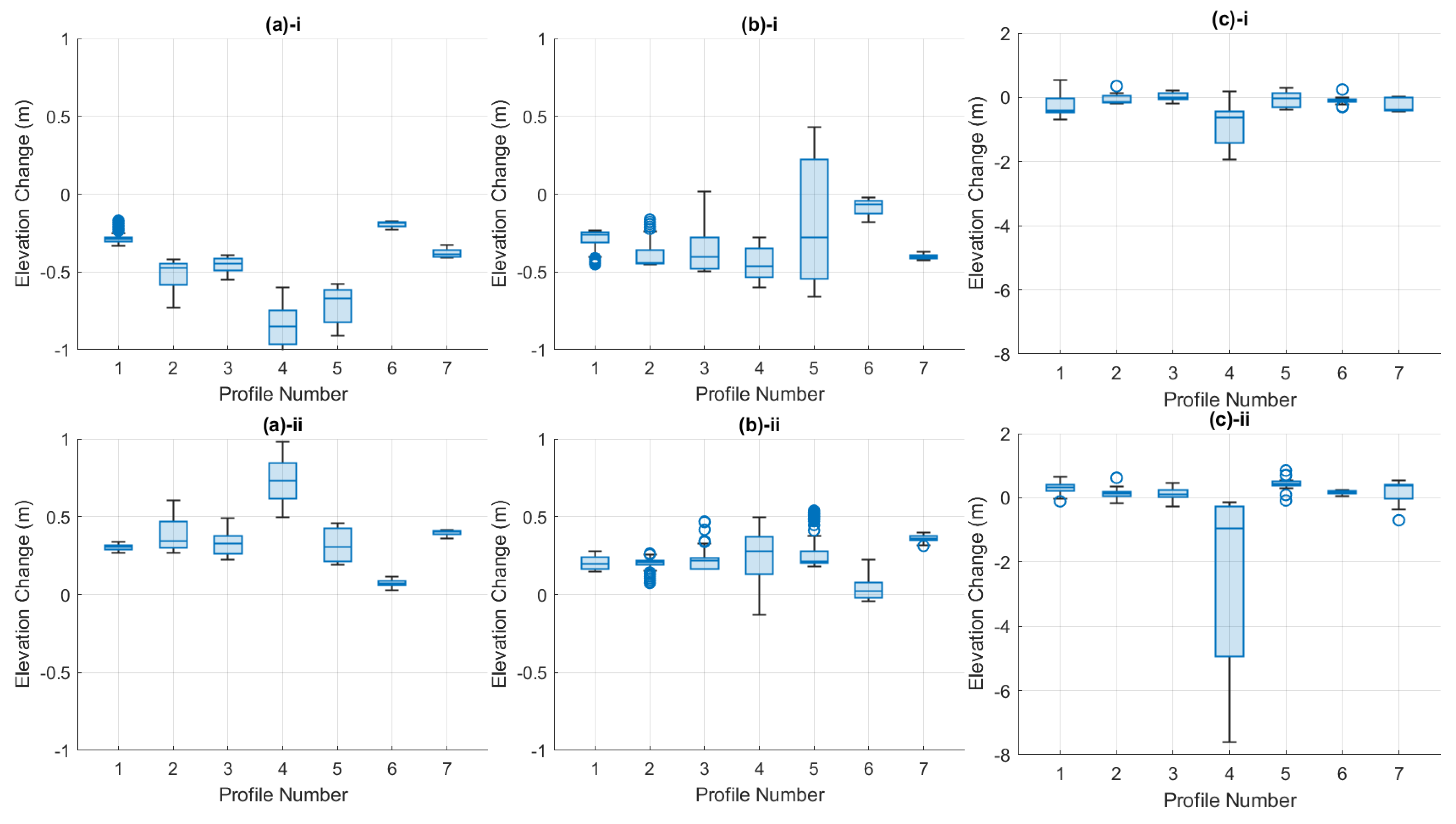
4.1. Survey Data
- The lower beach—extending from LAT to MSL;
- The middle beach—extending from MSL to HAT;
- The upper beach—extending from HAT to the dune crest.
4.1.1. Sensitivity Analysis
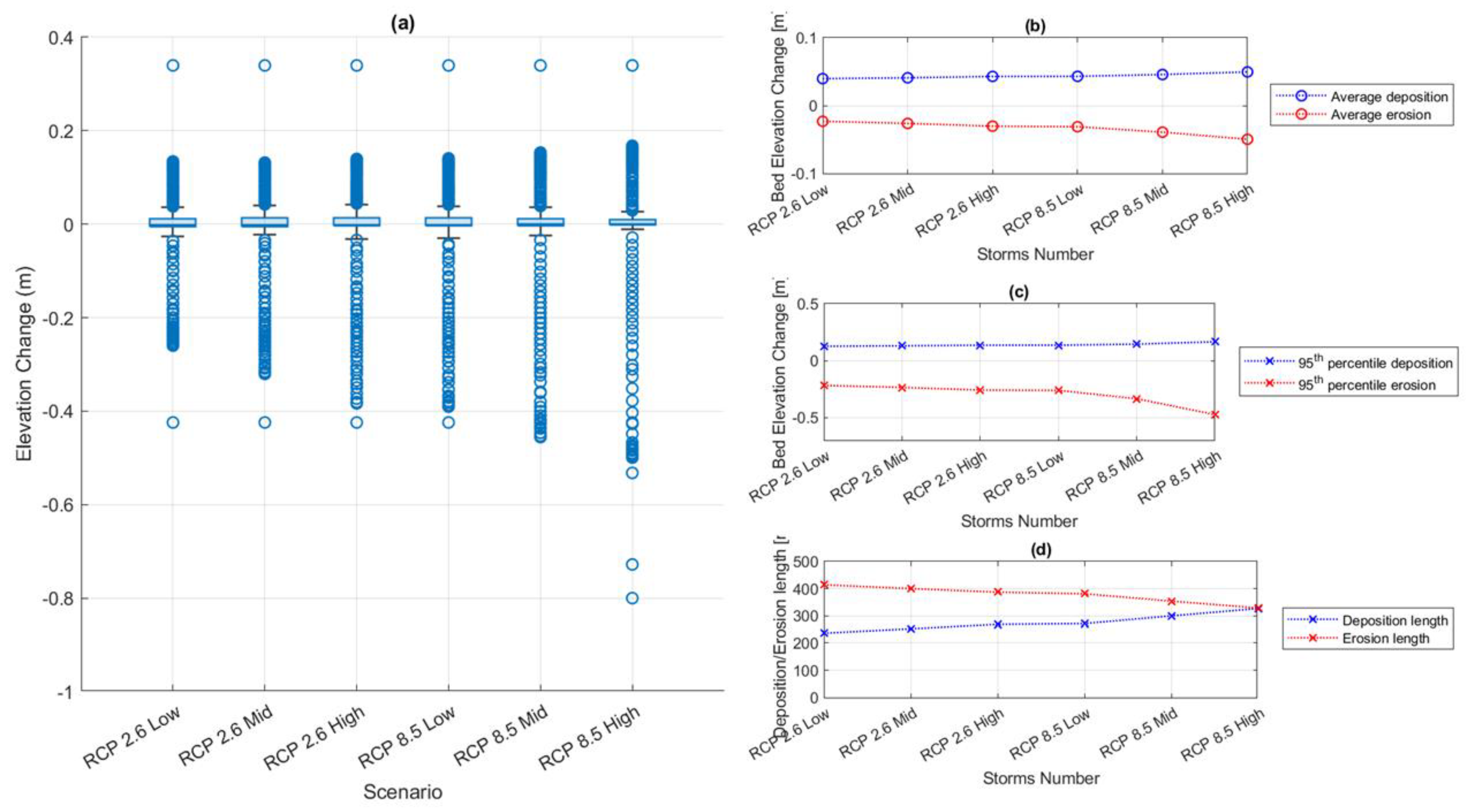
4.1.2. Future Climate Scenarios
Sea-Level Rise
Changing Wave Heights
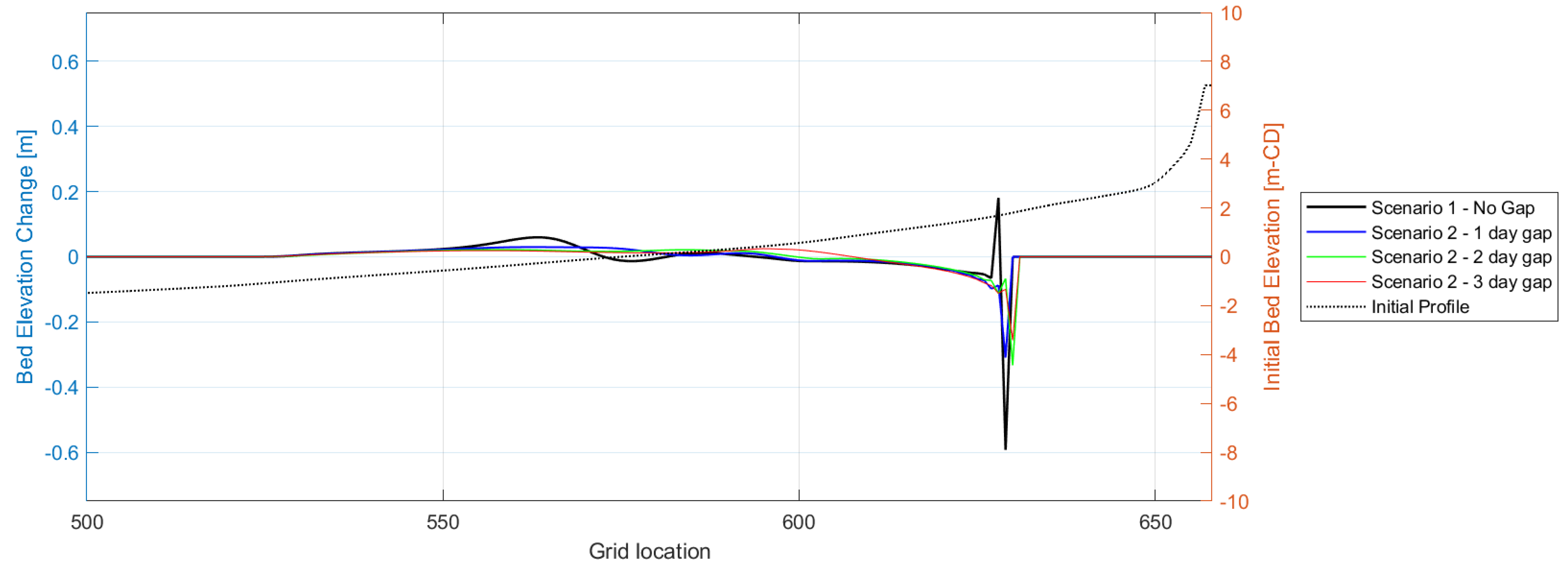
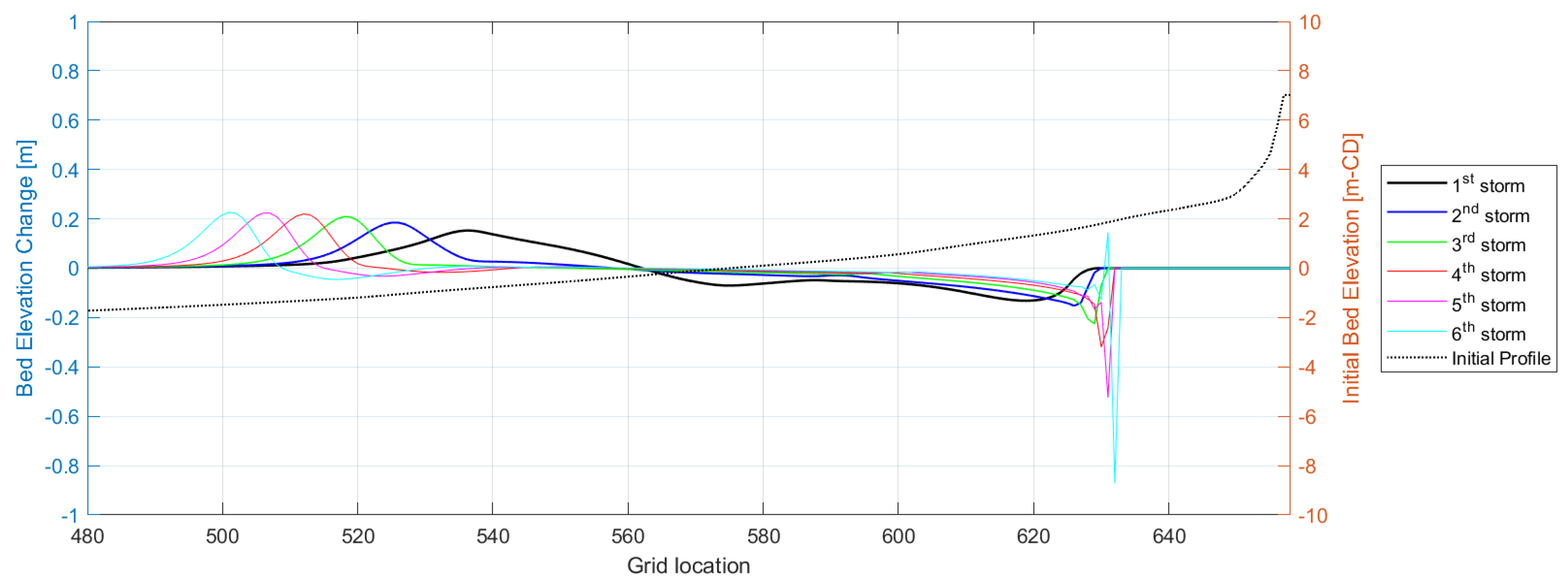
Greater Storm Frequency
5. Discussion
6. Summary and Conclusions
- The field survey results corroborate the classical seasonal erosion-deposition cycle typical of dissipative beaches, with significant winter storm-driven erosion (up to 1 m) and subsequent summer recovery However, long-term monitoring is needed to assess interannual variability and resilience.
- The 1D XBeach model effectively captured sediment erosion patterns on the mid and lower beachface, but showed lower accuracy on the upper beach and dune erosion. These discrepancies likely arise from the inherent simplifications of 1D modelling such as omission of alongshore processes and assumption of sediment heterogeneity. Model sensitivity to uncertainty in forcing wave data and sediment grain size highlights the importance of high-quality input data.
- Simulations incorporating sea-level rise scenarios indicate intensified erosion and dune vulnerability, particularly under high-end projections, while an increase in the frequency of storm events exacerbates cumulative erosion and impedes recovery. These are significant finding in light of future climate change.
- The approaches and findings from this study extend beyond Brandon Bay. The modelling framework, parameter sensitivity analysis, and discussion of equilibrium recovery trajectories are applicable to similar wave-dominated coastal embayments with dissipative beaches. The methods applied here can inform coastal risk assessments, climate adaptation planning, and management strategies in diverse geographical contexts. Furthermore, the integration of near-term storm modelling with long-term scenario-based analysis underscores the need for dynamic, process-based tools in managing increasingly vulnerable coastal environments.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dissanayake, P.; Brown, J.; Wisse, P.; Karunarathna, H. Effects of Storm Clustering on Beach/Dune Evolution. Mar. Geol. 2015, 370, 63–75. [Google Scholar] [CrossRef]
- Dissanayake, P.; Brown, J.; Karunarathna, H. Modelling Storm-Induced Beach/Dune Evolution: Sefton Coast, Liverpool Bay, UK. Mar. Geol. 2014, 357, 225–242. [Google Scholar] [CrossRef]
- Berard, N.A.; Mulligan, R.P.; da Silva, A.M.F.; Dibajnia, M. Evaluation of XBeach Performance for the Erosion of a Laboratory Sand Dune. Coast. Eng. 2017, 125, 70–80. [Google Scholar] [CrossRef]
- Itzkin, M.; Moore, L.J.; Ruggiero, P.; Hacker, S.D.; Biel, R.G. The Relative Influence of Dune Aspect Ratio and Beach Width on Dune Erosion as a Function of Storm Duration and Surge Level. Earth Surf. Dyn. 2021, 9, 1223–1237. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Callaghan, D.P.; Li, F.; Wainwright, D.J.; Duong, T.M. Assessing Coastline Recession for Adaptation Planning: Sea Level Rise versus Storm Erosion. Sci. Rep. 2023, 13, 8286. [Google Scholar] [CrossRef]
- Coco, G.; Senechal, N.; Rejas, A.; Bryan, K.R.; Capo, S.; Parisot, J.; Brown, J.A.; MacMahan, J.H. Beach Response to a Sequence of Extreme Storms. Geomorphology 2014, 204, 493–501. [Google Scholar] [CrossRef]
- Wright, L.D.; Short, A.D. Morphodynamic Variability of Surf Zones and Beaches: A Synthesis. Mar. Geol. 1984, 56, 93–118. [Google Scholar] [CrossRef]
- Aagaard, T.; Greenwood, B.; Hughes, M. Sediment Transport on Dissipative, Intermediate and Reflective Beaches. Earth-Sci. Rev. 2013, 124, 32–50. [Google Scholar] [CrossRef]
- Short, A.D.; Hesp, P.A. Wave, Beach and Dune Interactions in Southeastern Australia. Mar. Geol. 1982, 48, 259–284. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; Van Dongeren, A.; De Vries, J.V.T.; McCall, R.; Lescinski, J. Modelling Storm Impacts on Beaches, Dunes and Barrier Islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Sallenger, A.H., Jr. Storm Impact Scale for Barrier Islands. J. Coast. Res. 2000, 16, 890–895. [Google Scholar]
- Morton, R.A.; Paine, J.G.; Gibeaut, J. Stages and Durations of Post-Storm Beach Recovery, Southeastern Texas Coast, USA. J. Coast. Res. 1994, 10, 884–908. [Google Scholar]
- Leeder, M.R. Sedimentology: Process and Product; Chapman & Hall: London, UK, 1994; ISBN 13:978-0-412-53300-6. [Google Scholar]
- Masselink, G.; Castelle, B.; Scott, T.; Dodet, G.; Suanez, S.; Jackson, D.; Floc’h, F. Extreme Wave Activity during 2013/2014 Winter and Morphological Impacts along the Atlantic Coast of Europe. Geophys. Res. Lett. 2016, 43, 2135–2143. [Google Scholar] [CrossRef]
- Ranasinghe, R. Assessing Climate Change Impacts on Open Sandy Coasts: A Review. Earth-Sci. Rev. 2016, 160, 320–332. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Bianchi, A.; Dottori, F.; Feyen, L. Climatic and Socioeconomic Controls of Future Coastal Flood Risk in Europe. Nat. Clim. Change 2018, 8, 776–780. [Google Scholar] [CrossRef]
- Gorski, J.F.; Dietrich, J.C.; Passeri, D.L.; Mickey, R.C.; Luettich, R.A., Jr. Deterministic, Dynamic Model Forecasts of Storm-Driven Coastal Erosion. Nat. Hazards 2025, 121, 6257–6283. [Google Scholar] [CrossRef]
- Turner, I.L.; Leaman, C.K.; Harley, M.D.; Thran, M.C.; David, D.R.; Splinter, K.D.; Matheen, N.; Hansen, J.E.; Cuttler, M.V.W.; Greenslade, D.J.M.; et al. A Framework for National-Scale Coastal Storm Hazards Early Warning. Coast. Eng. 2024, 192, 104571. [Google Scholar] [CrossRef]
- O’Neill, A.C.; Nederhoff, K.; Erikson, L.H.; Thomas, J.A.; Barnard, P.L. A Dataset of Two-Dimensional XBeach Model Set-Up Files for Northern California. Data 2024, 9, 118. [Google Scholar] [CrossRef]
- Suzuki, T.; Cox, D.T. Evaluating XBeach Performance for Extreme Offshore-Directed Sediment Transport Events on a Dissipative Beach. Coast. Eng. J. 2021, 63, 517–531. [Google Scholar] [CrossRef]
- Chataigner, T.; Yates, M.L.; Le Dantec, N.; Harley, M.; Splinter, K.; Goutal, N. Sensitivity of a One-Line Longshore Shoreline Change Model to the Mean Wave Direction. Coast. Eng. 2022, 172, 104025. [Google Scholar] [CrossRef]
- Yu, H.; Weng, Z.; Chen, G.; Chen, X. Improved XBeach Model and Its Application in Coastal Beach Evolution under Wave Action. Coast. Eng. J. 2023, 65, 560–571. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Thompson, D.M.; Plant, N.G.; Long, J.W. Evaluation of Wave Runup Predictions from Numerical and Parametric Models. Coast. Eng. 2014, 92, 1–11. [Google Scholar] [CrossRef]
- Chardón-Maldonado, P.; Pintado-Patiño, J.C.; Puleo, J.A. Advances in Swash-Zone Research: Small-Scale Hydrodynamic and Sediment Transport Processes. Coast. Eng. 2016, 115, 8–25. [Google Scholar] [CrossRef]
- Sutherland, J.; Peet, A.; Soulsby, R. Evaluating the Performance of Morphological Models. Coast. Eng. 2004, 51, 917–939. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Almeida, L.; Ferreira, Ó. Modelling Storm-Induced Beach Morphological Change in a Meso-Tidal, Reflective Beach Using XBeach. J. Coast. Res. 2011, 64, 1916–1920. [Google Scholar]
- Williams, J.J.; de Alegría-Arzaburu, A.R.; McCall, R.T.; Van Dongeren, A. Modelling Gravel Barrier Profile Response to Combined Waves and Tides Using XBeach: Laboratory and Field Results. Coast. Eng. 2012, 63, 62–80. [Google Scholar] [CrossRef]
- RTE. How Healthy Kerry Sand Dunes Are Worth €9 Million a Year 2020. Available online: https://www.rte.ie/brainstorm/2024/0808/1124306-sand-dunes-maharees-kerry-economics-wild-atlantic-way/ (accessed on 1 September 2025).
- Met-Éireann Met.Ie, The Irish Meteorological Service Online, Storm Centre 2022. Available online: https://www.met.ie/climate/storm-centre (accessed on 1 September 2025).
- Egon, A.; Nash, S.; Farrell, E.; Fennell, S.; Iglesias, G. Development of Nested Local Scale Wave Model for Storm Study in Brandon Bay Using SWAN. In Proceedings of the 39th IAHR World Congress, Granada, Spain, 19 June 2022. [Google Scholar]
- Scullion, A. An Investigation of Sediment Transport Pathways and Shoreline Position Evolution in Brandon Bay, Co. Kerry. Master’s Thesis, National University of Ireland Galway, Galway, Ireland, 2017. [Google Scholar]
- Nuyts, S.; Farrell, E.J.; Fennell, S.; Nash, S. An Assessment of the Role of the Timex Sampling Strategy on the Precision of Shoreline Detection Analysis. Coasts 2024, 4, 347–365. [Google Scholar] [CrossRef]
- Komar, P.D. Beach Processes and Sedimentation; Prentice Hall: Upper Saddle River, NJ, USA, 1977. [Google Scholar]
- Bosboom, J.; Stive, M.J.F. Coastal Dynamics; TU Delft OPEN Publishing: Delft, The Netherlands, 2021; ISBN 978-94-6366-371-7. [Google Scholar]
- Davidson, M.; Lewis, R.; Turner, I. Forecasting Seasonal to Multi-Year Shoreline Change. Coast. Eng. 2010, 57, 620–629. [Google Scholar] [CrossRef]
- Williams, J.; Esteves, L.; Rochford, L. Modelling Storm Responses on a High-Energy Coastline with XBeach. Model. Earth Syst. Environ. 2015, 1, 3. [Google Scholar] [CrossRef]
- Williams, J.J.; Esteves, L.S. Guidance on Setup, Calibration, and Validation of Hydrodynamic, Wave, and Sediment Models for Shelf Seas and Estuaries. Adv. Civ. Eng. 2017, 2017, 5251902. [Google Scholar] [CrossRef]
- van Rijn, L.C.; Walstra, D.J.; Grasmeijer, B.; Sutherland, J.; Pan, S.; Sierra, J. The Predictability of Cross-Shore Bed Evolution of Sandy Beaches at the Time Scale of Storms and Seasons Using Process-Based Profile Models. Coast. Eng. 2003, 47, 295–327. [Google Scholar] [CrossRef]
- IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; IPCC: Geneva, Switzerland, 2019; Available online: https://www.ipcc.ch/site/assets/uploads/sites/3/2019/12/SROCC_FullReport_FINAL.pdf (accessed on 1 September 2025).
- Turner, I.L.; Harley, M.D.; Short, A.D.; Simmons, J.A.; Bracs, M.A.; Phillips, M.S.; Splinter, K.D. A Multi-Decade Dataset of Monthly Beach Profile Surveys and Inshore Wave Forcing at Narrabeen, Australia. Sci. Data 2016, 3, 160024. [Google Scholar] [CrossRef]
- Liu, X.; Kuang, C.; Huang, S.; He, L.; Han, X. Modelling and Evaluation of Beach Morphodynamic Behavior: A Case Study of Dongsha Beach in Eastern China. Ocean Coast. Manag. 2023, 240, 106661. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; Van Dongeren, A.; Van Thiel de Vries, J.; Lescinski, J.; McCall, R. XBeach Model Description and Manual. Unesco-IHE Inst. Water Educ. Deltares Delft Univ. Tecnhology. Rep. 2010, 21, 2. [Google Scholar]
- de Vries, J.v.T.; Van Gent, M.; Walstra, D.; Reniers, A. Analysis of Dune Erosion Processes in Large-Scale Flume Experiments. Coast. Eng. 2008, 55, 1028–1040. [Google Scholar] [CrossRef]
- Wang, Y.; Zamora, N.; Quiroz, M.; Satake, K.; Cienfuegos, R. Tsunami Resonance Characterization in Japan Due to trans-Pacific Sources: Response on the Bay and Continental Shelf. J. Geophys. Res. Ocean. 2021, 126, e2020JC017037. [Google Scholar] [CrossRef]






| Profile | LAT 1 to HAT 2 | LAT to MSL 3 | MSL to HAT | ||||||
|---|---|---|---|---|---|---|---|---|---|
| r | RMSE (m) | BSS | r | RMSE (m) | BSS | r | RMSE (m) | BSS | |
| 1 | 0.999 | 0.26 | −1.27 | 0.999 | 0.14 | 0.53 | 0.996 | 0.34 | −6.68 |
| 2 | 0.998 | 0.10 | 0.44 | 0.999 | 0.10 | 0.67 | 0.996 | 0.10 | −0.05 |
| 3 | 0.997 | 0.09 | 0.36 | 0.999 | 0.09 | −1.17 | 0.997 | 0.07 | 0.84 |
| 4 | 0.997 | 0.42 | 0.02 | 0.999 | 0.45 | −0.32 | 0.991 | 0.35 | 0.42 |
| 5 | 0.993 | 0.45 | −1.15 | 0.998 | 0.50 | −1.01 | 0.999 | 0.31 | −2.42 |
| 6 | 0.996 | 0.09 | 0.20 | 0.997 | 0.09 | 0.26 | 0.997 | 0.09 | 0.13 |
| 7 | 0.999 | 0.07 | 0.39 | 0.999 | 0.08 | 0.23 | 0.997 | 0.04 | 0.70 |
| Scenario | Wave Parameter Input | Sediment Characteristic Input | ||
|---|---|---|---|---|
| Wave Height HS | Wave Period TP | D50 | D90 | |
| Base | - | - | - | - |
| SA01 | ×0.8 | - | - | - |
| SA02 | ×1.2 | - | - | - |
| SA11 | - | ×0.8 | - | - |
| SA12 | - | ×1.2 | - | - |
| SA21 | - | - | ×1.1 | ×1.1 |
| SA22 | - | - | ×1.2 | ×1.2 |
| SA23 | - | - | ×1.5 | ×1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egon, A.; Farrell, E.; Iglesias, G.; Nash, S. Measurement and Modelling of Beach Response to Storm Waves: A Case Study of Brandon Bay, Ireland. Coasts 2025, 5, 32. https://doi.org/10.3390/coasts5030032
Egon A, Farrell E, Iglesias G, Nash S. Measurement and Modelling of Beach Response to Storm Waves: A Case Study of Brandon Bay, Ireland. Coasts. 2025; 5(3):32. https://doi.org/10.3390/coasts5030032
Chicago/Turabian StyleEgon, Andi, Eugene Farrell, Gregorio Iglesias, and Stephen Nash. 2025. "Measurement and Modelling of Beach Response to Storm Waves: A Case Study of Brandon Bay, Ireland" Coasts 5, no. 3: 32. https://doi.org/10.3390/coasts5030032
APA StyleEgon, A., Farrell, E., Iglesias, G., & Nash, S. (2025). Measurement and Modelling of Beach Response to Storm Waves: A Case Study of Brandon Bay, Ireland. Coasts, 5(3), 32. https://doi.org/10.3390/coasts5030032







