Seasonal to Multi-Decadal Shoreline Change on a Reef-Fringed Beach
Abstract
:1. Introduction
2. Study Area and Methodology
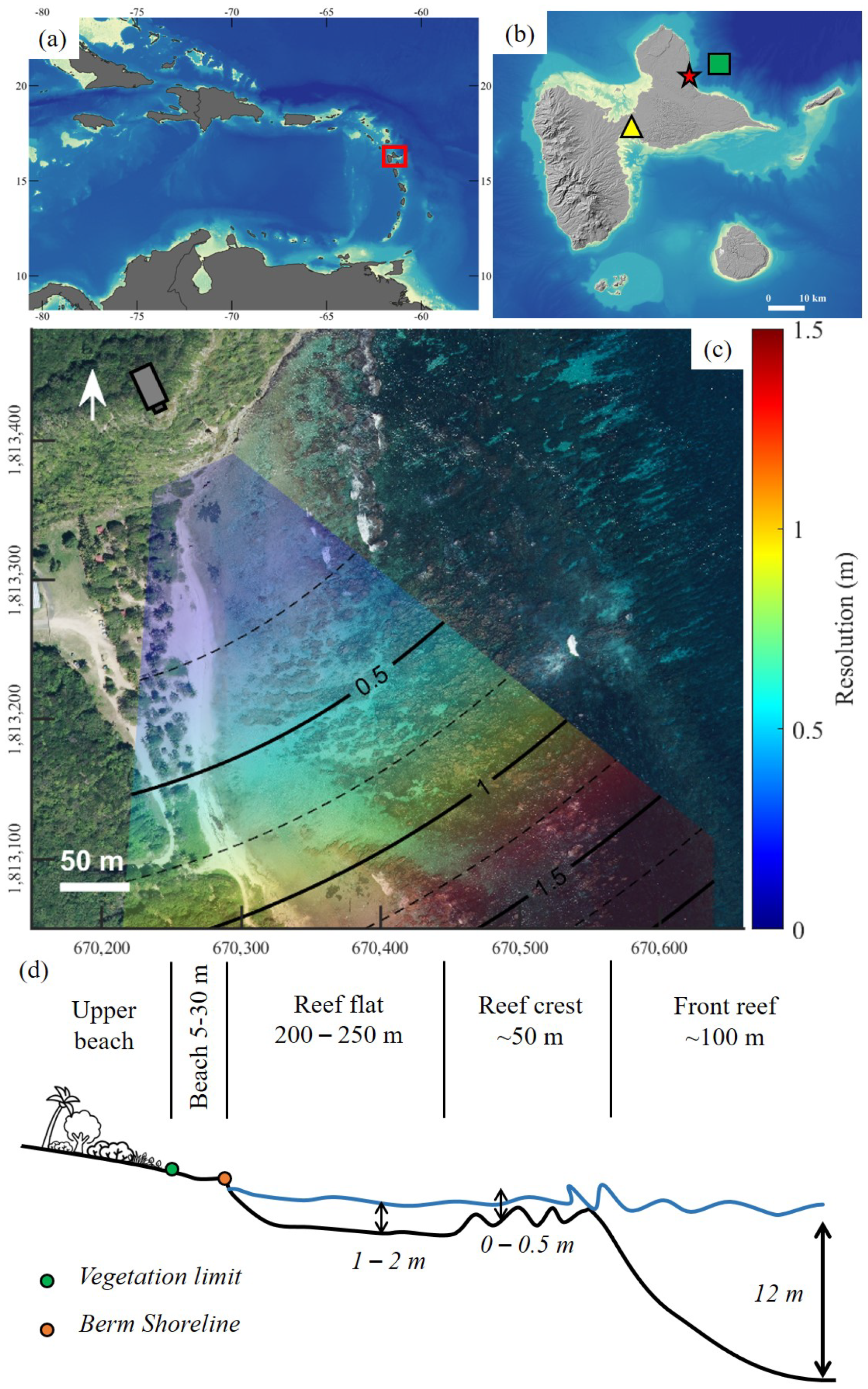
2.1. Study Site Description
2.2. Hydrodynamic Conditions
2.2.1. Waves and Still Water Level
2.2.2. Cyclones Tracks
2.3. Shoreline Datasets
2.3.1. Airborne, Satellite and UAV Derived Dataset
2.3.2. Fixed Video System Derived Dataset
2.3.3. Shoreline Digitalization and Processing
- The vegetation limit: This represents the boundary between the last vegetated area and the sandy beach. Serving as an indicator of the beach’s mid to long-term evolution (ranging from monthly to multi-annual scales), the vegetation boundary is typically affected only by storm events.
- The berm: This is identifiable either as a sedimentary vertical bulge on the beach or through marine deposits. The berm offers a more dynamic perspective, which informs the beach’s evolution, from short to long term (from weekly to multi-annual scales) changes.
2.4. Data Analysis
2.4.1. Interrupted Time Series Analysis and ARIMA Model
2.4.2. Cyclicity and Correlations
3. Results
3.1. Multi Decadal Shoreline Observations
3.2. High Frequency Shoreline Observations
4. Discussion
4.1. Short-Term Shoreline Evolution: Drivers and Processes
4.2. Long-Term Shoreline Evolution
5. Future Expectations and Potential Solutions
6. Conclusions and Perspectives
- Storms have a limited impact on long-term shoreline change, as sufficient recovery time allows a return to the pre-storm state. Extreme storm events have a significant influence on the vegetation limit shoreline, causing a retreat that may exceed 20 m and take several decades to recover, but that have little impact on the berm shoreline. More frequent and less intense storms, while having little influence on the vegetation limit, may strongly influence the berm shoreline.
- The annual cyclicity of is the driver of shoreline fluctuation, which is a novel observation. The wave attenuation by reefs is depth-dependent; seasonality triggers changes in the efficacy of the filter over the year, leading to significant annual fluctuation of the shoreline.
- Climate change, specifically SLR and potential changes in storm intensity and frequency, will affect shoreline dynamics. SLR may increase the depth over the reef, extending the retreat period and shortening the accretion phase within the cycle. Additionally, more frequent and intense storms could reduce the recovery time between events, possibly culminating in a future trend of increased shoreline retreat.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davidson, M.; Lewis, R.; Turner, I. Forecasting seasonal to multi-year shoreline change. Coast. Eng. 2010, 57, 620–629. [Google Scholar] [CrossRef]
- Hansen, J.; Barnard, P. Sub-weekly to interannual variability of a high-energy shoreline. Coast. Eng. 2010, 57, 959–972. [Google Scholar] [CrossRef]
- Kuriyama, Y.; Yanagishima, S. Regime shifts in the multi-annual evolution of a sandy beach profile. Earth Surf. Process. Landf. 2018, 43, 3133–3141. [Google Scholar] [CrossRef]
- Pianca, C.; Holman, R.; Siegle, E. Shoreline variability from days to decades: Results of long-term video imaging. J. Geophys. Res. Oceans 2015, 120, 2813–2825. [Google Scholar] [CrossRef]
- Ruggiero, P.; Kaminsky, G.; Gelfenbaum, G.; Voigt, B. Seasonal to Interannual Morphodynamics along a High-Energy Dissipative Littoral Cell. J. Coast. Res. 2005, 2005, 553–578. [Google Scholar] [CrossRef]
- Stive, M.; Aarninkhof, S.; Hamm, L.; Hanson, H.; Larson, M.; Wijnberg, K.; Nicholls, R.; Capobianco, M. Variability of shore and shoreline evolution. Coast. Eng. 2002, 47, 211–235. [Google Scholar] [CrossRef]
- Thom, B.; Hall, W. Behaviour of beach profiles during accretion and erosion dominated periods. Earth Surf. Process. Landf. 1991, 16, 113–127. [Google Scholar] [CrossRef]
- Turner, I.; Harley, M.; Short, A.; Simmons, J.; Bracs, M.; Phillips, M.; Splinter, K. A multi-decade dataset of monthly beach profile surveys and inshore wave forcing at Narrabeen, Australia. Sci. Data 2016, 3, 160024. [Google Scholar] [CrossRef]
- Winant, C.; Inman, D.; Nordstrom, C. Description of seasonal beach changes using empirical eigenfunctions. J. Geophys. Res. 1975, 80, 1979–1986. [Google Scholar] [CrossRef]
- Wright, L.; Short, A. Morphodynamic variability of surf zones and beaches: A synthesis. Mar. Geol. 1984, 56, 93–118. [Google Scholar] [CrossRef]
- Harley, M.; Masselink, G.; Alegria-Arzaburu, A.; Valiente, N.; Scott, T. Single extreme storm sequence can offset decades of shoreline retreat projected to result from sea-level rise. Commun. Earth Environ. 2022, 3, 112. [Google Scholar] [CrossRef]
- Lee, G.; Nicholls, R.; Birkemeier, W. Storm-driven variability of the beach-nearshore profile at Duck. Mar. Geol. 1998, 148, 163–177. [Google Scholar] [CrossRef]
- Masselink, G.; Castelle, B.; Scott, T.; Dodet, G.; Suanez, S.; Jackson, D.; Floc’h, F. Extreme wave activity during 2013/2014 winter and morphological impacts along the Atlantic coast of Europe. Geophys. Res. Lett. 2016, 43, 2135–2143. [Google Scholar] [CrossRef]
- Castelle, B.; Bujan, S.; Ferreira, S.; Dodet, G. Foredune morphological changes and beach recovery from the extreme 2013/2014 winter at a high-energy sandy coast. Mar. Geol. 2017, 385, 41–55. [Google Scholar] [CrossRef]
- Scott, T.; Masselink, G.; O’Hare, T.; Saulter, A.; Poate, T.; Russell, P.; Davidson, M.; Conley, D. The extreme 2013/2014 winter storms: Beach recovery along the southwest coast of England. Mar. Geol. 2016, 382, 224–241. [Google Scholar] [CrossRef]
- Anderson, T.; Frazer, L.; Fletcher, C. Transient and persistent shoreline change from a storm. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Beetham, E.; Kench, P.; O’Callaghan, J.; Popinet, S. Wave transformation and shoreline water level on Funafuti Atoll, Tuvalu Edward. J. Geophys. Res. Oceans 2016, 121, 6762–6778. [Google Scholar] [CrossRef]
- Ferrario, F.; Beck, M.; Storlazzi, C.; Micheli, F.; Shepard, C.; Airoldi, L. The effectiveness of coral reefs for coastal hazard risk reduction and adaptation. Nat. Commun. 2014, 5, 1–9. [Google Scholar] [CrossRef]
- Harris, D.; Rovere, A.; Casella, E.; Power, H.; Canavesio, R.; Collin, A.; Pomeroy, A.; Webster, J.; Parravicini, V. Coral reef structural complexity provides important coastal protection from waves under rising sea levels. Sci. Adv. 2018, 4, 1–8. [Google Scholar] [CrossRef]
- Péquignet, A.; Becker, J.; Merrifield, M.; Boc, S. The dissipation of wind wave energy across a fringing reef at Ipan. Coral Reefs 2011, 30, 71–82. [Google Scholar] [CrossRef]
- Mahabot, M.M.; Pennober, G.; Suanez, S.; Troadec, R.; Delacourt, C. Effect of Tropical Cyclones on Short-Term Evolution of Carbonate Sandy Beaches on Reunion Island, Indian Ocean. J. Coast. Res. 2017, 33, 839–853. [Google Scholar] [CrossRef]
- Ogg, J.G.; Koslow, J.A. The impact of Typhoon Pamela (1976) on Guam’s coral reefs and beaches. Pac. Sci. 1978, 32, 105–118. [Google Scholar]
- Spiske, M.; Pilarczyk, J.E.; Mitchell, S.; Halley, R.B.; Otai, T. Coastal erosion and sediment reworking caused by hurricane Irma—Implications for storm impact on low-lying tropical islands. Earth Surf. Process. Landf. 2022, 47, 891–907. [Google Scholar] [CrossRef]
- Hawkins, T.W.; Gouirand, I.; Allen, T.; Belmadani, A. Atmospheric Drivers of Oceanic North Swells in the Eastern Caribbean. J. Mar. Sci. Eng. 2022, 10, 183. [Google Scholar] [CrossRef]
- Rueda, A.; Vitousek, S.; Camus, P.; Tomás, A.; Espejo, A.; Losada, I.J.; Barnard, P.L.; Erikson, L.H.; Ruggiero, P.; Reguero, B.G.; et al. A global classification of coastal flood hazard climates associated with large-scale oceanographic forcing. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Jevrejeva, S.; Bricheno, L.; Brown, J.; Byrne, D.; Dominicis, M.D.; Rynders, S.; Palanisamy, H.; Wolf, J. Quantifying processes contributing to coastal hazards to inform coastal climate resilience assessments, demonstrated for the Caribbean Sea. Nat. Hazards Earth Syst. Sci. 2020, 20, 2609–2626. [Google Scholar] [CrossRef]
- Cambers, G. Beach changes in the eastern caribbean islands: Hurricane impacts and implications for climate change. J. Coast. Res. 1997, 24, 29–47. [Google Scholar]
- Vos, K.; Splinter, K.D.; Harley, M.D.; Simmons, J.A.; Turner, I.L. CoastSat: A Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Model. Softw. 2019, 122, 104528. [Google Scholar] [CrossRef]
- Valentini, N.; Saponieri, A.; Danisi, A.; Pratola, L.; Damiani, L. Exploiting remote imagery in an embayed sandy beach for the validation of a runup model framework. Estuar. Coast. Shelf Sci. 2019, 225, 106244. [Google Scholar] [CrossRef]
- Holman, R.A.; Stanley, J. The history and technical capabilities of Argus. Coast. Eng. 2007, 54, 477–491. [Google Scholar] [CrossRef]
- Plant, N.G.; Aarninkhof, S.G.; Turner, I.L.; Kingston, K.S. The performance of shoreline detection models applied to video imagery. J. Coast. Res. 2007, 23, 658–670. [Google Scholar] [CrossRef]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The State of the World’s Beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef] [PubMed]
- Mentaschi, L.; Vousdoukas, M.I.; Pekel, J.F.; Voukouvalas, E.; Feyen, L. Global long-term observations of coastal erosion and accretion. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Tsiakos, C.A.D.; Chalkias, C. Use of Machine Learning and Remote Sensing Techniques for Shoreline Monitoring: A Review of Recent Literature. Appl. Sci. 2023, 13, 3268. [Google Scholar] [CrossRef]
- Shoreline Variability at a Reef-Fringed Pocket Beach. Front. Mar. Sci. 2020, 7, 1–16. [CrossRef]
- Guillen, L.; Pallardy, M.; Legendre, Y.; Torre, Y.; Loireau, C. Morphodynamique du littoral Guadeloupéen. Phase 1: Définition et Mise en Place d’un Réseau D’observation et de Suivi du Trait de côte: Evaluation Historique du Trait de Côte Guadeloupéen; Rapport Final; BRGM: Petit Bourg, France, 2017. [Google Scholar]
- Bellwood, D.R.; Pratchett, M.S.; Morrison, T.H.; Gurney, G.G.; Hughes, T.P.; Álvarez-Romero, J.G.; Day, J.C.; Grantham, R.; Grech, A.; Hoey, A.S.; et al. Coral reef conservation in the Anthropocene: Confronting spatial mismatches and prioritizing functions. Biol. Conserv. 2019, 236, 604–615. [Google Scholar] [CrossRef]
- CEREMA. Fiches Synthétiques de Mesure des états de Mer-Tome 3–Outre-Mer; SHOM: Brest, France, 2021. [Google Scholar]
- Reguero, B.; Méndez, F.; Losada, I. Variability of multivariate wave climate in Latin America and the Caribbean. Glob. Planet. Change 2013, 100, 70–84. [Google Scholar] [CrossRef]
- Krien, Y.; Dudon, B.; Roger, J.; Zahibo, N. Probabilistic hurricane-induced storm surge hazard assessment in Guadeloupe, Lesser Antilles, 2015. Nat. Hazards Earth Syst. Sci. 2015, 15, 1711–1720. [Google Scholar] [CrossRef]
- SHOM. Références Altimétriques Maritimes—Édition 2020; Shom: Brest, France, 2020. [Google Scholar]
- Torres, R.; Tsimplis, M. Seasonal sea level cycle in the Caribbean Sea. J. Geophys. Res. Oceans 2012, 117, 1–18. [Google Scholar] [CrossRef]
- Data SHOM. Available online: https://data.shom.fr/ (accessed on 10 July 2023).
- Egbert, G.D.; Bennett, A.F.; Foreman, M.G.G. TOPEX/POSEIDON tides estimated using a global inverse model. J. Geophys. Res. Oceans 1994, 99, 24821–24852. [Google Scholar] [CrossRef]
- Modélisation et Analyse pour la Recherche Côtière. Available online: https://marc.ifremer.fr/resultats/vagues (accessed on 10 July 2023).
- Laigre, T.; Balouin, Y.; Nicolae-Lerma, A.; Moisan, M.; Valentini, N.; Villarroel-Lamb, D.; De La Torre, Y. Seasonal and Episodic Runup Variability on a Caribbean Reef-Lined Beach. J. Geophys. Res. Oceans 2023, 128, e2022JC019575. [Google Scholar] [CrossRef]
- Splinter, K.D.; Carley, J.T.; Golshani, A.; Tomlinson, R. A relationship to describe the cumulative impact of storm clusters on beach erosion. Coast. Eng. 2014, 83, 49–55. [Google Scholar] [CrossRef]
- Jarvinen, B.R.; Neumann, C.J.; Davis, M.A.S. A Tropical Cyclone Data Tape for the North Atlantic Basin, 1886–1983: Contents, Limitations, and Uses; Technical Report, National Hurricane Center (1965–1995); United States, National Oceanic and Atmospheric Administration: Washington, DC, USA, 1984.
- Landsea, C.W.; Franklin, J.L. Atlantic Hurricane Database Uncertainty and Presentation of a New Database Format. Mon. Weather Rev. 2013, 141, 3576–3592. [Google Scholar] [CrossRef]
- Barr, B.W.; Chen, S.S.; Fairall, C.W. Seastate-Dependent Sea Spray and Air-Sea Heat Fluxes in Tropical Cyclones: A New Parameterization for Fully Coupled Atmosphere-Wave-Ocean Models. J. Atmos. Sci. 2022, 80, 933–960. [Google Scholar] [CrossRef]
- Fan, Y.; Hwang, P.; Yu, J. Surface Gravity Wave Modeling in Tropical Cyclones. In Geophysics and Ocean Waves Studies; Essa, K.S., Risio, M.D., Celli, D., Pasquali, D., Eds.; IntechOpen: Rijeka, Croatia, 2020; Chapter 6. [Google Scholar] [CrossRef]
- Ruiz-Salcines, P.; Salles, P.; Robles-Díaz, L.; Díaz-Hernández, G.; Torres-Freyermuth, A.; Appendini, C.M. On the Use of Parametric Wind Models for Wind Wave Modeling under Tropical Cyclones. Water 2019, 11, 2044. [Google Scholar] [CrossRef]
- Saffir, H.S. Hurricane wind and storm surge. Military Eng. 1973, 423, 4–531. [Google Scholar]
- Simpson, R.H. The hurricane disaster-potential scale. Weatherwise 1974, 27, 169–186. [Google Scholar]
- Sai, S.; Tjahjadi, M.; Rokhmana, C. Geometric Accuracy Assessments of Orthophoto Production from UAV Aerial Images. KnE Eng. 2019, 333–344. [Google Scholar] [CrossRef]
- Doherty, Y.; Harley, M.D.; Vos, K.; Splinter, K.D. A Python toolkit to monitor sandy shoreline change using high-resolution PlanetScope cubesats. Environ. Model. Softw. 2022, 157, 105512. [Google Scholar] [CrossRef]
- García-Rubio, G.; Huntley, D.; Russell, P. Evaluating shoreline identification using optical satellite images. Mar. Geol. 2015, 359, 96–105. [Google Scholar] [CrossRef]
- Holland, K.; Holman, R.; Lippmann, T.; Stanley, J.; Plant, N. Practical use of video imagery in nearshore oceanographic field studies. IEEE J. Ocean. Eng. 1997, 22, 81–92. [Google Scholar] [CrossRef]
- Thieler, E.R.; Himmelstoss, E.A.; Zichichi, J.L.; Ergul, A. The Digital Shoreline Analysis System (DSAS) Version 4.0—An ArcGIS Extension for Calculating Shoreline Change; Technical Report; US Geological Survey: Reston, VA, USA, 2009. [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control, 5th ed.; Palgrave Macmillan: London, UK, 2015. [Google Scholar]
- Ferron, J.; Rendina-Gobioff, G. Interrupted Time Series Design. In Encyclopedia of Statistics in Behavioral Science; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Schaffer, A.; Dobbins, T.; Pearson, S.A. Interrupted time series analysis using autoregressive integrated moving average (ARIMA) models: A guide for evaluating large-scale health interventions. BMC Med. Res. Methodol. 2021, 21, 58. [Google Scholar] [CrossRef]
- Greene, C.A.; Thirumalai, K.; Kearney, K.A.; Delgado, J.M.; Schwanghart, W.; Wolfenbarger, N.S.; Thyng, K.M.; Gwyther, D.E.; Gardner, A.S.; Blankenship, D.D. The Climate Data Toolbox for MATLAB. Geochem. Geophys. Geosyst. 2019, 20, 3774–3781. [Google Scholar] [CrossRef]
- Burvingt, O.; Masselink, G.; Russell, P.; Scott, T. Classification of beach response to extreme storms. Geomorphology 2017, 295, 722–737. [Google Scholar] [CrossRef]
- Eiser, W.C.; Birkemeier, W.A. Beach Profile Response to Hurricane Hugo; ASCE: Reston, VR, USA, 1991. [Google Scholar]
- Aagaard, T.; Hughes, M.; Baldock, T.; Greenwood, B.; Kroon, A.; Power, H. Sediment transport processes and morphodynamics on a reflective beach under storm and non-storm conditions. Mar. Geol. 2012, 326–328, 154–165. [Google Scholar] [CrossRef]
- Becker, J.; Merrifield, M.; Ford, M. Water level effects on breaking wave setup for Pacific Island fringing reefs. J. Geophys. Res. Oceans 2014, 119, 3909–3925. [Google Scholar] [CrossRef]
- Cheriton, O.; Storlazzi, C.; Rosenberger, K. Observations of wave transformation over a fringing coral reef and the importance of low-frequency waves and offshore water levels to runup, overwash, and coastal flooding. J. Geophys. Res. Oceans 2016, 121, 3121–3140. [Google Scholar] [CrossRef]
- Ning, Y.; Liu, W.; Sun, Z.; Zhao, X.; Zhang, Y. Parametric study of solitary wave propagation and runup over fringing reefs based on a Boussinesq wave model. J. Mar. Sci. Technol. 2018, 24, 512–525. [Google Scholar] [CrossRef]
- Wandres, M.; Aucan, J.; Espejo, A.; Jackson, N.; De Ramon N’Yeurt, A.; Damlamian, H. Distant-Source Swells Cause Coastal Inundation on Fiji’s Coral Coast. Front. Mar. Sci. 2020, 7, 1–10. [Google Scholar] [CrossRef]
- Brenner, O.T.; Lentz, E.E.; Hapke, C.J.; Henderson, R.E.; Wilson, K.E.; Nelson, T.R. Characterizing storm response and recovery using the beach change envelope: Fire Island, New York. Geomorphology 2018, 300, 189–202. [Google Scholar] [CrossRef]
- Eichentopf, S.; Karunarathna, H.; Alsina, J.M. Morphodynamics of sandy beaches under the influence of storm sequences: Current research status and future needs. Water Sci. Eng. 2019, 12, 221–234. [Google Scholar] [CrossRef]
- Coco, G.; Senechal, N.; Rejas, A.; Bryan, K.; Capo, S.; Parisot, J.; Brown, J.; Macmahan, J. Beach response to sequence of extreme storms. Geomorphology 2013, 204, 493–501. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2022: Impacts, Adaptation and Vulnerability; Summary for Policymakers; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; pp. 3–33. [Google Scholar]
- Quataert, E.; Storlazzi, C.; Rooijen, A.; Cheriton, O.; Dongeren, A. The influence of coral reefs and climate change on wave-driven flooding of tropical coastlines. Geophys. Res. Lett. 2015, 42, 6407–6415. [Google Scholar] [CrossRef]
- Storlazzi, C.D.; Elias, E.; Field, M.E.; Presto, M.K. Numerical modeling of the impact of sea-level rise on fringing coral reef hydrodynamics and sediment transport. Coral Reefs 2011, 30, 83–96. [Google Scholar] [CrossRef]
- Storlazzi, C.D.; Gingerich, S.B.; Van Dongeren, A.; Cheriton, O.M.; Swarzenski, P.W.; Quataert, E.; Voss, C.I.; Field, D.W.; Annamalai, H.; Piniak, G.A.; et al. Most atolls will be uninhabitable by the mid-21st century because of sea-level rise exacerbating wave-driven flooding. Sci. Adv. 2018, 4, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Kench, P.S.; Beetham, E.P.; Turner, T.; Morgan, K.M.; Mclean, R.F.; Owen, S.D. Sustained coral reef growth in the critical wave dissipation zone of a Maldivian atoll. Commun. Earth Environ. 2022, 3, 9. [Google Scholar] [CrossRef]
- van Woesik, R.; Cacciapaglia, C.W. Keeping up with sea-level rise: Carbonate production rates in Palau and Yap, western Pacific Ocean. PLoS ONE 2018, 13, e0197077. [Google Scholar] [CrossRef]
- Perry, C.T.; Murphy, G.N.; Kench, P.S.; Smithers, S.G.; Edinger, E.N.; Steneck, R.S.; Mumby, P.J. Caribbean-wide decline in carbonate production threatens coral reef growth. Nat. Commun. 2013, 4, 1402. [Google Scholar] [CrossRef]
- Gardner, T.A.; Côté, I.M.; Gill, J.A.; Grant, A.; Watkinson, A.R. Long-term region-wide declines in Caribbean corals. Science 2003, 301, 958–960. [Google Scholar] [CrossRef]
- Wilkinson, C.R.; Souter, D. Status of Caribbean Coral Reefs after Bleaching and Hurricanes in 2005; NOAA: Silver Spring, MD, USA, 2008. [Google Scholar]
- Toth, L.T.; Storlazzi, C.D.; Kuffner, I.B.; Quataert, E.; Reyns, J.; McCall, R.; Stathakopoulos, A.; Hillis-Starr, Z.; Holloway, N.H.; Ewen, K.A.; et al. The potential for coral reef restoration to mitigate coastal flooding as sea levels rise. Nat. Commun. 2023, 14, 2313. [Google Scholar] [CrossRef]
- Roelvink, F.E.; Storlazzi, C.D.; van Dongeren, A.R.; Pearson, S.G. Coral Reef Restorations Can Be Optimized to Reduce Coastal Flooding Hazards. Front. Mar. Sci. 2021, 8, 653945. [Google Scholar] [CrossRef]
- Balaguru, K.; Foltz, G.R.; Leung, L.R. Increasing Magnitude of Hurricane Rapid Intensification in the Central and Eastern Tropical Atlantic. Geophys. Res. Lett. 2018, 45, 4238–4247. [Google Scholar] [CrossRef]
- Belmadani, A.; Dalphinet, A.; Chauvin, F.; Pilon, R.; Palany, P. Projected future changes in tropical cyclone-related wave climate in the North Atlantic. Clim. Dyn. 2021, 56, 3687–3708. [Google Scholar] [CrossRef]
- Bhatia, K.T.; Vecchi, G.A.; Knutson, T.R.; Murakami, H.; Kossin, J.; Dixon, K.W.; Whitlock, C.E. Recent increases in tropical cyclone intensification rates. Nat. Commun. 2019, 10, 635. [Google Scholar] [CrossRef] [PubMed]
- Chauvin, F.; Pilon, R.; Palany, P.; Belmadani, A. Future changes in Atlantic hurricanes with the rotated-stretched ARPEGE-Climat at very high resolution. Clim. Dyn. 2020, 54, 947–972. [Google Scholar] [CrossRef]
- Knutson, T.; Camargo, S.J.; Chan, J.C.; Emanuel, K.; Ho, C.H.; Kossin, J.; Mohapatra, M.; Satoh, M.; Sugi, M.; Walsh, K.; et al. Tropical cyclones and climate change assessment Part II: Projected Response to Anthropogenic Warming. Bull. Am. Meteorol. Soc. 2019, 100, 1987–2007. [Google Scholar] [CrossRef]
- Walsh, K.J.; Mcbride, J.L.; Klotzbach, P.J.; Balachandran, S.; Camargo, S.J.; Holland, G.; Knutson, T.R.; Kossin, J.P.; cheung Lee, T.; Sobel, A.; et al. Tropical cyclones and climate change. WIREs Clim. Chang. 2016, 7, 65–89. [Google Scholar] [CrossRef]











| Id | Date | Source | Photography Type | Device | Resolution (m) |
|---|---|---|---|---|---|
| 1 | 25 February 1947 | IGN | Argentic | Aircraft | 1 |
| 2 | 25 August 1948 | IGN | Argentic | Aircraft | 0.4 |
| 3 | 20 December 1950 | IGN | Argentic | Aircraft | 0.9 |
| 4 | 19 March 1954 | IGN | Argentic | Aircraft | 0.2 |
| 5 | 9 December 1955 | IGN | Argentic | Aircraft | 0.4 |
| 6 | 22 March 1964 | IGN | Argentic | Aircraft | 0.7 |
| 7 | 6 February 1969 | IGN | Argentic | Aircraft | 0.7 |
| 8 | 3 April 1975 | IGN | Argentic | Aircraft | 0.4 |
| 9 | ?? March 1979 | IGN | Argentic | Aircraft | 0.5 |
| 10 | 1 January 1980 | IGN | Argentic | Aircraft | 0.5 |
| 11 | 20 February 1984 | IGN | Argentic | Aircraft | 0.4 |
| 12 | 16 March 1988 | IGN | Argentic | Aircraft | 0.4 |
| 13 | 14 October 1989 | IGN | Argentic | Aircraft | 0.2 |
| 14 | 1 February 1999 | IGN | Argentic | Aircraft | 0.6 |
| 15 | ?? ?? 2004 | IGN | Numeric | Aircraft | 0.5 |
| 16 | 21 February 2010 | IGN | Numeric | Aircraft | 0.3 |
| 17 | ?? ?? 2014 | CNES\IGN | Numeric | Pleiades satellite | 0.5 |
| 18 | ?? ?? 2015 | CNES\IGN | Numeric | Spot 6-7 satellite | 2 |
| 19 | ?? ?? 2016 | CNES\IGN | Numeric | Spot 6-7 satellite | 2 |
| 20 | ?? ?? 2017 | IGN | Numeric | Aircraft | 0.2 |
| 21 | ?? ?? 2018 | CNES\IGN | Numeric | Pleiades satellite | 0.5 |
| 22 | ?? ?? 2019 | CNES\IGN | Numeric | Pleiades satellite | 0.5 |
| 23 | 28 September 2020 | BRGM | Numeric | UAV | 0.1 |
| 24 | 21 October 2022 | BRGM | Numeric | UAV | 0.1 |
| Event | Date | (m) | (sec) | (°) | Min. Distance (km) |
|---|---|---|---|---|---|
| Carol | 1 September 1953 | nd | nd | nd | 440 |
| Esther | 1 September 1961 | nd | nd | nd | 830 |
| Hugo | 17 September 1989 | 10 | 7.5 | 90 | 4 |
| Luis | 15 September 1995 | 5.6 | 7.5 | 82.0 | 150 |
| Edouard | 8 August 1996 | 3.6 | 8.6 | 71.0 | 600 |
| Gert | 15 September 1999 | 3.9 | 8.5 | 91.0 | 780 |
| Igor | 1 September 2010 | 4.8 | 8.3 | 62.0 | 740 |
| Erika | 28 August 2015 | 4.5 | 7.0 | 70.0 | 10 |
| Irma | 5 September 2017 | 6.3 | 7.6 | 83.0 | 140 |
| Jose | 9 September 2017 | 4.1 | 9.3 | 78.0 | 190 |
| Teddy | 1 August 2020 | 5.1 | 12.5 | 69.0 | 850 |
| Event | Date | (m) | (sec) | (°) | Min. Distance (km) |
|---|---|---|---|---|---|
| Jerry | 20 September 2019 | 2.6 | 10.3 | 356.0 | 320 |
| Sebastien | 19 November 2019 | 2.0 | 11.2 | 343.0 | 500 |
| Josephine | 15 August 2020 | 2.9 | 9.1 | 40.0 | 300 |
| Laura | 21 August 2020 | 2.9 | 7.7 | 87.0 | 80 |
| Teddy | 18 September 2020 | 5.1 | 12.5 | 69.0 | 850 |
| Grace | 14 August 2021 | 2.7 | 7.4 | 78.0 | 7 |
| Peter | 20 September 2021 | 1.9 | 7.7 | 74.0 | 310 |
| Sam | 29 September 2021 | 2.5 | 9.3 | 85.0 | 610 |
| Earl | 3 September 2022 | 2.0 | 7.6 | 84.0 | 280 |
| Fiona | 16 September 2022 | 4.6 | 7.9 | 98.0 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laigre, T.; Balouin, Y.; Villarroel-Lamb, D.; De La Torre, Y. Seasonal to Multi-Decadal Shoreline Change on a Reef-Fringed Beach. Coasts 2023, 3, 240-262. https://doi.org/10.3390/coasts3030015
Laigre T, Balouin Y, Villarroel-Lamb D, De La Torre Y. Seasonal to Multi-Decadal Shoreline Change on a Reef-Fringed Beach. Coasts. 2023; 3(3):240-262. https://doi.org/10.3390/coasts3030015
Chicago/Turabian StyleLaigre, Thibault, Yann Balouin, Deborah Villarroel-Lamb, and Ywenn De La Torre. 2023. "Seasonal to Multi-Decadal Shoreline Change on a Reef-Fringed Beach" Coasts 3, no. 3: 240-262. https://doi.org/10.3390/coasts3030015
APA StyleLaigre, T., Balouin, Y., Villarroel-Lamb, D., & De La Torre, Y. (2023). Seasonal to Multi-Decadal Shoreline Change on a Reef-Fringed Beach. Coasts, 3(3), 240-262. https://doi.org/10.3390/coasts3030015







