Physiochemical Changes to TTCF Ensilication Investigated Using Time-Resolved SAXS

Abstract

Successful eradication or control of prevailing infectious diseases is linked to vaccine efficacy, stability, and distribution. The majority of protein-based vaccines are transported at fridge (2–8 °C) temperatures, cold chain, to retain potency. However, this has been shown to be problematic. Proteins are inherently susceptible to thermal fluctuations, occurring during transportation, causing them to denature. This leads to ineffective vaccines and an increase in vaccine-preventable diseases, especially in low-income countries. Our research utilises silica to preserve vaccines at room temperature, removing the need for cold chain logistics. The methodology is based upon sol–gel chemistry in which soluble silica is employed to encapsulate and ensilicate vaccine proteins. This yields a protein-loaded silica nanoparticle powder which is stored at room temperature and subsequently released using a fast chemical process. We have previously shown that tetanus toxin C fragment (TTCF) ensilication is a diffusion-limited cluster aggregation (DLCA)-based process using time-resolved small-angle x-ray scattering (SAXS). Here, we present our expanded investigation on the modularity of this system to further the understanding of ensilication via time-resolved SAXS. Our results show that variations in the ensilication process could prove useful in the transition from batch to in-flow manufacturing of ensilicated nanoparticles.

1. Introduction

There is an urgent demand for thermostable vaccines [1,2]. Most of the adjuvant-based protein vaccines are liquid formulated and have to be transported via the cold chain infrastructure. This latter system is imperfect. It allows for problems to occur at any stage [3,4,5,6,7]. To minimise the dependency on the cold chain, we have to enable room temperature stable vaccines. There have been many attempts to stabilise vaccines, and there are several strategies being explored [8,9,10,11,12,13,14,15,16].

Ensilication is one of these strategies with several successes in vitro with evidence of its capacity in vivo [17,18,19,20]. This method enables room temperature storage and distribution by encasing proteins in a silica shell which is electrostatically attached. The silica source is tetraethyl orthosilicate (TEOS), which can be hydrolysed, subsequently condensed, and polymerised under optimised conditions [21]. The process of ensilication requires only a handful of reagents and produces a protein-loaded silica powder consisting of agglomerated silica–protein nanoparticles. The material is resilient against heating/freezing and does not require desiccation as many other methods do. The protein can be retrieved with full retention of protein structure and functionality afterwards using a fast chemical process [17,18,19,20].

The current process of ensilication is carried out via batch production which, in a diffusion-limited system, creates an agglomerated nanoparticulate material. In order to obtain significant control in this system, we are exploring variations in the experimental setup. Therefore, in this study, we expanded on the characterisation of the ensilication process in solution. We have established that ensilication occurs in three stages in a previous study [18]. Here, time-resolved SAXS was utilised to analyse the ensilication of tetanus toxin C fragment (TTCF) at different silica-to-bulk volume ratios and different pH levels, compared to our standard setting, 1:50 at pH 7. We applied mathematical modelling to the SAXS data and present our interpretation of the outcomes.

2. Materials and Methods

2.1. Tetanus Toxin C Fragment

TTCF was produced in-house by recombinant expression in BL21(DE3) E. coli according to a previously published protocol [22]. His-tag-purified TTCF was characterised using sodium dodecyl sulphate–polyacrylamide gel electrophoresis (SDS–PAGE), circular dichroism, and enzyme-linked immunosorbent assay (ELISA) before use in this study as shown in [18].

2.2. Time-Resolved SAXS at ID02 Beamline ESRF

Prehydrolysed TEOS was prepared by mixing TEOS and ultrapure H₂O 1:1 and the addition of HCl to catalyse the reaction. This was added to 10 mL of 1 mg/mL TTCF solution, once both phases turned homogenous, at 1:50 ratio at pH 7 in a glass beaker. Using a sterile syringe, 1 mL of sample was taken and injected into a quartz capillary. SAXS measurements were performed on the time-resolved ultra-small-angle scattering beamline ID02 at the European Synchrotron Research Facility (ESRF), Grenoble, France [23]. The incident X-ray energy was 12.46 keV and sample-detector distance was employed at 1.5 m. SAXS data were acquired using the Rayonix MX-170HS detector with exposure times between 0.01 and 0.03 s. The measured 2D patterns after normalisation by incident flux, sample transmission, and the solid angle were azimuthally averaged to obtain the 1D static scattering profiles as a function of the magnitude of scattering vector, $q$. Where $q$ is given by, $q=\frac{4\mathsf{\pi }\sin \mathsf{\theta }}{\mathsf{\lambda }}$, with $\mathsf{\lambda }$ the incident X-ray wavelength (=0.0996 nm) and $\mathsf{\theta }$ the scattering angle. This gave a $q$-range of 0.006 <$q$< 0.5 ${\AA }^{-1}$. The scattering background in each case was measured using a Tris buffer, and the normalised background-subtracted data are represented by $I\left(q\right)$.

2.3. TTCF Ensilication Ratios

Ensilication of TTCF at standard 1:50, (prehydrolysed) silica-to-bulk-volume, ratio occurs rapidly in standard conditions; therefore, in this study, additional ratios of ensilication were measured to investigate any differences in particle morphology and size. High, 1:20, and low, 1:100, silica to volume ratios were chosen to assess as they will have significantly different amounts of silica present in the solution. The procedure of measurement was the same as the 1:50 ratio; once the hydrolysed silica was added to the TTCF solution, a sample was injected into the capillary, and measurement was initiated.

2.4. TTCF Ensilication at pH 6 and 8

Ensilication is heavily influenced by pH affecting the ensilication process. pH 8 and 6, at a low silica ratio (1:100), were chosen to investigate whether these changes would influence particle morphology, size, and the overall process.

2.5. SAXS Data Fitting

The previous investigation via SAXS enabled us to categorise the ensilication process into three distinct stages (Figure 1). We modelled the system, using the SasView software package [24], according to a monodisperse particulate solution initially [25],

$$\mathsf{\Delta }I\left(q\right)=N\cdot I_0\cdot \mathsf{\Delta }{\rho }^2\cdot V_{particle}^2 \cdot P\left(q\right) \cdot S\left(q\right)$$

to which we add silicic acid in the form of hydrolysed TEOS where I: intensity; N: number of particles; P(q): form factor; S(q): structure factor; $\rho$: scattering length density; V: particle volume.

The scattering length densities used for fitting are 9.44 × 10⁻⁶ A² (solvent), 12.468 × 10⁻⁶ A² (TTCF protein), and 17.5 × 10⁻⁶ A² for (TEOS/SiOH₄) [26].

Stage I fitting included the cumulative effect of an ellipsoid [18,25] (protein) form factor P1(q), a mass fractal [27] (silica) model P2(q) $\cdot$ S2(q), and power law (to compensate for low q upturn):

$$I\left(q\right)=scale\cdot q^{-power}+P1+scale\cdot P2\left(q\right)\cdot S2\left(q\right)+background$$

where:

$$P1\left(q,\alpha \right)=\left(\frac{scale}{V}\cdot F^2\left(q,\alpha \right)\right)$$

The ellipsoidal form factor includes the Fourier transform.

$$F\left(q,\mathsf{\alpha }\right)=\frac{3\mathsf{\Delta }\rho V\left(\sin \left[qr\left(R_p,R_e,\mathsf{\alpha }\right)\right]-\cos \left[qr\left(R_p,R_e,\mathsf{\alpha }\right)\right]\right)}{{\left[qr\left(R_p,R_e,\mathsf{\alpha }\right)\right]}^3}$$

where $R_p$: polar radius, $R_e$: equatorial radius, $\mathsf{\Delta }\rho$: scattering length density (SLD) difference between particle and solvent, $\mathsf{\alpha }$: axis angle, $V$: ellipsoid volume ($V=\left(4/3\right)\mathsf{\pi }{R}_p{R}_e^2$).

The mass fractal includes both a form and structure factor as follows:

$$P2\left(q\right)=F{\left(qR\right)}^2 and S2\left(q\right)=\frac{\left(\mathsf{\Gamma }\left(D_f-1\right){\mathsf{\zeta }}^{\left(D_f^{-}1\right)}\right)}{{\left[1+{\left(q\mathsf{\zeta }\right)}^2\right]}^{\left(D_f-1\right)/2}}\cdot \frac{\left(\sin \left[\left(D_f-1\right){\tan }^{-1}\left(q\mathsf{\zeta }\right)\right]\right)}{q}$$

where $R$: radius building block, D_f: fractal dimension and $\mathsf{\zeta }$ $\left(zeta\right)$: cut-off length maximum resolvable particle size.

Stage II fitting combined the effect of a broad peak (scattering inhomogeneities) system with mass fractal as the process enters a heterogeneous particulate phase. The former model has a power law built in; therefore, there was no need to include low q interactions separately. Mathematically this model consists of the following:

$$I\left(q\right)=\frac{A}{q^n} + \frac{C}{1+{\left(\left|q-q_0\right|{\rm Z}\right)}^m} +scale\cdot P2\left(q\right)S2\left(q\right)+background$$

where $A$: Porod law scale factor; $n$: the Porod exponent; $C$: Lorentzian scale factor; $m$: the exponent of $q$; $\mathsf{{\rm Z}}$: the screening length.

Stage III is the final stage of ensilication where the silica scattering is overtaking the system. We modelled this using a combination of power law and the $P2\left(q\right)\cdot S2\left(q\right)$ equation.

$$I\left(q\right)=scale\cdot q^{-power}+scale\cdot P2\left(q\right)\cdot S2\left(q\right)+background$$

3. Results and Discussion

The standard ensilication condition (1:50) has been analysed in a previous study [18]. There, we found that ensilication is a three-staged diffusion-limited cluster aggregation process (DLCA [21]) with each stage transitioning relatively rapidly, in order of seconds to minutes (Figure 1). SAXS experiments on different ratios of silica in this study were intended to provide more resolution on the influence of these conditions during ensilication. The expected observations were based on the difference in rates of ensilication. From earlier experiments, it was shown that higher levels of silica added to the reaction volume increased the polymerisation rate and therefore speeds up ensilication. When there is less silica, it takes more time for the polymer fragments to find each other by diffusion and connect.

The time-resolved scattering data at a high ratio (1:20) showed a smoother interface (Figure 2A), while the opposite was observed when using a significantly lower ratio of silica, 1:100 (Figure 3A). There was a broad peak formation and some increase in scattering at low q. There was visual turbidity which verified the process of ensilication; however, this process was relatively slower (tens of minutes) than at 1:50 which happened in an order of minutes.

Observing the SAXS signal of this high silica ensilication indicated that only the third stage of ensilication was proceeding. Therefore, the power law + mass fractal fit was applied to these data. The output (Figure 2C) showed a similar trend comparable to the 1:50 data. The fractal dimension, D_f, and cut-off length seem to behave similarly to D_f ~ 2 (1:50 ratio D_f ~ 1.8,

Table 1. SAXS ensilication parameter overview. Key parameters displayed are grouped according to ratio, pH, and ensilication stages. Fractal dim: fractal dimension; Equatorial R; equatorial radius; Polar R: polar radius; Cut-off: static protein and silica aggregates; Lorentz length: average particle radius; Fractal R: radius fractal particles; Chi²: goodness of fit. Standard conditions adapted with permission from [18].

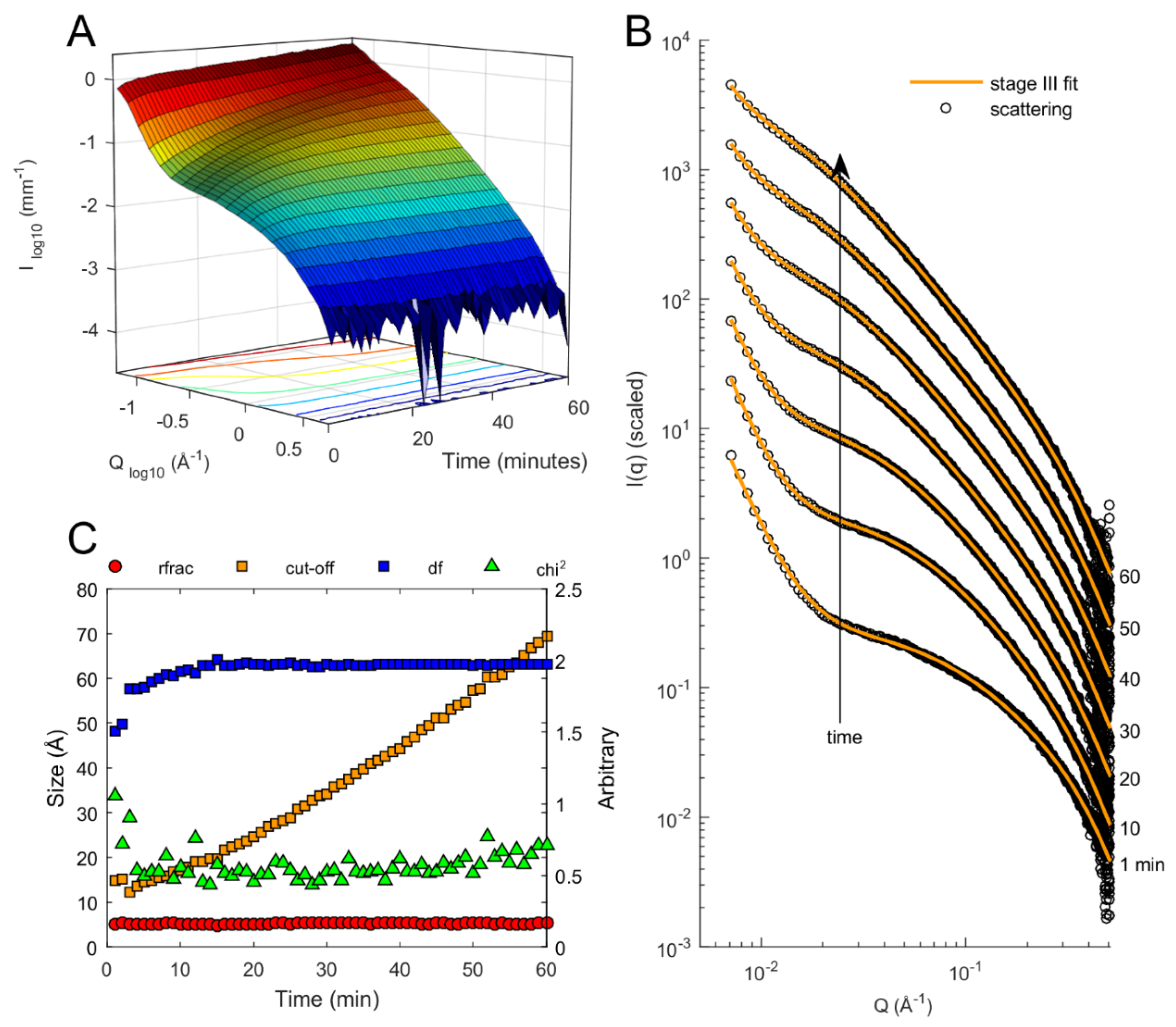
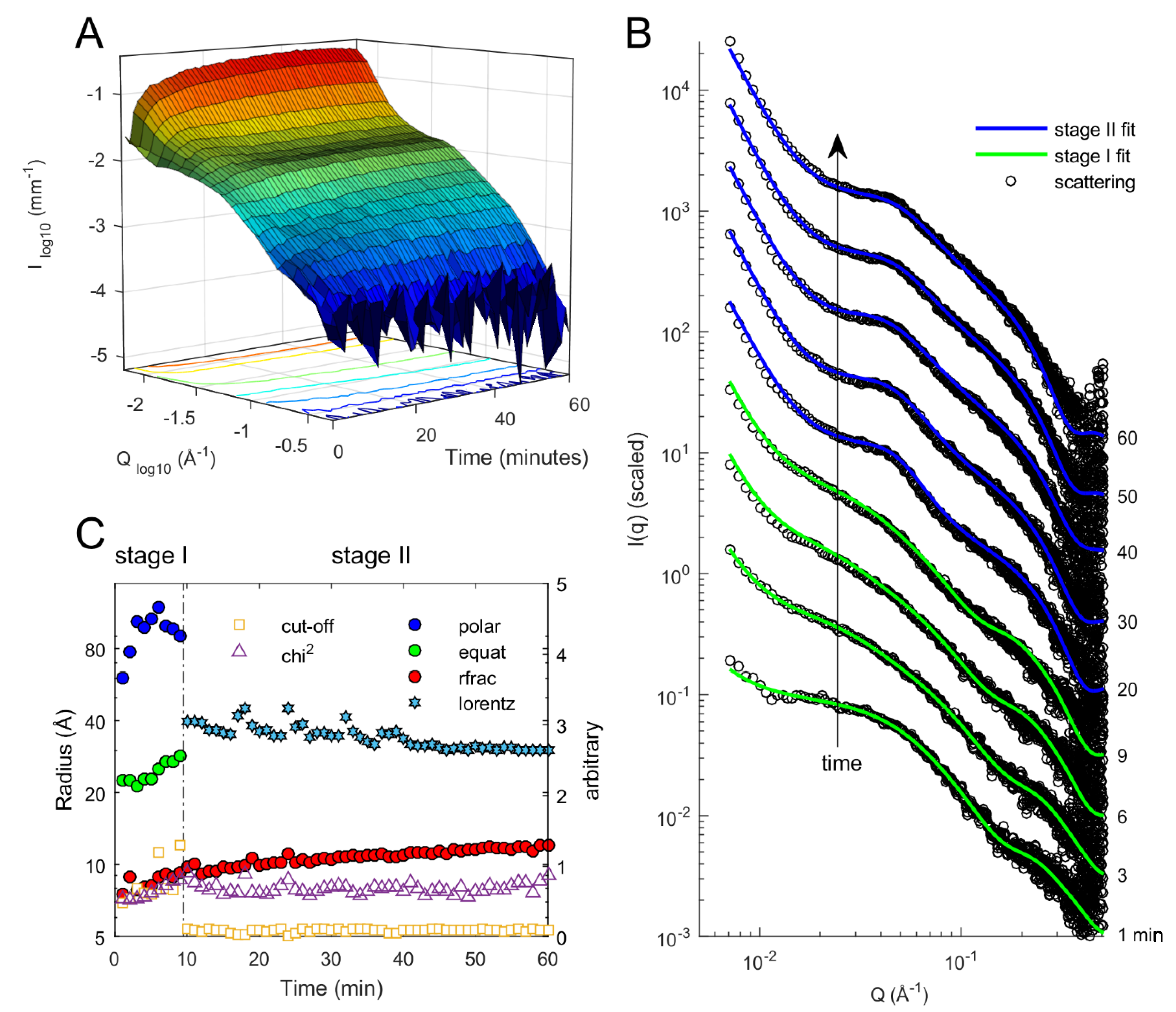
SAXS TTCF		Standard Conditions
Beamline	ID02	i22		ID02		ID02
Ratio	1:20	1:50		1:50		1:100
Time (min)	0–60	0–2		2–60		0–60		0–120
pH	7	7	7	7	7	7	7	8
Stage	III	I	II	II	III	I	II	I
Fractal dim.	1.5–2.0	1.1	1.1	1.1	1.6–1.9	-	-	1.0–1.5
Equatorial R	-	25–50	-	-	-	22–28	-	40–55
Polar R	-	50–165 −50	-	-	-	60–120–90	-	120–175
Cut-Off	14–69	10–600	165–20	12	20–80	>1	>1	50–300
Chi2	>1	3.0–12	5.0–12	>1	>1	>1	>1	>1
Lorentz	-	-	54–48	42–33	-	-	40–30	-
Fractal R	5	4.4–4.9	5.1–7.4	7.1–10	5.5–7.1	7.5–9.3	9.5–12	7.6–9.5

) and cut-off increasing linearly.

For the low silica ensilication, there is a slow transition (after 10 min) from the first stage of the ensilication proceeding towards the second stage (Figure 3B). This is indicated by the scattering moving towards a broad peak at mid q which slowly decreases over time with the slope at low q increasing gently. These observations are supported by the overall good fit for the models at each stage, I and II. The parameter output shows a similar trend to the 1:50 data in the first two stages (Figure 3C). The increase in polar and equatorial radii, the subsequent dip in these radii, and the following formation of an amorphous broad peak (Lorentz length) are identical to the transitions occurring in the 1:50 ratio. There is a difference in fractal dimension. However, after experimenting with different values for the D_f, there was no significant change in any of the associated parameters. Both fit models have good agreement on the radius of fractal building blocks at 10 Å (Table 1). Overall, the SAXS experiments on adjusting the ratio of hydrolysed TEOS to reaction volume show an increase of the ensilication speed with higher amounts of silica added. When lower amounts are used, the opposite is seen with both experiments at neutral pH.

After establishing the fact that varying ratios of silica influence the rate of ensilication, the following was to examine the effect of pH. As the 1:100 ratio already significantly slowed the ensilication process, this ratio was utilised to provide a greater resolution. This decision was based on the fast transition occurring during the 1:50 in situ flow experiment [18].

From the time-resolved scattering, it is apparent that no obvious transitions occur at pH 6 in the experimental timescale (data not shown). However, there are two scattering populations visible at pH 8 (Figure 4A). The visualised data showed a scattering of the reaction time, 120 min, at pH 8. There was an increase in the signal present during the initial moments of this run due to the introduction of silica to the system. These data were subsequently fitted with the stage I model. The sliced view of the fitted data showed a transition during the first 10 min of ensilication after which the solution stabilised. The signal showed no transition towards stage II or III, as observed in the other experiments. This suggested that the particles that are formed are stabilised in solution after adding the hydrolysed TEOS, and that this stabilisation occurs after 10 min. The fitted model provided several outputted parameters which helped to elucidate the effect of pH 8 on the ensilication of TTCF (Figure 4C). The model distinguishes the two populations where the low-mid q population is an ellipsoidal particle, representing the growing TTCF ensilicated particle, and the high q population is the fractal scattering caused by the colloidal polymeric silica particles. The radii for the ellipsoidal particle, polar, and equatorial displayed an increase in size. Especially, the polar radius increased from 120 Å to 175 Å over time (Table 1). The equatorial had a lower margin of growth but was still visible. The radius associated with the building blocks of the fractal structure displayed growth; however, the growth was only minimal. These parameters suggest that TTCF grows over its polar radius, similar to the 1:50 experiment. However, the signal of the particle does not disappear in the scattering signal and points towards the effect of pH.

It was previously understood that once TTCF–silica particles reach a particular size, aggregation is initiated. However, this was not observed at pH 8. This absence of aggregation is also supported by the calculated cut-off length for the polymer–protein particle. The scattering has large fluctuations present during the initial stages but does settle over time with particles having an approximate length of 200–300 Å. This trend is also visible in the fractal dimension (D_f) as this parameter can identify the kind of polymerisation process occurring. With a D_f of 1.45 stabilising towards the end, this indicates a slow sol–gel process as visual turbidity was observed.

4. Conclusions

This study investigated the effect of silica ratios and pH on the ensilication process classified as a DLCA type. The observation indicated an effect on the rate of ensilication while varying the added silica amounts. Additionally, the effect of pH demonstrated protein–silica particle growth and stabilisation at pH 8, low silica ratio.

The idea of individual stabilised TTCF–silica particles with a lower amount of silica is beneficial to increase surface area for release and is also cost effective. More attempts towards optimising the silica–protein ratio can identify the minimum concentration necessary to ensilicate all proteins in solution and optimise the time needed for this process. Fluctuating the pH indeed adds a layer of additional control in a diffusion-based system. These batch-type analyses will allow this method to progress into a more sophisticated means of nanoparticle synthesis using flow chemistry.

The effect of lower amounts of silica required will lead to a decreased cost in production. Changes to pH exert more control of the nanoparticle formation and drug release that; subsequently, a chemical release process might not be required. This further enhances the applicability of ensilication to existing protein-based vaccines and will make it more feasible to create thermostable vaccines that can be transported to regions in need of them.