Revealing Interactions between Temperature and Salinity and Their Effects on the Growth of Freshwater Diatoms by Empirical Modelling
Abstract
1. Introduction
2. Materials and Methods
2.1. Organisms and Culture Conditions
2.2. Temperature and Salinity Experiments
2.3. Calculation of Specific Growth Rate
2.4. Empirically Modelling Diatom Growth
2.4.1. Multiplicative and Decoupled Models
2.4.2. Polynomial Regression Equations
2.4.3. Data Fitting
3. Results and Discussion
3.1. Variations in the Response to Temperature and Salinity among Diatom Species
3.2. Empirical Modelling of Diatom Growth Considering Temperature and Salinity
3.2.1. Cymbella cf. incurvata
3.2.2. Nitzschia linearis
3.2.3. Cyclotella meneghiniana
3.2.4. Melosira varians
3.2.5. Ulnaria acus
3.2.6. Navicula gregaria
3.3. Temperature and Salinity Tolerance of Freshwater Diatoms
3.4. Ambiguity in Empirically Modelling Interactive Effects under Various Environmental Conditions
3.4.1. Diversity of Interaction Types
3.4.2. Ambiguity in Result Interpretation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Components and Final Concentration in Culture Medium | Stock Solution | Addition Per Litre of Culture Medium |
|---|---|---|
| 1. HEPES (1.00 mM) | 238.10 g/L dH2O | 1.0 mL |
| 2. Ca(NO3)2 × 4 H2O (0.21 mM) | 100.00 g/L dH2O | 0.5 mL |
| 3. MgSO4 × 7 H2O (0.203 mM) | 20.00 g/L dH2O | 2.5 mL |
| 4. K2 HPO4 × 3 H2O (13.20 µM) | 5.00 g/L dH2O | 0.6 mL |
| + NaNO3 (0.35 mM) | 50.00 g/L dH2O | |
| + Na2CO3 (0.19 mM) | 32.00 g/L dH2O | |
| 5. H3BO3 (16 µm) | 1.00 g/L dH2O | 1 mL |
| 6. Vitamin Solution | 1 mL | |
| Vitamin B12 (0.15 nM) | 0.20 mg/L dH2O | |
| Biotin (4.10 nM) | 1.00 mg/L dH2O | |
| Thiamine-HCl (0.30 µM) | 100.00 mg/L dH2O | |
| Niacinamide (0.80 nM) | 0.10 mg/L dH2O | |
| pH of the Vitamin Solution should be around pH 7 | ||
| 7. Trace Metals | 1 mL | |
| 7.1. Preparation of Trace Metal Solution | ||
| Na2EDTA × 2 H2O: 4.36 g | ||
| FeCl3 × 6 H2O: 3.15 g | ||
| Dissolve in 1000 mL dH2O, then add 1 mL of Primary Trace Metals each (see below). | ||
| Primary Trace Metals are stored frozen as 1 mL aliquots. | ||
| 7.2. Primary Trace Metals | ||
| 7.2.1. K2CrO4 | 0.194 g/100 mL dH2O | |
| 7.2.2. CoCl2 × 6 H2O | 1.00 g/100 mL dH2O | |
| 7.2.3. CuSO4 × 5 H2O | 0.25 g/100 mL dH2O | |
| 7.2.4. MnCl2 × 4 H2O5 | 18.00 g/100 mL dH2O | |
| 7.2.5. Na2MoO4 × 2 H2O | 1.89 g/100 mL dH2O | |
| 7.2.6. NiSO4 × 6 H2O | 0.27 g/100 mL dH2O | |
| 7.2.7. H2SeO3 | 0.13 g /100 mL dH2O | |
| 7.2.8. Na3VO4 | 0.184 g /100 mL dH2O | |
| 7.2.9. ZnSO4 × 7 H2O | 2.20 g/100 mL dH2O | |
| 8. Na2SiO3 × 9 H2O (0.50 mM)–optional | 28.42 g/L dH2O | 5 mL |
References
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P.G. Primary production of the biosphere: Integrating terrestrial and oceanic components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef]
- Wilhelm, C.; Buchel, C.; Fisahn, J.; Goss, R.; Jakob, T.; LaRoche, J.; Laavud, J.; Lohr, M.; Riebesell, U.; Stehfest, K.; et al. The regulation of carbon and nutrient assimilation in diatoms is significantly different green algae. Protist 2006, 157, 91–124. [Google Scholar] [CrossRef]
- Prestegard, S.K.; Knutsen, G.; Herfindal, L. Adenosine content and growth in the diatom Phaeodactylum tricornutum (Bacillariophyceae): Effect of salinity, light, temperature and nitrate. Diatom Res. 2014, 29, 361–369. [Google Scholar] [CrossRef]
- Smol, J.P.; Stoermer, E.F. The Diatoms: Applications for the Environmental and Earth Sciences; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Lobo, E.A.; Heinrich, C.G.; Schuch, M.; Wetzel, C.E.; Ector, L. Diatoms as bioindicators in rivers. In River Algae; Necchi, O., Jr., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 245–271. [Google Scholar]
- Stevenson, R.J.; Pan, Y.; Van Dam, H. Assessing environmental conditions in rivers and streams with diatoms. In The Diatoms: Applications for the Environmental and Earth Sciences; Smol, J.P., van Dam, H., Eds.; Cambridge University Press: Cambridge, MA, USA, 1999; pp. 57–85. [Google Scholar]
- Birks, H.J.B. Numerical methods for the analysis of diatom assemblage data. In The Diatoms: Applications for the Environmental and Earth Sciences, 2nd ed.; Smol, P.J., Stoermer, E.F., Eds.; Cambridge University Press: Cambridge, MA, USA, 2010; pp. 23–54. [Google Scholar]
- Pajunen, V.; Kahlert, M.; Soininen, J. Stream diatom assemblages as environmental indicators–A cross-regional assessment. Ecol. Indic. 2020, 113, 106183. [Google Scholar] [CrossRef]
- Crain, C.M.; Kroeker, K.; Halpern, B.S. Interactive and cumulative effects of multiple ahuman stressors in marine systems. Ecol. Lett. 2008, 11, 1304–1315. [Google Scholar] [CrossRef]
- Jackson, M.; Loewen, C.G.; Vinebrooke, R.D.; Chimimba, C.T. Net effects of multiple stressors in freshwater ecosystems: A meta-analysis. Glob. Chang. Biol. 2016, 22, 180–189. [Google Scholar] [CrossRef]
- Cote, I.M.; Darling, E.S.; Brown, C.J. Interactions among ecosystem stressors and their importance in conservation. Proc. R. Soc. B 2016, 283, 10152592. [Google Scholar] [CrossRef]
- Birk, S.; Chapman, D.; Carvalho, L.; Spears, B.M.; Andersen, H.E.; Argillier, C.; Auer, S.; Baattrup-Pedersen, A.; Banin, L.; Beklioğlu, M.; et al. Impacts of multiple stressors on freshwater biota across spatial scales and ecosystems. Nat. Ecol. Evol. 2020, 4, 1060–1068. [Google Scholar] [CrossRef]
- Boyd, P.W.; Collins, S.; Dupont, S.; Fabricius, K.; Gattuso, J.P.; Havenhand, J.; Hutchins, D.A.; Riebesell, U.; Rintoul, M.S.; Vichi, M.; et al. Experimental strategies to assess the biological ramifications of multiple drivers of global ocean change—A review. Glob. Chang. Biol. 2017, 24, 2239–2261. [Google Scholar] [CrossRef]
- Erofeeva, E.A. Plant hormesis and Shelford’s tolerance law curve. J. For. Res. 2021, 32, 1789–1802. [Google Scholar] [CrossRef]
- Low-Decarie, E.; Boatman, T.G.; Bennett, N.; Passfield, W.; Gavalas-Olea, A.; Siegel, P.; Geider, R.J. Predictions of response to temperature are contingent on model choice and data quality. Ecol. Evol. 2017, 7, 10467–10481. [Google Scholar] [CrossRef]
- Barton, S.; Yvon-Durocher, G. Quantifying the temperature dependence of growth rate in marine phytoplankton within an across species. Limnol. Oceanogr. 2019, 64, 2081–2091. [Google Scholar] [CrossRef]
- Grimaud, G.M.; Mairet, F.; Sciandra, A.; Bernard, O. Modeling the temperature effect on the specific growth rate of phytoplankton: A review. Rev. Environ. Sci. Biotechnol. 2017, 16, 625–645. [Google Scholar] [CrossRef]
- Brand, L.E. The salinity tolerance of forty-six marine phytoplankton isolates. Estuar. Coast. Shelf. S. 1984, 18, 542–556. [Google Scholar] [CrossRef]
- Kirst, G.O. Salinity tolerance of eukaryotic marine algae. Annu. Rev. Plant. Physiol. Plant Mol. Biol. 1989, 40, 21–53. [Google Scholar] [CrossRef]
- Albrecht, M.; Roshan, S.K.; Fuchs, L.; Karsten, U.; Schumann, R. Applicability and limitations of high-throughput algal growth rate measurements using in vivo fluorescence in microtiter plates. J. Appl. Phycol. 2022, 34, 2037–2049. [Google Scholar] [CrossRef]
- Mata, T.M.; Martins, A.A.; Caetano, N.S. Microalgae for biodiesel production and other applications: A review. Renew. Sustain. Energ. Rev. 2010, 14, 217–232. [Google Scholar] [CrossRef]
- Beliveau, D.J.; Hickman, M. Isolation and response to temperature of five diatom species. Arch. Protstenk. 1982, 126, 355–370. [Google Scholar] [CrossRef]
- Lee, E.; Jalalizadeh, M.; Zhang, Q. Growth kinetic models for microalgae cultivation: A review. Algal Res. 2015, 12, 497–512. [Google Scholar] [CrossRef]
- Gustavs, L.; Schumann, R.; Eggert, A.; Karsten, U. In vivo growth fluorometry: Accuracy and limits of microalgal growth rate measurements in ecophysiological innvestigations. Aquat. Microb. Ecol. 2009, 55, 95–104. [Google Scholar] [CrossRef]
- Cerco, C.F.; Cole, T. User’s Guide to the CE-QUAL-ICM Three-Dimensional Eutrophication Model; US Army Corps of Engineers: Washington, DC, USA, 1995. [Google Scholar]
- Gharagozloo, P.E.; Drewry, J.L.; Collins, A.M.; Dempster, T.A.; Choi, C.Y.; James, S.C. Analysis and modeling of Nannochloropsis growth in lab, greenhouse, and raceway experiments. J. Appl. Phycol. 2014, 26, 2303–2314. [Google Scholar] [CrossRef]
- Gao, S.; Waller, P.; Khawam, G.; Attalah, S.; Huesemann, M.; Ogden, K. Incorporation of salinity, nitrogen, and shading stress factors into the Huesemann Algae Biomass Growth model. Algal Res. 2018, 35, 462–470. [Google Scholar] [CrossRef]
- Dudley, B.D.; Barr, N.G.; Plew, D.R.; Scheuer, K. Experiments to parameterise a growth and nutrient storage model for Agarophyton spp. Estuar. Coast. Shelf Sci. 2022, 264, 107660. [Google Scholar] [CrossRef]
- Miller, R.L.; Kamykowski, D.L. Effects of temperature, salinity, irradiance and diurnal periodicity on growth and photosynthesis in the diatom Nitzschia americana: Light-saturated growth. J. Phycol. 1986, 22, 339–348. [Google Scholar] [CrossRef]
- Bosma, R.; van Zessen, E.; Reith, J.H.; Tramper, J.; Wijffels, R.H. Prediction of volumetric productivity of an outdoor photobioreactor. Biotechnol. Bioeng. 2007, 97, 1108–1120. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike. Springer Series in Statistics; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Bernard, O.; Remond, B. Validation of a simple model accounting for light and temperature on microalgal growth. Bioresour. Technol. 2012, 123, 520–527. [Google Scholar] [CrossRef]
- Singh, S.P.; Singh, P. Effect of temperature and light on the growth of algae species: A review. Renew. Sustain. Energy Rev. 2015, 50, 431–444. [Google Scholar] [CrossRef]
- Walter, B.; Peters, J.; van Beusekom, J.E.E.; John, M.A.S. Interactive effects of temperature and light during deep convection: A case study on growth and condition of the diatom Thalassiosira weissflogii. ICES J. Mar. Sci. 2015, 72, 2061–2071. [Google Scholar] [CrossRef][Green Version]
- Renaud, S.M.; Thinh, L.-V.; Lambrinidis, G.; Parry, D.L. Effect of temperature on growth, chemical composition and fatty acid composition of tropical Australian microalgae grown in batch cultures. Aquaculture 2002, 211, 195–214. [Google Scholar] [CrossRef]
- Ras, M.; Steyer, J.-P.; Bernard, O. Temperature effect on microalgae: A crucial factor for outdoor production. Rev. Environ. Sci. Bio/Technol. 2013, 12, 153–164. [Google Scholar] [CrossRef]
- Falk, S.; Maxwell, D.P.; Laudenbach, D.E.; Huner, N.P.A. Photosynthetic adjustment to temperature. In Photosynthesis and the Environment; Baker, N.R., Ed.; Springer: Dordrecht, The Netherlands, 1996; pp. 367–385. [Google Scholar]
- Roubeix, V.; Lancelot, C. Effect of salinity on growth, cell size and silicification of an euryhaline freshwater diatom: Cyclotella meneghiniana. Transit. Waters Bull. 2008, 1, 31–38. [Google Scholar]
- Yin, J.; Sun, X.; Zhao, R.; Qiu, X.; Eeswaran, R. Application of uniform design to evaluate the different conditions on the growth of algae Prymnesium parvum. Sci. Rep. 2021, 11, 12672. [Google Scholar] [CrossRef] [PubMed]
- Ritchie, R.J.; Larkum, A.W.D. Potassium transport in Enteromorpha intestinalis (L.) link. J. Exp. Bot. 1985, 164, 394–412. [Google Scholar] [CrossRef]
- Munns, R.; Greenway, H.; Kirst, G.O. Halotolerant eukaryotes. In Encyclopedia of Plant Physiology; Lange, O.L., Nobel, P.S., Osmond, C.B., Ziegler, H., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1983; Volume 12C, pp. 59–135. [Google Scholar]
- Underwood, G.J.C.; Provot, L. Determining the environmental preferences of four estuarine epipelic diatom taxa: Growth across a range of salinity, nitrate and ammonium conditions. Eur. J. Phycol. 2000, 35, 173–182. [Google Scholar] [CrossRef]
- Cumming, B.F.; Smol, J.P. Development of diatom-based salinity models for paleoclimatic research from lakes in British Columbia (Canada). van Dam, H., Ed.; In Twelfth International Diatom Symposium. Developments in Hydrobiology; Springer: Dordrecht, The Netherland, 1993; Volume 90. [Google Scholar]
- Clavero, E.; Hernandez-Marine, M.; Grimalt, J.O.; Garcia-Pichel, F. Salinity tolerance of diatoms from thalassic hypersaline environments. J. Phycol. 2000, 36, 1021–1034. [Google Scholar] [CrossRef]
- Wachnicka, A.; Gaiser, E.; Collins, L.; Frankovich, T.; Boyer, J. Distribution of diatoms and development of diatom-based models for inferring salinity and nutrient concentrations in Florida Bay and Adjacent Coastal Wetlands of South Florida. Estuar. Coast. 2010, 33, 1080–1098. [Google Scholar] [CrossRef]
- Potapova, M. Patterns of diatom distribution in relation to salinity. In The Diatom World; Seckbach, J., Kociolek, J.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 313–332. [Google Scholar]
- Saunders, K.M. A diatom dataset and diatom-salinity inference model for southeast Australian estuaries and coastal lakes. J. Paleolimnol. 2011, 46, 525–542. [Google Scholar] [CrossRef]
- Reed, J.M.; Mesquita-Joanes, F.; Griffiths, H.I. Multi-indicator conductivity transfer functions for quaternary palaeoclimate reconstruction. J. Paleolimnol. 2012, 47, 251–275. [Google Scholar] [CrossRef]
- Nodine, E.R.; Gaiser, E.E. Distribution of diatoms along environmental gradients in the Charlotte Harbor, Florida (USA), estuary and its watershed: Implications for bioassessment of salinity and nutrient concentrations. Estuar. Coast. 2014, 37, 864–879. [Google Scholar] [CrossRef]
- Rzodkiewicz, M.; Gabka, M.; Szpikowska, G.; Woszczyk, M. Diatom assemblages as indicators of salinity gradients: A case study from a coastal lake. Oceanol. Hydrobiol. Stud. 2017, 46, 325–339. [Google Scholar] [CrossRef]
- Tibby, J.; Richards, J.; Tyler, J.J.; Barr, C.; Fluin, J.; Goonan, P. Diatom-water quality thresholds in South Australian stream indicate a need for more stringent water quality guidelines. Mar. Freshw. Res. 2020, 71, 942–952. [Google Scholar] [CrossRef]
- Juggins, S. Quantitative reconstructions in palaeolimnology: New paradigm or sick science? Quarter. Sci. Rev. 2013, 64, 20–32. [Google Scholar] [CrossRef]
- Sogaard, D.H.; Hansen, P.J.; Rysgaard, S.; Glud, R.N. Growth limitation of three Arctic sea algal species: Effects of salinity, pH, and inorganic carbon availability. Polar Biol. 2011, 34, 1157–1165. [Google Scholar] [CrossRef]
- Remy, M.; Hillebrand, H.; Floder, S. Stability of marine phytoplankton communities facing stress related to global change: Interactive effects of heat waves and turbidity. J. Exp. Mar. Biol. Ecol. 2017, 497, 219–229. [Google Scholar] [CrossRef]
- Yan, T.; Zhou, M.; Qian, P. Combined effects of temperature, irradiance and salinity on growth of diatom Skeletonema costatum. Chi. J. Oceano. Limnol. 2002, 20, 237–243. [Google Scholar]
- Baek, S.H.; Jung, S.W.; Shin, K. Effects of temperature and salinity on growth of Thalassiosira pseudonana (Bacillariophyceae) isolated from ballast water. J. Freshw. Ecol. 2011, 26, 547–552. [Google Scholar]
- Krawiec, R.W. Autecology and clonal variability of the marine centric diatom Thalassiosira rotula (Bacillariphyceae) in response to light, temperature and salinity. Mar. Biol. 1982, 69, 79–89. [Google Scholar] [CrossRef]
- Collins, C.D.; Boylen, C.W. Physiological responses of Anabaena variabilis (Cyanophyceae) to instantaneous exposure to various combinations of light intensity and temperature. J. Phycol. 1982, 18, 206–211. [Google Scholar] [CrossRef]
- Arrigo, K.R.; Sullivan, C.W. A high resolution bio-optical model of microalgal growth: Tests using sea-ice algal community time-series data. Limnol. Oceanogr. 1994, 39, 609–631. [Google Scholar] [CrossRef]
- Moisan, J.R.; Moisan, T.A.; Abbott, M.R. Modelling the effect of temperature on the maximum growth rates of phytoplankton populations. Ecol. Model. 2002, 153, 197–215. [Google Scholar] [CrossRef]
- Montagnes, D.J.S.; Kimmance, S.A.; Atkinson, D. Using Q10: Can growth rates increase linearly with temperature? Aquat. Microb. Ecol. 2003, 32, 307–313. [Google Scholar] [CrossRef]
- Haario, H.; Kalachev, L.; Laine, M. Reduced models of algae growth. Bull. Mathe. Biol. 2009, 71, 1626–1648. [Google Scholar] [CrossRef] [PubMed]
- Pegallapati, A.K.; Nirmalakhandan, N. Modeling algal growth in bubble columns under sparging with CO2-enriched air. Bioresour. Technol. 2012, 124, 137–145. [Google Scholar] [CrossRef]
- Ketheesan, B.; Nirmalakhandan, N. Modeling microalgal growth in an airlift-driven raceway reactor. Bioresour. Technol. 2013, 136, 689–696. [Google Scholar] [CrossRef] [PubMed]
- Bordel, S.; Guieysse, B.; Munoz, R. Mechanistic model for the reclamation of industrial wastewaters using algal-bacterial photobioreactors. Environ. Sci. Technol. 2009, 43, 3200–3207. [Google Scholar] [CrossRef] [PubMed]
- Bernhardt, J.R.; Sunday, J.M.; Thompson, P.L.; O’Connor, M.I. Nonlinear averaging of thermal experience predicts population growth rates in a thermally variable environment. Proc. R. Soc. B. 2018, 285, 20181076. [Google Scholar] [CrossRef]
- Thomas, M.K.; Kremer, C.T.; Klausmeier, C.A.; Litchman, E. A global pattern of thermal adaptation in marine phytoplankton. Science 2012, 338, 1085–1088. [Google Scholar] [CrossRef]
- Cossins, A.R.; Bowler, K. Temperature Biology of Animals; Chapman and Hall: New York, NY, USA, 1987. [Google Scholar]
- James, S.C.; Janardhanam, V.; Hanson, D.T. Simulating pH effects in an algal growth hydrodynamics model. J. Phycol. 2013, 49, 608–615. [Google Scholar] [CrossRef]
- Cerco, C.F.; Cole, T. Three-Dimensional Eutrophication Model of Chesapeake Bay; US Army Corps of Engineers: Washington, DC, USA, 1994. [Google Scholar]
- Dauta, A.; Devaux, J.; Piquemal, F.; Boumnich, L. Growth rate of four freshwater algae in relation to light and temperature. Hydrobiologia 1990, 207, 221–226. [Google Scholar] [CrossRef]
- Martins, I.; Azevedo, A.; Gomez, I.; Valente, L.M.P. Variation on the standing stock of Gracilaria sp. In a temperature estuary under single-stressor and multiple-stressor climate change scenarios. Algal Res. 2020, 51, 102079. [Google Scholar] [CrossRef]
- Tevatia, R.; Demirel, Y.; Rudrappa, D.; Blum, P. Effects of thermodynamically coupled reaction diffusion in microalgae growth and lipid accumulation: Model development and stability analysis. Comp. Chem. Engineer. 2015, 75, 28–39. [Google Scholar] [CrossRef]
- Guterman, H.; Vonshak, A.; Ben-Yaakov, S. A macromodel for outdoor algal mass production. Biotechnol. Bioeng. 1990, 35, 809–819. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Fan, M.; Liu, R.; Wang, X.; Yuan, X.; Zhu, H. The dynamics of temperature and light on the growth of phytoplankton. J. Theor. Biol. 2015, 385, 8–19. [Google Scholar] [CrossRef]
- Di Toro, D.M.; O’Connor, D.J.; Thomann, R.V. A dynamic model of the phytoplankton population in the sacramento-san joaquin delta. Am. Chem. Soc. 1971, 106, 131–180. [Google Scholar]
- Ahlgren, G. Temperature functions in biology and their application to algal growth constants. Oikos 1987, 49, 177–190. [Google Scholar] [CrossRef]
- Blanchard, G.F.; Guarini, J.-M.; Richard, P.; Gros, P.; Mornet, F. Quantifying the short-term temperature effect on light-saturated photosynthesis of intertidal microphytobenthos. Mar. Ecol. Prog. Ser. 1996, 134, 309–313. [Google Scholar] [CrossRef]
- Slegers, P.M.; Loesing, M.B.; Wijffels, R.H.; van Straten, G.; van Boxtel, A.J.B. Scenario evaluation of open pond microalgae production. Algal Res. 2013, 2, 358–368. [Google Scholar] [CrossRef]
- Quinn, J.; de Winter, L.; Bradley, T. Microalgae bulk growth model with application to industrial scale systems. Bioresource Technol. 2011, 102, 5083–5092. [Google Scholar] [CrossRef]
- Geider, R.J.; MacIntyre, H.L.; Kana, T.M. Dynamic model of phytoplankton growth and acclimation: Responses of the balanced growth rate and the chlorophyll a:carbon ratio to light, nutrient-limitation and temperature. Mar. Ecol. Prog. Ser. 1997, 148, 187–200. [Google Scholar] [CrossRef]
- Wigmosta, M.S.; Coleman, A.M.; Skaggs, R.J.; Huesemann, M.H.; Lane, L.J. National microalgae biofuel production potential and resource demand. Water Resour. Res. 2011, 47, W00H04. [Google Scholar] [CrossRef]
- Kleiman, R.M.; Characklis, G.W.; Kern, J.D.; Gerlach, R. Characterizing weather-related biophysical and financial risks in algal biofuel production. App. Energ. 2021, 294, 116960. [Google Scholar] [CrossRef]
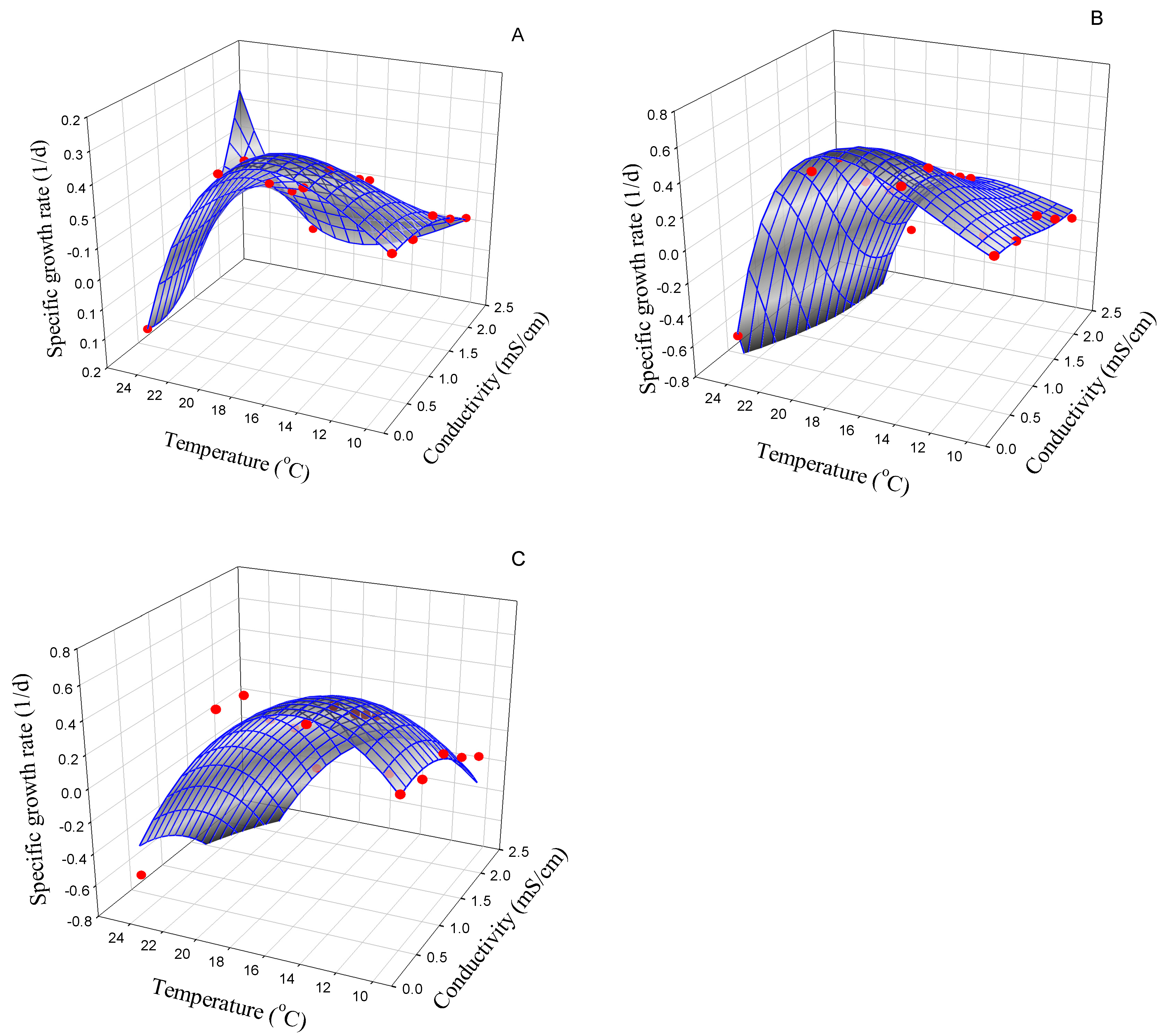
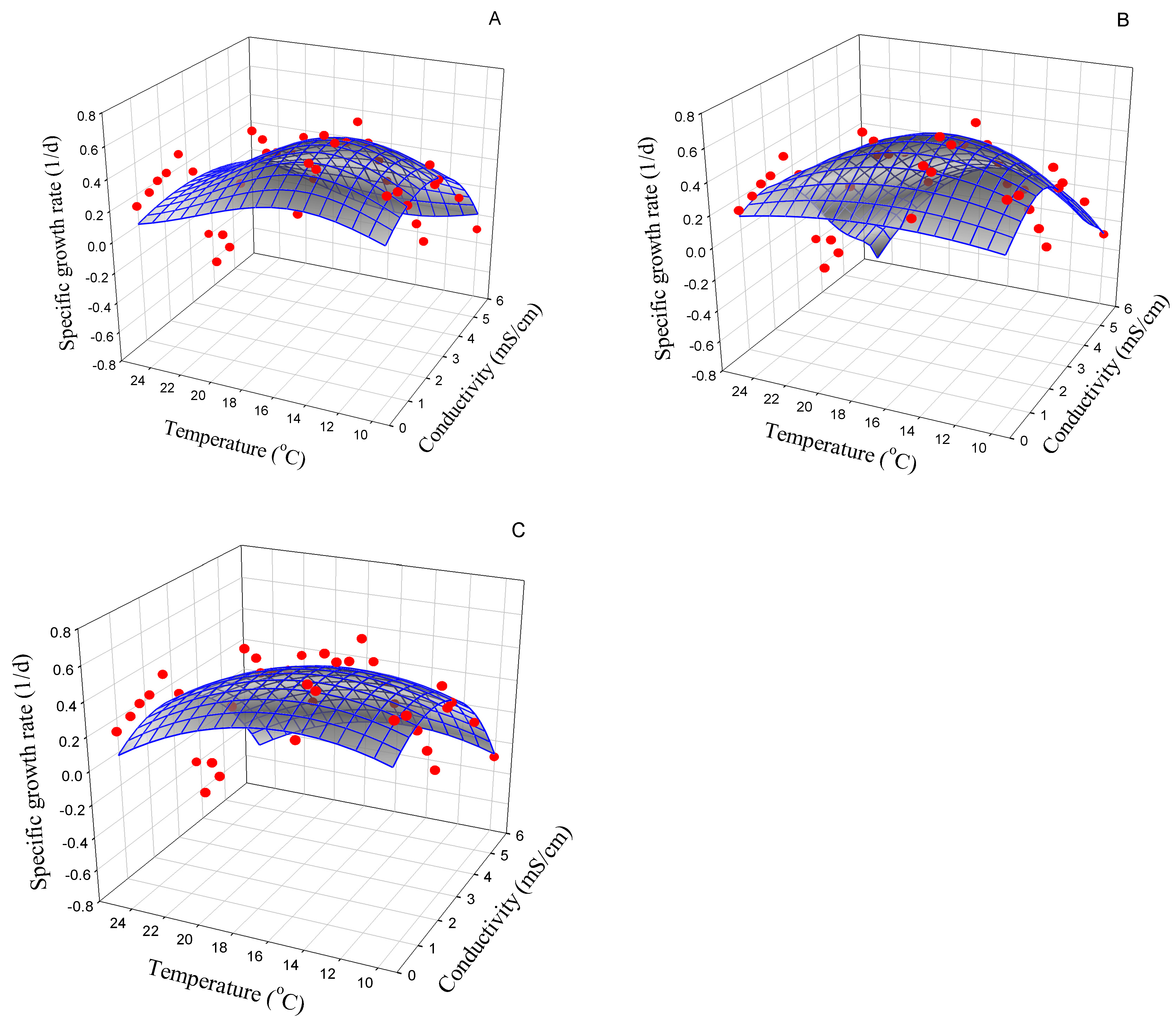

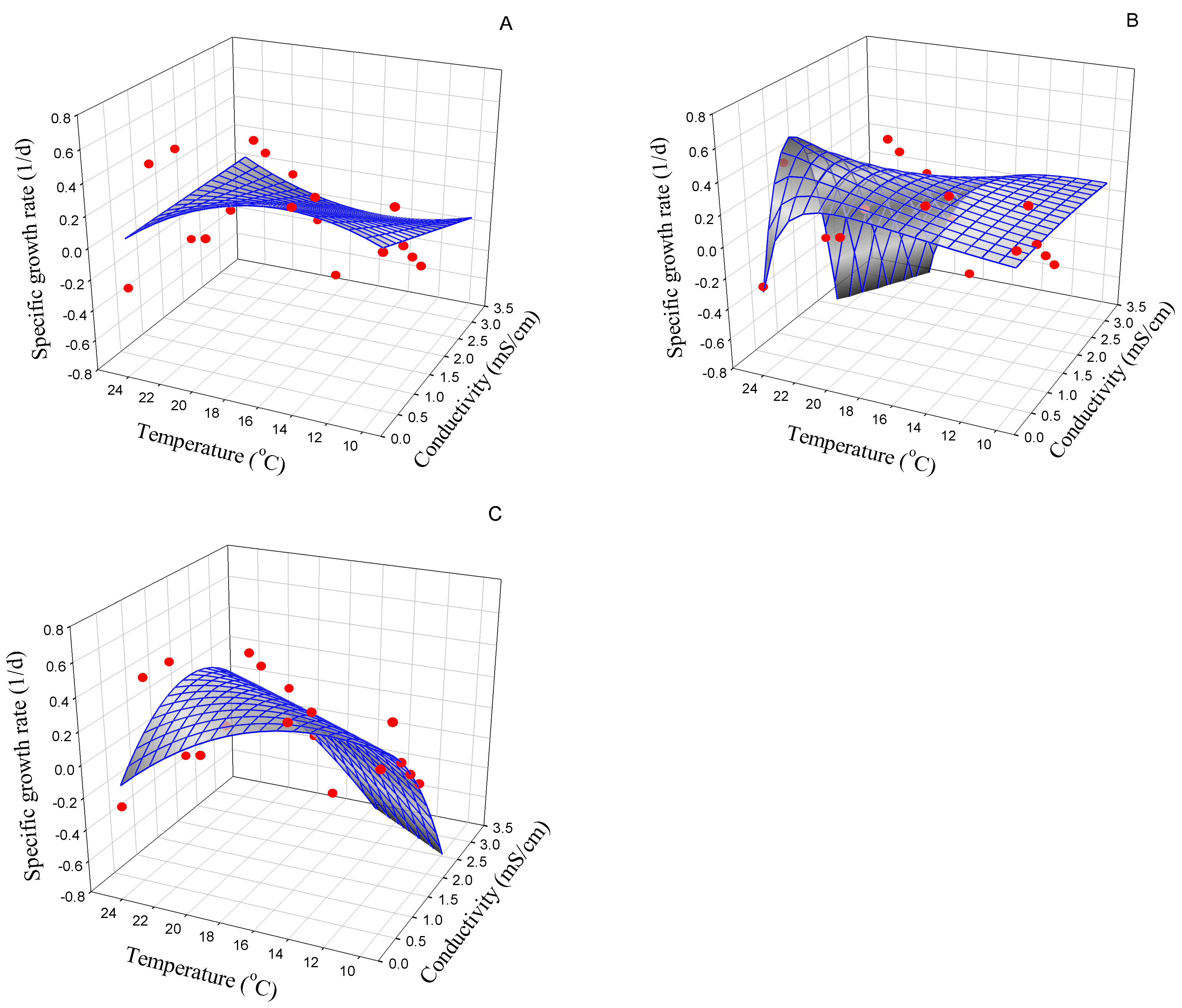

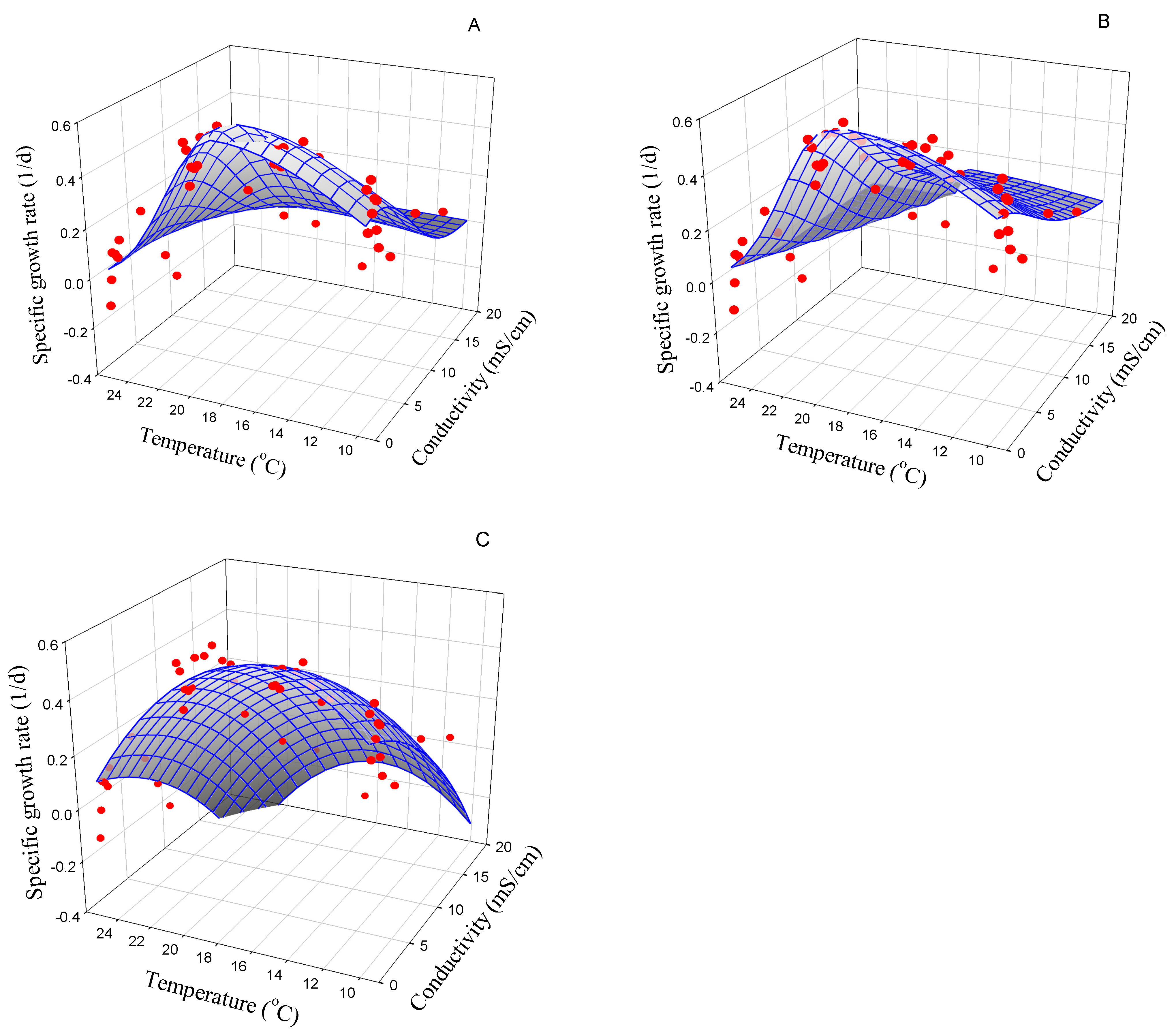
| Strain | Best Model | Symbol (Unit) | Model Parameter | AIC |
|---|---|---|---|---|
| Cymbella cf. incurvata | (°C) | Optimum temperature of the quadratic portion; when = 0, this value is identical to the optimum temperature of the whole curve (i.e., growth reaches the maximum rate, and the thermal response is symmetric) | −91.06 | |
| (°C) | the thermal breadth (i.e., the range over which diatoms grow) | |||
| (mS/cm) | Optimum conductivity | |||
| (mS/cm) | Maximum conductivity above which growth ceases | |||
| Nitzschia linearis | (1/d) | Maximum growth rate reached at the optimum temperature ; °C) and the optimum conductivity ; mS/cm) | −133.49 | |
| (°C) | Thermal breadth that can be affected by salinity depending on the interaction coefficien (cm/mS) | |||
| (cm2/mS2) | Salinity effect factor | |||
| Cyclotella meneghiniana | See above | See above | −43.90 | |
| Melosira varians | (1/d) | Growth rate at 20 °C | −51.79 | |
| (mS/cm) | Optimum conductivity | |||
| (mS/cm) | Maximum conductivity above which growth ceases | |||
| Ulnaria acus | (1/°C2) | Temperature effect factor describing the change in the growth rate with increasing temperature below or above the optimum ; °C) | −94.70 | |
| (mS/cm) | Optimum conductivity for growth | |||
| (mS/cm) | Maximum conductivity for growth | |||
| (cm/mS) | Represents the interactive effect | |||
| Navicula gregaria | (1/d) is | Maximum growth rate obtained at the optimum temperature (°C) and the optimum conductivity (mS/cm) | −229.82 | |
| (1/°C2) | Temperature effect factors at temperature below and above the optimum, respectively | |||
| (cm2/mS2) | Salinity effect factor. |
| Strain | Temperature Response | Salinity Response | ||||
|---|---|---|---|---|---|---|
| Optimum Temperature (°C) | Thermal Breadth (°C) | Temperature Tolerance Range (°C) | Optimum Conductivity (mS/cm) | Maximum Conductivity (mS/cm) | Half-Saturation Conductivity (mS/cm) | |
| Cymbella cf. incurvate | 15.8 (15.3–16.3) | 14.8 (12. 7–16.9) | 15.5 ± 7.4 | 0.63 (0.35–0.90) | 1.81 (1.75–1.88) | 0.81 (0.01–1.61) |
| Nitzschia linearis | 15.9 (14.7–17.1) | 31.8 (24.1–39.4) | 15.9 ± 15.9 | 2.44 (2.02–2.87) | 5.29 (4.84–5.74) | 4.60 (1.17–8.04) |
| Cyclotella meneghiniana | 17.3 (13.9–20.8) | 59.6 (0–121.0) | 17.3 ± 29.8 | 0.69 (0.58–0.81) | 1.38 (1.06–1.71) | |
| Melosira varians | 1.20 (1.06–1.34) | 6.41 (3.81–8.90) | ||||
| Ulnaria acus | 17.1 (12.2–22.0) | 28.1 (11.7–44.4) | 17.1 ± 14.1 | 1.08 (0.79–1.37) | 2.29 (2.02–2.56) | |
| Navicular gregaria | 18.4 (17.3–19.4) | 19.3 (17.9–20.6) | 18.4 ± 9.7 | 2.12 (0.29–3.96) | 9.01 (6.65–11.37) | |
| Interaction ID | Type of Interaction | Interactive Effects | Simulation |
|---|---|---|---|
| A | Stressor 1—modulated slope of the response to stressor 2 | Salinization increased or decreased the slope of the temperature–growth curve, which is accompanied by the narrowed or broadened thermal breadth, respectively. Similar effects can be exerted by temperature increases on the conductivity–growth curve. | 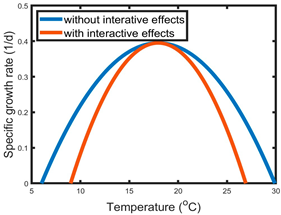 |
| B | Stressor 1—shifted optimum level of stressor 2 | Salinization increases the optimum temperature of the bell-shaped temperature–growth curve | 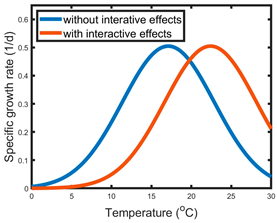 |
| C | Combination of A and B | The temperature–growth curve is modulated both vertically and horizontally by salinization. Salinization narrows the thermal breadth. Both the optimum temperature and the maximum growth rate are lowered. | 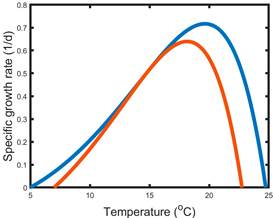 |
| Equation | Interaction ID | AIC | |||||
|---|---|---|---|---|---|---|---|
| Cymbella incurvata | Nitzschia linearis | Cyclotella meneghiniana | Melosia varians | Ulnaria acus | Navicula gregaria | ||
| ST7 | A | −52.53 | −33.02 | ||||
| ST15 | A | −133.49 ** | −43.90 ** | −173.43 | |||
| ST17 | A | −131.76 * | −90.30 * | ||||
| ST34 | A | −88.75 * | |||||
| ST11 | A | −56.91 | −51.79 ** | ||||
| ST21 | A | −120.46 | −32.72 | −42.93 | |||
| ST31 | A | −43.25 | |||||
| ST22 | A | −117.83 | −78.93 | ||||
| ST23 | A | −118.88 | −87.97 * | ||||
| ST37 | A | −88.43 * | |||||
| ST39 | A | −88.09 * | |||||
| ST27 | A | −42.19 | |||||
| ST29 | A | −44.10 | |||||
| ST28 | A | −42.85 | |||||
| ST30 | A | −44.78 | |||||
| ST32 | A | −41.02 | |||||
| ST36 | A | −87.56 | |||||
| ST38 | A | −89.24 * | |||||
| ST41 | A | −86.34 | |||||
| ST43 | A | −84.32 | |||||
| ST51 | A | −211.67 | |||||
| ST52 | A | −219.61 ** | |||||
| ST33 | B | −89.72 * | |||||
| ST35 | B | −94.70 ** | |||||
| ST2 | C | −62.08 ** | |||||
| ST4 | C | −60.63 * | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.T.Y.; Becker, A.; Kleinschmidt, J.; Mayombo, N.A.S.; Farias, L.; Beszteri, S.; Beszteri, B. Revealing Interactions between Temperature and Salinity and Their Effects on the Growth of Freshwater Diatoms by Empirical Modelling. Phycology 2023, 3, 413-435. https://doi.org/10.3390/phycology3040028
Le TTY, Becker A, Kleinschmidt J, Mayombo NAS, Farias L, Beszteri S, Beszteri B. Revealing Interactions between Temperature and Salinity and Their Effects on the Growth of Freshwater Diatoms by Empirical Modelling. Phycology. 2023; 3(4):413-435. https://doi.org/10.3390/phycology3040028
Chicago/Turabian StyleLe, T. T. Yen, Alina Becker, Jana Kleinschmidt, Ntambwe Albert Serge Mayombo, Luan Farias, Sára Beszteri, and Bánk Beszteri. 2023. "Revealing Interactions between Temperature and Salinity and Their Effects on the Growth of Freshwater Diatoms by Empirical Modelling" Phycology 3, no. 4: 413-435. https://doi.org/10.3390/phycology3040028
APA StyleLe, T. T. Y., Becker, A., Kleinschmidt, J., Mayombo, N. A. S., Farias, L., Beszteri, S., & Beszteri, B. (2023). Revealing Interactions between Temperature and Salinity and Their Effects on the Growth of Freshwater Diatoms by Empirical Modelling. Phycology, 3(4), 413-435. https://doi.org/10.3390/phycology3040028






