Estimation of Genetic Parameters for Litter Size and Growth Traits in a Prolific Line of Tunisian Barbarine Sheep
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Traits Analysed
2.3. Statistical Analysis
2.4. Bivariate Linear–Linear Model
2.5. Bivariate Threshold-Linear Model
2.6. Univariate Linear and Threshold Models
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bedhiaf-Romdhani, S.; Djemali, M.; Zaklouta, M.; Iniguez, L. Monitoring crossbreeding trends in native Tunisian sheep breeds. Small Rumin. Res. 2008, 74, 274–278. [Google Scholar] [CrossRef]
- Atti, N.; Ben Hamouda, M. Relationships among carcass composition and tail measurements in fat-tailed Barbarine sheep. Small Rumin. Res. 2004, 53, 151–155. [Google Scholar] [CrossRef]
- Bedhiaf-Romdhani, S.; Djemali, M. Estimation of sheep carcass traits by ultrasound technology. Livest. Sci. 2006, 101, 294–299. [Google Scholar] [CrossRef]
- Bedhiaf, S.; Abidi, S.; Atti, N.; Salem, H.; Ben Salem, M.; Lassoued, N.; Othmane, M. Caractérisation et Gestion des Ruminants Pour une Meilleure productivité: Un Demi-Siècle de Recherche Scientifique à l’INRAT. Annales de l’INRAT. 2013. Available online: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Caract%C3%A9risation+et+gestion+des+ruminants+pour+une+meilleure+productivit%C3%A9%3A+Un+demi-si%C3%A8cle+de+recherche+scientifique+%C3%A0+l%27INRAT&btnG= (accessed on 31 July 2017).
- Bedhiaf-Romdhani, S.; Djemali, M. New genetic parameters to exploit genetic variability in low input production systems. Livest. Sci. 2006, 99, 119–123. [Google Scholar] [CrossRef]
- Bedhiaf, S.; Jemmali, B.; Sassi, Y. Novel phenotype management using molecular characterization in Barbarine Prolific “W” sheep line raised under low input production system in Tunisia. In Proceedings of the Book of Abstracts of the 67th Annual Meeting of the European Federation of Animal Science, Belfast, UK, 29 August–2 September 2016. [Google Scholar] [CrossRef]
- Ben Gara, A. Définition des objectifs de la sélection des ovins de race Barbarine en Tunisie. In Analysis and Definition of the Objectives in Genetic Improvement Programmes in Sheep and Goats; An economic approach to increase their profitability; Gabiña, D., Ed.; Ciheam: Zaragoza, Spain, 2000; Volume 43, pp. 111–116. [Google Scholar]
- Wright, S. An Analysis of Variability in Number of Digits in an Inbred Strain of Guinea Pigs. Genetics 1934, 19, 506–536. [Google Scholar] [CrossRef]
- Matos, C.A.P.; Thomas, D.; Gianola, D.; Perez-Enciso, M.; Young, L. Genetic Analysis of Discrete Reproductive Traits in Sheep Using Linear and Nonlinear Models: II. Goodness of Fit and Predictive Ability. J. Anim. Sci. 1997, 75, 88–94. [Google Scholar] [CrossRef]
- Olesen, I.; Perez-Enciso, M.; Gianola, D.; Thomas, D. A comparison of normal and nonnormal mixed models for number lambs born in Norwegian sheep. J. Anim. Sci. 1994, 72, 1166–1173. [Google Scholar] [CrossRef]
- Ramírez-Valverde, R.; Misztal, I.; Bertrand, J.K. Comparison of threshold vs. linear and animal vs. sire models for predicting direct and maternal genetic effects on calving difficulty in beef cattle. J. Anim. Sci. 2001, 79, 333–338. [Google Scholar] [CrossRef]
- Moreno, C. Estudio de los Componentes Genéticos del Modelo Umbral. Ph.D. Thesis, Universidad de Zaragoza, Zaragoza, Spain, 1993. [Google Scholar]
- Ødegård, J.; Meuwissen, T.; Heringstad, B.; Madsen, P. A simple algorithm to estimate genetic variance in an animal threshold model using Bayesian inference. Genet. Sel. Evol. GSE 2010, 42, 29. [Google Scholar] [CrossRef]
- Warwick, B.L.; Cartwright, T.C. Adjustment of Milk Lamb Weaning Weights to a Standard Age. J. Anim. Sci. 1958, 17, 521–526. [Google Scholar] [CrossRef]
- Marschner, I. glm2: Fitting Generalized Linear Models with Convergence Problems. R J. 2011, 3, 12–15. [Google Scholar] [CrossRef]
- Notter, D.R. Genetic parameters for growth traits in Suffolk and Polypay sheep. Livest. Prod. Sci. 1998, 55, 205–213. [Google Scholar] [CrossRef]
- Sorensen, D.A.; Andersen, S.; Gianola, D.; Korsgaard, I. Bayesian inference in threshold models using Gibbs sampling. Genet. Sel. Evol. 1995, 27, 229. [Google Scholar] [CrossRef]
- Casellas, J.; Caja, G.; Ferret, A.; Piedrafita, J. Analysis of litter size and days to lambing in the Ripollesa ewe. I. Comparison of models with linear and threshold approaches. J. Anim. Sci. 2007, 85, 618–624. [Google Scholar] [CrossRef]
- Sorensen, D.; Gianola, D. Likelihood, Bayesian and MCMC Methods in Quantitative Genetics, 1st ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Legarra, A.; Varona, L.; Lopez de Maturana, E. Manual TM. Available online: https://snp.toulouse.inra.fr/~alegarra/manualtm.pdf (accessed on 31 July 2017).
- Djemali, M.; Aloulou, R.; Sassi, M.B. Adjustment factors and genetic and phenotypic parameters for growth traits of Barbarine lambs in Tunisia. Small Rumin. Res. 1994, 13, 41–47. [Google Scholar] [CrossRef]
- Lassoued, N.; Benkhlil, Z.; Woloszyn, F.; Rejeb, A.; Aouina, M.; Rekik, M.; Fabre, S.; Bedhiaf-Romdhani, S. FecX Bar a Novel BMP15 mutation responsible for prolificacy and female sterility in Tunisian Barbarine Sheep. BMC Genet. 2017, 18, 43. [Google Scholar] [CrossRef]
- Hamouda, M.B. Contrôle de croissance des ovins allaitants en Tunisie. i. ajustement d’une courbe globale et analyse critique du protocole officiel. Revue D’élevage Médecine Vétérinaire Pays Tropicaux 2012, 65, 31–39. [Google Scholar] [CrossRef]
- Safari, E.; Fogarty, N.; Gilmour, A.R. A review of genetic parameter estimates for wool, growth, meat and reproduction traits in sheep. Livest. Prod. Sci. 2005, 92, 271–289. [Google Scholar] [CrossRef]
- Boujenane, I. Productivity of Sardi, D’man and their crossbred ewes mated to terminal sires. Small Rumin. Res. 2012, 108, 22–27. [Google Scholar] [CrossRef]
- Mekkawy, W.; Roehe, R.; Lewis, R.M.; Davies, M.H.; Bünger, L.; Simm, G.; Haresign, W. Comparison of repeatability and multiple trait threshold models for litter size in sheep using observed and simulated data in Bayesian analyses. J. Anim. Breed. Genet. 2010, 127, 261–271. [Google Scholar] [CrossRef]
- Vazquez, A.I.; Weigel, K.A.; Gianola, D.; Bates, M.; Pérez-Cabal, M.; Rosa, G.; Chang, Y.M. Poisson versus threshold models for genetic analysis of clinical mastitis in US Holsteins. J. Dairy Sci. 2009, 92, 5239–5247. [Google Scholar] [CrossRef] [PubMed]
- Bedhiaf, S.; Bouix, J.; Clement, V.; Bibe, B.; François, D. Importance du choix du Modèles D’analyse dans L’estimation des Paramètres Génétiques de la Croissance des ovins à Viande en Tunisie. 2000. Available online: https://agris.fao.org/search/en/providers/122439/records/647472a3425ec3c088f2e6a4 (accessed on 15 April 2024).
- Robinson, D. Models which might explain negative correlations between direct and maternal genetic effects. Livest. Prod. Sci. 1996, 45, 111–122. [Google Scholar] [CrossRef]
- Barbosa, L.T.; Santos, G.d.B.; Muniz, E.N.; Azevedo, H.C.; Fagundes, J.L. Genetic parameters for growth traits of santa ines sheep using Gibbs sampling. Rev. Caatinga 2015, 28, 211–216. [Google Scholar] [CrossRef]
- Carvalho, G.; Barbosa, L.; Oliveira, T.; Fonseca, F.; Muniz, E.; Azevedo, H. Estimation of genetic parameters Santa Inês Sheep breed using single and two-traits models. Ciência Rural. 2014, 44, 111–116. [Google Scholar] [CrossRef]
- Aguirre, E.; Mattos, E.; Eler, J.; Barreto Neto, A.; Ferraz, J. Estimation of genetic parameters and genetic changes for growth characteristics of Santa Ines sheep. Genet. Mol. Res. 2016, 15, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Ziadi, C.; Bedhiaf-Romdhani, S. Genetic parameters of reproductive traits in a prolific «W» line. In Proceedings of the Barbarine Sheep. 69th Annual Meeting of the European Federation of Animal Science 2018, Dubrovnik, Croatia, 27–31 August 2018. [Google Scholar]
- El-Hentati, H.; Mhamdi, N.; Aloulou, R.; Hamouda, M.B.; Chriki, A. Estimates of Phenotypic and Genetic Parameters of weight productivity traits of Tunisian D’man ewes. Life Sci. J. 2013, 10, 4. [Google Scholar]
- Analla, M.; Serradilla, J.M. Estimation of correlations between ewe litter size and maternal effects on lamb weights in Merino sheep. Genet. Sel. Evol. 1998, 30, 493. [Google Scholar] [CrossRef]
- Norberg, E.; Berg, P.; Pedersen, J. Genetic parameters for birth weight, growth, and litter size in Nordic sheep breeds. Acta Agric. Scand. Sect. A 2005, 55, 123–127. [Google Scholar] [CrossRef]
- Hanford, K.J.; Van Vleck, L.D.; Snowder, G. Estimates of genetic parameters and genetic trend for reproduction, weight, and wool characteristics of Polypay sheep. Livest. Sci. 2006, 102, 72–82. [Google Scholar] [CrossRef]
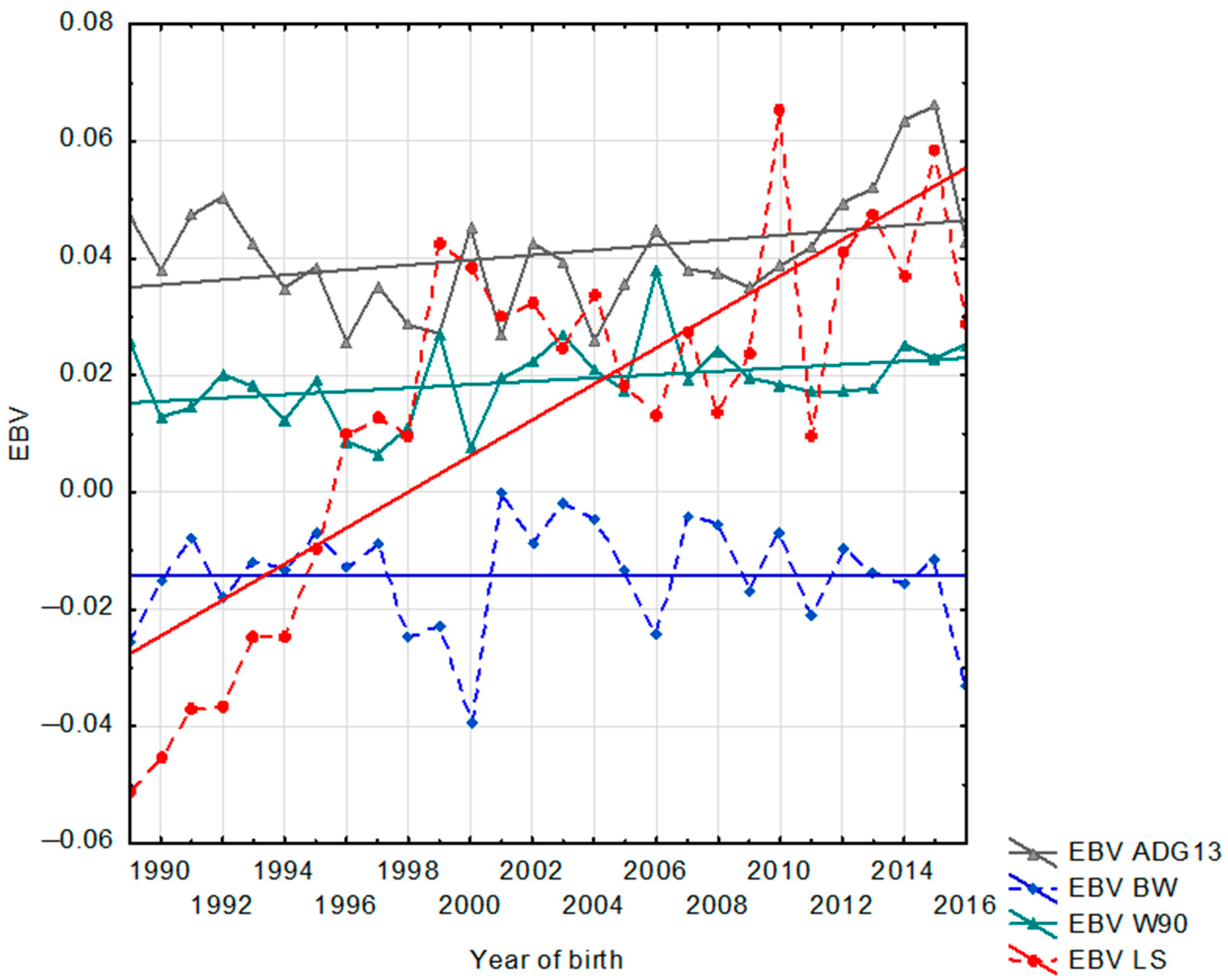
| Trait | n | Mean ± Sd | Minimum | Maximum | CV (%) |
|---|---|---|---|---|---|
| LS (n° of lambs) | 2725 | 1.56 ± 0.62 | 1.0 | 4.0 | 40.0 |
| BW (kg) | 3804 | 2.77 ± 0.55 | 1.50 | 4.10 | 19.9 |
| W90 (kg) | 3066 | 14.8 ± 3.87 | 4.97 | 26.47 | 26.1 |
| ADG13 (g) | 3090 | 135.1 ± 54.38 | 0.90 | 332.72 | 40.2 |
| Trait | |||||
|---|---|---|---|---|---|
| Parameter | LS a | LS b | BW | W90 | ADG13 |
| 0.03 (0.01) | 0.06 (0.02) | 0.04 (0.01) | 0.31 (0.24) | 89.62 (61.98) | |
| - | - | 0.02 (0.008) | 1.17 (0.51) | 252.03 (95.29) | |
| - | - | −0.02 (0.008) | −0.25 (0.28) | −86.43 (63.53) | |
| - | - | −0.86 (0.008) | −0.45 (0.029) | −0.66 (0.027) | |
| 0.025 (0.01) | 0.04 (0.01) | 0.04 (0.005) | 0.64 (0.26) | 144.30 (56.62) | |
| 0.29 (0.009) | 0.30 (0.01) | 0.14 (0.007) | 6.29 (0.23) | 1526.16 (57.94) | |
| Trait | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | LS a | LS b | BW a | BW b | W90 a | W90 b | ADG13 a | ADG13 b |
| 0.06 (0.01) | 0.06 (0.01) | 0.05 (0.01) | 0.04 (0.01) | 0.21 (0.17) | 0.11 (0.16) | 120.02 (65.78) | 109.73 (58.99) | |
| - | - | 0.025 (0.01) | 0.017 (0.007) | 1.40 (0.45) | 1.44 (0.42) | 298.46 (120.8) | 275.15 (103.32) | |
| - | - | −0.024 (0.009) | −0.018 (0.006) | −0.25 (0.29) | −0.17 (0.22) | −131.75 (83.42) | −123.38 (57.70) | |
| - | - | −0.74 (0.016) | −0.75 (0.012) | −0.57 (0.055) | −0.32 (0.054) | −0.76 (0.031) | −0.80 (0.024) | |
| 0.12 (0.01) | 0.18 (0.01) | 0.06 (0.007) | 0.06 (0.007) | 1.00 (0.31) | 1.13 (0.30) | 253.84 (74.78) | 326.19 (78.29) | |
| 0.21 (0.008) | 0.14 (0.009) | 0.16 (0.008) | 0.16 (0.008) | 6.79 (0.24) | 6.95 (0.26) | 1583.50 (61.25) | 1604.76 (62.06) | |
| h2 | r | |||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | Median | HPD95% | P | k | MCse | Median | HPD95% | MCse |
| LSlinear | 0.08 | 0.03, 0.15 | 0.37 | 0.04 | 0.00096 | 0.16 | 0.11, 0.20 | 0.00036 |
| LSthreshold | 0.14 | 0.05, 0.24 | 0.81 | 0.06 | 0.00167 | 0.24 | 0.18, 0.32 | 0.0006 |
| BWd | 0.18 | 0.07, 0.32 | 0.95 | 0.10 | 0.003 | 0.25 * | 0.20, 0.30 | 0.00088 |
| BWm | 0.07 | 0.009, 0.17 | 0.31 | 0.02 | 0.00285 | |||
| W90d | 0.03 | 0.00, 0.10 | 0.06 | 0.006 | 0.00168 | 0.20 * | 0.14, 0.26 | 0.00103 |
| W90m | 0.14 | 0.02, 0.26 | 0.75 | 0.04 | 0.00347 | |||
| ADG13d | 0.04 | 0.001, 0.11 | 0.09 | 0.007 | 0.00225 | 0.17 * | 0.13, 0.23 | 0.00073 |
| ADG13m | 0.13 | 0.04, 0.23 | 0.74 | 0.05 | 0.00265 | |||
| h2 | r | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Median | HPD95% | P | k | MCse | Median | HPD95% | MCse | |
| Linear | LS | 0.14 | 0.09, 0.20 | 0.95 | 0.10 | 0.00251 | 0.46 | 0.41, 0.51 | 0.00204 |
| BWd | 0.20 | 0.10, 0.27 | 0.98 | 0.11 | 0.00482 | 0.29 * | 0.24, 0.35 | 0.00226 | |
| BWm | 0.09 | 0.03, 0.19 | 0.45 | 0.03 | 0.00652 | ||||
| W90d | 0.02 | 0.00, 0.06 | 0.00 | 0.001 | 0.00211 | 0.24 * | 0.19, 0.30 | 0.0009 | |
| W90m | 0.15 | 0.06, 0.26 | 0.88 | 0.08 | 0.00367 | ||||
| ADG13d | 0.05 | 0.007, 0.11 | 0.18 | 0.01 | 0.00372 | 0.22 * | 0.17, 0.28 | 0.00145 | |
| ADG13m | 0.14 | 0.04, 0.27 | 0.76 | 0.05 | 0.00633 | ||||
| Threshold | LS | 0.15 | 0.09, 0.20 | 0.97 | 0.10 | 0.00258 | 0.62 | 0.56, 0.68 | 0.00172 |
| BWd | 0.13 | 0.08, 0.24 | 0.93 | 0.09 | 0.00374 | 0.29 * | 0.24, 0.33 | 0.00114 | |
| BWm | 0.06 | 0.02, 0.13 | 0.16 | 0.02 | 0.00295 | ||||
| W90d | 0.001 | 0.001, 0.03 | 0.00 | 0.001 | 0.00198 | 0.25 * | 0.20, 0.30 | 0.00167 | |
| W90m | 0.15 | 0.05, 0.24 | 0.87 | 0.06 | 0.00556 | ||||
| ADG13d | 0.05 | 0.006, 0.10 | 0.06 | 0.01 | 0.0025 | 0.24 * | 0.18, 0.29 | 0.00138 | |
| ADG13m | 0.12 | 0.05, 0.23 | 0.73 | 0.06 | 0.00436 | ||||
| Trait | Median | HPD95% | P | k | MCse | |
|---|---|---|---|---|---|---|
| Linear | LS, BW | −0.52 | −0.58, −0.46 | 1.00 | −0.57 | 0.00218 |
| LS, W90 | −0.38 | −0.44, −0.31 | 1.00 | −0.43 | 0.00124 | |
| LS, ADG13 | −0.34 | −0.42, −0.27 | 1.00 | −0.41 | 0.0021 | |
| Threshold | LS, BW | −0.60 | −0.65, −0.55 | 1.00 | −0.64 | 0.00112 |
| LS, W90 | −0.47 | −0.53, −0.40 | 1.00 | −0.52 | 0.00167 | |
| LS, ADG13 | −0.44 | −0.52, −0.36 | 1.00 | −0.51 | 0.00227 |
| Trait | Median | HPD95% | P | k | MCse | |
|---|---|---|---|---|---|---|
| Linear | LS, BW | −0.18 | −0.50, 0.13 | 0.09 | −0.45 | 0.01585 |
| LS, W90 | −0.49 | −0.99, 0.47 | 0.19 | −0.92 | 0.04214 | |
| LS, ADG13 | −0.53 | −0.91, 0.01 | 0.05 | −0.85 | 0.02072 | |
| Threshold | LS, BW | −0.24 | −0.53, 0.12 | 0.08 | −0.45 | 0.01154 |
| LS, W90 | −0.83 | −0.99, −0.37 | 0.00 | −0.99 | 0.02824 | |
| LS, ADG13 | −0.42 | −0.90, 0.13 | 0.09 | −0.82 | 0.0239 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziadi, C.; Bedhiaf-Romdhani, S.; Molina, A. Estimation of Genetic Parameters for Litter Size and Growth Traits in a Prolific Line of Tunisian Barbarine Sheep. Ruminants 2024, 4, 256-266. https://doi.org/10.3390/ruminants4020018
Ziadi C, Bedhiaf-Romdhani S, Molina A. Estimation of Genetic Parameters for Litter Size and Growth Traits in a Prolific Line of Tunisian Barbarine Sheep. Ruminants. 2024; 4(2):256-266. https://doi.org/10.3390/ruminants4020018
Chicago/Turabian StyleZiadi, Chiraz, Sonia Bedhiaf-Romdhani, and Antonio Molina. 2024. "Estimation of Genetic Parameters for Litter Size and Growth Traits in a Prolific Line of Tunisian Barbarine Sheep" Ruminants 4, no. 2: 256-266. https://doi.org/10.3390/ruminants4020018
APA StyleZiadi, C., Bedhiaf-Romdhani, S., & Molina, A. (2024). Estimation of Genetic Parameters for Litter Size and Growth Traits in a Prolific Line of Tunisian Barbarine Sheep. Ruminants, 4(2), 256-266. https://doi.org/10.3390/ruminants4020018





