Abstract
This article reviews the electrodynamic force law of Wilhelm Weber and its importance in electromagnetic theory. An introduction is given to Weber’s force and it is shown how it has been utilised in the literature to explain electromagnetism as well as phenomena in other disciplines of physics, where the force law has connections to the nuclear force, gravity, cosmology, inertia and quantum mechanics. Further, criticism of Weber’s force is reviewed and common misconceptions addressed and rectified. It is found that, while the theory is not without criticism and has much room for improvement, within the limitations of its validity, it is equally as successful as Maxwell’s theory in predicting certain phenomena. Moreover, it is discussed how Weber offers a valid alternative explanation of electromagnetic phenomena which can enrich and complement the field perspective of electromagnetism through a particle based approach.
1. Introduction
Wilhelm E. Weber formulated a generalised electrodynamic force law that was first published in 1846, only a few years prior to Maxwell’s first works on electromagnetism. However, Weber’s direct-action-at-a-distance theory is little known today and often dismissed a priori and without further thought in the scientific community, on the basis that it is old and superseded or taken as disproven. Whilst there are historic reasons that led to the dismissal of Weber’s theory and the success of Maxwell-Lorentz field theory, there seems to be some common misconceptions surrounding the theories and the existing criticism.
This manuscript aims to give a balanced and comprehensive review about Weber’s theory and show that it’s dismissal is premature. Criticism will be reviewed and refuted where appropriate, and for the sake of context it will be shown that field theory is not without criticism either. After analysing the achievements of Weber’s electrodynamics through its use in the literature and how it has been applied not only to electromagnetism, but several branches of physics, it will eventually be shown that both electromagnetic theories have great commonalities and they can be regarded as complementary rather than competing. Weber is shown to provide a viable alternative description of electrodynamics, and whilst it is not without limitations and has bounds of validity, as will be discussed, it is argued that neither theory is perfect and that their similarities far outweigh their differences.
Some have commented that the current state of physics is in a crisis, and that “new physics” is required to resolve current puzzles in particle physics and supersymmetry [1,2,3,4]. However, it may be possible that a re-examination of the foundations (i.e., electrodynamics in this case) can lead to new perspectives and insight which may guide and inform new solutions. It is argued that further pursuit and research of Weber electrodynamics can offer epistemological, physical and practical value.
2. Fundamentals of Weber’s Theory
Weber’s electrodynamic force is introduced to provide a mathematical overview and to familiarise the reader with Weber’s direct-action approach as an explanation for electricity and magnetism. Weber’s force describes the interaction of two point charges and was postulated before the electron was even discovered. Hence, it was originally based on Fechner’s hypothesis that a current consists of equal amounts of positive and negative charges moving in opposite directions, which was the conventional wisdom at the time, as scientists imagined so called “electrical fluidae” moving through wires and circuits when subjected to electromotive forces. Fechner’s hypothesis will be addressed separately (see Section 3.3) and it shall be noted that Weber’s theory can still be used when we assume that only electrons are charge carriers in motion responsible for conduction currents in circuits. With this restriction lifted we can now explain the general workings of Weber’s theory.
First, let us consider two charged particles, and , in a Cartesian coordinate system , at their respective positions and (see Figure 1).
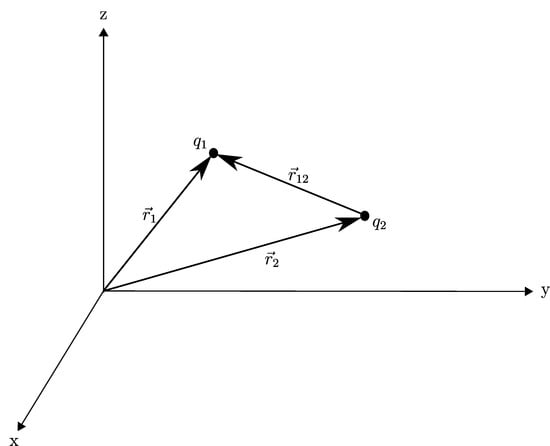
Figure 1.
Two charged particles and in a Cartesian coordinate system at positions and . Their relative position is a vector pointing from to .
The position of these particles, which are time dependent spatial coordinates, can be expressed by
where we have the unit vectors:
Their relative position is the difference between and :
and a distance given by the magnitude of
With this, the unit vector along can be defined as
and both as well as are pointing from to . The relative velocity and relative acceleration between the two charges can be calculated as first and second time derivatives of the relative position, Equations (6) and (7), respectively:
To arrive at the time derivative of the chain rule is utilised:
By analogy, the same procedure can be applied to arrive at the second time derivative, or the quotient and product rule along with the substitutions , , can be used:
With the help of these definitions, we can now examine Weber’s potential between the charges in question which will eventually lead us to Weber’s force. It was two years after Weber introduced his force law that he succeeded in showing that it could be derived from a potential, and this takes the form:
To arrive at the force, the principle of virtual work is invoked which states
(Note that the principle of virtual work by definition depends on a time dependent trajectory.) Now applying Equation (12) to (11) gives Weber’s force law in the following way:
where again the chain rule is necessary to derive the expression correctly,
We can see in (13) different notations of Weber’s force, for example, we can simply write the time derivatives indicated as dots, noting
Similarly, the following form can more readily be used to substitute quantities, which is especially handy when investigating the interaction between charge carriers for a given experiment or apparatus, for example:
We can see from these derivations that the force depends on the relative position, velocity and acceleration of the particles involved. The force is along the line joining them and follows Newton’s third law in the strong form, that is every action has an equal and opposite reaction. Furthermore, conservation of energy as well as conservation of linear and angular momentum are followed by this law. Additionally the principle of superposition applies to this force law, similar to the superposition principle with electric and magnetic fields of Maxwellian field theory.
Other formulations of Weber’s force formula exist in the literature, as will be discussed in Section 3.2.1, it has been shown that Weber can be formulated to incorporate electromagnetic fields [5,6,7,8,9] and especially in [8] the field-based Weber force is formulated with focus on the relation between source and test charges and how they define current elements and densities. Further, Hamiltonian and Lagrangian formulations of the force law have been obtained [6,10] and expressions like this have occasionally been used in the literature [11,12,13].
3. Literature Review
3.1. Two Different Theories of Electrodynamics
Historically, many scientists have worked on electrodynamics and electromagnetic phenomena, performing a wide range of experiments to investigate the nature of electricity and magnetism. From these experiments researchers have developed a multitude of hypotheses, laws and eventually attempted to merge them into cohesive theories, leading to several attempts to explain electrodynamics, some of them more successful than others. Many alternative theories have been proposed over the years with important contributions from several scientists. Some examples include Gauss, Neumann, Lorentz, Riemann, Weber, Helmholtz, Hertz, Ritz, Moon & Spencer, and Wheeler-Feynman direct-action theory, amongst others (see Appendix B of [6], also [14,15,16,17,18,19,20,21]).
In this section, some brief comments will be first given on the established theory of fields and ether by Maxwell, which forms the foundation of modern science and technological inventions, from particle accelerators to modern medical instrumentation. Following this, we will introduce Weber’s force law in the context of its development before engaging with the wider literature relating to its development and application.
3.1.1. Maxwell’s Equations and Field Theory
When James Clerk Maxwell presented his magnum opus on electromagnetic theory [22] in 1873, he formulated his ideas about the action of electric and magnetic fields partly in prose and partly as mathematical descriptions and equations he introduced. These can be summarised in the concise form of only four equations as widely disseminated in modern times [23]. The differential forms of Maxwell’s equations in a vacuum and in SI-units are commonly given as:
Here, is the local charge density, and are the vacuum permittivity and permeability and is the current density. and are the electric and magnetic field, respectively, through which charged particles interact, meaning contact-action where a particle always interacts with the field as a medium and the fields themselves can interact, as for example in the transmission of electromagnetic waves.
Equation (17) is Gauss’s law, which relates the electric field with the charge density, (18) is the law of non-existence of magnetic monopoles, (19) is the Maxwell-Faraday equation that expresses induction, and (20) is the Maxwell-Ampère equation that correlates currents and time-varying electric fields to magnetic fields, which is also a form of induction. Due to the time-dependent nature of (19) and (20) electromagnetic waves can be predicted, while Maxwell’s approach is originally based on the ether through which electromotive forces and waves would propagate, from today’s point of view the fields themselves have effectively replaced the ether as the dominant medium and are now considered to be responsible for interaction transmission. The ether as an original construct is largely and effectively ignored.
Further to the field equations, the Biot-Savart law is formulated to obtain the magnetic field for a current element integrated along a closed circuit path
where is a current element and r is the distance from to the point where the field is evaluated and is the corresponding unit vector. For forces between two current elements, Grassmann’s force is normally utilised based on the Biot-Savart law,
For any charged particle q in more general situations moving in the presence of electric and magnetic fields the interaction is usually given by the Lorentz force:
In general, field theory and Maxwell’s equations are a ‘macroscopic’ approach as they were developed from a continuous medium model (the ether). However, as we will see in the following section, Weber’s force is ‘microscopic’ in that sense as it describes the interaction between two charged particles in its standard form. For a better comparison between Maxwell’s and Weber’s theory, Assis shows the derived force between two point charges from field theory [24] up to second order in based on the work of Liénard, Wiechert and Schwarzschild, which was first obtained by O’Rahilly [25] as
In this formula is the test charge and is the source charge generating the fields and , where according to Assis time retardation, radiation and relativistic effects have been included. The constant c is the speed of light and denotes the acceleration of the point charge. It is apparent that the expression depends on the square of the source charge velocity and on its acceleration, whereas Weber’s force depends on the relative velocity and acceleration, as will be seen in Section 3.1.2. Assis also shows how this expression can be obtained from the Darwin Lagrangian ([6], Section 6.8), as the Darwin Lagrangian is more widely used in the literature to describe systems of point charges [26,27,28]. Both the Schwarzschild force (24) and Lorentz force (23) have been criticised as violating conservation of linear and angular momentum. To restore conservation it is usually argued that the energy is lost or gained by the electromagnetic field generated by the charges or that self force needs to be taken into account [29,30]. However, a system of two point charges seems extremely difficult to test. The general applicability (or non-applicability) of Newton’s third law to the Lorentz force and generally in electrodynamics has been discussed in [31,32,33]. Cornille [32] also claims that if the electrodynamic force laws indeed violate Newton’s third law, then it inevitably leads to the conclusion that energy can be extracted from the ether, as the ether exerts a force that is responsible for the violation.
It has further been criticised that the velocity in the Lorentz force formula (23) is not clearly defined, that is what it is defined with respect to, was not even given by Lorentz himself [6,34]. It thus remains ambiguous if the definition is w.r.t a coordinate system or a source charge, which might itself be moving, although there seems to be support to the idea that Lorentz viewed the velocity as relative to the ether [6,34]. However, in relativistic treatments this is usually resolved by a chosen inertial frame of reference and regarding the velocity relative to the measuring device or observer.
In an interesting review about Maxwell’s equations and the field approach Tran [35] concludes that there are only few experiments supporting the Maxwell-Ampère and Maxwell-Faraday equation, at least not to the same degree of accuracy that the continuity equation and the magnetic law are supported. There is further discussion about conceptual problems in classic electromagnetism and modern particle-field theories in the literature [36,37]. This mainly focuses on the problem of point charges and their diverging self-energy, as the calculated energy of an electron with its own field tends to infinity based on classic electromagnetism. One solution is the renormalisation approach in the quantum theory of Dirac where the point charge is treated as a singularity and the infinite energy is subtracted as a constant from the problem to renormalise the energy content. The other solution is the extended particle model, where elementary charges are not treated as point-like anymore and consequently the divergence in the singularity disappears. Pietsch [36] discusses both approaches and the associated cost of the proposed solutions, and for an interesting discussion of these approaches including a mathematical perspective, see [38], on which Pietsch bases their arguments. Pietsch then argues that both approaches are incompatible at a fundamental level and a better solution is needed, in which direct-action theories are proposed. Lazarovici [37] also discusses the self-energy problem and the Lorentz-Dirac as well as the extended particle solutions as unsatisfactory, but also involves free fields, among other philosophical, mathematical and physical arguments, and proposes the Wheeler-Feynman direct-action theory in particular as a solution to those problems. The renormalisation approach has also been criticised by other authors [39], including Feynman [40] and Dirac [41]. A similar argument has been made by Kastner about the Wheeler-Feynman direct-action theory, not only does it avoid self-energy problems, it is also not subject to Haag’s theorem and the consequent problems of free and interacting fields in quantum field theory (QFT) [42].
This concludes the brief overview of field theory and Maxwell’s equations and further reading where fields, waves, radiation and relativity are treated can be found in the works of other authors [26,43,44,45,46].
3.1.2. Weber’s Theory of Electrodynamics
Wilhelm Eduard Weber first published his force law to describe the interaction of charged particles in 1846, some 15 years before Maxwell published his first work on electromagnetism, ‘On physical lines of force’ [47], a concept which would only tangentially relate to the field concept later introduced in Maxwell’s Treatise [23]. Maxwell, as a contemporary of Weber, was well aware of his work and Maxwell positively mentions Weber in his Treatise, expressing admiration for Weber’s work. As a 19th century scientist, Weber engaged with several physical disciplines, but a collection of his original work on electrodynamics can be found in [48,49] and English translations of his eight major memoirs on electromagnetism can be found in [50,51,52,53,54,55,56,57].
The main difference between Weber’s theory and Maxwell’s field equations is that Weber’s is a direct-action-at-a-distance theory, such as Newton’s law of gravity or Coulomb’s force of electrostatic interaction, and the fields themselves are not conceptualised as a primary part of the mathematical description. Instead, Weber’s force depends on the direct interaction and force transmission between charges themselves, as opposed to contact action in field theory, where the charges give rise to fields so a source charge and a test charge only interact with the field of the other. Some aspects of how fields can still be conceived with Weber will be discussed later in Section 3.2.
In modern vector notation and SI units, Weber’s force can be expressed as
When Weber developed his force, the aim was to connect Coulomb’s force and Ampère’s force, arriving at a more general interaction law. Weber’s force acts along the line joining two interacting point charges, following Newton’s third law in the strong form with equal action and reaction, conserving linear and angular momentum. It depends only on the relative distance, relative velocity and relative acceleration of the interacting charges.
As this force is electrodynamic in nature, it contains electrostatic (i.e., Coulomb’s force) and magnetic (i.e., Ampère’s force) interactions, which is comparable with the Lorentz force (23) where a static (i.e., the electric field term) and a moving component (i.e., the magnetic field term) of the force are considered. The speed of light c in (15) was introduced as the ratio between electrostatic and electromagnetic units of charge, whose value was first determined experimentally in 1856 (10 years later) by Weber and Kohlrausch based on Weber’s force. In 1848, two years after the presentation of the force law, Weber also showed that the force can be derived from a velocity dependent potential, as shown in Section 2.
A further analysis of the capabilities of Weber’s theory will follow in Section 3.2 and the theory has undergone more development in recent decades. It is noteworthy that predominantly in the low velocity limit, Weber and Maxwell theory predict very similar results, if not the same results for a given phenomenon. Weber has also been shown to be consistent with field equations by a number of authors and the matter will be further addressed in Section 3.2.1.
However, it must be stressed, Weber’s electrodynamic theory has not yet been developed to anywhere near the same degree that other theories have, which includes the high velocity regime near the speed of light where the theory has problems. When quantum interactions are considered, the Wheeler-Feynmann approach to direct-action has undergone development by Davies who introduced a quantum theory based on Wheeler-Feynman electrodynamics [58]. In the case of Weber, only some initial connections between Weber’s theory and quantum mechanics have been made, as will be seen in Section 3.2.2, however, a rigorous treatment is yet to be developed. This is considered a work in progress and further research is needed before any conclusions can be drawn about Weber’s theory in the quantum realm.
3.2. Weber Electrodynamics in the Literature
After Maxwell’s success in the late 19th and early 20th century, Weber’s electrodynamic force law has not received a lot of attention except from a few, with important contributions from O’Rahilly [25], Wesley [9,59,60], Assis [6] and others. Over the years, many connections have been made from Weber’s theory of electrodynamics to different topics within physics, while Weber’s force is electromagnetic in nature and has been used to describe phenomena in that field, it is also shown to interconnect with mechanics, the structure of the atom, gravity, quantum mechanics and even some effects of general relativity theory (GRT) and topics that are usually referred to as “breakthrough physics”. A visual overview of the relations Weber has with electromagnetics and other disciplines can be seen in Figure 2.
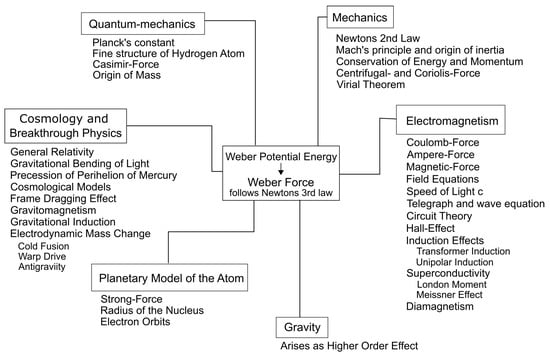
Figure 2.
A visual map providing an overview of the different subsidiary fields and phenomena that Weber’s theory has been shown to provide a basis for and connects with throughout the branches of physics and engineering.
3.2.1. Electromagnetic Phenomena
As Weber is essentially a theory of electrodynamics, it has been shown to explain many pure and applied phenomena in electricity and magnetism. From its basic form (15), it is easy to see that Weber’s force reduces to the Coulomb force for stationary charges. That means for static charges where their velocities are zero, the formula can be simplified to
Thus, Weber can be readily seen to describe purely electrostatic interactions. When interacting charges start moving, the force then changes, and for two current elements in a circuit Ampère’s force can be derived from Weber’s force as shown by Assis [61]. For two steady current elements and this takes the form:
Grassmann’s force (22) from Section 3.1.1, for comparison, is slightly different in its interaction. Assis’ extensive analysis indicates the similarities and differences between Ampère’s and Grassmann’s forces [6] and most notably shows, that Grassmann’s force violates Newton’s third law. However, it has been claimed that, when the respective force expressions are applied to any closed circuit, they are equivalent and lead to the same result [62]. There has been a discussion in the literature about which force is the correct one. For example, a paper by Cavalleri [63] claims that Grassmann’s force gives the correct result for any given circuit and Ampère’s does not; but as Assis commented in response [64], they did not consider all contributions of Ampère’s force in their deductions and when carried out, both models predict the same force values [62,65]. This inevitably leads to the conclusion that it is impossible to distinguish between the two forces for any closed circuit, which has been verified for several configurations [66,67].
In this context, it seems adequate to briefly discuss the Ampère force and note its importance, as even Maxwell himself stated that it must remain the cornerstone of electrodynamics. The divide in the literature between Ampère’s vs. Grassmann’s force seems to stem from the nature of the Ampère force, which includes a longitudinal force component along the wire in the direction of movement of the current elements. This feature complies with Newton’s third law but appears to be incompatible with the Lorentz force, whereas Grassmann’s force for current elements does not include a longitudinal component and is in turn compatible with the Lorentz force, but violates Newton’s third law. When Ampère conducted his original experiments, investigating the force between two wires [68,69,70,71], he found his force law as a result of these experiments and made sure to include the longitudinal component according to his observations. Further to the discussions about the general applicability of Newton’s third law in electrodynamics [31,32], Chaib and Lima [72] have re-iterated that Ampère did not find any evidence in his experiments that would contradict Newton’s third law and that it remains applicable in electrodynamics. They also clarify that Ampère regarded the third law as a consequence of his experiments, rather than an assumption he tried to conform to, and explain his philosophical reasoning in arriving at that conclusion. The authors of [72] also give a review of some of Ampère’s main work in the manuscript and show that Ampère was the first to obtain an expression similar to the Biot-Savart law from his experiments.
This special quality of the Ampère force to incorporate longitudinal forces has sparked the interest of researchers and in modern times more experiments have been performed to investigate it, where the force has also been connected to a variety of effects and applications. In particular Graneau et al. have investigated Ampère’s force [73,74,75,76,77,78,79,80,81,82], including water jet propulsion, exploding wires, fusion and railguns, as well as the electromagnetic impulse pendulum, liquid mercury experiments (e.g., Ampère’s bridge) and homopolar motors [83,84,85,86,87,88,89,90,91,92]. Even though the exploding wire phenomenon has been investigated further [93,94] and the longitudinal Ampère force component does not seem responsible for the bursting of wires, it is still important in other situations. For example, the importance of Ampère’s force to induction in general has been discussed along with the ability of the force to explain EM-waves in the near field [95]. A classical approach to derive longitudinal forces has been taken by Rambaut and Vigier [96], where they find longitudinal forces as an average effect of conduction electrons and lattice charges of a current element. In a follow-up paper [97] the authors then derive longitudinal forces with a different approach based on the Liénard-Wiechert potentials and discuss their influence on conductors in all phases, including plasmas and fusion applications. Recently Moyssides also succeeded in deriving longitudinal forces with the help of the Biot-Savart-Grassmann-Lorentz force law acting on a submarine projectile in mercury, showing that both forces are equivalent and both agree with experimental results presented in the paper [98]. Further experiments to detect longitudinal forces have been performed by Saumont [99], where difficulties in measurements of these forces due to thermal effects and rapid spurious forces are also addressed and the compatibility of longitudinal tensile forces with relativity theory and the Lorentz force is considered. An experiment by Graneau et al. [100] has investigated longitudinal forces utilising spark gaps in a circuit and found them consistent with Ampère’s force, which has been interpreted as a direct proof of the existence of longitudinal forces. A new experiment has recently investigated how the charges in a neon glow lamp are influenced in the near field of a capacitor dependent on the signal frequency [101]. It was found that there is a longitudinal force component on the charges moving in the plasma that agrees with predictions of a Weber-Ampère model calculated in the paper. We can deduce from this brief analysis that longitudinal forces appear in both classic and Weber approaches which shows the similarity of the two theories.
Moving on from current elements, Weber’s force in the general form (15) is a force between point charges and depends on the relative velocity between them, it is intrinsically electromagnetic in nature and so incorporates magnetic interaction by design. The magnetic force naturally arises from the movement of the charges, whereas the Lorentz force (23) is usually derived by considering special relativity theory (SRT) or Lorentz transformation of the Coulomb Force or electric field [46,102,103,104] and magnetism is considered to arise as a relativistic effect in this context. However, recently it has also been suggested that it may not be necessary to treat magnetism as a consequence of SRT and instead Maxwell’s equations can be derived from Coulomb’s force and time retardation without any further assumptions [105]. In Weber electrodynamics however, the intrinsic velocity dependence of the force can be used in combination with the concept of current elements to calculate magnetic interaction forces, such as has been applied to the fields of solenoids [106,107,108,109]. Specifically in the case of the magnetic field of a long straight wire [107] the Lorentz and Weber force on a charged particle have been found to be identical in the low velocity limit.
Further to the similarities between Ampère’s and Grassmann’s force as well as the Weber and the Lorentz force, Weber has been shown to be consistent with Maxwell’s field equations by a number of authors [5,6,8,9,110,111], even though it does not conceptually depend on them. For example, Wesley [9] derives field equations from Weber by introducing charge densities and current densities into Weber’s equation and integrates over a fixed volume. He arrives at the form
with
The primed quantities in this formula are sources acting on the unprimed test currents and charges separated by distance R. It is especially interesting that in addition to the usual electric potential and magnetic potential two new potentials, and appear and Wesley points out that the Lorentz force and Maxwell’s equations are a special case where only the first three terms on the left hand side of (27) appear. Wesley further argues that the representations through a force equation and field expression are mathematically isomorphic as long as the fields are intermediate without time retardation. However, when time retardation is introduced into (27), the field expressions then contain wave equations with velocity c.
While Assis [6] and Kinzer [5] have taken a similar approach to Wesley, starting from Weber’s formula and deriving the field equations from it, the opposite approach, starting from Maxwell’s equation and arriving at a Weber-type formulation, does also exist [8]. With extensive mathematical work the author of [8] shows that there are two implicit restrictions in Maxwell’s field equations and without these restrictions a set of Weber equations can be obtained. One limitation is the condition that the charge density function is a constant in time and the other is that the test charge velocity is required to be zero for mathematical consistency according to the author of [8]. The procedure of removing the restrictions from Maxwell’s field theory is then to allow for moving test charges and time varying charge densities, which emphasises Wesley’s argument that Maxwell’s equations are a special case of Weber’s law. Another important opposite approach has also been discussed where Weber’s and Ampère’s forces are obtained as a non-relativistic limit from the Liénard-Wichert potentials [97] and from a Fermi distribution of accelerated charges [112]. In the recent approach of Li [110] a field representation of Weber’s force is developed with the help of Einstein notation, where the velocity and acceleration dependent terms in Weber’s force can then each be identified with a respective Tensor field. Li states that this approach has the advantage of simplifying the necessary calculations in systems of many particles, reducing the number of required force calculations.
One of the strengths that is usually ascribed to Maxwell’s field equations is that the velocity of light appears from the wave equations as does the relation between permittivity and . However, it was not Maxwell who first discovered the relation between the speed of light c and electromagnetic waves, in fact it was Weber and Kohlrausch who first predicted the value of c from Weber’s equation and confirmed it experimentally [113,114]. Following this, Weber and Kirchhoff derived the telegraph equation for the propagation of electromagnetic signals through a wire independently of each other, and Assis has provided a modern derivation and analysis of the telegraph equation in this context [115,116,117]. This equation also reduces to a regular wave equation when the resistance of the wire goes to zero. Fukai [118] has further argued that modern views of the vacuum can be assumed, where the vacuum behaves as a medium with inductance and capacitance, similar to a coaxial cable or transmission line problem, Weber’s theory predicts a signal propagation at light velocity in vacuum and thus should be able to predict radiation as well.
In relation to circuit theory, Assis [119] has analysed the self inductance of circuits with the help of Weber’s force and Newton’s second law and compared them to similar derivations based on the Lorentz force and the Liénard-Schwarzschild force for circuits. He manages to derive the self inductance from Weber’s force by examining the acceleration that conductor charges will be subjected to. The result can be interpreted as an effective mass of the conduction electrons in the circuit, with the positive lattice ions opposing the motion of the accelerated electrons. In a further study [120] Assis and Bueno also show that the self inductance formulae for a single circuit of Weber and Maxwell are equivalent. This has added to the previously known fact that the mutual inductance formulae were the same, however when a single circuit is considered, the equivalence can be obtained by considering surface charge or volume charge elements instead of line charge elements. Weber himself also worked on circuit resistances [49], conducting many experiments to investigate their resistive behaviour and considered the derivation of an absolute unit of resistance based on his force law.
A possible derivation of the Hall effect from Weber’s force has been investigated by McDonald [121] and it is deduced that, under the condition that only negative charges are assumed to be charge carriers in Weber’s theory, and disregarding the original Fechner hypothesis, Weber does predict the Hall effect consistent with the Lorentz force derivation. Based on this assumption the Hall effect cannot distinguish between the two forces, as they are equivalent in this particular case. The Fechner hypothesis itself will be further discussed in Section 3.3.
In addition to self inductance and the generation of a Hall voltage, Weber’s theory has also been applied to voltages arising through induction. Smith et al. [122,123] have developed a model for transformer induction with the assumption of conduction electrons following accelerated motion. They arrive at an expression identical to Faraday’s law and predict voltages in receiver coils correctly. Maxwell even pointed out in his Treatise [22] that it is possible to derive Faraday’s law from Weber’s law, as Weber derived it himself from his force, and Wesley has also indicated the connection between Faraday’s law and Weber’s, besides consideration of induction in general [9,59].
Unipolar induction (also called homopolar induction), as another example, has been analysed by Assis [124] on the basis of Weber electrodynamics. He arrives at the conclusion that the phenomenon can only be predicted correctly if the closing wire is included in the analysis, thus considering the whole circuit that is influenced by the presence of a magnet in a Faraday generator setup. Recently, unipolar induction experiments have been found to be consistent with Weber electrodynamics [125,126] There are also recent claims in the literature [127] that not all observed induction effects can be explained by Faraday’s law or the flux cutting rule, mentioning Weber as a possible fuller explanation. Assis has even presented an analysis [128] where he explores beyond the regular scope of unipolar induction and describes a situation where an additional voltage is induced due to the presence of an electrostatic potential, calling it Weberian induction. In this scenario a spinning disk is placed inside a charged spherical shell, with or without the magnet. From the perspective of field theory and the Lorentz force, the charge on the shell cannot induce a voltage in the disk due to the absence of a field inside the shell, but in Weber’s electrodynamics the charge on the shell would still exert a force on the disk charges and an additional voltage should be induced. However, such an effect would be many orders of magnitude smaller than regular unipolar induction. This field-free electrostatic force is closely related to a criticism of Weber’s theory and will be further discussed in Section 3.2.3 and Section 3.3.
Related to unipolar induction is the so-called Feynman disk paradox [129], where metal spheres are mounted on a plastic disk free to rotate and a current carrying coil is situated on the same axis. Initially, the apparatus is at rest, but when the current is switched off, the paradox arises. Analysing the problem in terms of the change in magnetic flux one would expect the disk to rotate as an electric field is induced and seen by the spheres, however, analysing from the perspective of angular momentum would mean that the disk does not start to rotate, as the momentum is initially zero and since it must be conserved, the disk should remain stationary. The apparent contradiction in field theory is resolved by taking into account the electromagnetic angular momentum stored in the fields, so that initially the angular momentum was not zero [130]. Fukai argues that the problem is equally well explained by Weber’s theory [118] and considers the force on the sphere exerted by the change of current in the solenoid, which turns out to be non-zero, so the disk will move accordingly.
It was also shown recently that superconductivity can be derived from Weber’s theory according to two independent authors in two different ways. One approach by Prytz [131] considers a magnet or solenoid with a DC current at rest and the centripetal acceleration of the conductor charges. This acceleration causes the Meissner effect to appear in conduction materials according to their deductions. Assis and Tajmar [132] instead follow a more general treatment where AC currents are considered, and in turn the acceleration of the charges causes the Meissner effect and the London moment to appear from Weber’s force.
The so called Aharonov-Bohm effect (AB-effect) that describes a phase shift experienced by electrons when they are scattered around a finite solenoid is usually explained through the quantum mechanical influence of the vector potential . Wesley [133] managed to establish a connection between Weber’s force and the existence of the AB-effect. First, he takes a more classical approach and considers the force due to motional induction on the electron beam, which leads them to find a phase shift depending on the electron path due to this force component. Then, he shows that the same force is present when considering Weber’s potential and force, causing the appearance of the phase shift and thus the AB-effect. Unfortunately in the digital version there seems to be a misprint and large parts of the paper are missing, but his essential deductions can still be found in the first and last sections of the manuscript [133].
An initial connection between Weber’s force and antenna theory has been made by Prytz [134]. In this approach the concept of retarded time is considered to account for far distance effects and utilised with the acceleration dependent induction of Weber’s force. This can describe loop antennae by itself and also contributes to dipole antennae, and simultaneously relates back to the transmission of radio waves. This is, of course, similar to the approach taken by Moon and Spencer [19] who had derived the behaviour of the loop and dipole antenna about 60 years prior, and also arrived at Neumann’s inductance formula for circuits based on the acceleration dependent force in the process.
Weber also considered early forms of diamagnetism in his work, based on the molecular currents introduced by Ampère, where diamagnetism occurs when molecular currents are induced by an external field in a diamagnetic material that has otherwise no molecular currents. While the general idea of molecular currents remains to this day, present explanations necessitate quantum mechanical considerations to fully account for the existence of diamagnetism, due to the Bohr-Van Leeuwen theorem.
3.2.2. Relevance of Weber’s Force Beyond Electromagnetism
There are several aspects of Weber’s force that are not immediately obvious when just regarding it as an electrodynamic force law between charged particles. It holds wider consequences in its action and has been connected to a variety of topics in the literature. The first connection of note is the structure of the atom. Weber himself used his theory to devise a planetary model of the atom [135,136], where negative charges orbit around a positively charged centre, even before the electron was discovered. He realised a special feature of his force law by which an atomic structure emerges as a consequence, that is, a certain critical distance exists in the force law. It is most remarkable that below this critical distance like charges will start to attract instead of repel and opposite charges will still attract regardless. Furthermore, when two or more charges interact with only each other (no external forces are present in that scenario) they cannot transition to the inside or outside of that critical distance. If the interaction started below the critical radius, it would remain inside the radius, and if it began outside it would remain outside. Interestingly, the critical distance can be calculated to be of the order of the known diameter of the atomic nucleus when electron or positron interaction is considered. Thus, it seems possible to interpret Weber’s force as relating to the strong nuclear force that is responsible for the attraction inside the nucleus, even though it is not yet known how it would work for protons. Additionally, for two charges of opposite sign orbiting each other in this model a confinement to elliptical orbits is found which would experience a precession of the elliptical axis [135,136,137,138] and remain within an upper and lower bound of the orbit radius [135,137,139,140,141].
Weber also speculated based on his model of the atom on the mechanism of heat conduction and a possible connection between light and electricity. He related the orbital frequency of charged particles in his model to the wavelength of excited heat- and light-waves. Zöllner [142] even considered that from Weber’s model it would be possible to derive the spectral lines of chemical elements. Upon considering the possibility of multiple orbits in a molecule and that each orbit could be populated with a number of charges, Weber also deduced a classification system characterising the possible combinations of positive and negative charges in a table that has similarities to the periodic table of elements. He further concluded that these molecular configurations could attract other molecules and combine to form stable systems. Eventually he was led to the hypothesis that chemical bonds might have an electrical origin and arrived at a bond that is similar to a covalent bond between two atoms sharing an electron pair [135].
Unfortunately, Weber passed away before he could finish his planetary model of the atom, nevertheless it shows some very interesting properties, while Weber speculated about spectral lines emerging from their model, the fine structure of the atom was still in an early stage of discovery. There are relatively recent works in the literature [11,12] analysing the connections between Weber’s theory and quantised energy levels, they generally tend to show slightly different splittings for the fine structure of the atom. In 2015, Torres-Silva et al. [11] used the Hamiltonian formalism of Weber’s theory and also considered spin–orbit corrections, whereas Frauenfelder and J. Weber [12] used a Bohr-Sommerfeld quantisation on Weber’s Hamiltonian for a hydrogen atom. Wesley obtained a similar result in [143] where he considered the perturbation energy on the electron orbit in the hydrogen atom by utilising the Schrödinger perturbation method, which leads to energy levels different from the experimentally known splittings. It is also reviewed by Post [144] that Phipps’ modification to Weber’s potential leads to twice the number of observed splittings. As the experimental determinations of quantum electrodynamics (QED), such as the fine structure, lamb shift, Rydberg constant and anomalous dipole moments are among the most well tested predictions derived from field theory, this will remain the greatest challenge for Weber-type theories as it seems that it cannot make the necessary predictions in its current form. However, it seems worth noting that Feynman has directly utilised ideas of direct-action and retarded time in his approach to develop QED [40].
The Weber force has also been shown to be similar to velocity dependent forces in nuclear physics, such as nucleon-nucleon forces [145]. These are central forces and obey Newton’s third law, and in [145] the authors show that the momentum dependent inter-nucleon forces in the interaction potential and Hamiltonian are generalised Weber forces, pointing out that Weber’s force can be considered a special case of the forces appearing in nuclear physics. They state further that a similarity to Ampères force exists in nuclear physics as well for scattering processes of spinless projectiles and that it cannot be understood on the basis of only the Lorentz force analogy, but is consistent with a Weber force analogy.
Another interesting similarity with the forces of nature exists between Weber’s force and gravity, and Weber had already speculated about such a connection based on his atomic model. One of the underlying ideas is that the attractive force between charged particle assemblies is slightly larger than the repulsive force. Based on this idea, Assis [146,147] has developed a model to derive gravitational effects as a fourth order effect from the electromagnetic interaction through an extension of Weber’s formula. He considers a series expansion of Weber’s force law:
with numerical constants and and omitting any higher order terms of the series expansion. Equation (32) is then used to study the interaction of two neutral dipoles that consist of a positive charge in the centre and an oscillating negative charge. After an extensive analysis, Assis arrives at a non-zero force of attraction between the two dipoles which he proceeds to interpret as a gravitational interaction force. These derivations later led Tajmar [148] to analyse a minimum energy requirement between two neutral dipoles that is similar in nature to Planck’s constant. The approach used by Assis is then further investigated by Baumgärtel and Tajmar [149] yielding a slightly different result to that originally obtained by Assis. The authors of [149] interpret the resulting force to contain the Casimir force and inertial effects as well. Further analysis of this result in regards to a minimum energy requirement is pursued and the study finds a connection to Planck’s constant and the origin of mass establishing a general relation between Weber’s theory and Planck’s constant solely on electrodynamic properties of particles. One can generally see with the appearance of the Casimir force, Planck’s constant and the fine structure of the atom that Weber’s theory ties to certain quantum mechanical effects, however it still requires significant development on quantum theoretical aspects in the future.
There are other considerations about Weber’s force and gravitational interaction. A common approach in the literature is to utilise a gravitational force of the Weber type, such as has been investigated by Tisserand [150], Gerber [151], Schrödinger [152] and others. Utilising such a gravitational form of Weber’s law, Assis and Wesley [60,153] have shown that it is also possible to arrive at the origin of inertia in combination with Mach’s principle. Their derivations generally follow the form
where it is easy to see that the usual charges and have been replaced by masses , and gravitational constant G. As a consequence of this approach however, Newtons second law, , follows naturally from this formulation, so that the interaction with the distant masses is responsible for the existence of inertia. In essence, Assis calculates the force on a body by investigating its interaction with what is more or less a celestial sphere and the cosmic microwave background, while Wesley uses a gravitational field in his derivations. Additionally, in Assis’ model the resulting force contains terms that represent centrifugal and Coriolis forces.
Because there are many possible variations of Weber-type gravitational forces of similar nature, e.g., [60,150,151,152,154], their form has been further generalised by Bunchaft and Carneiro [155] as
Here, k is a parameter depending on the nature of the interacting bodies (like charges or masses) and the parameters and are positive constants of the velocity and acceleration terms usually of the order . Further aspects of these approaches, with regards to cosmology and conservation of energy, will be discussed in the next section.
Weber’s force law in its basic form (15), is a ’microscopic’ force law which obeys certain general principles of mechanics. It intrinsically follows Newton’s third law of action and reaction. Any action arising from Weber’s force has an opposing force of equal magnitude and inverse sign, making it consistent with linear momentum conservation. It can also be shown that Weber’s theory follows energy and angular momentum conservation [6,8], and Weber himself only succeeded in 1871 to show that conservation of energy is obeyed.
It is even possible to derive a virial theorem from Weber’s force as has been shown by Mendes and Assis [156]. The virial theorem states that the time average of kinetic energy in a system of discrete particles is related to the potential energy of the particles. For Weber’s formula this takes the form
with the potential energy being Weber’s potential (see Section 2). As a consequence, this offers the possibility for statistical treatments of problems with Weber, such as the formations of galaxies on an astronomical scale or plasma physics, although limitations have been indicated regarding the applicability to cold plasmas [157].
Weber’s force has also been used with a modified version of mechanics [158]. The idea is based on the relational nature of Weber’s force, making mechanics relational as well. In essence, Newton’s mechanical principles are extended with Mach’s principle and a Weber-type force for interacting masses is implemented. This has consequences for cosmology, affecting the interpretation of Hubble’s law and the cosmological redshift as light interacting on its journey. The cosmic microwave radiation background would then indicate an equilibrium state and the precession of mercury’s perihelion is due to the interaction with distant fixed stars. Although the idea is intricate and intriguing, this would of course be less compatible with the standard cosmological interpretation of an expanding universe.
3.2.3. Cosmology and Breakthrough Physics
From the previous section it was shown that Weber has ties to other forces of nature, like nuclear forces and gravity, and it was suggested that Weber’s force has significant links to cosmological theories and related phenomena. Based on the possibility of gravitational modifications to Weber’s force, there have been many investigations about planetary motion and in particular the precession of mercury’s perihelion [13,150,151,152,159,160,161,162,163,164]. In addition, some of these also investigate the bending of light in a gravitational field and the two effects are usually explained from GRT. From these investigations it can be seen that Weber generally offers a possible explanation for both observations, but the applicability has been shown to have limits.
The general form of Weber-type forces of the order (34), is further investigated by Bunchaft and Carneiro [155] with specific attention to energy conservation. The authors of [155] show that such a force is only conservative under a special condition when the parameters and of (34) obey the form . They deduce from this analysis that a Weber-type gravitational force cannot predict the correct values for the precession of mercury’s perihelion and the gravitational bending of light at the same time under the condition of being conservative. However, more generalised formulations of higher order might still be able to predict both effects whilst remaining conservative, and it is still evident from this that Weber’s force offers an alternative approach to phenomena that are usually attributed to GRT. A somewhat more general discussion about how GRT and Weber-type theories are related on a fundamental level can be found by Giné [165], although that approach has been challenged [166] in not having a proper Einsteinian approach. A further analysis by Tiandho [167] came to the conclusion that Weber-type gravitational forces are a weak field approximation of GRT and thus a special case, nonetheless, it shows some similarity and connection between the two theories.
Recently, Weber-like gravitational interactions in combination with Mach’s principle have been investigated with regards to their implications in cosmology [168]. The advantage of such an approach is that inertia arises naturally from the interaction with a celestial sphere and avoids the incompatibility of inertia in GRT with Mach’s principle; and additionally maintains the equivalence of gravitational and inertial mass and the equivalence of kinematic and dynamic rotation rates of the Earth. On the other hand, the resulting universe is non-expanding and the redshift arises from energy loss of light on its journey. Another cosmology model based on Mach’s principle has recently been developed and investigated by Das [169], where the universe is governed by Machian gravity. According to Das it is able to explain rotational curves and mass distribution of galaxies without dark matter or dark energy and when comparing the model to observed cosmological data it fits well with the measurements. Previous to these approaches, the general idea of a Machian cosmology had been suggested in the literature [158,170,171,172,173], where P. and N. Graneau [173] have even found a connection to the expanding universe, but Das seems to be the first to apply the concept to available data of galactic rotation curves.
Beyond the general connection of Weber’s theory and GRT, some works have analysed more specific effects arising from gravitational perturbations, for example spacecraft flyby anomalies [154,174]. These approaches also utilise gravitational formulations of Weber’s force, similar to the previously discussed modifications. The first of such gravitational-influenced effects is called frame dragging, also known as the Lense-Thirring-effect, which has its usual explanation in GRT. This effect adds a precession to a gyroscope or orbiting satellite in the presence of a large rotating mass. It is possible to arrive at a similar effect by utilising Weber’s theory [174] for gravitational interactions. The authors of [174] present the formula for the action of a large spinning shell with mass M, radius R and angular velocity on a test body, mass m, at position , velocity and acceleration to be
where G and c are the gravitational constant and speed of light, respectively. As can be seen it is similar to the previously presented gravitational-type Weber forces, with terms resulting from the rotation and acceleration, for example the second and third term in square brackets of (36) represent centrifugal and Coriolis’ force, which appear due to the implementation of Mach’s principle. After analysing the problem with the help of Newton’s second law, they arrive at a gravitationally induced azimuthal acceleration that will be experienced by the test body, similar to a frame dragging effect.
The gravitomagnetism arising from this principle has also led Tajmar and Assis to investigate flyby anomalies with a similar implementation of gravity-like Weber forces [154]. They found that flyby anomalies due to Weber-based interactions are several magnitudes smaller than currently measurable. They relate this to data of Rosetta flyby manoeuvres where expected anomalies have not been measured, even though the standard approach would have predicted them. However, if the effect is, according to the Weber-interaction, below the threshold of current detectability, this result would not be surprising.
Apart from the general and specific connections to GRT, an interesting possibility seems to exist in Weber’s theory that pushes the boundaries of known physics. A situation can be created according to Assis, where the mass of charged particles can be manipulated under the influence of a field-free electrostatic force [6,175]. If it is indeed possible to change the inertial mass of a charged particle through electrodynamic means, it can possibly be applied to breakthrough propulsion physics technologies, such as the warp drive, anti-gravity or even cold fusion [176,177,178] which could revolutionise space travel, energy production and transportation in general.
The approach taken by Assis shows the influence of a charged spherical shell on a point charge according to Weber’s force, whereby the force on the point charge can be interpreted as an inertial mass change of the particle. Assis considers a hollow spherical shell made of a dielectric with charge Q of radius R, with an angular velocity . This approach is similar in nature to the gravitational model of gravitomagnetism with Weber for a massive spherical shell producing a frame dragging effect. Here, the charged sphere acts on a point charge q at position , velocity and acceleration . For the point charge inside of the spherical shell, he arrives at the expression
which can further be simplified with the restriction , meaning the sphere being stationary, to:
With the help of Newton’s second law this can then be interpreted as a change in effective inertial mass of the particle due to the potential on the surrounding shell.
This is an especially interesting prediction of Weber’s theory, because in standard theory, the field inside a charged spherical shell is zero and such an effect is not intuitively expected. Assis also estimates an order of magnitude for the effect, which entails a sphere of radius and a potential on the shell of to double the mass of an electron, which is generally in the realm of the possible to obtain in the laboratory. However, from these values compared with the size and charge of the electron it can be seen that the effect is still considerably small in nature. However, as a logical conclusion, in theory a particle can be made to have an effective negative mass through the influence of an electrostatic potential at the cost of sufficient energy expenditure. This behaviour might then be applied to future breakthrough propulsion applications [176,177,178].
As this is an interesting prediction and experiment to determine boundaries of the validity of Weber’s force law, several experimental efforts have tried to investigate this predicted phenomenon, with recent evidence suggesting the non-existence of this effect. Mikhailov had first reported an experiment in 1999 [179] where he claims to have successfully observed the effect in question, with two follow-up experiments in 2001 and 2003 [180,181], which he reported to be equally successful. However, the attempts of independent researchers to repeat and, respectively, improve their experiments have not yielded positive results [182,183,184]. Since all of the re-evaluated experiments feature a refined methodology and uncover flaws in the settings of Mikhailov (e.g., coupling and detection methods), one inevitably concludes that the effect in question was not observed by Mikhailov. An important point is discussed by Lörincz and Tajmar [183] as to what degree a glow discharge is suited to produce and measure a possible mass change of charge carriers, because the discharge is always made up of a neutral plasma and hence probably not suited to show the effect, and Weikert and Tajmar also speculated that the oscillatory motion of electrons in a Barkhausen-Kurz configuration could mask the effect in question [184].
There is new evidence [185] that the sought after mass change effect does not seem to exist. Tajmar and Weikert tested electron beam deflections in a Perrin tube where under a certain magnetic field the beam would be deflected precisely into a Faraday cup measuring the beam current. The arrangement was located in an aluminium sphere that was charged up to ±20 and they simultaneously observed the current feeding a set of Helmholtz coils generating the magnetic field and the measured beam current of the Faraday cup. By observing the necessary current to keep the beam consistently in the Faraday cup they concluded that the sought after effect can be ruled out by two orders of magnitude. This makes this topic a valid point of criticism against Weber electrodynamics which will be discussed further in the following Section 3.3.
These many investigations of Weber’s force in the literature demonstrate the strength of the theory and how it links to many fields across physics, and therefore it is an interesting alternative model to standard electrodynamics. Weber’s force law has even been suggested in the literature as a unified theory of nature [146,186], especially as it includes the electromagnetic force, a form of nuclear or strong force, a gravitational-type force and additionally an explanation of the origin of inertia. We can see from this that Weber offers an elegant path towards the unification of theories and, to quote O’Rahilly ([25], Volume II, p. 535): ‘If any one man deserves credit for the synthetic idea which unifies the various branches of magnetic and electrical science, that man is Wilhelm Weber’. Weber’s theory connecting so many disciplines is of course not an accident, since it is an electromagnetic theory. Field theory and relativity which the standard model of modern physics is based on also show these properties and strive for a unified theory of physics. It is well known that three out of the four forces of nature can be unified in the standard model (magnetic force, strong nuclear force and electroweak force) and attempts are made through quantum gravity to connect the remaining force to those three. So in general, any theory attempting to explain the natural phenomena on a larger scale is likely to show the characteristics of a unified theory. However, Weber’s theory, despite the time that has elapsed since its inception, is still very much in an early stage of development and has not been researched to the same degree as conventional models. Nevertheless this should not be taken as discouraging, quite the opposite in fact, it gives motivation for further investigation of Weber’s force to explore its capabilities to describe and predict the universe. Needless to say, Weber’s theory is not without criticism.
3.3. Criticism of Weber’s Theory
Weber’s force is not pursued by mainstream physics as it was superseded by Maxwell’s theory of fields and ether, and so we must question just why the theory was largely abandoned in favour of another. Historically there were three main points of criticism leading to the neglect of Weber’s theory and a fourth factor of experimental nature. The points of criticism of Weber’s force were: (i) It is based on the Fechner hypothesis, i.e., currents being comprised of equal amounts of moving positive and negative charges, (ii) Helmholtz first criticised Weber’s force as violating energy conservation, and (iii) then criticised the theory for exhibiting unphysical behaviour in the form of negative mass and infinite acceleration. Finally, what was claimed as decisive evidence in favour of the field model were the successful experiments of Hertz, demonstrating electromagnetic waves and therefore taken as direct proof supporting Maxwell’s theory as opposed to Weber’s. We will now re-investigate these historical factors to see how they have aged and after that look at more modern criticisms or limitations of the theory. Another review of historic criticisms from a philosophical perspective of action-at-a-distance theories in general can be found in [187] with a strong focus on epistemologic aspects.
We will first consider the criticism that Weber’s force is originally based on Fechner’s hypothesis. In the middle of the 19th century it was assumed that a current in a circuit consisted of equal amounts of positive and negative charge (or electric “fluidae”) moving in opposite directions. While it is true that Weber designed his force based on this assumption to derive Ampère’s force, he himself moved away from the idea of a double current consisting of moving positive and negative charges towards a simple current where the positive charges remain fixed in the lattice and only the negative charges are considered to be moving in his later works. Despite this change in perspective, he did not alter the formulation of his force law because it would still remain valid in predicting observable effects. Assis showed [61] that it is possible to derive Ampère’s force regardless of the Fechner hypothesis from Weber’s force. The only assumptions made are the charge neutrality of current elements and the independence of velocities of positive and negative charge carriers therein. This means that it holds true for moving electrons and stationary lattice charges as well as oppositely moving positive and negative charges as, for example, in plasma states. Further the Hall effect can be explained with Weber’s theory when the Fechner hypothesis is abandoned, as reviewed in the previous section.
When discussing this matter it should be mentioned that Clausius was the first to claim in 1877 that Weber’s force would lead to unphysical situations when only one kind of charge is moving and the other kind is fixed in a conductor [188]. This criticism seems to have been taken as a decisive argument against the theory as reviewed by Woodruff [189] and persisted in the more recent literature when Pearson and Kilambi analysed the similarity with nuclear forces [145]. The argument is that in the situation where Weber’s force is not balanced by oppositely moving charge carriers, so called electrostatic induction occurs outside of a conductor and this has been considered an exclusion criterion of Weber’s theory as an explanation for electrodynamics in [145]. However, it must be said that an early extensive refutation of this argument has been given by Zöllner as early as 1877 [190] in response to Clausius, arguing that these electrostatic effects have been known since 1801 through experiments by Erman [191] and others, and Weber’s theory is erroneously criticised. Assis and Hernandes [192,193,194] have given a modern review of electrostatic induction effects in theory and experiment, showing that these effects do indeed exist on different orders of magnitude and that it is too early to dismiss Weber’s force law on such a basis. In fact, the existence of such effects could even provide experimental support for Weber’s theory. In conclusion we can say that at present there is no requirement for Fechner’s hypothesis in Weber’s theory and the criticism is not valid.
Helmholtz originally criticised the theory by saying it did not obey conservation of energy. He considered the potential and kinetic energy, especially with particles in circular motion and came to the conclusion that there are possible situations in Weber’s theory where energy can be lost or gained and thus objected to the theory. At the time, Maxwell was familiar with Weber’s theory and knew of Helmholtz’s argument, supporting the objection stated by him. It was only in 1869 and 1871 that Weber succeeded in showing that energy is conserved in his force law. After this proof Maxwell even acknowledged in his Treatise that Weber’s theory was mistakenly criticised in that regard [22] and reconsidered it as a possible theory of electrodynamics. Helmholtz erroneously came to the conclusion that energy conservation is violated as he only included the velocities between interacting charges and did not consider the complete form of Weber’s force which also depends on the acceleration of charges, leading him to an incomplete deduction [24].
Furthermore, Helmholtz issued a second major criticism of Weber’s theory, where he describes a situation that leads a particle to exert behaviour of negative mass and upon movement it could accelerate infinitely in the presence of an external force, such as friction, and an infinite amount of work would be done. He describes a particle inside a charged spherical shell that experiences friction from a fluid and as it is infinitely accelerating, it would continue to heat the fluid due to friction and thus perform an infinite amount of work. An argument ensued between the two parties with Weber trying to defend against the criticism, but Helmholtz again countered his arguments and the criticism prevailed [189] and to this day remains an open question in Weber electrodynamics.
This is indeed a similar situation to the suggested inertial mass change of Assis due to a field-free electrostatic force and the criticism has been further analysed by Assis and Caluzi [195]. They have suggested three possible ways to resolve the problem: (1) If instead of using Weber’s force and Newton’s mechanics, a modification of mechanics to a relativistic type kinetic energy is assumed, then the particle will not accelerate ad infinitum. The modified expression for mechanics has also been obtained by Schrödinger [152] and Wesley [60] by considering Weber-type forces. (2) It is also possible to avoid the problem by a modification of Weber’s potential energy, e.g., Phipps [196], which leads to a force expression where infinite acceleration does not occur. (3) It is still possible (though highly unlikely) that nature behaves this way, it just has not been sufficiently tested.
However, with the new experiment of Tajmar and Weikert [185] it seems very unlikely that nature behaves in a way where this change of mass or energy is involved. Especially when according to Helmholtz an infinite amount of work can be gained if a particle experiencing friction forces from a fluid would continue to increase the fluid’s temperature due to the friction. By implication this would violate the first law of thermodynamics and allow for a perpetual motion machine under the condition that the energy can be extracted from the closed system formed by the charged shell, fluid and point charge. It could theoretically still be possible that in order for the effect to manifest, a friction force is needed, as this is what Helmholtz originally considered and was also included in the analysis of Assis and Caluzi [195]. However, this seems unlikely as Assis also made the prediction for a mass change without the consideration of friction forces at first [175] and further a situation like this seems very unlikely to manifest in practice. As far as we know, a similar system has never been observed in nature and the proposed scenario seems unlikely to occur naturally.
If we now consider resolutions (1) and (2) suggested by Assis and Caluzi, we can say for point (1) that the infinite acceleration of a particle can be avoided through the assumption of modified mechanics, but this would change the behaviour mainly for velocities near the speed of light, as pointed out by Weikert and Tajmar [185]. Additionally, in this case Assis and Caluzi still speak of an effective inertial mass influenced by the electrodynamics, so an apparent mass change would still occur in this instance. As for point (2), the modification of Weber’s potential energy to Phipp’s potential, this can generally present a solution to the problem, however Phipp’s potential turns out to have other shortcomings [197]. Nevertheless, there might still be a more fundamental, more general Weber-type potential where the change in mass is avoided and the problem is resolved, such as suggested by Li [198]. So this criticism is a valid point, however, there might well be other ways not yet known to avoid the problem like a more general potential and here more research is needed. It must also be added to this discussion that due to the self-energy divergence in field theory, the Lorentz-Dirac renormalisation solution also leads to runaway behaviour with infinite self-acceleration of a particle [37]. Albeit a different situation where the particle interacts with its own field, as opposed to Weber’s theory where the particle interacts with a field-free charge distribution, this shows that we can find the same unphysical behaviour through infinite acceleration exhibited in the framework of field theory as well. It would seem inadequate to use this singular behaviour as a decisive argument against Weber’s theory when field theory is not rid of such a problem itself.
The fourth factor that was historically held against Weber’s theory are Hertz’s experiments that showed a finite propagation velocity of electromagnetic signals, and were taken as a direct verification of Maxwell’s field theory. However, we have seen in the previous sections that Weber’s theory has been shown to be consistent with fields and can indeed predict wave equations propagating with the speed of light and is related to radiation phenomena when the right physical methods and constraints are applied. So it remains questionable if Hertz’s experiments should only be taken as a direct proof of Maxwell’s equations. For example, the experiments are also consistent with Ritz’s theory (as pointed out by O’Rahilly [25]), and it would be premature to exclude Weber’s theory on that basis.
Additionally, it should be mentioned that Weber believed in a form of ether, i.e., the luminiferous ether, which nowadays has been effectively replaced by the electromagnetic field model. So one could argue that Weber’s theory is based on the same ethereal premise as Maxwell’s, as he tried to model the interactions of charges within the fluid of ether that was general scientific consensus at the time. Although it should be noted that Weber’s force does not conceptually depend on the ether due to only involving relative velocities. Furthermore when invoking the principle of Ockham’s razor, that is, entities should not be multiplied beyond necessity, it becomes apparent that Weber’s theory is considered to be preferable over Maxwell’s as it makes fewer assumptions. Weber being based only on the interaction of charges without invoking the concept of field entities conforms to minimal assumptions as only the charges and their motion is relevant. Additionally, there is an argument in the literature, when discussing contact-action through fields or emitted virtual particles, that entities like the ether or the field which cannot be observed directly should be avoided [199]. At its core this issue relates to a more general criticism of Weber’s theory being a direct-action-at-a-distance theory with apparent instantaneous transmission unlike a field theory. The instantaneous nature of force laws like this is usually argued to be a problem since it violates causality and since the propagation of electromagnetic effects are clearly of finite velocity, hence there is an apparent problem with the theory. Take, for example, Newton’s gravitational force law: if one body experiences a change in position, body two will immediately feel this change in force, no matter the distance between them. However, there exists a claim in the literature that Newtonian gravity actually propagates at the speed of light [200]. Although the analysis is based on dimensional, empirical and observational arguments, this is a remarkable postulate, and even though Newtonian gravity is formulated mathematically as instantaneous-action-at-a-distance, a finite propagation speed is implicitly contained within the formula, suggesting that the same could be true for other so called “instantaneous” force laws.
So the real question is how propagation velocities behave in Weber’s theory or how they can be limited. There are multiple factors to consider here. First, Weber’s force itself models a delay in propagation intrinsically with the constant c in the formula, and as argued by Brown [201], c should be viewed as a retardation constant at which cause and effect occur. Related to this Sokol’skii and Sadovnikov [13] have studied planetary orbits with a gravitational form of Weber and find that gravitational interaction propagates at the speed of light c in their model. In the previous Section 3.2.1 we have seen different considerations showing how Weber is able to predict wave propagation of electromagnetic signals at the speed of light, for example in combination with the principle of retarded time applied by Moon and Spencer, and Wesley who derived wave equations based on this premise. Additionally, Weber and Kohlrausch first obtained experimentally the value of c with Weber’s force and Kirchhoff and Weber both arrived at the telegraph equation for propagation of signals in a circuit independently from each other based on Weber’s force. From these considerations, we can see that Weber indeed expresses a delay in propagation and a finite propagation velocity despite it’s action-at-a-distance origin, meaning causality is not violated.
The overall concept of action-at-a-distance theories on a more philosophical basis has been discussed by Pietsch [36]. The discussion is on a more general level about energy conservation, necessity of contact for transmission of energy, locality criteria and metaphysical considerations and does not favour Weber’s theory over the Wheeler-Feynman type or other action-at-a-distance theories [21]. First the problem of divergent self energy of a point charge in classic electromagnetism is discussed, with the existing resolutions of renormalisation versus extension approaches. It is argued that both solutions come at a cost and that action-at-a-distance can offer an alternative to resolve either problem that arises in one approach or the other. Similarities of pure particle action and pure field theories are explored in the analysis [36] and then Pietsch continues to point out similarities of action-at-a-distance theories with modern particle-field theories of electrodynamics widely established today. Lentze [202] has argued that direct-action between charges as a general concept can provide deeper insight into explaining the origin of electromagnetic forces and the light speed principle, thus improving our understanding of nature. Further discussion of direct-action theories, also more focussed on the quantum version of the Wheeler-Feynman approach with respect to Haag’s inconsistency theorem and how direct-action can overcome the mathematical inconsistencies and problems arising from QED and QFT can be found in [42], but are beyond the scope of this review.
From a modern perspective, Weber’s force has been critiqued as it does not account for relativistic corrections of deflected electron beams, such as the Kaufmann-Bucherer or Bertozzi experiments [203,204] in its basic form. Additionally, Weber’s force does not impose the same relativistic speed limit of c on a particle [205] as is expected from SRT, and it does not seem to be compatible with SRT and the Lorentz transformation based on these shortcomings. In its standard form Weber is only an approximation in for high speed particles compared with relativistic corrections, as shown by [107,203]. There are, however, some approaches in the literature to address and solve these inconsistencies of Weber’s force. For example, this could suggest that the regular form of Weber’s force (15) might still be an incomplete theory and only modified forms may be able to overcome this problem. Attempts on limiting the velocity have been made by Montes [206], Wesley [204] and Phipps [196] which manage to include relativistic corrections to varying degrees. Assis [207] investigated Phipp’s potential and the inclusion of higher order terms similar to [146,147] in relation to their relativistic compatibility. He finds that these types of Weber theories either hold the speed limit c for an individual charge or their relative speed, but not both at the same time. In general these approaches consider some form of modification of Weber’s theory, which might involve other costs as analysed for the gravitational type forces and their energy conservation [155], and even if a suitable modification is discovered, its properties should be studied further on this basis. In a recent study, Li [198] utilises an extension of Weber’s potential and the additional assumption of modified mechanics and arrives at high velocity particle behaviour that is identical to the predictions made from SRT. This has certain similarities to Wesley’s approach [143] of modified mechanics in conjunction with a Weber-type force and indicates that further research is necessary in relation to the high velocity regime.
Another interesting approach to potentially resolve the problem was suggested by Bush [137]. Bush investigated a direct-action force of the Weber-Ampère type and instead of a variation of mass with velocity assumes a variation of charge with velocity. He deduces from these investigations that the ratio obtained with their approach is consistent with the Kaufmann-Bucherer experiments. Further, with this approach it is the force which tends to zero for a relative velocity between charges close or equal to the speed of light, rather than the mass tending to infinity. The reason why no superluminal particles are observed experimentally is then the lack of force transmission at the speed of light. From these different suggestions to reconcile Weber’s force with relativistic corrections it can thus be concluded that the theory has not been fully developed for high speed interactions yet, and more research is needed if Weber can be correctly used in that sense.
Recently, a new study by Kühn found that it is also possible to resolve the problem with wave equations derived from Weber electrodynamics [111], where the wave solutions are obtained in the reference frame of the receiver. The article first shows how Maxwell’s equations lead to Weber’s force within the low velocity limit and then further investigates how the wave propagation in the far field can be limited to the velocity of light. Interestingly, the Lorentz transformation is not a necessity in that approach and rather than viewing the propagation velocity as constant w.r.t. the transmitter, it is perceived as constant by the receiver. The physical mechanism responsible for this behaviour is discussed with regard to a newly developed emission theory by Kühn [208] and its implications for electrodynamics and SRT. Concluding from these different approaches, while in its standard form Weber’s force seems incompatible with SRT, we see that solutions have been suggested and further research is needed to investigate how Weber’s theory and relativistic physics are related.
Other modern criticisms have been issued where Weber’s force was shown to lead to unphysical results [157,209]. In the case of the investigation carried out by Clemente et al. Weber’s force is applied to cold plasmas and analysed for the resulting propagation of waves in the plasma oscillations. The authors of [157] find that Weber predicts a type of longitudinal wave propagation that is unphysical and contradicts the well established experimental evidence [210] about dispersion relations in cold plasmas. On this basis it is also concluded that only the existence of electromagnetic fields can account for this effect and that Weber’s force leads to erroneous results in this case because it strictly follows Newton’s third law. This is, of course, an important point of criticism and it shows that Weber’s theory has not yet been developed in relation to plasma physics at all. It might be interesting to see if Weber still leads to unphysical results if retarded action is taken into account (as it was discussed in Section 3.2.1 whereby Weber is consistent with fields in that case). It might be possible to arrive at the correct result by modification of Weber’s equation or potentially Ritz’s formula could account for the discrepancy, while this is a shortcoming of Weber’s force it would be of interest to further develop a plasma physics approach based on Weber’s force.
An analysis by Sherwin [209] compares the transmission and detection of an idealised radar system between Weber’s force and the Liénard-Wiechert force in the standard theory. While the magnitude is found to be the same for both approaches, the angular dependence, direction of signal transmission and propagation delay is different between the two. Sherwin states that the standard result through the Liénard-Wiechert equation is well supported by experiments in radar technology and disagrees with the Weber prediction. On the other hand, the field-model result cannot easily account for longitudinal forces, which the Weber force can, and at least the propagation delay can be introduced through a retarded time approach, such as Wesley’s [9,211]. From this, Sherwin concludes that neither theory agrees sufficiently well with observable phenomena yet. This seems to be a peculiar situation that neither theory fully agrees with expectations yet, as it is likely that the inclusion of longitudinal forces in the Liénard-Wiechert model would also change the angular dependence and transmission direction closer towards the Weber force result. Certainly, more research is needed to arrive at an answer to the problem and it would be advantageous to give Weber’s theory a further rigorous development for signal transmission and radar applications, also on the basis of the approaches reviewed herein [9,19,134,211].
We have outlined how Weber’s theory offers particular value in explaining phenomena arising in various areas of physics. Most of the original objections to the theory have been answered and the criticisms that remain are not yet completely resolved. Neither the Maxwellian field approach nor Weber’s electrodynamics are free of criticism and problems, each theory has its own advantages and disadvantages and unreconciled inconsistencies. In the same way that established theories are continually researched and developed further and eventually amended, we would make the argument that the same is necessary for direct-action theories, especially considering that there are significant parallels between both theories and many connections have been established between the two. Several authors have presented the view point that direct-action theories are a valid alternative to be considered in physics and can help overcome problems associated with field theory. None of the theories are perfect, so it is not wise to dismiss direct-action too early and it should be further developed to inform research and to investigate what explanations it can offer. Another useful approach might be to regard the two theories as complementary, and depending on the application to employ whichever theory is most suitable.
4. Perspective and Future Prospects
The present article has given a comprehensive review about an underrated contribution to the foundations of electrodynamics, namely the electrodynamic theory of Wilhelm Weber, and pointed out its many capabilities. However, even with the several strengths of Weber’s formula presented, the current limitations of the theory have also been explored and criticism of the theory addressed. Overall, it is found that Weber’s force in its standard form is only valid within certain limitations and further research is needed, but it can still complement Maxwell’s field equations within those bounds.
In the literature analysis both Maxwell’s theory of fields and Weber’s electrodynamics have been introduced, and it was then reviewed how Weber is capable of explaining several electromagnetic phenomena, including Coulomb’s force, Ampère’s force, field equations, induction and the telegraph and wave equations. Moreover, the importance of longitudinal forces and their role in Weber electrodynamics was emphasised, as well as their analogy in field theory, as they have been shown to exist in both approaches.
Further to just explaining electricity and magnetism, Weber’s theory provides a basis for other physics disciplines and has a unifying character connecting several branches of physics. It has been shown how Weber’s force connects to gravity and the strong nuclear force, Newton’s second law and Mach’s principle and relativistic phenomena such as the bending of light or frame dragging, however it is not yet known how the weak force relates to Weber’s force. For standard field theory it is well known that strong force and weak force can be related to the electromagnetic force but it is still unknown how gravity can be unified with the other forces in that approach, although it is being actively researched (e.g., quantum gravity). Lastly, field theory is compatible with SRT as well as quantum mechanics, but there is no extensive research yet how Weber’s theory can be related to these topics, if at all. We can see from this juxtaposition that both theories are similar, yet different, and a table is given below summarising some of the similarities and differences of both theories (Table 1).

Table 1.
A comparison between field and Weber theory in selected categories.
One can conclude that Weber’s theory is not without limitations and is only valid within the low velocity regime, with standing problems in relativistic physics (special as well as general), radiation and plasma applications as well as quantum electrodynamics. However, if the force law is considered as an addition to Maxwellian field theory, it can enrich one’s perspective on electromagnetic phenomena and beyond. It offers an explanation of observed phenomena from a particle perspective, as well as the prediction thereof. In this sense Weber’s theory can be regarded as an important component of electrodynamic theory, even though it has not been developed anywhere near to the same level as field theory. While experimental evidence in relativistic electrodynamics and QED supports Maxwell’s field theory, it has been found that Weber agrees with experiments in the near field and low velocity limit. This suggests, along with recent studies, that Weber’s force is a low velocity approximation up to second order in of a more fundamental underlying force, and needs further development. Several modifications are conceivable, with possible generalisations of the Ritz-type or corrections to the Weber potential as suggested by Li [198] and it will be subject to future work to investigate the full capabilities and boundaries of the theory and its modifications.
A benefit of Weber’s force is that it follows Newton’s third law of motion, thus conserving linear momentum, and additionally conserving angular momentum as well as energy, so it does not violate conservation laws. In the field approach it is usually argued that conservation laws are not violated when the energy content of the field is taken into account, i.e., the field can obtain energy or momentum from a system and store it as well as release energy and momentum. Further, Weber’s force accounts for longitudinal forces intrinsically, however, the absence of longitudinal forces seems to be desired in radar and plasma applications where the field approach benefits from this quality instead and Weber seems to fail to predict the expected results. However, Weber’s force can be calculated directly from the movement of the charges involved in an interaction and does not necessitate the calculation of one or more fields of those charges from which the force is calculated, which offers clear force and particle-based explanations, which avoids problems such as the self-energy divergence. Another benefit in Weber’s theory is that charge velocities are clearly defined, whereas in field theory there may be some ambiguity left as to what velocities are to be used in the Lorentz force equation. Lastly, Weber’s force offers the possibility to unify gravitational forces with those of electromagnetism. It is thus considered constructive to use both theories in cooperation with each other, as each can compensate for the other’s weakness and regarding a specific problem in question from both perspectives can potentially lead to new insight. Examples for this can be found not only in the flux cutting analogy of unipolar induction, but also transformer induction where the particle perspective considers the acceleration of the current electrons whereas the field perspective links the magnetic flux of either side of the transformer. Similarly, magnetic fields (e.g., of a solenoid) can be regarded from a particle perspective, where it is again the movement of the charges exerting an influence on the test body rather than the field mediating the force.
On the basis of the present review, one can identify certain aspects of Weber’s electrodynamics that would be especially interesting to research further. Firstly, the importance of Ampère longitudinal forces to determine how they influence specific applications, for example the present limitations surrounding the radar equation and cold plasmas, and further development of Weber’s force for signal transmission and radar applications would be of interest. Further, the general relevance of longitudinal forces to nuclear fusion applications has been suggested [82,97,212], and it remains to be determined how longitudinal forces could be applicable to plasma physics on a wider scale, especially as plasmas typically have a positive ion charge density and a negative electron charge density. There is not yet extensive experimental work giving a quantitative estimate of the influence of the longitudinal forces on plasmas of which the authors are aware. Some recent experiments [101] suggest that the influence is frequency dependent but relatively small. Further research into longitudinal forces would certainly be of general interest to clarify their overall role in electrodynamics.
Another aspect that should be further investigated is charged particle optics based on Weber’s electrodynamics, in particular the deflection of high-speed electrons as in the Bertozzi experiment and further exploring how Weber relates to mass change with velocity and SRT. In order to advance the simulation in the high velocity regime, Weber’s force will likely need modifications, such as suggested by Wesley, Assis, Montes and Li, along with other types of modification and generalisation still to be explored.
It could also be valuable to research further electrostatic induction and its connection to Weber’s force, Assis notably mentions the experiments performed by Jefimenko and Edwards et al. [213,214,215]. Nowadays, there are more modern experiments that have been performed and extended the work of Edwards et al. with superconductors and electrostatic induction in general, but it seems like they have not yet been analysed from a Weber-perspective and similar experiments could help to further investigate the boundaries and validity of Weber’s and field theory in these cases. Next to electrostatic induction, of course, investigating other induction experiments further and how Weber’s force can predict them seems logical as Weber has been successfully applied to transformer and unipolar induction already.
There have been some initial connections between Weber’s force and quantum mechanics (see Section 3.2.2), and it could be extremely valuable to extend Weber’s force to the quantum realm, as this could resolve existing problems with Weber’s force and might allow for new insight into particle physics from a Weber perspective relating to the nature and behaviour of the particles themselves. Similar to Weber’s model of the atom, it might be conceivable that a Weber-type theory leads to a quantum wave equation which resembles Schrödinger’s equation. Interestingly, a recent study by Zhao [216] has derived a wave equation similar to Schrödinger’s, that shows interesting similarities to Weber, as both Weber’s planetary model of the atom and Zhao’s approach can account for precessing electron orbits. So it might be worth investigating what quantum mechanical capabilities Weber-type forces might have. It may well offer yet unknown solutions and insight regarding present problems surrounding supersymmetric expectations in particle physics.
In conclusion, Weber’s force is an electrodynamic force law with limited validity that can complement Maxwell’s field equations, and particularly in the low velocity and near field limit it is indistinguishable from field theory. It can offer explanations not only for electromagnetic phenomena but also general physics, with many connections yet to be explored, holding great potential for further development.
Author Contributions
Conceptualization, C.B. and S.M.; formal analysis, C.B.; writing—original draft preparation, C.B.; writing—review and editing, S.M.; supervision, S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
One of the authors (CB) is funded by the School of Electrical Engineering, Electronics and Computer Science (EEE-CS), University of Liverpool. CB and SM are thankful to the EEE-CS School in this regard. The authors would also like to thank RT Smith for fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lykken, J.; Spiropulu, M. Supersymmetry and the Crisis in Physics. Sci. Am. 2014, 310, 34–39. [Google Scholar] [CrossRef]
- Crowther, K. Defining a crisis: The roles of principles in the search for a theory of quantum gravity. Synthese 2021, 198, 3489–3516. [Google Scholar] [CrossRef]
- Meucci, S. Physics has Evolved Beyond the Physical. Cosm. Hist. J. Nat. Soc. Philos. 2020, 16, 452–465. [Google Scholar]
- Hossenfelder, S. Lost in Math: How Beauty Leads Physics Astray; Hachette: Paris, France, 2018. [Google Scholar]
- Kinzer, E.; Fukai, J. Weber’s force and Maxwell’s equations. Found. Phys. Lett. 1996, 9, 457–461. [Google Scholar] [CrossRef]
- Assis, A.K.T. Weber’s Electrodynamics; Springer: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Gray, R.W. Candid Remarks On Introductory Classical Electrodynamics and Textbooks. Preprint 2020, 1–27. [Google Scholar] [CrossRef]
- Anonymous. Advances in Weber and Maxwell Electrodynamics; Amazon Fulfillment: Wroclaw, Poland, 2018. [Google Scholar]
- Wesley, J.P. Weber electrodynamics, Part I—General theory, steady current effects. Found. Phys. Lett. 1990, 3, 443–469. [Google Scholar] [CrossRef]
- Holzmüller, G. Über die Anwendung der Jacobi-Hamilton’schen Methode auf den Fall der Anziehung nach dem Electrodynamischen Gesetze von Weber; Universität Halle-Wittenberg: Halle, Germany, 1870. [Google Scholar]
- Torres-Silva, H.; López-Bonilla, J.; López-Vázquez, R.; Rivera-Rebolledo, J. Weber’s electrodynamics for the hydrogen atom. Indones. J. Appl. Phys. 2015, 5, 39–46. [Google Scholar] [CrossRef]
- Frauenfelder, U.; Weber, J. The fine structure of Weber’s hydrogen atom: Bohr–Sommerfeld approach. Z. Angew. Math. Phys. 2019, 70, 105. [Google Scholar] [CrossRef]
- Sokolskii, A.; Sadovnikov, A. Lagrangian Solutions for Weber’s Law of Attraction. Sov. Astron. 1987, 31, 90. [Google Scholar]
- Moon, P.; Spencer, D.E.; Mirchandaney, A.S.; Shama, U.Y.; Mann, P.J. The Electrodynamics of Gauss, Neumann, and Hertz. Phys. Essays 1994, 7, 28–33. [Google Scholar] [CrossRef]
- Lorentz, H.A. La Théorie Électromagnétique de Maxwell et son Application aux Corps Mouvants; EJ Brill: Leiden, The Netherlands, 1892; Volume 25. [Google Scholar]
- McCormmach, R. HA Lorentz and the electromagnetic view of nature. Isis 1970, 61, 459–497. [Google Scholar] [CrossRef]
- Woodruff, A.E. The contributions of Hermann von Helmholtz to electrodynamics. Isis 1968, 59, 300–311. [Google Scholar] [CrossRef]
- Martínez, A.A. Ritz, Einstein, and the emission hypothesis. Phys. Perspect. 2004, 6, 4–28. [Google Scholar] [CrossRef]
- Moon, P.; Spencer, D.E. A new electrodynamics. J. Frankl. Inst. 1954, 257, 369–382. [Google Scholar] [CrossRef]
- Wheeler, J.A.; Feynman, R.P. Interaction with the absorber as the mechanism of radiation. Rev. Mod. Phys. 1945, 17, 157. [Google Scholar] [CrossRef]
- Wheeler, J.A.; Feynman, R.P. Classical electrodynamics in terms of direct interparticle action. Rev. Mod. Phys. 1949, 21, 425. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism Unabridged; Dover: New York, NY, USA, 1954. [Google Scholar]
- Yaghjian, A.D. Reflections on Maxwell’s treatise. Prog. Electromagn. Res. 2014, 149, 217–249. [Google Scholar] [CrossRef]
- Assis, A.K.T.; Silva, H.T. Comparison between Weber’s electrodynamics and classical electrodynamics. Pramana 2000, 55, 393–404. [Google Scholar] [CrossRef]
- O’Rahilly, A. Electromagnetic Theory: A Critical Examination of Fundamentals; Dover Publications: New York, NY, USA, 1965; Volumes I and II. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Darwin, C.G. LI. The dynamical motions of charged particles. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1920, 39, 537–551. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Electrodynamics of Continuous Media, 2nd ed.; Pergamon: Oxford, UK, 1985. [Google Scholar]
- Page, L.; Adams, N.I., Jr. Action and reaction between moving charges. Am. J. Phys. 1945, 13, 141–147. [Google Scholar] [CrossRef]
- Steane, A.M. Nonexistence of the self-accelerating dipole and related questions. Phys. Rev. D 2014, 89, 125006. [Google Scholar] [CrossRef]
- Cornille, P. The Lorentz force and Newton’s third principle. Can. J. Phys. 1995, 73, 619–625. [Google Scholar] [CrossRef]
- Cornille, P. Review of the application of Newton’s third law in physics. Prog. Energy Combust. Sci. 1999, 25, 161–210. [Google Scholar] [CrossRef]
- Sebens, C.T. Forces on fields. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2018, 63, 1–11. [Google Scholar] [CrossRef]
- Assis, A.; Peixoto, F. On the velocity in the Lorentz force law. Phys. Teach. 1992, 30, 480–483. [Google Scholar] [CrossRef][Green Version]
- Tran, M. Evidence for Maxwell’s equations, fields, force laws and alternative theories of classical electrodynamics. Eur. J. Phys. 2018, 39, 063001. [Google Scholar] [CrossRef]
- Pietsch, W. On conceptual issues in classical electrodynamics: Prospects and problems of an action-at-a-distance interpretation. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2010, 41, 67–77. [Google Scholar] [CrossRef]
- Lazarovici, D. Against fields. Eur. J. Philos. Sci. 2018, 8, 145–170. [Google Scholar] [CrossRef]
- Muller, F.A. Inconsistency in classical electrodynamics? Philos. Sci. 2007, 74, 253–277. [Google Scholar] [CrossRef]
- Frisch, M. Inconsistency, Asymmetry, and Non-Locality: A Philosophical Investigation of Classical Electrodynamics; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Feynman, R.P. Space-time approach to quantum electrodynamics. In Selected Papers of Richard Feynman; Brown, L.M., Ed.; World Scientific: Singapore, 2000; pp. 99–119. [Google Scholar]
- Dirac, P.A.M. The evolution of the physicist’s picture of nature. Sci. Am. 1963, 208, 45–53. [Google Scholar] [CrossRef]
- Kastner, R.E. Haag’s Theorem as a Reason to Reconsider Direct-Action Theories. arXiv 2015, arXiv:1502.03814. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics; Pearson Prentice Hall: Hoboken, NJ, USA, 2005. [Google Scholar]
- Cullwick, E.G. Electromagnetism and Relativity: With Particular Reference to Moving Media and Electromagnetic Induction; Longmans: London, UK, 1959. [Google Scholar]
- Moon, P.H.; Spencer, D.E. Foundations of Electrodynamics; Boston Technical Publishers Inc: Cambridge, MA, USA, 1965. [Google Scholar]
- Lorrain, P.; Corson, D.R. Electromagnetic Fields and Waves; Courier Corporation: North Chelmsford, MA, USA, 1970. [Google Scholar]
- Maxwell, J.C. XXV. On physical lines of force: Part I—the theory of molecular vortices applied to magnetic phenomena. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1861, 21, 161–175. [Google Scholar] [CrossRef]
- Weber, W.E. Wilhelm Weber’s Werke; First Part; Julius Springer: Berlin, Germany, 1893; Volume 3. [Google Scholar]
- Weber, W.E. Wilhelm Weber’s Werke; Second Part; Julius Springer: Berlin, Germany, 1893; Volume 4. [Google Scholar]
- Weber, W. Determinations of Electrodynamic Measure: Concerning a Universal Law of Electrical Action; 21st Century Science and Technology: Leesburg, VA, USA, 2007. [Google Scholar]
- Weber, W. Electrodynamic Measurements, Especially Measures of Resistance. 2021. Available online: https://www.ifi.unicamp.br/~assis/Weber-EM2.pdf (accessed on 5 July 2022).
- Weber, W. Electrodynamic Measurements, Especially on Diamagnetism. 2021. Available online: https://www.ifi.unicamp.br/~assis/Weber-EM3.pdf (accessed on 5 July 2022).
- Kohlrausch, R.; Weber, W. Electrodynamic Measurements, Especially Attributing Mechanical Units to Measures of Current Intensity. 2021. Available online: http://www.ifi.unicamp.br/~assis/Weber-EM4.pdf (accessed on 5 July 2022).
- Weber, W. Electrodynamic Measurements, Especially on Electric Oscillations. 2021. Available online: http://www.ifi.unicamp.br/~assis/Weber-EM5.pdf (accessed on 5 July 2022).
- Weber, W. Electrodynamic measurements—Sixth memoir, relating specially to the principle of the conservation of energy. Lond. Edinb. Dublin Philos. Mag. J. Sci. Fourth Ser. 1872, 43, 1–20. [Google Scholar]
- Weber, W. Electrodynamic Measurements, Especially on the Energy of Interaction. 2021. Available online: http://www.ifi.unicamp.br/~assis/Weber-EM7.pdf (accessed on 5 July 2022).
- Weber, W. Determinations of Electrodynamic Measure: Particularly in Respect to the Connection of the Fundamental Laws of Electricity with the Law of Gravitation; 21st Century Science and Technology: Leesburg, VA, USA, 2021; Available online: https://www.ifi.unicamp.br/~assis/Weber_EM8.pdf (accessed on 5 July 2022).
- Davies, P. A quantum theory of Wheeler–Feynman electrodynamics. In Proceedings of the Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1970; Volume 68, pp. 751–764. [Google Scholar] [CrossRef]
- Wesley, J. Weber electrodynamics, part II unipolar induction, Z-antenna. Found. Phys. Lett. 1990, 3, 471–490. [Google Scholar] [CrossRef]
- Wesley, J.P. Weber electrodynamics: Part III. mechanics, gravitation. Found. Phys. Lett. 1990, 3, 581–605. [Google Scholar] [CrossRef]
- Assis, A.K.T. Deriving Ampere’s law from Weber’s law. Hadron. J. 1990, 13, 441–451. [Google Scholar]
- Moyssides, P.G. Calculation of the sixfold integrals of the Ampere force law in a closed circuit. IEEE Trans. Magn. 1989, 25, 4307–4312. [Google Scholar] [CrossRef]
- Cavalleri, G.; Bettoni, G.; Tonni, E.; Spavieri, G. Experimental proof of standard electrodynamics by measuring the self-force on a part of a current loop. Phys. Rev. E 1998, 58, 2505. [Google Scholar] [CrossRef]
- Assis, A.K.T. Comment on “Experimental proof of standard electrodynamics by measuring the self-force on a part of a current loop”. Phys. Rev. E 2000, 62, 7544. [Google Scholar] [CrossRef]
- Assis, A.K.T.; Bueno, M.A. Equivalence between Ampere and Grassmann’s forces. IEEE Trans. Magn. 1996, 32, 431–436. [Google Scholar] [CrossRef]
- Bueno, M.; Assis, A.K.T. Proof of the identity between Ampère and Grassmann’s forces. Phys. Scr. 1997, 56, 554. [Google Scholar] [CrossRef]
- Assis, A.K.; Bueno, M. Bootstrap effect in classical electrodynamics. Rev. Fac. Ing. 2000, 7, 49–55. [Google Scholar]
- Hofmann, J.R. André-Marie Ampère: Enlightenment and Electrodynamics; Cambridge University Press: Cambridge, UK, 1996; Volume 7. [Google Scholar]
- Ampère, A.M. Mémoire présenté à l’Académie royale des Sciences, le 2 octobre 1820, où se trouve compris le résumé de ce qui avait été lu à la même Académie les 18 et 25 septembre 1820, sur les effets des courans électriques. In Proceedings of the Annales de Chimie et de Physique, Paris, France, 2 October 1820; Volume 15, pp. 59–76. [Google Scholar]
- Ampère, A. The effects of electric currents. In Early Electrodynamics—The First Law of Circulation; Tricker, R.A.R., Ed.; Pergamon: Oxford, UK, 1965; pp. 140–154. [Google Scholar]
- Assis, A.; Souza Filho, M.; Caluzi, J.; Chaib, J. From Electromagnetism to Electrodynamics: Ampère’s Demonstration of the Interaction between Current Carrying Wires. In Proceedings of the 4th International Conference on Hands-on Science, University of Azores, Ponta Delgada, Portugal, 23 July 2007; pp. 9–16. [Google Scholar]
- Chaib, J.; Lima, F. Resuming Ampère’s experimental investigation of the validity of Newton’s third law in electrodynamics. Ann. Fond. Louis Broglie 2020, 45, 19. [Google Scholar]
- Graneau, P. Electromagnetic jet-propulsion in the direction of current flow. Nature 1982, 295, 311. [Google Scholar] [CrossRef]
- Graneau, P. Application of Ampere’s force law to railgun accelerators. J. Appl. Phys. 1982, 53, 6648–6654. [Google Scholar] [CrossRef]
- Graneau, P. First indication of Ampere tension in solid electric conductors. Phys. Lett. A 1983, 97, 253–255. [Google Scholar] [CrossRef]
- Graneau, P. Ampere tension in electric conductors. IEEE Trans. Magn. 1984, 20, 444–455. [Google Scholar] [CrossRef][Green Version]
- Graneau, P. Ampère-Neumann Electrodynamics of Metals; Hadronic Press, Inc.: Nonantum, MA, USA, 1985. [Google Scholar]
- Graneau, P. The Ampere-Neumann Electrodynamics of Metallic Conductors. Fortschritte Der Phys. 1986, 34, 457–501. [Google Scholar]
- Graneau, P.; Graneau, N. The electromagnetic impulse pendulum and momentum conservation. Il Nuovo Cimento D 1986, 7, 31–45. [Google Scholar] [CrossRef]
- Graneau, P. Amperian recoil and the efficiency of railguns. J. Appl. Phys. 1987, 62, 3006–3009. [Google Scholar] [CrossRef]
- Graneau, P.; Thompson, D.S.; Morrill, S.L. The motionally induced back-emf in railguns. Phys. Lett. A 1990, 145, 396–400. [Google Scholar] [CrossRef]
- Graneau, P.; Graneau, N. The role of Ampere forces in nuclear fusion. Phys. Lett. A 1992, 165, 1–13. [Google Scholar] [CrossRef]
- Assis, A.K.T. On the mechanism of railguns. Galilean Electrodyn. 1992, 3, 93–95. [Google Scholar]
- Nasiłowski, J. A note on longitudinal Ampere forces in gaseous conductors. Phys. Lett. A 1985, 111, 315–316. [Google Scholar] [CrossRef]
- Pappas, P. The original Ampere force and Biot-Savart and Lorentz forces. Il Nuovo Cimento B (1971–1996) 1983, 76, 189–197. [Google Scholar] [CrossRef]
- Phipps, T.; Phipps, T., Jr. Observation of Ampere forces in mercury. Phys. Lett. A 1990, 146, 6–14. [Google Scholar] [CrossRef]
- Phipps, T.E. New evidence for Ampère longitudinal forces. Phys. Essays 1990, 3, 198. [Google Scholar] [CrossRef]
- Wesley, J. Pinch effect and Ampere tension to drive Hering’s pump. Found. Phys. Lett. 1994, 7, 95–104. [Google Scholar] [CrossRef]
- Peoglos, V. Measurement of the magnetostatic force of a current circuit on a part of itself. J. Phys. D Appl. Phys. 1988, 21, 1055. [Google Scholar] [CrossRef]
- Achilles, R. Again on the Guala-Valverde homopolar induction experiments. Spacetime Subst. 2002, 3, 235. [Google Scholar]
- Achilles, R.; Guala-Valverde, J. Action at a Distance: A Key to Homopolar Induction. Apeiron Stud. Infin. Nat. 2007, 14, 169–183. [Google Scholar]
- Guala-Valverde, J.; Achilles, R. A Manifest Failure of Grassmann’s Force. Apeiron Stud. Infin. Nat. 2008, 15, 202–205. [Google Scholar]
- Papageorgiou, C.; Raptis, T. Fragmentation of Thin Wires Under High Power Pulses and Bipolar Fusion. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2010; Volume 1203, pp. 955–960. [Google Scholar] [CrossRef]
- Alfaro, A.D. Ampre’s Longitudinal Forces Revisited; Technical Report; Naval Postgraduate School, United States: Monterey, CA, USA, 2018. [Google Scholar]
- Pappas, P.; Pappas, L.; Pappas, T. Ampère cardinal forces-electrodynamics—Proof and prediction of empirical Faraday induction. Phys. Essays 2014, 27, 570–579. [Google Scholar] [CrossRef]
- Rambaut, M.; Vigier, J. The simultaneous existence of EM Grassmann-Lorentz forces (acting on charged particles) and Ampère forces (acting on charged conducting elements) does not contradict relativity theory. Phys. Lett. A 1989, 142, 447–452. [Google Scholar] [CrossRef]
- Rambaut, M.; Vigier, J. Ampere forces considered as collective non-relativistic limit of the sum of all Lorentz interactions acting on individual current elements: Possible consequences for electromagnetic discharge stability and tokamak behaviour. Phys. Lett. A 1990, 148, 229–238. [Google Scholar] [CrossRef]
- Moyssides, P.G. The anticipated longitudinal forces by the Biot-Savart-Grassmann-Lorentz force law are in complete agreement with the longitudinal Ampère forces. Eur. Phys. J. Plus 2014, 129, 1–17. [Google Scholar] [CrossRef]
- Saumont, R. Ampère Force: Experimental Tests. In Advanced Electromagnetism: Foundations, Theory and Applications; World Scientific: Singapore, 1995; pp. 620–635. [Google Scholar]
- Graneau, N.; Phipps, T., Jr.; Roscoe, D. An experimental confirmation of longitudinal electrodynamic forces. Eur. Phys. J. D At. Mol. Opt. Plasma Phys. 2001, 15, 87–97. [Google Scholar] [CrossRef]
- Kühn, S. Experimental investigation of an unusual induction effect and its interpretation as a necessary consequence of Weber electrodynamics. J. Electr. Eng. 2021, 72, 366–373. [Google Scholar] [CrossRef]
- Einstein, A. Zur elektrodynamik bewegter körper. Ann. Der Phys. 1905, 354, 769–822. [Google Scholar] [CrossRef]
- Frisch, D.H.; Wilets, L. Development of the Maxwell-Lorentz equations from special relativity and Gauss’s law. Am. J. Phys. 1956, 24, 574–579. [Google Scholar] [CrossRef]
- Field, J. Derivation of the Lorentz force law, the magnetic field concept and the Faraday–Lenz and magnetic Gauss laws using an invariant formulation of the Lorentz transformation. Phys. Scr. 2006, 73, 639. [Google Scholar] [CrossRef]
- Dodig, H. Direct derivation of Lienard–Wiechert potentials, Maxwell’s equations and Lorentz force from Coulomb’s law. Mathematics 2021, 9, 237. [Google Scholar] [CrossRef]
- Smith, R.T.; Jjunju, F.P.; Maher, S. Evaluation of Electron Beam Deflections across a Solenoid Using Weber-Ritz and Maxwell-Lorentz Electrodynamics. Prog. Electromagn. Res. 2015, 151, 83–93. [Google Scholar] [CrossRef][Green Version]
- Smith, R.T.; Maher, S. Investigating Electron Beam Deflections by a Long Straight Wire Carrying a Constant Current Using Direct Action, Emission-Based and Field Theory Approaches of Electrodynamics. Prog. Electromagn. Res. 2017, 75, 79–89. [Google Scholar] [CrossRef][Green Version]
- Baumgärtel, C.; Smith, R.T.; Maher, S. Accurately predicting electron beam deflections in fringing fields of a solenoid. Sci. Rep. 2020, 10, 10903. [Google Scholar] [CrossRef] [PubMed]
- Baumgärtel, C.; Maher, S. A Charged Particle Model Based on Weber Electrodynamics for Electron Beam Trajectories in Coil and Solenoid Elements. Prog. Electromagn. Res. C 2022, 123, 151–166. [Google Scholar] [CrossRef]
- Li, Q. Electric Field Theory Based on Weber’s Electrodynamics. Int. J. Magn. Electromagn. 2021, 7, 1–6. [Google Scholar]
- Kühn, S. The Inhomogeneous Wave Equation, Liénard-Wiechert Potentials, and Hertzian Dipole in Weber Electrodynamics. 2022. Available online: https://www.researchgate.net/publication/358747323_The_inhomogeneous_wave_equation_Lienard-Wiechert_potentials_and_Hertzian_dipole_in_Weber_electrodynamics (accessed on 5 July 2022). [CrossRef]
- Rambaut, M. Macroscopic non-relativistic Ampère EM interactions between current elements reflect the conducting electron accelerations by the ion’s electric fields. Phys. Lett. A 1991, 154, 210–214. [Google Scholar] [CrossRef]
- Weber, W.; Kohlrausch, R. Ueber die Elektricitätsmenge, welche bei galvanischen Strömen durch den Querschnitt der Kette fliesst. Ann. Phys. 1856, 175, 10–25. [Google Scholar] [CrossRef]
- Assis, A.K. On the first electromagnetic measurement of the velocity of light by Wilhelm Weber and Rudolf Kohlrausch. In Volta and the History of Electricity; Università degli Studi di Pavia and Editore Ulrico Hoepli: Milano, Italy, 2003; pp. 267–286. [Google Scholar]
- Kirchhoff, G. Ueber die Bewegung der Elektricität in Leitern. Ann. Phys. 1857, 178, 529–544. [Google Scholar] [CrossRef]
- Weber, W. Elektrodynamische Maassbestimmungen Insbesondere über Elektrische Schwingungen; Teubner: Leipzig, Germany, 1864; Volume 6, pp. 105–241. [Google Scholar]
- Assis, A.K.T.; Hernandes, J. Telegraphy equation from Weber’s electrodynamics. IEEE Trans. Circuits Syst. II Express Briefs 2005, 52, 289–292. [Google Scholar] [CrossRef]
- Fukai, J. A Promenade Along Electrodynamics; Vales Lake Publishing: Pueblo West, CO, USA, 2003. [Google Scholar]
- Assis, A.K.T. Circuit theory in Weber electrodynamics. Eur. J. Phys. 1997, 18, 241. [Google Scholar] [CrossRef]
- Bueno, M.; Assis, A.K.T. Equivalence between the formulas for inductance calculation. Can. J. Phys. 1997, 75, 357–362. [Google Scholar] [CrossRef]
- McDonald, K.T. Weber’s Electrodynamics and the Hall Effect. 2020, pp. 1–15. Available online: http://kirkmcd.princeton.edu/examples/weber.pdf (accessed on 5 July 2022).
- Smith, R.T.; Taylor, S.; Maher, S. Modelling electromagnetic induction via accelerated electron motion. Can. J. Phys. 2014, 93, 802–806. [Google Scholar] [CrossRef]
- Smith, R.T.; Jjunju, F.P.; Young, I.S.; Taylor, S.; Maher, S. A physical model for low-frequency electromagnetic induction in the near field based on direct interaction between transmitter and receiver electrons. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160338. [Google Scholar] [CrossRef]
- Assis, A.K.; Thober, D.S. Unipolar induction and Weber’s electrodynamics. In Frontiers of Fundamental Physics; Springer: Berlin, Germany, 1994; pp. 409–414. [Google Scholar]
- Baumgärtel, C.; Maher, S. A Novel Model of Unipolar Induction Phenomena Based on Direct Interaction Between Conductor Charges. Prog. Electromagn. Res. 2021, 171, 123–135. [Google Scholar] [CrossRef]
- Baumgärtel, C.; Maher, S. Resolving the Paradox of Unipolar Induction—New Experimental Evidence on the Influence of the Test Circuit. Sci. Rep. 2022, 12, 16791. [Google Scholar] [CrossRef]
- Härtel, H. Unipolar Induction-a Messy Corner of Electromagnetism. Eur. J. Phys. Educ. 2020, 11, 47–59. [Google Scholar]
- Assis, A.K.T.; Fukai, J.; Carvalho, H. Weberian induction. Phys. Lett. A 2000, 268, 274–278. [Google Scholar] [CrossRef]
- Feynman, R. Lectures in Physics; Chapter 17 The Laws of Induction; California Institute of Technology: Pasadena, CA, USA, 1963; Volume II. [Google Scholar]
- Ma, T.C.E. Field angular momentum in Feynman’s disk paradox. Am. J. Phys. 1986, 54, 949–950. [Google Scholar] [CrossRef]
- Prytz, K.A. Meissner effect in classical physics. Prog. Electromagn. Res. 2018, 64, 1–7. [Google Scholar] [CrossRef][Green Version]
- Assis, A.; Tajmar, M. Superconductivity with Weber’s electrodynamics: The London moment and the Meissner effect. Ann. Fond. Louis Broglie 2017, 42, 307. [Google Scholar]
- Wesley, J. Induction Produces Aharonov-Bohm Effect. Apeiron 1998, 5, 73–82. [Google Scholar]
- Prytz, K. Antenna Theory—The Loop and the Dipole. In Electrodynamics: The Field-Free Approach; Springer: Berlin, Germany, 2015; pp. 219–238. [Google Scholar]
- Assis, A.K.T.; Wiederkehr, K.H.; Wolfschmidt, G. Weber’s Planetary Model of the Atom; Tredition Science: Hamburg, Germany, 2011. [Google Scholar]
- Weber, W.E. Electrodynamische Maassbestimmungen; S. Hirzel: Leipzig, Germany, 1871; Volume 2. [Google Scholar]
- Bush, V. The force between moving charges. J. Math. Phys. 1926, 5, 129–157. [Google Scholar] [CrossRef]
- Clemente, R.; Assis, A.K.T. Two-body problem for Weber-like interactions. Int. J. Theor. Phys. 1991, 30, 537–545. [Google Scholar] [CrossRef]
- Riecke, E. Ueber Molecularbewegung zweier Theilchen, deren Wechselwirkung durch das webersche Gesetz der elektrischen Kraft bestimmt wird. In Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen; Dieterich: Göttingen, Germany, 1874; p. 665. [Google Scholar]
- Lolling, G. Ueber Bewegungen elektrischer Theilchen nach dem Weber’schen Grundgesetz der Elektrodynamik. In Verhandlungen der Kaiserlichen Leopoldinisch-Carolinischen Deutschen Akademie der Naturforscher; Kaiserlich-Leopoldinisch-Carolinische Deutsche Akademie der Naturforscher: Halle, Germany, 1882; Volume 44, pp. 273–336. [Google Scholar]
- Ritter, E., II. Bewegung eines materiellen mit Eletricität geladenen Theilchens unter der Einwirkung eines ruhenden Centrum bei Giltigkeit des Weber’schen Gesetzes. Z. Math. Und Phys. Organ Angew. Math. 1892, 37, 8–24. [Google Scholar]
- Zöllner, J.F. Principien einer Elektrodynamischen Theorie der Materie; Engelmann: Leipzig, Germany, 1876; Volume 1. [Google Scholar]
- Wesley, J.P. Evidence for Weber–Wesley electrodynamics. In Proceedings of the Conference on Foundations of Mathematics and Physics, Perugia, Italy, 27–29 September 1989; pp. 27–29. [Google Scholar]
- Post, E.J. A Tale of Fine Structure Coincidences. In Quantum Reprogramming; Springer: Berlin, Germany, 1995; pp. 151–168. [Google Scholar]
- Pearson, J.; Kilambi, A. Velocity-dependent nuclear forces and Weber’s electrodynamics. Am. J. Phys. 1974, 42, 971–975. [Google Scholar] [CrossRef]
- Assis, A.K.T. Deriving gravitation from electromagnetism. Can. J. Phys. 1992, 70, 330–340. [Google Scholar] [CrossRef]
- Assis, A.K.T. Gravitation as a fourth order electromagnetic effect. In Advanced Electromagnetism: Foundations, Theory and Applications; Barret, T.W., Gales, D.M., Eds.; World Scientific Publishers: Singapore, 1995; pp. 314–331. [Google Scholar]
- Tajmar, M. Derivation of the Planck and Fine-Structure Constant from Assis’s Gravity Model. J. Adv. Phys. 2015, 4, 219–221. [Google Scholar] [CrossRef]
- Baumgärtel, C.; Tajmar, M. The Planck Constant and the Origin of Mass Due to a Higher Order Casimir Effect. J. Adv. Phys. 2018, 7, 135–140. [Google Scholar] [CrossRef]
- Tisserand, F. Sur le Mouvement des Planètes Autour du Soleil, D’après la loi Électrodynamique de Weber; Gauthier-Villars: Paris, France, 1872. [Google Scholar]
- Gerber, P. Die räumliche und zeitliche Ausbreitung der Gravitation. Z. Math. Phys. 1898, 43, 415–444. [Google Scholar]
- Schrödinger, E. Die Erfüllbarkeit der Relativitätsforderung in der klassischen Mechanik. Ann. Phys. 1925, 382, 325–336. [Google Scholar] [CrossRef]
- Assis, A.K.T. On Mach’s principle. Found. Phys. Lett. 1989, 2, 301–318. [Google Scholar] [CrossRef]
- Tajmar, M.; Assis, A.K.T. Influence of Rotation on the Weight of Gyroscopes as an Explanation for Flyby Anomalies. J. Adv. Phys. 2016, 5, 176–179. [Google Scholar] [CrossRef][Green Version]
- Bunchaft, F.; Carneiro, S. Weber-like interactions and energy conservation. Found. Phys. Lett. 1997, 10, 393–401. [Google Scholar] [CrossRef][Green Version]
- Mendes, R.; Malacarne, L.; Assis, A. Virial Theorem For Weber’s Law. In Has the Last Word Been Said on Classical Electrodynamics? New Horizons; Chubykalo, A., Espinoza, A., Onoochin, V., Smirnov-Rueda, R., Eds.; Rinton Press: Paramus, NJ, USA, 2004; pp. 67–70. [Google Scholar]
- Clemente, R.A.; Cesar, R.G. Cold plasma oscillations according to Weber’s law. An unphysical result. Int. J. Theor. Phys. 1993, 32, 1257–1260. [Google Scholar] [CrossRef]
- Assis, A.K.T. Relational Mechanics and Implementation of Mach’s Principle with Weber’s Gravitational Force; C. Roy Keys Inc.: Montreal, QC, Canada, 2014. [Google Scholar]
- Seegers, C. Über die Bewegung und die Störungen der Planeten, Wenn Dieselben Sich Nach dem Weberschen Elektrodynamischen Gesetz um die Sonne Bewegen; Springer: Berlin, Germany, 2013. [Google Scholar]
- Servus, H. Untersuchungen über die Bahn und die Störungen der Himmelskörper mit Zugrundelegung des Weber’schen Electrodynamischen Gesetzes. Ph.D. Thesis, Universität Halle-Wittenberg, Halle, Germany, 1885. [Google Scholar]
- Zöllner, J.K.F. Über die Natur der Cometen: Beiträge zur Geschichte und Theorie der Erkenntniss; Engelmann: Leipzig, Germany, 1872. [Google Scholar]
- Eby, P. On the perihelion precession as a Machian effect. Nuovo C. Lett. 1977, 18, 93–96. [Google Scholar] [CrossRef]
- Ragusa, S. Gravitation with a modified Weber force. Found. Phys. Lett. 1992, 5, 585–589. [Google Scholar] [CrossRef]
- Lévy, M. Sur l’application des lois électrodynamiques au mouvement des planétes. Comput. Rend. Acad. Sci. 1890, 110, 545. [Google Scholar]
- Giné, J. Is gravitational quantization another consequence of General Relativity? Chaos Solitons Fractals 2009, 42, 1893–1899. [Google Scholar] [CrossRef]
- Kholodenko, A. Newtonian Limit of Einsteinian Gravity and Dynamics of Solar System. In Relativity, Gravitation, Cosmology: Foundations; Nova Science Publishers: Hauppauge, NY, USA, 2015; pp. 101–152. [Google Scholar]
- Tiandho, Y. Weber’s gravitational force as static weak field approximation. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2016; Volume 1708, p. 070012. [Google Scholar]
- Lima, F. Nonzero Gravitational Force Exerted by a Spherical Shell on a Body Moving Inside It, and Cosmological Implications. Gravit. Cosmol. 2020, 26, 387–398. [Google Scholar] [CrossRef]
- Das, S. Mach Principle and a new theory of gravitation. arXiv 2012, arXiv:1206.6755. [Google Scholar]
- Roscoe, D. Mach’S Principle and Instantaneous Action at a Distance. In Instantaneous Action at a Distance in Modern Physics: “Pro” and “Contra”; Andrew E. Chubykalo, V.P., Smirnov-Rueda, R., Eds.; Nova Science Publishers, Inc.: Commack, NY, USA, 1999; pp. 175–188. [Google Scholar]
- Assis, A. Assis, A. A steady-state cosmology. In Progress in New Cosmologies; Springer: Berlin, Germany, 1993; pp. 153–167. [Google Scholar]
- Assis, A.K.; Graneau, P. Nonlocal forces of inertia in cosmology. Found. Phys. 1996, 26, 271–283. [Google Scholar] [CrossRef]
- Graneau, P.; Graneau, N. Machian inertia and the isotropic universe. Gen. Relativ. Gravit. 2003, 35, 751–770. [Google Scholar] [CrossRef]
- Tajmar, M.; Assis, A. Gravitational induction with Weber’s force. Can. J. Phys. 2015, 93, 1571–1573. [Google Scholar] [CrossRef]
- Assis, A.K.T. Changing the inertial mass of a charged particle. J. Phys. Soc. Jpn. 1993, 62, 1418–1422. [Google Scholar] [CrossRef]
- Tajmar, M. Propellantless propulsion with negative matter generated by electric charges. In Proceedings of the AIAA Joint Propulsion Conference, AIAA-2013, San Jose, CA, USA, 14–17 July 2013; Volume 3913. [Google Scholar]
- Tajmar, M.; Assis, A.K.T. Particles with negative mass: Production, properties and applications for nuclear fusion and self-acceleration. J. Adv. Phys. 2015, 4, 77–82. [Google Scholar] [CrossRef][Green Version]
- Tajmar, M. Revolutionary Propulsion Research at TU Dresden. In Proceedings of the Advanced Propulsion Workshop, Estes Park, CO, USA, 19–22 September 2016; pp. 20–22. [Google Scholar]
- Mikhailov, V. The Action of an Electrostatic Potential on the Electron Mass. Ann. Fond. Louis Broglie 1999, 24, 161. [Google Scholar]
- Mikhailov, V.F. Influence of an electrostatic potential on the inertial electron mass. Ann. Fond. Louis Broglie 2001, 26, 633–638. [Google Scholar]
- Mikhailov, V. Influence of a field-less electrostatic potential on the inertial electron mass. Ann. Fond. Louis Broglie 2003, 28, 231. [Google Scholar]
- Junginger, J.E.; Popovic, Z.D. An experimental investigation of the influence of an electrostatic potential on electron mass as predicted by Weber’s force law. Can. J. Phys. 2004, 82, 731–735. [Google Scholar] [CrossRef]
- Lorincz, I.; Tajmar, M. Experimental Investigation of the Influence of Spatially Distributed Charges on the Inertial Mass of Moving Electrons as Predicted by Weber’s Electrodynamics. Can. J. Phys. 2017, 95, 1023. [Google Scholar] [CrossRef]
- Weikert, M.; Tajmar, M. Investigation of the Influence of a field-free electrostatic Potential on the Electron Mass with Barkhausen-Kurz Oscillation. arXiv 2019, arXiv:1902.05419. [Google Scholar]
- Tajmar, M.; Weikert, M. Evaluation of the Influence of a Field-Less Electrostatic Potential on Electron Beam Deflection as Predicted by Weber Electrodynamics. Prog. Electromagn. Res. M 2021, 105, 1–8. [Google Scholar] [CrossRef]
- Assis, A. On the unification of forces of nature. Ann. Fond. Louis Broglie 2002, 27, 149–161. [Google Scholar]
- Fricke, H. Two Rival Programmes in 19th. Century Classical Electrodynamics Action-at-a-Distance versus field Theories. Ph.D. Thesis, The London School of Economics and Political Science (LSE), London, UK, 1982. [Google Scholar]
- Clausius, R. Ueber die Ableitung eines neuen elektrodynamischen Grundgesetzes. J. Reine Angew. Math. 1877, 82, 85. [Google Scholar]
- Woodruff, A.E. Action at a distance in nineteenth century electrodynamics. Isis 1962, 53, 439–459. [Google Scholar] [CrossRef]
- Zöllner, F. Ueber die Einwendungen von Clausius gegen das Weber’sche Gesetz. Ann. Phys. 1877, 236, 514–537. [Google Scholar] [CrossRef]
- Erman, P. Über die electroskopischen Phänomene des Gasapparats an der Voltaischen Säule. Ann. Phys. 1802, 10, 1–23. [Google Scholar] [CrossRef]
- Assis, A.K.T.; Hernandes, J.A. The Electric Force of a Current: Weber and the Surface Charges of Resistive Conductors Carrying Steady Currents; Apeiron, C. Roy Keys Inc.: Montreal, QC, Canada, 2007. [Google Scholar]
- Hernandes, J.; Assis, A.K.T. Electric potential due to an infinite conducting cylinder with internal or external point charge. J. Electrost. 2005, 63, 1115–1131. [Google Scholar] [CrossRef]
- Assis, A.K.T.; Rodrigues, W.; Mania, A. The electric field outside a stationary resistive wire carrying a constant current. Found. Phys. 1999, 29, 729–753. [Google Scholar] [CrossRef]
- Caluzi, J.; Assis, A.K.T. A critical analysis of Helmholtz’s argument against Weber’s electrodynamics. Found. Phys. 1997, 27, 1445–1452. [Google Scholar] [CrossRef]
- Phipps, T.E. Toward modernization of Weber’s force law. Phys. Essays 1990, 3, 414. [Google Scholar] [CrossRef]
- Caluzi, J.; Assis, A.K.T. An analysis of Phipps’s potential energy. J. Frankl. Inst. 1995, 332, 747–753. [Google Scholar] [CrossRef]
- Li, Q. Extending Weber’s Electrodynamics to High Velocity Particles. Int. J. Magn. Electromagn. 2022, 8, 1–9. [Google Scholar]
- Assis, A.K.T. Arguments in favour of action at a distance. In Instantaneous Action at a Distance in Modern Physics: “Pro” and “Contra”; Chubykalo, A.E., Pope, V., Smimov-Rueda, R., Eds.; Nova Science Publishers: Commack, NY, USA, 1999; pp. 45–56. [Google Scholar]
- Haug, E.G. Demonstration that Newtonian gravity moves at the speed of light and not instantaneously (infinite speed) as thought! J. Phys. Commun. 2021, 5, 025005. [Google Scholar] [CrossRef]
- Brown, G.B. Retarded Action-at-a-Distance: The Change of Force with Motion; Cortney Publications: Luton, Bedfordshire, UK, 1982. [Google Scholar]
- Lentze, G. Dialogue concerning magnetic forces. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2019, 68, 158–162. [Google Scholar] [CrossRef]
- Assis, A.K.T. Weber’s law and mass variation. Phys. Lett. A 1989, 136, 277–280. [Google Scholar] [CrossRef]
- Wesley, J.P. Empirically correct electrodynamics. Found. Phys. Lett. 1997, 10, 189–204. [Google Scholar] [CrossRef]
- Assis, A.K.T.; Caluzi, J. A limitation of Weber’s law. Phys. Lett. A 1991, 160, 25–30. [Google Scholar] [CrossRef]
- Montes, J. On Limiting Velocity with Weber-like Potentials. Can. J. Phys. 2017, 95, 770–776. [Google Scholar] [CrossRef]
- Assis, A.K.T.; Clemente, R. The ultimate speed implied by theories of Weber’s type. Int. J. Theor. Phys. 1992, 31, 1063–1073. [Google Scholar] [CrossRef]
- Kühn, S. Analysis of a stochastic emission theory regarding its ability to explain the effects of special relativity. J. Electromagn. Anal. Appl. 2020, 12, 169–187. [Google Scholar] [CrossRef]
- Sherwin, C.W. The Weber Radar. Phys. Essays 1991, 4, 417–419. [Google Scholar] [CrossRef]
- Barrett, P.; Jones, H.; Franklin, R. Dispersion of electron plasma waves. Plasma Phys. 1968, 10, 911. [Google Scholar] [CrossRef]
- Wesley, J. Weber electrodynamics extended to include radiation. Specul. Sci. Technol. 1987, 10, 50–53. [Google Scholar]
- Phipps, T. Electromagnetic Force Laws and Hot Fusion. Galilean Electrodyn. 2016, 27, 79–80. [Google Scholar]
- Edwards, W.F.; Kenyon, C.; Lemon, D. Continuing investigation into possible electric fields arising from steady conduction currents. Phys. Rev. D 1976, 14, 922. [Google Scholar] [CrossRef]
- Jefimenko, O. Demonstration of the electric fields of current-carrying conductors. Am. J. Phys. 1962, 30, 19–21. [Google Scholar] [CrossRef]
- Jefimenko, O.D. Electricity and Magnetism: An Introduction to the Theory of Electric and Magnetic Fields, 2nd ed.; Electret Scientific Company: Star City, WV, USA, 1989. [Google Scholar]
- Zhao, Y. A Novel Two-Particle Steady-State Wave Equation. IRanian J. Sci. Technol. Trans. A Sci. 2022, 46, 1019–1026. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).