Hydroxyl Spectroscopy of Laboratory Air Laser-Ignition
Abstract
1. Introduction
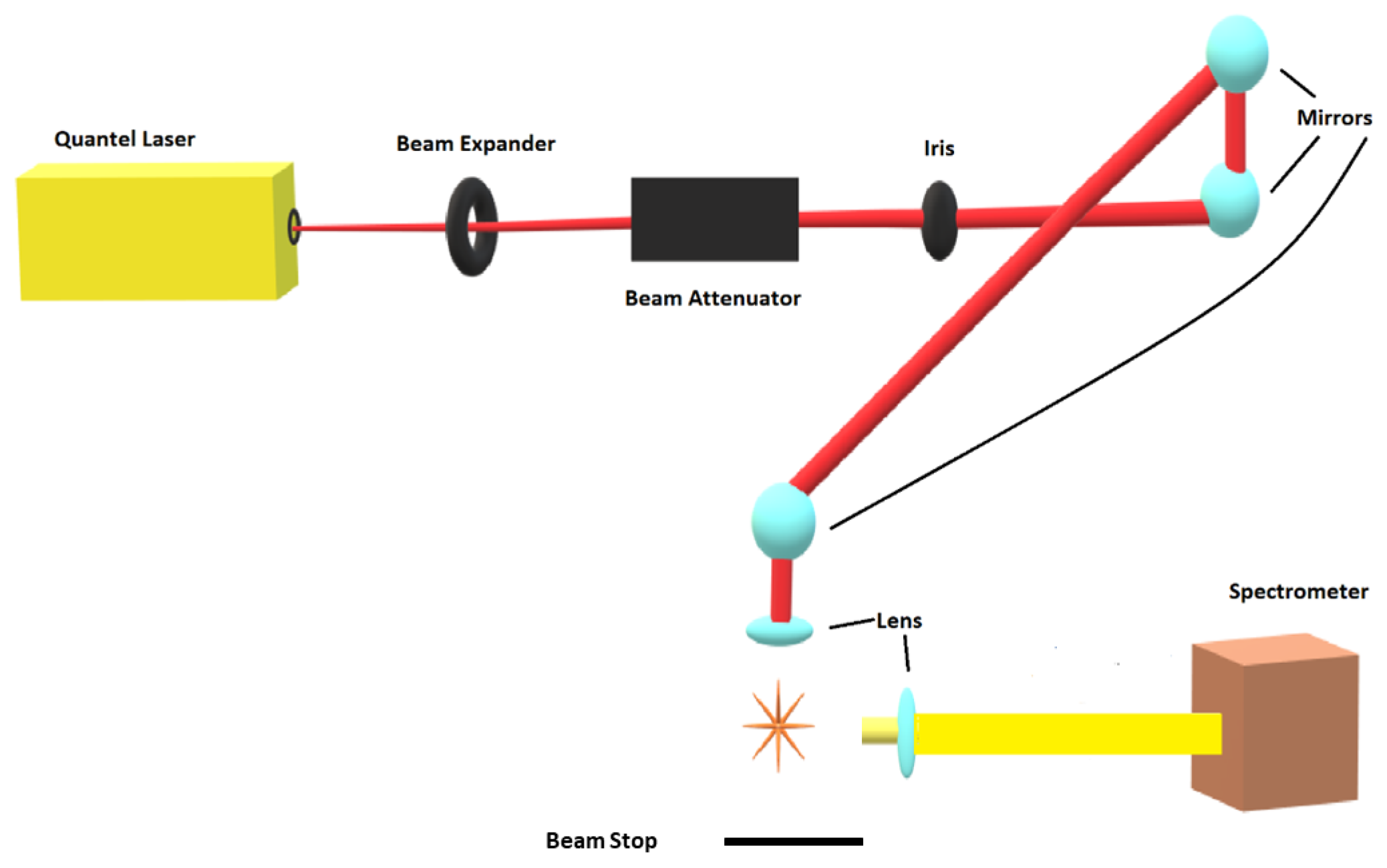
2. Materials and Methods
3. Results and Discussion
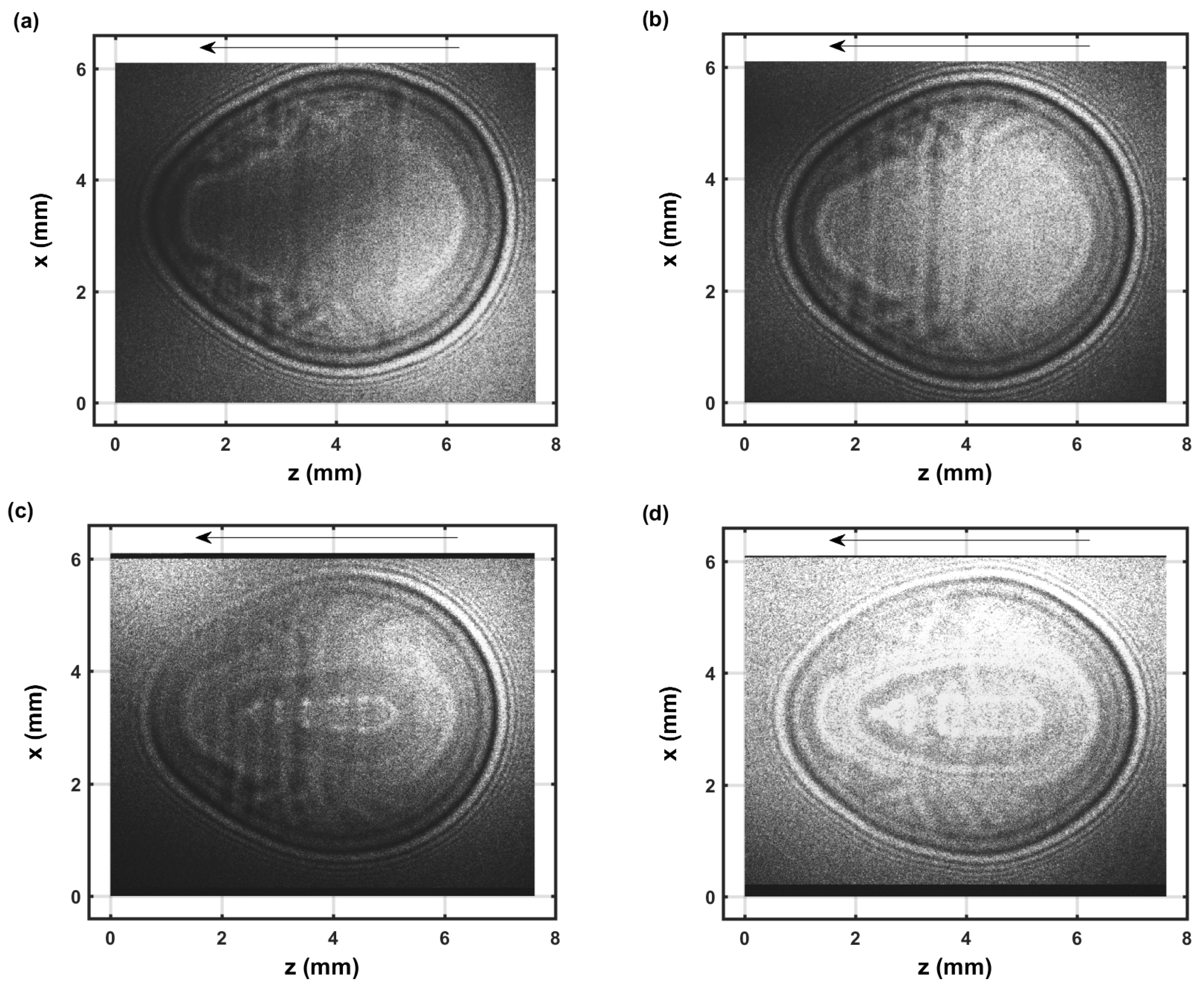
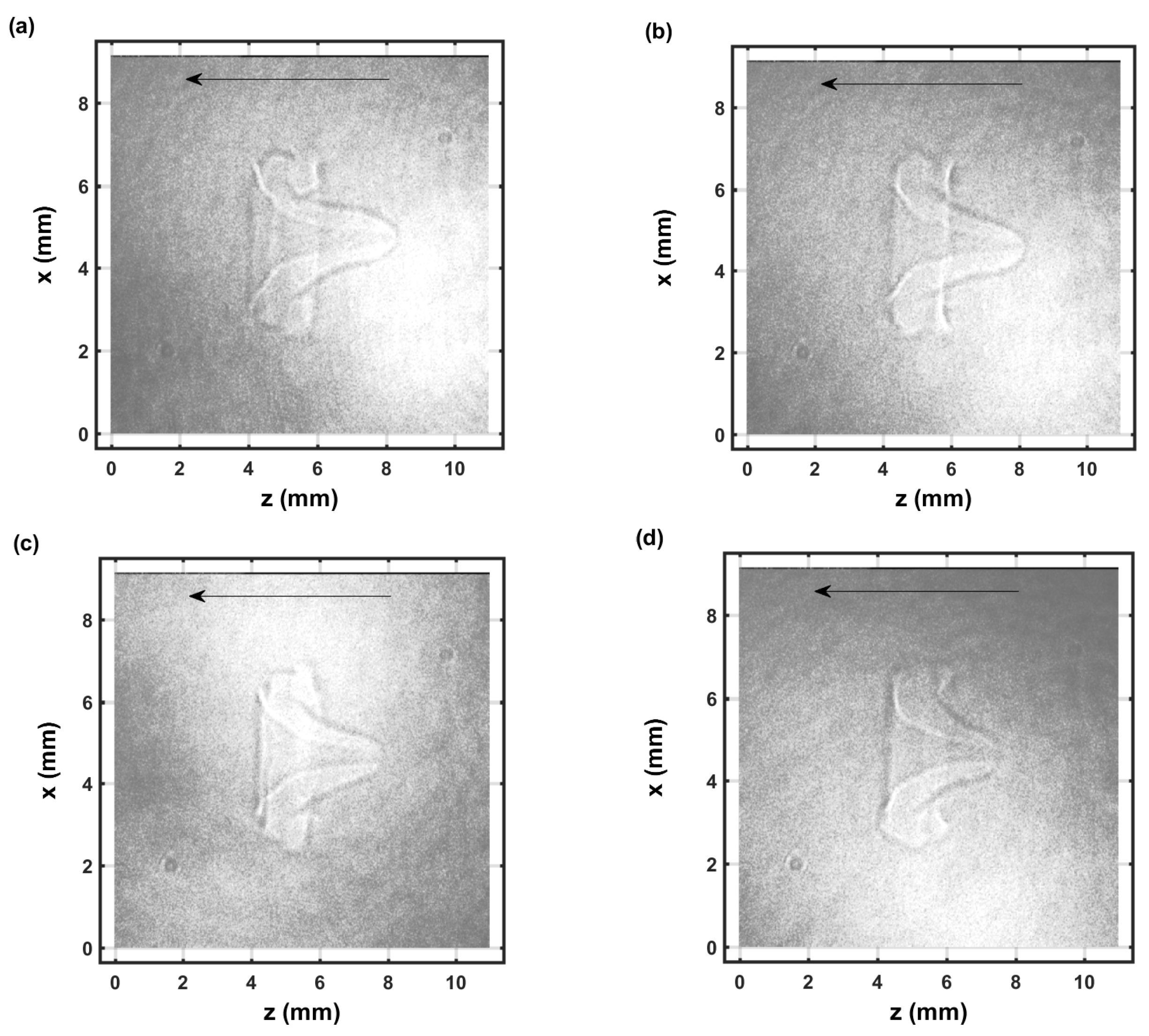
3.1. Shadow Graphs
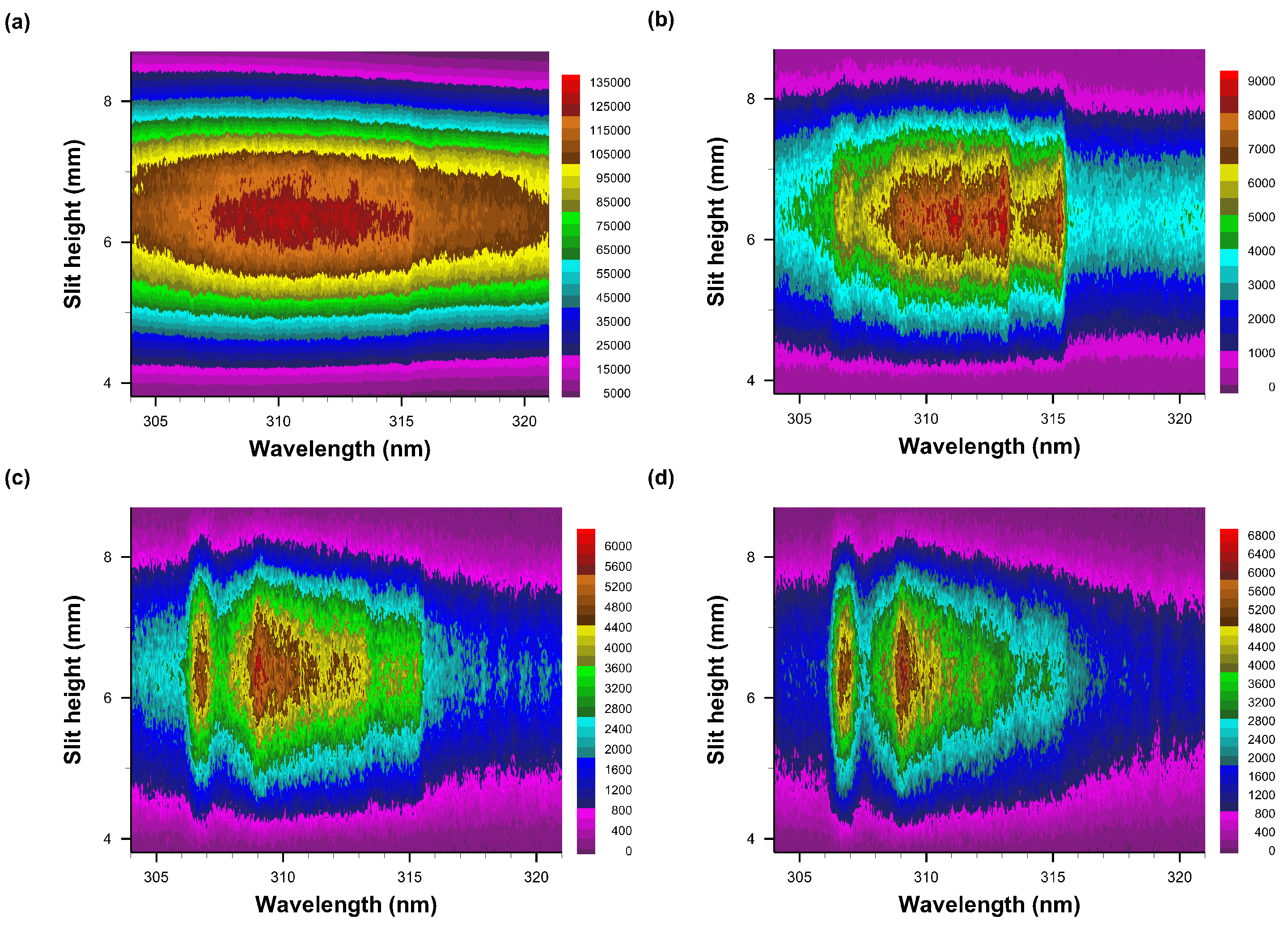
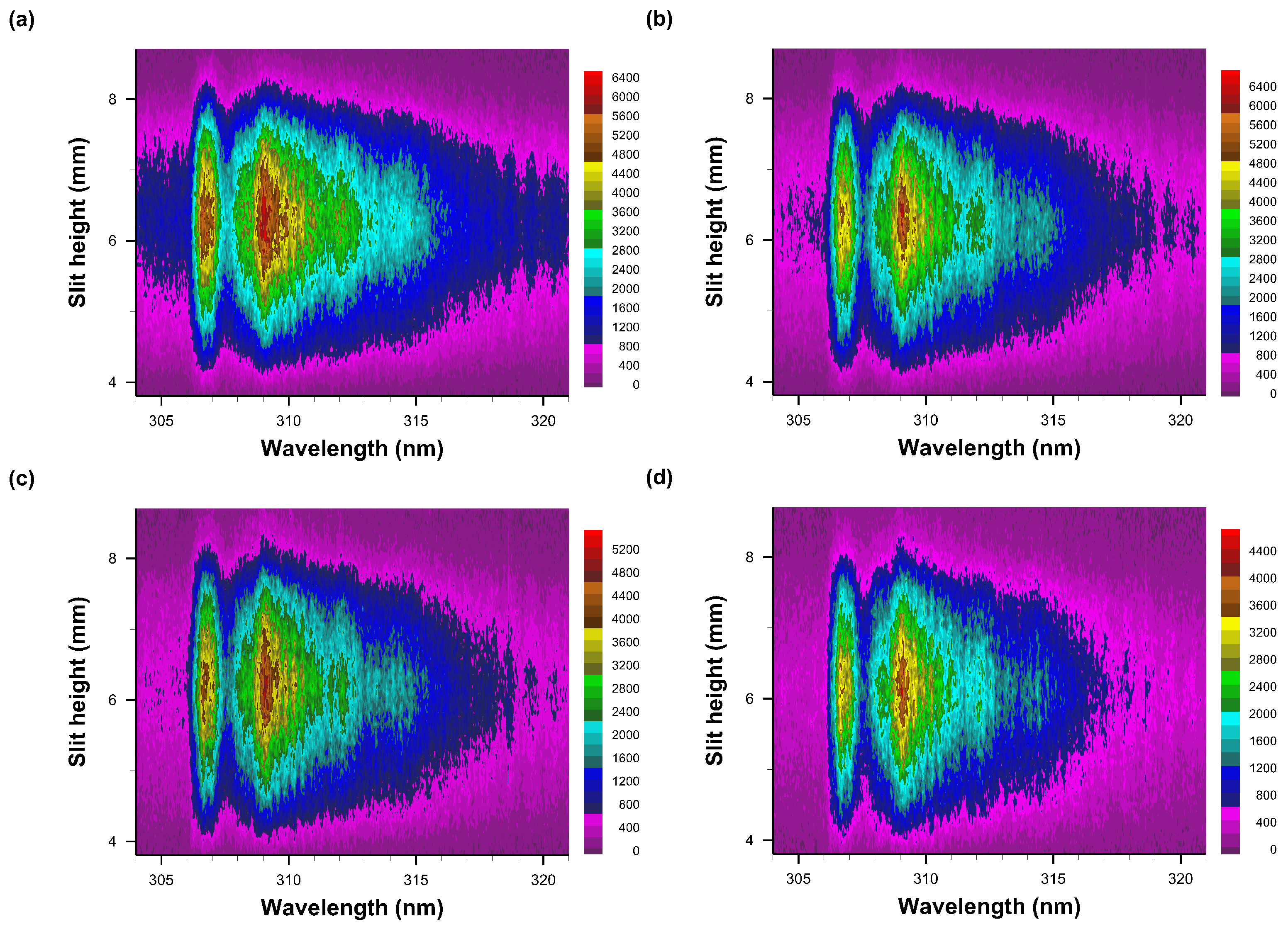
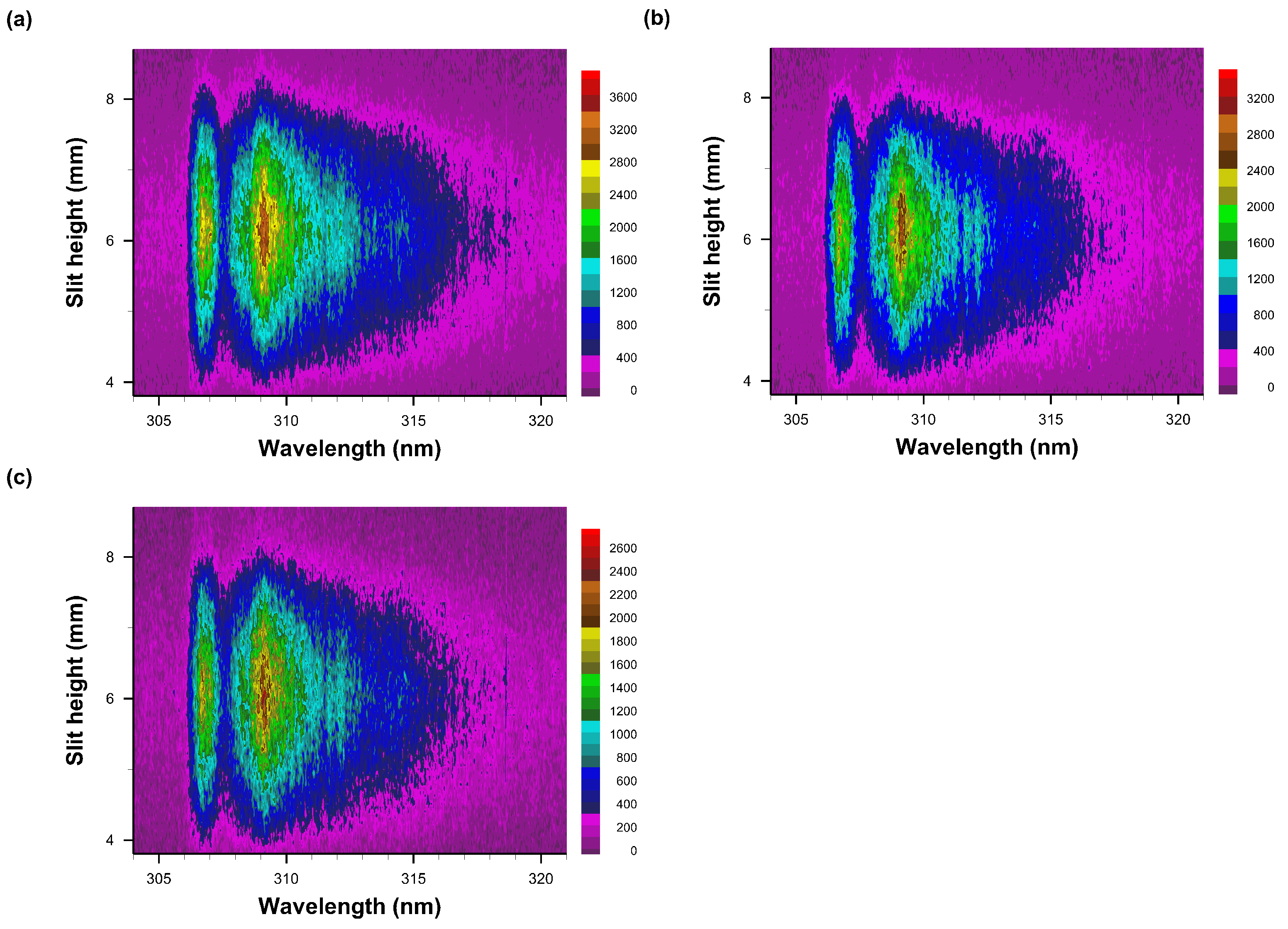
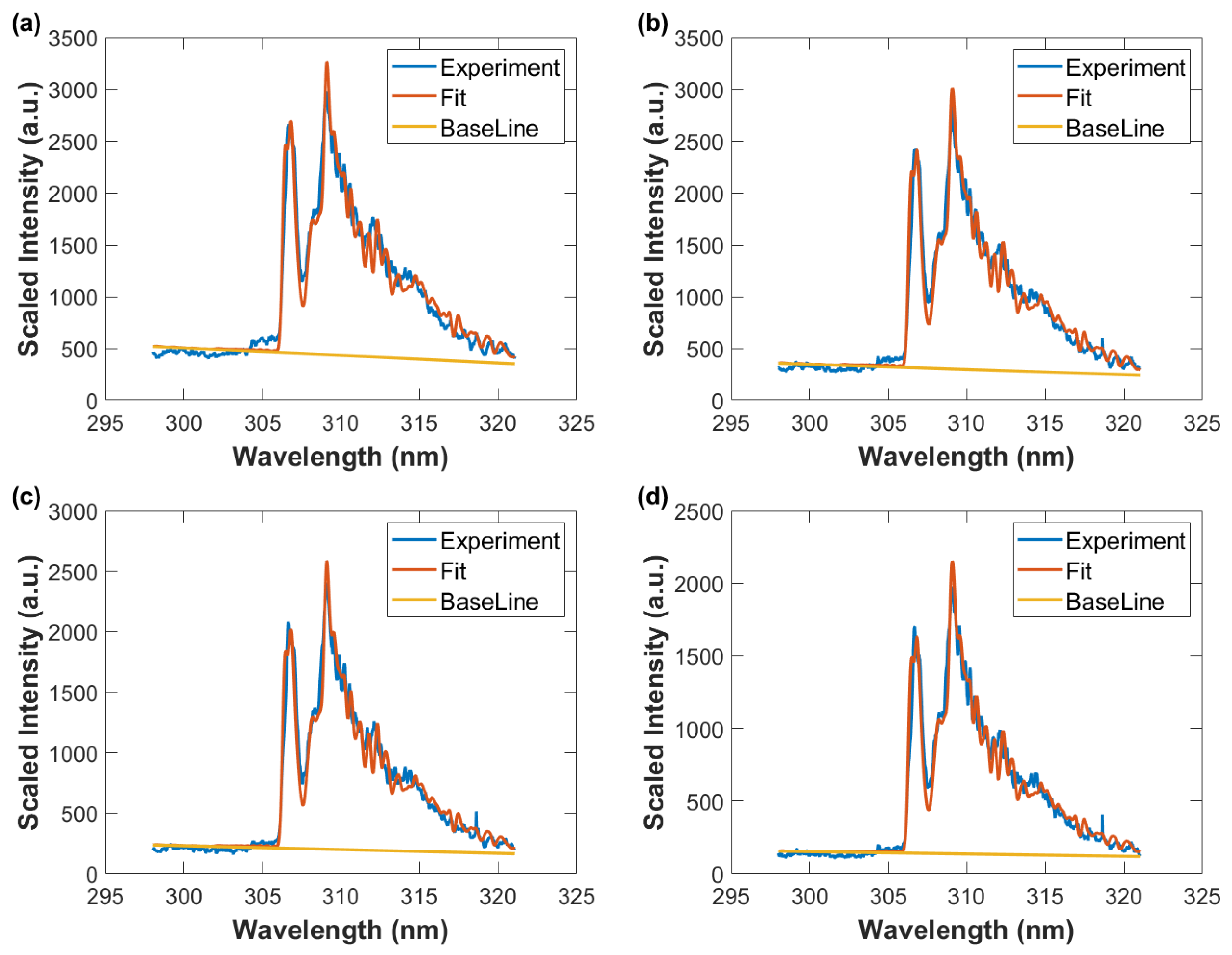
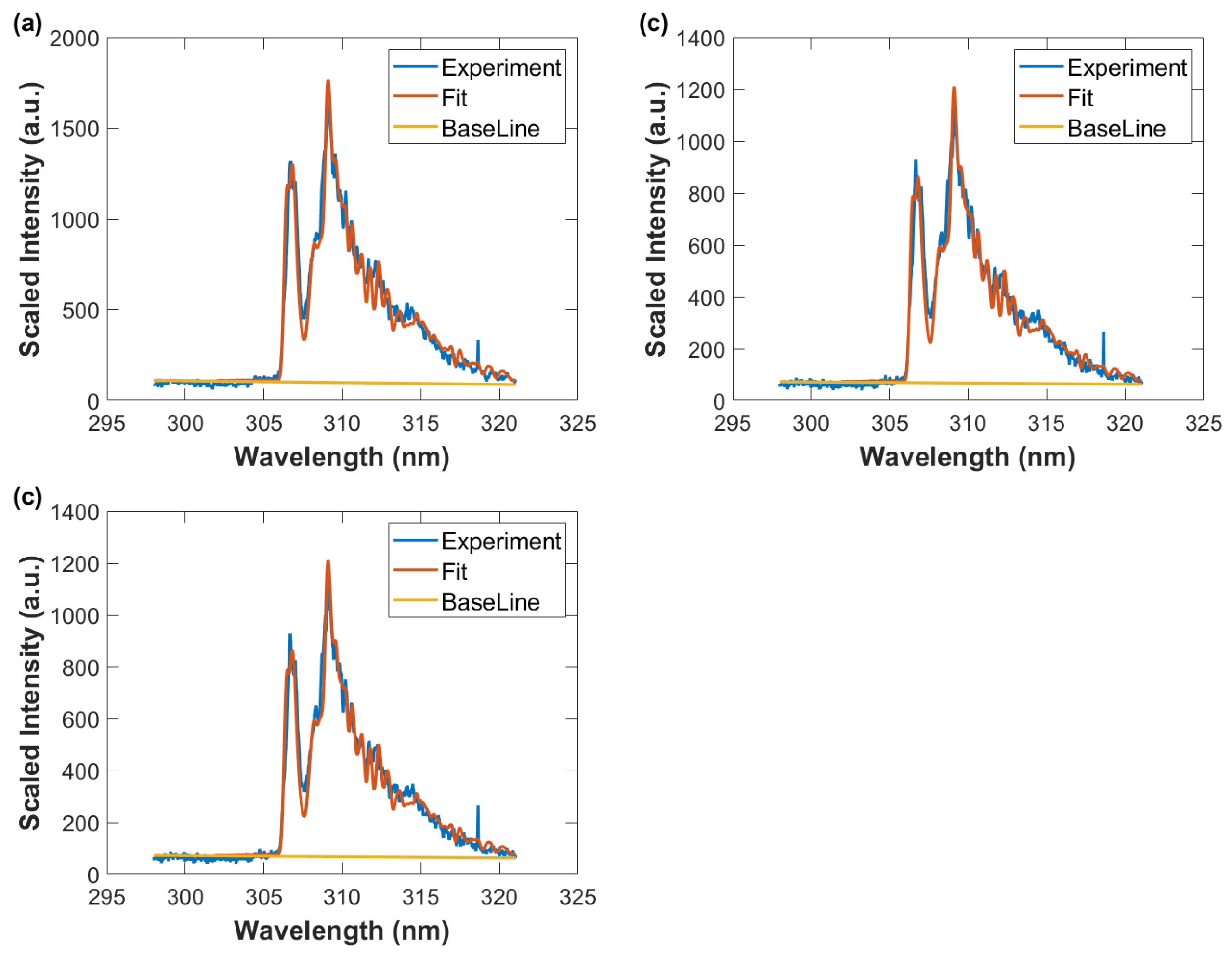
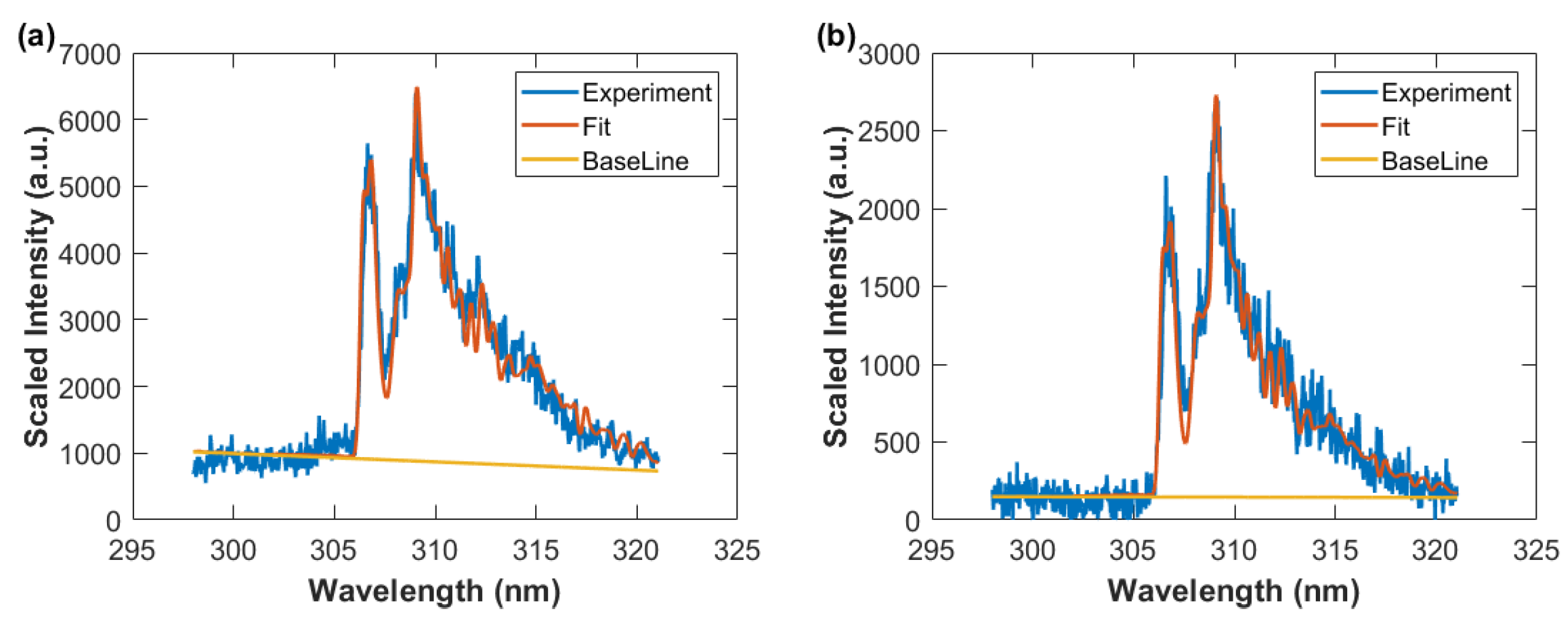
3.2. Emission Spectra
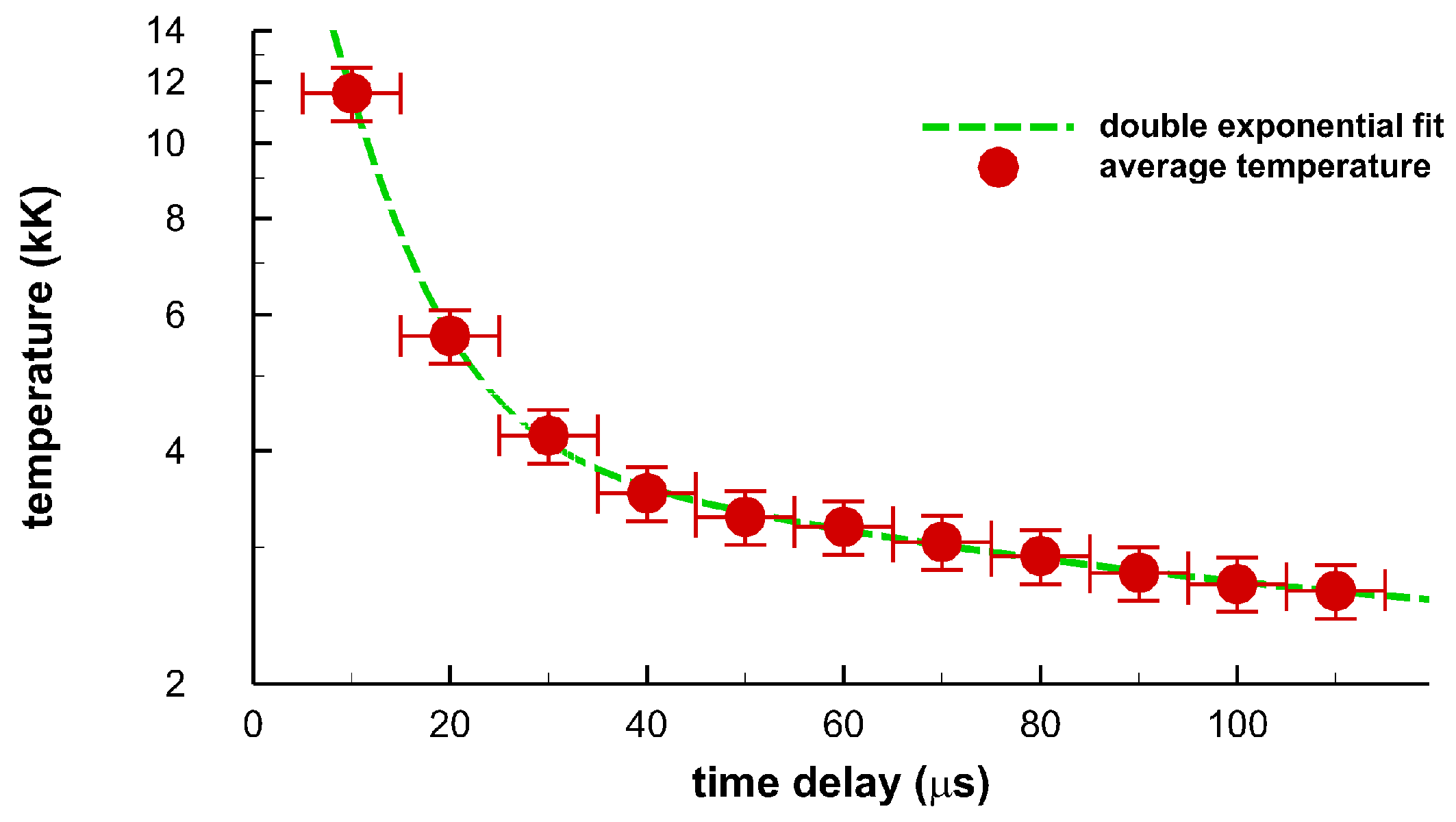
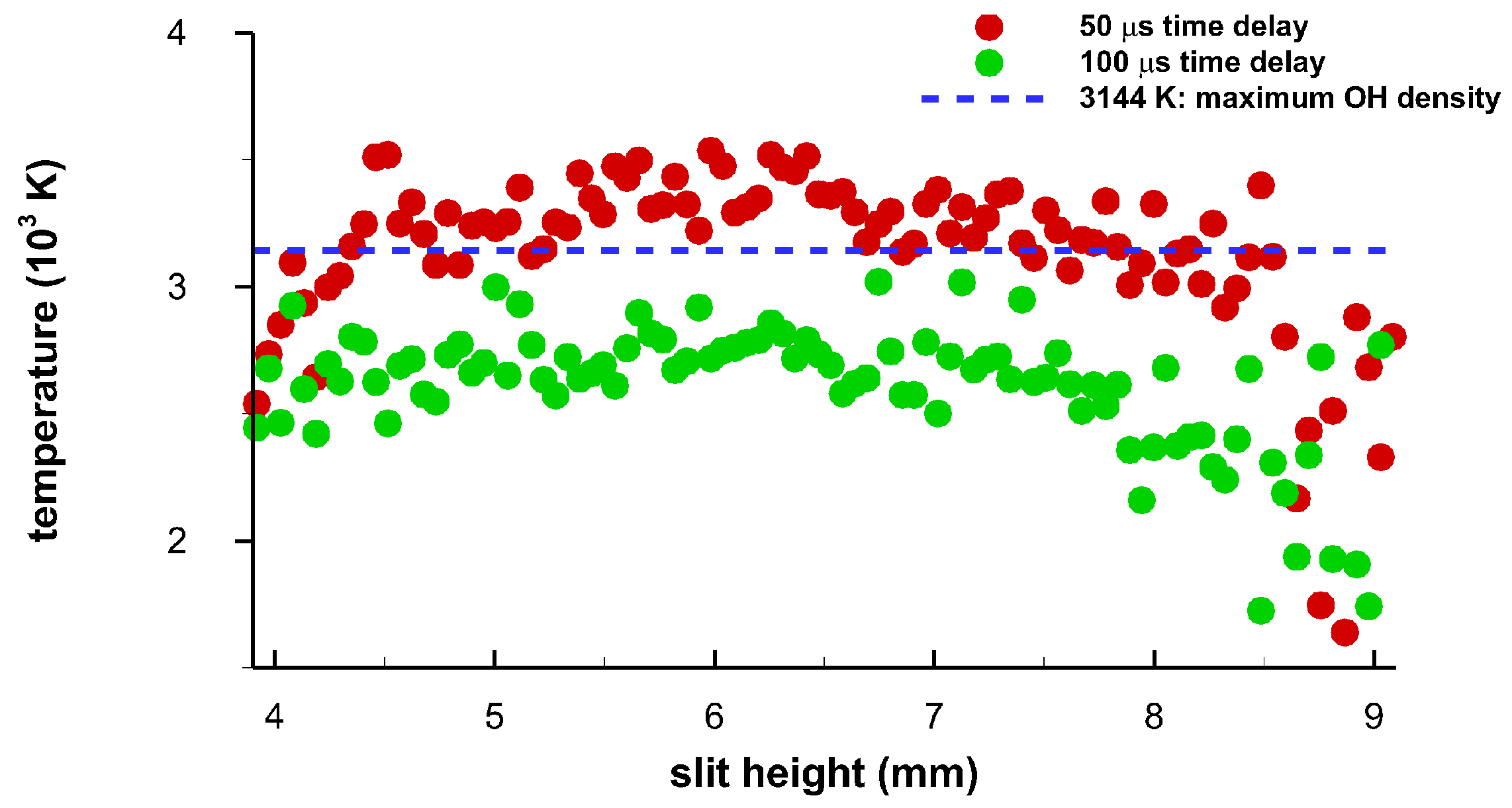
3.3. Correlation of OH Emission Spectra and of Shadow Graphs
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CN | Cyanide |
| BESP | Boltzmann Equilibrium Spectrum Program |
| ICCD | intensified Charge-Coupled Device |
| LIBS | Laser-Induced Breakdown Spectroscopy |
| Nd:YAG | Neodymium-doped Yttrium Aluminium Garnet |
| NMT | Nelder-Mead Temperature |
| OH | Hydroxyl |
| SATP | Standard Ambient Temperature Pressure |
References
- Kunze, H.-J. Introduction to Plasma Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Fujimoto, T. Plasma Spectroscopy; Clarendon Press: Oxford, UK, 2004. [Google Scholar]
- Ochkin, V.N. Spectroscopy of Low Temperature Plasma; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Boulos, M.I.; Fauchais, P.; Pfender, E. Thermal Plasmas. Fundamentals and Applications; Plenum Press: London, UK, 1994. [Google Scholar]
- Nugroho, S.K.; Kawahara, H.; Gibson, N.P.; de Mooij, E.J.W.; Hirano, T.; Kotani, T.; Kawashima, Y.; Masuda, K.; Brogi, M.; Birkby, J.L.; et al. First Detection of Hydroxyl Radical Emission from an Exoplanet Atmosphere: High-dispersion Characterization of WSAP-33b Using Subaru/IRD. Astrophys. J. Lett. 2021, 910, L9. [Google Scholar] [CrossRef]
- Stützer, R.; Oschwald, M. The Hyperfine Structure of the OH* Emission Spectrum and its Benefits for Combustion Analysis. In Proceedings of the 8th European Conference for Aeronautics and Space Sciences (EUCASS), Madrid, Spain, 1–4 July 2019; p. 2019–839. [Google Scholar]
- Radziemski, L.J.; Cremers, D.A. (Eds.) Laser-Induced Plasmas and Applications; Dekker: New York, NY, USA, 1989. [Google Scholar]
- Miziolek, A.W.; Palleschi, V.; Schechter, I. (Eds.) Laser Induced Breakdown Spectroscopy (LIBS): Fundamentals and Applications; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Singh, J.P.; Thakur, S.N. (Eds.) Laser-Induced Breakdown Spectroscopy, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- De Giacomo, A.; Hermann, J. Laser-induced plasma emission: From atomic to molecular spectra. J. Phys. D Appl. Phys. 2017, 50, 183002. [Google Scholar] [CrossRef]
- Parigger, C.G.; Helstern, C.M.; Jordan, B.S.; Surmick, D.M.; Splinter, R. Laser-Plasma Spectroscopy of Hydroxyl with Applications. Molecules 2020, 25, 988. [Google Scholar] [CrossRef] [PubMed]
- Parigger, C.G. Features of Hydroxyl Emission Spectroscopy in Laboratory-Air Laser-Plasma. Int. Rev. At. Mol. Phys. 2022, 13, 15–25. [Google Scholar]
- Fatima, H.; Ullah, M.U.; Ahmad, S.; Imran, M.; Sajjad, S.; Hussain, S.; Qayyum, A. Spectroscopic evaluation of vibrational temperature and electron density in reduced pressure radio frequency nitrogen plasma. SN Appl. Sci. 2021, 3, 646. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Lewis, J.W.L. Visualization of laser-induced breakdown and ignition. Opt. Express 2001, 9, 360–372. [Google Scholar] [CrossRef] [PubMed]
- Qin, W.; Chen, Y.-L.; Lewis, J.W.L. Time-resolved temperature images of laser-ignition using OH two-line laser-induced fluorescence (LIF) thermometry. Int. Flame Res. Found. (IFRF) Combust. J. 2005, 8, 200508. [Google Scholar]
- Parigger, C.G.; Guan, G.; Hornkohl, J.O. Measurement and analysis of OH emission spectra following laser-induced optical breakdown in air. Appl. Opt. 2003, 42, 5986–5991. [Google Scholar] [CrossRef] [PubMed]
- Parigger, C.G. Laser-induced breakdown in gases: Experiments and simulation. In Laser Induced Breakdown Spectroscopy (LIBS): Fundamentals and Applications; Miziolek, A.W., Palleschi, V., Schechter, I., Eds.; Cambridge University Press: New York, NY, USA, 2006; Chapter 4; pp. 171–193. [Google Scholar]
- Parigger, C.G.; Surmick, D.M.; Helstern, C.M.; Gautam, G.; Bol’shakov, A.A.; Russo, R. Molecular Laser-Induced Breakdown Spectroscopy. In Laser Induced Breakdown Spectroscopy, 2nd ed.; Singh, J.P., Thakur, S.N., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Chapter 7, pp. 167–212. [Google Scholar]
- Parigger, C.G.; Hornkohl, J.O. Quantum Mechanics of the Diatomic Molecule with Applications; IOP Publishing: Bristol, UK, 2020. [Google Scholar]
- Parigger, C.G.; Woods, A.C.; Surmick, D.M.; Gautam, G.; Witte, M.J.; Hornkohl, J.O. Computation of diatomic molecular spectra for selected transitions of aluminum monoxide, cyanide, diatomic carbon, and titanium monoxide. Spectrochim. Acta Part B At. Spectrosc. 2015, 107, 132–138. [Google Scholar] [CrossRef]
- Parigger, C.G. Review of spatiotemporal analysis of laser-induced plsama in gases. Spectrochim. Acta Part B At. Spectrosc. 2021, 179, 106122. [Google Scholar] [CrossRef]
- Parigger, C.G.; Helstern, C.M.; Jordan, B.S.; Surmick, D.M.; Splinter, R. Laser-Plasma Spatiotemporal Cyanide Spectroscopy and Applications. Molecules 2020, 25, 615. [Google Scholar] [CrossRef]
- Gordon, S.; McBride, B. Computer Program for Calculation of Complex Equilibrium Compositions, Rocket Performance, Incident and Reflected Shocks, and Chapman-Jouguet Detonations; NASA Lewis Research Center, Interim Revision, NASA Report SP-273; NASA: Washinton, DC, USA, 1976. [Google Scholar]
- McBride, B.J.; Gordon, S. Computer Program for Calculating and Fitting Thermodynamic Functions; NASA RP-1271; 2005 Version; NASA: Washinton, DC, USA, 1992. Available online: https://cearun.grc.nasa.gov/ (accessed on 14 December 2019).
- Thiyagarajan, M.; Thompson, S. Optical breakdown threshold investigation of 1064 nm laser induced air plasmas. J. Appl. Phys. 2012, 111, 073302. [Google Scholar] [CrossRef]
- Budnik, A.P.; Vakulovskii, A.S. Constant of Optical-Breakdown Avalanche Development in Moist Air; Atmospheric Optics (A91-29962 11-46); Gidrometeoizdat: Moscow, Russia, 1990; pp. 33–37. (In Russian) [Google Scholar]
- Condon, E.U.; Shortley, G. The Theory of Atomic Spectra; Cambridge University Press: Cambridge, UK, 1953. [Google Scholar]
- MATLAB Release R2022a Update 5; The MathWorks, Inc.: Natick, MA, USA, 2022.
- Surmick, D.M.; Hornkohl, J.O. (The University of Tennessee, University of Tennessee Space Institute, Tullahoma, TN, USA). Personal communication, 25 April 2016.
- Deans, S.R. The Radon Transform and Some Of Its Applications; John Wiley: New York, NY, USA, 1983. [Google Scholar]
- Radon, J. On the determination of functions from their integral values along certain manifolds. J. IEEE Trans. Med. Imaging 1986, 5, 170–176. [Google Scholar] [CrossRef] [PubMed]
- Eschlböck-Fuchs, S.; Demidov, A.; Gornushkin, I.B.; Schmid, T.; Rössler, R.; Huber, N.; Panne, U.; Pedarnig, J.D. Tomography of homogenized laaser-induced plasma by Radon transform technique. Spectrochim. Acta Part B At. Spectrosc. 2016, 123, 59–67. [Google Scholar] [CrossRef]
- Hertel, I.V.; Schulz, C.-P. Atoms, Molecules and Optical Physics 1, Atoms and Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]






| Species | Mole Fraction for 2500 K | Mole Fraction for 3100 K | Mole Fraction for 3750 K |
|---|---|---|---|
| e− | 4.147 × 10−10 | 4.916 × 10−8 | 1.3111 × 10−6 |
| Ar | 9.1983 × 10−3 | 8.9044 × 10−3 | 8.1562 × 10−3 |
| H | 2.7114 × 10−4 | 4.4885 × 10−3 | 1.3839 × 10−2 |
| H+ | - | - | 1.585 × 10−12 |
| H− | - | - | 1.653 × 10−10 |
| HNO | 9.4651 × 10−8 | 4.3791 × 10−7 | 3.7013 × 10−7 |
| HNO2 | 8.4537 × 10−8 | 6.3610 × 10−8 | 9.598 × 10−9 |
| HO2 | 4.0794 × 10−6 | 6.6671 × 10−6 | 1.8016 × 10−6 |
| H2 | 1.1744 × 10−4 | 4.5033 × 10−4 | 1.9256 × 10−4 |
| H2O | 8.7192 × 10−3 | 2.8062 × 10−3 | 1.3692 × 10−4 |
| H2O2 | 2.7318 × 10−8 | 2.1904 × 10−8 | 1.424 × 10−9 |
| N | 2.524 × 10−7 | 2.192 × 10−5 | 5.4050 × 10−4 |
| N+ | - | - | 1.489 × 10−14 |
| N− | - | - | 2.236 × 10−12 |
| NH | 3.634 × 10−9 | 1.943 × 10−7 | 1.3517 × 10−6 |
| NH2 | 1.103 × 10−10 | 2.329 × 10−9 | 3.358 × 10−9 |
| NO | 2.1548 × 10−2 | 4.3043 × 10−2 | 4.6896 × 10−2 |
| NO+ | 4.410 × 10−10 | 5.107 × 10−8 | 1.3420 × 10−6 |
| NO2 | 1.8594 × 10−5 | 1.9773 × 10−5 | 9.4889 × 10−6 |
| N2 | 7.5738 × 10−1 | 7.2208 × 10−1 | 6.5741 × 10−1 |
| N2− | - | - | 7.627 × 10−13 |
| N2+ | - | - | 5.901 × 10−11 |
| N2O | 1.1849 × 10−6 | 2.3699 × 10−6 | 2.5855 × 10−6 |
| N3 | - | - | 2.874 × 10−10 |
| O | 6.3014 × 10−3 | 6.0120 × 10−2 | 2.1044 × 10−1 |
| O+ | - | - | 2.075 × 10−11 |
| O− | 7.548 × 10−12 | 1.339 × 10−9 | 3.0021 × 10−8 |
| OH | 4.5941 × 10−3 | 1.0814 × 10−2 | 5.4876 × 10−3 |
| O2 | 1.918 × 10−1 | 1.4724 × 10−1 | 5.6886 × 10−2 |
| O2+ | - | - | 1.346 × 10−9 |
| O2− | - | - | 1.124 × 10−9 |
| O3 | 3.0933 × 10−8 | 9.5514 × 10−8 | 7.9000 × 10−8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parigger, C.G. Hydroxyl Spectroscopy of Laboratory Air Laser-Ignition. Foundations 2022, 2, 934-948. https://doi.org/10.3390/foundations2040064
Parigger CG. Hydroxyl Spectroscopy of Laboratory Air Laser-Ignition. Foundations. 2022; 2(4):934-948. https://doi.org/10.3390/foundations2040064
Chicago/Turabian StyleParigger, Christian G. 2022. "Hydroxyl Spectroscopy of Laboratory Air Laser-Ignition" Foundations 2, no. 4: 934-948. https://doi.org/10.3390/foundations2040064
APA StyleParigger, C. G. (2022). Hydroxyl Spectroscopy of Laboratory Air Laser-Ignition. Foundations, 2(4), 934-948. https://doi.org/10.3390/foundations2040064






