Optimizing Daylight Performance of Digital Fabricated Adobe Walls
Abstract
1. Introduction
2. Literature Benchmarks
2.1. Topology Optimization
2.2. Daylight Analysis
2.2.1. Daylight Calculation Methods
2.2.2. Sky Models
2.3. Digital Fabrication and Adobe Bricks: Pioneering Construction with 3D Printed Steel Molds
The Power of 3D Printed Steel Molds for the TO Wall
- Customization and Design Freedom: Unlike traditional manufacturing methods, which are constrained by the limitations of molds and tooling, 3D printing allows for the creation of highly customized molds tailored to specific architectural designs and project requirements (like daylight performance). Constructors can experiment with intricate patterns, textures, and shapes, pushing the boundaries of creativity and unlocking new aesthetic possibilities.
- Optimized Material Usage: 3D printing optimizes material usage by only depositing material where it is needed, minimizing waste and reducing environmental impact. This efficiency is particularly beneficial in adobe brick production, where sustainable practices are paramount.
- Rapid Prototyping and Iteration: The iterative nature of 3D printing enables rapid prototyping and design iteration, facilitating a more agile and responsive approach to construction. Constructors can quickly test different mold designs, refine their prototypes, and implement changes on the fly, accelerating the development process and reducing time-to-market.
- Complex Geometry and Structural Integrity: 3D printed steel molds can achieve intricate geometries and complex shapes that would be difficult or impossible to produce using traditional methods. This capability is invaluable for creating structurally sound adobe bricks with enhanced thermal performance and aesthetic appeal.
- Scalability and Cost-Effectiveness: While the initial investment in 3D printing equipment may be significant, the scalability and cost-effectiveness of additive manufacturing make it a viable long-term solution for adobe brick production. As technology matures and becomes more widespread, economies of scale will drive down costs, making 3D printed steel molds accessible to a broader range of builders and developers.
2.4. The Novelty of Proposed Design Framework
- The specific details of the framework (analysis methods, optimization algorithms) would determine its effectiveness.
- The research justifying its stability is important.
- Stability refers to the framework’s ability to produce consistent and reliable results across various design scenarios.
3. Methodology and Design Parameters
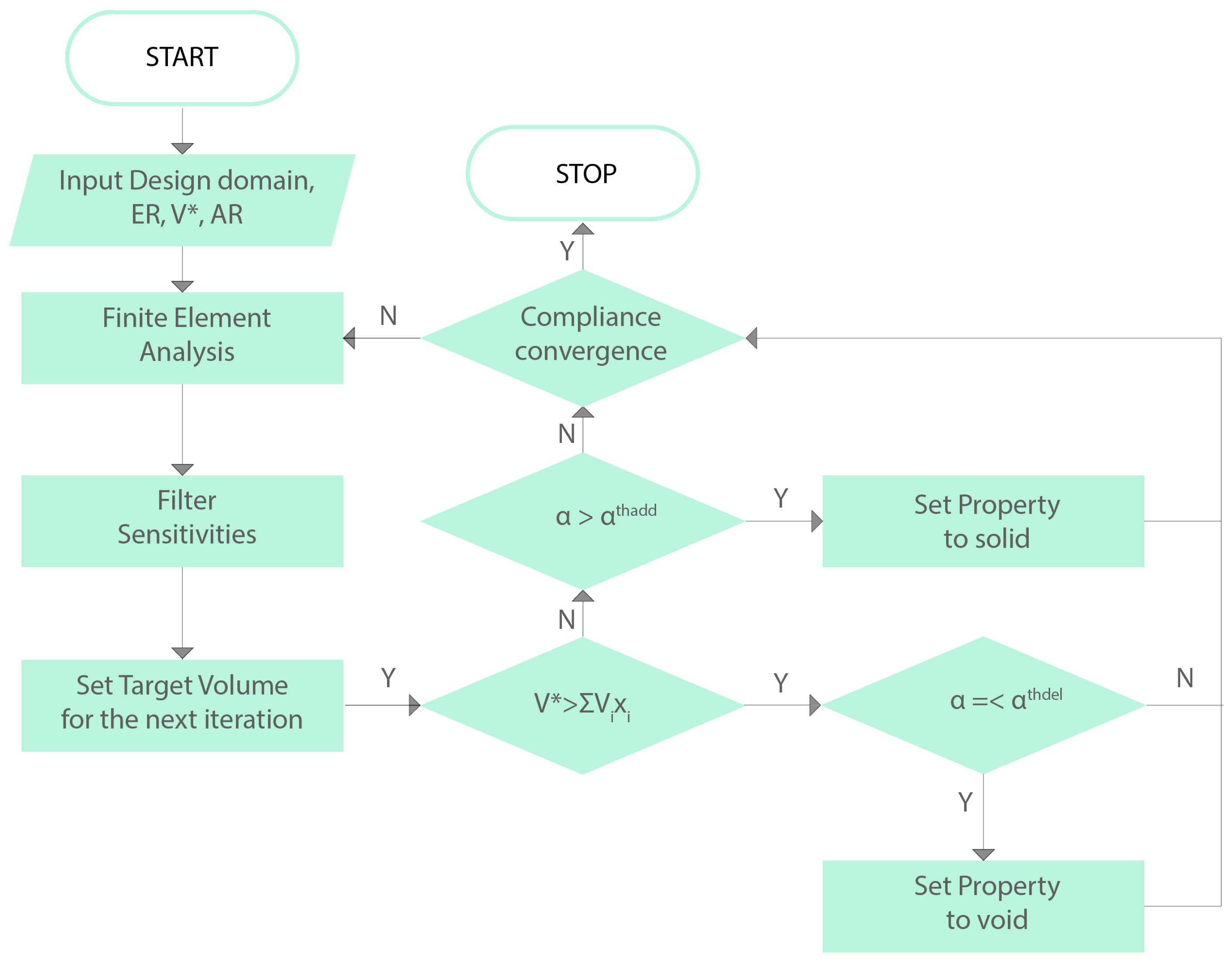
3.1. The TO-Based Design Process
- Discretize the design domain with the proper finite element mesh and introduce the constraints and other design variables (, and )
- Run the finite element analysis and calculate the sensitivity number of each element
- Filtering the sensitivity numbers.
- Set target Volume for the next iteration.
- Check the removal threshold and remove the elements with sensitivity number smaller than the threshold, if the target volume is greater to the subjected one.
- Check the addition threshold and remove the elements with sensitivity number greater than the threshold, if the target volume is smaller to the subjected one.
- Check the compliance convergence if the error is greater than the tolerance, repeat the procedure from step 2.
3.2. Split Flux Formula’s Direct Component Function
3.3. The Updated Flowchart
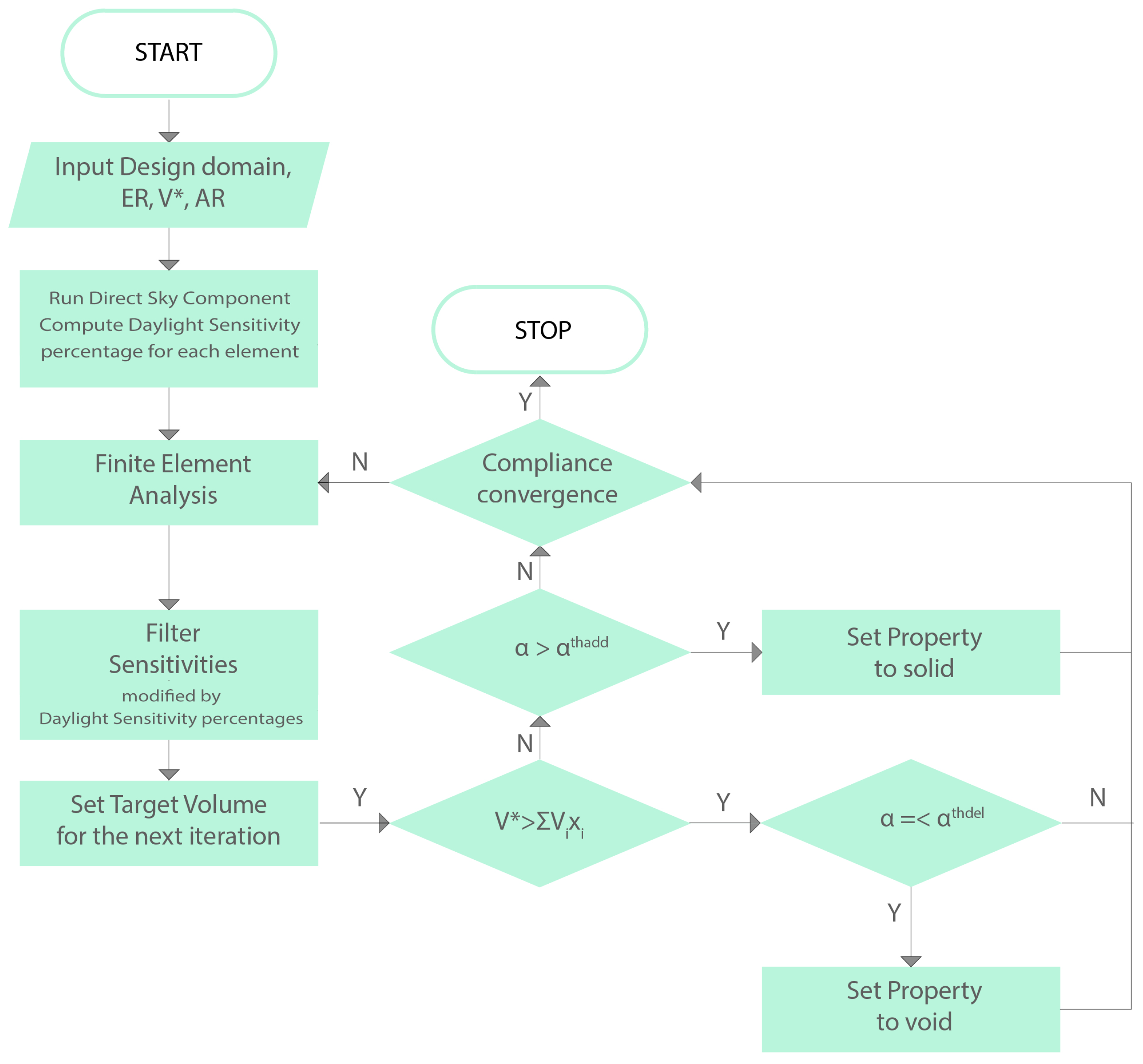
- Discretize the design domain with finite element mesh and introduce the constraints and other design variables (, and )
- Run the direct Sky Component Tool (Appendix B)
- Run the finite element analysis and calculate the modified, by daylight sensitivity percentage, sensitivity number of each element
- Filtering the modified sensitivity numbers by daylight sensitivity percentages.
- Set target Volume for the next iteration.
- If the target volume is greater to the subjected one, check the removal threshold and remove the elements with sensitivity number smaller than the threshold.
- If the target volume is smaller to the subjected one, check the addition threshold and remove the elements with sensitivity number greater than the threshold.
- Check the compliance convergence if the error is greater than the tolerance, repeat the procedure from step 3.
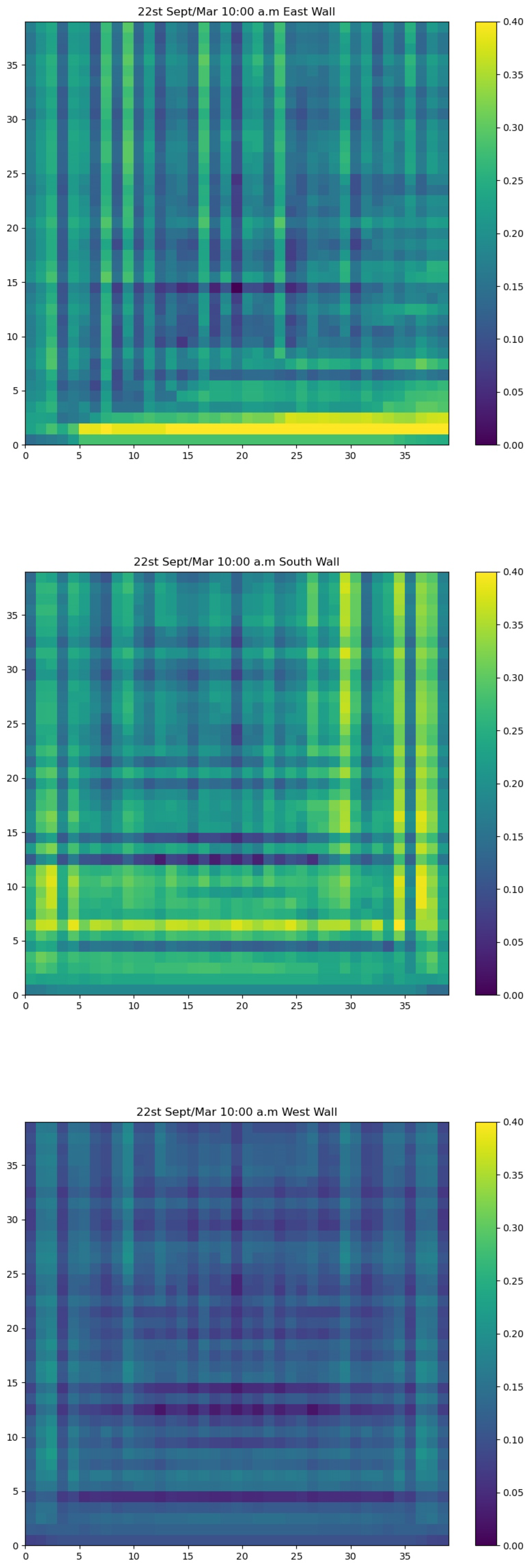
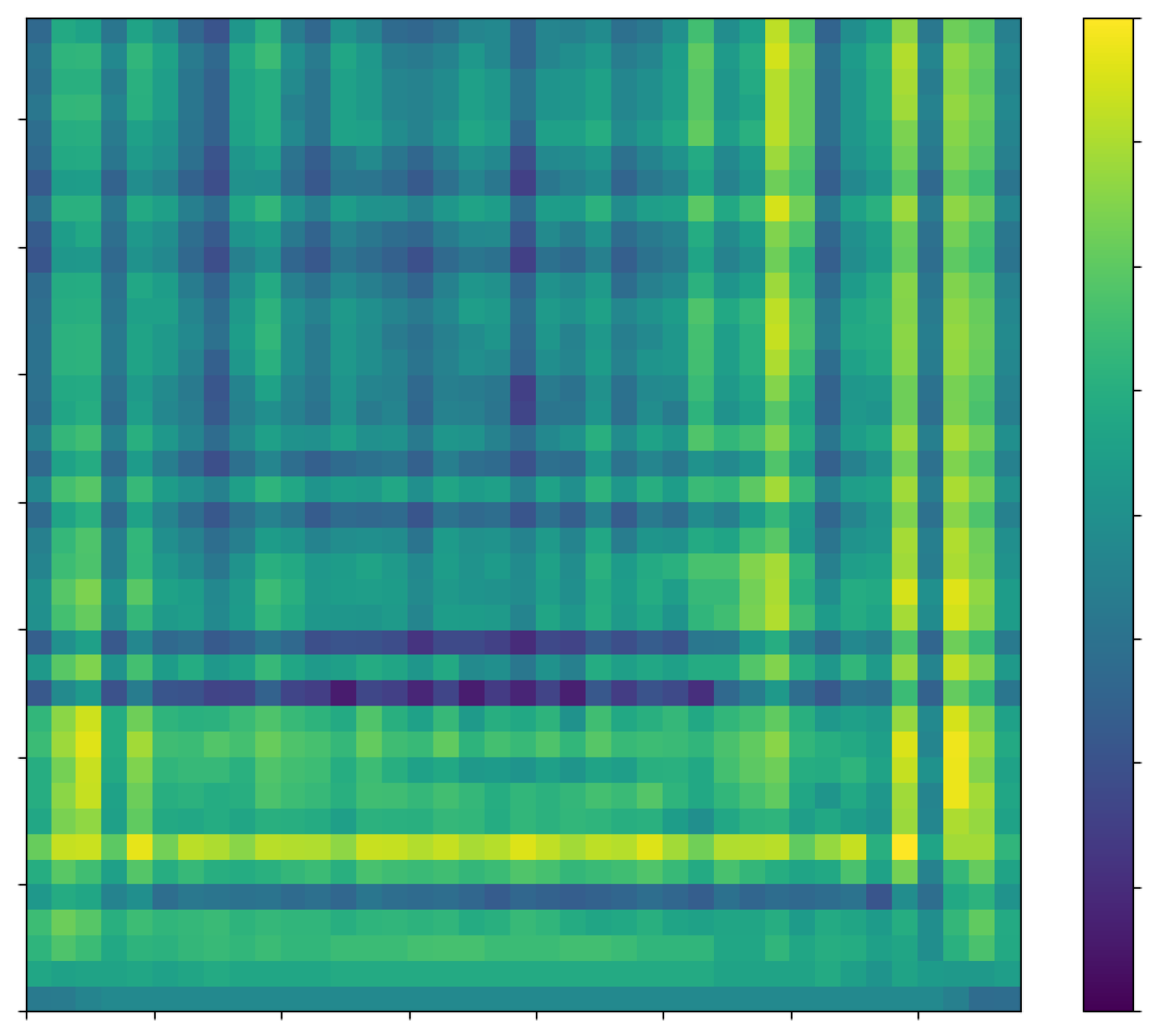
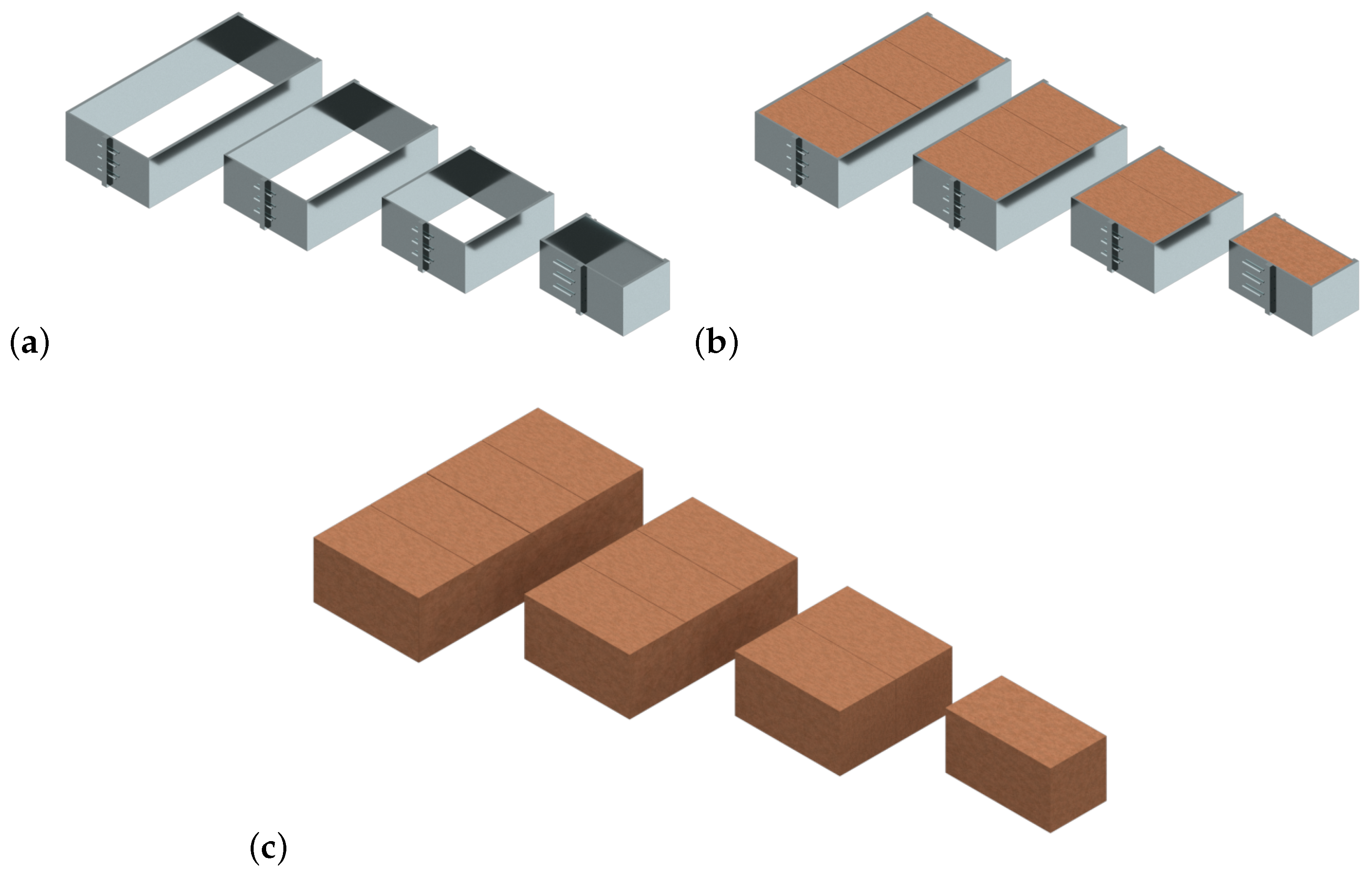
4. The Case Study
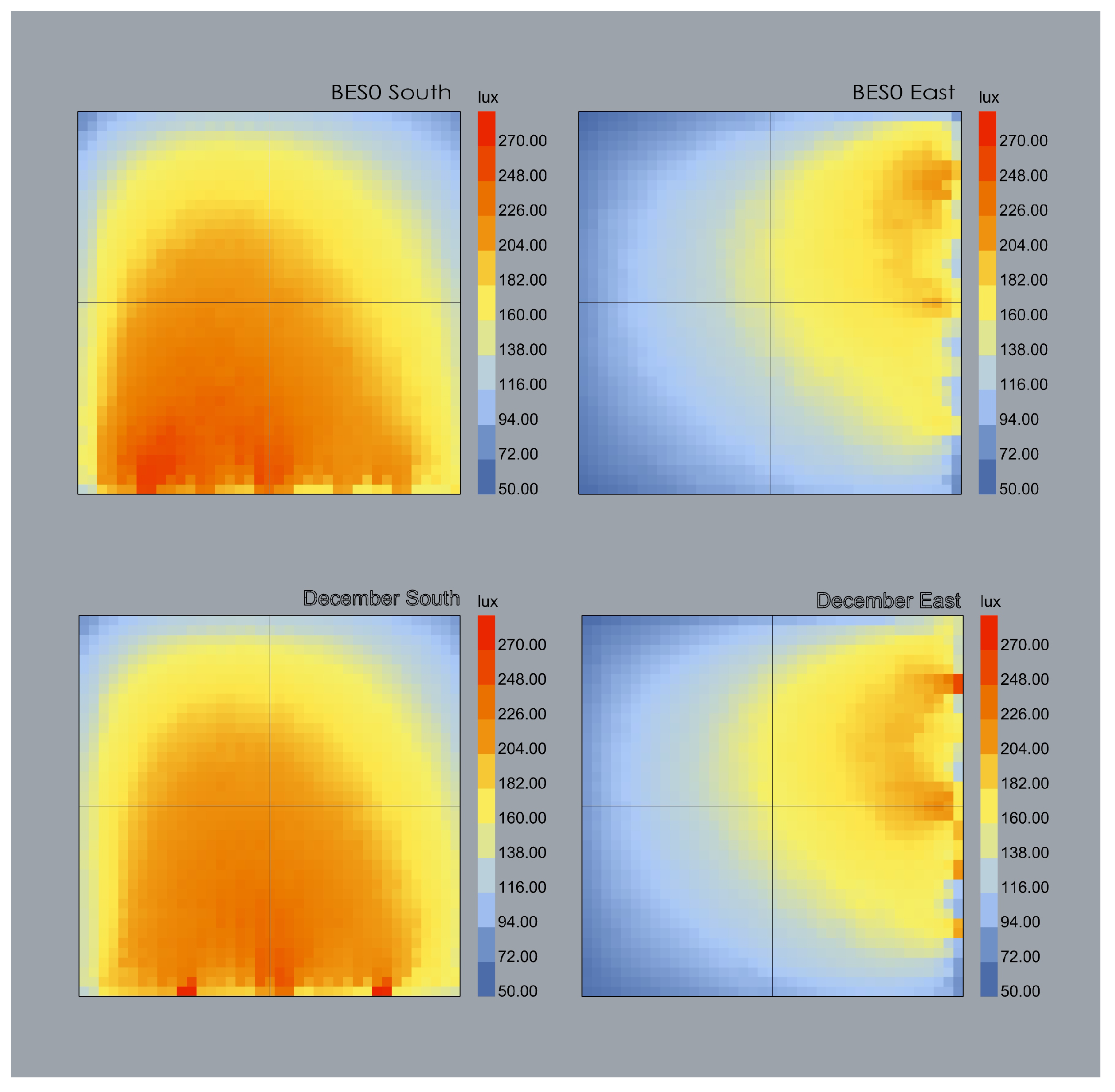
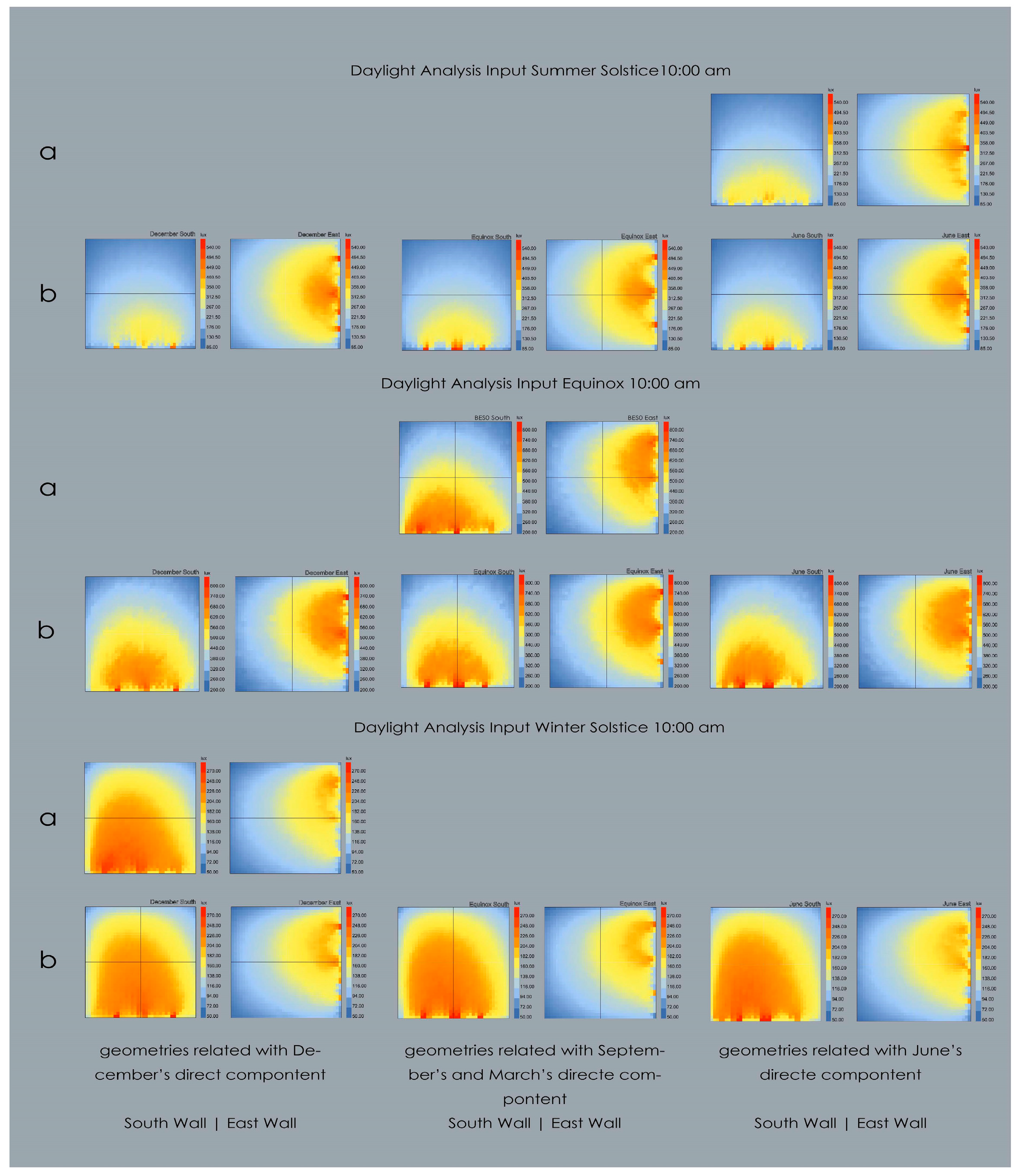
5. Results
- Design the walls, floor, roof and optimized wall in Rhinoceros 3d and assign the on HB Face toggle
- Design the window elements and assign the on HB Aperture toggle
- Define daylight sensors’ grid-size and assign it to HB Sensor grid size.
- Download weather Data for Athens Region and connect them in Climate-based sky toggle.
- Connect all the above with HB point-in-time grid-based recipe.
- Run the HB point-in-time grid based recipe.
- Choose the type of results for example Useful Daylight Illuminance (UDI) or Daylight Autonomy (DA)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


Appendix B
- The ground reflected light
- The upper surfaces of the room reflected light
- The light which is entered from the window and is reflected by the lower surfaces of the room
Appendix C
References
- Lagaros, N.D. The environmental and economic impact of structural optimization. Struct. Multidiscip. Optim. 2018, 58, 1751–1768. [Google Scholar] [CrossRef]
- UN Environment Programme. Global Status Report for Buildings and Construction. 2022. Available online: https://www.unep.org/resources/publication/2022-global-status-report-buildings-and-construction (accessed on 10 March 2024).
- UN World Commission on Environment and Development. Report of the World Commission on Environment and Development: Our Common Future; United Nations: New York, NY, USA, 1987.
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Lagaros, N.D.; Plevris, V.; Kallioras, N.A. The Mosaic of Metaheuristic Algorithms in Structural Optimization. Arch. Comput. Methods Eng. 2022, 29, 5457–5492. [Google Scholar] [CrossRef]
- Rozvany, G.I. A critical review of established methods of structural topology optimization. Struct. Multidiscip. Optim. 2009, 37, 217–237. [Google Scholar] [CrossRef]
- Zhou, M.; Rozvany, G. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization. Comput. Methods Appl. Mech. Eng. 1991, 89, 309–336. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Huang, Y. An improved multi-objective topology optimization model based on SIMP method for continuum structures including self-weight. Struct. Multidiscip. Optim. 2021, 63, 211–230. [Google Scholar] [CrossRef]
- Kim, H.; Querin, O.; Steven, G.; Xie, Y. Improving efficiency of evolutionary structural optimization by implementing fixed grid mesh. Struct. Multidiscip. Optim. 2002, 24, 441–448. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. A simple evolutionary procedure for structural optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y. A new look at ESO and BESO optimization methods. Struct. Multidiscip. Optim. 2008, 35, 89–92. [Google Scholar] [CrossRef]
- Radman, A. Bi-Directional Evolutionary Structural Optimization (BESO) for Topology Optimization of Material’s Microstructure. Ph.D. Thesis, RMIT University, Melbourne, Australia, 2013. [Google Scholar]
- Xia, L.; Xia, Q.; Huang, X.; Xie, Y.M. Bi-directional evolutionary structural optimization on advanced structures and materials: A comprehensive review. Arch. Comput. Methods Eng. 2018, 25, 437–478. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Van Dijk, N.P.; Maute, K.; Langelaar, M.; Van Keulen, F. Level-set methods for structural topology optimization: A review. Struct. Multidiscip. Optim. 2013, 48, 437–472. [Google Scholar] [CrossRef]
- Mei, Y.; Wang, X. A level set method for structural topology optimization and its applications. Adv. Eng. Softw. 2004, 35, 415–441. [Google Scholar] [CrossRef]
- Li, H.; Yamada, T.; Jolivet, P.; Furuta, K.; Kondoh, T.; Izui, K.; Nishiwaki, S. Full-scale 3D structural topology optimization using adaptive mesh refinement based on the level-set method. Finite Elem. Anal. Des. 2021, 194, 103561. [Google Scholar] [CrossRef]
- Wu, J.; Sigmund, O.; Groen, J.P. Topology optimization ofmulti-scale structures: A review. Struct. Multidiscip. Optim. 2021, 63, 1455–1480. [Google Scholar] [CrossRef]
- Ypsilantis, K.I.; Kazakis, G.; Lagaros, N.D. An efficient 3D homogenization-based topology optimization methodology. Comput. Mech. 2021, 67, 481–496. [Google Scholar] [CrossRef]
- Iversen, A.; Roy, N.; Hvass, M.; Jørgensen, M.; Christoffersen, J.; Osterhaus, W.; Johnsen, K. Daylight Calculations in Practice: An Investigation of the Ability of Nine Daylight Simulation Programs to Calculate the Daylight Factor in Five Typical Rooms; Danish Building Research Institute, Aalborg University: Copenhagen, Denmark, 2013. [Google Scholar]
- Tregenza, P.R.; Waters, I. Daylight coefficients. Light. Res. Technol. 1983, 15, 65–71. [Google Scholar] [CrossRef]
- Yoon, Y.B.; Jeong, W.R.; Lee, K.H. Window Material Daylighting Performance Assessment Algorithm: Comparing Radiosity and Split-Flux Methods. Energies 2014, 7, 2362–2376. [Google Scholar] [CrossRef]
- Watt, A. 3D Computer Graphics; Addison-Wesley: Boston, MA, USA, 2000. [Google Scholar]
- Xiao, D.; Wuyun, G.; Pan, Z. Indoor Daylight Simulation Using Radiosity Method. In Proceedings of the 2011 Workshop on Digital Media and Digital Content Management, Hangzhou, China, 15–16 May 2011; pp. 158–161. [Google Scholar]
- Larson, G.W.; Shakespeare, R.A. Rendering with Radiance: The Art and Science of Lighting Visualization; BookSurge: Charleston, SC, USA, 1998. [Google Scholar]
- Pope, J. Multi-Sensory Rendering for Viewpoint-Independent Scenes. Ph.D. Thesis, University of Bristol, Bristol, UK, 2000. [Google Scholar]
- Darula, S.; Kittler, R. CIE general sky standard defining luminance distributions. Proc. eSim 2002, 11, 13. [Google Scholar]
- Kimball, H.H.; Hand, I.F. Sky-Brightness and Daylight-Illumination Measurements. Mon. Weather. Rev. 1921, 49, 481–488. [Google Scholar] [CrossRef]
- Kimball, H.H.; Hand, I.F. Daylight Illumination on Horizontal, Vertical, and Sloping Surfaces. Mon. Weather. Rev. 1922, 50, 615–628. [Google Scholar] [CrossRef]
- Moon, P. Illumination from a non-uniform sky. Illum. Energy 1942, 37, 707–726. [Google Scholar]
- McDermott, L.; Gordon-Smith, G. Daylight illumination recorded at Teddington. In Proceedings of the Building Resource Congress, London, UK, September 1951; Volume 3. [Google Scholar]
- CIE 1955. Natural Daylight, Official Recommendation; International Commission on Illumination: Vienna, Austria, 1955. [Google Scholar]
- Hopkinson, G.; Petherbridge, P.; Longmore, J. Daylighting; Heinemann: London, UK, 1966. [Google Scholar]
- Kittler, R. Standardization of outdoor condition for the calculation of daylight factor with clear skies. In Proceedings of the CIE International Conference Sunlight in Buildings, Rotterdam, The Netherlands, 5–9 April 1967; pp. 273–285. [Google Scholar]
- Perez, R.; Seals, R.; Michalsky, J. All-weather model for sky luminance distribution—preliminary configuration and validation. Sol. Energy 1993, 50, 235–245. [Google Scholar] [CrossRef]
- Mardaljevic, J. Daylight Simulation: Validation, Sky Models and Daylight Coefficients. Ph.D. Thesis, De Montfort University, Leicester, UK, 1999. [Google Scholar]
- Antonanzas-Torres, F.; Urraca, R.; Polo, J.; Perpiñán-Lamigueiro, O.; Escobar, R. Clear sky solar irradiance models: A review of seventy models. Renew. Sustain. Energy Rev. 2019, 107, 374–387. [Google Scholar] [CrossRef]
- Kolarevic, B. Digital fabrication: Manufacturing architecture in the information age. Reinventing the Discourse—How Digital Tools Help Bridge and Transform Research, Education and Practice in Architecture. In Proceedings of the Twenty First Annual Conference of the Association for Computer-Aided Design in Architecture, Buffalo, NY, USA, 11–14 October 2001; pp. 268–278, ISBN 1-880250-10-1. [Google Scholar] [CrossRef]
- Gomaa, M.; Jabi, W.; Soebarto, V.; Xie, Y.M. Digital manufacturing for earth construction: A critical review. J. Clean. Prod. 2022, 338, 130630. [Google Scholar] [CrossRef]
- Geneidy, O.; Ismaeel, W.S.E.; Abbas, A.S. A critical review for applying three-dimensional concrete wall printing technology in Egypt. Archit. Sci. Rev. 2019, 62, 438–452. [Google Scholar] [CrossRef]
- Gomaa, M.S.; Jabi, W.; Reyes, A.V.; Soebarto, V. 3D printing system for earth-based construction: Case study of cob. Autom. Constr. 2021, 124, 103577. [Google Scholar] [CrossRef]
- de Soto, B.G.; Agustí-Juan, I.; Hunhevicz, J.; Joss, S.; Graser, K.; Habert, G.; Adey, B.T. Productivity of digital fabrication in construction: Cost and time analysis of a robotically built wall. Autom. Constr. 2018, 92, 297–311. [Google Scholar] [CrossRef]
- Ford, S.; Despeisse, M. Additive manufacturing and sustainability: An exploratory study of the advantages and challenges. J. Clean. Prod. 2016, 137, 1573–1587. [Google Scholar] [CrossRef]
- Siddika, A.; Mamun, M.A.A.; Ferdous, W.; Saha, A.K.; Alyousef, R. 3D-printed concrete: Applications, performance, and challenges. J. Sustain. Cem.-Based Mater. 2020, 9, 127–164. [Google Scholar] [CrossRef]
- Gomaa, M.; Carfrae, J.; Goodhew, S.; Jabi, W.; Veliz Reyes, A. Thermal performance exploration of 3D printed cob. Archit. Sci. Rev. 2019, 62, 230–237. [Google Scholar] [CrossRef]
- Minke, G. Building with Earth: Design and Technology of a Sustainable Architecture; De Gruyter: Berlin, Germany, 2006. [Google Scholar]
- Martín, S.; Mazarrón, F.R.; Cañas, I. Study of thermal environment inside rural houses of Navapalos (Spain): The advantages of reuse buildings of high thermal inertia. Constr. Build. Mater. 2010, 24, 666–676. [Google Scholar] [CrossRef]
- Chandel, S.; Sharma, V.; Marwah, B.M. Review of energy efficient features in vernacular architecture for improving indoor thermal comfort conditions. Renew. Sustain. Energy Rev. 2016, 65, 459–477. [Google Scholar] [CrossRef]
- Hamard, E.; Cazacliu, B.; Razakamanantsoa, A.; Morel, J.C. Cob, a vernacular earth construction process in the context of modern sustainable building. Build. Environ. 2016, 106, 103–119. [Google Scholar] [CrossRef]
- Liu, J.; Hu, R.; Wang, R.; Yang, L. Regeneration of vernacular architecture: New rammed earth houses on the upper reaches of the Yangtze River. Front. Energy Power Eng. China 2010, 4, 93–99. [Google Scholar] [CrossRef]
- Frangedaki, E.; Sargentis, G.F. Optimization in Engineering Aspects of Constructions with Earth by Laboratory Tests. A Proposed Methodology for the Proper Soil. Examples of Modern Houses Built with Earth in Greece; Zenodo: Geneva, Switzerland, 2019. [Google Scholar] [CrossRef]
- Morton, T.; Stevenson, F.; Taylor, B.; Smith, N.C. Low Cost Earth Brick Construction; Arc Chartered Architects: Fife, WA, USA, 2005. [Google Scholar]
- Silveira, D.; Oliveira, C.; Varum, H.; Ioannou, I.; Miccoli, L.; Tarque, N.; Parisi, F.; Fenu, L.; Solís, M.; Rodríguez-Mariscal, J.D. Mechanical characterization of adobe bricks. In Structural Characterization and Seismic Retrofitting of Adobe Constructions: Experimental and Numerical Developments; Springer: Cham, Switzerland, 2021; pp. 35–54. [Google Scholar]
- Technologies, R. Robotic Brickwork. Available online: https://rob-technologies.com/robotic-brickwork (accessed on 17 April 2024).
- Construction-Robotics. SAM2. Available online: https://www.construction-robotics.com/sam-2/ (accessed on 17 April 2024).
- Ahmad, A.; Kumar, A.; Prakash, O.; Aman, A. Daylight availability assessment and the application of energy simulation software—A literature review. Mater. Sci. Energy Technol. 2020, 3, 679–689. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y. Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elem. Anal. Des. 2007, 43, 1039–1049. [Google Scholar] [CrossRef]
- Gonidakis, D.N. Combining Structural Topology Optimization with Daylight Analysis. Master’s Thesis, National Technical University of Athens, Athens, Greece, 2020. [Google Scholar] [CrossRef]
- Oh, S.; Haberl, J.S. Origins of analysis methods used to design high-performance commercial buildings: Daylighting simulation. Sci. Technol. Built Environ. 2016, 22, 107–117. [Google Scholar] [CrossRef]
- Tregenza, P. Analysing sky luminance scans to obtain frequency distributions of CIE Standard General Skies. Light. Res. Technol. 2004, 36, 271–279. [Google Scholar] [CrossRef]
- Kittler, R.; Darula, S. Redistributions of luminance patterns on standard sky types. Light. Res. Technol. 2022, 54, 61–73. [Google Scholar] [CrossRef]
- Tregenza, P.R. Subdivision of the sky hemisphere for luminance measurements. Light. Res. Technol. 1987, 19, 13–14. [Google Scholar] [CrossRef]
- Cen, E. 12464-1 Light and Lighting-Lighting of Work Places-Part 1: Indoor Work Places; European Committee for Standardization (CEN): Brussels, Belgium, 2011. [Google Scholar]
- Miccoli, L.; Müller, U.; Fontana, P. Mechanical behaviour of earthen materials: A comparison between earth block masonry, rammed earth and cob. Constr. Build. Mater. 2014, 61, 327–339. [Google Scholar] [CrossRef]
- Mousourakis, A.; Arakadaki, M.; Kotsopoulos, S.; Sinamidis, I.; Mikrou, T.; Frangedaki, E.; Lagaros, N.D. Earthen architecture in greece: Traditional techniques and revaluation. Heritage 2020, 3, 1237–1268. [Google Scholar] [CrossRef]
- LadyBugTools. EPW Map. Available online: https://www.ladybug.tools/epwmap/ (accessed on 17 April 2024).





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonidakis, D.N.; Frangedaki, E.I.; Lagaros, N.D. Optimizing Daylight Performance of Digital Fabricated Adobe Walls. Architecture 2024, 4, 515-540. https://doi.org/10.3390/architecture4030028
Gonidakis DN, Frangedaki EI, Lagaros ND. Optimizing Daylight Performance of Digital Fabricated Adobe Walls. Architecture. 2024; 4(3):515-540. https://doi.org/10.3390/architecture4030028
Chicago/Turabian StyleGonidakis, Dimitrios N., Evangelia I. Frangedaki, and Nikos D. Lagaros. 2024. "Optimizing Daylight Performance of Digital Fabricated Adobe Walls" Architecture 4, no. 3: 515-540. https://doi.org/10.3390/architecture4030028
APA StyleGonidakis, D. N., Frangedaki, E. I., & Lagaros, N. D. (2024). Optimizing Daylight Performance of Digital Fabricated Adobe Walls. Architecture, 4(3), 515-540. https://doi.org/10.3390/architecture4030028







