A Two-Phase Genetic Algorithm Approach for Sleep Scheduling, Routing, and Clustering in Heterogeneous Wireless Sensor Networks

Abstract

Heterogeneous wireless sensor networks (HWSNs), comprising super nodes and normal sensors, offer a promising solution for monitoring diverse environments. However, their deployment is constrained by the limited battery life of sensors. To address this issue, clustering and routing techniques have been employed to conserve energy. Nevertheless, existing approaches often struggle with suboptimal energy distribution and weak network coverage. Additionally, they mostly failed to exploit other energy saving techniques such as sleep scheduling. This paper proposes a novel genetic algorithm (GA)-based approach to optimize sleep scheduling, routing, and clustering in HWSNs. The method comprises two phases, namely join sleep scheduling and tree construction, and clustering of normal nodes. Inspired by the concept of unequal clustering, the HWSN is split into some rings in the first phase, and the number of awake super nodes in each ring keeps the same. This approach addresses the challenges of balancing energy consumption and network lifetime. Furthermore, including network coverage and energy-related criteria in the proposed GA yields long-lasting network operation. Through rigorous simulations, we demonstrate that, on average, our algorithm reduces energy consumption and improves network coverage by 23% and 21.9%, respectively, and extends network lifetime by 501 rounds, compared to the state-of-the-art methods.

1. Introduction

Wireless sensor networks (WSNs) have emerged as cost-effective solutions for monitoring diverse environments, particularly in harsh or inaccessible conditions. However, their performance and longevity are often limited by the constrained energy resources of sensor nodes. To overcome this issue, heterogeneous WSNs (HWSNs) have been introduced [1,2,3], incorporating two types of nodes: normal sensors and super nodes [4,5]. Normal nodes are responsible for sensing tasks, while super nodes aggregate and forward data to the Base Station (BS). By employing high-energy super nodes as cluster heads (CHs), HWSNs can improve energy efficiency, extend network lifetime, and enhance data delivery.

Despite these advantages, super nodes consume energy more rapidly due to their heavier communication and computation load, which can shorten network lifetime. Therefore, achieving energy-efficient data gathering with balanced energy usage among super nodes remains a critical challenge. Existing studies have explored several strategies such as clustering [6,7], routing [8,9], clustering and routing [4,5,10,11,12], and sleep scheduling [13], to address this issue. The proposed algorithms in [4,5,10,11,12], which used both clustering and routing for efficient energy management, used different meta-heuristic algorithms such as genetic algorithm (GA) [5,12,14] and gray wolf optimization (GWO) [11]. Most of these algorithms arranged clustering and routing into two phases and solved them consecutively. These studies mainly lacked customized chromosome/particle representations, problem-specific operators/decoding methods, and effective cost functions. The other main drawback of the mentioned methods is that most of them treated clustering, routing, and sleep scheduling mechanisms separately, without considering their strong interdependence. A more integrated approach can yield better coordination among the mentioned mechanisms, ultimately improving energy efficiency and coverage.

To bridge this gap, this paper presents a unified GA-based framework for data collection in HWSNs that jointly optimizes sleep scheduling, clustering, and routing. The proposed method determines which super nodes should remain awake, constructs an energy-efficient routing tree among them, and assigns normal nodes to appropriate CHs. To manage complexity, the problem is divided into two GA-optimized phases: (1) simultaneous sleep scheduling and tree construction among super nodes, and (2) clustering of normal nodes based on awake CHs. Each phase employs problem-specific chromosome representations, customized initialization methods, and tailored genetic operators to achieve rapid convergence and effective load balancing. The customized cost functions introduced in both phases further enhance load balancing across super nodes, ensuring prolonged network sustainability.

The innovations of this paper can be summarized as follows:

• The proposed solution for reducing the state space effectively addresses the challenges of sleep scheduling, clustering, and tree construction on awake nodes by dividing the process into two phases, each optimized using a GA.
• Considering the strong interdependence between the sleep scheduling of super nodes and the construction of a tree on these nodes—since the tree must be built on awake super nodes—these two problems are tackled simultaneously through an innovative modeling approach.
• In the first phase, a novel cost function is employed to enhance environmental monitoring by selecting a set of super nodes as awake ones while minimizing the energy consumption of super nodes.
• Network clustering is modeled and optimized using a GA in the second phase, with a new cost function specifically designed to reduce energy consumption with distributing normal nodes among the awake CHs.
• Considering the pivotal role of initialization in the ultimate solution of GA, we propose a custom initialization in the first phase which helps GA to converge more quickly. The proposed method splits the HWSN into rings and selects equal number of awake super nodes per ring. This scheme, which is inspired by unequal clustering, helps balancing energy exhaustion of super nodes and prolongs network lifetime.
• We modify and customize the GA operators (crossover and mutation) to fit our problem and help achieving better solutions.
• The proposed solution has been rigorously evaluated in simulation environments, consistently demonstrating its superiority over existing methods.

The remainder of this paper is organized as follows: Section 2 reviews the related work, while Section 3 outlines the network model. Section 4 provides a comprehensive description of the proposed method, and Section 5 presents the results obtained using this method. Finally, Section 6 concludes the paper.

2. Related Works

We review related research in three key areas. First, we explore sleep scheduling studies on heterogenous and homogenous WSNs. The second part investigates clustering algorithms within the field. Finally, in the last part, we consider research on tree construction and routing protocols. The mentioned algorithms used different techniques for solving considered problems including greedy, meta-heuristic, and learning methods.

The literature on sleep scheduling and resource allocation in WSNs explored various approaches to optimize energy efficiency. Alwasel et al. [13] considered HWSNs and proposed an energy-efficient sleep-and-awake scheme to manage sleep states based on node resources, prioritizing network lifetime. In their work, they proposed iterative local search strategy to construct disjoint dominating sets, activating nodes of one dominating set each time instance. The algorithm prioritized nodes with higher residual energy for being awake while transitioning others to sleep mode. However, their method introduced computational complexity due to exhaustive search processes, limiting scalability in large-scale HWSNs. Additionally, it did not consider clustering and routing problems.

Sleep scheduling in homogenous WSNs was explored in [15,16,17]. Niyato et al. [15] used factors like energy level of nodes, the number of packets in their buffers, and channel condition, to determine sleep scheduling policies for solar-powered networks. The algorithm aimed to awaken nodes with higher energies, less congested buffers, and better channel conditions. The proposed method in [18] clustered sensor nodes and determined the sleep nodes per cluster based on the correlation of generated data by Cluster Members (CMs). The algorithm constructed a graph considering the correlation degree between the neighboring nodes and applied it to determine sleep and awake nodes. Bertanha et al. [19] performed sleep scheduling in two phases. A greedy algorithm was proposed for sleep scheduling in the first phase, which only focused on preserving connectivity throughout the network and did not take into account the coverage. For routing data packets, a next-hop toward the BS was adopted per node in the second phase, considering its residual energy and distance from the BS. References [16,17,20,21,22] employed Reinforcement Learning (RL) to determine the awake and sleep schedule of the nodes. Studies in [16,17,20] developed RL-driven sleep scheduling for star topology networks. Among the mentioned algorithms, references [17,22] focused on wireless body area networks, and considered criteria such as energy level of nodes, emergency of gathered data by sensors, and transmission delay, to decide on awake/sleep statuses of sensors. The algorithm proposed in [21] determined CHs and performed clustering using a greedy approach, followed by applying RL for sleep scheduling.

Clustering is vital in WSNs for efficient data collection and transmission. Mughal et al. [7] introduced a RL-based clustering model for IoT and HWSNs, aimed at optimizing resource utilization and reducing energy consumption. In [23], a scheme was presented that categorized sensors into normal and super nodes based on initial energy levels. Clusters were formed with energy-efficient CH selection, which prioritize super nodes by assigning more weights to them. Bhasker et al. [24] introduced a cluster-based data gathering technique for farm irrigation systems, focusing on reducing sensor node energy use and balancing the workload on CHs. They proposed a method that selects and rotates CHs near the energy centroid within clusters and designates gateway nodes to assist CHs. In the proposed algorithm in [25], CH selection was guided by a fitness function derived from multi-objective optimization. The objectives included minimizing energy usage and the distance between CHs and their CMs. The algorithm applied deep residual network to optimize number of clusters and CH selection. Afterwards, the Binary Horse Herd Optimization (BHHO) algorithm was used for route selection and data transmission.

The problem of routing in homogenous WSNs has been widely studied in the literature. Gupta et al. [26] assumed an event-driven system model in which a node sends packets upon detecting an event, such as the temperature exceeding a predefined threshold. The algorithm conserved energy by omitting redundant data packets generated by different sensor nodes. Chaurasia et al. [27] integrated Q-learning with Bald Eagle Search (BES).

Q-learning was used to evaluate the properness of closer neighbors to the BS per node for selection as its next-hop. The obtained Q-values were used by BES to construct best routes toward the BS. The considered criteria in BES were the amount of energy consumption and network lifetime. Reference [28] considered both residual energy of nodes and network load to improve energy efficiency and packet delivery. The algorithm used GWO to route construction. To construct the routing tree, the proposed algorithm in [29] first estimated the optimal number of children per node, namely $k$. Next, it started tree construction from the BS. For each node on the tree, it chose its $k$ closest nodes that are not on the tree, as its children.

The problem of clustering and routing in homogenous WSNs has been studied in various research including [30,31,32,33,34]. Authors in [31] presented an optimization approach for CH selection in IoT-assisted WSNs. They used factors like energy, delay, and distance as fitness criteria. Additionally, they employed tunicate swarm GWO algorithm for multipath routing. Reference [33] proposed a fuzzy logic-based CH selection method, which used the Mamdani inference engine to evaluate factors such as residual energy, node centrality, and distance to the BS, mimicking human decision-making for optimal CH selection. In [35], the authors introduced a hybrid Particle Swarm Optimization (PSO) and Artificial Bee Colony (ABC) algorithm to reduce routing costs. Shahid et al. [36] improved packet delivery and energy efficiency by using proper links, where the criteria for link selection was the link quality, energy of nodes, and distance between nodes. The quality of links was estimated using exponential moving average.

References [4,5,12,14,37] studied clustering and routing in HWSNs. Shafique et al. [37] considered energy heterogeneity and proposed a greedy algorithm for updating CHs of static clusters. The criteria for CH selection were the energy level of node and the exhausted energy by other sensors to send data to that node. To forward data of a CH toward the BS, its closer neighbors to the BS were examined, and the node with highest residual energy was adopted as the next-hop. Meta-heuristic algorithms have also been applied to clustering and routing in HWSNs [4,5,10,11,12,14]. Reference [8] proposed a greedy algorithm for clustering and applied Ant Colony Optimization (ACO) for routing. In [4], PSO was used to assign super nodes as CHs and build a spanning tree. The criteria in PSO-based clustering were network lifetime and distances between CMs and CHs, while average energy of routes and distances between successive super nodes on routes were considered for tree construction. Reference [10] also employed PSO for clustering and routing, focusing on energy and reliability. Wang et al. [12] performed join clustering and tree construction using bipartite chromosomes. The algorithm aimed to balance energy consumption of CHs while reducing overall energy consumption. Additionally, an improved chaos logistic map was applied to generate initial population to increase population diversity.

In [5], a two-phase GA handled clustering and tree construction for multi-channel HWSNs with normal and super nodes. The multi-radio super nodes were designated as CH, while the single-radio normal nodes were assigned to one of its neighboring CHs and connected to it using one of its assigned channels. In the tree construction phase, the algorithm balanced energy of super nodes based on their distances to the BS, which improved network lifetime considerably. Additionally, it offered a novel criterion for even distribution of normal nodes among CHs, further balancing the energy consumption of super nodes. The proposed algorithm in [5] was extended in [11], where authors employed GWO to optimize Transmission Power Control (TPC) in a HWSN with TPC-enabled super nodes. Reference [14] presented a novel algorithm for efficient data gathering in HWSNs. The approach consisted of two key phases: clustering and spanning tree construction. GA was employed in both phases, utilizing a problem-specific chromosome representation, a tailored population initialization scheme, and customized genetic operators (i.e., mutation and crossover). Specifically, in the tree construction phase, chromosomes were structured as trees, facilitating designing an effective initialization scheme and GA operations.

Table 1. The characteristics of the related works (HT: Heterogenous, HM: Homogenous, S: Seep scheduling, C: Clustering, R: Routing, G: Greedy, DL: Deep Learning, TPO: Taylor-Political optimizer, ROA: Remora Optimization Algorithm, F: Fuzzy).

Reference	Node Type	Problem	Approach	Features
[4,10]	HT	C, R	PSO	Limited performance due to using standard PSO
[5]	HT	C, R	GA	Even energy consumption in the network
[6]	HT	C	GWO	Excessive energy consumption due to direct data transmission form CHs to the BS
[8]	HT	C, R	G, ACO	Limited performance due to proposing greedy method for clustering and standard ACO for routing
[9]	HT	C, R	G	Limited performance due to proposing greedy methods for clustering and routing
[11]	HT	C, R	GWO	Optimizing transmission power and energy efficiency
[12]	HT	C, R	GA	Complexity in chromosome design, yielding lower performance
[13]	HT	S	G	High computational complexity Limited scalability
[14]	HT	C, R	GA	Problem-specific chromosome and operators improve performance Computationally intensive
[15]	HM	S	G	Customized to solar-powered WSNs, considering variations in energy harvesting rate
[16,17,20,22]	HM	S	RL	Customized to solar-powered WSNs, considering variations in energy harvesting rate Training overhead
[18]	HM	S, C	G	Limited performance due to proposing greedy methods for sleep scheduling and clustering
[19]	HM	S, C, R	G	Limited performance due to proposing greedy methods for sleep scheduling, clustering, and routing
[21]	HM	S, C, R	RL	Assuming static CMs Training overhead
[23]	HT	C	G	Limited performance due to proposing a greedy method for clustering Excessive energy consumption due to direct data transmission form CHs to the BS
[24]	HM	C	G	Limited performance due to proposing a greedy method for clustering Excessive energy consumption due to direct data transmission form CHs to the BS
[25]	HM	C, R	DL, BHH	Higher computational cost
[26]	HM	R	G	Assuming event-driven model
[27]	HM	R	RL, BES	No clustering method
[28]	HM	R	GWO	No clustering method
[29]	HM	R	G	Limited performance due to proposing a greedy method for routing
[30]	HM	C, R	RL, G	Assuming static CMs Training overhead
[31]	HM	C, R	TPO, GWO	Higher computational cost
[32]	HM	C, R	G	Performing power control Limited performance due to proposing greedy methods for clustering and routing
[33]	HM	C	F	Depending on proper rule design Excessive energy consumption due to direct data transmission form CHs to the BS
[34]	HM	C	ROA	Excessive energy consumption due to direct data transmission form CHs to the BS
[35]	HM	R	PSO, ABC	No clustering method Complexity of the hybrid algorithm
[36]	HM	R	G	Limited performance due to proposing a greedy method for routing Considering link quality
[37]	HT	C, R	G	Assuming static CMs Limited performance due to proposing greedy methods for CH selection and routing

summarizes the related works discussed in this study, highlighting their target problems and approaches. Despite the advancements in sleep scheduling, clustering, and tree construction for HWSNs, existing methods often suffer from key limitations. Our proposed solution addresses these deficits through an integrated two-phase approach that simultaneously optimizes sleep scheduling, clustering, and tree construction. The proposed GAs for the phases includes customized initialization methods and operators, and novel cost functions, yielding further energy efficiency and network lifetime. Rigorous simulations confirm the robustness of our approach, demonstrating its superiority over existing methods in key performance metrics.

3. Network Model

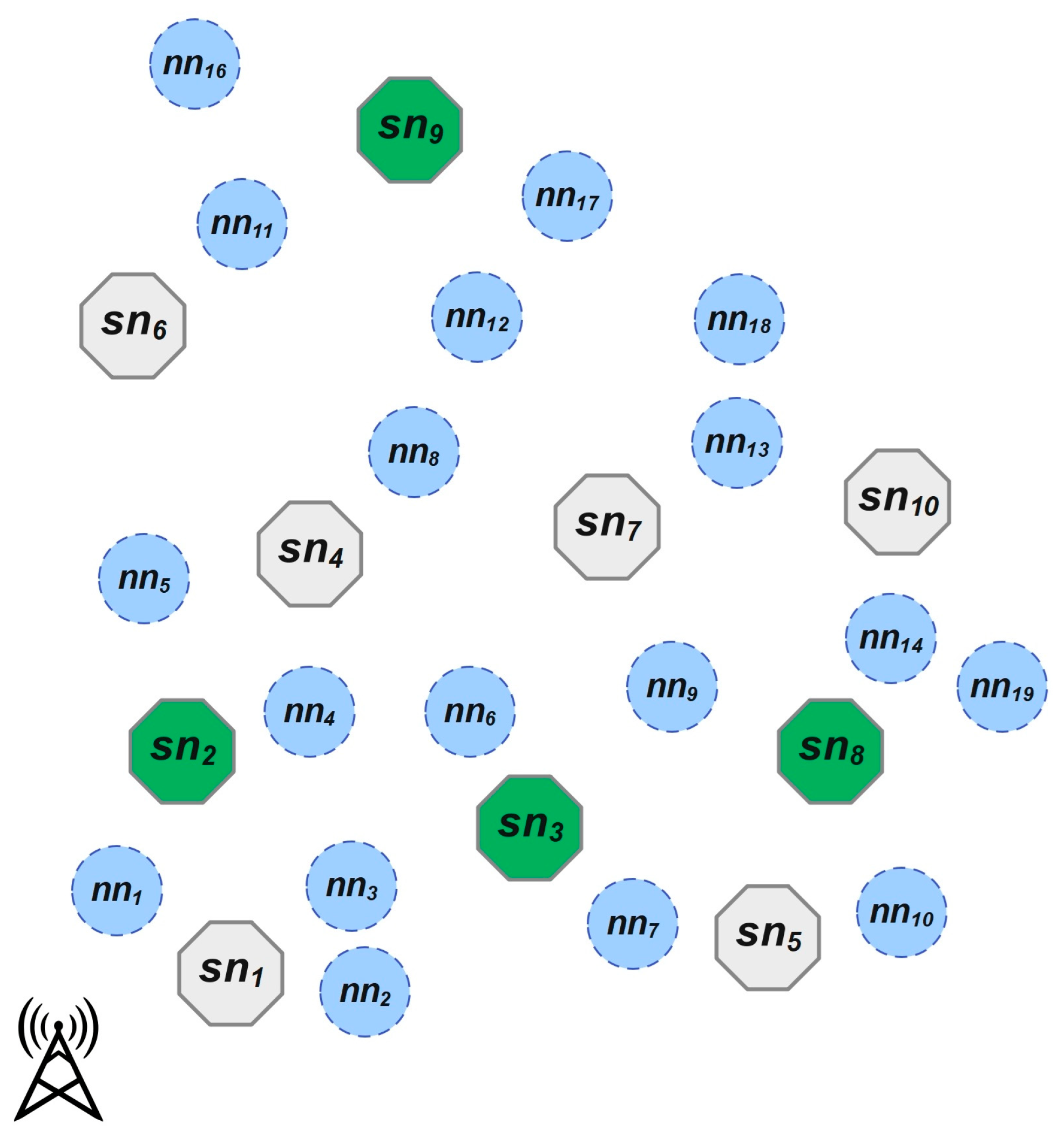
In the assumed network model, there are two types of nodes: super nodes and normal nodes. A sample HWSN is illustrated in Figure 1. We use $S$ and $N$ to show the set of super nodes and normal sensors, respectively. Every node, either super node or normal sensor, uses a battery with limited capacity. Super nodes possess greater initial energy and a larger transmission range compared to normal nodes. The initial energy and transmission range of super nodes are shown by $e_S$ and ${tr}_S$, respectively. These parameters are presented by $e_N$ and ${tr}_N$ for normal sensors. Additionally, there are fewer super nodes than normal sensors in the HWSN. The term $e_i$ refers to the remaining energy of the $i^{th}$ node, which can be a super node or a normal sensor. Finally, $|.|$ shows the cardinality of an assumed set.

Normal nodes are tasked with environmental monitoring. They collect data and send it to a nearby super node, which serves as their CH. The potential CHs for a normal node $n_i$ are super nodes within its transmission range. Each super node aggregates data of its assigned CMs. Since the BS might not be directly reachable by all super nodes, data needs to be relayed. For a super node $s_i$, other super nodes closer to the BS and within its transmission range are considered as its potential parents. One of these super nodes is selected as the parent for forwarding the data.

The network employs Time Division Multiple Access (TDMA) at the Medium Access Control (MAC) layer, which divides channel into timeslots. The data exchange process includes intra-cluster communication, where normal nodes transmit their collected data to their designated CHs during allocated timeslots, and inter-cluster communication, where super nodes use multi-hop forwarding to relay the gathered data toward the BS during their assigned timeslots.

The proposed energy model in [38] is used to compute required energy for data transmission/reception. The model proposes (1) and (2) for calculating consumed energy needed for transmission ($e_{trs}$) and reception ($e_{rec}$) based on packet size ($l$), respectively. These formulas incorporate factors like internal circuit energy ($e_{elec}$) and signal amplification energy. The amplification model varies with distance: the free space model for shorter distances, and the multipath fading model for distances beyond the threshold $d_0$. Amplifier energy consumption is denoted by ${\epsilon }_{fs}$ and ${\epsilon }_{mp}$ for these models, respectively.

$$e_{trs}\left(l, d_{tr}\right)=\left\{\begin{array}{c}l e_{elec}+l {\epsilon }_{fs} d_{tr}^2, d_{tr}<d_0\\ l e_{elec}+l {\epsilon }_{mp} d_{tr}^4, d_{tr}\ge d_0\end{array}\right.$$

(1)

$$e_{rec}\left(l\right)=l e_{elec}$$

(2)

In our study, path loss effects related to carrier frequency are not considered, as the focus is on evaluating the algorithmic performance under uniform propagation conditions. All studies used for comparison also follow the same assumption. It is worth mentioning our algorithm is fully applicable to environments with path loss.

The defined network model serves as the foundation for the proposed GA-based framework, where the relationships among nodes, their energy consumption, and communication structure guide the optimization of sleep scheduling, clustering, and routing. In the next section, we formulate these relationships into an optimization problem and detail how the GA is designed to solve it efficiently.

4. The Proposed Method

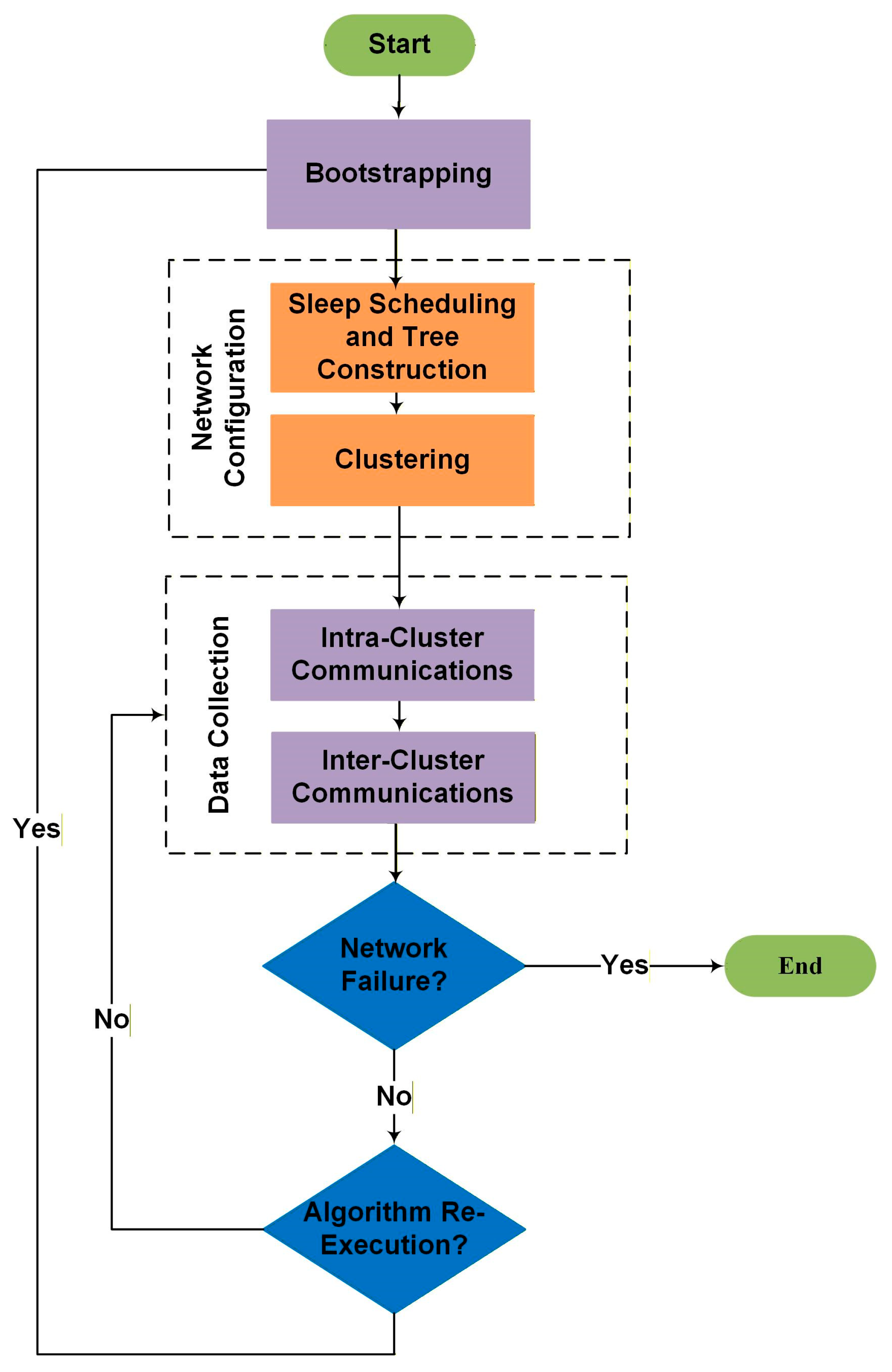
Figure 2 illustrates the workflow cycle during network lifetime. The network lifetime is divided into multiple rounds, each consisting of several time slices. During each time slice, data collected by normal nodes is first transmitted to super nodes via intra-cluster communication. Subsequently, super nodes relay this data to the BS through inter-cluster communication. The proposed algorithm is executed at the start of each round, where the BS gathers network information, such as the remaining energy of the nodes, to configure the network for optimal performance. This configuration is then applied throughout the time slices of the round. At the end of each round, the BS re-runs the algorithm to adjust for any changes in node characteristics, ensuring continuous network operation.

Our algorithm enhances data collection in HWSNs through integrating sleep scheduling, clustering, and routing. Considering the wide solution space of the mentioned problems, we divide the process into two phases to reduce complexity. Additionally, we employ a GA to obtain efficient solutions for each phase within a reasonable time. In the first phase, GA is used to solve the problem of selecting awake nodes and constructing a communication tree. The second phase focuses on network clustering. The specific steps involved in each phase are detailed in Section 4.1 and Section 4.2, respectively.

4.1. Sleep Scheduling and Tree Construction

In WSNs, efficient energy management is crucial for prolonging the network lifetime, particularly in heterogeneous environments where nodes have varying capabilities. Sleep scheduling plays a pivotal role in conserving energy by allowing nodes to enter the sleep mode when not actively transmitting or receiving data. This approach extends the lifetime of nodes, ensuring that critical tasks such as data transmission and routing are handled thoroughly. Simultaneously, during tree construction, it should be ensured that the network avoids overloading certain nodes, preventing premature depletion of their energy resources. The process of tree construction is intrinsically linked to the sleep scheduling, because the awake nodes form the backbone for data gathering within the network. Therefore, the combined approach of optimal sleep scheduling and tree construction is essential for maintaining a balanced load distribution, enhancing the overall efficiency, and extending the longevity of the HWSN. Accordingly, we propose an innovative approach that combines sleep scheduling and tree construction into a single-step process. This unified model, optimized using a GA, is designed to efficiently find the best solution within a reasonable time. The following sections will detail the chromosome representation, initial population construction, cost function, and GA operators proposed in our approach.

4.1.1. Chromosome Representation

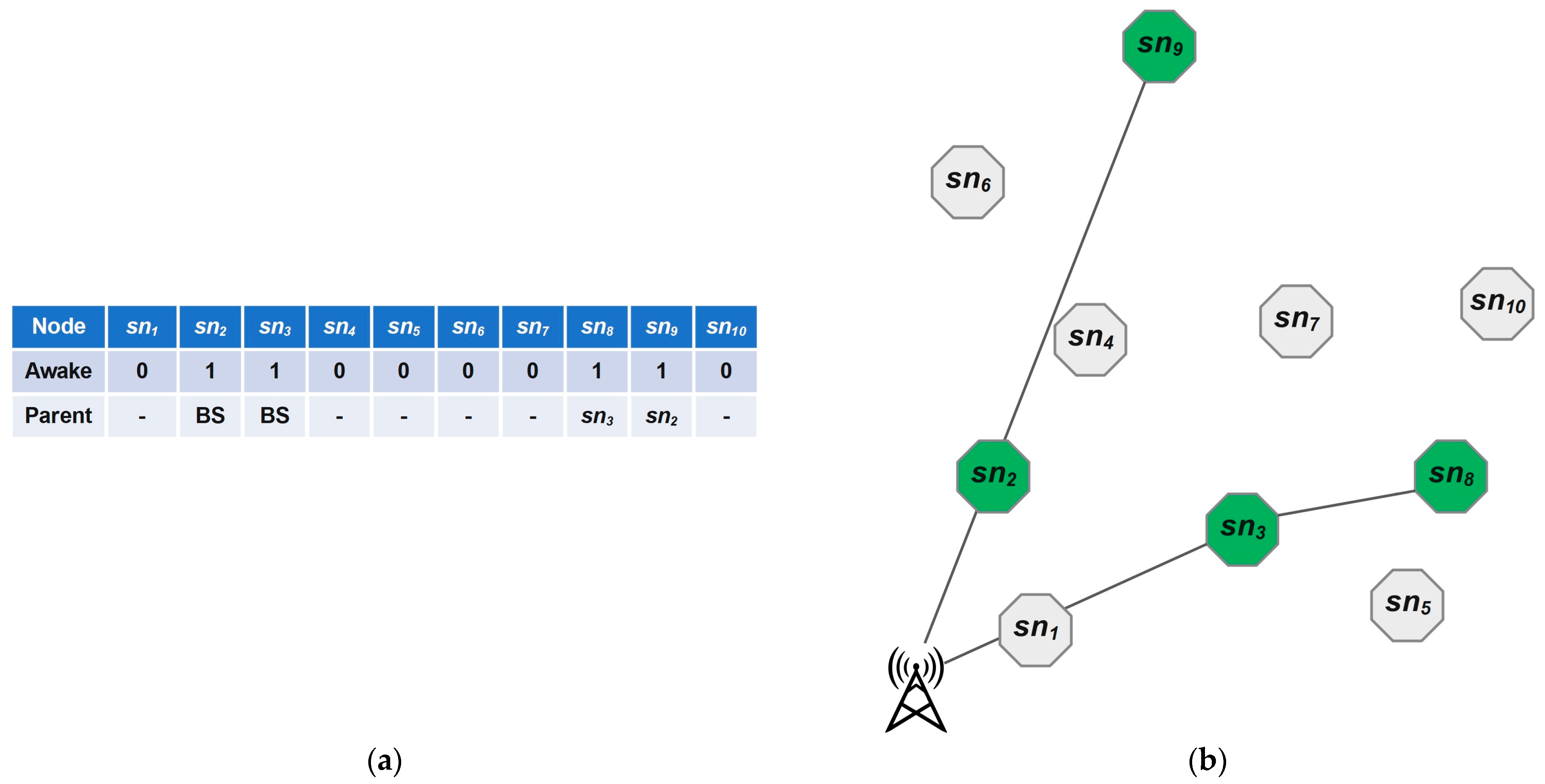
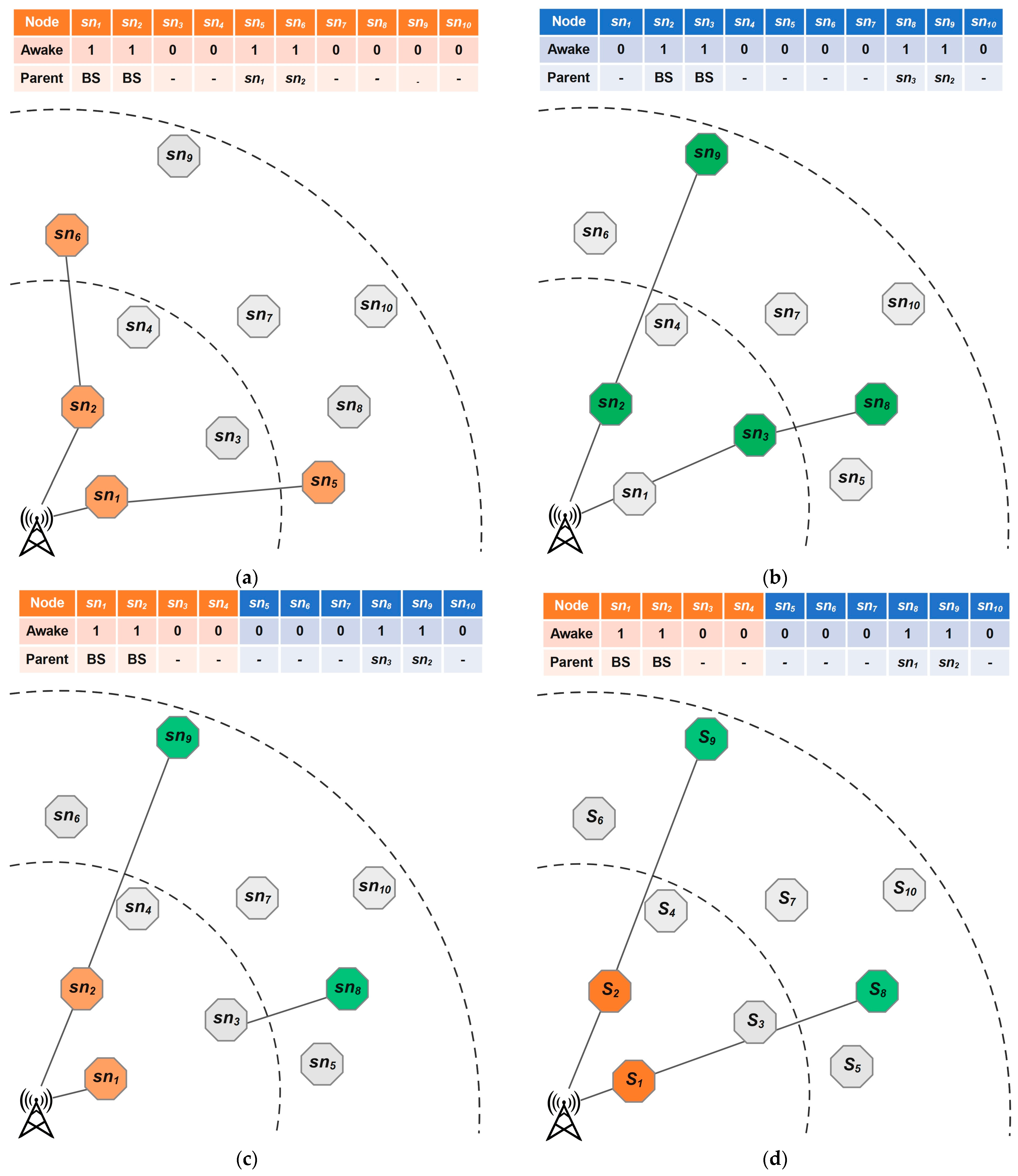
The proposed GA aims to simultaneously address the dual issues of sleep scheduling and tree construction in HWSNs. To achieve this, we design a chromosome structure represented as a matrix with dimensions of $2\times \left|S\right|$. Each column within this matrix corresponds to a specific super node in the network. The first row of the matrix corresponds to sleep state of super nodes, while the second row is dedicated to the tree construction problem. The values in the first row are binary: zero indicates that a super node is in the sleep state, and one indicates that it is awake. Additionally, the second row presents the selected parents for super nodes. In a chromosome, the super nodes are arranged sequentially based on their distance to the BS. Thus, the super node closest to the BS occupies the first column, while the one farthest away is positioned in the last column. Figure 3 shows an example chromosome and its representative tree. In the figure, green octagons represent awake super nodes, while gray octagons represent those in sleep mode. The lines between awake super nodes indicate links of the constructed tree.

4.1.2. Population Initialization

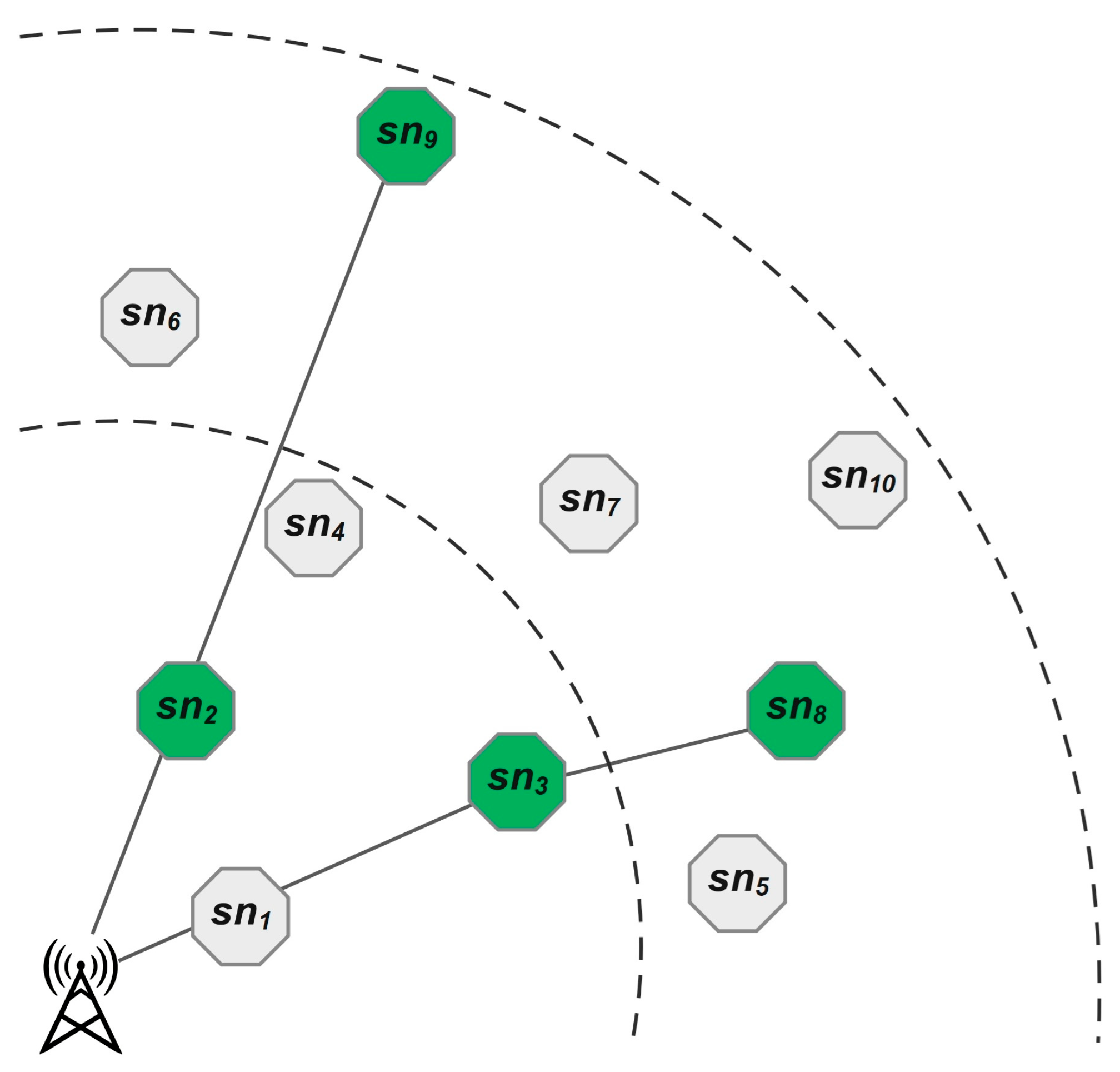
The elements of the proposed chromosome structure are populated according to the following scheme. A critical consideration to construct a chromosome is to select proper awake nodes, ensuring they are evenly distributed across the network. This distribution is essential for having at-least one super node within proximity to each normal node, allowing it to serve as the CH for gathering and forwarding data to the BS.

We divide the network into concentric rings centered around the BS and wake up $ar$ super nodes per ring (Figure 4). This unequal clustering idea was previously comprehensively discussed in [39] and proved to be a good solution to hot-spot problem. Determining the optimal number of rings is a complex process, refined through trial and error. Rings that are too narrow may limit the selection of suitable nodes, while excessively large rings could lead to suboptimal configurations. Furthermore, the value of $ar$ is determined based on different parameters such as the number of normal nodes and density of super nodes. The selection of awake nodes within each ring is carried out randomly, based on a weighted probability that considers remaining energy of super nodes. Equation (3) calculates $p{r}_{awake}\left(s_i\right)$, the probability of selecting $s_i$ to serve as an awake node. In this equation, $R\left(s_i\right)$ shows the ring which $s_i$ belongs to.

$$p{r}_{\mathit{awake}}\left(s_i\right)={\displaystyle \frac{e_i}{\sum _{s_k\in R\left(s_i\right)}{e}_k}}$$

(3)

Since the tree construction relies on awake nodes, columns corresponding to super nodes that are in the sleep state do not process. However, for super nodes that are awake (with a value of one), a subsequent step is required to construct the tree. This step involves selecting a random neighbor for each awake super node $s_i$, which must be both awake and positioned closer to the BS than $s_i$, to form the tree structure. If none of the neighbors of $s_i$ is awake, the chromosome is discarded. The selection of the parent among the super nodes which fulfill these constraints is influenced by their remaining energy, as shown in (4). According to this equation, super nodes with higher remaining energy have a greater probability of being selected as the parent, thereby ensuring that the tree construction process favors nodes with sufficient energy reserves. This approach not only helps in balancing the energy consumption across the network but also enhances the overall robustness and longevity of the HWSN.

$$p{r}_{\mathit{parent}}\left(s_j\right)={\displaystyle \frac{e_j}{\sum _{s_k\in N\left(s_i\right)\bigwedge dist\left(s_k,BS\right)<dist\left(s_i,BS\right)\bigwedge s_i is awake}{e}_k}},$$

(4)

where $N\left(s_i\right)$ is the set of neighbor super nodes of $s_i$, and $dist$ is the distance function.

4.1.3. Cost Function

GA uses a cost function to evaluate the acceptability of a particular solution (or chromosome). This function assigns a numerical value to each solution that reflects its quality or fitness. Our objective is to investigate two key factors: (1) the quality of the selection of awake nodes and (2) the quality of the constructed tree.

To evaluate the first factor, we examine the number of normal nodes that lack an awake super node in their neighborhood, as defined by (5). In this equation, $X_j^T$ stands for the $j^{th}$ chromosome. Additionally, $ON$ shows the set of orphan normal nodes that there is not an awake super node in their vicinity. The smaller value of $facto{r}_1$ indicates choosing better awake nodes, as it designates that the selected awake nodes are distributed evenly in the network, ensuring each normal node has at-least one awake super node nearby. The division by the total number of awake nodes is intended to normalize this metric, making it comparable with other factors.

$$facto{r}_1\left(X_j^T\right)={\displaystyle \frac{\left|ON\right|}{\left|N\right|}}$$

(5)

The coverage criterion related to the sleep scheduling problem. The proposed sleep scheduling algorithm for HWSNs in [13] preserved connectivity between the awake nodes and did not take into account the coverage measure. Other sleep scheduling algorithms considered homogenous WSNs and considered the connectivity of awake nodes and coverage of the monitoring area. It should be noted that our algorithm preserved connectivity through applying the proposed repair method in Section 4.1.4 to the outcome of crossover and mutation operators.

Another factor for evaluating the chromosomes is the quality of the constructed tree. To assess this, we aim to increase the minimum remaining energy of the nodes, as described in (6). In this equation, $e{r}_{ji}$ demonstrates the remaining energy of super node $s_i$ at the end of the round assuming the proposed network configuration by $X_j^T$. This approach ensures that tree structures which route data through nodes with higher energy levels are considered more suitable.

$$facto{r}_2\left(X_j^T\right)={\displaystyle \frac{{\mathrm{m}\mathrm{i}\mathrm{n}}_{s_k\in S} {er}_{jk}}{e_s}}$$

(6)

There are various energy-related criteria for data collection in WSNs. The most common metrics are energy consumption and network lifetime [4,5,10]. The proposed factor in (6) includes both of these metrics. It prioritizes configurations with lower energy usage. Additionally, it prolongs network lifetime by increasing the remaining energy of nodes at the end of the round.

Finally, our cost function is defined by (7), and our objective is to minimize it.

$$cos{t}_1\left(X_j^T\right)=w_1\times facto{r}_1\left(X_j^T\right)-w_2\times facto{r}_2\left(X_j^T\right), w_1+w_2=1$$

(7)

4.1.4. GA Operators

The key components of GA, including selection, crossover, and mutation operators, are introduced in this section. We customize each of these operators to suit the specific problem at hand and to align with the proposed chromosome structure model, which we will detail in the following.

Selection: The selection operator in GA is responsible for choosing which individuals from the current population will contribute to the creation of the next generation. The idea is to select the fittest individuals, those that are better suited to the problem according to the fitness function, to pass on their genes to their offspring. We employ Roulette Wheel Selection (RWS) as our selection operator, detailed in (8). In this equation, the term ${pop}^T$ refers to the population of chromosomes. In the RWS method, the chance of each chromosome to being selected as a parent is proportional to its cost. The lower the cost value, the higher the probability of selection, and conversely, chromosomes with higher cost values have a reduced chance of selection. This approach increases the likelihood that superior chromosomes, which demonstrate more effective network structures, will produce the next generation. However, we do not completely eliminate the possibility of selecting weaker chromosomes. They are still given a chance to contribute as parents, with the hope that some aspects of their structure might offer a valuable solution to the problem.

$$RWS\left(X_j^T\right)={\displaystyle \frac{1/cos{t}_1\left(X_j^T\right)}{\sum _{X_k^T\in {pop}^T}1/cos{t}_1\left(X_k^T\right)}}$$

(8)

Crossover: The crossover operator in GA is responsible for combining the genetic information of two parent chromosomes to produce offspring. This process mimics biological reproduction and aims to create new solutions (chromosomes) that inherit features from both parents, potentially leading to better solutions. In this phase, we employ the single-point crossover operator. Accordingly, a point is selected on two chromosomes, and the genes on the left side of one chromosome are combined with the genes on the right side of the other chromosome, and vice versa, resulting in two new offspring.

It is crucial to note that this crossover operation may not always yield valid chromosomes. The first issue is that a node may have no awake parent toward the BS. The other concern is that the number of awake nodes may deviate from the desired quantity. To address these issues, a repair procedure is proposed. The method ensures that the number of awake nodes in each ring is equal to $ar$. Accordingly, the number of awake nodes in each ring is examined: if it matches $ar$, no action is required. If there are more awake nodes than desired, we probabilistically reduce their number by switching some of them to the sleep state, based on their remaining energy levels (Equation (9)). Conversely, if there are fewer awake nodes than necessary, additional sleeping nodes are selected, once again probabilistically, based on their remaining energy according to (10), and switched to the awake state. Once the number of awake nodes has been adjusted, we proceed to validate the offspring. For nodes whose have at least one potential parent in the resultant offspring, no change is required. Otherwise, one of the closer super nodes to the BS is activated probabilistically considering their remaining energy, as shown in (11).

$$p{r}_{\mathit{remove}}\left(s_i\right)={\displaystyle \frac{e_i}{\sum _{s_k\in R\left(s_i\right)\wedge s_k is awake}{e}_k}}$$

(9)

$$p{r}_{\mathit{add}}\left(s_i\right)={\displaystyle \frac{e_i}{\sum _{s_k\in R\left(s_i\right)\wedge s_k is sleep}{e}_k}}$$

(10)

$$p{r}_{\mathit{parent}}\left(s_j\right)={\displaystyle \frac{e_j}{\sum _{s_k\in N\left(s_i\right)\bigwedge dist\left(s_k,BS\right)<dist\left(s_i,BS\right)\bigwedge s_i is sleep}{e}_k}}$$

(11)

The pseudocode of the proposed crossover operator is presented in Algorithm 1. In this algorithm, $R$ presents the set of rings, and ${na}_r$ is the number of awake nodes in ring $r$. Additionally, ${PP}_i$ is the set of potential parents of super node $s_i$.

Algorithm 1. Crossover operator of the first phase

Input: $X_i^T$, $X_j^T$ Output: $O_{1ij}^T$, $O_{2ij}^T$ Steps: 1.  $O_{1ij}^T$, $O_{2ij}^T\leftarrow$ Apply crossover operator to $X_i^T$ and $X_j^T$. 2.  For each chromosome $X_k^T\in \left\{O_{1ij}^T,O_{2ij}^T\right\}$ do 3.  For each ring $r\in R$ do 4.  If ${na}_r<ar$ do 5.    Awake $ar-{na}_r$ sleeping nodes consecutively, where the probability of awaking a node is computed using (9). 6.  If $ar<{na}_r$ do 7.    Put to sleep ${na}_r-ar$ awake nodes consecutively, where the probability of putting to sleep a node is computed using (10). 8.  End 9.  For each $s_m\in S$ do 10. ${PP}_m\leftarrow s_p\in N\left(s_m\right)\bigwedge dist\left(s_p,BS\right)<dist\left(s_m,BS\right)$. 11. If all nodes of ${PP}_m$ are in sleep mode do 12. Awake a node in ${PP}_m$, where the probability of awaking a node is computed using (11). 13. End 14. End

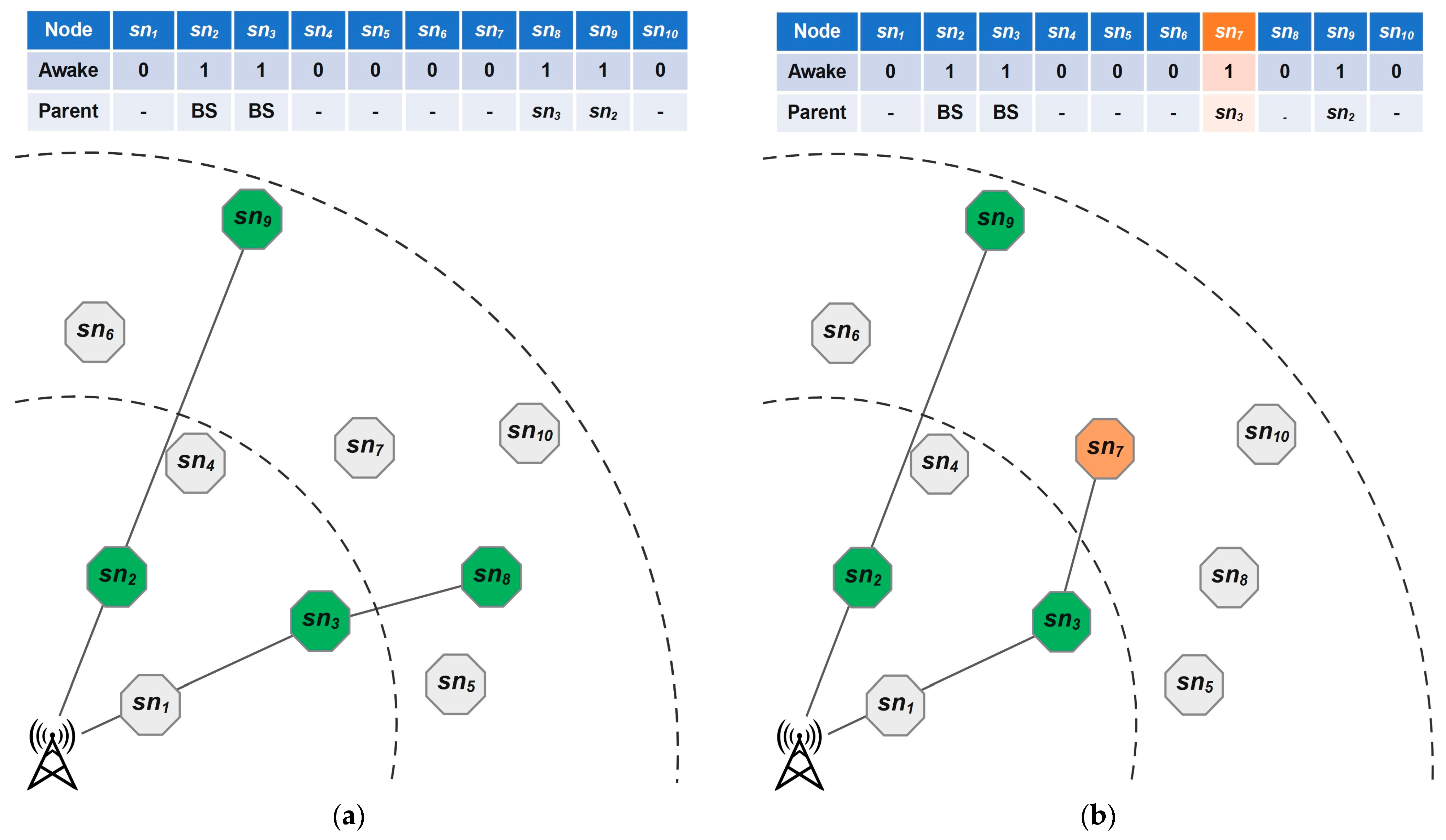
Figure 5 demonstrates an example of the proposed crossover operator. In this figure, the single-point crossover is applied to parent chromosomes, which are shown in Figure 5a,b, to produce two offspring. Here, $s_4$ is selected as the crossover point. We demonstrate one of the offsprings in Figure 5c. After generation of the offspring, we check for the validity of chromosome and change the structure of the chromosome to produce a valid chromosome (Figure 5d).

Mutation: The mutation operator in GA introduces random changes to the genes of a chromosome to maintain genetic diversity within the population. This operator is crucial because, without it, GA might converge too quickly to a suboptimal solution, getting stuck in local optima. According to the chromosome structure, we propose a customized mutation operator. In this approach, the number of genes of adopted chromosomes undergoing mutation is higher in the initial iterations of the algorithm and gradually decreases as the algorithm progresses. The number of genes undergoing mutation at iteration $t$, $m\left(t\right)$, is calculated as

$$m\left(t\right)=m_{\max }\left(1-{\displaystyle \frac{t}{t_{\max }}}\right).$$

(12)

where $m_{\max }$ and $t_{\max }$ are the initial number of genes undergoing mutation and the total number of iterations, respectively. This strategy enables extensive exploration of the solution space in the early iterations and shifts towards exploitation in the later ones.

The corresponding super nodes to the adopted genes are investigated, and the awake ones are switched from the awake to the sleep state. For each of these asleep super nodes, a node in the same ring must be woken up. This activation is controlled by the given probabilistic function in (10).

The pseudocode of the proposed mutation operator is presented in Algorithm 2.

Algorithm 2. Mutation operator of the first phase

Input: $X_i^T$ Output: $M_i^T$ Steps: $M_i^T\leftarrow X_i^T$. For $m\left(t\right)$ times do $s_j\leftarrow$ Select a random awake super node. Put to sleep $s_j$, and awake a sleeping node $s_k\in R$, which is selected probabilistically using (10). End

Figure 6 demonstrates an example of the mutation operator. In this figure, based on the mutation operator, $s_8$ goes to sleep mode. Accordingly, one other super node, for example $s_7$, is woken up in the ring and a parent is selected for this node from the awake super nodes.

4.2. Clustering

After completing the first phase, which involves introducing awake nodes in the network and constructing a tree on them, we proceed to the second phase, in which each normal node selects an awake super node in their neighborhood to act as their CH. To achieve this aim, we employ a GA, the details of which are outlined in the following.

4.2.1. Chromosome Representation and Population Initialization

The proposed chromosome structure for network clustering consists of an array of length $\left|N\right|$. Each gene of this chromosome corresponds to a normal node of the HWSN. To ensure a consistent structure across all chromosomes, the normal nodes in each chromosome are sorted based on their distance to the BS. Each gene presents the randomly selected CH for each corresponding normal node, which is selected from the awake super nodes within its transmission range. Figure 7 illustrates an example clustering chromosome and its corresponding network structure.

4.2.2. Cost Function

A cost function is proposed to assess the quality of clustering chromosomes. In this context, we consider two key criteria: The first metric promotes even clustering by ensuring an equal number of CMs for each CH, and the second one aims to maximize the minimum energy of CHs. The former helps evenly distribute the load of the network, while the latter accounts for the energy levels of the CHs to prevent any super node from depleting prematurely. Equation (13) describes the first measure, where $AS$ represents the set of awake super nodes selected in the previous phase, and ${nm}_{ji}$ indicates the number of cluster members assigned to the super node $s_i$ according to clustering chromosome $X_j^C$. Additionally, $inm$ represents the ideal number of cluster members and is calculated by dividing the number of available normal nodes by the number of awake super nodes:

$$facto{r}_3\left(X_j^C\right)=\underset{s_i\in \mathit{AS}}{\mathit{std}}{\displaystyle \frac{{nm}_{ji}}{inm}}.$$

(13)

Equation (14) describes $facto{r}_4$, which is similar to $facto{r}_2$ in the tree construction phase. The difference is that $facto{r}_2$ relies solely on the structure of the proposed tree, without knowledge of the number of CMs for each super node. On the other hand, $facto{r}_4$ accounts for the exact number of CMs per super node in the clustering phase, enabling more precise calculation of ${er}_{ji}$:

$$facto{r}_4\left(X_j^C\right)={\displaystyle \frac{{\mathrm{m}\mathrm{i}\mathrm{n}}_{s_k\in S} {er}_{jk}}{e_s}}.$$

(14)

Finally, the energy level of normal nodes is balanced as described in (15):

$$facto{r}_5\left(X_j^C\right)={\displaystyle \frac{{\mathrm{m}\mathrm{i}\mathrm{n}}_{n_k\in N} {er}_{jk}}{e_N}}.$$

(15)

Our cost function is defined by (16), and our objective is to minimize this function:

$$cos{t}_2\left(X_j^C\right)=w_3\times facto{r}_3\left(X_j^C\right)- w_4\times facto{r}_4\left(X_j^C\right)+w_5\times facto{r}_5\left(X_j^C\right), w_3+w_4+w_5=1.$$

(16)

4.2.3. GA Operators

Our GA uses three core operators to iteratively refine the population and guide it towards high-quality solutions including selection, crossover, and mutation. These operators are explored in the following.

Selection: We use RWS as the selection operator, which selects chromosomes based on the value returned by the cost function using a similar probability function to (8). Chromosomes with lower costs (indicating better solutions) have a higher probability of being chosen to produce the next generation.

Crossover: The crossover operator is employed to explore the solution space. In this case, a single-point crossover is used. All offspring produced by this operator are valid solutions for the clustering problem.

Mutation: In the proposed mutation process, for a random chromosome, a number of genes—which are corresponded to CHs of normal nodes—are randomly selected. The CH of each chosen normal node is changed from its current CH to another awake super node within its transmission range.

5. Experimental Results and Discussion

In this section, we evaluate the performance of the proposed method and compare it with HEDHMG (High-throughput and Energy-efficient Data gathering in Heterogeneous Multi-channel WSNs using GA) [5], EFCRPSO (Energy eFficient Clustering and Routing algorithms for WSNs using PSO) [10], EFEBPSO (Energy-eFficient and Energy-Balanced routing and clustering in WSNs using PSO) [4], and CRCGA (Clustering Routing protocol using a Chaotic Genetic Algorithm) [12]. The reason for selecting the mentioned methods is that they are addressing similar clustering, routing, and energy optimization problems in HWSNs. HEDHMG used a two-phase GA for clustering and tree construction. CRCGA employed GA to solve the joint problem of clustering and tree construction, using a bipartite chromosome representation and chaos-based initialization. EFEBPSO and EFCRPSO were applied PSO to construct the tree and clusters in two consecutive phases. The mentioned algorithms adopted different energy-related criteria to preserve energy efficiency such as the amount of consumed energy and lifetime of nodes.

The performance metrics used for comparison include area coverage, total energy consumption, First Node Die (FND), Last Node Die (LND), and number of available super nodes. The algorithms are implemented using WSNSimPy, a Python 3 library for discrete event simulation of WSNs. We evaluate three different networks, ${WSN}_1$, ${WSN}_2$, and ${WSN}_3$ which differ in node density and network dimensions. The network ${WSN}_1$ consists of 60 super nodes and 200 normal nodes, with the BS positioned in the lower-left corner of the area. The network ${WSN}_2$ is denser, featuring 80 super nodes and 250 normal nodes, and also has the BS located in the corner, similar to ${WSN}_1$. Both ${WSN}_1$ and ${WSN}_2$ are networks with dimensions of 200 m × 200 m. To evaluate the performance of the proposed method on the large networks, we use another network with dimensions of 300 m × 300 m which is named as ${WSN}_3$. This network consists of 120 super nodes and 500 normal nodes.

Table 2. Simulation parameters.

Parameter	Value	Reference
Network dimensions	200 m × 200 m, 300 m × 300 m
$e_N$	2 J	[5]
$e_S$	10 J	[5]
${tr}_N$	30 m	[5]
${tr}_S$	90 m	[5]
$e_{elec}$	50 nJ/bit	[38]
$e_{fs}$	$10 \mathrm{pJ}/\mathrm{bit}/{\mathrm{m}}^2$	[38]
$e_{mp}$	$0.0013 \mathrm{pJ}/\mathrm{bit}/{\mathrm{m}}^4$	[38]
$d_0$	$\sqrt{e_{fs}/e_{mp}}$	[38]
Time slices per round	50	[5]
Number of rings	4
$ar$	50% of all the super nodes

outlines the parameters used in the simulations. The parameters of the energy model, including $e_{elec}$, $e_{fs}$, $e_{mp}$, and $d_0$, are taken from [38]. Additionally, parameters $e_N$, $e_S$, ${tr}_N$, and ${tr}_S$, are adopted from HEDHMG [5] to ensure consistency and fairness in performance comparison. In this table, we set the number of rings to four and the number of awake super nodes to 50% of all super nodes. These values are determined through preliminary simulations in which different configurations were tested. The results showed that dividing the network into four rings provides the best performance. Increasing the number of rings makes the rings too narrow, reducing the pool of suitable nodes. Conversely, decreasing the number of rings yields rings that are too large, resulting in suboptimal configurations. Similarly, keeping 50% of the super nodes awake ensures an optimal balance between network connectivity and energy consumption, as higher percentages lead to unnecessary energy drain while lower ones increase the risk of connectivity loss.

Table 3. GA parameters.

Parameter	Value
Population size	30
Number of iterations	50
$w_1$	0.5
$w_2$	0.5
$w_3$	0.3
$w_4$	0.4
$w_5$	0.3

provides the GA parameters for the proposed method, including the weights for the criteria used in the cost functions, the number of iterations, and the population size. The weights in the proposed cost functions are determined based on preliminary experiments to balance the impact of different factors such as energy consumption, coverage, and connectivity. These experiments evaluate how varying each weight affects overall network performance, allowing us to select values that provide a reasonable trade-off among competing objectives.

5.1. Normal Node Coverage

This metric quantifies the number of normal nodes that have a super node as their CH. It serves as an indicator of how effectively the first phase of the algorithm selects awake super nodes. In this way, the algorithm can ensure super nodes are evenly spread across the network which increases the likelihood that normal nodes have an accessible awake super node nearby. Effective network coverage is critical for achieving performance and efficiency goals.

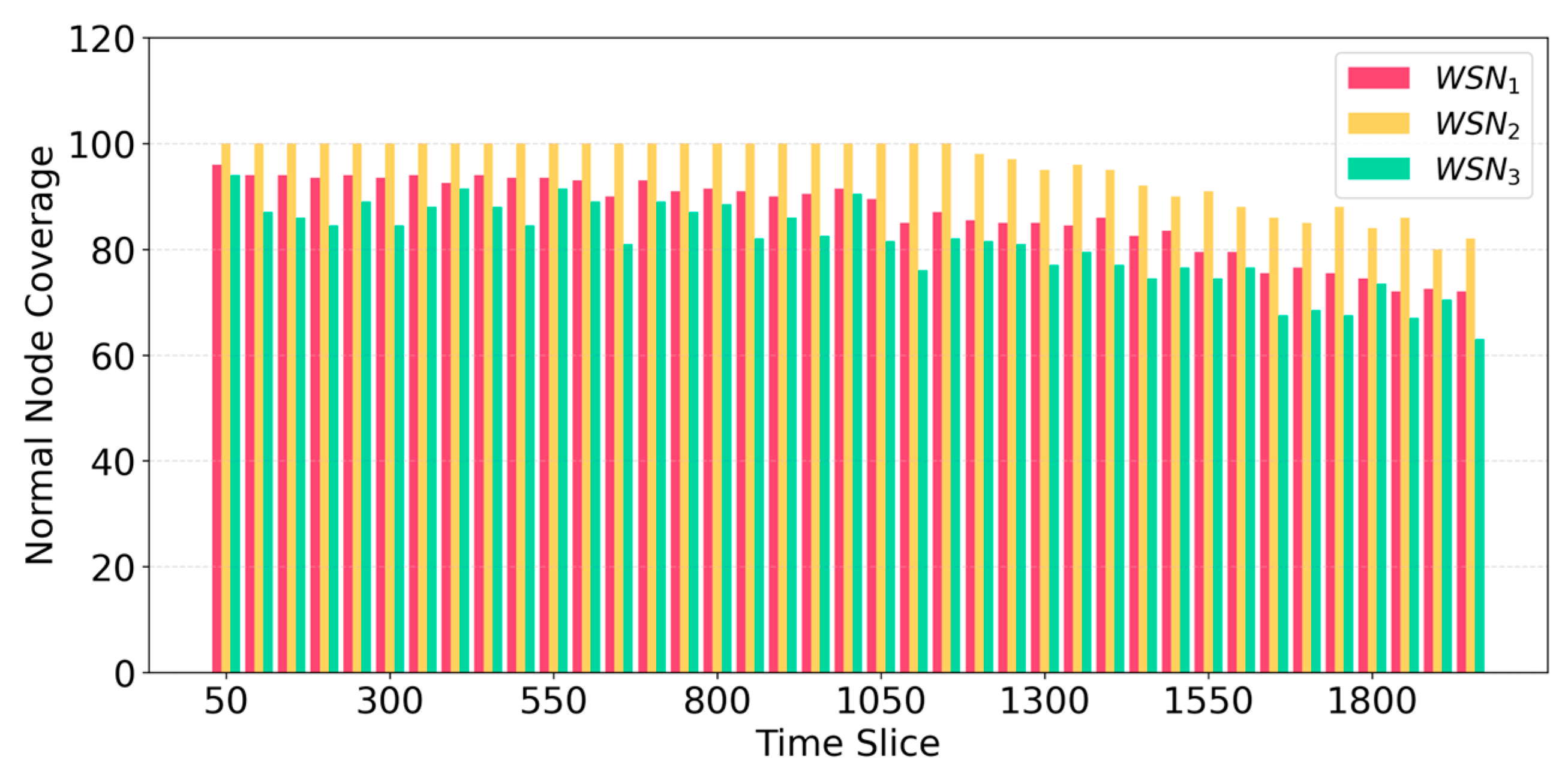
Figure 8 illustrates area coverage for $WS{N}_1$, $WS{N}_2$ and $WS{N}_3$, using the proposed method. In the early rounds, ${WSN}_2$ achieves almost full coverage, primarily because it contains a greater density of super nodes compared to $WS{N}_1$ and $WS{N}_3$. This higher super node density facilitates finding an awake super node in the neighborhood of normal nodes, supporting a strong coverage. Conversely, ${WSN}_1$, and $WS{N}_3$, which have fewer super nodes density, display slightly lower coverage, as the reduced number of super nodes limits the availability of CHs across the network. As time progresses, coverage decreases in all networks due to the depletion of super nodes. The decrease in the network coverage over time can be attributed to the energy consumption and eventual failure of super nodes, which reduces the ability of the HWSN to maintain consistent communication routes. However, even with this gradual reduction, the area coverage remains within acceptable thresholds in all of the networks.

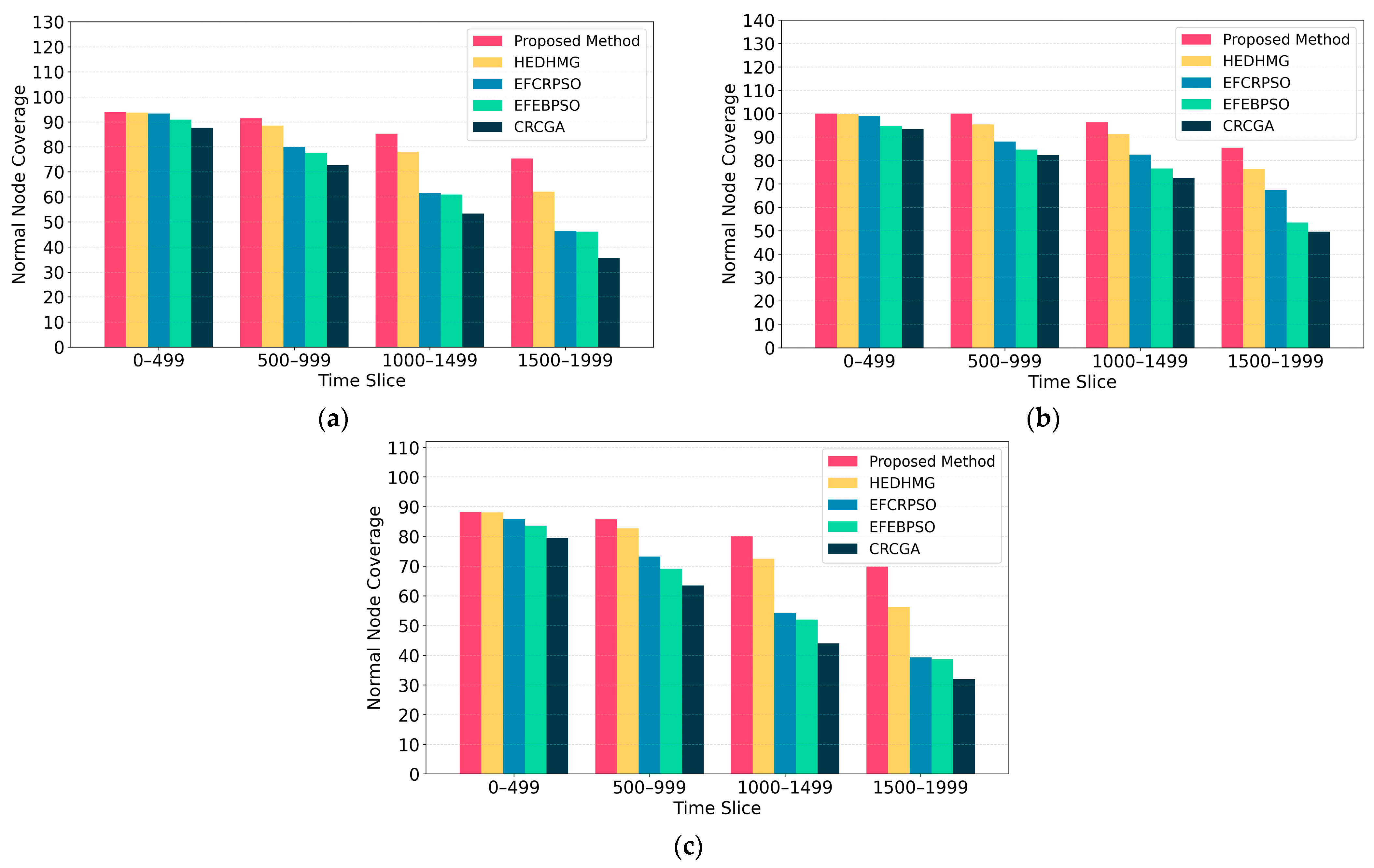
Figure 9 illustrates a comparison of normal node coverage between the proposed algorithm and other considered approaches. As depicted in the figure, the proposed algorithm significantly outperforms HEDHMG, EFCRPSO, EFEBPSO, and CRCGA in all of the networks. Specifically, in ${WSN}_1$, the proposed algorithm achieves an average coverage improvement of 8.6%, 29%, 31.1%, and 51.1% over HEDHMG, EFCRPSO, EFEBPSO, and CRCGA, respectively. Similarly, in ${WSN}_2$, the proposed algorithm surpasses these algorithms by 5.6%, 14.5%, 27.4%, and 33.4%, respectively. The average normal node coverage improvements in $WS{N}_3$ are 9%, 36%, 41%, and 61% regarding the competitive methods, respectively.

To better contextualize the results,

Table 4. Summary of resultant normal node coverage.

Network	Proposed Algorithm			Competitive Algorithms
	Min	Max	Expected	Min	Max	Expected
${WSN}_1$	76%	94%	85%	36%	94%	65%
${WSN}_2$	86%	100%	93%	50%	99%	74.5%
${WSN}_3$	70%	89%	79.5%	32%	88%	60%

summarizes the expected, minimum, and maximum normal node coverage values. In general, prior research indicates that coverage in HWSNs ranges from approximately 32% to 99%, depending on super node density and network topology. Our proposed algorithm achieves coverage within or above these ranges for all networks. Specifically, ${WSN}_1$ achieves coverage between 76% and 94% over the simulation rounds, while ${WSN}_2$, with higher super node density, maintains coverage between 86% and near-full coverage. The coverage for ${WSN}_3$ are 70% to 89%. These results confirm that the algorithm effectively balances sleep scheduling and CH selection, leading to sustained high coverage compared to HEDHMG, EFCRPSO, EFEBPSO, and CRCGA.

This sustained coverage is largely due to the inclusion of $facto{r}_1$ in the algorithm, which optimizes the sleep scheduling of super nodes. Using this factor ensures that super nodes are cyclically activated, balancing their load to delay their energy depletion. By minimizing the extent of orphan nodes through effective sleep scheduling, this factor enhances network coverage and functionality. Consequently, despite the inevitable death of super nodes, the proposed method ensures that the network retains satisfactory coverage levels over time, supporting continued data collection in the HWSN. The other factor enhancing our algorithm is proposing customized initialization, and crossover and mutation operators. According to these schemes, the HWSNs are divided into ring of equal width, and it is tried to keep the number of awake super nodes in different rings the same. Therefore, the awake nodes distribute evenly throughout the network.

5.2. Total Consumed Energy

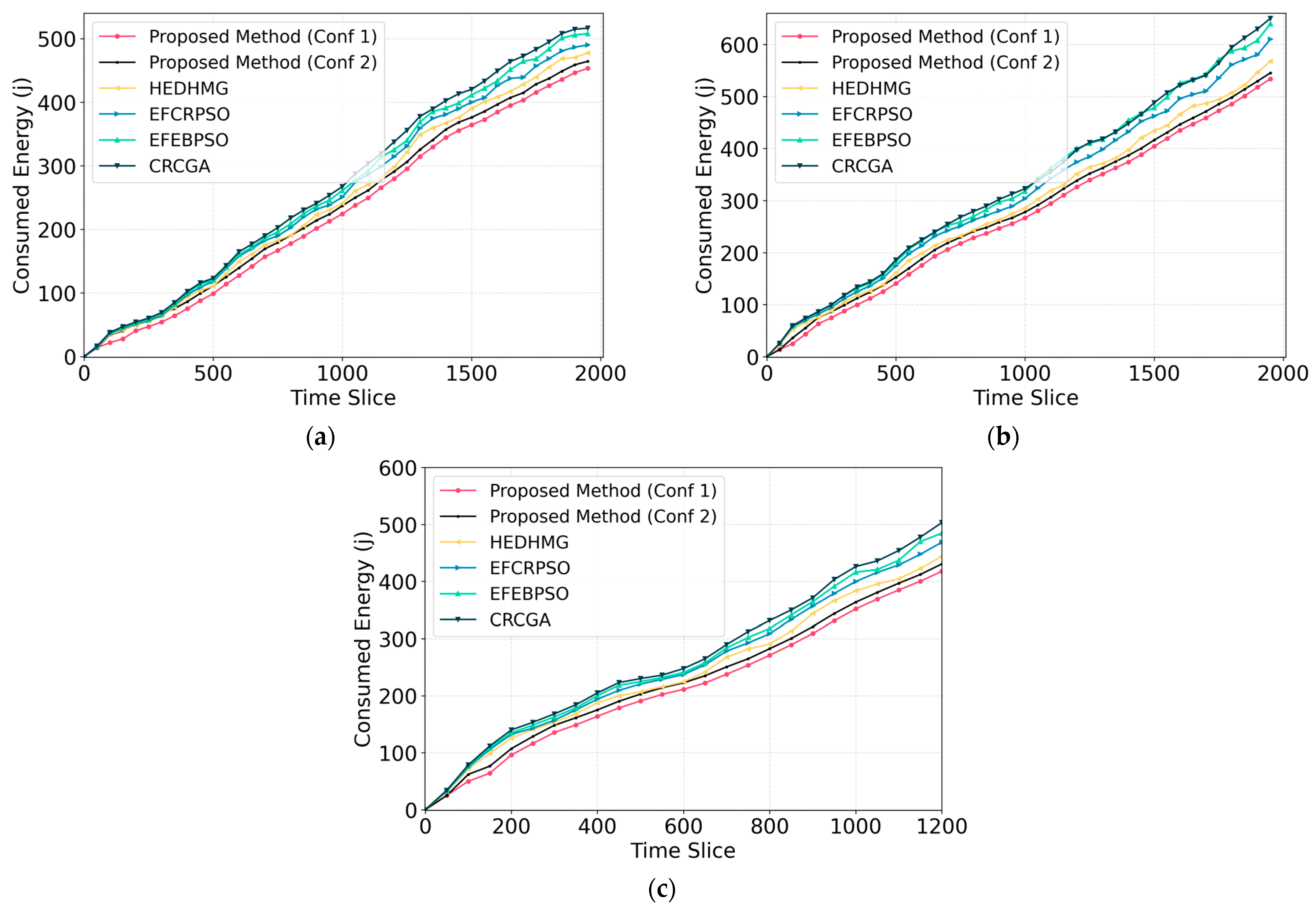
The next metric under consideration is the total consumed energy, which calculates the cumulative energy usage of super nodes that handle the primary task of data transmission and delivery within the network. Each awake super node in the routing tree receives data from its child nodes and forwards the gathered data along with the data of its own cluster toward the BS through its parent. The amount of energy consumed by the node for data reception and forwarding is calculated using (2) and (1), respectively. The total consumed energy metric is essential for evaluating the efficiency of the network, as nodes have limited, non-rechargeable energy sources, and conserving this energy directly influences network longevity. Figure 10 compares total energy consumption of the proposed method with other algorithms in ${WSN}_1$, ${WSN}_2$, and ${WSN}_3$. In this figure, to assess the impact of variations in the weight setup on the performance of the proposed algorithm, a new configuration, where $w_1$, $w_2$, $w_3$, $w_4$, and $w_5$ are set to 0.65, 0.35, 0.25, 0.5, and 0.25, is examined. This configuration is named Conf 2, while the primary configuration that assumes the given values in Table 3 is called Conf 1.

In all networks, the proposed method outperforms competing algorithms in terms of energy exhaustion. Specifically, for ${WSN}_1$, it reduces energy consumption by 10.5%, 14%, 16.4%, and 18.7% when compared to the HEDHMG, EFCRPSO, EFEBPSO, and CRCGA algorithms, respectively. These values are equal to 10.7%, 16.9%, 20.7%, and 21%, for ${WSN}_2$, and 11.5%, 15.5%, 17.7%, and 20%, for ${WSN}_3.$ Additionally, as shown in the figure, Conf 1 yields lower energy consumption compared to Conf 2.

The enhanced energy efficiency of our proposed approach in the considered network types highlights the robustness of the proposed method under varying conditions. This superiority is achieved due to the integration of four critical factors that we apply within the tree construction and clustering phases. The first factor, $facto{r}_1,$ ensures that awake super nodes are distributed uniformly across the network, which is particularly important for the tree construction phase. By spreading awake super nodes evenly, $facto{r}_1$ enables the formation of balanced communication routes. Without such uniform distribution, awake super nodes could become concentrated in some areas, leaving other sections without adequate awake super node coverage. This imbalance would limit the routing options in those uncovered areas, leading to increased energy consumption as nodes are forced to transmit data to distant parents. Furthermore, $facto{r}_2$ prioritizes routes with higher remaining energy in the tree construction phase, helping balance energy consumption across the WSN. Finally, proposing customized initialization method and GA operators enhances the performance of the proposed algorithm and reduces energy consumption.

In the clustering phase, additional efficiency is achieved through $facto{r}_3$ and $facto{r}_4$. The third factor plays a critical role by distributing normal nodes among super nodes as evenly as possible. This distribution balances the load across all super nodes, reducing the likelihood of any single node being overwhelmed by a large number of connections. Such even distribution not only conserves the energy of individual super nodes but also enhances the overall energy efficiency of the network. By preventing excessive energy consumption in specific nodes, $facto{r}_3$ contributes to a more sustainable energy usage scheme throughout the network. Additionally, $facto{r}_4$ focuses on energy conservation of super nodes. This metric prevents premature exhaustion of any single super node by distributing node responsibilities based on energy levels, similar to the prioritization strategy in the tree construction phase. Finally, $facto{r}_5$ reduces energy consumption of normal nodes and prevents choosing far super nodes as CHs, which require high energy levels for data transmission.

The employed factors in the cost functions create an energy management strategy that optimizes the selection of awake super nodes. This approach not only conserves energy in individual nodes but also maximizes overall network efficiency and ensures that HWSNs maintain robust coverage and functionality over lengthy periods. Using customized initialization, crossover, and mutation in the tree construction phase also improves energy efficiency. Even distribution of awake super nodes avoids long distances between normal nodes and their CHs, reducing exhausted energy for intra-cluster communication.

5.3. Network Lifetime

The network lifetime is measured as the time slice of occurring first death and last death in the network. In the literature, the mentioned metrics are named as First Node Die (FND) and Last Node Die (LND). Figure 11 compares the obtained FDN and LND of super nodes by the competitive algorithms. As the figure illustrates, in our algorithm, both FND and LND occur significantly later compared to competitive algorithms. Specifically, using the proposed method in $WS{N}_1$ results in improvement of 56, 167, 293, and 402 rounds or FND compared to HEDHMG, EFCRPSO, EFEBPSO, and CRCGA, respectively. For LND in ${WSN}_1$, the improvements are 140, 620, 615, and 810 rounds regarding the same algorithms. In ${WSN}_2$, the proposed method yields FND improvements of 161, 311, 487, and 532 rounds, and LND improvements of 128, 508, 681, and 757 rounds compared to HEDHMG, EFCRPSO, EFEBPSO, and CRCGA, respectively. Finally, in ${WSN}_3$, the proposed method yields FND improvements of 23, 122 161, and 175 rounds, and LND improvements of 150, 480, 570, and 560 rounds compared to HEDHMG, EFCRPSO, EFEBPSO, and CRCGA, respectively.

The enhancements in these results can be attributed to effective sleep scheduling and robust tree construction in the first phase, and efficient clustering in the latter phase. To be more precise, $facto{r}_1$ plays a crucial role in ensuring a uniform distribution of awake super nodes across the network, which yields load-balanced trees and reduces the likelihood of energy depletion in concentrated areas. The second factor, $facto{r}_2$, operating in the tree construction phase, focuses on maximizing the minimum remaining energy of super nodes within the tree. This factor gives priority to choosing super nodes with higher energy reserves, helping avoid overusing specific nodes and thus balancing energy consumption across the network. By distributing energy usage among super nodes more evenly, $facto{r}_2$ helps extend the lifetime of each node and mitigates the risk of network segmentation due to energy depletion in specific regions. Additionally, the proposed initialization method and GA operators balance the number of awake super nodes in the rings, yielding more even energy exhaustion and longer network lifetime.

In the clustering phase, $facto{r}_3$ and $facto{r}_4$ aid in evenly distributing normal nodes among awake super nodes, further contributing to energy efficiency by preventing any single super node from becoming overloaded. Together, these factors significantly extend the operational lifetime of nodes within the network, leading to delayed FND and LND. Furthermore, $facto{r}_5$ balances energy consumption of normal nodes and prevents their early death.

5.4. Number of Available Super Nodes

We define available super nodes as those that are alive and have other super nodes in their neighborhood capable of sending data toward the BS. Accordingly, a super node with a good amount of energy is considered unavailable if the BS is out of its transmission range and there is no other nearby super node to catch its data and forward it. The number of available super nodes is an important factor. This is due to a higher number of available super nodes improves area coverage, enabling the network to fulfill its primary goal of data delivery to the BS more efficiently.

Figure 12 reports the number of available super nodes in each round. As shown in this figure, the proposed method consistently demonstrates a higher number of available super nodes compared to competitive algorithms in all rounds for all networks. In ${WSN}_1$, the proposed method shows improvements of 5 super nodes over HEDHMG, 16 super nodes over EFCRPSO, 21 super nodes over EFEBPSO, and 35 super nodes over CRCGA, after 1800 time slices. In ${WSN}_2$, the improvements are 5 super nodes over HEDHMG, 15 super nodes over EFCRPSO, 26 super nodes over EFEBPSO, and 28 super nodes over CRCGA, after 1800 time slices. In ${WSN}_3$, the proposed method shows improvements of 23 super nodes over HEDHMG, 32 super nodes over EFCRPSO, 44 super nodes over EFEBPSO, and 40 super nodes over CRCGA, after 1200 time slices. Additionally, CRCGA has the worst performance. In ${WSN}_1$, in round 1800, it has 25, 18, 9, 4 less super nodes compared to the proposed method, HEDHMG, EFCRPSO, and EFEBPSO. The numbers are 29, 23, 13, 2, in ${WSN}_2$, and 47, 17, 8, and 4, in ${WSN}_3$.

The main factor in achieving a higher number of alive super nodes of our algorithm regarding the competitive schemes is the even distribution of awake nodes. The proposed initialization scheme, customized operators, and $facto{r}_1$ in the first phase, ensures an even distribution of awake super nodes throughout the network. This evenness reduces the chances of energy depletion in localized areas and promotes better coverage, which increases the likelihood of data being successfully forwarded to the BS. The other factors used in $cos{t}_1$ and $cos{t}_2$ also play a significant role in achieved results. The $facto{r}_2$ prioritizes super nodes for more energy for tree construction, increasing the chances of sustaining more alive super nodes, contributing to their availability. The third factor, $facto{r}_3$, used in the clustering, focuses on evenly distributing normal nodes among super nodes. This balance prevents individual super nodes from becoming overloaded, allowing them to remain operational and available for data forwarding. The application of customized initialization and GA operators in the first phase for balancing the distribution of super nodes throughout the HWSN increases the number of available super nodes. Additionally, CRCGA, while effective in some clustering tasks, shows lower availability because it does not explicitly ensure an even distribution of awake super nodes or consider energy balancing during cluster formation and tree construction.

5.5. Time Complexity

An important factor in data-gathering algorithms is their time complexity. For practical applicability, an effective algorithm should maintain low time complexity.

Table 5. Comparison of time complexity (in seconds).

Network	Proposed Method	HEDHMG	EFEBPSO	EFCRPSO	CRCGA
${WSN}_1$	12.1	12.8	22.9	23.1	14.1
${WSN}_2$	14.3	15.9	27.1	27.9	16.8
${WSN}_3$	20.6	22.7	39.9	41.1	23

compares the time complexity of the proposed method with the other algorithms. The results show that the proposed scheme achieves better runtime than the others.

6. Conclusions and Future Works

This paper proposed an algorithm for efficient sleep scheduling and data gathering in HWSNs. The algorithm consisted of two main phases, each utilizing a GA to optimize network performance. In the first phase, sleep scheduling and tree construction were handled simultaneously, considering their high dependency. Clustering of normal nodes using the awake super nodes as CHs was performed in the second phase. The objectives of these phases focused on energy efficiency and preserving network coverage. The first objective maximized normal node coverage by selecting proper awake super nodes, ensuring each normal node had an awake super node within its neighborhood. The second objective prioritized energy efficiency by balancing remaining energy of super nodes, encouraging routes that have nodes with higher energy levels, prolonging network lifetime. This energy-centric prioritization was also applied in the clustering phase, where normal nodes were evenly distributed among the awake super nodes to prevent overloading and balance energy use. The other advantage of our algorithm was proposing customized initialization scheme, and crossover and mutation operators in its first phase. These schemes aimed at even distribution of awake super nodes. For this purpose, the HWSN was divided into rings, and the initialization method and GA operators tried to adopt equal number of awake super nodes in these rings.

For the future work, we aim to explore other energy saving techniques, such as dynamic modulation scaling. Furthermore, we will examine other meta-heuristic algorithms to attain better network configurations. Swarm intelligence algorithms, such as GWO, have been shown to generate high-quality solutions. Therefore, combining these methods with GA can improve performance. In addition, using normal nodes as CH increases flexibly, improving energy efficiency. This idea, however, considerably expands the solution space and increases complexity, making it difficult to converge to an optimal solution. Therefore, we aim to propose an approach with acceptable time complexity to use normal nodes as CHs. Finally, we will investigate security aspects in HWSNs. Different security issues, such as trust-aware routing and mitigating attacks, have been widely studied in homogeneous WSNs. However, they have not been considered carefully in HWSNs. Additionally, using forecasting techniques [40] can help identify suspect nodes in event-based data gathering in HWSNs.