Abstract
Natural convection of liquid metals under magnetic fields is a phenomenon of interest in various industrial and scientific applications, including fusion reactor blankets and magnetohydrodynamic (MHD) power systems. While the application of a magnetic field generally suppresses convection and reduces the heat transfer rate, recent studies have reported cases where the Nusselt number increases under certain magnetic field conditions. In this study, we conduct numerical simulations of natural convection in an annular container filled with a liquid metal, subject to a circumferential static magnetic field. The governing equations, incorporating both temperature and electromagnetic fields, are solved using a high-order finite difference scheme. The results show that, within a specific range of parameters, the Nusselt number increases at moderate Hartmann numbers, even under low Rayleigh number conditions. Notably, this enhancement in heat transfer occurs alongside a reduction in kinetic energy, indicating that convective strength is not necessarily the dominant factor. Further analysis confirms that this phenomenon weakens and eventually vanishes as the Rayleigh number approaches 106. These findings provide evidence that magnetic field-induced heat transfer enhancement can occur without a corresponding increase in convective motion, thereby challenging conventional assumptions in magnetoconvection theory.
1. Introduction
Contrary to conventional expectations, this study demonstrates that heat transfer in liquid metal natural convection can be enhanced even when the fluid motion is suppressed by an applied magnetic field. This counterintuitive result challenges the widely accepted assumption that stronger convection necessarily yields greater thermal transport. By elucidating this unusual behavior, the present work contributes new insight into the fundamental mechanisms of magnetoconvective heat transfer.
In many engineering and natural systems, heat is transported from hot regions to cold regions not only by conduction but also through fluid motion—a process known as convection. When the fluid motion arises solely from temperature differences, it is referred to as natural convection. In such systems, the intensity of heat transfer is commonly quantified by the Nusselt number (Nu), while the strength of fluid motion is typically represented by the kinetic energy (TK). It is generally accepted that stronger fluid motion leads to more efficient heat transfer, meaning that higher kinetic energy is associated with a higher Nusselt number. However, in electrically conducting fluids such as liquid metals, externally applied magnetic fields can profoundly alter both the fluid motion and the associated heat transfer. The interaction between fluid flow and magnetic fields is described by magnetohydrodynamics (MHD).
Thermal convection of liquid metals plays a critical role in various scientific and engineering applications, including fusion reactor blankets, MHD power generation, single crystal growth of semiconductors, metallurgy, and planetary dynamos [1,2,3,4]. Due to their high electrical conductivity, liquid metals strongly interact with magnetic fields, enabling external control over flow structures and thermal behavior [5].
When a magnetic field is applied, it generally suppresses convective motion and reduces the heat transfer rate, as reflected by a decrease in the Nusselt number. This phenomenon has widely been studied in configurations such as cubic enclosures with differentially heated vertical walls. However, several studies have reported that, under high Rayleigh number conditions, the Nusselt number may increase within a certain range as the magnetic field strength increases [6]. This unexpected enhancement has been attributed to changes in flow structure [7], although the underlying mechanism remains unresolved.
In our previous work, we performed numerical simulations of natural convection of a liquid metal in an annular enclosure subjected to a circumferential static magnetic field [8,9,10,11]. These simulations revealed that, even at relatively low Rayleigh numbers, the Nusselt number can increase within a specified range as the Hartmann number rises [8]. More surprisingly, we observed that this enhancement in heat transfer was in some cases accompanied by a reduction in the total kinetic energy of the flow field [11], suggesting a departure from the typical positive correlation between convection strength and thermal transport.
This paradox defines the central question of the present study: how can thermal transport increase while convective motion is suppressed? Since convective heat transfer is generally assumed to scale with fluid motion, this observation raises fundamental questions about the mechanisms governing heat transfer in magnetoconvective systems.
To address this issue, we performed numerical simulations of liquid metal natural convection in an annular geometry under a circumferential magnetic field. To ensure high numerical accuracy, we adopt a configuration that avoids the formation of Hartmann boundary layers—thin regions near walls perpendicular to the magnetic field that become increasingly difficult to resolve at high Hartmann numbers. By orienting the magnetic field tangentially along the circumference, we enable precise simulation of bulk flow behavior without the complications of boundary layer resolution.
Previous studies on annular geometries, such as those by Kakarantzas et al. [12,13,14], applied uniform horizontal magnetic fields but did not report any increase in the Nusselt number within a specified range. In cubic enclosures, Chen et al. [15] observed an increase in heat transfer along with a reduction in kinetic energy under stronger magnetic fields. However, their definition of kinetic energy was based on only two velocity components, leaving the behavior of the total energy uncertain. A comparison with relevant previous studies is summarized in Table 1.

Table 1.
Comparison with previous studies.
It is also noteworthy that natural convection of low-Prandtl-number fluids, such as liquid metals, can exhibit unsteady behavior even in laminar regimes. For example, Rayleigh–Bénard convection may show irregular variations in the number of convection rolls depending on magnetic field strength and enclosure size [16]. Similar phenomena have been reported in our previous works [10,11], suggesting that time-averaged turbulence models may not reliably capture the dynamics of such flows.
Recently, the concept of “ultimate heat transfer” has been proposed, which assumes that turbulence universally enhances thermal transport [17]. However, the present study provides evidence to the contrary, demonstrating that heat transfer can be enhanced even when convective strength is weakened, thereby challenging the fundamental assumptions underlying this theory.
This study thus aims to clarify the relationship between convection intensity and heat transfer under the influence of a magnetic field in a novel configuration: liquid metal natural convection in an annular enclosure with isothermal inner and outer walls subjected to a circumferential static magnetic field. Through this work, we seek to advance the understanding of magnetoconvection in low-Prandtl-number fluids and contribute to the refinement of heat transfer theory in such systems.
In fusion reactors, cooling systems capable of withstanding high heat fluxes are essential, and blankets employing liquid metals (e.g., lithium, lead-lithium alloys) are commonly used. Since these systems operate under strong magnetic fields, magnetohydrodynamic (MHD) effects become dominant. Identifying conditions under which heat transfer can be maintained or even enhanced despite flow suppression by the magnetic field is therefore highly advantageous for cooling system design. A reduction in kinetic energy may also lead to savings in pumping power. In MHD power generation, where conductive fluids flow in a magnetic field to directly extract electricity, efficient control of both heat and fluid flow is critical. The key finding of this study—that heat transfer can be enhanced even when flow is suppressed by a magnetic field—could be applied to the design of heat exchangers in MHD systems and to minimizing heat loss.
2. Problem Configuration
Figure 1 illustrates a schematic of the problem configuration investigated in this study. The configuration represents a circulating structure typically used in thermal transport devices utilizing liquid metals. The annular container is filled with a liquid metal, such as mercury. The inner wall of the container is heated, while the outer wall is cooled. The top and bottom walls are thermally insulated. At the center of the annular enclosure, an infinitely long, straight coil is positioned to generate a static magnetic field within the liquid metal. The working fluid is assumed to be an incompressible Newtonian fluid. The magnetic flux density ( is the unit vector in the -direction) has only an azimuthal component, which is introduced by Ampère’s law as , where is constant current through the coil, and is the magnetic permeability of fluid.
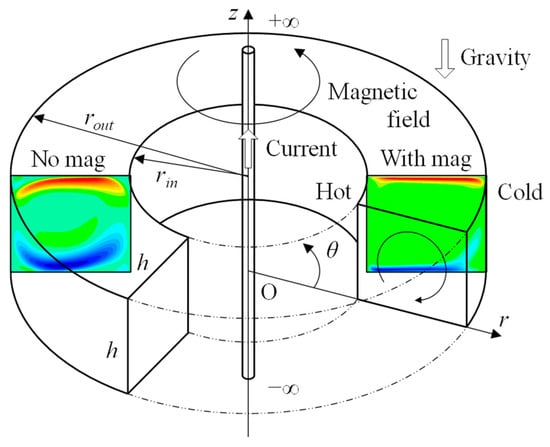
Figure 1.
Analysis model. The contours represent the radial velocity component . The left and right convection are without and with a magnetic field, respectively.
In formulating the governing equations for this study, the following assumptions are adopted:
- Electric currents induced by displacement and convection are negligible compared to the conduction current.
- The magnetic Reynolds number is sufficiently small, allowing the induced magnetic field to be neglected.
- The Boussinesq approximation is applied.
- Heat sources, including viscous dissipation and Joule heating, are neglected.
Viscous dissipation and Joule heating are intentionally omitted to focus on the convection characteristics under the simplest possible conditions. The negligible contribution of Joule heating has been validated in the authors’ previous paper [8] through evaluation based on the Eckert number, Hartmann number, and Prandtl number.
The governing equations, presented in Equation (1) through (5), correspond, respectively, to the continuity equation, momentum equation, energy equation, charge conservation equation, and Ohm’s law:
- Here,
- : velocity vector [m/s],
- : current density vector [A/m2],
- : pressure [Pa],
- : density at reference temperature [kg/m3],
- : kinematic viscosity [m2/s],
- : reference temperature [K],
- : magnetic flux density [T],
- : temperature [K],: thermal diffusivity [m2/s],
- : gravitational acceleration [m/s2],
- : unit vector in the -direction,: electric potential [V], and
- : thermal expansion coefficient at [K−1].
Equation (6) through (10) are the nondimensionalized forms of Equation (1) through (5), and are used in the present analysis.
- Here, the nondimensional variables are defined as follows:
- : dimensionless velocity,
- : dimensionless pressure,
- : dimensionless temperature,
- : dimensionless current density,
- : dimensionless magnetic flux density,
- : dimensionless electric potential,
- : reference velocity, and
- : radius ratio.
The nondimensional parameters are the Prandtl number , Rayleigh number , and Hartmann number , which are defined by the following Equations (11). In this study, the Prandtl number is fixed at .
- Here,
- : temperature of the inner (cold) cylinder [K],
- : temperature of the outer (hot) cylinder [K],
- : characteristic length of the container (e.g., side length) [m],
- : reference radius [m], and
- : value of at radius [T].
The boundary conditions were set on the walls as follows:
The no-slip boundary condition was adopted for the velocity. The walls were electrically insulated. The boundary condition of the temperature was mentioned as presented above. The initial value is uniformity zero.
In addition, the kinetic energy per unit volume is introduced as follows:
3. Methods
In MHD flows, Hartmann layers form on walls perpendicular to the magnetic field, with a characteristic thickness scaling as δH ∼ Ha−1. These layers are extremely thin and strongly resistive to flow, requiring fine resolution in numerical simulations. Shercliff layers form on walls parallel to the magnetic field, with a thickness scaling as δS ∼ Ha−1/2. These layers are generally thicker and play a key role in momentum transport in the presence of magnetic fields. Understanding both is essential for analyzing liquid metal flows under strong magnetic fields.
In general, the Shercliff boundary layer is thicker than the Hartmann boundary layer; however, it still becomes thinner as the magnetic flux density increases. In this study, the Hartmann boundary layer does not exist. Under strong magnetic field conditions, the boundary layer becomes significantly thin. Therefore, it is essential to use a dense, nonuniform grid near the wall boundaries. However, if the conservation properties of the numerical scheme are insufficient, the time step must be set extremely small, which, in the worst case, can lead to immediate numerical instability.
In this study, a custom numerical code was developed based on the high-order finite difference scheme proposed by Morinishi et al. [18], extended to incorporate temperature and electromagnetic field calculations. Although this scheme poses challenges in handling boundary conditions, fourth-order central differences were successfully applied to a rectangular cross-section container by introducing virtual cells.
A standard staggered grid was employed for spatial discretization. The grid spacing is nonuniform and defined by the following equations:
Here, denotes the number of cells, and is the grid spacing coefficient.
The mesh structure used in the present study is the same as that used in the authors’ previous studies, in which its reliability has been verified through three-dimensional simulations and linear stability analysis. Therefore, we believe that mesh dependency in this study is minimal [19].
The discretized governing equations are solved sequentially: the flow field governed by Equations (6) and (7), the temperature field by Equation (8), and the electromagnetic field by Equations (9) and (10). The simplified marker and cell (SMAC) method is used for the pressure-velocity coupling in the flow field, and the BiCGSTAB method is employed for iterative linear solvers. The energy equation is solved using the SOR method, and the same solver framework as the flow field is reused for solving the electromagnetic field.
A fourth-order central difference scheme is adopted for the discretization of the advection terms, which improves accuracy compared to previous studies. Second-order central differences are used for all other spatial discretizations. For the time integration, a third-order low-storage Runge–Kutta method is applied, and the diffusion term in the energy equation is solved using the second-order Crank–Nicolson scheme. All simulations in this study were conducted in an unsteady (time-dependent) manner. Additionally, parallel computation using OpenMP is employed as necessary.
4. Results and Discussion
4.1. Comparison with Previous Study
Figure 2 compares the present results with the previous work by Masuda and Tagawa [8]. As shown in the figure, within a specified range of Ha and Ra numbers, an increase in the Nusselt number at moderate Hartmann numbers is observed, consistent with the findings of the previous study. Notably, the discretization schemes for the advection term differ between the two studies, with the present study employing a more accurate scheme. Despite this difference, the same phenomenon is reproduced, indicating that the results reported in the previous work were not artifacts arising from numerical errors, but rather reflect a genuine physical effect. The present study therefore provides additional evidence supporting those earlier findings.
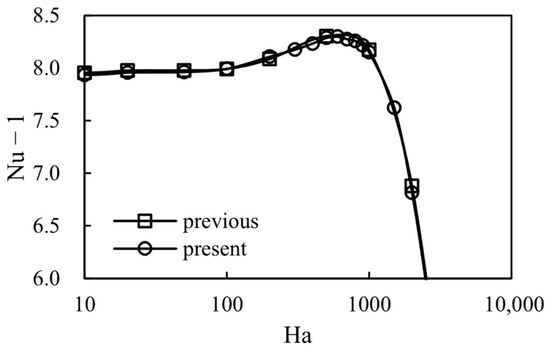
Figure 2.
Comparison of the Nusselt number with the previous study [8].
4.2. Effects of Grid Number and Grid Spacing Coefficient
The relationship between the grid number and the grid spacing coefficient is summarized in Table 2. The values in the table show the error relative to the reference case of and . The calculation conditions are and . Even when comparing the highest-accuracy case ( and ) with the lowest-accuracy case ( and ), the difference is less than 2.5%.

Table 2.
Errors due to grid number and grid spacing coefficient .
Accurately capturing boundary-layer flow phenomena requires a sufficiently large number of grid points, particularly at high Hartmann numbers where the boundary layer becomes thinner and demands finer resolution to resolve its structure. However, increasing the grid number and the spacing coefficient inevitably raises the computational cost. In future simulations, a grid resolution of is considered to offer a reasonable balance between accuracy and computational efficiency.
4.3. Boundary Layer
Figure 3 and Figure 4 show the contour plots of and , respectively. In addition, Figure 5 shows stream function Ψ. These contours represent the thickness of the Shercliff boundary layer. The simulation for was conducted using and to facilitate comparison with previous studies, while the simulations for to were performed using and , based on the results of the earlier grid resolution verification.
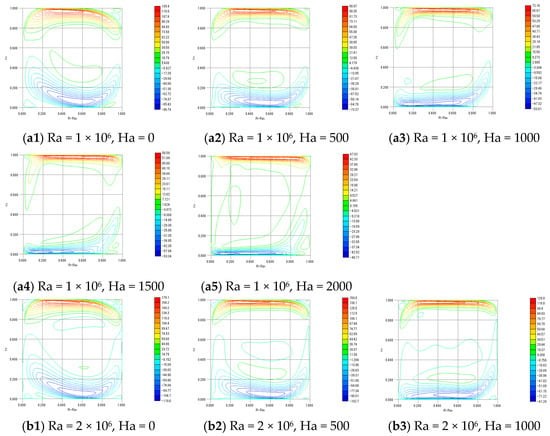
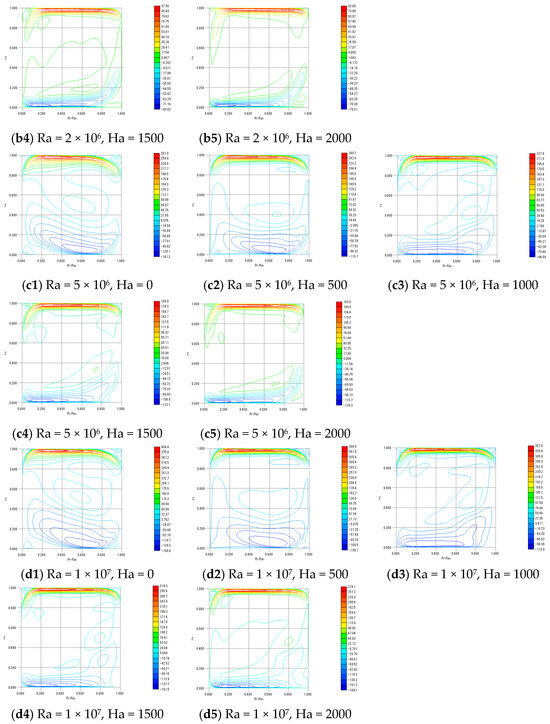
Figure 3.
Contours of .
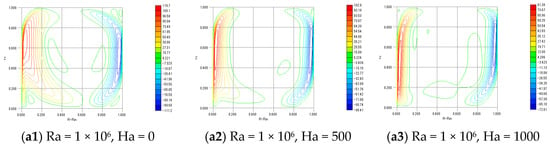
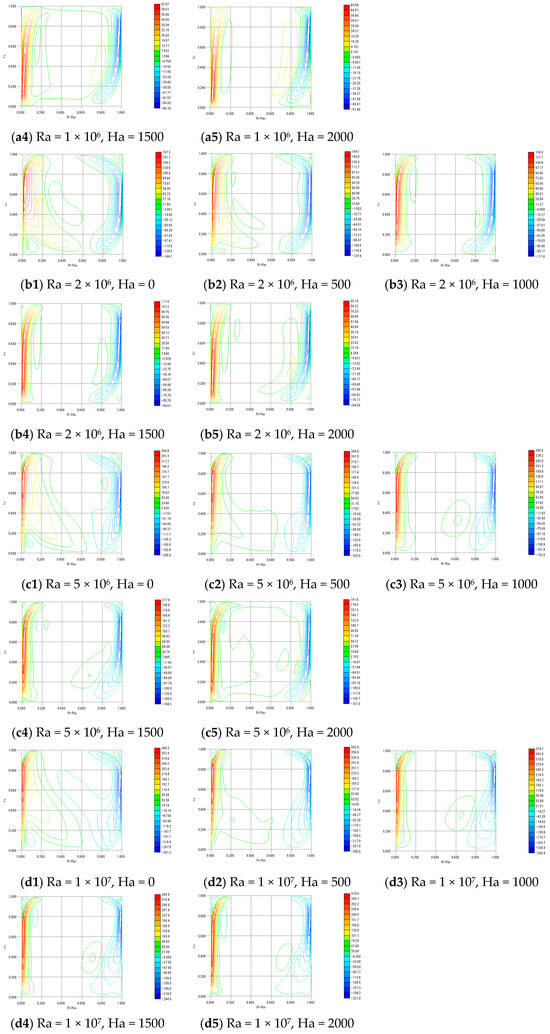
Figure 4.
Contours of .
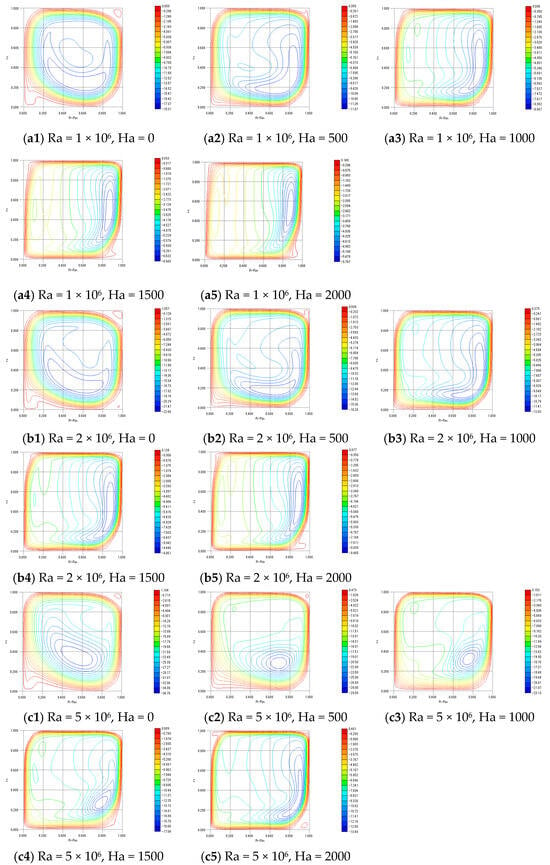
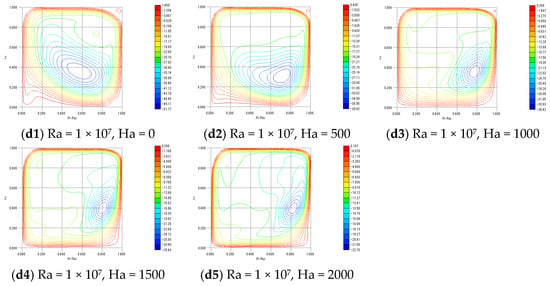
Figure 5.
Contours of stream function Ψ.
All contour plots exhibit similar profiles, with the velocity within the boundary layer well resolved. Therefore, the results obtained with a grid resolution of and a spacing coefficient of are considered sufficiently reliable.
Figure 6 shows the distribution of boundary layer thickness δ. The thickness was determined based on the location near the wall where the velocity component reaches its maximum. The coordinates of the grid points were used directly for this determination, resulting in a discontinuous distribution in the figure. In uniform flow, the Shercliff boundary layer thickness is known to scale with the square root of the Hartmann number (Ha1ᐟ2); however, no such trend was observed in the present study.
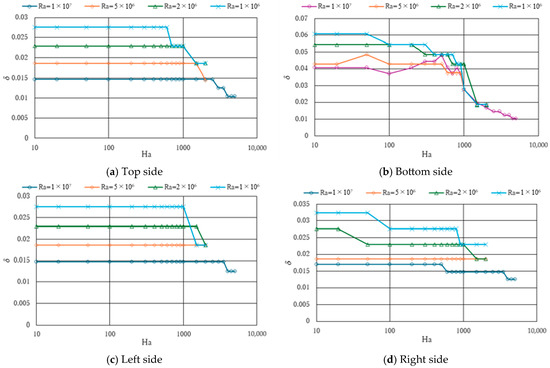
Figure 6.
Thickness of boundary layer δ.
4.4. Relationship Between Hartmann Number and Nusselt Number
Figure 7 shows the relationship between the Hartmann number and the Nusselt number . For each Rayleigh number (Ra), the resulting graphs exhibit generally similar trends. It was observed that as decreases, the magnitude of the increase in becomes smaller within a specified range of Ha and Ra numbers, and this phenomenon almost completely disappears around .
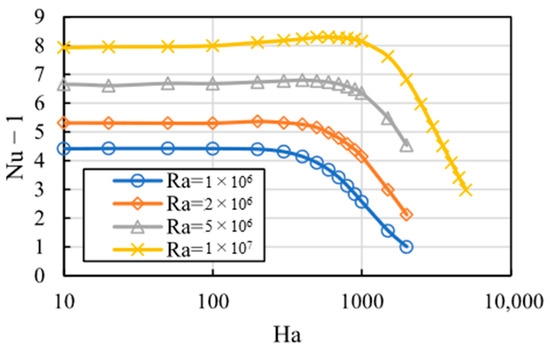
Figure 7.
Relationship between the Hartmann number (Ha) and the Nusselt number (Nu) for various Rayleigh numbers (Ra). An increase in Nu at moderate Ha values is observed for higher Ra, but this effect diminishes as Ra decreases and disappears around Ra = 106. These results suggest a lower Ra threshold below which the phenomenon no longer occurs.
In the previous study [8], it was reported that for and , no increase in was observed at moderate values. These results suggest the existence of a lower threshold near this range, below which the phenomenon no longer appears.
4.5. Relationship Between Hartmann Number and Kinetic Energy
Figure 8 presents a graph summarizing the relationship between the Hartmann number and the kinetic energy . As shown in Figure 7, the variations of with respect to at each exhibit generally similar trends, confirming that decreases as increases.
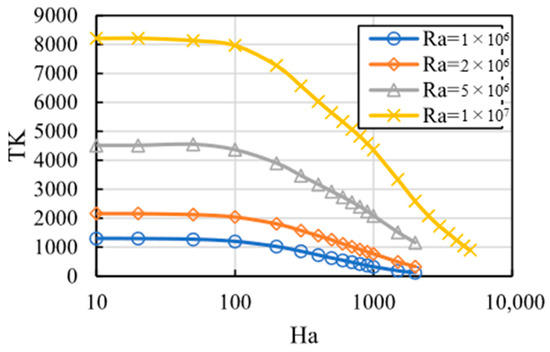
Figure 8.
Relationship between the Hartmann number (Ha) and the kinetic energy (TK) for various Rayleigh numbers (Ra). TK, representing the strength of convection, generally decreases as Ha increases. Comparison with Figure 5 shows that the peaks of TK and Nu occur at different Ha values, indicating no clear correlation between convection intensity and heat transfer. This suggests that the increase in Nu is not driven by stronger convection.
Here, serves as a parameter indicating the strength of convection, while indicates the degree of heat transfer. Although it is often assumed that stronger convection enhances heat transfer, a comparison of Figure 7 and Figure 8 reveals that the Hartmann numbers at which and reach their respective maxima differ. Therefore, no direct correlation between and can be established.
Based on this, it is concluded that the increase in within a specified range of Ha and Ra numbers is not caused by the intensity of convection.
The mechanism by which the Nusselt number (Nu) increases despite a decrease in kinetic energy (TK) can be explained as follows. The velocity field can be decomposed into a mean component and a fluctuating component (). While TK is evaluated based on the square of the total velocity, only the mean component contributes to heat transport, i.e., to Nu. Therefore, if the flow is rectified by the applied magnetic field such that increases and decreases, an increase in Nu and a simultaneous decrease in TK can occur.
4.6. Estimation of Ra for Liquid Metal Systems
As a practical reference, the Rayleigh number (Ra) for typical liquid metal systems can be estimated using representative thermophysical properties. For example, in a lead-bismuth eutectic system with a temperature difference of ΔT = 100 K, characteristic length h = 0.1 m, thermal expansion coefficient β = 1.3 × 10−4 K−1, kinematic viscosity ν = 1.2 × 10−7 m2/s, and thermal diffusivity α = 6.0 × 10−5 m2/s, the resulting Rayleigh number is approximately Ra ≈ 1.8 × 107. Similarly, for a mercury-based system under more compact conditions (e.g., ΔT = 20 K, h = 0.05 m), Ra is on the order of 106. These values indicate that Ra in liquid metal systems often falls within the transitional or weakly turbulent regime, making the range explored in this study highly relevant to real-world applications such as MHD power generation and fusion reactor blankets.
5. Conclusions
Through numerical simulations, the present study investigated and analyzed changes in flow behavior of thermal convection in a liquid metal under the influence of a magnetic field, across various conditions. The main conclusions are as follows:
- Similar results were reproduced even when the computational methods differed from those used in the previous study.
- Variations in grid number and grid-spacing coefficient had only minimal effects on accuracy.
- The boundary layer structures and distributions at each Ra number were generally similar, with notable changes occurring around Ha = 1000.
- An increase in the Nusselt number was observed at moderate Ha within a specified range of Ha and Ra; however, this effect disappeared around Ra = 1 × 106.
- The increase in the Nusselt number at moderate Ha values is not influenced by the kinetic energy of the flow.
Whether the flow is axisymmetric or not depends on the Rayleigh number (Ra) and the Hartmann number (Ha). Under conditions of low Ra or high Ha, the flow is axisymmetric, whereas under high Ra and low Ha, the flow exhibits three-dimensional characteristics. In a previous study [7], the phenomenon of increasing Nusselt number with increasing Ha was explained as being related to a transition of the flow structure from three-dimensional to two-dimensional. However, in the present study, this phenomenon was observed even though the flow remained entirely two-dimensional under all conditions. This contributes one of the key findings of the present work.
Author Contributions
Conceptualization, T.M. and T.T.; methodology, T.M.; software, T.M.; validation, S.K. and T.M.; investigation, S.K.; writing—original draft preparation, S.K. and T.M.; writing—review and editing, M.S., M.M.A.A. and T.T.; visualization, S.K.; supervision, T.T.; project administration, T.M.; funding acquisition, Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pinheiro, M.J. New Framework to Study Electromagnetic Turbulence. Magnetism 2022, 2, 356–367. [Google Scholar] [CrossRef]
- Radcliffe, A. Quasi-Stable, Non-Magnetic, Toroidal Fluid Droplets in a Ferrofluid with Annular Magnetic Field. Magnetism 2022, 2, 380–391. [Google Scholar] [CrossRef]
- Mişicu, Ş. Hydromagnetic Waves in Cold Nuclear Matter. Magnetism 2023, 3, 148–157. [Google Scholar] [CrossRef]
- Kubiak, T. The Influence of Blood and Serum Microenvironment on Spin-Labeled Magnetic Nanoparticles. Magnetism 2024, 4, 114–124. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, K.; Ayub, A.; Bashir, U.; Rashid, F.L.; Aryanfar, Y.; Ali, M.R.; Hendy, A.S.; Shah, I.; Ali, L. Localized magnetic fields and their effects on heat transfer enhancement and vortices generation in tri-hybrid nanofluids: A novel investigation. Case Stud. Therm. Eng. 2023, 50, 103408. [Google Scholar] [CrossRef]
- Okada, K.; Ozoe, H. Experimental heat transfer rates of natural convection of molten gallium suppressed under an external magnetic field in either the X, Y, or Z direction. J. Heat Transf. 1992, 114, 107–114. [Google Scholar] [CrossRef]
- Tagawa, T.; Ozoe, H. Enhancement of heat transfer rate by application of a static magnetic field during natural convection of liquid metal in a cube. J. Heat Transf. 1997, 119, 265–271. [Google Scholar] [CrossRef]
- Masuda, T.; Tagawa, T. Axisymmetric natural convection of liquid metal in an annular enclosure under the influence of azimuthal magnetic field. Energies 2020, 13, 2896. [Google Scholar] [CrossRef]
- Masuda, T.; Tagawa, T. Linear stability analysis of three-dimensional natural convection at low Prandtl number in an annular enclosure in the presence of a toroidal magnetic field. AIP Adv. 2020, 10, 125208. [Google Scholar] [CrossRef]
- Masuda, T.; Tagawa, T. Transition of natural convection of liquid metal in an annular enclosure. Phys. Fluids 2022, 34, 024107. [Google Scholar] [CrossRef]
- Masuda, T.; Tagawa, T.; Alam, M.M.A.; Hayamizu, Y. Transition of natural convection of liquid metal in an annular enclosure under a magnetic field. Phys. Fluids 2023, 35, 014112. [Google Scholar] [CrossRef]
- Kakarantzas, S.C.; Grecos, A.P.; Vlachos, N.S.; Sarris, I.E.; Knaepen, B.; Carati, D. Direct numerical simulation of a heat removal configuration for fusion blankets. Energy Convers. Manag. 2007, 48, 2775–2783. [Google Scholar] [CrossRef]
- Kakarantzas, S.C.; Sarris, I.E.; Vlachos, N.S. Natural convection of liquid metal in a vertical annulus with lateral and volumetric heating in the presence of a horizontal magnetic field. Int. J. Heat Mass Transf. 2011, 54, 3347–3356. [Google Scholar] [CrossRef]
- Kakarantzas, S.C.; Benos, L.T.; Sarris, I.E.; Knaepen, B.; Grecos, A.P.; Vlachos, N.S. MHD liquid metal flow and heat transfer between vertical coaxial cylinders under horizontal magnetic field. Int. J. Heat Fluid Flow 2017, 65, 342–351. [Google Scholar] [CrossRef]
- Chen, L.; Liu, B.Q.; Ni, M.J. Study of natural convection in a heated cavity with magnetic fields normal to the main circulation. Int. J. Heat Mass Transf. 2018, 127, 267–277. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Yamagishi, Y.; Hamano, Y.; Tasaka, Y.; Takeda, Y. Spontaneous flow reversals in Rayleigh-Bénard convection of a liquid metal. Phys. Rev. E 2011, 83, 036307. [Google Scholar] [CrossRef] [PubMed]
- Kawano, K.; Motoki, S.; Shimizu, M.; Kawahara, G. Ultimate heat transfer in ‘wall-bounded’ convective turbulence. J. Fluid Mech. 2021, 914, A13. [Google Scholar] [CrossRef]
- Morinishi, Y.; Vasilyev, O.V.; Ogi, T. Fully conservative finite difference scheme in cylindrical coordinates for incompressible flow simulations. J. Comput. Phys. 2004, 197, 686–710. [Google Scholar] [CrossRef]
- Omle, I.; Kovács, E.; Betti, B. The effect of surface triangular roughness inspired by nature with different angles on the interaction between free convection and surface radiation in a square cavity. Heat Transf. Res. 2023, 55, 1–21. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).