Magnetic Toroidal Monopole in a Single-Site System
Abstract
1. Introduction
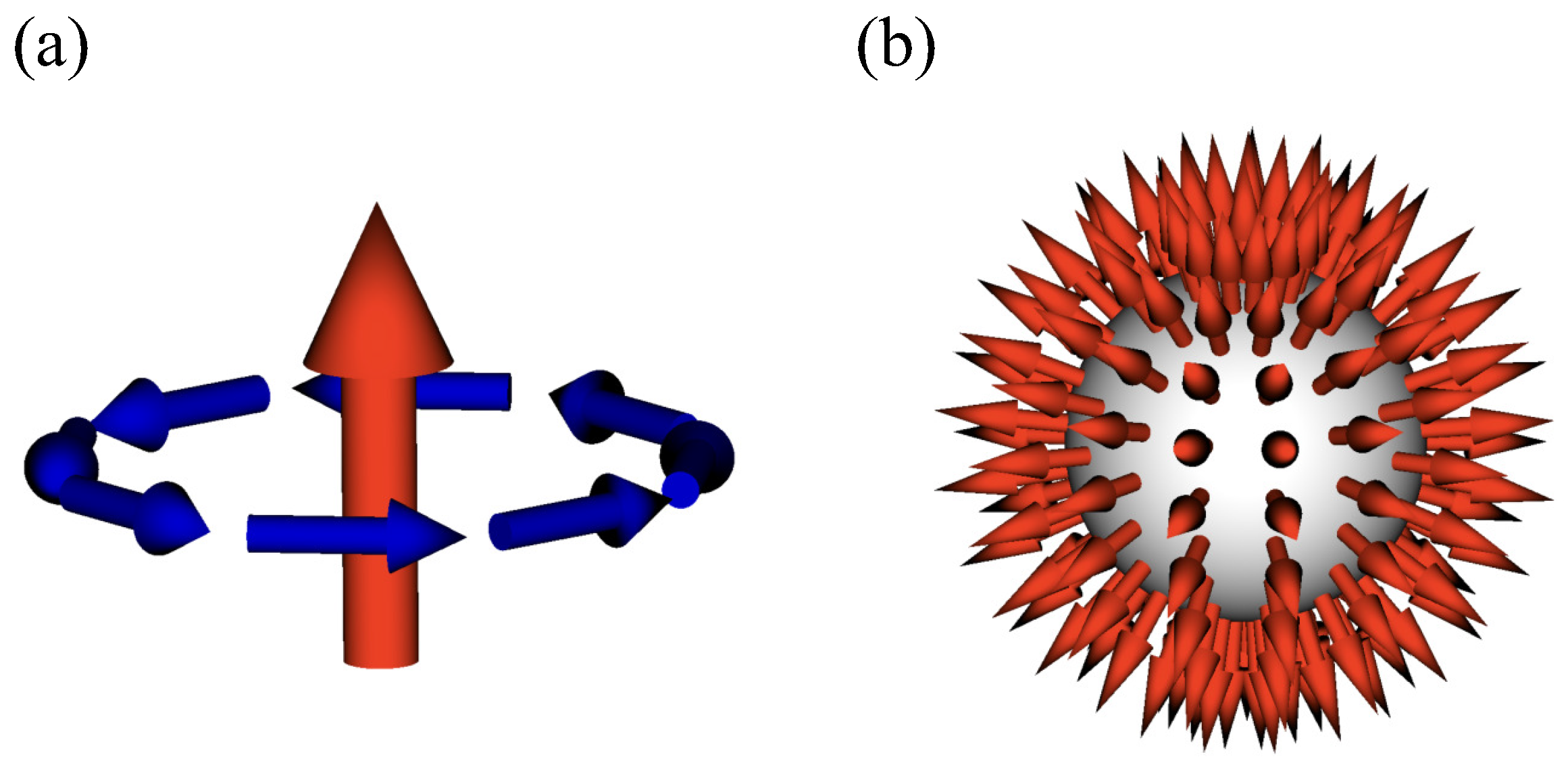
2. Magnetic Toroidal Monopole
3. Cluster Description
4. Atomic-Scale Description
5. Model Analysis
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kane, C.L.; Mele, E.J. Z2. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef] [PubMed]
- Moore, J.E. The birth of topological insulators. Nature 2010, 464, 194–198. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Moore, J.E. Three-dimensional topological insulators. Annu. Rev. Condens. Matter Phys. 2011, 2, 55–78. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Senthil, T. Symmetry-protected topological phases of quantum matter. Annu. Rev. Condens. Matter Phys. 2015, 6, 299–324. [Google Scholar] [CrossRef]
- Karplus, R.; Luttinger, J.M. Hall Effect in Ferromagnetics. Phys. Rev. 1954, 95, 1154–1160. [Google Scholar] [CrossRef]
- Smit, J. The spontaneous Hall effect in ferromagnetics II. Physica 1958, 24, 39–51. [Google Scholar] [CrossRef]
- Maranzana, F.E. Contributions to the Theory of the Anomalous Hall Effect in Ferro- and Antiferromagnetic Materials. Phys. Rev. 1967, 160, 421–429. [Google Scholar] [CrossRef]
- Berger, L. Side-Jump Mechanism for the Hall Effect of Ferromagnets. Phys. Rev. B 1970, 2, 4559–4566. [Google Scholar] [CrossRef]
- Nozieres, P.; Lewiner, C. A simple theory of the anomalous Hall effect in semiconductors. J. Phys. 1973, 34, 901–915. [Google Scholar] [CrossRef]
- Ye, J.; Kim, Y.B.; Millis, A.J.; Shraiman, B.I.; Majumdar, P.; Tešanović, Z. Berry Phase Theory of the Anomalous Hall Effect: Application to Colossal Magnetoresistance Manganites. Phys. Rev. Lett. 1999, 83, 3737–3740. [Google Scholar] [CrossRef]
- Jungwirth, T.; Niu, Q.; MacDonald, A.H. Anomalous Hall Effect in Ferromagnetic Semiconductors. Phys. Rev. Lett. 2002, 88, 207208. [Google Scholar] [CrossRef]
- Gosálbez-Martínez, D.; Souza, I.; Vanderbilt, D. Chiral degeneracies and Fermi-surface Chern numbers in bcc Fe. Phys. Rev. B 2015, 92, 085138. [Google Scholar] [CrossRef]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. Anomalous Hall effect. Rev. Mod. Phys. 2010, 82, 1539–1592. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef]
- Solovyev, I.V. Magneto-optical effect in the weak ferromagnets LaMO3 (M = Cr, Mn, and Fe). Phys. Rev. B 1997, 55, 8060–8063. [Google Scholar] [CrossRef]
- Sivadas, N.; Okamoto, S.; Xiao, D. Gate-Controllable Magneto-optic Kerr Effect in Layered Collinear Antiferromagnets. Phys. Rev. Lett. 2016, 117, 267203. [Google Scholar] [CrossRef]
- Li, X.; MacDonald, A.H.; Chen, H. Quantum Anomalous Hall Effect through Canted Antiferromagnetism. arXiv 2019, arXiv:1902.10650. [Google Scholar]
- Šmejkal, L.; González-Hernández, R.; Jungwirth, T.; Sinova, J. Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets. Sci. Adv. 2020, 6, eaaz8809. [Google Scholar] [CrossRef]
- Samanta, K.; Ležaić, M.; Merte, M.; Freimuth, F.; Blügel, S.; Mokrousov, Y. Crystal Hall and crystal magneto-optical effect in thin films of SrRuO3. J. Appl. Phys. 2020, 127, 213904. [Google Scholar] [CrossRef]
- Naka, M.; Hayami, S.; Kusunose, H.; Yanagi, Y.; Motome, Y.; Seo, H. Anomalous Hall effect in κ-type organic antiferromagnets. Phys. Rev. B 2020, 102, 075112. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Essential role of the anisotropic magnetic dipole in the anomalous Hall effect. Phys. Rev. B 2021, 103, L180407. [Google Scholar] [CrossRef]
- Feng, Z.; Zhou, X.; Šmejkal, L.; Wu, L.; Zhu, Z.; Guo, H.; González-Hernández, R.; Wang, X.; Yan, H.; Qin, P.; et al. An anomalous Hall effect in altermagnetic ruthenium dioxide. Nat. Electron. 2022, 5, 735–743. [Google Scholar] [CrossRef]
- Tomizawa, T.; Kontani, H. Anomalous Hall effect in the t2g orbital kagome lattice due to noncollinearity: Significance of the orbital Aharonov-Bohm effect. Phys. Rev. B 2009, 80, 100401. [Google Scholar] [CrossRef]
- Chen, H.; Niu, Q.; MacDonald, A.H. Anomalous Hall Effect Arising from Noncollinear Antiferromagnetism. Phys. Rev. Lett. 2014, 112, 017205. [Google Scholar] [CrossRef] [PubMed]
- Nakatsuji, S.; Kiyohara, N.; Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 2015, 527, 212. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Koretsune, T.; Ochi, M.; Arita, R. Cluster multipole theory for anomalous Hall effect in antiferromagnets. Phys. Rev. B 2017, 95, 094406. [Google Scholar] [CrossRef]
- Chen, H.; Wang, T.C.; Xiao, D.; Guo, G.Y.; Niu, Q.; MacDonald, A.H. Manipulating anomalous Hall antiferromagnets with magnetic fields. Phys. Rev. B 2020, 101, 104418. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Shindou, R.; Nagaosa, N. Orbital Ferromagnetism and Anomalous Hall Effect in Antiferromagnets on the Distorted fcc Lattice. Phys. Rev. Lett. 2001, 87, 116801. [Google Scholar] [CrossRef] [PubMed]
- Taguchi, Y.; Oohara, Y.; Yoshizawa, H.; Nagaosa, N.; Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 2001, 291, 2573–2576. [Google Scholar] [CrossRef]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef]
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123. [Google Scholar] [CrossRef]
- Katsura, H.; Nagaosa, N.; Balatsky, A.V. Spin Current and Magnetoelectric Effect in Noncollinear Magnets. Phys. Rev. Lett. 2005, 95, 057205. [Google Scholar] [CrossRef] [PubMed]
- Mostovoy, M. Ferroelectricity in Spiral Magnets. Phys. Rev. Lett. 2006, 96, 067601. [Google Scholar] [CrossRef]
- Tokura, Y.; Seki, S.; Nagaosa, N. Multiferroics of spin origin. Rep. Prog. Phys. 2014, 77, 076501. [Google Scholar] [CrossRef] [PubMed]
- Ott, H.R.; Rudigier, H.; Rice, T.M.; Ueda, K.; Fisk, Z.; Smith, J.L. p-Wave Superconductivity in UBe13. Phys. Rev. Lett. 1984, 52, 1915–1918. [Google Scholar] [CrossRef]
- Sigrist, M.; Rice, T.M. Phenomenological theory of the superconductivity phase diagram of U1−xThxBe13. Phys. Rev. B 1989, 39, 2200–2216. [Google Scholar] [CrossRef]
- Ghosh, H. Time-reversal symmetry-breaking superconductivity. Phys. Rev. B 1999, 59, 3357–3360. [Google Scholar] [CrossRef]
- Sigrist, M. Time-reversal symmetry breaking states in high-temperature superconductors. Prog. Theor. Phys. 1998, 99, 899–929. [Google Scholar] [CrossRef]
- Mackenzie, A.P.; Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 2003, 75, 657–712. [Google Scholar] [CrossRef]
- Schemm, E.; Gannon, W.; Wishne, C.; Halperin, W.; Kapitulnik, A. Observation of broken time-reversal symmetry in the heavy-fermion superconductor UPt3. Science 2014, 345, 190–193. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.K.; Smidman, M.; Shang, T.; Annett, J.F.; Hillier, A.D.; Quintanilla, J.; Yuan, H. Recent progress on superconductors with time-reversal symmetry breaking. J. Phys. Condens. Matter 2020, 33, 033001. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Jorio, A. Group Theory: Application to the Physics of Condensed Matter; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hayami, S.; Kusunose, H. Time-reversal switching responses in antiferromagnets. Phys. Rev. B 2023, 108, L140409. [Google Scholar] [CrossRef]
- Šmejkal, L.; Sinova, J.; Jungwirth, T. Beyond Conventional Ferromagnetism and Antiferromagnetism: A Phase with Nonrelativistic Spin and Crystal Rotation Symmetry. Phys. Rev. X 2022, 12, 031042. [Google Scholar] [CrossRef]
- Schmid, H. On ferrotoroidics and electrotoroidic, magnetotoroidic and piezotoroidic effects. Ferroelectrics 2001, 252, 41–50. [Google Scholar] [CrossRef]
- Schmid, H. Some symmetry aspects of ferroics and single phasemultiferroics. J. Phys. Condens. Matter 2008, 20, 434201. [Google Scholar] [CrossRef]
- Hayashida, T.; Matsumoto, K.; Kimura, T. Electric Field-Induced Nonreciprocal Directional Dichroism in a Time-Reversal-Odd Antiferromagnet. Adv. Mater. 2024, 20, 2414876. [Google Scholar] [CrossRef]
- Kusunose, H.; Hayami, S. Generalization of microscopic multipoles and cross-correlated phenomena by their orderings. J. Phys. Condens. Matter 2022, 34, 464002. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Kusunose, H. Unified description of electronic orderings and cross correlations by complete multipole representation. J. Phys. Soc. Jpn. 2024, 93, 072001. [Google Scholar] [CrossRef]
- Dubovik, V.; Cheshkov, A. Multipole expansion in classical and quantum field theory and radiation. Sov. J. Part. Nucl. 1975, 5, 318–337. [Google Scholar]
- Dubovik, V.; Tugushev, V. Toroid moments in electrodynamics and solid-state physics. Phys. Rep. 1990, 187, 145–202. [Google Scholar] [CrossRef]
- Gorbatsevich, A.; Kopaev, Y.V. Toroidal order in crystals. Ferroelectrics 1994, 161, 321–334. [Google Scholar] [CrossRef]
- Kopaev, Y.V. Toroidal ordering in crystals. Physics-Uspekhi 2009, 52, 1111–1125. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Fiebig, M.; Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys. Condens. Matter 2008, 20, 434203. [Google Scholar] [CrossRef]
- Papasimakis, N.; Fedotov, V.; Savinov, V.; Raybould, T.; Zheludev, N. Electromagnetic toroidal excitations in matter and free space. Nat. Mater. 2016, 15, 263. [Google Scholar] [CrossRef]
- Talebi, N.; Guo, S.; van Aken, P.A. Theory and applications of toroidal moments in electrodynamics: Their emergence, characteristics, and technological relevance. Nanophotonics 2018, 7, 93–110. [Google Scholar] [CrossRef]
- Cheong, S.W.; Talbayev, D.; Kiryukhin, V.; Saxena, A. Broken symmetries, non-reciprocity, and multiferroicity. NPJ Quantum Mater. 2018, 3, 19. [Google Scholar] [CrossRef]
- Xu, X.; Huang, F.T.; Cheong, S.W. Magnetic toroidicity. J. Phys. Condens. Matter 2024, 36, 203002. [Google Scholar] [CrossRef]
- Popov, Y.F.; Kadomtseva, A.; Belov, D.; Vorob’ev, G.; Zvezdin, A. Magnetic-field-induced toroidal moment in the magnetoelectric Cr2O3. J. Exp. Theor. Phys. Lett. 1999, 69, 330–335. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Towards a microscopic theory of toroidal moments in bulk periodic crystals. Phys. Rev. B 2007, 76, 214404. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Thöle, F.; Spaldin, N.A. Magnetoelectric multipoles in metals. Philos. Trans. R. Soc. A 2018, 376, 20170450. [Google Scholar] [CrossRef] [PubMed]
- Saito, H.; Uenishi, K.; Miura, N.; Tabata, C.; Hidaka, H.; Yanagisawa, T.; Amitsuka, H. Evidence of a New Current-Induced Magnetoelectric Effect in a Toroidal Magnetic Ordered State of UNi4B. J. Phys. Soc. Jpn. 2018, 87, 033702. [Google Scholar] [CrossRef]
- Yanagi, Y.; Hayami, S.; Kusunose, H. Manipulating the magnetoelectric effect: Essence learned from Co4Nb2O9. Phys. Rev. B 2018, 97, 020404. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides AOsO4 (A = K, Rb, and Cs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Nonreciprocal Directional Dichroism and Toroidalmagnons in Helical Magnets. J. Phys. Soc. Jpn. 2012, 81, 023712. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Theory of magneto-optical effects in helical multiferroic materials via toroidal magnon excitation. Phys. Rev. B 2014, 89, 195145. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Okuma, N. Nonreciprocal superposition state in antiferromagnetic optospintronics. Phys. Rev. B 2019, 99, 094401. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayami, S. Nonreciprocal magnons due to symmetric anisotropic exchange interaction in honeycomb antiferromagnets. Phys. Rev. B 2020, 101, 224419. [Google Scholar] [CrossRef]
- Sawada, K.; Nagaosa, N. Optical Magnetoelectric Effect in Multiferroic Materials: Evidence for a Lorentz Force Acting on a Ray of Light. Phys. Rev. Lett. 2005, 95, 237402. [Google Scholar] [CrossRef] [PubMed]
- Kawaguchi, H.; Tatara, G. Effective Hamiltonian theory for nonreciprocal light propagation in magnetic Rashba conductor. Phys. Rev. B 2016, 94, 235148. [Google Scholar] [CrossRef]
- Watanabe, H.; Yanase, Y. Nonlinear electric transport in odd-parity magnetic multipole systems: Application to Mn-based compounds. Phys. Rev. Res. 2020, 2, 043081. [Google Scholar] [CrossRef]
- Watanabe, H.; Yanase, Y. Photocurrent response in parity-time symmetric current-ordered states. Phys. Rev. B 2021, 104, 024416. [Google Scholar] [CrossRef]
- Suzuki, Y. Tunneling spin current in systems with spin degeneracy. Phys. Rev. B 2022, 105, 075201. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in -symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Kondo, H.; Akagi, Y. Nonlinear magnon spin Nernst effect in antiferromagnets and strain-tunable pure spin current. Phys. Rev. Res. 2022, 4, 013186. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Kusunose, H. Nonlinear spin Hall effect in -symmetric collinear magnets. Phys. Rev. B 2022, 106, 024405. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Y.; Xiao, D. Intrinsic Nonlinear Hall Effect in Antiferromagnetic Tetragonal CuMnAs. Phys. Rev. Lett. 2021, 127, 277201. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhao, J.; Huang, Y.X.; Wu, W.; Sheng, X.L.; Xiao, C.; Yang, S.A. Intrinsic Second-Order Anomalous Hall Effect and Its Application in Compensated Antiferromagnets. Phys. Rev. Lett. 2021, 127, 277202. [Google Scholar] [CrossRef]
- Kirikoshi, A.; Hayami, S. Microscopic mechanism for intrinsic nonlinear anomalous Hall conductivity in noncollinear antiferromagnetic metals. Phys. Rev. B 2023, 107, 155109. [Google Scholar] [CrossRef]
- Ota, K.; Shimozawa, M.; Muroya, T.; Miyamoto, T.; Hosoi, S.; Nakamura, A.; Homma, Y.; Honda, F.; Aoki, D.; Izawa, K. Zero-field current-induced Hall effect in ferrotoroidic metal. arXiv 2022, arXiv:2205.05555. [Google Scholar]
- Folen, V.J.; Rado, G.T.; Stalder, E.W. Anisotropy of the Magnetoelectric Effect in Cr2O3. Phys. Rev. Lett. 1961, 6, 607–608. [Google Scholar] [CrossRef]
- Krotov, S.; Kadomtseva, A.; Popov, Y.F.; Zvezdin, A.; Vorob’ev, G.; Belov, D. Magnetoelectric interactions and induced toroidal ordering in Cr2O3. J. Magn. Magn. Mater. 2001, 226, 963–964. [Google Scholar] [CrossRef]
- Arima, T.; Jung, J.H.; Matsubara, M.; Kubota, M.; He, J.P.; Kaneko, Y.; Tokura, Y. Resonant magnetoelectric X-ray scattering in GaFeO3: Observation of ordering of toroidal moments. J. Phys. Soc. Jpn. 2005, 74, 1419–1422. [Google Scholar] [CrossRef]
- Staub, U.; Bodenthin, Y.; Piamonteze, C.; García-Fernández, M.; Scagnoli, V.; Garganourakis, M.; Koohpayeh, S.; Fort, D.; Lovesey, S.W. Parity- and time-odd atomic multipoles in magnetoelectric GaFeO3 as seen via soft x-ray Bragg diffraction. Phys. Rev. B 2009, 80, 140410. [Google Scholar] [CrossRef]
- Staub, U.; Piamonteze, C.; Garganourakis, M.; Collins, S.P.; Koohpayeh, S.M.; Fort, D.; Lovesey, S.W. Ferromagnetic-type order of atomic multipoles in the polar ferrimagnetic GaFeO3. Phys. Rev. B 2012, 85, 144421. [Google Scholar] [CrossRef]
- Nie, Y.M. First-principles approach to investigate toroidal property of magnetoelectric multiferroic GaFeO3. J. Appl. Phys. 2016, 119. [Google Scholar] [CrossRef]
- Van Aken, B.B.; Rivera, J.P.; Schmid, H.; Fiebig, M. Observation of ferrotoroidic domains. Nature 2007, 449, 702–705. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, A.S.; Meier, D.; Fiebig, M. Ferroic nature of magnetic toroidal order. Nat. Commun. 2014, 5, 4796. [Google Scholar] [CrossRef]
- Fogh, E.; Zaharko, O.; Schefer, J.; Niedermayer, C.; Holm-Dahlin, S.; Sørensen, M.K.; Kristensen, A.B.; Andersen, N.H.; Vaknin, D.; Christensen, N.B.; et al. Dzyaloshinskii-Moriya interaction and the magnetic ground state in magnetoelectric LiCoPO4. Phys. Rev. B 2019, 99, 104421. [Google Scholar] [CrossRef]
- Tóth, B.; Kocsis, V.; Tokunaga, Y.; Taguchi, Y.; Tokura, Y.; Bordács, S. Imaging antiferromagnetic domains in LiCoPO4 via the optical magnetoelectric effect. Phys. Rev. B 2024, 110, L100405. [Google Scholar] [CrossRef]
- Murakawa, H.; Onose, Y.; Miyahara, S.; Furukawa, N.; Tokura, Y. Ferroelectricity Induced by Spin-Dependent Metal-Ligand Hybridization in Ba2CoGe2O7. Phys. Rev. Lett. 2010, 105, 137202. [Google Scholar] [CrossRef]
- Yamauchi, K.; Barone, P.; Picozzi, S. Theoretical investigation of magnetoelectric effects in Ba2CoGe2O7. Phys. Rev. B 2011, 84, 165137. [Google Scholar] [CrossRef]
- Toledano, P.; Khalyavin, D.D.; Chapon, L.C. Spontaneous toroidal moment and field-induced magnetotoroidic effects in Ba2CoGe2O7. Phys. Rev. B 2011, 84, 094421. [Google Scholar] [CrossRef]
- Hutanu, V.; Sazonov, A.; Murakawa, H.; Tokura, Y.; Náfrádi, B.; Chernyshov, D. Symmetry and structure of multiferroic Ba2CoGe2O7. Phys. Rev. B 2011, 84, 212101. [Google Scholar] [CrossRef]
- Baum, M.; Schmalzl, K.; Steffens, P.; Hiess, A.; Regnault, L.P.; Meven, M.; Becker, P.; Bohatý, L.; Braden, M. Controlling toroidal moments by crossed electric and magnetic fields. Phys. Rev. B 2013, 88, 024414. [Google Scholar] [CrossRef]
- Tolédano, P.; Ackermann, M.; Bohatý, L.; Becker, P.; Lorenz, T.; Leo, N.; Fiebig, M. Primary ferrotoroidicity in antiferromagnets. Phys. Rev. B 2015, 92, 094431. [Google Scholar] [CrossRef]
- Lee, C.; Kang, J.; Hong, J.; Shim, J.H.; Whangbo, M.H. Analysis of the difference between the pyroxenes LiFeSi2O6 and LiFeGe2O6 in their spin order, spin orientation, and ferrotoroidal order. Chem. Mater. 2014, 26, 1745–1750. [Google Scholar] [CrossRef]
- Wadley, P.; Novák, V.; Campion, R.; Rinaldi, C.; Martí, X.; Reichlová, H.; Železnỳ, J.; Gazquez, J.; Roldan, M.; Varela, M.; et al. Tetragonal phase of epitaxial room-temperature antiferromagnet CuMnAs. Nat. Commun. 2013, 4, 2322. [Google Scholar] [CrossRef] [PubMed]
- Wadley, P.; Howells, B.; Železnỳ, J.; Andrews, C.; Hills, V.; Campion, R.P.; Novák, V.; Olejník, K.; Maccherozzi, F.; Dhesi, S.; et al. Electrical switching of an antiferromagnet. Science 2016, 351, 587–590. [Google Scholar] [CrossRef] [PubMed]
- Godinho, J.; Reichlová, H.; Kriegner, D.; Novák, V.; Olejník, K.; Kašpar, Z.; Šobáň, Z.; Wadley, P.; Campion, R.; Otxoa, R.; et al. Electrically induced and detected Néel vector reversal in a collinear antiferromagnet. Nat. Commun. 2018, 9, 4686. [Google Scholar] [CrossRef]
- Manchon, A.; Železný, J.; Miron, I.M.; Jungwirth, T.; Sinova, J.; Thiaville, A.; Garello, K.; Gambardella, P. Current-induced spin–orbit torques in ferromagnetic and antiferromagnetic systems. Rev. Mod. Phys. 2019, 91, 035004. [Google Scholar] [CrossRef]
- Ding, L.; Xu, X.; Jeschke, H.O.; Bai, X.; Feng, E.; Alemayehu, A.S.; Kim, J.; Huang, F.T.; Zhang, Q.; Ding, X.; et al. Field-tunable toroidal moment in a chiral-lattice magnet. Nat. Commun. 2021, 12, 5339. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Huang, F.T.; Admasu, A.S.; Kratochvílová, M.; Chu, M.W.; Park, J.G.; Cheong, S.W. Multiple ferroic orders and toroidal magnetoelectricity in the chiral magnet BaCoSiO4. Phys. Rev. B 2022, 105, 184407. [Google Scholar] [CrossRef]
- Nakamura, R.; Aoki, I.; Kimura, K. Ferrotoroidic State Induced by Structural Rotation and Falsely Chiral Antiferromagnetism in PbMn2Ni6Te3O18. J. Phys. Soc. Jpn. 2024, 93, 063703. [Google Scholar] [CrossRef]
- Mentink, S.A.M.; Drost, A.; Nieuwenhuys, G.J.; Frikkee, E.; Menovsky, A.A.; Mydosh, J.A. Magnetic Ordering and Frustration in Hexagonal UNi4B. Phys. Rev. Lett. 1994, 73, 1031–1034. [Google Scholar] [CrossRef]
- Oyamada, A.; Kondo, M.; Fukuoka, K.; Itou, T.; Maegawa, S.; Li, D.X.; Haga, Y. NMR studies of the partially disordered state in a triangular antiferromagnet UNi4B. J. Phys. Condens. Matter 2007, 19, 145246. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Matsumori, H.; Saito, H.; Hidaka, H.; Amitsuka, H.; Nakamura, S.; Awaji, S.; Gorbunov, D.I.; Zherlitsyn, S.; Wosnitza, J.; et al. Electric Quadrupolar Contributions in the Magnetic Phases of UNi4B. Phys. Rev. Lett. 2021, 126, 157201. [Google Scholar] [CrossRef] [PubMed]
- Yatsushiro, M.; Kusunose, H.; Hayami, S. Multipole classification in 122 magnetic point groups for unified understanding of multiferroic responses and transport phenomena. Phys. Rev. B 2021, 104, 054412. [Google Scholar] [CrossRef]
- Knight, K.S.; Khalyavin, D.D.; Manuel, P.; Bull, C.L.; McIntyre, P. Nuclear and magnetic structures of KMnF3 perovskite in the temperature interval 10 K–105 K. J. Alloys Compd. 2020, 842, 155935. [Google Scholar] [CrossRef]
- Porter, D.G.; Granata, V.; Forte, F.; Di Matteo, S.; Cuoco, M.; Fittipaldi, R.; Vecchione, A.; Bombardi, A. Magnetic anisotropy and orbital ordering in Ca2RuO4. Phys. Rev. B 2018, 98, 125142. [Google Scholar] [CrossRef]
- Garlea, V.O.; Jin, R.; Mandrus, D.; Roessli, B.; Huang, Q.; Miller, M.; Schultz, A.J.; Nagler, S.E. Magnetic and Orbital Ordering in the Spinel MnV2O4. Phys. Rev. Lett. 2008, 100, 066404. [Google Scholar] [CrossRef] [PubMed]
- Karigerasi, M.H.; Lam, B.H.; Avdeev, M.; Shoemaker, D.P. Two-step magnetic ordering into a canted state in ferrimagnetic monoclinic Mn3As2. J. Solid State Chem. 2021, 294, 121901. [Google Scholar] [CrossRef]
- Muñoz, A.; Alonso, J.A.; Martínez-Lope, M.J.; Casáis, M.T.; Martínez, J.L.; Fernández-Díaz, M.T. Magnetic structure of hexagonal RMnO3 (R= Y, Sc): Thermal evolution from neutron powder diffraction data. Phys. Rev. B 2000, 62, 9498–9510. [Google Scholar] [CrossRef]
- Garca-Muoz, J.L.; Rodrguez-Carvajal, J.; Obradors, X.; Vallet-Reg, M.; González-Calbet, J.; Parras, M. Complex magnetic structures of the rare-earth cuprates R2Cu2O5 (R = Y, Ho, Er, Yb, Tm). Phys. Rev. B 1991, 44, 4716–4719. [Google Scholar] [CrossRef]
- Morosan, E.; Fleitman, J.A.; Huang, Q.; Lynn, J.W.; Chen, Y.; Ke, X.; Dahlberg, M.L.; Schiffer, P.; Craley, C.R.; Cava, R.J. Structure and magnetic properties of the Ho2Ge2O7 pyrogermanate. Phys. Rev. B 2008, 77, 224423. [Google Scholar] [CrossRef]
- Eriksson, T.; Bergqvist, L.; Nordblad, P.; Eriksson, O.; Andersson, Y. Structural and magnetic characterization of Mn3IrGe and Mn3Ir (Si1−xGex): Experiments and theory. J. Solid State Chem. 2004, 177, 4058–4066. [Google Scholar] [CrossRef]
- Li, M.R.; Retuerto, M.; Walker, D.; Sarkar, T.; Stephens, P.W.; Mukherjee, S.; Dasgupta, T.S.; Hodges, J.P.; Croft, M.; Grams, C.P.; et al. Magnetic-Structure-Stabilized Polarization in an Above-Room-Temperature Ferrimagnet. Angew. Chem. Int. Ed. 2014, 53, 10774. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin–orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous Multipole Ordering by Local Parity Mixing. J. Phys. Soc. Jpn. 2015, 84, 064717. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent spin-valley-orbital physics by spontaneous parity breaking. J. Phys. Condens. Matter 2016, 28, 395601. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, M.T.; Ikeda, H.; Oppeneer, P.M. First-principles theory of magnetic multipoles in condensed matter systems. J. Phys. Soc. Jpn. 2018, 87, 041008. [Google Scholar] [CrossRef]
- Kusunose, H.; Oiwa, R.; Hayami, S. Complete Multipole Basis Set for Single-Centered Electron Systems. J. Phys. Soc. Jpn. 2020, 89, 104704. [Google Scholar] [CrossRef]
- Hlinka, J. Eight Types of Symmetrically Distinct Vectorlike Physical Quantities. Phys. Rev. Lett. 2014, 113, 165502. [Google Scholar] [CrossRef]
- Hlinka, J.; Privratska, J.; Ondrejkovic, P.; Janovec, V. Symmetry Guide to Ferroaxial Transitions. Phys. Rev. Lett. 2016, 116, 177602. [Google Scholar] [CrossRef]
- Jin, W.; Drueke, E.; Li, S.; Admasu, A.; Owen, R.; Day, M.; Sun, K.; Cheong, S.W.; Zhao, L. Observation of a ferro-rotational order coupled with second-order nonlinear optical fields. Nat. Phys. 2020, 16, 42–46. [Google Scholar] [CrossRef]
- Hayashida, T.; Uemura, Y.; Kimura, K.; Matsuoka, S.; Morikawa, D.; Hirose, S.; Tsuda, K.; Hasegawa, T.; Kimura, T. Visualization of ferroaxial domains in an order-disorder type ferroaxial crystal. Nat. Commun. 2020, 11, 4582. [Google Scholar] [CrossRef]
- Nasu, J.; Hayami, S. Antisymmetric thermopolarization by electric toroidicity. Phys. Rev. B 2022, 105, 245125. [Google Scholar] [CrossRef]
- Hayami, S.; Oiwa, R.; Kusunose, H. Electric Ferro-Axial Moment as Nanometric Rotator and Source of Longitudinal Spin Current. J. Phys. Soc. Jpn. 2022, 91, 113702. [Google Scholar] [CrossRef]
- Cheong, S.W.; Lim, S.; Du, K.; Huang, F.T. Permutable SOS (symmetry operational similarity). NPJ Quantum Mater. 2021, 6, 58. [Google Scholar] [CrossRef]
- Hayami, S.; Yanagi, Y.; Kusunose, H. Spontaneous antisymmetric spin splitting in noncollinear antiferromagnets without spin–orbit coupling. Phys. Rev. B 2020, 101, 220403. [Google Scholar] [CrossRef]
- Oiwa, R.; Kusunose, H. Systematic Analysis Method for Nonlinear Response Tensors. J. Phys. Soc. Jpn. 2022, 91, 014701. [Google Scholar] [CrossRef]


| L | Orbital | # | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | s-s | 2 | E/MT | – | – | – | – | – | – |
| 1 | p-p | 18 | E/MT | M/ET | E/MT | – | – | – | – |
| 2 | d-d | 50 | E/MT | M/ET | E/MT | M/ET | E/MT | – | – |
| 3 | f-f | 98 | E/MT | M/ET | E/MT | M/ET | E/MT | M/ET | E/MT |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Magnetic Toroidal Monopole in a Single-Site System. Magnetism 2025, 5, 15. https://doi.org/10.3390/magnetism5030015
Hayami S. Magnetic Toroidal Monopole in a Single-Site System. Magnetism. 2025; 5(3):15. https://doi.org/10.3390/magnetism5030015
Chicago/Turabian StyleHayami, Satoru. 2025. "Magnetic Toroidal Monopole in a Single-Site System" Magnetism 5, no. 3: 15. https://doi.org/10.3390/magnetism5030015
APA StyleHayami, S. (2025). Magnetic Toroidal Monopole in a Single-Site System. Magnetism, 5(3), 15. https://doi.org/10.3390/magnetism5030015






