Double-Q Instability in Noncentrosymmetric Tetragonal Magnets with Bond-Dependent Magnetic Anisotropy Under an In-Plane Magnetic Field
Abstract
1. Introduction
2. Model and Method
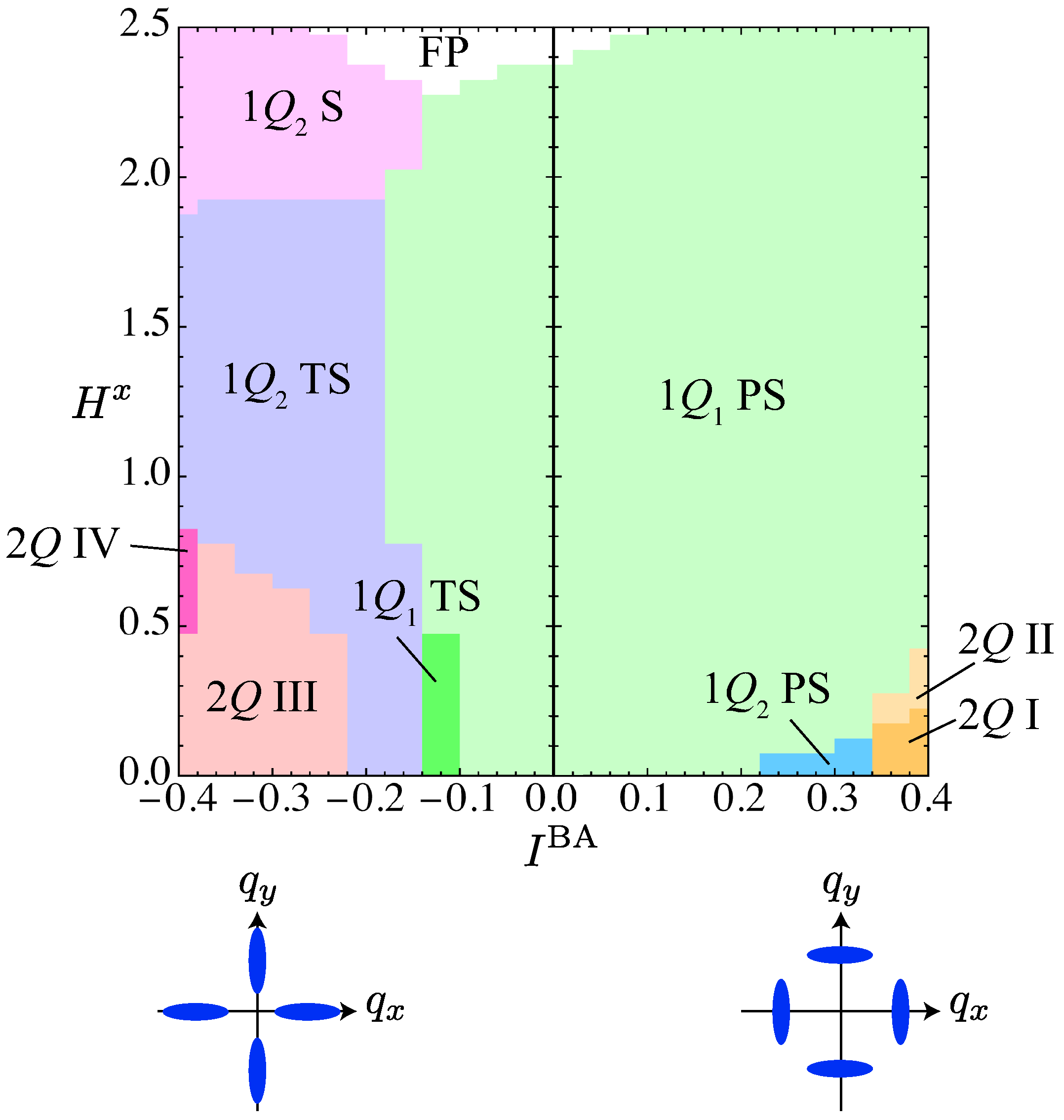
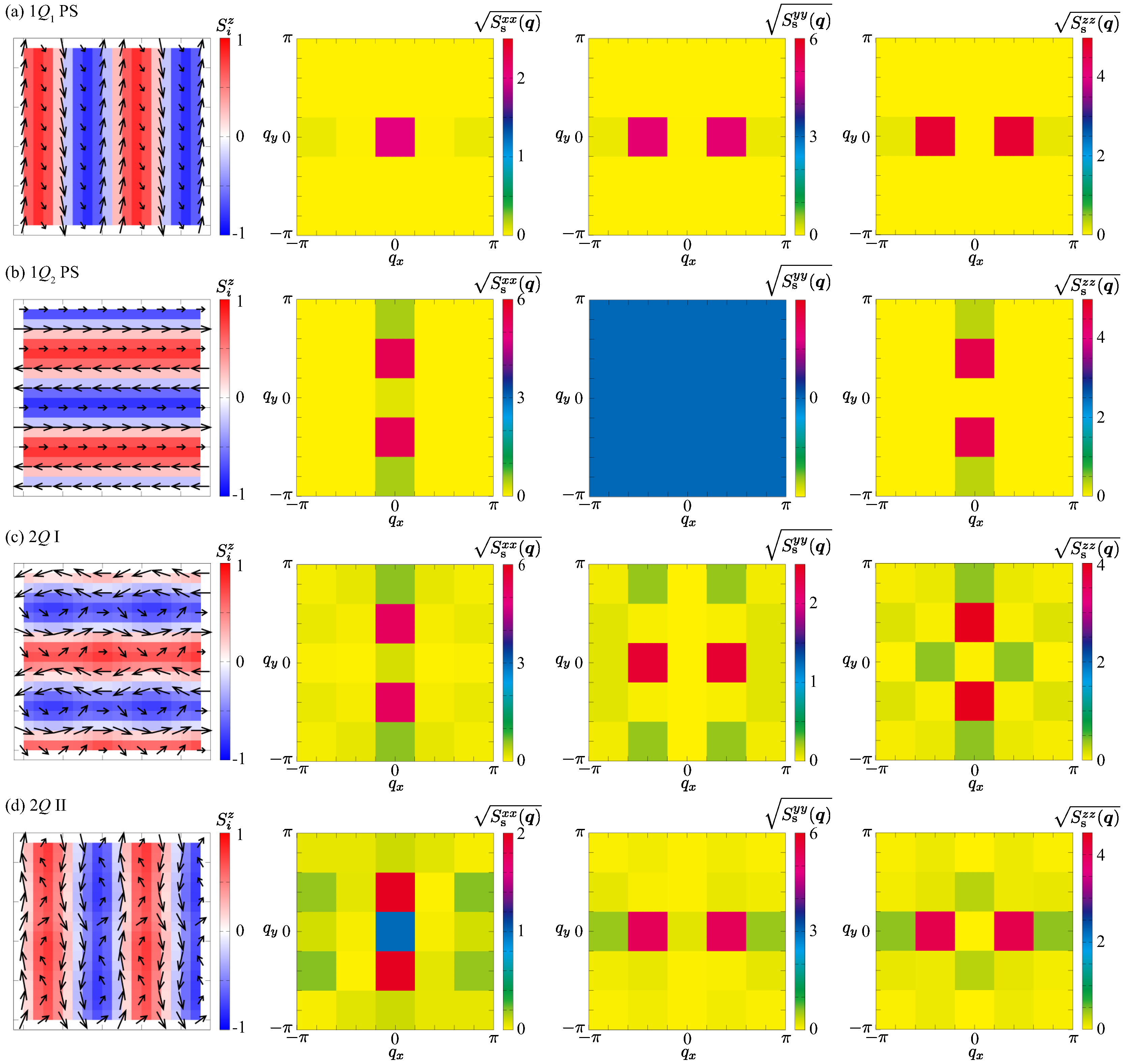
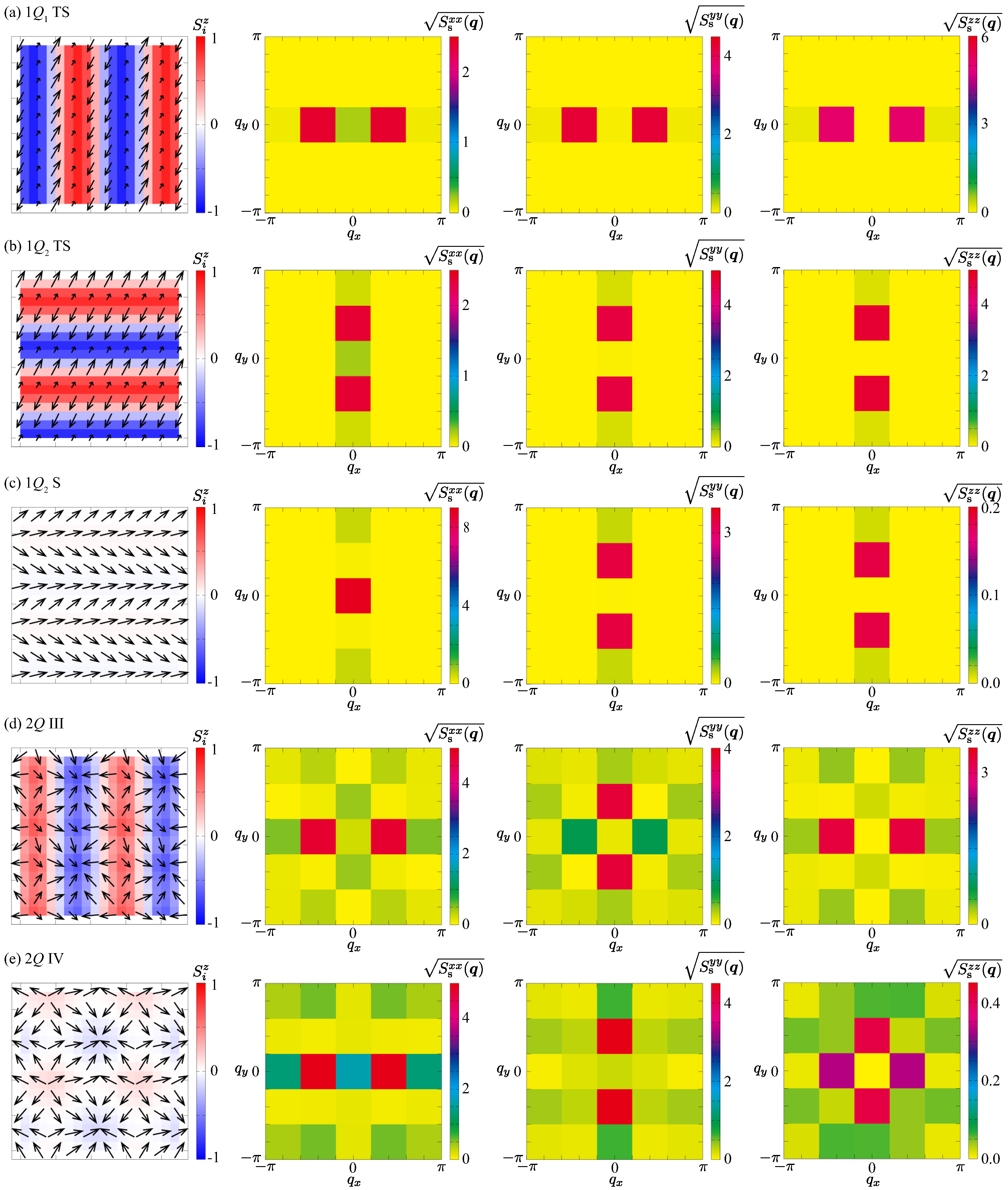
3. Results
3.1. Case of
3.2. Case of
3.3. Case of
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bak, P.; Lebech, B. “Triple-” Modulated Magnetic Structure and Critical Behavior of Neodymium. Phys. Rev. Lett. 1978, 40, 800–803. [Google Scholar] [CrossRef]
- McEwen, K.A.; Walker, M.B. Free-energy analysis of the single-q and double-q magnetic structures of neodymium. Phys. Rev. B 1986, 34, 1781–1783. [Google Scholar] [CrossRef] [PubMed]
- Zochowski, S.; McEwen, K. Thermal expansion study of the magnetic phase diagram of neodymium. J. Magn. Magn. Mater. 1986, 54, 515–516. [Google Scholar] [CrossRef]
- Forgan, E.; Rainford, B.; Lee, S.; Abell, J.; Bi, Y. The magnetic structure of CeAl2 is a non-chiral spiral. J. Phys. Condens. Matter 1990, 2, 10211. [Google Scholar] [CrossRef]
- Longfield, M.J.; Paixão, J.A.; Bernhoeft, N.; Lander, G.H. Resonant x-ray scattering from multi-k magnetic structures. Phys. Rev. B 2002, 66, 054417. [Google Scholar] [CrossRef]
- Bernhoeft, N.; Paixão, J.A.; Detlefs, C.; Wilkins, S.B.; Javorský, P.; Blackburn, E.; Lander, G.H. Resonant x-ray scattering from UAs0.8Se0.2: Multi-k configurations. Phys. Rev. B 2004, 69, 174415. [Google Scholar] [CrossRef]
- Stewart, J.; Ehlers, G.; Wills, A.; Bramwell, S.T.; Gardner, J. Phase transitions, partial disorder and multi-k structures in Gd2Ti2O7. J. Phys. Condens. Matter 2004, 16, L321. [Google Scholar] [CrossRef]
- Watson, D.; Forgan, E.M.; Nuttall, W.J.; Stirling, W.G.; Fort, D. High-resolution magnetic x-ray diffraction from neodymium. Phys. Rev. B 1996, 53, 726–730. [Google Scholar] [CrossRef]
- Harris, A.B.; Schweizer, J. Theoretical analysis of the double-q magnetic structure of CeAl2. Phys. Rev. B 2006, 74, 134411. [Google Scholar] [CrossRef]
- Schweizer, J.; Givord, F.; Boucherle, J.; Bourdarot, F.; Ressouche, E. The accurate magnetic structure of CeAl2 at various temperatures in the ordered state. J. Phys. Condens. Matter 2008, 20, 135204. [Google Scholar] [CrossRef]
- Szabó, A.; Orlandi, F.; Manuel, P. Fragmented Spin Ice and Multi-k Ordering in Rare-Earth Antiperovskites. Phys. Rev. Lett. 2022, 129, 247201. [Google Scholar] [CrossRef] [PubMed]
- Kurz, P.; Bihlmayer, G.; Hirai, K.; Blügel, S. Three-Dimensional Spin Structure on a Two-Dimensional Lattice: Mn/Cu(111). Phys. Rev. Lett. 2001, 86, 1106–1109. [Google Scholar] [CrossRef] [PubMed]
- Martin, I.; Batista, C.D. Itinerant Electron-Driven Chiral Magnetic Ordering and Spontaneous Quantum Hall Effect in Triangular Lattice Models. Phys. Rev. Lett. 2008, 101, 156402. [Google Scholar] [CrossRef] [PubMed]
- Akagi, Y.; Motome, Y. Spin Chirality Ordering and Anomalous Hall Effect in the Ferromagnetic Kondo Lattice Model on a Triangular Lattice. J. Phys. Soc. Jpn. 2010, 79, 083711. [Google Scholar] [CrossRef]
- Kato, Y.; Martin, I.; Batista, C.D. Stability of the Spontaneous Quantum Hall State in the Triangular Kondo-Lattice Model. Phys. Rev. Lett. 2010, 105, 266405. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Multiple-Q instability by (d-2)-dimensional connections of Fermi surfaces. Phys. Rev. B 2014, 90, 060402(R). [Google Scholar] [CrossRef]
- Liu, C.; Yu, R.; Wang, X. Semiclassical ground-state phase diagram and multi-Q phase of a spin-orbit-coupled model on triangular lattice. Phys. Rev. B 2016, 94, 174424. [Google Scholar] [CrossRef]
- Hayami, S.; Lin, S.Z.; Kamiya, Y.; Batista, C.D. Vortices, skyrmions, and chirality waves in frustrated Mott insulators with a quenched periodic array of impurities. Phys. Rev. B 2016, 94, 174420. [Google Scholar] [CrossRef]
- Hayami, S.; Okubo, T.; Motome, Y. Phase shift in skyrmion crystals. Nat. Commun. 2021, 12, 6927. [Google Scholar] [CrossRef]
- Domenge, J.C.; Sindzingre, P.; Lhuillier, C.; Pierre, L. Twelve sublattice ordered phase in the J1 − J2 model on the kagomé lattice. Phys. Rev. B 2005, 72, 024433. [Google Scholar] [CrossRef]
- Janson, O.; Richter, J.; Rosner, H. Modified Kagome Physics in the Natural Spin-1/2 Kagome Lattice Systems: Kapellasite Cu3Zn(OH)6Cl2 and Haydeeite Cu3Mg(OH)6Cl2. Phys. Rev. Lett. 2008, 101, 106403. [Google Scholar] [CrossRef] [PubMed]
- Messio, L.; Lhuillier, C.; Misguich, G. Lattice symmetries and regular magnetic orders in classical frustrated antiferromagnets. Phys. Rev. B 2011, 83, 184401. [Google Scholar] [CrossRef]
- Barros, K.; Venderbos, J.W.F.; Chern, G.W.; Batista, C.D. Exotic magnetic orderings in the kagome Kondo-lattice model. Phys. Rev. B 2014, 90, 245119. [Google Scholar] [CrossRef]
- Ghosh, S.; O’Brien, P.; Henley, C.L.; Lawler, M.J. Phase diagram of the Kondo lattice model on the kagome lattice. Phys. Rev. B 2016, 93, 024401. [Google Scholar] [CrossRef]
- Zhitomirsky, M.; Gvozdikova, M.; Ziman, T. Noncoplanar multi-k states in frustrated spinel and kagome magnets. Ann. Phys. 2022, 447, 169066. [Google Scholar] [CrossRef]
- Gembé, M.; Schmidt, H.J.; Hickey, C.; Richter, J.; Iqbal, Y.; Trebst, S. Noncoplanar magnetic order in classical square-kagome antiferromagnets. Phys. Rev. Res. 2023, 5, 043204. [Google Scholar] [CrossRef]
- Rosales, H.D.; Cabra, D.C.; Lamas, C.A.; Pujol, P.; Zhitomirsky, M.E. Broken discrete symmetries in a frustrated honeycomb antiferromagnet. Phys. Rev. B 2013, 87, 104402. [Google Scholar] [CrossRef]
- Jiang, K.; Zhang, Y.; Zhou, S.; Wang, Z. Chiral Spin Density Wave Order on the Frustrated Honeycomb and Bilayer Triangle Lattice Hubbard Model at Half-Filling. Phys. Rev. Lett. 2015, 114, 216402. [Google Scholar] [CrossRef]
- Venderbos, J.W.F. Multi-Q hexagonal spin density waves and dynamically generated spin-orbit coupling: Time-reversal invariant analog of the chiral spin density wave. Phys. Rev. B 2016, 93, 115108. [Google Scholar] [CrossRef]
- Shimokawa, T.; Kawamura, H. Ripple State in the Frustrated Honeycomb-Lattice Antiferromagnet. Phys. Rev. Lett. 2019, 123, 057202. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Ferrochiral, antiferrochiral, and ferrichiral skyrmion crystals in an itinerant honeycomb magnet. Phys. Rev. B 2023, 107, 014417. [Google Scholar] [CrossRef]
- Gembé, M.; Gresista, L.; Schmidt, H.J.; Hickey, C.; Iqbal, Y.; Trebst, S. Noncoplanar orders and quantum disordered states in maple-leaf antiferromagnets. Phys. Rev. B 2024, 110, 085151. [Google Scholar] [CrossRef]
- Chattopadhyay, T.; Brückel, T.; Burlet, P. Spin correlation in the frustrated antiferromagnet MnS2 above the Néel temperature. Phys. Rev. B 1991, 44, 7394–7402. [Google Scholar] [CrossRef]
- Balla, P.; Iqbal, Y.; Penc, K. Degenerate manifolds, helimagnets, and multi-Q chiral phases in the classical Heisenberg antiferromagnet on the face-centered-cubic lattice. Phys. Rev. Res. 2020, 2, 043278. [Google Scholar] [CrossRef]
- Yokota, T. Various Ordered States in Heisenberg FCC Antiferromagnets with Dipole–Dipole Interactions. J. Phys. Soc. Jpn. 2022, 91, 064003. [Google Scholar] [CrossRef]
- Hagihala, M.; Zheng, X.G.; Kawae, T.; Sato, T.J. Successive antiferromagnetic transitions with multi-k and noncoplanar spin order, spin fluctuations, and field-induced phases in deformed pyrochlore compound Co2(OH)3Br. Phys. Rev. B 2010, 82, 214424. [Google Scholar] [CrossRef]
- Okubo, T.; Nguyen, T.H.; Kawamura, H. Cubic and noncubic multiple-q states in the Heisenberg antiferromagnet on the pyrochlore lattice. Phys. Rev. B 2011, 84, 144432. [Google Scholar] [CrossRef]
- Chern, G.W. Noncoplanar Magnetic Ordering Driven by Itinerant Electrons on the Pyrochlore Lattice. Phys. Rev. Lett. 2010, 105, 226403. [Google Scholar] [CrossRef]
- Huang, Y.P.; Dong, J.W.; Kotetes, P.; Zhou, S. Antiferromagnetic chiral spin density wave and strain-induced Chern insulator in the square lattice Hubbard model with frustration. Phys. Rev. B 2020, 102, 195120. [Google Scholar] [CrossRef]
- Steffensen, D.; Christensen, M.H.; Andersen, B.M.; Kotetes, P. Topological superconductivity induced by magnetic texture crystals. Phys. Rev. Res. 2022, 4, 013225. [Google Scholar] [CrossRef]
- Utesov, O.I. Thermodynamically stable skyrmion lattice in a tetragonal frustrated antiferromagnet with dipolar interaction. Phys. Rev. B 2021, 103, 064414. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Meron, skyrmion, and vortex crystals in centrosymmetric tetragonal magnets. Phys. Rev. B 2021, 103, 104408. [Google Scholar] [CrossRef]
- Hayami, S. Multiple skyrmion crystal phases by itinerant frustration in centrosymmetric tetragonal magnets. J. Phys. Soc. Jpn. 2022, 91, 023705. [Google Scholar] [CrossRef]
- Venderbos, J.W.F.; Daghofer, M.; van den Brink, J.; Kumar, S. Switchable Quantum Anomalous Hall State in a Strongly Frustrated Lattice Magnet. Phys. Rev. Lett. 2012, 109, 166405. [Google Scholar] [CrossRef] [PubMed]
- Shahzad, M.; Sengupta, P. Noncollinear magnetic ordering in a frustrated magnet: Metallic regime and the role of frustration. Phys. Rev. B 2017, 96, 224402. [Google Scholar] [CrossRef]
- Khalyavin, D.D.; Brunt, D.; Qureshi, N.; Wildes, A.R.; Ouladdiaf, B.; Johnson, R.D.; Balakrishnan, G.; Petrenko, O.A. Magnetic ground state of NdB4: Interplay between anisotropic exchange interactions and hidden order on a Shastry-Sutherland lattice. Phys. Rev. B 2024, 109, L220411. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices" in magnetically ordered crystals: The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A.; Aji, V. Theory of the Helical Spin Crystal: A Candidate for the Partially Ordered State of MnSi. Phys. Rev. Lett. 2006, 96, 207202. [Google Scholar] [CrossRef] [PubMed]
- Binz, B.; Vishwanath, A. Theory of helical spin crystals: Phases, textures, and properties. Phys. Rev. B 2006, 74, 214408. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A. Chirality induced anomalous-Hall effect in helical spin crystals. Phys. B 2008, 403, 1336. [Google Scholar] [CrossRef]
- Yi, S.D.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef]
- Fert, A.; Reyren, N.; Cros, V. Magnetic skyrmions: Advances in physics and potential applications. Nat. Rev. Mater. 2017, 2, 17031. [Google Scholar] [CrossRef]
- Park, J.H.; Han, J.H. Zero-temperature phases for chiral magnets in three dimensions. Phys. Rev. B 2011, 83, 184406. [Google Scholar] [CrossRef]
- Yang, S.G.; Liu, Y.H.; Han, J.H. Formation of a topological monopole lattice and its dynamics in three-dimensional chiral magnets. Phys. Rev. B 2016, 94, 054420. [Google Scholar] [CrossRef]
- Tanigaki, T.; Shibata, K.; Kanazawa, N.; Yu, X.; Onose, Y.; Park, H.S.; Shindo, D.; Tokura, Y. Real-space observation of short-period cubic lattice of skyrmions in MnGe. Nano Lett. 2015, 15, 5438–5442. [Google Scholar] [CrossRef]
- Kanazawa, N.; Seki, S.; Tokura, Y. Noncentrosymmetric magnets hosting magnetic skyrmions. Adv. Mater. 2017, 29, 1603227. [Google Scholar] [CrossRef]
- Fujishiro, Y.; Kanazawa, N.; Nakajima, T.; Yu, X.Z.; Ohishi, K.; Kawamura, Y.; Kakurai, K.; Arima, T.; Mitamura, H.; Miyake, A.; et al. Topological transitions among skyrmion-and hedgehog-lattice states in cubic chiral magnets. Nat. Commun. 2019, 10, 1059. [Google Scholar] [CrossRef] [PubMed]
- Kanazawa, N.; Kitaori, A.; White, J.S.; Ukleev, V.; Rønnow, H.M.; Tsukazaki, A.; Ichikawa, M.; Kawasaki, M.; Tokura, Y. Direct Observation of the Statics and Dynamics of Emergent Magnetic Monopoles in a Chiral Magnet. Phys. Rev. Lett. 2020, 125, 137202. [Google Scholar] [CrossRef] [PubMed]
- Aoyama, K.; Kawamura, H. Hedgehog-lattice spin texture in classical Heisenberg antiferromagnets on the breathing pyrochlore lattice. Phys. Rev. B 2021, 103, 014406. [Google Scholar] [CrossRef]
- Eto, R.; Mochizuki, M. Theory of Collective Excitations in the Quadruple-Q Magnetic Hedgehog Lattices. Phys. Rev. Lett. 2024, 132, 226705. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: Chiral spin state based on a ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Taguchi, Y.; Oohara, Y.; Yoshizawa, H.; Nagaosa, N.; Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 2001, 291, 2573–2576. [Google Scholar] [CrossRef]
- Tatara, G.; Kawamura, H. Chirality-driven anomalous Hall effect in weak coupling regime. J. Phys. Soc. Jpn. 2002, 71, 2613–2616. [Google Scholar] [CrossRef]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef]
- Hamamoto, K.; Ezawa, M.; Nagaosa, N. Quantized topological Hall effect in skyrmion crystal. Phys. Rev. B 2015, 92, 115417. [Google Scholar] [CrossRef]
- Nakazawa, K.; Bibes, M.; Kohno, H. Topological Hall effect from strong to weak coupling. J. Phys. Soc. Jpn. 2018, 87, 033705. [Google Scholar] [CrossRef]
- Tai, L.; Dai, B.; Li, J.; Huang, H.; Chong, S.K.; Wong, K.L.; Zhang, H.; Zhang, P.; Deng, P.; Eckberg, C.; et al. Distinguishing the two-component anomalous Hall effect from the topological Hall effect. ACS Nano 2022, 16, 17336–17346. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Momoi, T.; Kubo, K.; Niki, K. Possible Chiral Phase Transition in Two-Dimensional Solid 3He. Phys. Rev. Lett. 1997, 79, 2081–2084. [Google Scholar] [CrossRef]
- Heinze, S.; von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Yoshida, Y.; Schröder, S.; Ferriani, P.; Serrate, D.; Kubetzka, A.; von Bergmann, K.; Heinze, S.; Wiesendanger, R. Conical Spin-Spiral State in an Ultrathin Film Driven by Higher-Order Spin Interactions. Phys. Rev. Lett. 2012, 108, 087205. [Google Scholar] [CrossRef]
- Ueland, B.; Miclea, C.; Kato, Y.; Ayala-Valenzuela, O.; McDonald, R.; Okazaki, R.; Tobash, P.; Torrez, M.; Ronning, F.; Movshovich, R.; et al. Controllable chirality-induced geometrical Hall effect in a frustrated highly correlated metal. Nat. Commun. 2012, 3, 1067. [Google Scholar] [CrossRef]
- Mankovsky, S.; Polesya, S.; Ebert, H. Extension of the standard Heisenberg Hamiltonian to multispin exchange interactions. Phys. Rev. B 2020, 101, 174401. [Google Scholar] [CrossRef]
- Paul, S.; Haldar, S.; von Malottki, S.; Heinze, S. Role of higher-order exchange interactions for skyrmion stability. Nat. Commun. 2020, 11, 4756. [Google Scholar] [CrossRef]
- Brinker, S.; dos Santos Dias, M.; Lounis, S. Prospecting chiral multisite interactions in prototypical magnetic systems. Phys. Rev. Res. 2020, 2, 033240. [Google Scholar] [CrossRef]
- Lounis, S. Multiple-scattering approach for multi-spin chiral magnetic interactions: Application to the one-and two-dimensional Rashba electron gas. New J. Phys. 2020, 22, 103003. [Google Scholar] [CrossRef]
- Leonov, A.O.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef] [PubMed]
- Amoroso, D.; Barone, P.; Picozzi, S. Spontaneous skyrmionic lattice from anisotropic symmetric exchange in a Ni-halide monolayer. Nat. Commun. 2020, 11, 5784. [Google Scholar] [CrossRef] [PubMed]
- Yambe, R.; Hayami, S. Skyrmion crystals in centrosymmetric itinerant magnets without horizontal mirror plane. Sci. Rep. 2021, 11, 11184. [Google Scholar] [CrossRef] [PubMed]
- Amoroso, D.; Barone, P.; Picozzi, S. Interplay between Single-Ion and Two-Ion Anisotropies in Frustrated 2D Semiconductors and Tuning of Magnetic Structures Topology. Nanomaterials 2021, 11, 1873. [Google Scholar] [CrossRef]
- Shekhtman, L.; Aharony, A.; Entin-Wohlman, O. Bond-dependent symmetric and antisymmetric superexchange interactions in La2CuO4. Phys. Rev. B 1993, 47, 174–182. [Google Scholar] [CrossRef]
- Khomskii, D.; Mostovoy, M. Orbital ordering and frustrations. J. Phys. A 2003, 36, 9197. [Google Scholar] [CrossRef]
- Jackeli, G.; Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: From Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 2009, 102, 017205. [Google Scholar] [CrossRef]
- Becker, M.; Hermanns, M.; Bauer, B.; Garst, M.; Trebst, S. Spin-orbit physics of j = Mott insulators on the triangular lattice. Phys. Rev. B 2015, 91, 155135. [Google Scholar] [CrossRef]
- Lee, E.K.H.; Kim, Y.B. Theory of magnetic phase diagrams in hyperhoneycomb and harmonic-honeycomb iridates. Phys. Rev. B 2015, 91, 064407. [Google Scholar] [CrossRef]
- Li, Y.D.; Wang, X.; Chen, G. Anisotropic spin model of strong spin-orbit-coupled triangular antiferromagnets. Phys. Rev. B 2016, 94, 035107. [Google Scholar] [CrossRef]
- Janssen, L.; Andrade, E.C.; Vojta, M. Honeycomb-Lattice Heisenberg-Kitaev Model in a Magnetic Field: Spin Canting, Metamagnetism, and Vortex Crystals. Phys. Rev. Lett. 2016, 117, 277202. [Google Scholar] [CrossRef] [PubMed]
- Rousochatzakis, I.; Rössler, U.K.; van den Brink, J.; Daghofer, M. Kitaev anisotropy induces mesoscopic Z2 vortex crystals in frustrated hexagonal antiferromagnets. Phys. Rev. B 2016, 93, 104417. [Google Scholar] [CrossRef]
- Yao, X.; Dong, S. Topological triple-vortex lattice stabilized by mixed frustration in expanded honeycomb Kitaev-Heisenberg model. Sci. Rep. 2016, 6, 26750. [Google Scholar] [CrossRef] [PubMed]
- Chern, G.W.; Sizyuk, Y.; Price, C.; Perkins, N.B. Kitaev-Heisenberg model in a magnetic field: Order-by-disorder and commensurate-incommensurate transitions. Phys. Rev. B 2017, 95, 144427. [Google Scholar] [CrossRef]
- Maksimov, P.A.; Zhu, Z.; White, S.R.; Chernyshev, A.L. Anisotropic-Exchange Magnets on a Triangular Lattice: Spin Waves, Accidental Degeneracies, and Dual Spin Liquids. Phys. Rev. X 2019, 9, 021017. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayami, S. Nonreciprocal magnons due to symmetric anisotropic exchange interaction in honeycomb antiferromagnets. Phys. Rev. B 2020, 101, 224419. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Hayami, S.; Gao, S.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Takagi, R.; Motome, Y.; Tokura, Y.; et al. Zoology of Multiple-Q Spin Textures in a Centrosymmetric Tetragonal Magnet with Itinerant Electrons. Adv. Sci. 2022, 9, 2105452. [Google Scholar] [CrossRef]
- Matsuyama, N.; Nomura, T.; Imajo, S.; Nomoto, T.; Arita, R.; Sudo, K.; Kimata, M.; Khanh, N.D.; Takagi, R.; Tokura, Y.; et al. Quantum oscillations in the centrosymmetric skyrmion-hosting magnet GdRu2Si2. Phys. Rev. B 2023, 107, 104421. [Google Scholar] [CrossRef]
- Wood, G.D.A.; Khalyavin, D.D.; Mayoh, D.A.; Bouaziz, J.; Hall, A.E.; Holt, S.J.R.; Orlandi, F.; Manuel, P.; Blügel, S.; Staunton, J.B.; et al. Double-Q ground state with topological charge stripes in the centrosymmetric skyrmion candidate GdRu2Si2. Phys. Rev. B 2023, 107, L180402. [Google Scholar] [CrossRef]
- Eremeev, S.; Glazkova, D.; Poelchen, G.; Kraiker, A.; Ali, K.; Tarasov, A.V.; Schulz, S.; Kliemt, K.; Chulkov, E.V.; Stolyarov, V.; et al. Insight into the electronic structure of the centrosymmetric skyrmion magnet GdRu2Si2. Nanoscale Adv. 2023, 5, 6678–6687. [Google Scholar] [CrossRef] [PubMed]
- Yoshimochi, H.; Takagi, R.; Ju, J.; Khanh, N.; Saito, H.; Sagayama, H.; Nakao, H.; Itoh, S.; Tokura, Y.; Arima, T.; et al. Multistep topological transitions among meron and skyrmion crystals in a centrosymmetric magnet. Nat. Phys. 2024, 20, 1001. [Google Scholar] [CrossRef]
- Singh, D.; Fujishiro, Y.; Hayami, S.; Moody, S.H.; Nomoto, T.; Baral, P.R.; Ukleev, V.; Cubitt, R.; Steinke, N.J.; Gawryluk, D.J.; et al. Transition between distinct hybrid skyrmion textures through their hexagonal-to-square crystal transformation in a polar magnet. Nat. Commun. 2023, 14, 8050. [Google Scholar] [CrossRef] [PubMed]
- Matsumura, T.; Kurauchi, K.; Tsukagoshi, M.; Higa, N.; Nakao, H.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Helicity Unification by Triangular Skyrmion Lattice Formation in the Noncentrosymmetric Tetragonal Magnet EuNiGe3. J. Phys. Soc. Jpn. 2024, 93, 074705. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Kaplan, T. Single-band Hubbard model with spin-orbit coupling. Z. Für Phys. B Condens. Matter 1983, 49, 313–317. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Noncoplanar multiple-Q spin textures by itinerant frustration: Effects of single-ion anisotropy and bond-dependent anisotropy. Phys. Rev. B 2021, 103, 054422. [Google Scholar] [CrossRef]
- Hirschberger, M.; Hayami, S.; Tokura, Y. Nanometric skyrmion lattice from anisotropic exchange interactions in a centrosymmetric host. New J. Phys. 2021, 23, 023039. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Helicity locking of a square skyrmion crystal in a centrosymmetric lattice system without vertical mirror symmetry. Phys. Rev. B 2022, 105, 104428. [Google Scholar] [CrossRef]
- Holanda, J.; Campos, C.; Franca, C.; Padrón-Hernández, E. Effective surface anisotropy in polycrystalline ferromagnetic nanowires. J. Alloys Compd. 2014, 617, 639–641. [Google Scholar] [CrossRef]
- Holanda, J.; Silva, D.; Padrón-Hernández, E. Angular dependence of the coercivity in arrays of ferromagnetic nanowires. J. Magn. Magn. Mater. 2015, 378, 228–231. [Google Scholar] [CrossRef]
- Holanda, J. Analyzing the magnetic interactions in nanostructures that are candidates for applications in spintronics. J. Phys. D Appl. Phys. 2021, 54, 245004. [Google Scholar] [CrossRef]
- Silva, W.W.; Hildever, L.M.; Santos, M.C.; Estrada, F.; Holanda, J. Analyzing the magnetic influence on magneto-optical interactions. J. Supercond. Nov. Magn. 2023, 36, 951–955. [Google Scholar] [CrossRef]
- Reichhardt, C.; Reichhardt, C.J.O.; Milošević, M.V. Statics and dynamics of skyrmions interacting with disorder and nanostructures. Rev. Mod. Phys. 2022, 94, 035005. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Effective spin model in momentum space: Toward a systematic understanding of multiple-Q instability by momentum-resolved anisotropic exchange interactions. Phys. Rev. B 2022, 106, 174437. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Néel- and Bloch-Type Magnetic Vortices in Rashba Metals. Phys. Rev. Lett. 2018, 121, 137202. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hayami, S. In-plane magnetic field-induced skyrmion crystal in frustrated magnets with easy-plane anisotropy. Phys. Rev. B 2021, 103, 224418. [Google Scholar] [CrossRef]
- Hayami, S.; Kato, Y. Widely-sweeping magnetic field–temperature phase diagrams for skyrmion-hosting centrosymmetric tetragonal magnets. J. Magn. Magn. Mater. 2023, 571, 170547. [Google Scholar] [CrossRef]
- Zhang, Z.; Vogel, M.; Holanda, J.; Jungfleisch, M.B.; Liu, C.; Li, Y.; Pearson, J.E.; Divan, R.; Zhang, W.; Hoffmann, A.; et al. Spin-wave frequency division multiplexing in an yttrium iron garnet microstripe magnetized by inhomogeneous field. Appl. Phys. Lett. 2019, 115. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Double-Q Instability in Noncentrosymmetric Tetragonal Magnets with Bond-Dependent Magnetic Anisotropy Under an In-Plane Magnetic Field. Magnetism 2024, 4, 412-423. https://doi.org/10.3390/magnetism4040027
Hayami S. Double-Q Instability in Noncentrosymmetric Tetragonal Magnets with Bond-Dependent Magnetic Anisotropy Under an In-Plane Magnetic Field. Magnetism. 2024; 4(4):412-423. https://doi.org/10.3390/magnetism4040027
Chicago/Turabian StyleHayami, Satoru. 2024. "Double-Q Instability in Noncentrosymmetric Tetragonal Magnets with Bond-Dependent Magnetic Anisotropy Under an In-Plane Magnetic Field" Magnetism 4, no. 4: 412-423. https://doi.org/10.3390/magnetism4040027
APA StyleHayami, S. (2024). Double-Q Instability in Noncentrosymmetric Tetragonal Magnets with Bond-Dependent Magnetic Anisotropy Under an In-Plane Magnetic Field. Magnetism, 4(4), 412-423. https://doi.org/10.3390/magnetism4040027





