Abstract
The rare earth-free Mn5Ge3 compound shows magnetocaloric properties similar to those of pure Gd; therefore, it is a good candidate for magnetic refrigeration technology. In this work, we investigate the influence of chemical substitution on the crystal structure and the magnetic, thermodynamic, and magnetocaloric properties of a polycrystalline Mn5Ge3 compound prepared by induction melting. For this purpose, we replaced 5% of the Mn with Cr or Co and 5% of the Ge with B or Al. The additional chemical elements were shown not to change the crystal structure of the parent compound (space group P63/mcm, No. 193). In the case of the magnetic properties, all samples remained ferromagnetic with the ordering temperature (TC) lower than for the original compound (TC = 295(1) K). The exception was the sample with B, where we observed an increase in TC by 3 K. The maximum value of the magnetic entropy change, |∆Sm|MAX (for a magnetic field change of 5 T), decreased from 7.1(1) for Mn5Ge3 to 6.2(1), 6.8(1), 4.8(1), and 5.8(1) J kg−1 K−1 for the alloys with B, Al, Cr, and Co, respectively. The adiabatic temperature change (∆Tad) (for a magnetic field change of 1 T) was determined from the specific heat measurements and was equal to 1.1(1), 1.2(1), 1.2(1), 0.8(1), and 0.8(1) K for Mn5Ge3, Mn5Ge2.85B0.15, Mn5Ge2.85Al0.15, Mn4.75Cr0.25Ge3, and Mn4.75Co0.25Ge3, respectively. The obtained data were compared with those from the literature. It was found that the substitution allowed for tuning of the ordering temperature in a wide temperature range. At the same time, the reduction in the magnetocaloric parameters’ values was relatively small. Therefore, the produced Mn5Ge3-based alloys allow for the expansion of the operation temperature range of the parent compound as a magnetocaloric material.
1. Introduction
The magnetocaloric effect is a phenomenon that leads to a change in the temperature of a magnetic material under the influence of an external magnetic field [1], and it can be employed in various devices (e.g., refrigerators) operating over a wide temperature range [2]. It has been shown that household appliances based on this technology (e.g., refrigerators and air conditioners) can consume less electricity and be more environmentally friendly, as they do not work with greenhouse or ozone-depleting gases. New materials with suitable properties are necessary for the development of magnetic cooling technology [3,4,5]. The search for such materials has been going on continuously for many years. Materials that exhibit a large magnetocaloric effect around room temperature include Gd [6,7], Gd5(Si,Ge)4 [8,9], FeRh [10,11], La(Fe,Si,X)13Hx [12], La(Fe,Si)13 [13], Ni–Mn–In Heusler alloys [14,15], Mn–Fe–P–As alloys [16], and MnAs alloys [17].
The same technology can be used to build coolers that operate at low temperatures, which can be used to liquefy helium, hydrogen, or natural gas [18]. Therefore, magnetocaloric materials capable of working in a wide temperature range are also being sought. The such hitherto known materials include many intermetallic alloys and compounds (e.g., Laves phases [19,20]), especially those containing rare earth elements [21,22,23,24].
Another subgroup of magnetocaloric materials with high potential are the compounds and alloys containing Mn [25,26,27,28]. This is because the value of MCE strongly depends on the value of the magnetic moment, which is particularly high for Mn and thus also for Mn-based materials. One of the most interesting compounds based on Mn is Mn5Ge3, which has attracted attention in many research fields for more than 50 years, e.g., in magnetic domain structure studies [29] or in spintronics as a possible efficient spin-injector due to the high spin-polarization of Mn5Ge3 and compatibility with Ge-based technology [30,31,32,33,34,35]. Mn5Ge3 is a promising magnetocaloric material because it is a soft ferromagnet showing second-order phase transition with a Curie temperature (TC) near room temperature, a large magnetic entropy change of ∆Sm = 7–9 J kg−1 K−1 for a magnetic field change of 5 T [36,37,38], and an adiabatic temperature change of ∆Tad = 1 K for a magnetic field change of 1 T [36]. This compound, owing to its physical properties, may be used in magnetic refrigerators [39,40]. The attractive properties of Mn5Ge3 initiated studies of, for example, off-stoichiometric Mn5+xGe3-x alloys [41] or systems modified chemically by introducing elements such as Co [42,43,44,45], Fe [42,44,45,46,47], or Ni [48] into the Mn position or by replacing Ge with Si [49,50], Ga [51], Sb [52], Al [53], Ag [54,55], or even Fe [56]. Moreover, simultaneous substitutions of Fe for Mn and Si for Ge have also been attempted [57,58]. The goal of all these modifications was to increase the application potential of Mn5Ge3. In addition, due to the high price of pure Ge (>1000 USD/kg), the cost of raw materials for an Mn5Ge3 compound is too high for commercial application in terms of magnetic refrigeration [5]. Therefore, partial replacement of Ge with cheaper elements may not only improve its magnetocaloric properties, but also reduce the cost.
In this work, we joined the trend of investigating the effect of chemical composition modification on the magnetocaloric properties of the Mn5Ge3 compound. For this purpose, we prepared samples with novel substitutions or with a level of modification not yet investigated. The alloys with the chemical composition Mn5Ge2.85B0.15, Mn5Ge2.85Al0.15, Mn4.75Cr0.25Ge3, and Mn4.75Co0.25Ge3 were examined from the point of view of their structural, magnetic, thermodynamic, and magnetocaloric properties. It was found that any changes in the stoichiometry of the starting material had a considerable effect on its properties. The most interesting results were obtained for the compound Mn5Ge2.85B0.15.
Unlike previous studies in the literature where arc-melting was used for synthesis, here the induction melting process was used to obtain the materials studied.
2. Materials and Methods
Polycrystalline samples of (Mn1−xMex)5(Ge1−yOey)3 (Me = Co, Cr; Oe = B, Al; x, y = 0.05) alloys were synthesized by induction melting of pure (i.e., Mn, 99.9%; Ge, 99.9999%; Co, 99.998%; Cr, 99.99%; B, 99.999%; Al, 99.999%) constituent elements in a water-cooled copper hearth under a high-purity argon atmosphere. Pellets of approximately 2 g each were remelted and flipped several (at least five) times to ensure homogeneity. No additional Mn was added to the initially calculated mass. However, Mn was remelted before adding it to the batch to improve its quality. The total mass loss for each sample was less than 0.1%. Afterwards, no further heat treatment was applied. The density of the samples was determined by the Archimedes method at room temperature. To measure the mass of the samples, a Radwag (Radom, Poland) XA 110.4Y.A electronic scale was used.
The phase purity of all the compounds was checked by Rietveld analysis of the X-ray diffraction (XRD) patterns collected at room temperature. A diffractometer with a Bragg–Brentano configuration equipped with a Cu-Kα radiation source was used. The structure refinement was carried out by employing the program FullProf (version 6.30) [59].
Scanning electron microscopy (SEM) images and the elemental compositions were obtained using an FEI Nova NanoSEM 650 with an energy-dispersive spectroscopy (EDS) attachment. An electron energy of 30 keV was used for imaging and excitation of the characteristic radiation of the elements. Analysis of the EDS data was performed with the license software delivered with the instrument using the P/B ZAF (standardless) method.
Magnetic field and temperature dependent magnetization data were collected using a Physical Property Measurement System (PPMS, Quantum Design, San Diego, CA, USA) equipped with a vibrating sample magnetometer (VSM). Measurements of magnetization as a function of temperature were made in two modes. First, the zero-field cooling (ZFC) mode was used, i.e., the sample was first cooled down to 2 K without magnetic field and then the measurement was performed during heating. Next, the field cooling (FC) mode was employed in which the sample was cooled in a constant non-zero magnetic field down to the lowest temperatures while the magnetization measurement was performed. Both measurements were made in the temperature range from 2 to 400 K.
Measurements of the specific heat in the temperature range from 260 to 380 K were made using the 2τ relaxation method with the heat capacity option of the PPMS. Samples of ~10 mg were attached to the platform with Apiezone H.
3. Results and Discussion
First, the structures of the obtained samples were determined. The room temperature XRD patterns for all studied (Mn1−xMex)5(Ge1−yOey)3 alloys are presented in Figure 1. The Rietveld refinement of the powder XRD patterns of all the compounds showed a hexagonal crystal structure with a space group P63/mcm (No. 193). In this structure, Mn atoms occupied two positions, 4d (1/3, 2/3, 0) and 6g (x1, 0, 1/4), whereas Ge atoms occupied only the 6g (x2, 0, 1/4) sites [60]. Exemplary results of the Rietveld analysis are shown in Figure 1a,b for selected samples (modified by B and Co substitution). The lattice parameters estimated for all of the compounds from the refinement are shown in Table 1. It was found that the lattice parameters values did not change significantly, and for the Co substitution, they were comparable with those from the literature [42,44,45]. In addition to the main diffraction peaks originating from the hexagonal structure, some small peaks (marked by the star symbol in Figure 1) assigned to minor unknown impurity phases can be observed for some of the samples.
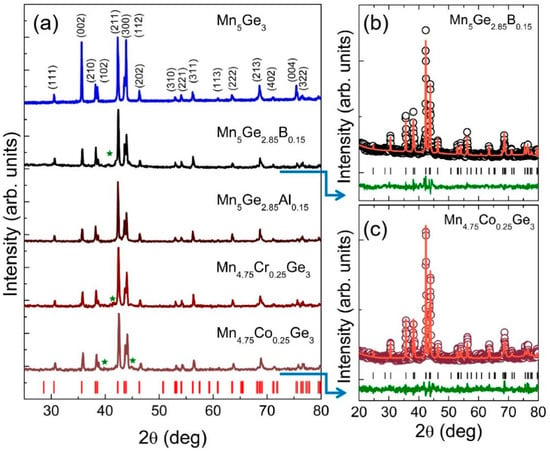
Figure 1.
(a) XRD data obtained at room temperature for all of the studied (Mn1−xMex)5(Ge1−yOey)3 alloys. Vertical ticks at the bottom indicate the Bragg maxima positions for Mn5Ge3 labeled with the Miller indices at the top. Stars mark the peaks due to the impurity phases. Panels (b,c) show examples of Rietveld refinement for the selected Mn5Ge2.85B0.15 and Mn4.75Co0.25Ge3 alloys, respectively. The solid line through the experimental points represents a fitted model. The difference between the experimental and theoretical curves is represented by the bottom solid green curve.

Table 1.
The estimated chemical composition, the lattice parameters (a, c) values, the unit-cell volume (V), the average crystallite size (D), and the theoretical (dt) and experimental (d) densities for the (Mn1−xMex)5(Ge1−yOey)3 alloys.
As shown previously, the average size of the crystallites, D, can strongly influence the magnetic and magnetocaloric properties of different materials [36,61,62]. Therefore, for comparative studies, it is preferred to study materials with crystallites of similar size. D was calculated from the standard Scherrer formula: D = 0.89λ/Bcosθd, where λ is the X-ray wavelength, B is the full width at half maximum of a peak, and θd is the Bragg angle [63]. The values of D for the (Mn1−xMex)5(Ge1−yOey)3 alloys are listed in Table 1. It turns out that for our samples, the values of D were very similar and close to 50 nm.
The experimentally determined density (d) values were in good agreement with those obtained from the diffractogram analysis (see Table 1). The observed differences between the experimental and theoretical values resulted from the imperfections of the actual samples in the form of cracks or voids and were less than 6%. Density measurements allowed for the determination of the entropy change values in volumetric units (mJ cm−3 K−1), which is more meaningful for design and construction purposes [64,65].
The EDS measurements were carried out at different spots along the samples. The refined average compositions for all the obtained samples are summarized in Table 1. The chemical composition ratio was in good agreement with the nominal one.
The temperature dependencies of the magnetic susceptibilities of these compounds in the ZFC mode and in the field of 0.1 T are shown in Figure 2. The magnetic transition temperatures (TC) for each alloy were determined from the derivative of the ZFC magnetization (Figure 3a) and are given in Table 2. The TC values for all tested alloys were smaller than for the parent compound (TC = 295(1) K), except for the sample containing B, for which a 3 K increase in TC was observed. The largest reduction in TC was seen for the samples with Co (281(1) K) and Cr (288(1) (K)). The TC values are in good agreement with those presented in the literature (see Table 5). In addition, for the sample (Mn0.95Co0.05)5Ge3, the obtained TC value was higher than that obtained by Kim et al. (TC = 273 K) [42] and by Kang et al. (TC = 266 K) [45]. These results suggest that the magnetic properties of Mn5Ge3 are sensitive to the synthesis conditions.
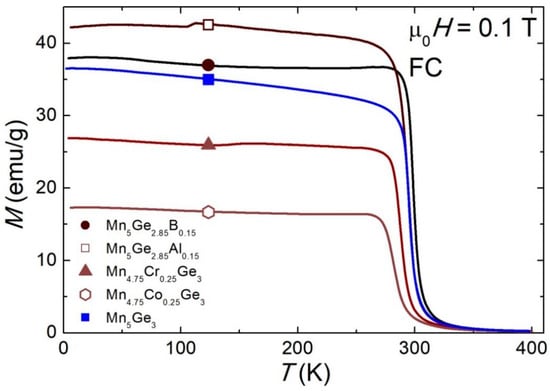
Figure 2.
Temperature dependence of the field cooled (FC) magnetization of the (Mn1−xMex)5(Ge1−yOey)3 alloys in the magnetic field of 0.1 T.
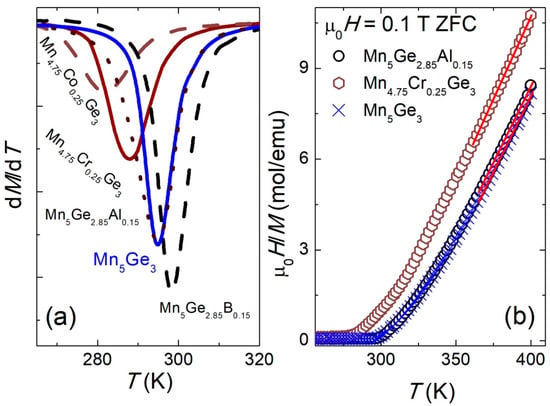
Figure 3.
(a) The derivative of magnetization (dM/dT) versus temperature; (b) temperature dependence of μ0H/M between 260 and 400 K. The solid lines represent the fits of the Curie–Weiss law to the data between 360 and 400 K for selected compositions of the (Mn1−xMex)5(Ge1−yOey)3 series.

Table 2.
The magnetic properties of the (Mn1−xMex)5(Ge1−yOey)3 alloys: values of the magnetic Curie temperature (TC), the paramagnetic Curie–Weiss temperature (ΘCW), the effective magnetic moments (μeff) per Mn atom, and the saturation magnetization (σS) per Mn atom at 4 K.
The inverse susceptibility data (Figure 3b) were fitted with the Curie–Weiss (CW) law:
where μeff is the effective magnetic moment, and ΘCW is the paramagnetic Curie–Weiss temperature. The effective magnetic moment per Mn ion was calculated and is provided in Table 2. Figure 3b indicates that above the ordering temperatures, the CW law was well obeyed. The values of μeff and ΘCW estimated from the CW fit are also given in Table 2. For all alloys, the value of μeff was practically the same, approximately 2 μB. This value, as in many other materials containing Mn, was lower than the theoretical value for Mn2+ ion (5.92 μB) due to the influence of the crystal field [66]. For the pure Mn5Ge3, the value of μμeff was in good agreement with previous measurements [51,67]. The performed chemical modifications led to a small decrease in the μeff value compared to that of the pure sample. Moreover, the obtained μeff values were typical of other Mn-based alloys and compounds [68,69,70]. It was also observed that the used substitutions resulted in the lowering of ΘCW. Similar magnetic behavior and changes in TC and magnetization were found for other Mn5Ge3-based alloys [41,43,71].
Figure 4 shows the field dependence of the magnetization σ(μ0H) measured at T = 4 K. The values of the characteristic parameters for the starting compound Mn5Ge3, such as saturation magnetization (σS = 2.60(8) μB/Mn), saturation field (μ0HS = 1.5(1) T), and coercivity field (μ0HC~10 mT), are in good agreement with literature values [72]. The value of σS decreased as a result of all the chemical composition changes made (see Table 2), consistent with results reported earlier [41,43,49,52]. On the other hand, a small amount of B or Al in the place of Ge reduced μ0HS to 1.2(1) T, making these samples easier to magnetize. From the inset of Figure 4, it is evident that after the chemical modification no hysteresis loop appeared in the samples studied.
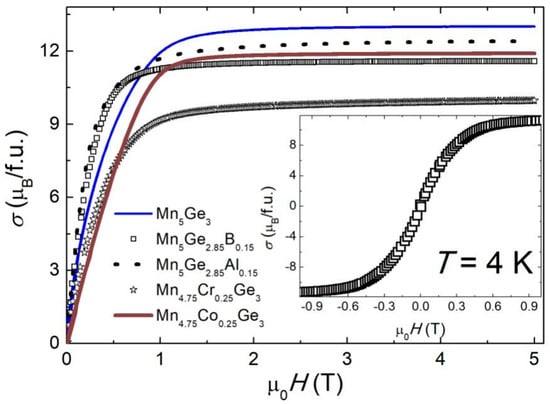
Figure 4.
The first quadrant of the magnetization loop for (Mn1−xMex)5(Ge1−yOey)3 alloys at 4 K. Inset: close-up of the weak-field range for the sample with B.
Figure 5 shows the Arrott plots [73] for the alloys with Co and Cr as examples. The positive slopes of the Arrott plots indicate that the paramagnetic (PM) to ferromagnetic (FM) transitions were of the second order.
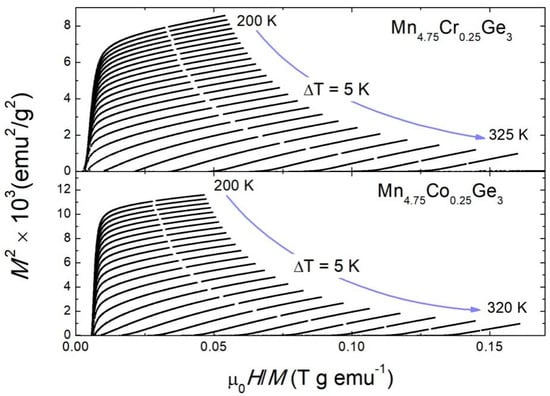
Figure 5.
The Arrott plots, M2 vs. μ0H/M, measured in the temperature range around TC for the selected samples.
To calculate the isothermal entropy change, ∆Sm, the standard Maxwell equation was used [3,5,74]:
The temperature dependencies of the ∆Sm calculated from M(μ0H) for different samples are presented in Figure 6. For all materials, ∆Sm(T) showed a negative value and the plot of this dependence took the shape of a symmetrical peak located at TC. Such properties of the ∆Sm(T) curve are typical of materials showing a second-order phase transition from the PM to the FM state, which is in line with the analysis of the Arrott plots. The Mn5Ge3 parent compound showed the highest value of |∆Sm| for a magnetic field change of 5 T as |∆Sm|MAX = 7.1(1) J kg−1 K−1 at 300(1) K. For the remaining materials, the |∆Sm|MAX value was lower (see Table 3). The greatest reduction was observed for the sample with Cr, for which the value of |∆Sm|MAX decreased by 32% compared to that of the starting material. On the other hand, for the Al sample, the |∆Sm|MAX value was only 4% lower than that of Mn5Ge3. The temperature at which the |∆Sm|MAX occurred also shifted towards lower values for modified materials. The exception was the sample with B for which the temperature of |∆Sm|MAX (Tmax = 302(1) K) was higher than for the pure compound Mn5Ge3, as the TC.
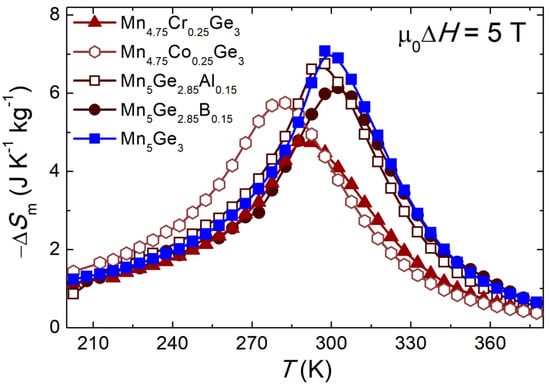
Figure 6.
The entropy change ∆Sm vs. temperature for a magnetic field change μ0∆H = 5 T for the (Mn1−xMex)5(Ge1−yOey)3 alloys. The lines in the figure are a guide for the eye.

Table 3.
Magnetocaloric performance of the (Mn1−xMex)5(Ge1−yOey)3 alloys: the maximum entropy change (|∆Sm|MAX) in mass (J kg−1 K−1) and volumetric (mJ cm−3 K−1) units, the adiabatic temperature change (ΔTad), the relative cooling power (RCP), and the temperature-averaged entropy change (TEC) for temperature lifts, ΔTlift = 3, 5, and 10 K. The values of all the parameters were collected for different values of the magnetic field change (μ0∆H).
We also calculated the relative cooling power (RCP) according to the equation RCP = |∆Sm|MAX × ∆TFWHM, where ∆TFWHM is the full-width at half-maximum of ∆Sm. RCP determines the amount of heat that can be transferred between cold and hot reservoirs and is one of the parameters determining the performance of magnetocaloric materials [1]. As with the |∆Sm|MAX value, the materials after the chemical modification showed lower RCP values than the original compound (see Table 3). This was mainly due to the lower |∆Sm|MAX value of these materials.
The RCP value is easy to calculate, which is why it is often reported in publications and makes it easier to compare the performance of individual magnetocaloric materials. However, as it is determined for a wide range of temperatures, it is of little use in the construction of specific devices. Therefore, another magnetocaloric parameter called temperature averaged entropy change (TEC) has been proposed [75]. The value of the TEC was calculated using the formula [75]:
where ΔTlift and Tmid denote the temperature lift and averaged temperature, respectively. The values of TEC for ΔTlift equal to 3, 5, and 10 K for the studied materials are collected in Table 3. For individual materials, the TEC values were close to the maximum |∆Sm|MAX value for a given value of μ0∆H. This behavior is typical of materials with a second-order phase transition [75].
The dependencies of |∆Sm|MAX, RCP, and TEC(5) on the magnetic field change μ0∆H are plotted in Figure 7. From these graphs, one can read the value of the magnetocaloric parameters for any value of μ0∆H. For all parameters, we observed the power-type dependence ~μ0∆Hn. From the fitting of the |∆Sm|MAX and RCP data, the values of the critical exponents could be determined with the following relations: |∆Sm|MAX(μ0∆H) ~μ0∆H(1+(1/δ)(1−1/β)) and RCP(μ0∆H) ~μ0∆H(1+1/δ) [76]. At first, from the relation RCP(μ0∆H), we determined the value of δ = 1/(n − 1). Then, using the obtained value of δ and the parameter of the fit determined from the relation |∆Sm|MAX(μ0∆H) ~μ0∆Hn, the value of β was calculated according to the formula β = 1/(1 − δ(n − 1)). The obtained exponents β, δ, and n (for |∆Sm|MAX(μ0∆H)) and their expected values based on the relevant theoretical models are collected in Table 4. For Mn5(Ge0.95B0.05)3, Mn5(Ge0.95Al0.05)3, and (Mn0.95Co0.05)5Ge3, the obtained values of n and δ were closest to the 3D Heisenberg model, while for the Mn5Ge3 and (Mn0.95Cr0.05)5Ge3 alloys, they were closest to the mean-field model [77]. For TEC(5), the values of the critical exponent were very similar to those obtained for |∆Sm|MAX and equal to 0.72(2), 0.67(2), 0.72(2), 0.75(2), and 0.86(3) for Mn5Ge3, Mn5Ge2.85B0.15, Mn5Ge2.85Al0.15, Mn4.75Cr0.25Ge3, and Mn4.75Co0.25Ge3, respectively.
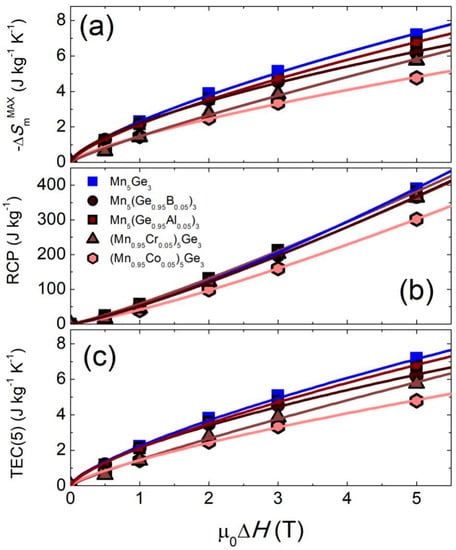
Figure 7.
(a) The curves of ∆Sm vs. μ0∆H; (b) RCP vs. μ0∆H; (c) TEC(5) vs. μ0∆H for the (Mn1−xMex)5(Ge1−yOey)3 alloys. The lines show the results of the fit with the ~μ0∆Hn-type dependency, where n is a critical exponent.

Table 4.
The critical exponent values β, δ, and n for the (Mn1−xMex)5(Ge1−yOey)3 alloys.
Table 3 summarizes the magnetocaloric properties of all the studied alloys. No enhancement of the magnetocaloric effect was observed for any of the samples tested when the chemical composition of the Mn5Ge3 was modified by 5%.
To gain more information about the magnetocaloric properties of the (Mn1−xMex)5(Ge1−yOey)3 alloys, the phenomenological universal curve can be constructed by normalizing the entropy change to ∆S’ = ∆Sm/∆SmMAX and rescaling the temperature axis below and above TC:
where Tr1 and Tr2 are the temperatures at which ∆Sm = ∆SmMAX/2 [76]. Figure 8 shows the θ dependence of ΔS’ for a magnetic field change of 5 T. The peaks of the curves collapsed onto the same universal curve, which is associated with the FM ordering transition of the second order and reveals a universal behavior of the (Mn1−xMex)5(Ge1−yOey)3 alloys. Similar results have been obtained in other studies [37,38].
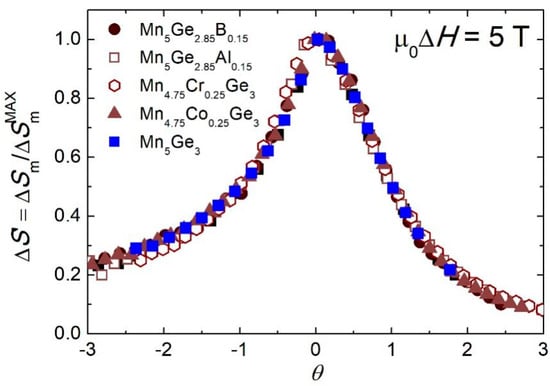
Figure 8.
Magnetocaloric universal curves of the (Mn1−xMex)5(Ge1−yOey)3 alloys for a magnetic field change of 5 T.
Additionally, the specific heat (Cp) data (Figure 9) were used to calculate the adiabatic temperature change ∆Tad = −∆Sm × T/Cp [78]. For this purpose, the maximum value of −∆Sm and the Cp value at TC were used. The obtained values of the magnetocaloric parameters are summarized in Table 3. For all samples, the ∆Tad value fluctuated around 1 K for μ0∆H = 1 T. For the samples with Al and B, the ∆Tad value was slightly higher (by ~0.1 K) than for pure Mn5Ge3, but the difference was within the estimated measurement error. For the samples containing Cr and Co, the values of ∆Tad were clearly lower but in line with previous results of direct measurements by Kang et al. [45]. Thus, for all of the abovementioned chemical modifications, the decrease in the ∆Tad value was due to the blurring of the magnetic transition and lower magnetic entropy.
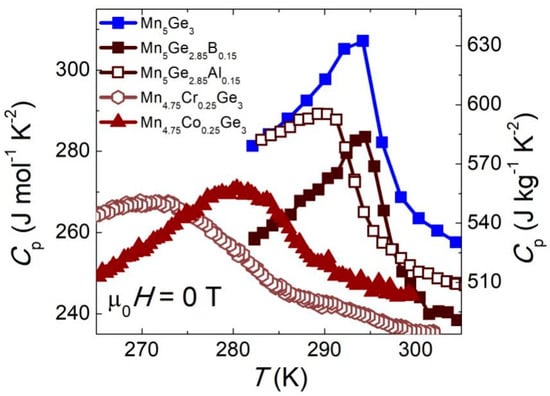
Figure 9.
Specific heat vs. temperature near the phase transition of the studied (Mn1−xMex)5(Ge1−yOey)3 samples. The lines in the figure are a guide for the eye.
For some composites, an enhancement of the magnetocaloric properties was observed [79]. Therefore, we calculated the magnetic entropy change for an exemplary composite according to the equation: ∆Smcomp(T) = (1 − z)∆SmI(T) + z∆SmII(T), where ∆SmI(T) and ∆SmII(T) represent the experimental data for the composite components. In Figure 10, the calculated result (for selected z = 0.4 value) is compared with the experimental data for the Mn5Ge3 and (Mn0.95Co0.05)5Ge3 samples. Although the maximum value of ∆Sm was reduced to ~5 J kg−1 K−1, the composite sample showed a broad table-like magnetocaloric effect in a wide temperature range. Therefore, the RCP value was enhanced in this case up to 405(9) J kg−1, and the magnetocaloric properties were improved.
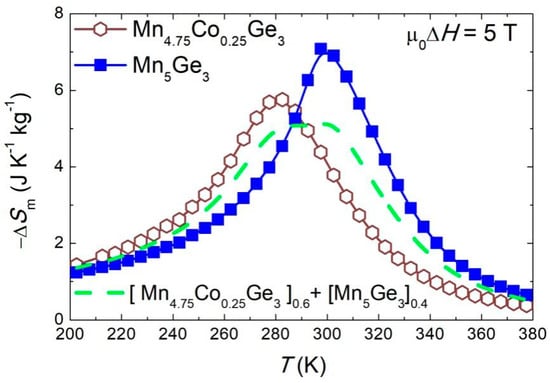
Figure 10.
The calculated temperature dependence of the magnetic entropy change ∆Sm for the ((Mn0.095Co0.05)5Ge3)0.6(Mn5Ge3)0.4 composite material (dashed line) compared with the results for its constituent compounds. The results are presented for a magnetic field change of 5 T. The solid lines in the figure are a guide for the eye.
Finally, we summarize the present and literature data for the Mn5Ge3 and Mn5Ge3-based alloys. In Table 5, the values of the ordering temperature (TC), the maximum entropy change (|∆Sm|MAX), and the relative cooling power (RCP) for a magnetic field change of 1 T and 2 T are collected. We chose the |∆Sm|MAX and RCP values for a field changes of 1 T and 2 T because they are most often presented in the publications and are the closest to the values of the magnetic field changes that can be used in actual devices. In addition, Figure 11 shows a graph with the |∆Sm|MAX values (for a magnetic field change of 2 T) as a function of TC for various samples of the Mn5Ge3 compound and its alloys. The data were divided into groups according to the type of element modifying the chemical composition. This graph clearly shows that by using an appropriate modification of the chemical composition, it is possible to significantly expand the operating range of the magnetocaloric material based on Mn5Ge3; a practically constant value of |∆Sm|MAX ≈ 3.5 J kg−1 K−1 can be achieved in the range from 280 to 303 K. The graph also shows a clear trend of changes in the magnetocaloric properties due to the modification of the chemical composition. The points are arranged in a convex arc that has an extremity that is determined by the pure Mn5Ge3 compound. By substituting different chemical elements, we can modify the TC. For example, the addition of Ni in the place of Mn leads to a lower TC, while the addition of Sb in place of Ge can increase the TC. The second important conclusion is that the |∆Sm|MAX value did not increase as a result of the known chemical composition modifications. In practice, the|∆Sm|MAX value for Mn5Ge3-based alloys is always lower than for the parent compound. In a few cases, the observed increased |∆Sm|MAX value may result from measurement errors not included in the calculation. The collected data also show how the parameter values are distributed for Mn5Ge3 samples obtained by different authors. The TC values range between 293 and 300 K, |∆Sm|MAX values (for μ0∆H = 2 T) range from 3.6 to 4.1 J kg−1 K−1, and RCP values (for μ0∆H = 2 T) range from 100 to 145 J kg−1. These differences result from different microstructural properties of different samples such as slightly different stoichiometries, different crystallites size, and different shapes of the sample for magnetic measurements. Figure 11 can be used as a signpost for further research on the improvement of the magnetocaloric properties of the Mn5Ge3 compound in terms of chemical composition modification.

Table 5.
The ordering temperature (TC), the maximum entropy change (|∆Sm|MAX), and the relative cooling power (RCP) for a 1 T and 2 T magnetic field change for Mn5Ge3 and Mn5Ge3-based alloys.
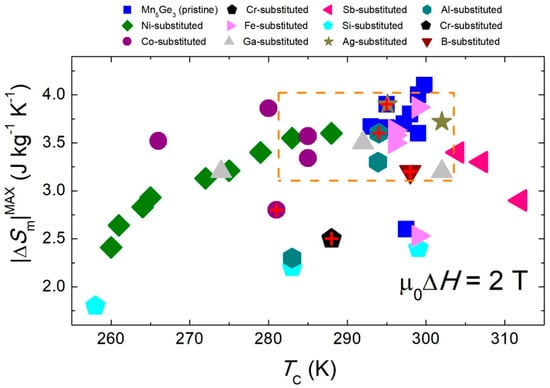
Figure 11.
Maximum values of magnetic entropy change |∆Sm|MAX for different samples of Mn5Ge3 and Mn5Ge3-based alloys for a magnetic field change of 2 T taken from the literature (see Table 4). In the graph, the data for Mn5Ge3-based alloys are grouped according to the type of the substituted chemical element. The values obtained for the samples of the present work are marked with red crosses. The symbols within the rectangle correspond to the samples with an almost constant |∆Sm|MAX value in a wide temperature range.
4. Conclusions
In this work, the effect of chemical composition modification on the magnetocaloric properties of Mn5Ge3 was investigated. The following samples were prepared by induction melting: Mn5Ge3, Mn5(Ge0.95B0.05)3, Mn5(Ge0.95Al0.05)3, (Mn0.95Cr0.05)5Ge3, and (Mn0.95Co0.05)5Ge3. The X-ray diffraction measurements revealed that the tested materials crystallized in the same hexagonal crystal structure (space group P63/mcm, No. 193) as the parent Mn5Ge3 compound. According to the magnetic measurements, all the studied compositions show soft ferromagnetic properties at room temperature. Modification of the chemical composition changed the Curie temperature from TC = 295(1) K for the starting compound to 298(1), 294(1), 288(1), and 281(1) K for the alloys with 5% of B, Al, Cr, and Co, respectively. The magnetic entropy change, characterizing the magnetocaloric effect, was reduced from −∆Sm = 7.1(1) J kg−1 K−1 for the starting material to 6.2(1), 6.8(1), 4.8(1), and 5.8(1) J kg−1 K−1 for the alloys with B, Al, Cr, and Co substitution, respectively. For the samples with Al and B, the adiabatic temperature change ∆Tad value was practically the same as for the parent compound, i.e., 1.1(1) K (for a magnetic field change of 1 T). However, for the samples with Co and Cr, the value of ∆Tad decreased by 27%, i.e., down to 0.8(1) K. For all the performed chemical composition modifications, the RCP values were also reduced. Therefore, there was no enhancement of the magnetocaloric properties in the studied materials. The prepared samples fit well with the general trend of changes in the magnetocaloric properties of the Mn5Ge3 compound as a result of the modification of its chemical composition. Analysis of the literature data showed that appropriate modification of the chemical composition makes it possible to obtain a set of alloys with very similar magnetocaloric properties over a wide temperature range (i.e., 280–303 K). Therefore, a promising track to improve the MCE performance seems to be preparation of composites. An exemplary simulation of the ((Mn0.095Co0.05)5Ge3)0.6(Mn5Ge3)0.4 composite based on the experimentally measured components built a broad table-like magnetocaloric effect that improved the relative cooling power by 4%.
Author Contributions
Conceptualization, K.S. and T.T.; methodology, K.S., K.U., P.S. and H.G.; validation, K.S., K.U., P.S. and T.T.; formal analysis, K.S.; investigation, K.S., K.U., P.S. and H.G.; resources, T.T.; data curation, K.S.; writing—original draft preparation, K.S.; writing—review and editing, K.S., K.U., H.G., P.S. and T.T.; visualization, K.S.; supervision, T.T.; project administration, K.S. and T.T.; funding acquisition, T.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors thank Daria Szewczyk for the technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Franco, V.; Blázquez, J.S.; Ingale, B.; Conde, A. The Magnetocaloric Effect and Magnetic Refrigeration Near Room Temperature: Materials and Models. Annu. Rev. Mater. Res. 2012, 42, 305–342. [Google Scholar] [CrossRef] [Green Version]
- Barclay, J.A. Magnetic Refrigeration: A Review of a Developing Technology. In Advances in Cryogenic Engineering; Fast, R.W., Ed.; A Cryogenic Engineering Conference Publication; Springer: Boston, MA, USA, 1988; Volume 33, pp. 719–731. ISBN 978-1-4613-9876-9. [Google Scholar]
- Franco, V.; Blázquez, J.S.; Ipus, J.J.; Law, J.Y.; Moreno-Ramírez, L.M.; Conde, A. Magnetocaloric Effect: From Materials Research to Refrigeration Devices. Prog. Mater. Sci. 2018, 93, 112–232. [Google Scholar] [CrossRef]
- Gottschall, T.; Skokov, K.P.; Fries, M.; Taubel, A.; Radulov, I.; Scheibel, F.; Benke, D.; Riegg, S.; Gutfleisch, O. Making a Cool Choice: The Materials Library of Magnetic Refrigeration. Adv. Energy Mater. 2019, 9, 1901322. [Google Scholar] [CrossRef] [Green Version]
- Dzekan, D.; Waske, A.; Nielsch, K.; Fähler, S. Efficient and Affordable Thermomagnetic Materials for Harvesting Low Grade Waste Heat. APL Mater. 2021, 9, 011105. [Google Scholar] [CrossRef]
- Brown, G.V. Magnetic Heat Pumping near Room Temperature. J. Appl. Phys. 1976, 47, 3673–3680. [Google Scholar] [CrossRef] [Green Version]
- Synoradzki, K.; Nowotny, P.; Skokowski, P.; Toliński, T. Magnetocaloric Effect in Gd5(Si,Ge)4 Based Alloys and Composites. J. Rare Earths 2019, 37, 1218–1223. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant Magnetocaloric Effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494–4497. [Google Scholar] [CrossRef]
- Provenzano, V.; Shapiro, A.J.; Shull, R.D. Reduction of Hysteresis Losses in the Magnetic Refrigerant Gd5Ge2Si2 by the Addition of Iron. Nature 2004, 429, 853–857. [Google Scholar] [CrossRef]
- Annaorazov, M.P.; Nikitin, S.A.; Tyurin, A.L.; Asatryan, K.A.; Dovletov, A.K. Anomalously High Entropy Change in FeRh Alloy. J. Appl. Phys. 1996, 79, 1689–1695. [Google Scholar] [CrossRef]
- Chirkova, A.; Skokov, K.P.; Schultz, L.; Baranov, N.V.; Gutfleisch, O.; Woodcock, T.G. Giant Adiabatic Temperature Change in FeRh Alloys Evidenced by Direct Measurements under Cyclic Conditions. Acta Mater. 2016, 106, 15–21. [Google Scholar] [CrossRef]
- Gozdur, R.; Gębara, P.; Chwastek, K. A Study of Temperature-Dependent Hysteresis Curves for a Magnetocaloric Composite Based on La(Fe, Mn, Si)13-H Type Alloys. Energies 2020, 13, 1491. [Google Scholar] [CrossRef] [Green Version]
- Gębara, P.; Pawlik, P. Broadening of Temperature Working Range in Magnetocaloric La(Fe,Co,Si)13-Based Multicomposite. J. Magn. Magn. Mater. 2017, 442, 145–151. [Google Scholar] [CrossRef]
- Pathak, A.K.; Khan, M.; Dubenko, I.; Stadler, S.; Ali, N. Large Magnetic Entropy Change in Ni50Mn50−xInx Heusler Alloys. Appl. Phys. Lett. 2007, 90, 262504. [Google Scholar] [CrossRef] [Green Version]
- Planes, A.; Mañosa, L.; Acet, M. Magnetocaloric Effect and Its Relation to Shape-Memory Properties in Ferromagnetic Heusler Alloys. J. Phys. Condens. Matter 2009, 21, 233201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tegus, O.; Brück, E.; Buschow, K.H.J.; de Boer, F.R. Transition-Metal-Based Magnetic Refrigerants for Room-Temperature Applications. Nature 2002, 415, 150–152. [Google Scholar] [CrossRef]
- Wada, H.; Tanabe, Y. Giant Magnetocaloric Effect of MnAs1−xSbx. Appl. Phys. Lett. 2001, 79, 3302–3304. [Google Scholar] [CrossRef]
- Zhang, H.; Gimaev, R.; Kovalev, B.; Kamilov, K.; Zverev, V.; Tishin, A. Review on the Materials and Devices for Magnetic Refrigeration in the Temperature Range of Nitrogen and Hydrogen Liquefaction. Phys. B Condens. Matter 2019, 558, 65–73. [Google Scholar] [CrossRef]
- Ćwik, J.; Koshkid’ko, Y.; Nenkov, K.; Mikhailova, A.; Małecka, M.; Romanova, T.; Kolchugina, N.; de Oliveira, N.A. Experimental and Theoretical Analysis of Magnetocaloric Behavior of Dy1−xErxNi2 Intermetallics ( x = 0.25, 0.5, 0.75 ) and Their Composites for Low-Temperature Refrigerators Performing an Ericsson Cycle. Phys. Rev. B 2021, 103, 214429. [Google Scholar] [CrossRef]
- Ćwik, J.; Koshkid’ko, Y.; Małecka, M.; Weise, B.; Krautz, M.; Mikhailova, A.; Kolchugina, N. Magnetocaloric Prospects of Mutual Substitutions of Rare-Earth Elements in Pseudobinary Tb1−xHoxNi2 Compositions (x = 0.25–0.75). J. Alloy. Compd. 2021, 886, 161295. [Google Scholar] [CrossRef]
- Andreenko, A.S.; Belov, K.P.; Nikitin, S.A.; Tishin, A.M. Magnetocaloric Effects in Rare-Earth Magnetic Materials. Sov. Phys. Uspekhi 1989, 32, 649–664. [Google Scholar] [CrossRef]
- Kuz’min, M.D.; Tishin, A.M. Magnetic Refrigerants for the 4.2-20 K Region: Garnets or Perovskites? J. Phys. D Appl. Phys. 1991, 24, 2039–2044. [Google Scholar] [CrossRef]
- Gschneidner, K.A.; Pecharsky, V.K. Rare Earths and Magnetic Refrigeration. J. Rare Earths 2006, 24, 641–647. [Google Scholar] [CrossRef]
- Li, L.; Yan, M. Recent Progresses in Exploring the Rare Earth Based Intermetallic Compounds for Cryogenic Magnetic Refrigeration. J. Alloy. Compd. 2020, 823, 153810. [Google Scholar] [CrossRef]
- Brück, E.; Tegus, O.; Cam Thanh, D.T.; Trung, N.T.; Buschow, K.H.J. A Review on Mn Based Materials for Magnetic Refrigeration: Structure and Properties. Int. J. Refrig. 2008, 31, 763–770. [Google Scholar] [CrossRef]
- Phan, M.-H.; Yu, S.-C. Review of the Magnetocaloric Effect in Manganite Materials. J. Magn. Magn. Mater. 2007, 308, 325–340. [Google Scholar] [CrossRef]
- Dubenko, I.; Khan, M.; Pathak, A.K.; Gautam, B.R.; Stadler, S.; Ali, N. Magnetocaloric Effects in Ni–Mn–X Based Heusler Alloys with X = Ga, Sb, In. J. Magn. Magn. Mater. 2009, 321, 754–757. [Google Scholar] [CrossRef]
- Chaudhary, V.; Chen, X.; Ramanujan, R.V. Iron and Manganese Based Magnetocaloric Materials for near Room Temperature Thermal Management. Prog. Mater. Sci. 2019, 100, 64–98. [Google Scholar] [CrossRef]
- Wrzeciono, A.; Gemperle, R. Abhängigkeit der Bereichsstruktur in Mn5Ge3 von der Kristalldicke. Phys. Status Solidi (B) 1966, 14, 491–497. [Google Scholar] [CrossRef]
- Panguluri, R.P.; Zeng, C.; Weitering, H.H.; Sullivan, J.M.; Erwin, S.C.; Nadgorny, B. Spin Polarization and Electronic Structure of Ferromagnetic Mn5Ge3 Epilayers. Phys. Status Solidi B 2005, 242, R67–R69. [Google Scholar] [CrossRef] [Green Version]
- Olive-Mendez, S.; Spiesser, A.; Michez, L.A.; Le Thanh, V.; Glachant, A.; Derrien, J.; Devillers, T.; Barski, A.; Jamet, M. Epitaxial Growth of Mn5Ge3/Ge(111) Heterostructures for Spin Injection. Thin Solid Film. 2008, 517, 191–196. [Google Scholar] [CrossRef]
- Ndiaye, W.; Richter, M.C.; Heckmann, O.; De Padova, P.; Mariot, J.-M.; Stroppa, A.; Picozzi, S.; Wang, W.; Taleb-Ibrahimi, A.; Le Fèvre, P.; et al. Bulk Electronic Structure of Mn5Ge3/Ge(111) Films by Angle-Resolved Photoemission Spectroscopy. Phys. Rev. B 2013, 87, 165137. [Google Scholar] [CrossRef]
- Tang, J.; Wang, C.-Y.; Chang, L.-T.; Fan, Y.; Nie, T.; Chan, M.; Jiang, W.; Chen, Y.-T.; Yang, H.-J.; Tuan, H.-Y.; et al. Electrical Spin Injection and Detection in Mn5Ge3/Ge/Mn5Ge3 Nanowire Transistors. Nano Lett. 2013, 13, 4036–4043. [Google Scholar] [CrossRef] [PubMed]
- Spiesser, A.; Saito, H.; Jansen, R.; Yuasa, S.; Ando, K. Large Spin Accumulation Voltages in Epitaxial Mn5Ge3 Contacts on Ge without an Oxide Tunnel Barrier. Phys. Rev. B 2014, 90, 205213. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Yuan, Y.; Birowska, M.; Zhang, C.; Cao, L.; Wang, M.; Grenzer, J.; Kriegner, D.; Doležal, P.; Zeng, Y.-J.; et al. Strain-Induced Switching between Noncollinear and Collinear Spin Configuration in Magnetic Mn5Ge3 Films. Phys. Rev. B 2021, 104, 064416. [Google Scholar] [CrossRef]
- Toliński, T.; Synoradzki, K. Specific Heat and Magnetocaloric Effect of the Mn5Ge3 Ferromagnet. Intermetallics 2014, 47, 1–5. [Google Scholar] [CrossRef]
- Zheng, T.F.; Shi, Y.G.; Hu, C.C.; Fan, J.Y.; Shi, D.N.; Tang, S.L.; Du, Y.W. Magnetocaloric Effect and Transition Order of Mn5Ge3 Ribbons. J. Magn. Magn. Mater. 2012, 324, 4102–4105. [Google Scholar] [CrossRef]
- Lalita; Rathi, A.; Pardeep; Verma, A.K.; Gahtori, B.; Gautam, A.; Pant, R.P.; Babu, P.D.; Basheed, G.A. Field Dependence of Magnetic Entropy Change in Mn5Ge3 near Room Temperature. J. Alloy. Compd. 2021, 876, 159908. [Google Scholar] [CrossRef]
- Maraytta, N.; Voigt, J.; Salazar Mejía, C.; Friese, K.; Skourski, Y.; Perßon, J.; Salman, S.M.; Brückel, T. Anisotropy of the Magnetocaloric Effect: Example of Mn5Ge3. J. Appl. Phys. 2020, 128, 103903. [Google Scholar] [CrossRef]
- Wang, S.; Fan, C.; Liu, D. Large Anisotropic Magnetocaloric Effect, Wide Operating Temperature Range, and Large Refrigeration Capacity in Single-Crystal Mn5Ge3 and Mn5Ge3/Mn3.5Fe1.5Ge3 Heterostructures. ACS Appl. Mater. Interfaces 2021, 13, 33237–33243. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, E.J.; Choi, K.; Han, W.B.; Kim, H.-S.; Yoon, C.S. Magnetocaloric Effect of Mn5+xGe3−x Alloys. J. Alloy. Compd. 2015, 620, 164–167. [Google Scholar] [CrossRef]
- Kim, Y.; Kang, K.H.; Kim, J.H.; Kim, E.J.; Choi, K.; Han, W.B.; Kim, H.-S.; Oh, Y.; Yoon, C.S. Magnetocaloric Refrigerant with Wide Operating Temperature Range Based on Mn5−xGe3(Co,Fe)x Composite. J. Alloy. Compd. 2015, 644, 464–469. [Google Scholar] [CrossRef]
- Carroll, P.; Williams, A.; Caudle, M.; Darkins, L.; Eaton, A.; Fitzgerald, B.; Knauf, B.; Rurka, M.; Shlonsky, E.; Wilson, P.; et al. Enhanced Magnetic Refrigeration Capacities in Minutely Co Doped Mn5-xCoxGe3 Compounds. Intermetallics 2017, 89, 10–15. [Google Scholar] [CrossRef]
- Kang, K.H.; Kim, J.H.; Oh, Y.; Kim, E.J.; Yoon, C.S. Critical Behavior and Magnetocaloric Effect of Mn4.75Ge3(Co, Fe)0.25 Alloys. J. Alloy. Compd. 2017, 696, 931–937. [Google Scholar] [CrossRef]
- Kang, K.H.; Kim, J.H.; Kim, J.W.; Chung, K.C.; Yoon, C.S. Direct Measurement of the Magnetocaloric Effect (ΔTad) of Mn5−x(Fe,Co)xGe3. J. Alloy. Compd. 2017, 729, 603–606. [Google Scholar] [CrossRef]
- Zhang, Q.; Du, J.; Li, Y.B.; Sun, N.K.; Cui, W.B.; Li, D.; Zhang, Z.D. Magnetic Properties and Enhanced Magnetic Refrigeration in (Mn1−xFex)5Ge3 Compounds. J. Appl. Phys. 2007, 101, 123911. [Google Scholar] [CrossRef]
- Brock, J.; Bell-Pactat, N.; Cai, H.; Dennison, T.; Fox, T.; Free, B.; Mahyub, R.; Nar, A.; Saaranen, M.; Schaeffer, T.; et al. The Effect of Fe Doping on the Magnetic and Magnetocaloric Properties of Mn5-xFexGe3. Adv. Mater. Sci. Eng. 2017, 2017, 9854184. [Google Scholar] [CrossRef] [Green Version]
- Kang, K.H.; Kim, E.J.; Kim, J.; Yoon, C.S. Mn5−xGe3Nix Refrigerant for Active Magnetic Refrigeration. J. Appl. Phys. 2020, 128, 223903. [Google Scholar] [CrossRef]
- Liu, X.B.; Altounian, Z. Magnetocaloric Effect in Mn5Ge3−xSix Pseudobinary Compounds. J. Appl. Phys. 2006, 99, 08Q101. [Google Scholar] [CrossRef]
- Zhao, F.Q.; Dagula, W.; Tegus, O.; Buschow, K.H.J. Magnetic-Entropy Change in Mn5Ge3−xSix Alloys. J. Alloy. Compd. 2006, 416, 43–45. [Google Scholar] [CrossRef]
- Xi-Bin, L.; Shao-Ying, Z.; Bao-Gen, S. Magnetic Properties and Magnetocaloric Effects of Mn5Ge3xGax. Chin. Phys. 2004, 13, 397–400. [Google Scholar] [CrossRef]
- Songlin; Dagula; Tegus, O.; Brück, E.; de Boer, F.R.; Buschow, K.H.J. Magnetic and Magnetocaloric Properties of Mn5Ge3−xSbx. J. Alloy. Compd. 2002, 337, 269–271. [Google Scholar] [CrossRef]
- Zheng, T.F.; Shi, Y.G.; Fan, J.Y.; Shi, D.N.; Tang, S.L.; Lv, L.Y.; Zhong, W. Critical Behavior and the Universal Curve for Magnetocaloric Effect in Textured Mn5Ge3−xAlx Ribbons. J. Appl. Phys. 2013, 113, 17A944. [Google Scholar] [CrossRef]
- Si, X.; Liu, Y.; Zhang, Z.; Ma, X.; Lin, J.; Luo, X.; Zhong, Y.; Si, H. Analysis of the Magnetic Transition and Magnetocaloric Effect in Mn5Ge2.9Ag0.1 Compound. J. Alloy. Compd. 2019, 795, 304–313. [Google Scholar] [CrossRef]
- Qian, Y.; Ma, X.; Si, X.; Liu, H.; Luo, X.; Lin, J.; Liu, Y. The Analysis of Magnetocaloric Effect and Magnetic Critical Behavior in Mn5Ge3−xAgx Compounds. Phys. Scr. 2020, 95, 065701. [Google Scholar] [CrossRef]
- Swathi, S.; Arun, K.; Remya, U.D.; Dzubinska, A.; Reiffers, M.; Nagalakshmi, R. Ising Critical Behavior and Room Temperature Magnetocaloric Effect in Itinerant Ferromagnetic Mn5Ge2.9Fe0.1 Compound. Intermetallics 2021, 132, 107164. [Google Scholar] [CrossRef]
- Halder, M.; Yusuf, S.M.; Nigam, A.K. Magnetocaloric Effect and Its Implementation in Critical Behavior Study of Mn4FeGe3−xSix Intermetallic Compounds. J. Appl. Phys. 2011, 110, 113915. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.W.; Yan, J.L.; Feng, E.L.; Tang, G.W.; Zhou, K.W. Effect of Fe Substitution on the Structure and Magnetocaloric Effect of Mn5−xFexGeSi2 Alloys. J. Magn. Magn. Mater. 2017, 422, 356–361. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Forsyth, J.B.; Brown, P.J. The Spatial Distribution of Magnetisation Density in Mn5Ge3. J. Phys. Condens. Matter 1990, 2, 2713–2720. [Google Scholar] [CrossRef]
- Synoradzki, K.; Kowalski, W.; Falkowski, M.; Toliński, T.; Kowalczyk, A. Magnetic Properties and Magnetocaloric Effect of DyNi4Si. Acta Phys. Pol. A 2014, 126, 162–163. [Google Scholar] [CrossRef]
- Zhang, F.; Taake, C.; Huang, B.; You, X.; Ojiyed, H.; Shen, Q.; Dugulan, I.; Caron, L.; van Dijk, N.; Brück, E. Magnetocaloric Effect in the (Mn,Fe)2(P,Si) System: From Bulk to Nano. Acta Mater. 2022, 224, 117532. [Google Scholar] [CrossRef]
- Langford, J.I.; Wilson, A.J.C. Scherrer after Sixty Years: A Survey and Some New Results in the Determination of Crystallite Size. J. Appl. Crystallogr. 1978, 11, 102–113. [Google Scholar] [CrossRef]
- Gschneidner, K.A., Jr.; Pecharsky, V.K.; Tsokol, A.O. Recent Developments in Magnetocaloric Materials. Rep. Prog. Phys. 2005, 68, 1479–1539. [Google Scholar] [CrossRef]
- Toliński, T.; Falkowski, M.; Kowalczyk, A.; Synoradzki, K. Magnetocaloric Effect in the Ternary DyCo3B2 Compound. Solid State Sci. 2011, 13, 1865–1868. [Google Scholar] [CrossRef]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-521-81614-4. [Google Scholar]
- Ciszewski, R. Magnetic Structure of the Mn5Ge3 Alloy. Phys. Status Solidi (B) 1963, 3, 1999–2004. [Google Scholar] [CrossRef]
- Synoradzki, K.; Toliński, T. Effective Mass Enhancement and Spin-Glass Behaviour in CeCu4MnyAl1−y Compounds. J. Phys. Condens. Matter 2012, 24, 136003. [Google Scholar] [CrossRef] [PubMed]
- Synoradzki, K. Spin-Glass Behavior in LaCu4Mn Compound. Acta Phys. Pol. A 2017, 131, 1024–1026. [Google Scholar] [CrossRef]
- Synoradzki, K. Magnetocaloric Effect in Spin-Glass-like GdCu4Mn Compound. J. Magn. Magn. Mater. 2022, 546, 168857. [Google Scholar] [CrossRef]
- Kang, K.H.; Oh, Y.; Kim, J.H.; Kim, E.J.; Kim, H.-S.; Yoon, C.S. Magnetocaloric Effect of Compositionally Partitioned Mn5-xGe3Nix Alloys Produced by Solid State Sintering. J. Alloy. Compd. 2016, 681, 541–546. [Google Scholar] [CrossRef]
- Kappel, G.; Fischer, G.; Jaegle, A. On the Saturation Magnetization of Mn5Ge3. Phys. Lett. A 1973, 45, 267–268. [Google Scholar] [CrossRef]
- Arrott, A. Criterion for Ferromagnetism from Observations of Magnetic Isotherms. Phys. Rev. 1957, 108, 1394–1396. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A. Magnetocaloric Effect from Indirect Measurements: Magnetization and Heat Capacity. J. Appl. Phys. 1999, 86, 565–575. [Google Scholar] [CrossRef]
- Griffith, L.D.; Mudryk, Y.; Slaughter, J.; Pecharsky, V.K. Material-Based Figure of Merit for Caloric Materials. J. Appl. Phys. 2018, 123, 034902. [Google Scholar] [CrossRef]
- Franco, V.; Blázquez, J.S.; Conde, A. Field Dependence of the Magnetocaloric Effect in Materials with a Second Order Phase Transition: A Master Curve for the Magnetic Entropy Change. Appl. Phys. Lett. 2006, 89, 222512. [Google Scholar] [CrossRef]
- Le Guillou, J.C.; Zinn-Justin, J. Critical Exponents from Field Theory. Phys. Rev. B 1980, 21, 3976–3998. [Google Scholar] [CrossRef] [Green Version]
- Zverev, V.I.; Tishin, A.M.; Kuz’min, M.D. The Maximum Possible Magnetocaloric ΔT Effect. J. Appl. Phys. 2010, 107, 043907. [Google Scholar] [CrossRef]
- Law, J.Y.; Franco, V. Magnetocaloric Composite Materials. In Encyclopedia of Materials: Composites; Elsevier: Amsterdam, The Netherlands, 2021; pp. 461–472. ISBN 978-0-12-819731-8. [Google Scholar]
- de Oliveira, R.C.; Demaille, D.; Casaretto, N.; Zheng, Y.J.; Marangolo, M.; Mosca, D.H.; Varalda, J. Magnetic and Structural Properties of Mn5+xGe3+y Thin Films as a Function of Substrate Orientation. J. Magn. Magn. Mater. 2021, 539, 168325. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).