1. Introduction
The Montreal (1987) and Kyoto (1997) protocols were designed to reduce the emission of gases depleting the ozone layer and contributing to the greenhouse effect, respectively. Consequently, alternative more efficient systems, avoiding the use of such gases, have been researched. Among them, the most relevant systems are those based on the thermoelectric (TE) or Peltier effect and those based on the the magnetocaloric (MC) effect. The former is based on the fact that, in P- and N-type semiconductors, the charge carriers, also heat carriers, move in opposite directions when a given electric current flows through them. A thermolectric cell is formed by a couple of such semiconductors connected electrically in series and thermally in parallel. The heat flows to one side of the cell when the current goes from the N to the P direction and to the opposite side if the current is reversed. Therefore, the junction cools in one case and heats if the current is inverted. This is an extremely simple conception, since the system has no moving parts, avoids the use of fluids, and can work on very small devices (e.g., electronic components) or in spacecraft. Moreover, the system can also work as a thermal electric generator when a hot source and a cold sink are available (e.g., TE generation for solar energy conversion [
1]).
The weak point of TE refrigerators is their low coefficient of performance (COP), defined as the ratio between the heat extracted from a cold source and the work performed in doing so,
. This is a consequence of three conflicting properties: a good TE material should have a high Seebeck coefficient
, high electrical conductivity
, and low thermal conductivity
(a TE couple with ideal materials with
and
has the maximum or Carnot’s
). But a high Seebeck coefficient needs a high effective mass and low carrier density (Mott’s formula), which implies low electrical conductivity. On the other hand, high
usually also implies high
(Wiedemann–Franz law), but this law is not necessarily obeyed by semiconductors and, in practical TE materials, the phonon heat conduction is more important than the electron or hole conduction. A way to reduce the phonon contribution to
is the use of semiconductors of high molar mass, such as Bi
Te
. A practical index to characterize the efficiency of a material is the figure of merit
. The maximum
of a TE refrigerator working between a cold heat source at temperature
and a hot heat sink at
is [
2].
where
corresponds to the Carnot efficiency. Today,
for Bi-doped PbSeTe/PbTe [
3], but commercial TE materials usually have
. This means, that near room temperature, at
= 300 K, and for a temperature interval of 20 K (i.e.,
= 280 K),
cannot be higher than 31% of the Carnot efficiency with the most advanced TE materials, and with commercial Peltier cells
14% of Carnot’s
at most. For revision of the TE materials, we suggest reference [
3].
On the other hand, since the discovery of the so-called “giant magnetocaloric effect” [
4], MC refrigeration has become a real alternative to traditional systems. From the thermodynamic point of view, this method is highly efficient (up to 60% Carnot efficiency [
5]), but there are also several difficulties with these systems. First, the limited temperature span that is achieved with MC materials (MCM). This is solved via regeneration, which is essentially a battery or a continuum of systems working in series, one delivering heat to the next one at a higher temperature. Second, the means of transferring heat from the cold heat source to the MCM and from this source to the hot heat sink. Thermal diodes or switches have been proposed [
6], but, in most room temperature prototypes, the heat transfer is achieved via a fluid consisting of water with anti-corrosion additives. Use of this fluid generates new problems: weak thermal contact (and then, low frequency and low cooling power), the pressure to move the fluid, viscose dissipation, thermal and fluid leakages, and so on. A review of the materials and systems for magnetocaloric refrigeration is provided in the book by Tishin and Spichkin [
5]. For a recent review, we suggest, among others [
7].
The possibility exists of combining the strengths of the TE and MC methods to produce a hybrid system. Tomc et al. [
8] and Egolf et al. [
9] proposed a combination of TE and MC methods to achieve a substantial improvement compared to use of the MC method alone. This occurs because the TE method has low efficiency for a high temperature span
, but increases strongly for low, or even negative,
, which can be supplied by the MC subsystem. As outlined in
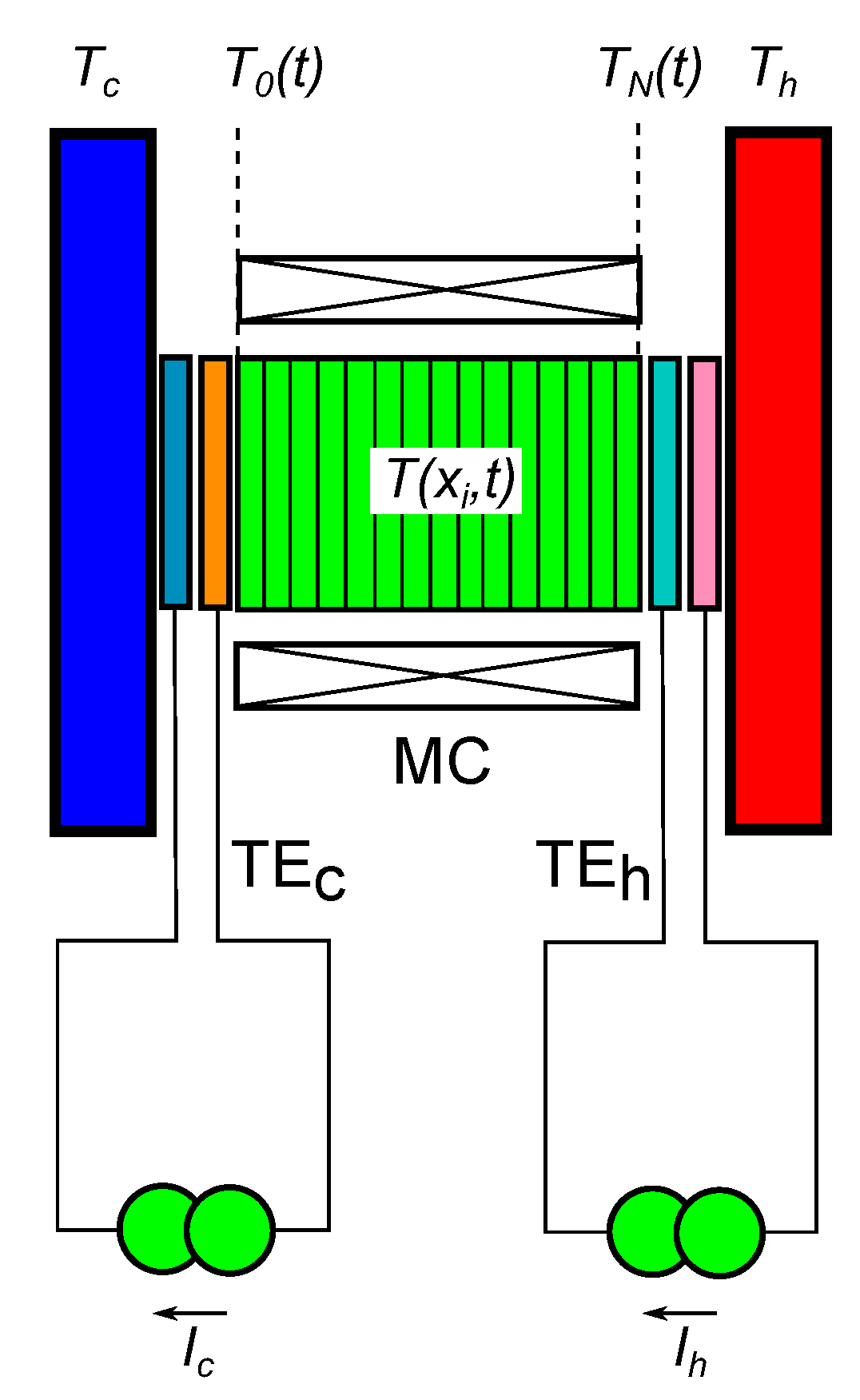
Figure 1, a TE-MC-TE sandwich is placed between a cold heat source at temperature
and a hot heat sink at
. An alternating magnetic field is applied to the MCM. When the magnetic field is on, the MCM is at its highest temperature, close to
. Then, the right-side TE cell is activated and pumps heat from the MCM to the hot sink. When the magnetic field is off, the MCM is cold, eventually being near or colder than
. The left side TE cell is then activated, transferring heat from the cold source to the MCM. De Vries and van der Meer [
10] performed a simulation of a similar system, concluding that the cooling capacity was similar to that of Peltier cells alone, but their system used a fluid as a regenerator. Moreover, it is likely that the working parameters were not optimized. Huang et al. [
11], very recently, reported a simulation for a complete MC system using Peltier cells as thermal diodes. This study involved simulation of Gd as the MC material and obtained moderate efficiencies. The key problem, that of using a material with second-order transition, was diluted among many other influences on heat losses and leaks. We presented some preliminary results of the simulation of a single sandwich in the conference THERMAG VIII [
12], concluding that the TE-MC hybrid system was an interesting procedure, but that there were many variables to be optimized. Monfared [
13] simulated a battery of sandwiches which were designed to reach higher temperature spans.
In this investigation, we found that the properties and dimensions of the MCM require to be correlated with the TE cells to achieve optimum performance in
or in cooling power. We simplified the properties of a TE cell, characterizing it with only three parameters: the effective Seebeck coefficient
, the electrical resistance
, and the thermal conductance
. The simulations undertaken take into account the properties of commercial TE cells. For the MCM, a material with a first-order transition and low hysteresis provides virtually infinite heat capacity, which is crucial to improve the efficiency. This is because, in the coexistence paramagnetic/ferromagnetic phase, the temperature is entirely determined by the magnetic field. The experimental properties of some doped La(Fe,Si)
alloys are considered. A new master equation is derived for the heat transfer in the MCM, since the most used equation [
13] is not valid for a material with a first-order transition, leading to a
indetermination. The output of the simulation program (
, magnetocaloric and thermoelectric work, extracted and released heat, etc.) is monitored for very slow continuous variation of certain working parameters. To simplify the case, only one sandwich is focused on, considering that a battery is essentially a superposition of sandwiches.
The potential applications of the system are not different to those of a refrigeration system with MC or TE materials, and are not discussed further here. The object of this investigation is to show that the combined TE-MC system results in higher efficiency and versatility than that achieved for pure magnetocaloric or thermoelectric systems.
Section 2 describes a simplified, but very faithful, model of the operation of a typical commercial Peltier cell.
Section 3 presents, in a simplified manner, the working principles of a hybrid TE-MC system using materials with a first-order transition, such as La(Fe,Si)
, to highlight the essential details.
Section 4 describes a numerical simulation using realistic parameters.
Section 4.1 introduces an original master equation for the heat flow in an MCM having a first-order transition and the finite difference approximation that is used to solve the master equation.
Section 4.2 discusses the realistic values for the working parameters. The following sub-sections present the simulation results for the cooling efficiency, the extracted and released heat powers, and the thermal evolution for the three cases being compared. A pure Peltier system is described in
Section 4.3, a pure MC system with quasi-ideal thermal diodes is described in
Section 4.4, and the combined MC-TE system with two Peltier cells and one MCM is described in
Section 4.5. Finally,
Section 5 presents the conclusions from a comparison of the three systems.
2. Model for Thermoelectric Cells
The effective values of , , and for a module consisting of many thermoelectric elements were used. The modelization was tested using the reported curves of extracted heat power against the temperature difference for several electric current supplies I, and against the voltage V for different I values. In particular, the data for a cell from RTM Ltd. were tested against the model.
From first principles of irreversible thermodynamics [
14], assuming a constant Seebeck coefficient, the voltage in a Peltier cell connected between two heat sources/sinks at temperatures
and
is,
The extracted heat power from side 1 (let us assume the cold side),
, the heat power released to side 2 (the hot side),
, and the work power supplied by the cell,
, are given by
From these equations, it follows that if
and
,
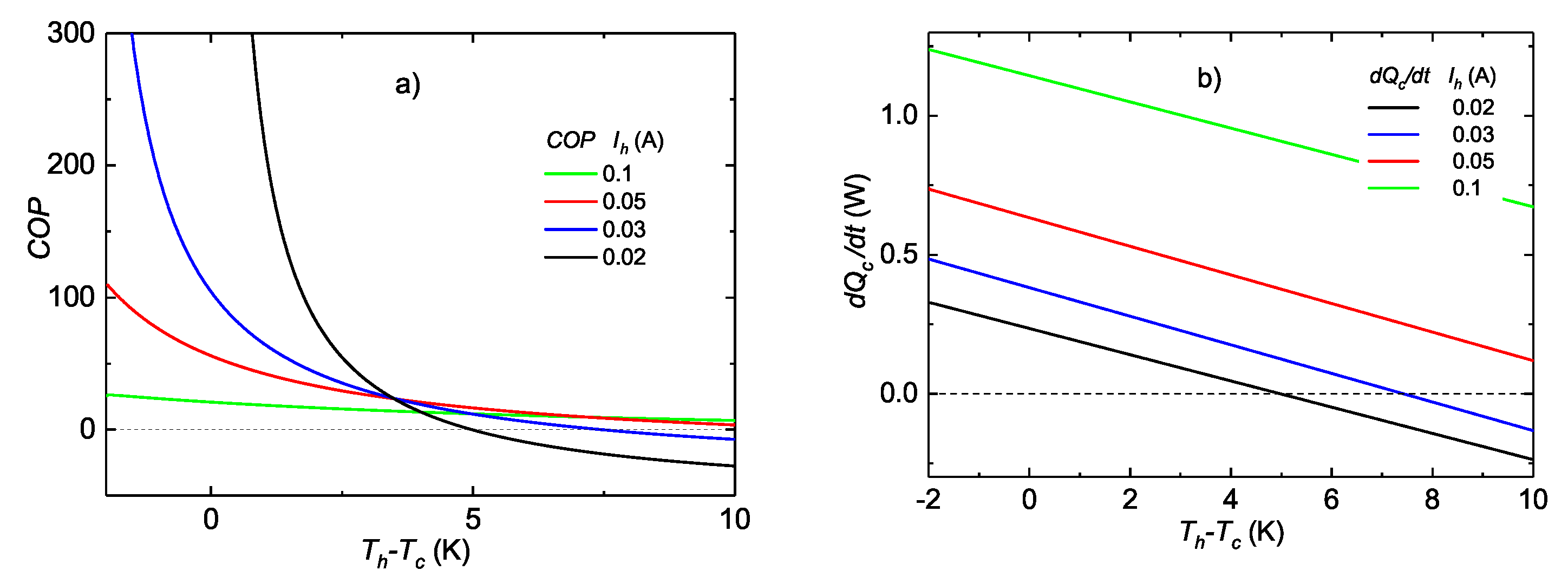
, and then, the efficiency of a Peltier cell is the Carnot efficiency. A very important detail is that, for small temperature differences, the conduction term can be neglected, resulting in
For the cell 1ML07-050-15AN25 from RMS Ltd. at
K, the parameters set are (
Table 1)
,
mW/K and
mV/K (the cell is a combination of many TE elemental couples). For
,
, producing an enormous value for low currents. For instance, for
A,
. For a negative temperature difference
K, and
A,
. However, for higher positive differences, the performance decays rapidly and the cell can barely transfer heat to the hot side if
K (
) with
0.1 A. Nevertheless, it is able to prevent heat leakage from the hot side to the cold side.
A magnetocaloric material (i.e., a LaFeSi-type alloy) can increase the temperature by
K upon application of a magnetic field, making the transfer possible very efficiently, for starting
. Consequently, the statement in [
10] that the hybrid system produces the same performance as a TE system, is only valid for a particular, and not very fortunate, choice of parameters, but it is not generalizable. It is most likely that, in the simulation performed in this study, the Peltier subsystem was much more powerful than the MC system, preventing its effective action. Both subsystems should be adequately dimensioned.
3. Simple Model for a Sandwich Having an Ideal MCM with a First-Order Transition
The typical values of the parameters used in this section are listed in
Table 1.
In this section, to establish the main physical principles of the combined system, we perform some simple mathematics using a proposed model for a TE cell and a simple model for the behavior of the MCM in the phase coexistence region. Let us assume that there is a heat “reservoir” (it will be seen that this has to be a heat pump), representing the MCM, that is assumed to be of infinite heat capacity at temperature
T, regulated externally by a magnetic field. An MCM with a first-order transition fulfills these conditions under paramagnetic/ferromagnetic phase coexistence. As a simple case, let us consider that
T has a constant low value,
, for a time
and a higher value,
, for the same time, the period being
. Let us assume that we apply some electrical current to the high and low temperature cells
and
in the following way
with constant values of
,
,
and
. The current
is intended to prevent heat leakage to the cold source at
, through the TE cell on the left side (the cold TE cell), when the MCM is at its highest temperature
. During this time, the cold TE cell plays the role of a thermal diode, but it requires a small electrical work supply to achieve this purpose.
is intense enough to extract heat from the cold source when the MCM is at its lower temperature,
, and the transfer can be performed efficiently. During this stage, the TE cell is an active device. Similarly, in the hot TE cell,
prevents heat leakage to the MCM, when it is at
, and
transfers heat from the MCM when it is at
to the hot sink at
. We also assume that the change between
and
takes a negligible time. In the interim, the magnetic subsystem performs an adiabatic process from
to
or vice versa. This assumption is an idealization, but not far removed from the real case. Equations (
3)–(
5), replacing
and
by the temperatures at both sides of each cell, give the following instantaneous heat powers extracted from the cold source by the cold TE cell:
, released to the intermediate system,
, extracted from the intermediate system by the hot TE cell,
, released to the hot source,
, and the work power made by each cell,
and
. We assign the subscript 1 or 2 to these powers, according to the temperature of the intermediate MCM, obtaining
These equations are trivially integrated to give the extracted and released heats by every subsystem and the thermoelectric work in a cycle resulting
The intermediate “reservoir” should actually be a thermodynamic heat pump which receives
at a temperature
or
and transfers
, making a work value of
in a cycle. We assume that the intermediate system works cyclically, without any thermal connection with the environment (in a real device this point is not fulfilled, since the magnetic subsystem has a weak thermal leakage to or from the environment). Hence, the work performed by the magnetic subsystem is
and the total work
. For compatibility with the second law of thermodynamics, the entropy released by the intermediate device should be higher than that extracted; this is
with
. The value
holds for an ideal Carnot device, working without entropy production.
Moreover, the value of
is determined by the properties of the MCM for a given
and
(i.e.,
is the area of the thermodynamic cycle in the magnetization/field or entropy/temperature diagrams for that substance), which imposes another relation between
and
. The pair of relations (
17) and (
18), involving
,
,
,
,
, and
, indicate that only four of these six quantities can be chosen arbitrarily. Let us assume that
and the four currents through the TE cells are fixed. Then, the intermediate system has to adapt its maximum and minimum temperatures
and
to achieve the Carnot efficiency, since the extracted and released heats are determined by the currents at the TE cells. If the MCM is a typical ferromagnet without a phase transition (strictly, a second-order transition at the Curie temperature occurs only at zero field, but there is no transition for any other field in a typical ferromagnet), the steady regime is reached when Equation (
21) is obeyed and
.
In an MCM with a first–order transition, such as a La(Fe,Si)
alloy, working in the phase coexistence region, the temperatures
and
are both determined by the minimum and maximum magnetic fields (this is a requirement of the Gibbs phase rule, i.e., the state of the MCM is a point of the phase coexistence line in a
diagram and
B determines the temperature). However, if the relation (
21) is not fulfilled, the MCM will gain or lose net heat every cycle (then,
). This net heat will gradually transform one phase to the other phase and the material will change to a single-phase state when one of the phases is exhausted. After this, the temperature of the resulting phase,
or
, will change slowly until Equation (
21) is satisfied, reaching a steady regime. It is desirable to have the MCM in the phase coexistence region as long as possible, where the MC effect is much more powerful. Most often, the lowest magnetic field is zero, and then
is the transition temperature at zero field,
, (frequently referred to as the Curie temperature, but its character differs markedly from that of a typical ferromagnet). On the other hand, the phase coexistence line is very approximately a straight line
and
is determined by the maximum applied field. Therefore, for an MCM with a first-order transition, and for a maximum applied field
B, only three parameters can be chosen among
,
,
, and
, if we want to work in the steady regime and always in the phase coexistence region. For instance, if we apply equal currents to both TE cells, making
and
(two constraints), the MCM will leave the coexistence state region before reaching the steady regime, except for the precise value of the magnetic field
B, which determines
, such that the relation (
21) is satisfied.
A natural working hypothesis is to take
and
as the minimum values which prevent thermal leakage from the MCM to the cold source and from the hot sink to the MCM. This is achieved in Equation (
12) imposing
and in Equation (
10)
. These relations determine the two low currents. We can arbitrarily choose the maximum current at the cold cell,
, which determines the heat-per-cycle extracted from the cold source, according to Equation (
15). With given
and
, and chosen
,
, and
, Equation (
21) gives the value of
for the steady regime. The cooling power,
, and the other heat and work values are obtained via Equations (
15)–(
20). Finally the COP in the steady regime is computed as
Assuming the linear dependence of
T with
B for the phase coexistence line,
can be tailored by manipulating the chemical composition of several MC alloys.
K/T for typical alloys derived from La(Fe,Si)
. Let us assume that the magnetic subsystem follows a Carnot cycle between the magnetic fields 0 and
B. Then, the temperatures of the MCM are
and
. The steady regime, while keeping the MCM in the phase coexistence region, imposes the relation of Equation (
21).
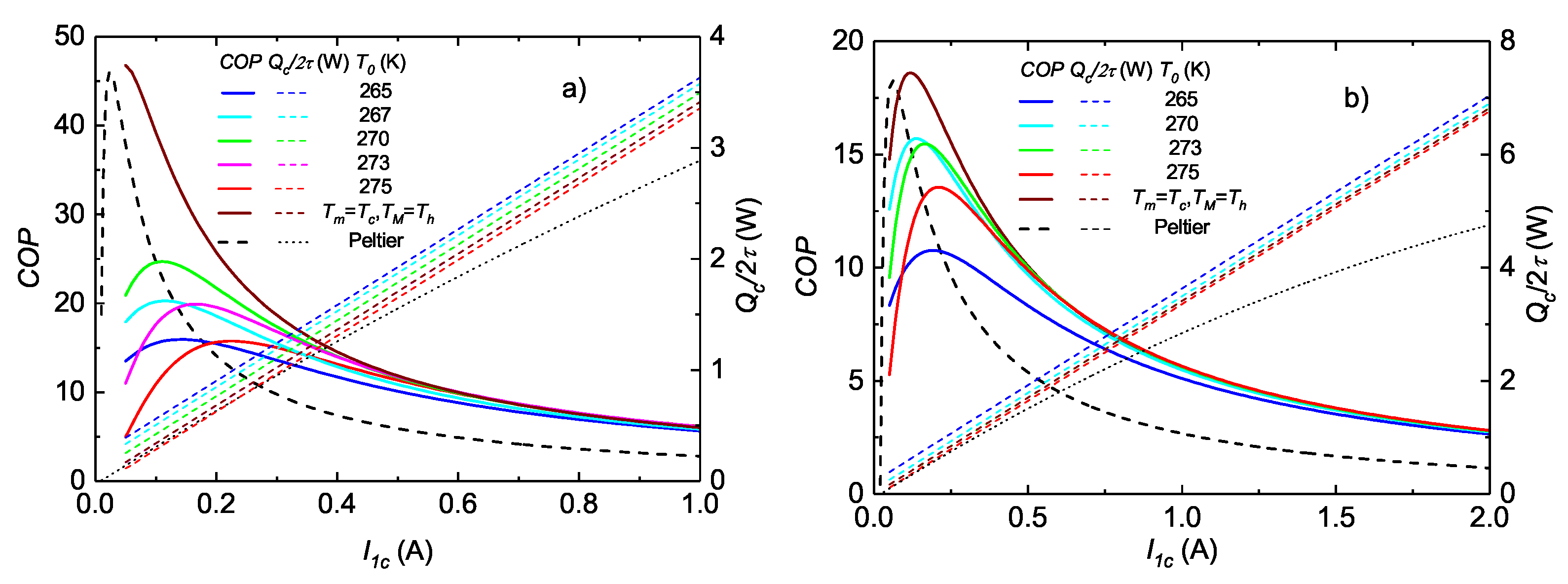
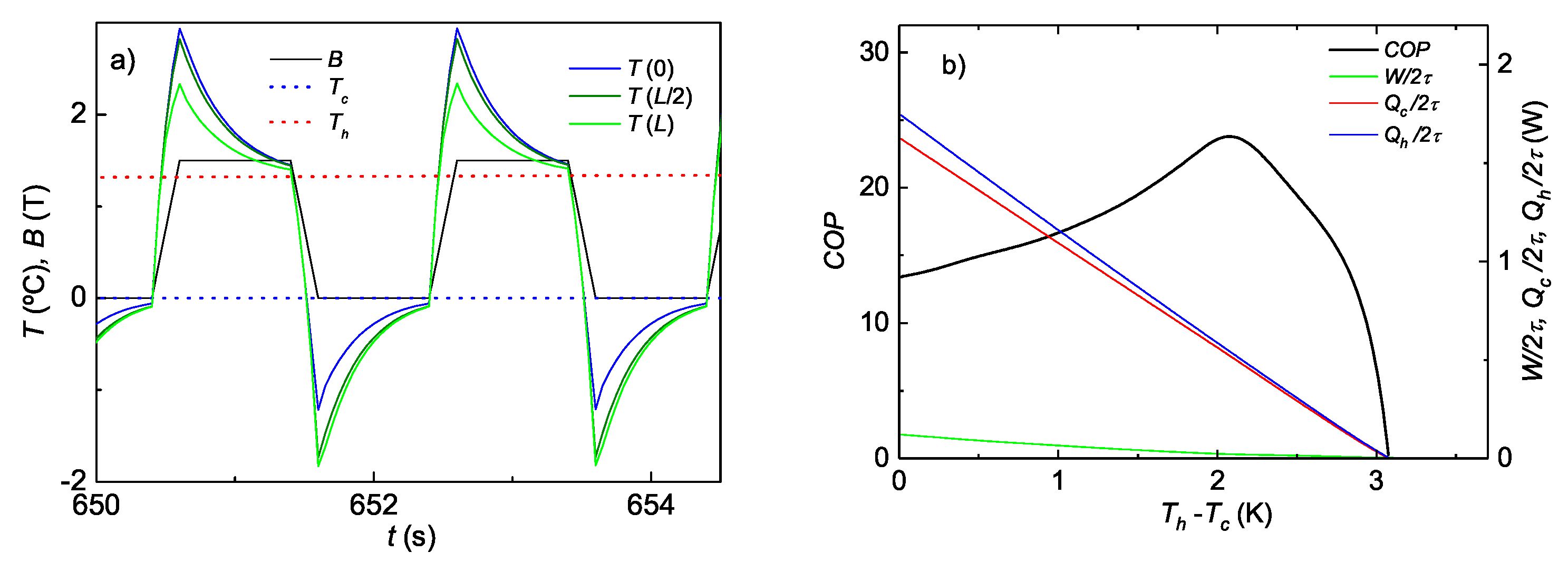
Figure 2a shows
and the cooling power
for
K,
K (
2 K), for several characteristic temperatures of the MCM and a fixed increment
K. For the interesting case, included in the figures, in which the low and high temperatures of the MCM coincide with the temperatures of the cold source and the hot sink, respectively,
and
, the magnetic field is adjusted to be
instead of 2 T. This figure also shows the data for a pure Peltier heat transfer; that is, two Peltier cells in series, working continuously, with the same current,
, without any intermediate system. To compare with the hybrid system, the power of the pure Peltier method is divided by two, because, in the hybrid system, each cell works actively only during one half of the period.
The curves in
Figure 2a show how the choice of the transition temperature of the material,
at zero field, and the applied magnetic field, which fixes the maximum temperature of the MCM, are critical. For a cold source at
K and a hot sink at
K, and a maximum applied field of 2 T (therefore,
K), the maximum COP is obtained for
K, and decays sharply for higher or lower values. If
and the magnetic field is regulated to reach the maximum temperature
, the efficiency (brown curve in
Figure 2a) increases dramatically and overcomes that of a pure Peltier system by a large amount, doubling its COP except for very low heat flow given for low currents. Similar features occur, but with lower COP, for a higher temperature span.
Figure 2b shows the results for
K and
K. Except for very weak currents, the
is clearly higher for the hybrid system, even more than twice in most of the range
A. The cooling power is also greater than that of the pure Peltier method. The
of the hybrid system decreases if
(e.g., for
K) or
(e.g., for
K,
K = 273 K). The highest
occurs if the MCM and the magnetic field are chosen to have
and
(brown curves in
Figure 2).
As the main conclusion of this section, a hybrid sandwich in which the MCM has a first-order transition improves the efficiency with respect to a pure TE system if working in the phase coexistence region, but the working parameters have to be properly chosen.