An Analytical Approach for Computing the Coefficient of Refrigeration Performance in Giant Inverse Magnetocaloric Materials

Abstract

An analytical approach for computing the coefficient of refrigeration performance (CRP) was described for materials that exhibited a giant inverse magnetocaloric effect (MCE), and their governing thermodynamics were reviewed. The approach defines the magnetic work input using thermodynamic relationships rather than isothermal magnetization data discretized from the literature. The CRP was computed for only cyclically reversible temperature and entropy changes in materials that exhibited thermal hysteresis by placing a limit on their operating temperature in a thermodynamic cycle. The analytical CRP serves to link meaningful material properties in first-order MCE refrigerants to their potential work and efficiency and can be employed as a metric to compare the behaviors of dissimilar alloy compositions or for materials design. We found that an optimum in the CRP may exist that depends on the applied field level and Clausius–Clapeyron (CC) slope. Moreover, through a large literature review of NiMn-based materials, we note that NiMn(In/Sn) alloys offer the most promising materials properties for applications within the bounds of the developed framework.

1. Introduction

Giant inverse magnetocaloric materials have gained recent attention in the scientific community due to their high magnetic-to-thermal energy conversion efficiencies and potential for eliminating environmentally harmful chemicals typically used in conventional vapor-compression refrigeration units. Residential and commercial heating and cooling appliances account for nearly 40% of the United States’ energy consumption, totaling 20.26 quadrillion British thermal units (BTU) annually. As global populations continue to grow, the amount of energy allocated for heating and cooling applications is expected to increase by 84% by the year 2050, compared to energy levels from 2010 [1,2]. The environmentally damaging fluids used in vapor compression systems, such as chlorofluorocarbons (CFCs) or hydrofluorocarbons (HCFCs) [3,4], are well-known to be leading contributors to greenhouse gas emissions and can destroy stratospheric ozone [5,6].

Solid-state refrigeration devices, such as magnetocaloric and thermoelastic regenerators, have the potential to mitigate greenhouse gas emissions [7], as they do not require HCFCs in thermodynamic cooling cycles. In a report submitted to the U.S. Department of Energy [8], magnetocaloric and thermoelastic technologies are projected to reduce energy demands for HVAC systems in both commercial and residential sectors by at least 20%. However, to succeed in that goal, there must be further development of caloric materials. Thus, the authors aim to define an analytical approach for computing a performance metric useful for comparing the energy conversion efficiency in novel solid-state refrigerant materials to facilitate high-throughput performance screening.

In previous works, Wood and Potter developed a thermodynamic metric, namely the refrigeration capacity (RC), that could be applied to materials that exhibited second-order magnetic transitions without hysteretic loss [9]. Nearly 20 years following their work, Pecharsky and Gsneidner conceived a similar metric, namely the relative cooling power, RCP, which was applied to the first-order magnetostructural transition observed in GdSiGe [10,11]. They also employed the RCP to compare materials that exhibited a second-order magnetic transition, such as pure Gd [10]. However, using the RCP to compare materials that exhibited hysteretic losses across magnetostructural transitions with those that did not (e.g., across purely magnetic second-order transitions) led to misleading comparisons. More recently, other metrics applicable to materials exhibiting first-order magnetostructural transitions have been derived by the present author [12], Moya [13,14], and Brück [15]. For instance, Brück et al. defined a coefficient of performance, COP, which accounted for hysteretic losses through its implementation and was applicable to the physics across first-order structural phase transformations. It was mentioned that, in quantifying the applied magnetic-work required to generate the cooling in the magnetocaloric material (i.e., energy input), the isothermal magnetization loops needed to be numerically integrated. Data for complete magnetization loops across magnetostructural transitions were limited in the literature and were cumbersome to digitize.

Here, we aim to analytically compute the metric so that commonly measured and reported materials properties can be used to quickly compare the performance of novel magnetocaloric materials. In this way, solid refrigerants that exhibit a first-order magnetostructural transition with transformation hysteresis can be quickly assessed. First, the thermodynamics governing the conventional (second-order) caloric effects in solids are briefly described, which can be defined for any externally applied stimuli (thermodynamic force) that influences a material’s free energy. The thermodynamics are then incorporated into Wood and Potter’s RC parameter. Next, the thermodynamics governing first-order structural phase transformations are described. The entropy change and adiabatic temperature change are derived from the Clausius–Clapeyron relationship and a method developed by Porcari et al., [16,17], respectively. These are later applied to Wood and Potter’s RC parameter, and the disadvantages of employing this metric to first-order structural transitions are revealed.

Finally, we present an analytical approach to compute the coefficient of refrigeration performance (CRP) that is directly applicable to first-order structural phase transitions. The analytical approach accounts for hysteretic losses and employs basic and commonly reported materials properties in the literature, rather than cumbersome digitized magnetization data. The development of the analytical CRP is followed with a discussion and examples used for comparing the caloric effects in first-order magnetostructural materials.

2. Thermodynamic Quantities of Interest

A caloric, or thermal, effect is defined by a material’s isothermal entropy ($\Delta S_{iso}$) or adiabatic temperature ($\Delta T_{ad}$) change in response to some external stimulus (force). For the elastocaloric effect (ECE), this stimulus is mechanical load, and for the magnetocaloric effect (MCE), a magnetic field. Reversible heating and cooling effects can be generated in a solid material by a change in the material’s free energy, which might include latent heat effects from a structural transition. Heating can also be generated through any irreversible processes that occur at the time of applying the external field. Magnetic and structural hystereses serve as indicators that thermodynamically irreversible processes take place, and through the second law of thermodynamics, the entropy produced (and thus heat) from these irreversible processes will always be greater than zero.

The internal energy of a substance changes with an applied thermodynamic “force”, such as stress, temperature, and magnetic field. These forces do not depend on the material’s volume and are referred to, herein, as intensive thermodynamic variables.[18] Since we aim to determine the caloric effects resulting from a change in internal energy, we consider the Gibbs free energy, $G$, which implicitly assumes intensive variables are applied to the substance in question during experiments [18]. Here, the $G$ describes the free energy of a single structural phase. The change in free energy, $dG$, of that phase is defined as [18]

$$dG=VdP-SdT-{\displaystyle \sum }_{i=1}^n{X}_{i}d{y}_i$$

(1)

where $V$ is specific volume (m³·kg⁻¹), $P$ is hydrostatic pressure (Pa), $S$ is the entropy (J·kg⁻¹·K⁻¹), $T$ is temperature (K), $X_i$ are extensive (volume dependent) material properties, such as bulk magnetization $M$ (emu·g⁻¹) or specific strain $\epsilon$ (m³·kg⁻¹), and $y_i$ are their thermodynamic intensive-force conjugates, such as applied magnetic field, ${\mu }_{0}H$ (Tesla), or uniaxial stress,$\sigma$ (Pa), respectively. Note that ${\mu }_0$ is the permeability of free space in Henry·m⁻¹, and $H$ is the applied magnetic field in A·m⁻¹.

The isothermal entropy change defining the caloric effect can then be quantified using Equation (1). This is performed by employing Maxwell relations, first assuming that the application of the external stimuli is performed at atmospheric pressure and that all other applied forces are constant, i.e., $dP=d{y}_i=0$. The entropy, $S$, is expressed as

$$-S={\left(\frac{dG}{dT}\right)}_{\left\{P,y_{n=i}\right\}}.$$

(2)

The forces that are assumed constant in Equation (2) are denoted by subscripts. Similarly, other extensive thermodynamic quantities can be solved for from Equation (1) using the same approach. In the case, below, pressure and temperature are assumed constant. Here, $X_i$ can be expressed as

$$-X_i={\left(\frac{dG}{d{y}_i}\right)}_{\left\{P,T,y_{n\ne i}\right\}}$$

(3)

where $P$, $T$, and all other $y_i$ are constant intensive variables.

Next, Equations (2) and (3) can be differentiated with respect to the other’s independent variable. Equation (2) is differentiated with respect to $y_i$ resulting in

$$-\frac{dS}{d{y}_i}=\frac{d}{d{y}_i}{\left(\frac{dG}{dT}\right)}_{\left\{P,y_{n=i}\right\}}$$

(4)

and Equation (3) with respect to $T$, resulting in

$$-\frac{d{X}_i}{dT}=\frac{d}{dT}{\left(\frac{dG}{d{y}_i}\right)}_{\left\{P,T,y_{n\ne i}\right\}}.$$

(5)

Assuming that the second partial derivative of $G$ is smooth and continuous, the right-hand side of Equations (4) and (5) are identical, and therefore, the left-hand sides are also mathematically equivalent. The incremental isothermal entropy change and “caloric effect”, $d{S}_{iso}$, from stimulus $y_i$ can then be denoted as

$$d{S}_{iso}=\left(\frac{d{X}_i}{dT}\right)d{y}_i\Rightarrow \int d{S}_{iso}=\int \left(\frac{d{X}_i}{dT}\right)d{y}_i,$$

(6)

which simplifies to

$${S|}_{y_i}-{S|}_{y_i=0}=\Delta S_{iso}\left(0\to y_i\right)={{\displaystyle \int }}_0^{y_i}\left(\frac{d{X}_i}{dT}\right)d{y}_i$$

(7)

In Equation (7), the isothermal entropy change has been derived for any single phase exposed to the intensive force $y_i$ in $G$. It is important to note that, in experiments where strain drives the caloric effect and is thus the independent variable, the Helmholtz free energy expression should be employed, instead of $G$, to insure consistency between the measured and predicted caloric behaviors [19].

2.1. Conventional Magnetocaloric Cooling with Second-Order Transitions

A wide range of crystalline and amorphous materials exhibit the MCE. Laves phases [20], ferromagnetic lanthanum manganites [21,22,23], and other rare-earth containing crystalline compounds [24,25,26,27] are commonly studied. Many Laves phase compounds, such as HoCo2 [28,29], TbCo2 [30], and TbFe2 [31], are of interest, because they exhibit a significant change in magnetization, $M$, across their ferromagnetic/paramagnetic Curie temperatures, $T_{Curie}$. Many well-performing conventional MCE materials are not employed in regenerative cycles due to limited availability and the cost of rare earths.

If a magnetic field, $y_i={\mu }_{0}H$, is applied to a magnetocaloric refrigerant, the resulting entropy change is defined as ${{\displaystyle \int }}_0^{{\mu }_{0}H}\left(\frac{dM}{dT}\right)d\left({\mu }_{0}H\right)$ by Equation (7), where $X_i$ has been replaced with $M$ and is the energetic conjugate of ${\mu }_{0}H$. The MCE, or magnetic field-induced isothermal entropy change across a second-order magnetic transition, is illustrated in Figure 1a,b.

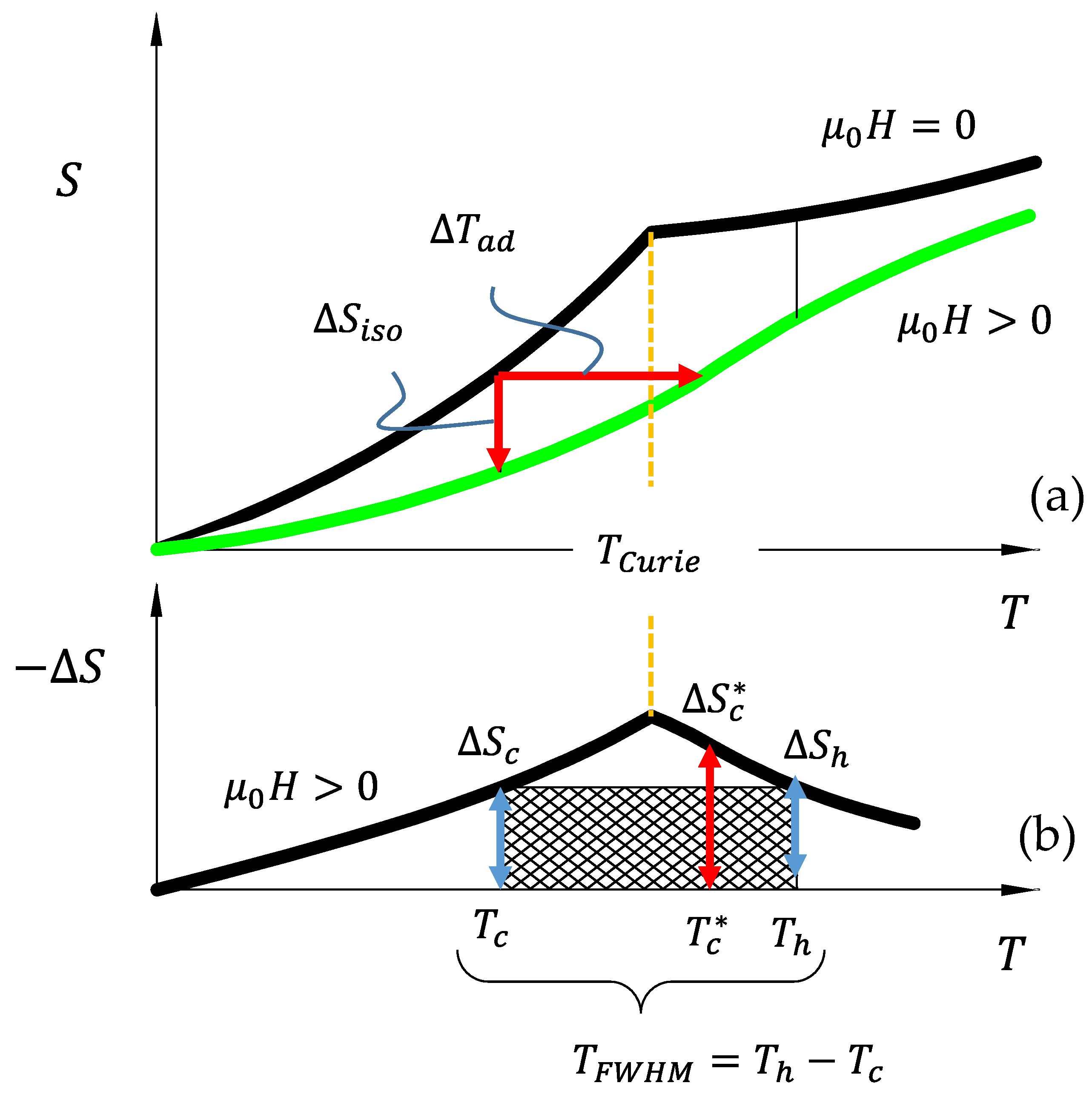
In Figure 1a, the entropy versus temperature diagram of a ferromagnetic material is depicted around its $T_{Curie}$. Under zero magnetic field (top curve), the entropy is shown to exhibit a cusp at $T_{Curie}$ [32]. According to Equation (2), the entropy curve is defined by the partial derivative of the $G$ with respect to temperature. Clearly, the second temperature derivative of the free energy, i.e., $dS/dT$, exhibits a discontinuity at $T_{Curie}$, thus making the change in magnetization at $T_{Curie}$ a second-order magnetic transition. Interestingly, the assumption of commutativity, described above, no longer holds exactly at $T_{Curie}$ due to the inability to quantify the derivative of $G$. However, at temperatures above and below $T_{Curie}$, Equation (7) is applicable for determining magnetic field-induced $\Delta S_{iso}$.

Upon applying ${\mu }_{0}H$ to a ferromagnetic material around its $T_{Curie}$, the total entropy (magnetic disorder) decreases, as depicted in Figure 1a,b. This can manifest an increase in temperature. Consequently, the MCE in most ferromagnetic materials that exhibit second-order magnetic transitions is achieved through adiabatic or isentropic demagnetization, i.e., removing the applied magnetic field.

The adiabatic temperature change corresponding to a decrease in entropy is illustrated by a red horizontal arrow labeled as $\Delta T_{ad}$ in Figure 1a. The magnitude of $\Delta T_{ad}$ in a single structural phase material (described with the above Gibbs free energy) can be derived using the following thermodynamic assumptions and analyses. It is assumed that the total change in entropy, $d{S}_{total}$, is a function of all other thermodynamic quantities as posited by the Truesdell’s theory of equipresence and the structure of thermodynamic state functions [33]. As such, $d{S}_{total}$ is defined as

$$d{S}_{total}=\left(\frac{dS}{dP}\right)dP+\left(\frac{dS}{dT}\right)dT+{\displaystyle \sum }_{i=1}^n\left(\frac{dS}{d{y}_i}\right)d{y}_i.$$

(8)

According to Figure 1a, the $\Delta T_{ad}$ is produced when $d{S}_{total}=0$. Assuming isobaric ($dP=0$) and isentropic ($d{S}_{total}=0$) conditions in Equation (8) to match the condition of adiabatic experiments, Equation (8) reduces to

$$0=\left(\frac{dS}{dT}\right)d{T}_{ad}+\left(\frac{dS}{d{y}_i}\right)d{y}_i$$

(9)

when only one driving force, $y_i$ is applied. Substituting the Maxwell relation from Equation (6) into (9) for $\frac{dS}{d{y}_i}$ results in

$$0=\left(\frac{dS}{dT}\right)d{T}_{ad}+\left(\frac{d{X}_i}{dT}\right)d{y}_i$$

(10)

where by the entropy change generated from applying $y_i$ can be moved to the left side of the equality. Thus,

$$-\left(\frac{d{X}_i}{dT}\right)d{y}_i=\left(\frac{dS}{dT}\right)d{T}_{ad},$$

(11)

where $\left(\frac{dS}{dT}\right)=\frac{C_p}{T}$ per the second law of thermodynamics, and $C_p$ is the isobaric heat capacity [18]. Therefore,

$$-\left(\frac{d{X}_i}{dT}\right)d{y}_i=\left(\frac{C_p}{T}\right)d{T}_{ad}.$$

(12)

Finally, the terms in Equation (12) can be separated and integrated, leading to

$$\Delta T_{ad}\left(0\to y_i\right)=-{{\displaystyle \int }}_0^{y_i}\frac{T}{C_p}{\left(\frac{\partial X_i}{\partial T}\right)}_{\left\{y_{n\ne i}\right\}}d{y}_i,$$

(13)

where the adiabatic temperature change can be computed for any isochoric driving force, $y_i$, if the isobaric heat capacity, $C_p$, and extensive $X_i$ histories are known. Oftentimes, $C_p$ is assumed to be independent of the driving force, $y_i$, and $\Delta T_{ad}$ is approximated as [34]

$$\Delta T_{ad}\approx -\frac{T}{C_p}\Delta S_{iso}.$$

(14)

It is important to note that Equation (14) has been developed using $G$ for a single structural phase. Furthermore, this is simply an approximation, assuming only small fluctuations occur in $C_p$ by applying the external stimuli. Moreover, $T$ in Equation (14) is nominally assumed to equal the starting temperature at which $y_i$ is applied during the adiabatic temperature change.

2.2. Wood and Potters Refrigeration Capacity for Magnetic Cooling

The refrigeration capacity (RC) defines the suitability of a magnetic material for cooling applications and was originally conceived by Wood and Potter [9] approximately forty years following the seminal work of Weiss and Piccard [35]. Wood and Potter proposed that a measure of how well a magnetic refrigerant will operate should be based on its capability to perform thermal work through field cycling used in magnetic regenerative heat cycles. They considered that the entropy change at the cold end of a heat cycle should not exceed that at the hot end to satisfy the second law of thermodynamics. As such, the “thermal work” that was performed by a magnetocaloric material was defined as the entropy change achieved at the cold temperature reservoir of a heat cycle, $\Delta S_c$, multiplied by the temperature gradient across which the heat was moved, $\Delta T$. Originally, the $\Delta T$ was defined as the difference between the hot ($T_h$) and cold ($T_c$) reservoir temperature of a regenerative cycle, i.e., $\Delta T=T_h-T_c$. Due to the ambiguity of the proposed hot and cold temperature reservoirs, in practice, these temperatures were assumed to be the full-width-half-maximum ($T_{FWHM}$) of the entropy change versus temperature diagram, as shown in Figure 1b [32].

Figure 1b illustrates the RC computed for conventional second-order magnetocaloric refrigerants from the above entropy change versus temperature diagram. To generate the entropy change versus temperature curves, the difference was computed between the zero field (${\mu }_{0}H=0$) and applied field (${\mu }_{0}H>0$) curves from Figure 1a. As shown in Figure 1b, an entropy change at some cold temperature, $T_c$, is defined as $\Delta S_c$, whereas an entropy change of $\Delta S_h$ is achievable at temperature $T_h$. Thus, the RC, was defined as [9]

$$RC=\Delta S_c\Delta T=\Delta S_c{T}_{FWHM}$$

(15)

Clearly, the goal of much present-day research is increasing the RC in state-of-the-art MCE materials [7,36], because it corresponds to the amount of reversible thermal work performed by the refrigerant.

In magnetocaloric refrigerants exhibiting a second-order magnetic transition, the largest entropy change occurs around the $T_{Curie}$, but this temperature does not change as a function of applied field. As such, applying greater magnetic fields to second-order magnetocaloric compounds simply increases the $\Delta S_c$ and only marginally broadens the entropy change peak (i.e., $T_{FWHM}$ in Equation (15)). To compare materials using Wood and Potter’s RC parameter, Equations (14) and (7) were substituted into Equation (15), so $RC=\Delta S_c\Delta T_{ad}$. Using $\Delta T_{ad}$ in place of $T_{FWHM}$ leading to a thermodynamic performance metric for second-order phase transforming materials in heat cycles around their $T_{Curie}$ [10]. It is important to note, however, that $\Delta S_c$ and $\Delta T_{ad}$ are both dependent on the applied field level and operating temperature. In the following section, we describe the magnetocaloric effects that are generated across first-order magnetostructural phase transitions and how they differ from those in the above sections. Performance criteria are analytically developed for reversible behavior in first-order materials so they may be properly compared with reversible second-order systems.

3. Thermodynamics of Giant Caloric Effects across First-Order Meta-Magnetic Transitions

First-order magnetostructural transitions are observed in many multifunctional alloys [37]. For simplicity, we focus on the observed behaviors in a well-known NiMnIn meta-magnetic shape memory alloy (MMSMA) [38,39]. MMSMAs are rare-earth-free intermetallic compounds that exhibit a reversible first-order magnetostructural diffusionless phase transformation between low temperature martensite (M) and high temperature austenite (A) and are candidates for cooling applications [40,41,42]. In our analyses, isothermal magnetization data measured in Ni₄₈Mn₃₈In₁₄ (at.%) polycrystals were used to describe the meta-magnetic behavior across first-order magnetostructural transitions and the caloric effect. The NiMnIn polycrystals, herein, were subjected to a homogenization treatment at 1123 K for 24 h in a protective argon atmosphere and then water quenched.

At temperatures below a critical transformation temperature, $T_0$, NiMnIn alloys are composed of a non-magnetic M-phase (paramagnetic, superparamagnetic, etc.) [43,44,45,46,47]. This is illustrated by the thermomagnetic curves in Figure 2a. On heating the M-phase in a small ${\mu }_{0}H$, the MMSMA begins to spontaneously magnetize (see green curve) as it transforms into the high temperature A-phase and is accompanied by an endothermic (cooling) reaction from the latent heat of the martensitic transition. On heating, critical M-to-A transformation temperatures are referred to as the austenite start ($A_s)$ temperature and austenite finish ($A_f$) temperatures. Conversely, cooling causes an exothermic A-to-M transformation at the critical temperatures denoted as martensite start ($M_s$) and martensite finish ($M_f$). The difference in $A_f$ and $M_f$ has been used to describe energy barriers to the martensitic transformation, including elastic and irreversible parts [48,49,50,51,52], and is the main reason for developing an analytical performance metric for only the reversible behavior in first-order materials, as second-order materials do not exhibit these same energy losses or barriers. Moreover, second-order materials exhibit the conventional magnetocaloric effect as described by Equation (7), but first-order materials exhibit magneto-structural transformations which are accompanied by a latent heat component and therefore exhibit “giant” magnetocaloric effects.

Upon applying a constant magnetic field, $H^{*}$, to the MMSMA and measuring magnetization across the reversible martensitic transition, the $M_f$, $M_s$, $A_s$, and $A_f$ temperatures experience a decrease (see blue curve in Figure 2a), indicating that the magnetic field stabilized the high-temperature ferromagnetic A-phase. Indeed, each critical temperature exhibits a unique sensitivity to the applied field, also referred to as the Clausius–Clapeyron (CC) slopes, $d{M}_f/d\left({\mu }_{0}H\right)$, $d{M}_s/d\left({\mu }_{0}H\right)$, $d{A}_s/d\left({\mu }_{0}H\right)$, and $d{A}_f/d\left({\mu }_{0}H\right)$. Often, in the literature, these slopes are assumed to be equivalent to $d{M}_s/d\left({\mu }_{0}H\right)$; however, this can be an oversimplification. In inverse giant MCE materials, the CC slopes are negative in sign.

If the MMSMA is held at constant temperature $M_f$ under zero magnetic field, $M_f^{{\mu }_{0}H=0}$, then there exists a field level (${\mu }_{0}H=H^{*}$) at which the M-phase will completely transform to the A-phase, as shown in Figure 2a by a vertical red dashed line. The magnetization response during this isothermal magnetic field-driven transformation at $M_f^{{\mu }_{0}H=0}$ is depicted in Figure 2b by a blue curve. To complete the isothermal transformation at $M_f^{{\mu }_{0}H=0}$, the $A_f^{{\mu }_{0}H=0}$ must effectively decrease (at the rate defined by $d{A}_f/d\left({\mu }_{0}H\right)$) to match $M_f^{{\mu }_{0}H=0}$. Therefore, we can define $H^{*}$ as the field level needed achieve a complete and reversible isothermal martensitic transformation at $M_f^{{\mu }_{0}H=0}$, as $H^{*}=\left(A_f^{{\mu }_{0}H=0}-M_f^{{\mu }_{0}H=0}\right)d\left({\mu }_{0}H\right)/A_f$ [52]. In this expression, $d\left({\mu }_{0}H\right)/A_f$ is assumed to be a positive quantity that simply denotes the sensitivity of the $A_f$ temperature to the applied ${\mu }_{0}H$. Similarly, the magnetic field required to initiate the meta-magnetic transition at $M_f^{{\mu }_{0}H=0}$ can be defined by $H_{req}=\left(A_s^{{\mu }_{0}H=0}-M_f^{{\mu }_{0}H=0}\right)d\left({\mu }_{0}H\right)/A_s$, assuming $d\left({\mu }_{0}H\right)/A_s$ is a positive quantity. In this context of isothermal meta-magnetic magnetic field-driven transformations, the volume fraction of stabilized A-phase, $\xi$, can be computed as $\xi =\left({\mu }_{0}H-H_{req}\right)/\left(H^{*}-H_{req}\right)$, where $H_{req}<{\mu }_{0}H<H^{*}$.

Clearly, if the MMSMA is constrained to a constant temperature equal to $M_f^{{\mu }_{0}H=0}$ and then $H^{*}$ is applied, the complete M-to-A transition will occur. Moreover, subsequent removal of the field will produce the complete A-to-M transformation, making it cyclically reversible. If the same process was performed above $M_f^{{\mu }_{0}H=0}$, only partial or no transformation will occur on subsequent field cycling.

The magnetization and demagnetization response across the complete magnetic field induced transformation at $M_f^{{\mu }_{0}H=0}$ in NiMnIn is depicted (blue) in Figure 2b up to $H^{*}$. In application, the endothermic reaction resulting from the M-to-A transition during adiabatic loading contributes to the temperature change of the MMSMA. Therefore, if the MMSMA was originally exposed to a magnetic field large enough to initiate transformation (see $H_{req}$ in the figure) at $M_f^{{\mu }_{0}H=0}$, the adiabatic temperature change must be overcome by applying an even greater magnetic field to progress the transformation to completion. For instance, if the complete M-to-A transformation produced $\Delta T_{ad}$ of −5 K, then the temperature barrier that must be overcome to complete the transition could be described by $\left(A_f^{{\mu }_{0}H=0}-(M_f^{{\mu }_{0}H=0}-5 K)\right)$. In terms of quantifying the magnetic field needed to complete the adiabatic transition, we assume the starting temperature is less than $M_f^{{\mu }_{0}H=0}$ by an amount equal to $\Delta T_{ad}$. The magnetic field required to complete the adiabatic transformation at $M_f^{{\mu }_{0}H=0}$, shown in Figure 2b as $H_{ad}^{*}$, was defined as $H_{ad}^{*}=\left(A_f^{{\mu }_{0}H=0}-[M_f^{{\mu }_{0}H=0}-\left|\Delta T_{ad}\right|]\right)d\left({\mu }_{0}H\right)/A_f$, and is again a positive quantity by assuming $d\left({\mu }_{0}H\right)/A_f$ is positive. To illustrate the adiabatic magnetization curve up to $H_{ad}^{*}$, we have depicted an isothermal magnetization curve of our NiMnIn alloy at a temperature lower than $M_f^{{\mu }_{0}H=0}$ (green) and then found the average magnetization response (see dash-dot-dot curve) between the two temperatures. The adiabatic magnetization curve is essential for later development of the analytical CRP, as it defines the input energy required by the MMSMA to achieve the giant MCE.

First-order phase transitions are associated with a change in crystal symmetry (structure), which implies the $G$ is discontinuous at the thermodynamic equilibrium temperature, $T_0$. The free energy above and below $T_0$ describe that of two separate structural phases with independent physical properties including $C_p$, $M$, $V$, etc. At $T_0$, thermodynamic equilibrium between the two phases leads to the well-known CC relations [18,52,53]. According to Equation (1), the $G$ in either phase of the bulk material is influenced by external stimuli including hydrostatic pressure, temperature, and $y_i$ (stress or magnetic field).

In the case of M-to-A first-order structural phase transitions [49,53,54,55] the $G$ of each phase is equivalent at the point of the transition; thus, so is their differential,

$$d{G}^A=d{G}^M.$$

(16)

Since each phase is exposed to the same driving forces at the point of transition,

$$V^{A}dP-S^{A}d{T}_0-{\displaystyle \sum }_{i=1}^n{X}_i^{A}d{y}_i=V^{M}dP-S^{M}d{T}_0-{\displaystyle \sum }_{i=1}^n{X}_i^{M}d{y}_i$$

(17)

Assuming the phase transition occurs in a constant pressure atmosphere, $dP=0$, Equation (17) can be simplified to

$$\left(S^M-S^A\right)d{T}_0={\displaystyle \sum }_{i=1}^n\left(X_i^A-X_i^M\right)d{y}_i$$

(18)

Or

$$\Delta S^{M\to A}={\displaystyle \sum }_{i=1}^n\left(-\Delta X_i^{M\to A}\right)\frac{d{y}_i}{d{T}_0}$$

(19)

where $\Delta S^{M\to A}$ is the entropy change, or difference, between the two phases at $T_0$, $\Delta X_i^{M\to A}$ is the measured change in the i^th extensive property across the first-order transition, and $d{y}_i/d{T}_0$ is the inverse CC slope [53]. For partial transformations, i.e., $\xi <1$, only a fraction of the $\Delta X_i^{M\to A}$ and $\Delta S^{M\to A}$ are achieved.

Equation (19) is applicable to magnetocaloric materials that exhibit first-order magneto-structural phase transitions, such as NiMnIn, where $y_i={\mu }_{0}H$ and $\Delta X_i$ = $\Delta M^{M\to A}$; thus, $\Delta S^{M\to A}=-\Delta M^{M\to A}\xi ·d\left({\mu }_{0}H\right)/d{T}_0$ and $\xi =1$ for a complete transformation. Equation (19) appears to be similar to Equation (7); however, these two expressions were derived under dissimilar thermodynamic conditions and therefore provide the $\Delta S_{iso}$ for fundamentally different processes. There has been much debate in the literature whether Equation (7) and its discretized form [56] are applicable to quantify $\Delta S^{M\to A}$ across first-order transitions [57]. While we recognize the large body of contributing discussions, this topic is out of the scope of the present work.

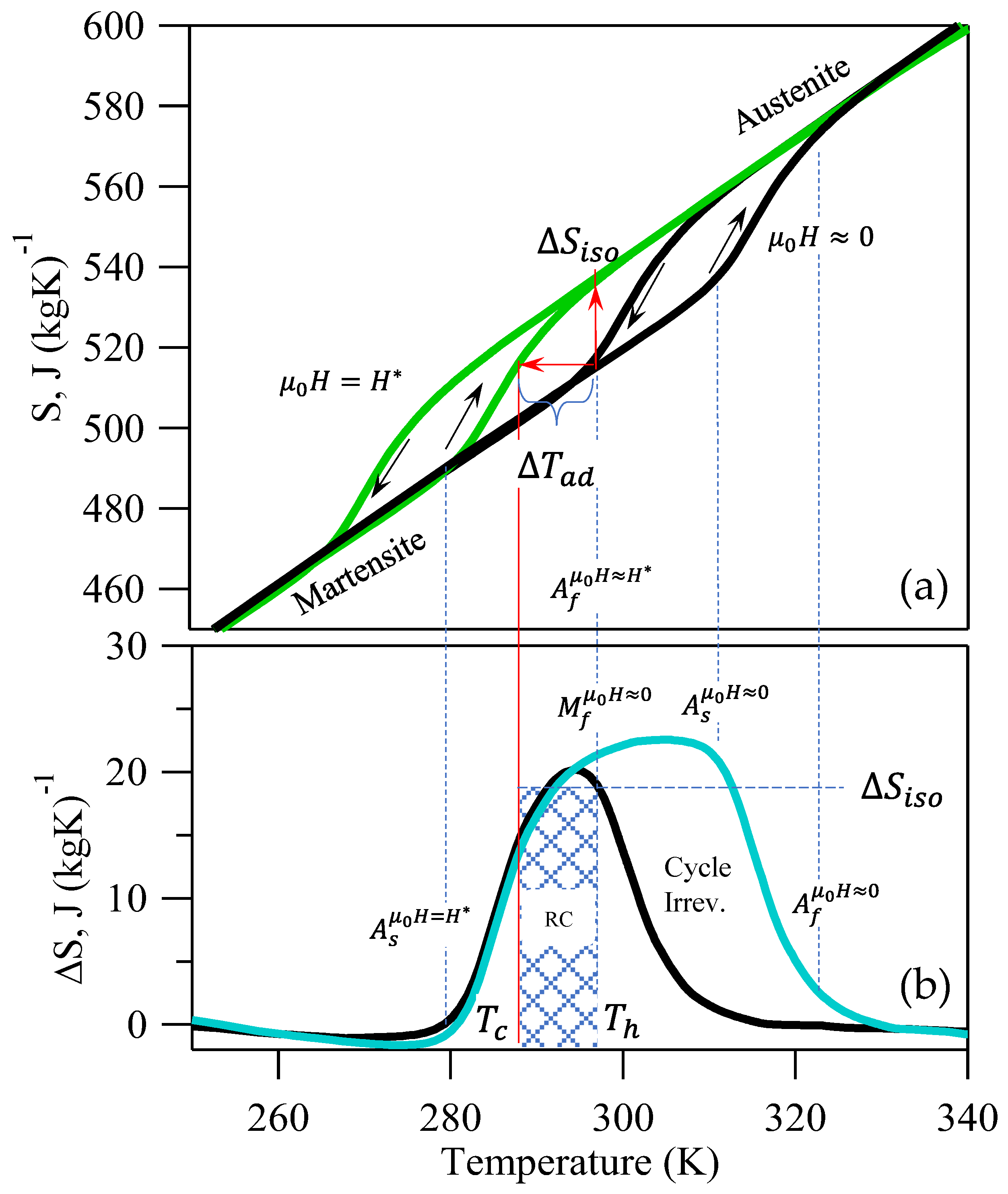
Using the described physics, we aim to develop an analytical form for the CRP that accounts for the cyclic irreversibility in first-order materials. We thus turn our attention to the entropy ($S$) versus temperature ($T$) diagrams, as was done with second-order materials (in Figure 1). The isofield total $S$ vs. $T$ curves are depicted in Figure 3 for our NiMnIn alloy [52]. Since $S$ is an extensive thermodynamic property, its behavior parallels the thermomagnetic response depicted in Figure 2a. On heating the M-phase under no applied magnetic field, the MMSMA undergoes a structural transition starting at the $A_s^{{\mu }_{0}H=0}$ temperature and finishing at $A_f^{{\mu }_{0}H=0}$, as indicated by the abrupt increase in $S$. On subsequent cooling, a thermal hysteresis is clearly observed when the material transforms back to the M-phase, and the $S$ decreases abruptly.

Similar to the thermomagnetic response in Figure 2a, the $S$ vs. $T$ response in Figure 3a depicts a decrease in transformation temperatures under $H^{*}$. It can be seen clearly in Figure 3a that if the MMSMA was originally at the $M_f^{{\mu }_{0}H=0}$ temperature and $H^{*}$ was applied, then $\Delta S_{iso}$ will equal approximately the entropy difference between A and M. Applying this field results in a decrease in critical transformation temperatures.

Using the applied- and zero-field entropy versus temperature ($S-T$) data in Figure 3, the entropy change, $\Delta S$, has been plotted below by computing the difference between the curves. The entropy change versus temperature depicted by the $\Delta S-T$ curve in Figure 3 and the corresponding labels are representative of the physics in all inverse NiMn-based first-order magnetostructural transitions. The cyan curve describing the entropy change represents those which are most commonly reported in giant magnetocaloric studies of MMSMAs [12]. It is crucial to note that the features of the $\Delta S-T$ curve align with critical transformation temperatures from the $S-T$ diagram above, so they have been labeled explicitly.

Typically, in studies on giant MCE materials, the RC is computed using the commonly reported cyan $\Delta S-T$ curve by multiplying $\Delta S_{iso}$ by $T_{FWHM}$, as was done in Equation (15). Note the $T_{FWHM}$ encompasses the thermal hysteresis of the $S-T$ diagram above. If field cycling was performed at a temperature above $M_f^{{\mu }_{0}H=0}$, the MMSMA would only exhibit a partial entropy change on the first field ramping and zero on subsequent, and therefore would be cyclically irreversible—a large difference in the behavior that was described for second-order materials.

As mentioned in Section 2.2, $RC=\Delta S_c\Delta T$, where $\Delta T$ was assumed to equal $T_{FWHM}$, and more recently, $\Delta T=\Delta T_{ad}$ [10,15]. In first-order materials, we propose $\Delta S_c=\Delta S_{iso}$, which is nearly equivalent to the entropy change across the transition (see Equation (19)). It is interesting to note that $T_{FWHM}$ appears to be related to critical transformation temperatures in Figure 3. Since $\Delta T=T_h-T_c$, we assume $T_h=M_f^{{\mu }_{0}H=0}$, or $\Delta T=M_f^{{\mu }_{0}H=0}-T_c$ and $RC=\Delta S_{iso}\Delta T_{ad}$. Note that if $T_h=A_f^{{\mu }_{0}H=0}$, the RC parameter will yield erroneously high values. Since it is assumed that $T_h=M_f^{{\mu }_{0}H=0}$, $\Delta S_{iso}$ will be reversible with field cycling. Moreover, $\Delta T_{ad}$ is expected to be cyclically reversible under these constraints.

Oftentimes, in the literature, $\Delta T_{ad}$ is approximated using Equations (8)–(14) [58] for first-order phase transitions. However, through the author’s experience, this method of computing $\Delta T_{ad}$ often leads to approximations that nearly double that of measured values. In published works, similar discrepancies are typically attributed to non-ideal experimental conditions; however, the author posits that they are the result of neglecting the original assumptions imposed in the development of Equation (8). That is, the expression for $d{S}_{total}$ is only valid for one of the two structural phases that exist across first-order phase transitions, and Equation (8) is not applicable when two or more phases co-exist. In the simplification of Equation (14), we assumed $dS/dT=C_p/T$ from the second law of thermodynamics. However, A and M phases in first-order materials are well-known to exhibit differences in $C_p$ as large as 50 J·kg^-1·K⁻¹ [59]. Conversely, accurate predictions for $\Delta T_{ad}$ have been developed by Cugini and Porcari et al. [16,17], whereby the $S-T$ diagrams (see Figure 3) have been analyzed across first-order phase transitions with a discontinuous change in $G$.

In their work, $\Delta T_{ad}$ was derived across a first-order phase transition in NiMn-based materials through graphical analysis of $S-T$ diagrams, such as those shown in Figure 3. The $\Delta T_{ad}$ was determined by assuming isentropic conditions ($d{S}_{total}=0$, as was performed in deriving Equation (9)) on the same diagram. Cugini and Porcari et al. solved $\Delta T_{ad}$ empirically using similar triangles on the $S-T$ diagram as

$$\Delta T_{ad}=\frac{\Delta S·\xi ·\left(\frac{d{T}_0}{d{y}_i}\right)y_i}{\Delta S·\xi +\left(\frac{d{T}_0}{d{y}_i}\right)y_i·\frac{C_p^M}{T}}$$

(20)

where $C_p^M$ is the isobaric heat capacity of the M phase depicted in Figure 3, and $\Delta S$ is the entropy change produced by applying $y_i$, i.e., $\Delta S^{\left(M\to A\right)}$. It is important to note that, since Equation (20) is empirical, $d{T}_0/d{y}_i$ was assumed to be a positive quantity used in defining the length of one side of the similar triangles. Similar to $H^{*}$, the sign of the CC slope is neglected here and simply represents the sensitivity of the transformation temperatures to an applied field. When comparing $\Delta T_{ad}$ computed using Equations (14) and (20) with measured values across first-order transitions in the literature, it is clear that predictions computed from Equation (20) more closely match experiments [52]. Thus, for developing the analytical CRP, herein, Equation (20) was used to compute $\Delta T_{ad}$ for materials demonstrating first-order magnetostructural transitions.

3.1. Refrigeration Capacity (RC) in First-Order Phase Transforming Materials

In a process similar to that applied to second-order materials, Equations (19) and (20) are substituted into Equation (15) to compute the RC in first-order systems. Assuming that the A-phase in the first-order material is ferromagnetic and the M-phase is non-magnetic, such as those depicted in Figure 2, applying a sufficient magnetic field to the M phase is expected to produce the M-to-A transition. On removing the applied field, the material will return to the M-phase if the temperature was at or below $M_f^{{\mu }_{0}H=0}$.

As such, cycling a sufficient magnitude of magnetic field at temperatures at or below $M_f^{{\mu }_{0}H=0}$ will produce reversible and repeatable entropy or temperature changes in the magnetocaloric solid. Such reversibility is analogous to that of second-order systems. Therefore, from Equations (19) and (20), assuming the only applied force is ${\mu }_{0}H$ under isothermal conditions and that the magnetocaloric material was originally in the M-phase at the $M_f^{{\mu }_{0}H=0}$ temperature, the RC can be defined as

$$RC=\Delta S^{M\to A }\left|\Delta T_{ad}\right|$$

(21)

which simplifies to

$$RC=\frac{1}{\frac{1}{\Delta M^{M\to A}·\xi }\left(\frac{1}{{\mu }_{0}H}+{\left(\frac{d{T}_0}{d\left({\mu }_{0}H\right)}\right)}^2\frac{C_p^M}{\Delta M^{M\to A}·\xi ·M_f^{{\mu }_{0}H=0}}\right)}$$

(22)

where $d{T}_0/d\left({\mu }_{0}H\right)=d{A}_f/d\left({\mu }_{0}H\right)$, and ${\mu }_{0}H$ is, in fact, the isothermally applied magnetic field consistent with Equations (19) and (20) and bound between $H_{req}$ and $H^{*}$. Within these constraints, if ${\mu }_{0}H<H_{req}$, then $RC=0$, and if ${\mu }_{0}H>H^{*}$, the $RC$ will saturate at a maximum.

Per Equation (22), the $RC$ in first-order materials can be approximated using the magnetization change across the magnetostructural transformation, $\Delta M^{M\to A}$, the $A_f$ and $A_s$ temperature field sensitivity, the field-free transformation temperatures, and the heat capacity of the M-phase, $C_p^M$, at $M_f^{{\mu }_{0}H=0}$.

3.2. Coefficient of Performance (CRP) in First-Order Phase Transforming Materials

Recent works [15,34,37,60,61,62,63,64,65] have described the problems in using the RC as a metric to compare the MCE performance of first-order materials because it does not account for the energy input needed to drive the magnetostructural transformation. Moreover, the thermal gradient across which heat is moved is assumed to be the $T_{FWHM}$ (the bigger cyan curve in Figure 3b). A metric that addresses these shortcomings is the coefficient of (refrigeration) performance, CRP, defined as $\eta =\dot{Q}/\dot{W}$, where $\dot{Q}$ is the reversible thermal work that can be achieved using the solid refrigerant, and $\dot{W}$ is the work (in this case magnetic work) required to excite the system. The coefficient of performance applied to a first-order materials was described as [15,37,62]

$$CRP=\frac{RC}{{{\displaystyle \int }}_0^{B_{max}}M\left(T_{Curie},B\right)dB}$$

(23)

where the numerator was the $RC$ in Equation (15), and the denominator was the magnetic work applied to the first-order material at $T_{Curie}$, where $B={\mu }_{0}H$. The magnetic field applied to the first-order material in the present case is at $M_f^{{\mu }_{0}H=0}$. As shown for completely reversible first-order transitions with field cycling, $T_{Curie}$ in Equation (23) must equal $M_f^{{\mu }_{0}H=0}$. In the literature, the CRP was tabulated with Equation (23) for various materials using different quantities for $\Delta T$ for the $RC$ in the numerator [37]. $\Delta T$ has been assumed to be $T_{FWHM}$ of the $\Delta S-T$ curve, $\Delta T_{ad}$, or $\Delta T_{cyclic}$, where $\Delta T_{cyclic}$ was described to be the cyclically reversible $\Delta T_{ad}$ at $T_{Curie}$. Since no standard is used in the literature, CRPs greater than unity were found when assuming $\Delta T=T_{FWHM}$, because the effect of hysteresis was not removed from the calculation [37]. In these past works, it is still unclear whether (1) $\Delta T_{ad}$ was computed using Equations (14) or (20) or was from direct measurement, and (2) if $T_{Curie}$ in Equation (23) corresponded to a thermodynamic equilibrium temperature, $T_0$. In the NiMn-based material mentioned above, the ferromagnetic A-phase exhibited its own ferromagnetic $T_{Curie}$, which is often above $A_f^{{\mu }_{0}H=0}$. Thus, $T_{Curie}\ne M_f^{{\mu }_{0}H=0}$.

3.3. Analytical Approach for Computing the CRP in First-Order Phase Transforming Materials

In the present work, $RC=\Delta S^{M\to A}\left|\Delta T_{ad}\right|$ as imposed by the bounds defining the $RC$-, i.e., the first-order material is only cyclically reversible, and thus comparable to second-order materials when excited at or below $M_f^{{\mu }_{0}H=0}$. As such, the numerator in Equation (23) has been defined by Equation (22). Furthermore, we have defined $T_h=M_f^{{\mu }_{0}H=0}$, and the denominator of Equation (23) has become ${{\displaystyle \int }}_0^{B_{max}}M\left(M_f^{{\mu }_{0}H=0},B\right)dB$ to be consistent with $\Delta S-T$ diagram in Figure 3.

In application, the $\Delta T_{ad}$ is achieved by ramping the magnetic field on the first-order material in thermally insulated conditions, and therefore, the magnetic field required to achieve the full temperature and entropy change at $T_h=M_f^{{\mu }_{0}H=0}$ was defined by $H_{ad}^{*}$ (see Section 3) and is depicted in Figure 2b. The magnetization change across the complete martensitic transition was defined as $\Delta M^{M\to A}$, and therefore, the denominator of Equation (23) has been approximated as the area of a triangle (see magnetization response in Figure 2b), or

$$\dot{W}=\underset{0}{\overset{H_{ad}^{*}}{{\displaystyle \int }}}M\left(M_f^{{\mu }_{0}H=0}, {\mu }_{0}H\right)d{H}_{ad}^{*}\approx \frac{1}{2}{H}_{ad}^{*}\left(\Delta M^{M\to A}·\xi \right)$$

(24)

Substituting Equations (24) and (22) in to Equation (23), and assuming $H_{ad}^{*}=\left(A_f^{{\mu }_{0}H=0}-\left\{M_f^{{\mu }_{0}H=0}-\left|\Delta T_{ad}\right|·\xi \right\}\right)d\left({\mu }_{0}H/d{A}_f\right)$, per the above descriptions, results in the analytical form of the CRP for first-order materials. The analytical CRP reduces to

$$CRP=\frac{\left(\frac{1}{\frac{1}{\Delta M^{M\to A}·\xi }\left(\frac{1}{{\mu }_{0}H}+{\left(\frac{d{A}_f}{d\left({\mu }_{0}H\right)}\right)}^2\frac{C_p^M}{\Delta M^{M\to A}·\xi ·M_f^{{\mu }_{0}H=0}}\right)}\right)}{\frac{1}{2}\left(A_f^{{\mu }_{0}H=0}-\{M_f^{{\mu }_{0}H=0}-\left|\Delta T_{ad}\right|·\xi \}\right)\left(\frac{d\left({\mu }_{0}H\right)}{d{A}_f}\right)·\Delta M^{M\to A}·\xi }$$

(25)

and is confirmed to be a dimensionless parameter, with limits from zero to unity, that can be quantified with basic and commonly reported materials properties in giant inverse MCE materials. The $d{A}_f/d\left({\mu }_{0}H\right)$ in Equation (25) is assumed to be a positive quantity as a result of employing Equation (20) to empirically quantify $\Delta T_{ad}$. In a previous work [15], the community was encouraged to publish complete datasets, so that the CRP could be computed with numerically integrated digitized magnetization loops; however, here we find that the CRP can be approximated with $\Delta M^{M\to A}$, $d{A}_f/d\left({\mu }_{0}H\right)$, $d{A}_s/d\left({\mu }_{0}H\right)$, $M_f^{{\mu }_{0}H=0}$, $A_s^{{\mu }_{0}H=0}$, $A_f^{{\mu }_{0}H=0}$, and $C_p^M$ from only a few basic thermal and thermomagnetic experiments. Moreover, binding $T_h$ to $M_f^{{\mu }_{0}H=0}$ ensures that the CRP will be computed for only the reversible part of first-order transformations, which then lends the ability to employ the metric to compare the performance of first-order materials that undergo magnetostructural transformations and hysteresis with those that do not, i.e., purely ferromagnetic coolants.

4. Comparison of CRP in NiMn-Based Meta-Magnetic SMA

The analytical form of the CRP was given in Equation (25), which was defined by physically meaningful and fundamental materials properties. The metric can be used to compare the performance of magnetic refrigerants that exhibit inverse first-order magnetostructural transformations. Moreover, it allows for a uniform comparison in performance in both second-order and first-order materials. Thus, it can serve as a materials design tool to determine the optimal candidate for a solid-state cooling application with a specific $T_h$ and applied field level. In the present case, $T_h$ is bound to $M_f^{{\mu }_{0}H=0}$, and $T_c$ is defined as $M_f^{{\mu }_{0}H=0}-\left|\Delta T_{ad}\right|$. Note that the CRP is expected to be zero if ${\mu }_{0}H<H_{req}$, which would suggest that the thermal hysteresis and ($A_s^{{\mu }_{0}H=0}-M_f^{{\mu }_{0}H=0})$ is too large in comparison with $d{A}_s/d\left({\mu }_{0}H\right)$ for any meaningful phase change to take place [66].

To demonstrate the use of the analytic CRP, data for inverse MCE materials were tabulated in

Table 1. CRP computed with Equation (25) for NiMn-based MSMAs with an applied field of 5 Tesla.

Alloy Composition [at.%]	${\mathit{C}}_{\mathit{p}}^{\mathit{M}}$ [J ⋅ (kgK)−1]	$\Delta {\mathit{M}}^{\mathit{M}\to \mathit{A}}$ [emu ⋅ g−1]	${\mathit{M}}_{\mathit{f}}^{{\mathit{\mu }}_0\mathit{H}=0}$ [K]	${\mathit{A}}_{\mathit{s}}^{{\mathit{\mu }}_0\mathit{H}=0}$ [K]	${\mathit{A}}_{\mathit{f}}^{{\mathit{\mu }}_0\mathit{H}=0}$ [K]	$\frac{\mathit{d}{\mathit{A}}_{\mathit{s}}}{\mathit{d}\left({\mathit{\mu }}_0\mathit{H}\right)}$ [K · T−1]	$\frac{\mathit{d}{\mathit{A}}_{\mathit{f}}}{\mathit{d}\left({\mathit{\mu }}_0\mathit{H}\right)}$ [K · T−1]	CRP	Ref.
Ni40Co10Mn33Al17	488+	104	319	349	372	−4.60	−2.73	0.00	[67]
Ni40Co10Mn34Al16	500+	75	369	388	403	−1.58	−0.43	0.00	[67]
Ni45Co5Mn32Al18	469+	43	254	261	290	−0.86	−0.14	0.00	[67]
Ni26.5Co5.5Mn48Ga20	390+	70	109	162	175	−4.00	−4.00	0.00	[68]
Ni41Co9Mn31Ga19	390+	110	202	253	278	−8.14	−7.04	0.00	[69]
Ni43Co7Mn30Ga20	390+	110	197	212	220	−4.93	−3.52	0.30	[69]
Ni40Co10.8Mn31.4Ga16.5In1.4	480	53	325	355	389	−4.50	−4.50	0.00	[70]
Ni41.7Co8.1Mn33.3Ga13.8In3.2	480	49	330	350	380	−3.50	−3.50	0.00	[70]
Ni41.7Co8.6Mn32.3Ga14.1In3.3	480	62	310	333	355	−4.60	−4.60	0.00	[70]
Ni42.4Co7.1Mn33.0Ga15.3In2.3	480	16	370	380	388	−2.40	−2.40	0.12	[70]
Ni45Co5Mn36.5In13.5 *	350+	125	238	254	277	−10.50	−10.50	0.29	[47]
Ni49.8Co1.2Mn33.5In25.5	350	90	242	250	256	−4.90	−4.90	0.65	[71]
Ni45.2Co5.1Mn36.7In13	350	98	311	317	327	−5.50	−5.50	0.66	[71]
Ni45Co5Mn37.5In12.5	480	60	358	368	383	−3.38	−3.78	0.34	[71]
Ni45Co5Mn38Sb12	380+	60	245	260	280	−1.63	−1.63	0.00	[72]
Ni45Co5Mn38Sb12	380+	62	253	272	280	−2.28	−1.90	0.00	[73]
Ni41Co9Mn39Sb11	380+	105	251	260	269	−3.18	−3.50	0.67	[74]
Ni43Co4Mn42Sn11	423	73	189	216	243	−3.85	−3.85	0.00	[12]
Ni43Co4Mn42Sn11	418	84	185	214	230	−4.35	−4.35	0.00	[12]
Ni43Co4Mn42Sn11	433	79.3	198	224	233	−4.55	−4.55	0.00	[12]
Ni43Co4Mn42Sn11	455	67	213	232	246	−4.17	−4.17	0.06	[12]
Ni43Co4Mn42Sn11	430	81	193	217	225	−4.35	−4.35	0.00	[12]
Ni43Co4Mn42Sn11	452	73	209	230	240	−3.70	−3.70	0.00	[12]
Ni43Co4Mn42Sn11	452	84	210	229	238	−4.00	−4.00	0.07	[12]
Ni43Co6Mn40Sn11	420	50	263	279	287	−4.55	−3.64	0.19	[75]
Ni45.2Co5.1Mn37.0Sn12.7	450	92	251	260	285	−3.57	−3.57	0.23	[76]
Ni50Co1Mn36Sn13	405	45	270	280	309	−0.93	−0.93	0.00	[77]
Ni43Co7Mn39Sn11	420	85	282	295	300	−3.57	−3.29	0.58	[42]
Ni45.5Co5.0Mn37.2Sn12.3	450	63	321	327	344	−1.64	−1.64	0.20	[76]
Ni46Cu4Mn38Sn12	590	60	269	283	291	−0.53	−0.53	0.00	[78]
Ni54Fe1Mn20Ga25	420+	60	276	284	302	−5.00	−5.00	0.36	[79]
Ni52Fe3Mn20Ga25	405+	80	230	242	250	−1.31	−1.31	0.00	[79]
Ni53Fe2Mn20Ga25	416+	70	268	279	288	−1.12	−1.12	0.00	[79]
Ni50Mn31Al19	484+	7	303	310	322	−0.14	−0.58	0.00	[67]
Ni55Mn20Ga25	439+	50	310	317	337	−1.83	−1.83	0.12	[79]
Ni50.4Mn34.8In14.8	358+	110	181	191	200	−9.04	−9.55	0.38	[58]
Ni50Mn36In14	400	16	340	344	351	−0.19	−0.22	0.00	[52]
Ni49.8Mn35In15.2	372+	97	231	238	243	−9.55	−8.04	0.56	[58]
Ni50Mn34.5In15.5	366	69	259	265	271	−5.70	−5.05	0.61	[52]
Ni50Mn35.5In14.5	400	6.7	325	331	337	−0.85	−0.28	0.00	[52]
Ni50Mn35In15	372	41	294	296	303	−3.0	−0.85	0.55	[52]
Ni37Mn54Sn9	386+	57	208	224	243	−1.40	−1.40	0.00	[80]

⁺$C_p^M$ was approximated using Thermocalc * Alloy is single crystal.

for over forty MMSMAs with various compositions. We found that $C_p^M$ and $d{A}_s/d\left({\mu }_{0}H\right)$ were scarce in the literature; therefore, Thermocalc was employed to approximate $C_p^M$ at $M_f^{{\mu }_{0}H=0}$ for a few of the compositions and the $d{A}_s/d\left({\mu }_{0}H\right)$, which was needed to compute $H_{req}$, were obtained through digitization of commonly reported isofield thermomagnetization curves. The CRP was computed for each alloy, assuming 5 T was applied at the $M_f^{{\mu }_{0}H=0}$ temperature.

As shown in Table 1, nearly half of the listed MMSMA exhibited a non-zero CRP. The alloys that exhibited a CRP of zero required $H_{req}>$ 5 T. Since no M-to-A transformation would be generated by applying 5 T, for these alloys, the RC, i.e., the numerator of the CRP, was also zero. A larger applied field would result in more alloys exhibiting a non-zero CRP, because a M-to-A transformation may begin to take place. By subjecting all the MMSMAs listed in Table 1 to the same applied field, the alloys most suitable for a given MCE application could be identified as those with the largest CRP. Interestingly, the alloys containing indium offered the most prevalent non-zero CRP for all the NiMn-based MMSMAs with an applied field of 5 T.

Upon inspecting values in Table 1, the CRP was non-intuitive and could not be simply predicted using a single material property, such as $d{A}_f/d\left({\mu }_{0}H\right)$. A parametric analysis of each material property would reveal its effect on CRP and would provide a clearer understanding of the important factors dictating performance. Prior to performing a parametric analysis, the CRP was computed for an architype MMSMA to use as a reference. Ni₅₀Mn₃₅In₁₅ at.% was selected as the archetypal alloy, which exhibited the properties listed in

Table 2. Properties of archetype Ni₅₀Mn₃₅In₁₅ at.% MMSMA polycrystals and their typical upper and lower bounds for parametric analysis [52].

Property	Value in Ni50Mn35In15 at.%	Lower Bound	Upper Bound	Unit
$M_f^{{\mu }_{0}H=0}$	294	109	370	K
$A_s^{{\mu }_{0}H=0}$	296	162	388	K
$A_f^{{\mu }_{0}H=0}$	303	175	403	K
$\Delta M$	41	7	125	emu · g−1
$C_p^M$	372	350	590	J · kg−1K−1
$d{A}_s/d\left({\mu }_{0}H\right)$	−3.0	−0.14	−10.50	K · T−1
$d{A}_f/d\left({\mu }_{0}H\right)$	−0.85	−0.14	−10.50	K · T−1

. Using the characterization parameters in Table 2, the Ni₅₀Mn₃₅In₁₅ alloy exhibited a $H^{*}$ of 10.5 T, a $H_{req}$ of 0.6 T, and a $H_{ad}^{*}$ of 19 T. Thus, if ${\mu }_{0}H$ = 5 T, nearly 44% of the M-to-A transformation would take place at $M_f^{{\mu }_{0}H=0}$. This material would offer a $\Delta T_{ad}$ of 7.2 K, RC of 71.6 J·kg⁻¹ and would require 128.5 J ·kg⁻¹ to drive 44% of the transformation, resulting in a CRP of 0.55.

With the cumulative data in Table 1 for all the NiMn-based MMSMA compositions, upper and lower bounds in $\Delta M^{M\to A}$, $C_p^M$, $M_f^{{\mu }_{0}H=0}$, $A_s^{{\mu }_{0}H=0}$, $A_f^{{\mu }_{0}H=0}$, $d{A}_f/d\left({\mu }_{0}H\right)$, and $d{A}_s/d\left({\mu }_{0}H\right)$ were identified and listed in Table 2. These bounds were used to perform a parametric analysis in the CRP (Equation (25)) as a function of the given material property. The other properties (not varied) were those of the architype NiMnIn alloy.

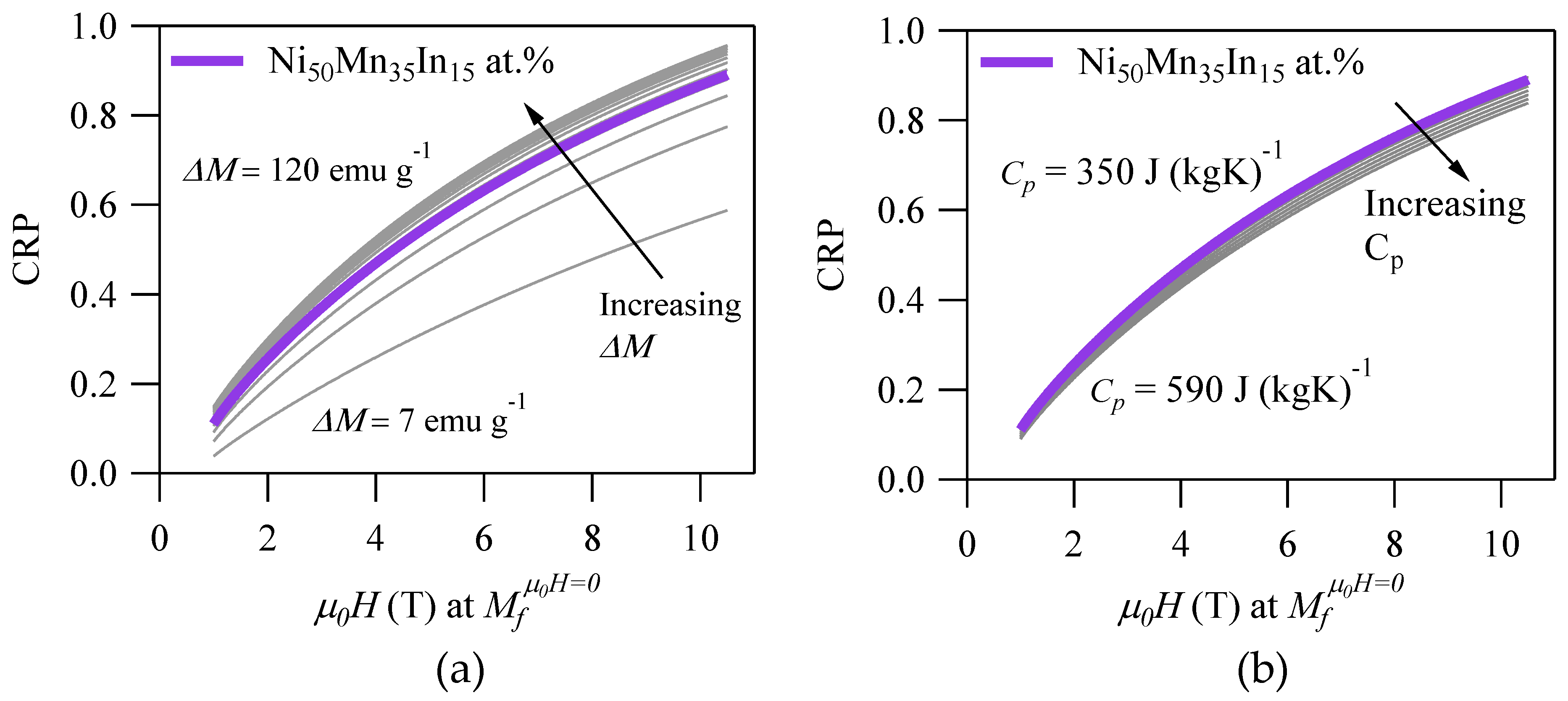
For instance, Figure 4a depicts the CRP vs. ${\mu }_{0}H$ for various $\Delta M^{M\to A}$ within the bounds in Table 2. From the figure, it is clear that the CRP would be reduced significantly for alloys that exhibit $\Delta M^{M\to A}$ < 27 emu·g⁻¹. In practice, this would eliminate MMSMAs that are characterized by a paramagnetic austenite from consideration for MCE applications. By decreasing $\Delta M^{M\to A}$ from 27 emu·g⁻¹ to only 7 emu·g⁻¹, the CRP would be reduced by 25% when cycling $H^{*}$. The CRP exhibited less sensitivity to $\Delta M$ above 27 emu·g⁻¹, and therefore, this value should be used as a threshold when selecting materials for MCE applications.

Figure 4b depicts the CRP vs. ${\mu }_{0}H$ for various $C_p^M$. Since the $C_p^M$ is present in only one term of the $\Delta T_{ad}$ in Equation (20), and the ratio of the highest to lowest values as given in Table 2 is low (a factor of two times, compared to nearly 17 times for $\Delta M^{M\to A}$), the effect to the CRP is minor. Nonetheless, lower values would obviously produce greater $\Delta T_{ad}$ and a higher RC. Higher $\Delta T_{ad}$ would, in turn, increase $H_{ad}^{*}$, which might decrease the CRP, because greater magnetic work would need to be applied to the material to generate the cooling effect. Thus, the CRP of an alloy may be increased by decreasing $C_p^M$, although the change is relatively small.

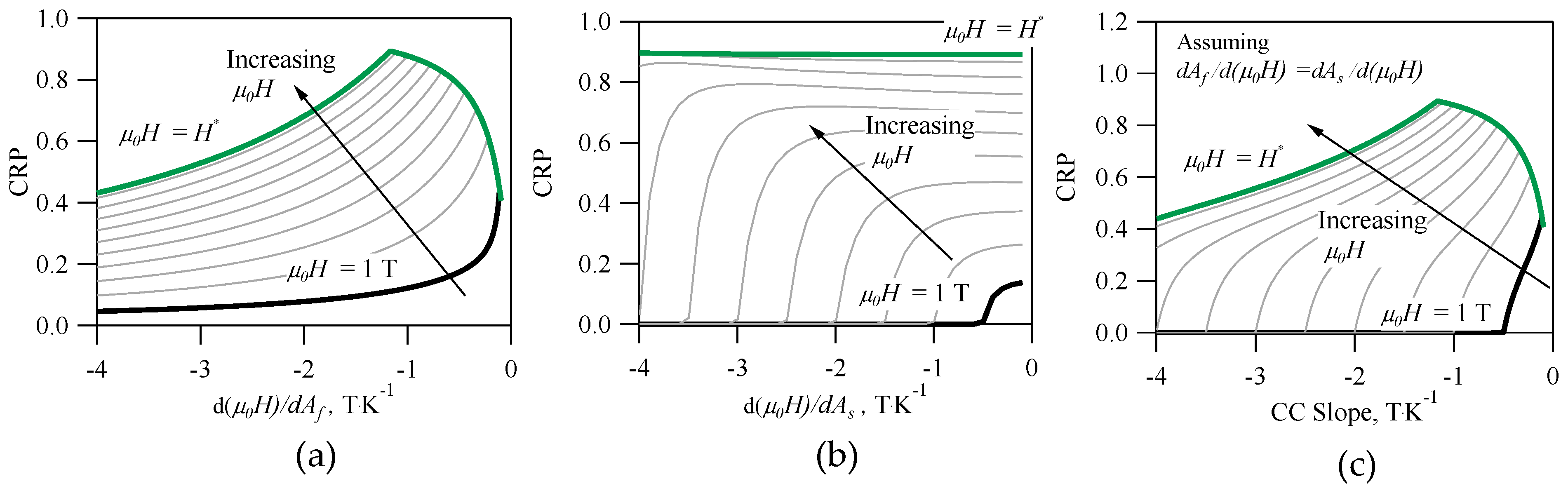
Finally, Figure 5a–c depict the CRP vs. inverse CC slopes for an alloy with the same properties as the architype NiMnIn. The inverse CC slopes appear to have the greatest influence on the CRP out of all the material properties in Equation (25). This is not surprising, because the entropy change, or $\Delta S^{M\to A}$ in Equation (19), depends on the inverse CC slope. In Figure 5a, the CRP is depicted as a function of $d\left({\mu }_{0}H\right)/d{A}_f$ for ${\mu }_{0}H$ = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 10.5 Tesla. For the Ni₅₀Mn₃₅In₁₅ alloy, $H^{*}$ = 10.5 T. As mentioned earlier, $d{A}_f/d\left({\mu }_{0}H\right)$ was used to compute $H_{ad}^{*}$, $H^{*}$, and the RC in Equation (22); therefore, the influence of $d\left({\mu }_{0}H\right)/d{A}_f$ on the CRP is highly nonlinear. Interestingly, the results in Figure 5a suggest an optimum may exist in the CRP, which appears to be dependent on ${\mu }_{0}H$. For example, if the cycled magnetic field was ${\mu }_{0}H$ = 2 T, a CRP of 0.61 would be achievable if $d{A}_f/d\left({\mu }_{0}H\right)$ = −4.5 K·T⁻¹. If ${\mu }_{0}H$ = 5 T, a CRP of 0.79 would be achievable if $d{A}_f/d\left({\mu }_{0}H\right)$ = −1.81 K·T⁻¹. Under the given framework, an absolute maximum in the CRP of 0.89 is attainable if $H^{*}$ was applied to the Ni₅₀Mn₃₅In₁₅ alloy as long as $d{A}_f/d\left({\mu }_{0}H\right)$ = −0.85 K·T⁻¹. The maximum CRP rapidly decreases if the magnitude of $d{A}_f/d\left({\mu }_{0}H\right)$ is less −0.85 K·T⁻¹. Many, but not all, of the compositions in Table 1 that exhibit a CRP of zero also exhibit a $d{A}_f/d\left({\mu }_{0}H\right)$ with a magnitude less than −0.85 K·T⁻¹.

Similarly, the CRP vs. $d\left({\mu }_{0}H\right)/d{A}_s$ was plotted in Figure 5b for an alloy with materials properties matching those of Ni₅₀Mn₃₅In₁₅ at.%. The $d{A}_s/d\left({\mu }_{0}H\right)$ parameter was only used in quantifying $H_{req}$, therefore affecting $\xi$ for a given ${\mu }_{0}H$. The $d{A}_s/d\left({\mu }_{0}H\right)$ parameter does not appear to affect the maximum attainable CRP; however, the results in Figure 5b can be used to determine acceptable ${\mu }_{0}H$ needed achieve a non-zero CRP.

In most literature, only one CC slope is reported, i.e., the thermodynamic equilibrium point of the forward (A-to-M) martensitic transformation, but in most MMSMAs, there are four separate CC slopes. In the case of the inverse MCE, we focus on the reverse (M-to-A) martensitic transformation, and therefore, the $d{A}_s/d\left({\mu }_{0}H\right)$ and $d{A}_f/d\left({\mu }_{0}H\right)$ slopes are the most important. Assuming the thermodynamic equilibrium from M-to-A at the $A_f^{{\mu }_{0}H=0}$ and $A_s^{{\mu }_{0}H=0}$ exhibit the same sensitivity to ${\mu }_{0}H$, the CRP vs. the inverse CC slope would exhibit features from both Figure 5a,b, as depicted in Figure 5c. In Figure 5c, non-zero CRP is attained at specific inverse CC slopes and ${\mu }_{0}H$ that also correspond to some CRP maximum.

5. Conclusions and Future Work

In the present work, an analytical approach for computing the coefficient of refrigeration performance (CRP) was described in the context of the giant inverse magnetocaloric effect (MCE), whereby discretized isothermal magnetization data were not required to compute the input work. The framework developed for computing the CRP from first-order magnetostructural and meta-magnetic transformations was intended to mirror the cyclic reversibility attainable in second-order and strictly magnetic transitions. While computing the refrigeration capacity (RC), we found that cyclic reversibility was achieved if the “hot temperature reservoir”, namely $T_h$, was bound to the zero-field martensite finish temperature, $M_f^{{\mu }_{0}H=0}$. Due to this limitation, not all first-order meta-magnetic transformations were capable of exhibiting non-zero RC or CRP.

A parametric analysis of the analytical CRP was performed, revealing that optimum Clausius–Clapeyron (CC) slopes may exist for a given magnitude of an applied magnetic field. Moreover, we found that the CRP can be maximized by ensuring a magnetization change across the martensitic transition, $\Delta M^{M\to A}$, is greater than 27 emu·g⁻¹, which suggests non-magnetic martensite-to-paramagnetic austenite transformations are not useful for giant MCE applications.

Finally, due to the highly nonlinear behavior of the CRP with respect to the CC slopes, NiMnIn and NiMnSn alloys were found to exhibit the most favorable properties for giant inverse MCE applications when compared to over forty meta-magnetic shape memory alloys. This was attributed to the favorable CC slopes, $\Delta M^{M\to A}$, and $C_p^M$. In future work, we aim to employ the given framework to compare the CRP in first-order MCE materials with that in second-order materials at their respective $T_h$ (or $M_f^{{\mu }_{0}H=0}$) to identify the most favorable compositions for a specific application and operating temperature interval.