Energy Storage Flywheel Rotors—Mechanical Design
Definition
1. Introduction
2. Applications and Performance
3. Manufacture
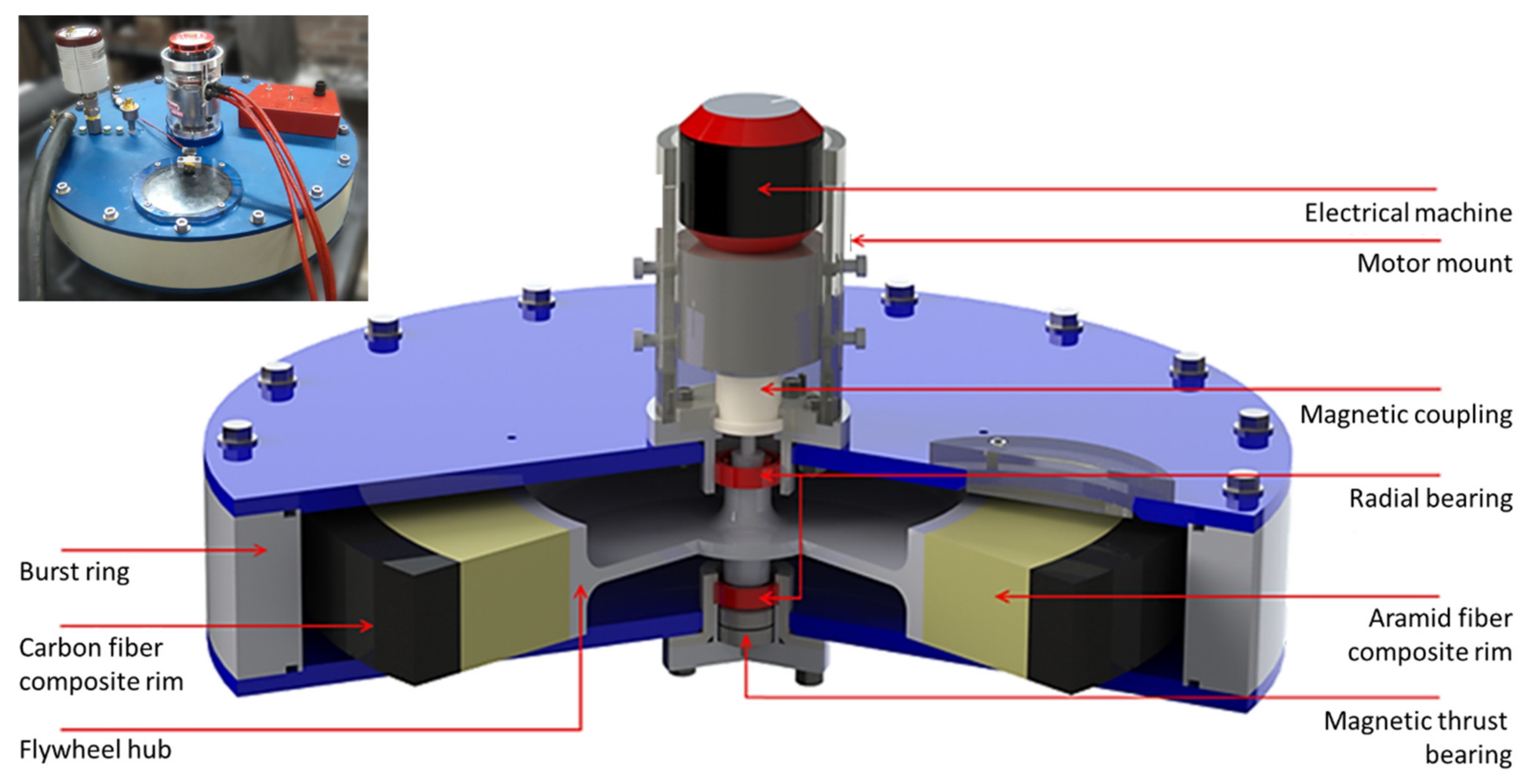
3.1. Hub Construction
3.2. Rim Construction
3.3. Assembly
4. Analytical Modeling
4.1. Energy Storage and Power Capacity
4.2. Material Characterization
4.2.1. Hygroscopic Effects
4.2.2. Temperature Effects
4.2.3. Aging Effects
4.2.4. Stress Magnitude
4.3. Quasi-Static Analysis
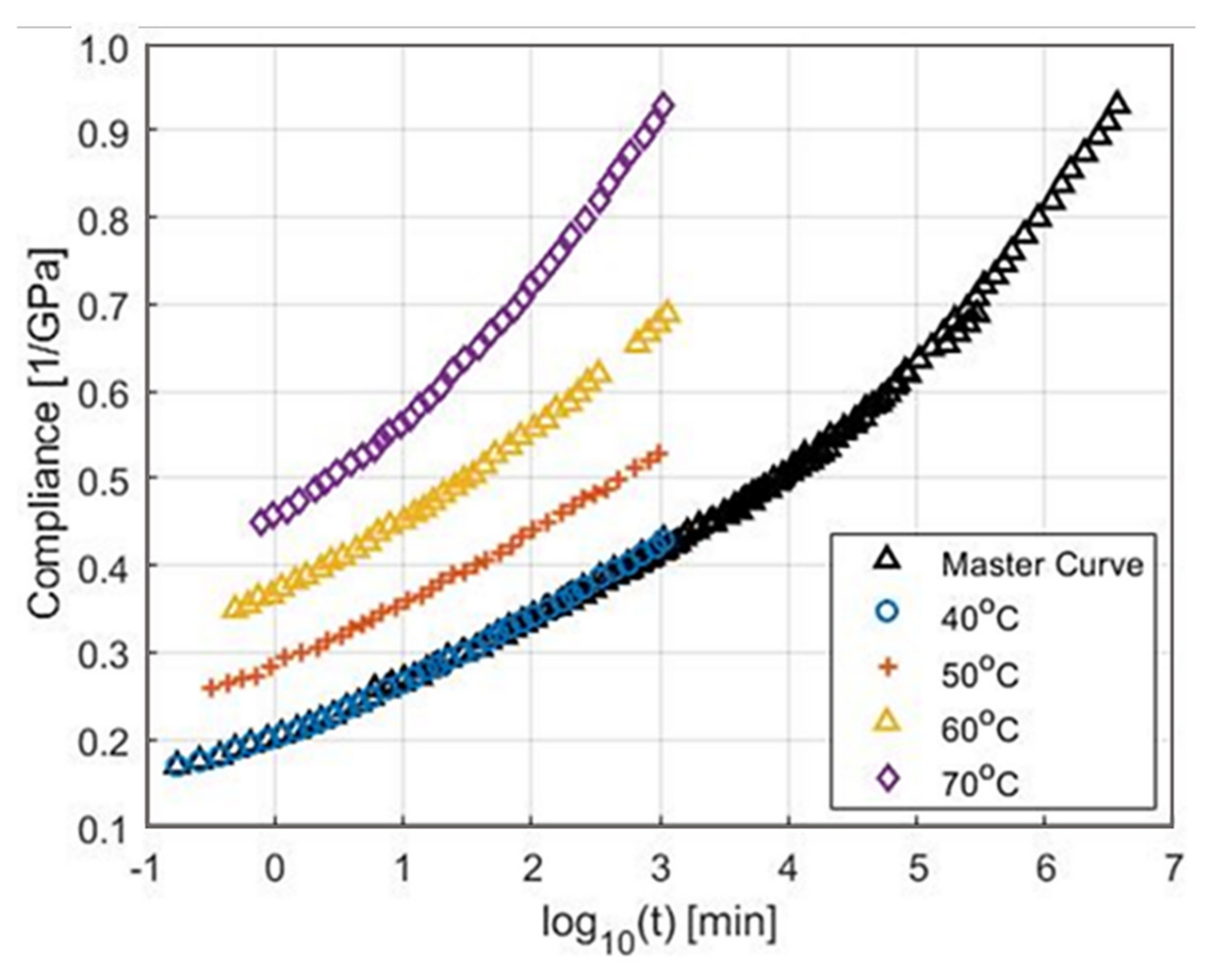
4.4. Viscoelastic Analysis
4.5. Shear Stress
5. Failure Analysis
5.1. Failure Criteria
5.2. Maximum Stress Criterion
5.3. Tsai-Wu Criterion
5.4. Progressive Failure Analysis
6. Conclusions and Prospects
Author Contributions
Funding
Conflicts of Interest
Entry Link on the Encyclopedia Platform
References
- British Petroleum Statistical Review of World Energy. Globally Consistent Data on World Energy Markets and Authoritative Publications in the Field of Energy; British Petroleum: London, UK, 2021; Volume 70. [Google Scholar]
- Chen, H.; Cong, T.N.; Yang, W.; Tan, C.; Li, Y.; Ding, Y. Progress in electrical energy storage system: A critical review. Prog. Nat. Sci. 2009, 19, 291–312. [Google Scholar] [CrossRef]
- Kåberger, T. Progress of renewable electricity replacing fossil fuels. Glob. Energy Interconnect. 2018, 1, 48–52. [Google Scholar] [CrossRef]
- Moriarty, P.; Honnery, D. Can renewable energy power the future? Energy Policy 2016, 93, 3–7. [Google Scholar] [CrossRef]
- Hadjipaschalis, I.; Poullikkas, A.; Efthimiou, V. Overview of current and future energy storage technologies for electric power applications. Renew. Sustain. Energy Rev. 2009, 13, 1513–1522. [Google Scholar] [CrossRef]
- Denholm, P.; O’Connell, M.; Brinkman, G.; Jorgenson, J. Overgeneration from Solar Energy in California: A Field Guide to the Duck Chart; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2015.
- Amiryar, M.E.; Pullen, K.R. A review of flywheel energy storage system technologies and their applications. Appl. Sci. 2017, 7, 286. [Google Scholar] [CrossRef]
- Sabihuddin, S.; Kiprakis, A.E.; Mueller, M. A numerical and graphical review of energy storage technologies. Energies 2015, 8, 172–216. [Google Scholar] [CrossRef]
- Ilan, D. The ground stone components of drills in the ancient Near East: Sockets, flywheels, cobble weights, and drill bits. J. Lithic Stud. 2016, 3, 261–277. [Google Scholar] [CrossRef]
- Skinner, M. Characterization of Passibe Sischarge Losses in a Flywheel Energy Storage System. Masters’s Thesis, University of Alberta, Edmonton, AB, Canada, 2017. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Hebner, R.; Beno, J.; Walls, A. Flywheel batteries come around again. IEEE Spectr. 2002, 39, 46–51. [Google Scholar] [CrossRef]
- Bolund, B.; Bernhoff, H.; Leijon, M. Flywheel energy and power storage systems. Renew. Sustain. Energy Rev. 2007, 11, 235–258. [Google Scholar] [CrossRef]
- Krack, M.; Secanell, M.; Mertiny, P. Rotor Design for High-Speed Flywheel Energy Storage Systems. In Energy Storage in the Emerging Era of Smart Grids; InTech: London, UK, 2011. [Google Scholar]
- Skinner, M.; Suess, M.; Secanell, M.; Mertiny, P. Design of a Composite Flywheel Rotor For Long-Term Energy Storage in Residential Applications. In Proceedings of the The Canadian Society of Mechanical Engineering International Congress, Kelowna, BC, Canada, 26–29 June 2016; pp. 1–5. [Google Scholar]
- Skinner, M.; Mertiny, P. Effects of Viscoelasticity on the Stress Evolution over the Lifetime of Filament-Wound Composite Flywheel Rotors for Energy Storage. Appl. Sci. 2021, 11, 9544. [Google Scholar] [CrossRef]
- Pullen, K. The Status and Future of Flywheel Energy Storage. Joule 2019, 3, 1394–1399. [Google Scholar] [CrossRef]
- The GYROBUS: Something New Under the Sun? Motor Trend, January 1952; 37.
- Wakefield, E. History of the Electric Automobile: Hybrid Electric Vehicles; Society of Automotive Engineers: Warrendale, PA, USA, 1998; ISBN 978-0-7680-0125-9. [Google Scholar]
- Weiss, C.C. Volvo Confirms Fuel Savings of 25 Percent with Flywheel KERS. Available online: https://newatlas.com/volvo-flywheel-kers-testing/27273/ (accessed on 9 December 2021).
- Porche GT3R Technical Specs. Available online: https://www.porsche.com/international/_iceland_/motorsportandevents/motorsport/customerracing/racingcars/991-2nd-gt3-r/ (accessed on 9 December 2021).
- Rupp, A.; Baier, H.; Mertiny, P.; Secanell, M. Analysis of a Flywheel Energy Storage System for Light Rail Transit. Energy 2016, 107, 625–638. [Google Scholar] [CrossRef]
- Tarrant, C. Kinetic Energy Storage Wins Acceptance. Available online: https://www.railwaygazette.com/kinetic-energy-storage-wins-acceptance/27250.article (accessed on 9 December 2021).
- NRStor Inc. 2 MW Minto Flywheel Facility: A Fast-Ramping Resource for Grid Regulation and Other Electricity Services. Available online: http://nrstor.com/2019/11/21/2-mw-minto-flywheel-facility-market-impact-case-study-power-advisory/ (accessed on 9 December 2021).
- Beacon Power, Operating Plants Stephenton, New York. Available online: https://beaconpower.com/stephentown-new-york/ (accessed on 9 December 2021).
- Amber Kinetics. The World’s Only Flywheel Innovation Hub. Available online: https://amberkinetics.com/installation/the-worlds-only-flywheel-innovation-hub/ (accessed on 9 December 2021).
- Genta, G. Kinetic Energy Storage: Theory and Practice of Advanced Flywheel Sysstems; Butterworth-Heinemann: London, UK, 2014; ISBN 0-408-01396-6. [Google Scholar]
- Ha, S.K.; Han, H.H.; Han, Y.H. Design and manufacture of a composite flywheel press-fit multi-rim rotor. J. Reinf. Plast. Compos. 2008, 27, 953–965. [Google Scholar] [CrossRef]
- Kale, V.; Thomas, M.; Secanell, M. On determining the optimal shape, speed, and size of metal flywheel rotors with maximum kinetic energy. Struct. Multidiscip. Optim. 2021, 64, 1481–1499. [Google Scholar] [CrossRef]
- Wang, Y.; Dai, X.; Wei, K.; Guo, X. Progressive failure behavior of composite flywheels stacked from annular plain profiling woven fabric for energy storage. Compos. Struct. 2018, 194, 377–387. [Google Scholar] [CrossRef]
- Ornaghi, H.L.; Neves, R.M.; Monticeli, F.M.; Almeida, J.H.S. Viscoelastic characteristics of carbon fiber-reinforced epoxy filament wound laminates. Compos. Commun. 2020, 21, 100418. [Google Scholar] [CrossRef]
- Takkar, S.; Gupta, K.; Tiwari, V.; Singh, S.P. Dynamics of Rotating Composite Disc. J. Vib. Eng. Technol. 2019, 7, 629–637. [Google Scholar] [CrossRef]
- Eggers, F.; Almeida, J.H.S.; Azevedo, C.B.; Amico, S.C. Mechanical response of filament wound composite rings under tension and compression. Polym. Test. 2019, 78, 105951. [Google Scholar] [CrossRef]
- Rejab, R.; Kumar, N.M.; Ma, Q.; Idris, M.S.; Zhang, B.; Merzuki, M.N.M. Wireless technology applied in 3-axis filament winding machine control system using MIT app inventor Wireless technology applied in 3-axis filament winding machine control system using MIT app inventor. IOP Conf. Ser. Mater. Sci. Eng. 2019, 469, 012030. [Google Scholar]
- Wild, P.M.; Vickers, G.W. Analysis of filament-wound cylindrical shells under combined centrifugal, pressure and axial loading. Compos. Part A Appl. Sci. Manuf. 1997, 28, 47–55. [Google Scholar] [CrossRef]
- Sayem Uddin, M.; Morozov, E.V.; Shankar, K. The effect of filament winding mosaic pattern on the stress state of filament wound composite flywheel disk. Compos. Struct. 2014, 107, 260–275. [Google Scholar] [CrossRef]
- Tzeng, J.T.; Emerson, R.P.; O’Brien, D.J. Viscoelasticity Analysis and Experimental Validation of Anisotropic Composite Overwrap Cylinders. In Proceedings of the ASME 2012 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 9–15 November 2012; p. 429. [Google Scholar] [CrossRef]
- Ertz, G. Development, Manufacturing and Testing of a Multi-Rim (Hybrid) Flywheel Rotor. Diploma Thesis, Leibniz Universität Hannover, Hannover, Germany, 2014. [Google Scholar]
- Skinner, M.; Mertiny, P. Experimental Characterization of Low-Speed Passive Discharge Losses of a Flywheel Energy Storage System. Appl. Mech. 2021, 2, 1–15. [Google Scholar] [CrossRef]
- Kale, V.; Secanell, M. A comparative study between optimal metal and composite rotors for flywheel energy storage systems. Energy Rep. 2018, 4, 576–585. [Google Scholar] [CrossRef]
- Zheng, Y.; Bahaloo, H.; Mousanezhad, D.; Mahdi, E.; Vaziri, A.; Nayeb-Hashemi, H. Stress analysis in functionally graded rotating disks with non-uniform thickness and variable angular velocity. Int. J. Mech. Sci. 2016, 119, 283–293. [Google Scholar] [CrossRef]
- Yeh, K.Y.; Han, R.P.S. Analysis of high-speed rotating disks with variable thickness and inhomogeneity. J. Appl. Mech. Trans. ASME 1994, 61, 186–191. [Google Scholar] [CrossRef]
- Ertz, G.; Twiefel, J.; Krack, M. Feasibility Study for Small Scaling Flywheel-Energy-Storage Systems in Energy Harvesting Systems. Energy Harvest. Syst. 2014, 1, 233–241. [Google Scholar] [CrossRef]
- Ha, S.K.; Kim, M.H.; Han, S.C.; Sung, T.H. Design and spin test of a hybrid composite flywheel rotor with a split type hub. J. Compos. Mater. 2006, 40, 2113–2130. [Google Scholar] [CrossRef]
- Hartl, S.; Schulz, A.; Sima, H.; Koch, T.; Kaltenbacher, M. A Static Burst Test for Composite Flywheel Rotors. Appl. Compos. Mater. 2016, 23, 271–288. [Google Scholar] [CrossRef]
- Han, Y.; Ren, Z.; Tong, Y. General Design Method of Flywheel Rotor for Energy Storage System. Energy Procedia 2012, 16, 359–364. [Google Scholar] [CrossRef][Green Version]
- Mittelstedt, M.; Hansen, C.; Mertiny, P. Design and multi-objective optimization of fiber-reinforced polymer composite flywheel rotors. Appl. Sci. 2018, 8, 1256. [Google Scholar] [CrossRef]
- Krack, M.; Secanell, M.; Mertiny, P. Cost optimization of hybrid composite flywheel rotors for energy storage. Struct. Multidiscip. Optim. 2010, 41, 779–795. [Google Scholar] [CrossRef]
- Skinner, M.; Secanell Gallart, M.; Mertiny, P. Observed Effects of Vibrationally Induced Fretting on Bearing–Shaft Systems in Flywheel Energy Storage Systems. J. Fail. Anal. Prev. 2018, 18, 837–845. [Google Scholar] [CrossRef]
- Allam, M.N.M.; Tantawy, R.; Yousof, A.; Zenkour, A.M. Elastic and viscoelastic stresses of nonlinear rotating functionally graded solid and annular disks with gradually varying thickness. Arch. Mech. Eng. 2017, 64, 423–440. [Google Scholar] [CrossRef]
- Long, Z.; Zhiping, Q. Review of Flywheel Energy Storage System. In Proceedings of ISES World Congress 2007 (Vol. I–Vol. V); Springer: Berlin/Heidelberg, Germany, 2008; pp. 2815–2819. [Google Scholar]
- Lai, W.M.; Rubin, D.; Krempl, E. Chapter 5: The Elastic Solid. In Introduction to Continuum Mechanics; Elsevier: Amsterdam, The Netherlands, 2010; pp. 201–352. [Google Scholar]
- Ding, H.; Chen, W.L.Z. Elasticity of Transversely Isotropic Materials; Gladwell, G.M.L., Ed.; Springer: Dordrecht, The Netherlands, 2006; ISBN 9781119130536. [Google Scholar]
- Zhao, J.; Song, X.; Liu, B. Standardized compliance matrixes for general anisotropic materials and a simple measure of anisotropic degree based on shear extension coupling coefficient. Int. J. Appl. Mech. 2011, 8, 1–28. [Google Scholar]
- Lakes, R. Viscoelastic Materials; Cambridge University Press: Cambridge, UK, 2009; Volume 1, ISBN 9780511626722. [Google Scholar]
- Buchroithner, A.; Haidl, P.; Birgel, C.; Zarl, T.; Wegleiter, H. Design and experimental evaluation of a low-cost test rig for flywheel energy storage burst containment investigation. Appl. Sci. 2018, 8, 2622. [Google Scholar] [CrossRef]
- Rojas, J.I.; Nicolás, J.; Crespo, D. Study on mechanical relaxations of 7075 (Al-Zn-Mg) and 2024 (Al-Cu-Mg) alloys by application of the time-temperature superposition principle. Adv. Mater. Sci. Eng. 2017, 2017, 2602953. [Google Scholar] [CrossRef]
- Mahdavi, R.; Goodarzi, V.; Jafari, S.H.; Saeb, M.R.; Shojaei, S.; Khonakdar, H.A. Experimental analysis and prediction of viscoelastic creep properties of PP/EVA/LDH nanocomposites using master curves based on time—Temperature superposition. J. Appl. Polym. Sci. 2018, 135, 46725. [Google Scholar] [CrossRef]
- Barbero, E.J. Time-Temperature-Age Superposition Principle for Predicting Long-Term Response of Linear Viscoelastic Materials, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780081026014. [Google Scholar]
- Yeow, Y.; Morris, D.; Brinson, H. Time-Temperature Behavior of a Unidirectional Graphite/Epoxy Composite. In Fifth Conference on Composite Materials: Testing and Design; ASTM International: West Conshohocken, PA, USA, 1979; pp. 1–37. [Google Scholar]
- Koyanagi, J.; Sato, M. Time and Temperature Dependence of Transverse Tensile Failure of Unidirectional Carbon Fiber-Reinforced Polymer Matrix Composites, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780081026014. [Google Scholar]
- Emerson, R.P. Viscoelastic Flywheel Rotors: Modeling and Measurement. Ph.D. Thesis, Pennsylvania State University, State College, PA, USA, 2002. [Google Scholar]
- Aniskevich, A.; Glaskova-Kuzmina, T. Effect of Moisture on Elastic And Viscoelastic Properties of Fiber Reinforced Plastics: Retrospective and Current Trends, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780081026014. [Google Scholar]
- Alwis, K.G.N.C.; Burgoyne, C.J. Time-temperature superposition to determine the stress-rupture of aramid fibres. Appl. Compos. Mater. 2006, 13, 249–264. [Google Scholar] [CrossRef]
- Sihn, S.; Tsai, S. Automated shift for time-temperature superposition. In Proceedings of the 12th International Comittee on Composite Materials, Paris, France, 5–9 July 1999; Volume 51. [Google Scholar]
- Brinson, H.F.; Griffith, W.I.; Morris, D.H. Creep Rupture of Polymer-matrix Composites. Exp. Mech. 1981, 57, 329–335. [Google Scholar] [CrossRef]
- Brinson, H.F. Mechanical and optical viscoelastic characterization of Hysol 4290. Exp. Mech. 1968, 8, 561–566. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Akulichev, A.G.; Gagani, A.I.; Echtermeyer, A.T. Time-temperature-plasticization superposition principle: Predicting creep of a plasticized epoxy. Polymers 2019, 11, 1848. [Google Scholar] [CrossRef] [PubMed]
- Ganß, M.; Satapathy, B.K.; Thunga, M.; Weidisch, R.; Pötschke, P.; Janke, A. Temperature dependence of creep behavior of PP-MWNT nanocomposites. Macromol. Rapid Commun. 2007, 28, 1624–1633. [Google Scholar] [CrossRef]
- Jain, N.; Verma, A.; Singh, V.K. Dynamic Mechanical Analysis and Creep-recovery behaviour of Polyvinyl Alcohol based cross-linked Biocomposite reinforced with Basalt fiber. Mater. Res. Express 2019, 6, 105373. [Google Scholar] [CrossRef]
- Gergesova, M.; Zupančič, B.; Saprunov, I.; Emri, I. The closed form t-T-P shifting (CFS) algorithm. J. Rheol. 2011, 55, 1–16. [Google Scholar] [CrossRef]
- Bradshaw, R.D.; Brinson, L.C. Recovering nonisothermal physical aging shift factors via continuous test data: Theory and experimental results. J. Eng. Mater. Technol. Trans. ASME 1997, 119, 233–241. [Google Scholar] [CrossRef]
- Sullivan, J.L. Creep and physical aging of composites. Compos. Sci. Technol. 1990, 39, 207–232. [Google Scholar] [CrossRef]
- Lou, Y.C. Viscoelastic Characterization of Nonlinear Fiber-Reinforced Plastic. J. Compos. Mater. 1971, 5, 208–234. [Google Scholar] [CrossRef]
- Stinchcomb, W.W.; Bakis, C.E. Fatigue Behavior of Composite Laminates. Compos. Mater. Ser. 1991, 4, 105–180. [Google Scholar] [CrossRef]
- Lekhnitskiy, S.G. Anisotropic Plates; Tekhniko-Teoreticheskoy Literatury; Air Force Systems Command: Moscow, Russia, 1957. [Google Scholar]
- Chdnis, C.C.; Kiruly, L.J. Rim-Spoke Composite Flywheels—Stress a N D Vibration Analysis; NASA Lewis Research Center: Cleveland, OH, USA, 1976.
- Gabrys, C.W.; Bakis, C.E. Design and Testing of Composite Flywheel Rotors. In Composite Materials: Testing and Design, Thirteenth Volume; ASTM International: West Conshohocken, PA, USA, 1997; pp. 1–22. [Google Scholar]
- Ha, S.K.; Yang, H.-I.; Kim, D.-J. Optimum design of a hybrid composite flywheel with permanent magnet rotor. J. Compos. Mater. 1999, 33, 1544–1575. [Google Scholar] [CrossRef]
- Kelly, P. Mechanics Lecture Notes. Available online: http://homepages.engineering.auckland.ac.nz/~pkel015/SolidMechanicsBooks/index.html (accessed on 15 November 2021).
- Ha, S.K.; Kim, D.J.; Sung, T.H. Optimum design of multi-ring composite flywheel rotor using a modified generalized plane strain assumption. Int. J. Mech. Sci. 2001, 43, 993–1007. [Google Scholar] [CrossRef]
- Hearn, C.S.; Flynn, M.M.; Lewis, M.C.; Thompson, R.C.; Murphy, B.T.; Longoria, R.G. Low cost flywheel energy storage for a fuel cell powered transit bus. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Arlington, TX, USA, 9–12 September 2007; pp. 829–836. [Google Scholar] [CrossRef]
- Krack, M.; Secanell, M.; Mertiny, P. Advanced optimization strategies for cost-sensitive design of energy storage flywheel rotors. J. Adv. Mater. 2011, 43, 65–78. [Google Scholar] [CrossRef]
- Kheawcum, M.; Sangwongwanich, S. A Case Study on Flywheel Energy Storage System Application for Frequency Regulation of Islanded Amphoe Mueang Mae Hong Son Microgrid. In Proceedings of the 17th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, ECTI-CON 2020, Phuket, Thailand, 24–27 June 2020; pp. 421–426. [Google Scholar]
- Pérez-Aparicio, J.L.; Ripoll, L. Exact, integrated and complete solutions for composite flywheels. Compos. Struct. 2011, 93, 1404–1415. [Google Scholar] [CrossRef]
- Eraslan, A.N.; Akis, T. On the plane strain and plane stress solutions of functionally graded rotating solid shaft and solid disk problems. Acta Mech. 2006, 181, 43–63. [Google Scholar] [CrossRef]
- Saleeb, A.F.; Arnold, S.M.; Al-Zoubi, N.R. A study of time-dependent and anisotropic effects on the deformation response of two flywheel designs. In Proceedings of the 14th Symposium on Composite Materials: Testing and Design, Pittsburgh, PA, USA, 11–12 March 2003. [Google Scholar]
- Trufanov, N.A.; Smetannikov, O.Y. Creep of Composite Energy Accumulators. Strength Mater. 1991, 23, 671–675. [Google Scholar]
- Portnov, G.G. Estimation of Limit Strains in Disk-Type Flywheels Made of Compliant Elastomeric Matrix Composite Undergoing Radial Creep. Mech. Compos. Mater. 2000, 36, 55–58. [Google Scholar] [CrossRef]
- Tzeng, J.T. Viscoelastic Analysis of Composite Flywheel for Energy Storage; Army Research Laboratory: Aberdeen Proving Ground, Aberdeen, MD, USA, 2001. [Google Scholar]
- Ghosh, T.N.; Tzeng, J.T.; Emerson, R.P.; O’Brien, D.J.; Ghosh, T.N. Viscoelasticity Analysis and Experimental Validation of Anisotropic Composite Overwrap Cylinders. Trans. Ophthalmol. Soc. UK 2012, 101, 200–202. [Google Scholar] [CrossRef]
- Levistor Boosting Forecourt Grid Power for the Next Generation of Fast Charging Electric Vehicles. Available online: https://levistor.com/#about (accessed on 9 December 2021).
- Stornetic GmbH Powerful Storage System for Grid Services. Available online: https://stornetic.com/assets/downloads/stornetic_general_presentation.pdf (accessed on 9 December 2021).
- Tang, S. Note on acceleration stress in a rotating disk. Int. J. Mech. Sci. 1970, 12, 205–207. [Google Scholar] [CrossRef]
- Reddy, T.Y.; Srinath, H. Effects of acceleration stresses on the yielding of rotating disks. Int. J. Mech. Sci. 1974, 16, 593–596. [Google Scholar] [CrossRef]
- Salehian, M.; Shahriari, B.; Yousefi, M. Investigating the effect of angular acceleration of the rotating disk having variable thickness and density function on shear stress and tangential displacement. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–11. [Google Scholar] [CrossRef]
- Li, S. The Maximum Stress Failure Criterion and the Maximum Strain Failure Criterion: Their Unification and Rationalization. J. Compos. Sci. 2020, 4, 157. [Google Scholar] [CrossRef]
- Ha, S.K.; Lee, D.G.; Kim, D.J. Optimization of hybrid composite rotor in flywheel battery. SAE Tech. Pap. 1998. [Google Scholar] [CrossRef]
- Corbin, C.K. Burst Failure Prediction of Composite Flywheel Rotors: A Progressive Damage Approach via Stiffness Degredation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2005. [Google Scholar]
- Tsai, S.W.; Wu, E.M. A General Theory of Strength for Anisotropic Materials. J. Comp. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Li, S.; Sitnikova, E.; Liang, Y.; Kaddour, A.S. The Tsai-Wu failure criterion rationalised in the context of UD composites. Compos. Part A Appl. Sci. Manuf. 2017, 102, 207–217. [Google Scholar] [CrossRef]
- Roy, A.K.; Tsai, S.W. Design of Thick Composite Cylinders. J. Press. Vessel Technol. 2009, 110, 255. [Google Scholar] [CrossRef]
- Chen, Q.; Li, C.; Tie, Y.; Liu, K. Progressive Failure Analysis of Composite Flywheel Rotor Based on Progressive Damage Theory. J. Mech. Eng. 2013, 49, 1–6. [Google Scholar] [CrossRef]
- Kotelnikova-Weiler, N.; Baverel, O.; Ducoulombier, N.; Caron, J.F. Progressive damage of a unidirectional composite with a viscoelastic matrix, observations and modelling. Compos. Struct. 2018, 188, 297–312. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Lifetime [years] | >20 [5] |
| Charge/discharge cycles | <107 [5] |
| Energy density [Wh/kg] | <130 [17] |
| Price [(USD)/kWh] | 400–6960 [5,17] |
| Power density [W/kg] | ~1000 [5] |
| Shape | Cross Section | k-Value |
|---|---|---|
| Laval disk |  | 1.00 |
| Laval disk real |  | 0.70–0.90 |
| Conical disk |  | 0.70–0.85 |
| Solid disk |  | 0.606 |
| Thin ring |  | 0.50 |
| Thick rim |  | 0.303 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skinner, M.; Mertiny, P. Energy Storage Flywheel Rotors—Mechanical Design. Encyclopedia 2022, 2, 301-324. https://doi.org/10.3390/encyclopedia2010019
Skinner M, Mertiny P. Energy Storage Flywheel Rotors—Mechanical Design. Encyclopedia. 2022; 2(1):301-324. https://doi.org/10.3390/encyclopedia2010019
Chicago/Turabian StyleSkinner, Miles, and Pierre Mertiny. 2022. "Energy Storage Flywheel Rotors—Mechanical Design" Encyclopedia 2, no. 1: 301-324. https://doi.org/10.3390/encyclopedia2010019
APA StyleSkinner, M., & Mertiny, P. (2022). Energy Storage Flywheel Rotors—Mechanical Design. Encyclopedia, 2(1), 301-324. https://doi.org/10.3390/encyclopedia2010019







