1. Introduction
Virtual experiments (VEs) and digital twins (DTs) have attracted substantial attention in the metrological community [
1,
2,
3,
4,
5], also illustrated by the fact that virtual metrology is listed as a key area in the strategic research agenda of EURAMET’s European Metrology Network Mathmet [
6]. Uncertainty evaluation involving VEs and DTs is an important area of interest. Recent papers considered uncertainty evaluation for the applications of, e.g., coordinate measuring machines [
7,
8,
9,
10,
11,
12], tilted wave interferometry [
13,
14], flow measurements [
15,
16] and scatterometry [
17,
18]. Some more theoretically oriented papers considered the exact replication of JCGM-101 [
19] distributions by means of using samples of VEs [
20,
21,
22]. In [
23] various possible procedures for uncertainty evaluation based on VEs were discussed and assessed using computer experiments involving a Virtual Coordinate Measuring Machine (VCMM). It was found that resulting uncertainties and coverage intervals could be significantly different for measurands that have a complex dependency on their input quantities, like the peak-to-valley value as a measure of the circularity of an approximately circular shape. Bayesian methods applied to VEs are also regularly studied [
24,
25], in particular because Bayesian methods naturally allow for uncertainty quantification of the estimated parameters. Comparing different ways of evaluating measurement uncertainty has been conducted in many different contexts. See, e.g., [
26] for an example involving the analysis of heteroscedastic measurement data.
The problem addressed by this paper is the question of how a regularly employed uncertainty calculation procedure [
9] in the context of VEs compares with the procedure based on the propagation of distributions (PoD), as presented in JCGM-101. This comparison will be performed in detail for a simple example model, which will be formally presented in
Section 2. It is important to understand possible differences between these procedures, as the first procedure is often used in practice, while claiming consistency with the second procedure, i.e., with JCGM-101. These differences do not seem to have been studied in the past.
In
Section 2, we present these procedures in detail. To obtain a better understanding of possible differences, we approximate the variances in the distributions resulting from both procedures using the law of propagation of uncertainty from JCGM-100 [
27] and we give an analytical formula indicating how much the calculated uncertainties by both procedures can be different in specific adverse circumstances. In
Section 3, we present some concrete numerical examples using the full Monte Carlo procedures, in order to confirm the intuition gained from the analytical formula. We also present an example with a simplified VCMM. In
Section 4, we discuss the results and our conclusions are presented in
Section 5.
2. Method
A VE models how an
-dimensional measurement data vector
is generated in an experiment, given an
-dimensional vector
containing the values of the (possibly) multi-dimensional measurand, an
-dimensional vector
containing influence quantities not varying over repeated measurements, and an
-dimensional vector
containing influence quantities that vary between different measurements. This leads to the VE function
g:
Typically,
affects the measurement data in the form of
-dimensional additive measurement noise, leading to the function
not depending on
:
If
is once continuously differentiable with respect to
, the VE can be expanded in powers of
as
where
denotes the Landau big O symbol, where the implied bounding constant can still depend on
. We will, therefore, focus our study on a first-order VE of the form
This class of functions is regularly studied, e.g., in [
28]. Furthermore, many models for the measurand can be represented as the partial inverse of this function, e.g., in calibration or correction models [
29].
We assume Gaussian noise with zero mean and covariance matrix , and that an estimate of the other influence quantities is given, as well as its covariance matrix . Given a data sample , the central question is to determine and its covariance matrix .
We will now discuss two common procedures for evaluating . The first is the procedure from JCGM-101 based on the propagation of distributions (PoD), the second procedure relies on creating multiple data samples using the VE and applying a data analysis function (DA) to the sampled data (VE-DA). To clarify analytically what is happening in these sampling-based procedures, we use the law of the propagation of uncertainty (LPU) from JCGM-100 to approximate the variance in the distributions, which can be used to construct an approximate distribution for the measurand when a normal distribution is assumed.
2.1. Propagation of Distributions
The Monte Carlo method-based PoD procedure from JCGM-101 prescribes that the VE-equation (
4) is first transformed into a measurement function
f expressing the measurand as a function of all other variables. This can readily be conducted in our case, leading to
where
denotes the left Moore–Penrose inverse of the matrix
and gives the least-squares solution
for
in (
4) given measured data
and estimates
for
and
for
.
In the PoD procedure, the estimate
and covariance matrix
are calculated by repeatedly creating samples
and
from the state-of-knowledge probability distributions characterizing the input quantities
and
, respectively. The function
f from Equation (
5) is applied to the measured data
and each sample pair
, resulting in samples
. These samples
can be used to estimate the value of the measurand by means of the mean
of the samples, and the standard uncertainty of the measurand by means of the empirical covariance matrix
of the samples. While the PoD procedure outlined here might deviate from the description of the Monte Carlo method presented in JCGM-101, as we have introduced a separate variable
for the measurement noise affecting the measured data
, it is equivalent, since we assume a normal distribution for
with known covariance
and a single measured value for
.
Using the LPU, a covariance matrix
approximating
can be computed by means of
where
and
are assumed independent, and where
is treated as known, as the measurement noise is separately modeled by
.
To be able to apply the LPU, the derivative
of the matrix
is needed, which is given by [
30]:
where
. Note that
and
are 3-dimensional tensors when each of
,
and
have more than one dimension and the operations in (
8) and (
9) correspond to tensor contractions over the appropriate dimensions. In most of the subsequent examples
is one-dimensional; therefore, we will not focus on this aspect in the following equations.
Writing
and
, the application of the LPU and the product rule of differentiation yields for the approximation
of
All matrices are evaluated at the estimate
. To simplify the notation, we have removed this dependence on
from the notation.
2.2. VE-Based Sampling Procedure
In the procedure VE-DA a data analysis function
must be available to compute an estimate of the measurand based on the measurement data only:
If a full explicit measurement model
f as in Equation (
5) is available, then
can be derived from
f by fixing the inputs
and
to some estimates
and
(most often
).
An estimate
of the measurand is fixed, which can be based on the measurement data, e.g.,
or on a nominal value for the measurand. Once
is chosen, repeatedly samples
and
are drawn from the probability distributions characterizing the input quantities
and
, respectively. These samples are used to generate simulated data samples
using the VE from (
1), or in our case, from (
4). Next, the function
is applied to the simulated data
, yielding samples
. Statistics like the covariance matrix
can be computed from these samples. In the case
is unbiased, the mean
of the samples
will be close to
. In other cases,
may be simply disposed of, or it can be used for a bias correction [
23]. The reported value of the measurand is typically
and not
, though this choice is irrelevant as regards the uncertainty evaluation and will not be discussed any further in this paper.
The procedure VE-DA finds application in VCMMs [
9], with which simulated measurement data are repeatedly generated, to which the DA is then subsequently applied. This DA may consist of, e.g., fitting a geometrical element like a circle to the simulated data, and the diameter may be the parameter of interest. As fixed
either the nominal values for the measurand or an estimate based on the measured coordinates are typically used. On top of this geometrical shape, measurement errors due to CMM and object imperfections are simulated, resulting in simulated measurement data in the form of simulated point clouds.
The main discrepancy between the VE-DA and PoD procedures is that in VE-DA, possible measurement errors resulting in possible measurement data are simulated based on the parameter , whereafter a relatively simple data analysis function that is independent of , is applied to evaluate the measurement data. In the PoD procedure, an explicit mathematical model for the measurand of the form is created first by inverting the function that models the data generation process. Hereafter, all uncertain influence factors as modeled by and are simulated and applied as possible corrections to the observed measurement data.
We again calculate the LPU-based covariance matrix
approximating the covariance matrix
that would be obtained using the Monte Carlo method-based VE-DA procedure. In a first step, we assess the covariance matrix of the data
, which, using
, is given by
This covariance matrix is then propagated through the function
yielding
Comparing Equations (
18) and (
12) we observe that Equation (
12) has two additional terms involving
, which do not necessarily sum up to zero, and therefore, the VE-DA procedure does not always give identical results as the PoD procedure from JCGM-101. The reason is that the impact of the uncertainty of
on
and
is not evaluated in an equivalent way. The matrix
is related to the null-space of
B. In the first order, uncertainties lying in this null-space are not taken into account by the VE-DA procedure, whereas they are taken into account by the PoD procedure. If
B was fixed, then any noise orthogonal to
B would not matter, as it would not affect the calculated value for
. However, due to the uncertainty in
, a perturbed matrix
may actually start containing components aligning with the noise, which results in additional uncertainty for
. This part of the uncertainty is neglected by the VE-DA procedure. Note that if
then both procedures yield the same result, as this would result in
.
2.3. Ratio Between VE-DA and PoD Uncertainties
In this section, we analyze how large or small the ratio of the standard uncertainties calculated according to the different procedures for a single measurand
y can become. We define the ratio
where
denotes the standard uncertainty of the scalar measurand
y using the PoD procedure, and similarly
for the VE-DA procedure. We assume that the estimate
corresponds to the true value of
, such that we can write
and that we do not mix in this analysis the effects of an incorrect estimate of
with the effect of using a different procedure for uncertainty evaluation. To approximate the ratio
r we will analytically study the ratio
which is based on the LPU approximation of the variances resulting from applying VE-DA and PoD. We call the standard deviations of these approximations
and
. The analytical approximations are used to find models for which the VE-DA and PoD procedures may give substantially different results. Therefore, the approximation error is not a primary concern, as long as the results based on the LPU help to identify interesting cases for which the procedures yield different results. Nevertheless, we have excluded pathological examples corresponding to cases in which
is almost singular and for which the resulting PoD distribution had a very long tail, in contrast to the VE-DA solution.
From Equations (
12) and (
18) we see that the difference in the covariance matrices
and
is equal to
and that it is governed by the matrix-vector products
and
. Two extreme cases for the value of the difference shown in Equation (
21) are given by
, in which the VE-DA uncertainty is larger than the PoD uncertainty, and
and
, in which the VE-DA uncertainty is smaller than the PoD uncertainty. Furthermore, we choose
to get rid of the term
that would draw the ratio (
20) towards unity.
We now assume that both
and
are one-dimensional, whereas
remains
-dimensional. By choosing the physical units of
y and
z and/ or scaling and/ or translating
y and
z appropriately, we can arrange
Let
. By appropriate scaling of
we can arrange that
, where
is actually a vector in the case of a single-dimensional measurand. To alleviate the notation, we will remove
from quantities depending on
z when they are evaluated at
. We obtain
and
. By an appropriate choice of the basis vectors of the
-dimensional space, we can, without loss of generality, assume that
for some constants
and
. Note however that in this paper, we only intend to present some examples of cases in which uncertainty evaluation methods start to differ, so we do not strictly need to cover all cases. For the extreme cases, we choose
to have only noise components in the relevant directions, while keeping the norm
as small as possible. Using these definitions, we find that
Plugging Equations (
28) and (
29) into (
12) and (
18) and the resulting expressions into Equation (
20) leads to the ratio
2.3.1. VE-DA Uncertainty Larger than PoD Uncertainty
In order to maximize
in Equation (
30), corresponding to
, we can choose as model parameters
where both components of
have standard uncertainty
, and
denotes an arbitrary factor. Assuming that the estimate
for the measurand
y equals
, this leads to the ratio
It can be seen that the ratio (
32) is always larger than 1 and increases when either the uncertainty in
z becomes large or the impact of the additive effect of
z orthogonal to
B in the model for the measurand increases, i.e.,
; choosing
,
and
leads to
. Note that by an appropriate choice of the unit for the
z-values, either
or
can be assumed to be equal to 1, as long as
and
. Numerical simulations show that the ratio
is approximately attainable for the Monte Carlo method-based procedures VE-DA and PoD, from which we conclude that the approximation
to
r is appropriate for such cases. For larger values of
or
the approximation
to
r becomes poor and cannot be relied on. In such cases, the obtained distribution for
y using the PoD procedure becomes highly skewed with a long tail.
2.3.2. VE-DA Uncertainty Smaller than PoD Uncertainty
We now turn to the opposite case in which we aim to minimize
from Equation (
30) corresponding to
and large
. Setting the model parameters to
we find the ratio
The ratio in (
34) is actually the inverse of the ratio in (
32), the only difference between the two cases being the choice for the value of
. Causes for a ratio significantly different from unity are a large derivative in the direction orthogonal to
B (i.e., large
), a large uncertainty
or a large realization of the noise vector
(i.e., large
), whereby the noise vector should be orthogonal to
B. Simulations show that, in particular, by assuming a very large
, one can obtain a very small
and
r.
The mathematical intuition for achieving and large is as follows. The matrix will vanish if is orthogonal to . The matrix equals the product of essentially three factors: the orthogonal projection , the factor and the factor . As (as and ) and is the orthogonal projection to the space orthogonal to the column space of B, the product has the largest Euclidian norm for vectors of fixed length if is orthogonal to the columns of B and will then be equal to . The product has the largest absolute value for vectors of fixed norm if is parallel to . Finally, is only a one-dimensional scalar if is one-dimensional.
3. Numerical Simulations
In this section, we present some numerical simulations illustrating the difference in calculated uncertainty using the VE-DA and PoD procedures. We start with five synthetic cases with the identifiers (IDs) ‘Lin-Hetero-Large’, ‘Lin-Hetero-Small’, ‘Lin-Homo-Large’, ‘Lin-Homo-Small’ and ‘Trigon’ which were constructed to clearly demonstrate the possibility of obtaining different uncertainties as presented in the last section. The sixth case with ID ‘Circle’ is a more realistic example based on coordinate metrology and a VCMM.
In the Monte Carlo method-based calculations, we used
repetitions for the numerical values presented in
Table 1, and
repetitions for the generation of the histograms due to calculation time. We assumed a one dimensional measurand and an
dimensional data-space for the
x-values with
such that
. All cases used the following values:
(by an appropriate scaling of the
y-axis),
(by an appropriate translation of the
z-axis),
(by an appropriate scaling of the
z-axis) and
(a concrete realization of the noise vector equal to 3 times the standard deviation). The values
,
and
were chosen according to Equation (
31) for the cases ‘Lin-Hetero-Large’ and ‘Lin-Homo-Large’, resulting in a VE-DA uncertainty larger than the PoD uncertainty, whereas they were chosen according to Equation (
33) for the cases ‘Lin-Hetero-Small’, ‘Lin-Homo-Small’ and ’Trigon’, resulting in a VE-DA uncertainty smaller than the PoD uncertainty. The value
was chosen as large as possible while ensuring that, in particular, the PoD procedure still resulted in an approximately normal distribution for
y, and in a similar way
was selected. In all cases, the noise components
and
of the noise vector
were independent. In the cases ‘Lin-Hetero-Large’ and ‘Lin-Hetero-Small’, the noise was heteroscedastic (i.e., different variance), whereas in the cases ‘Lin-Homo-Large’, ‘Lin-Homo-Small’ and ‘Trigon’ the noise was homoscedastic (i.e, same variance). In the cases where the ID starts with ‘Lin’ we considered a linear function of the form
with
from Equation (
24) and
from Equation (
25), whereas in the case ‘Trigon’ the function
involving trigoniometric functions was used.
The case ‘Circle’ has a 3-dimensional vector
in contrast to the 1-dimensional
of the preceding cases. Here, we consider a more realistic situation corresponding to a least-squares circle fit for determining the mid-point
and radius
to four geometrical points with coordinates
with nominal measurement directions
parallel to the coordinate axes in the horizontal plane. For the uncertainty structure the simplified VCMM from [
23] has been used. This problem can be cast in the form of the model of Equation (
4) by expressing the measured data, the linear scale errors
and
and the squareness error
as
and defining
This model of shape (
4) can be used for simulating the generation of measurement data. For the inverse operation, i.e., for fitting the circle parameters, Equation (
5) cannot directly applied in practice, as the angles
needed for the computation of
are only approximately known when performing a measurement. Therefore, a general least-squares fitting routine for fitting circle parameters to data [
31] is used, like what is conducted in practice.
A worst case situation in terms of the ratio
r occurs when both the realization of the noise vector
and the derivative
of
are parallel to each other and orthogonal to
, e.g., if they are both parallel to
In
Figure 1 a schematic overview of the situation is shown including a measurement noise vector aligning with
. However, it turned out that the derivative
for this practical case is not at all orthogonal to
, leading to virtually identical uncertainties for both uncertainty procedures. In the simulation we used
m,
m and
mm.
A summary of the results of the simulations is shown in
Table 1. The calculated estimates
and
were both reasonably close to
in each case. We chose not to present them in
Table 1 in order not to distract the attention from the calculated uncertainties, which is the focus of this study.
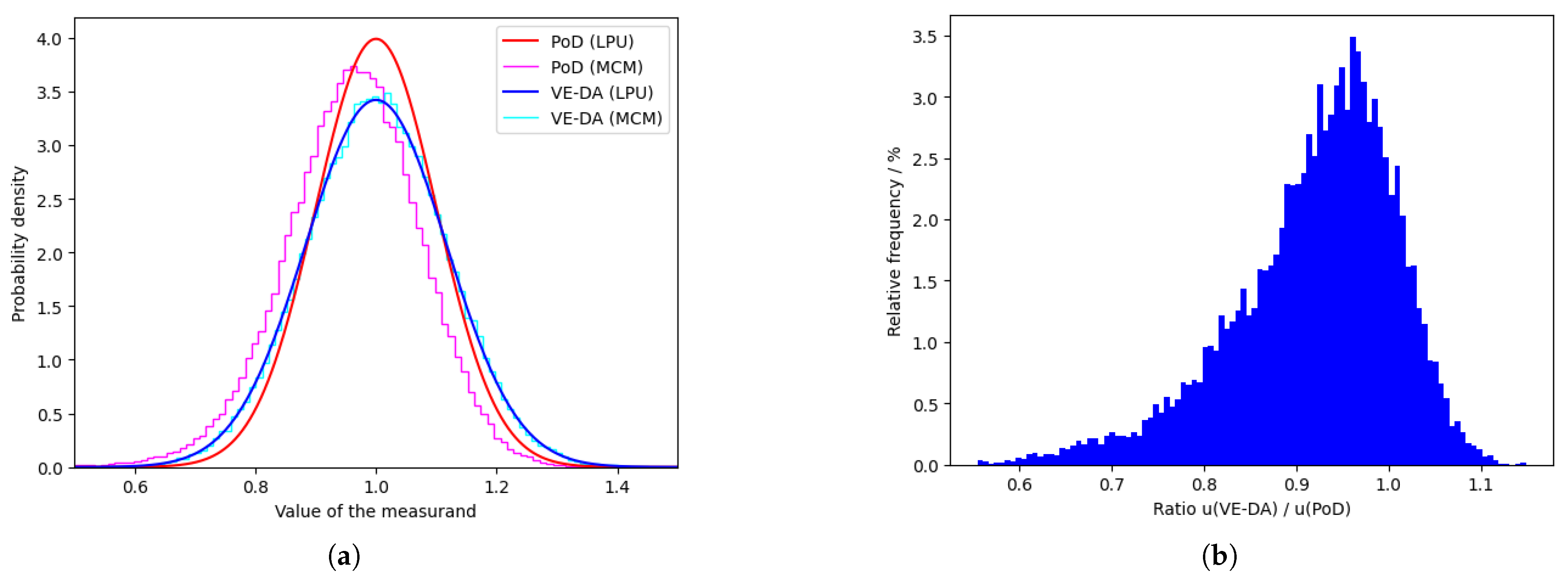
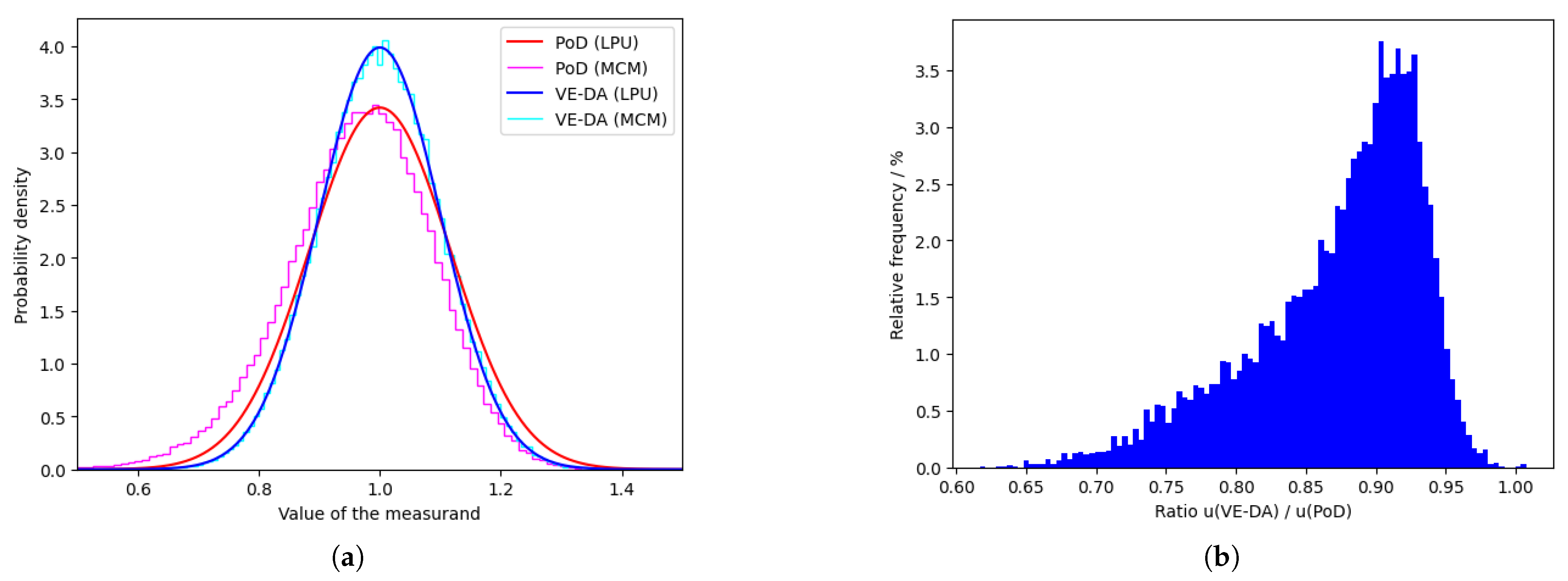
In the left parts of
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6 the distributions for the five synthetic cases are shown. Both the smooth Gaussian distribution using the LPU approximation as well as the stair-case plots resulting from the histograms based on the Monte Carlo samples are shown. In all cases, the approximation is reasonable to very good. If we were to allow more wild distributions or larger values of
, then the ratio
r would attain more extreme values than shown in this paper.
Table 1 presents the ratios and in the left part of
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6 the distributions are shown for particular values of the noise
, which were chosen to obtain extreme values of the ratio. We also performed experiments in which we kept the model shape fixed, but drew random samples for both
and
to obtain an impression of the distribution of the ratio in a random case, rather than in the worst case, although the model structure is still the worst case. In the right part of
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6 histograms are drawn for the resulting ratios based on 10,000 repetitions. For case ‘Circle’ the resulting histogram is entirely concentrated at 1 and, therefore, we did not present similar figures for this last case.
4. Discussion
From the results in
Table 1 we conclude that significant differences can occur between the VE-DA and PoD procedures, with the ratio
r ranging from 0.51 to 1.35 in the cases considered. The numerical experiments also made it clear that it is easier to find examples with the PoD uncertainty being larger than the VE-DA uncertainty than the opposite. Further increasing the factor
is possible but unrealistic and not conducted in this paper. It would nevertheless show that both analysis procedures can, in theory, give even more different results. Increasing
and/ or
makes the distributions behave in a non-Gaussian way, resulting in ratios
r quite different from
, though in some cases still very different from unity. The histograms show that also in the case of randomly generated noise and an estimate of the additional
z-parameter not coinciding with its true values, the ratio can still deviate considerably from unity, as long as the VE model itself has the particular shape with
approximately orthogonal to
B. Also, the values shown in
Table 1 are covered by the histogram, indicating that the presented numerical values and, in particular, the employed value of
are realistic for each case.
Figure 2b and
Figure 4b show that ratios below unity are more likely, even if the model structure was constructed to obtain a ratio larger than one. In
Figure 3b,
Figure 5b, and
Figure 6b, we do not observe the opposite effect: all ratios are at most equal to one in these histograms.
In general, we observe that using a Monte Carlo method for drawing samples from the distribution for
z and for the measurement noise and using this in combination with a mathematical model for the measurement is not sufficient to obtain the same result as the PoD procedure from JCGM-101. The point in the procedure at which the measured data
is converted to a value
for the measurand matters. The VE-DA procedure neglects, in the first order, some of the uncertainty related to the null-space of
B, caused by the absence of the factor
in Equation (
18). However, in practical cases, the factor
will often be very close to unity, as the product
will generally be small.
One may ask the question what the ‘correct’ uncertainty is, which is actually a general topic for which a considerable body of literature exists, including diverging views on it [
32,
33,
34,
35]. From a normative viewpoint, that would be the one based on the PoD procedure, as this procedure is described in JCGM-101, which is also known as ISO/IEC Guide 98-3-1. From a Bayesian point of view, one may also opt for the PoD procedure, as the propagation of distributions procedure aligns with the idea of propagating state-of-knowledge distributions through a model, while the JCGM-101 approach is not always compatible with a complete Bayesian point of view. Classical statisticians may want to consider the success rates of calculated coverage intervals, which have also been studied inside the metrological community [
18,
36]. We assessed the success rates, but did not find significant differences on average. The success rates of 95% coverage intervals constructed for both procedures in all five cases, as determined for the 10,000 repetitions considered for each of the histograms, were close to 95%. However, for specific choices of the parameters, there were sometimes large differences, and therefore, simply preferring the method yielding on average the shortest intervals did not seem ideal either, in particular as worst-case parameter settings are of main interest to this paper. So, no clear best procedure was identified by this criterion.
In this paper, we considered a first-order model in both
and
and used a least-squares inversion. When considering stronger non-linear models and other types of inversion and data processing, like Chebyshev or minimum-zone fitting, larger differences may occur. However, such models are much harder to analyze analytically than the model of Equation (
4) studied in this paper, though a numerical comparison can be performed as long as the VE model can be transformed to a measurement model expressing the measurand explicitly as a function of the input quantities. Note that in practice it is often easier to apply the VE-DA procedure, whereas it can be practically infeasible to properly invert the virtual experiment and to express the measurand directly as a function of the measured data and other influence quantities.
A limitation of this study is that we illustrated the difference between the procedures only for a few, mainly synthetic, cases, whereas one may wonder what the difference is for a large number of practical cases. The fact that we did not find an example from real-life measurements for which both procedures give different results also limits the direct impact of the study.
The broader implication of this study is that metrologists cannot apply the VE-DA procedure to evaluate the measurement uncertainty and claim that it is compliant with JCGM-101 without any further thoughts. It needs to be assessed if, for the employed measurement model, both procedures give identical results or not.