1. Introduction
Traceability is a fundamental concept in metrology. Quantities must be expressed on a metrologically traceable measurement scale to enable meaningful comparison. For this reason, traceability is critical to the functioning of international quality infrastructures (QIs) and to the dissemination of measurement units within the global measurement system [
1]. Also for this reason, traceability is often mandated when critical decisions depend on measurements of physical quantities.
A pair of international arrangements that rely on traceability have been established. These arrangements have fostered the development of national and international quality infrastructure, which provides access to necessary traceable measurement services in society. In 1999, the International Committee for Weights and Measures (CIPM) Mutual Recognition Arrangement (MRA) provided a framework for national metrology institutes (NMIs) to demonstrate the equivalence of their measurement capabilities to those of international peers [
2]. Similarly, in 2001, the International Laboratory Accreditation Cooperation (ILAC) multi-lateral MRA provided a framework to support the provision of calibration and testing services across the developed world [
3].
The concept of traceability emerged late in the 20th century [
4]. Four possible definitions for
traceability were considered in an early paper by Belanger [
5,
6]. In 1982, Nicholas and White, in their monograph
Traceable Temperatures, proposed a variation on one of Belanger’s suggestions [
7]. Then, in 1984, the first edition of the
Vocabulary of Metrology (VIM) included an entry for traceability, drawing on another of Belanger’s suggestions ([
8], 6.12). Later editions of the VIM expanded and refined the definition of traceability. The second edition, in 1993, emphasised that traceability was a quantitative characteristic of measurement by including reference to
uncertainty ([
9], 6.10). This revision coincided with the release of the first edition of the
Guide to the Expression of Uncertainty in Measurement (GUM) [
10]. The current definition of traceability in the third edition of the VIM is as follows ([
11], 2.41):
metrological traceability
property of a measurement result whereby the result can be related to a reference through a documented unbroken chain of calibrations, each contributing to the measurement uncertainty.
This incorporates terms with specific meanings—
measurement result,
calibration, and
measurement uncertainty—which are also defined in the VIM. The definition is accompanied by eight explanatory notes, one of which elaborates on the meaning of
reference.
It is notable that the definition of traceability includes a requirement for documentation. Metrology is a scientific discipline, and traceability is one of its fundamental principles. It is unusual to see such a practical requirement being specified in a scientific definition. However, traceability plays the functional role in society of ensuring the reliability of measurements. The need for documentation stems from the real-world requirement to audit the reliability of the measuring stages along a traceability chain. Thus, the VIM definition integrates both the scientific concept of traceability and the practical necessity of generating records that can be audited.
The term “traceability” encompasses a range of meanings. As De Biève notes, “traceability is a general (superordinate) concept” [
12]. The description of
metrological traceability in the VIM is a specialised interpretation. The VIM associates traceability with measurement uncertainty; however, it is beneficial to distinguish between them. De Biève opines that traceability is a prerequisite for the evaluation of measurement uncertainty [
13]; thus, measurement uncertainty cannot be meaningfully assessed without first establishing traceability—a view shared by Ehrlich and Rasberry [
14]. This highlights the importance of structure—or configuration—in traceability: the way in which stages in a traceable measurement are designed to provide a link back to a metrological reference.
In this article, we emphasise the importance of modelling such configurations and suggest that this task should be clearly distinguished from the evaluation of uncertainty; however, in practice, they are often conflated. For example, Cox and Harris describe the evaluation of uncertainty as comprising two phases: first, the
formulation of a model; and second, its
evaluation [
15]. They emphasise that the first phase must be carried out by metrologists, to identify and capture all relevant information, whereas the second is a computational task. The GUM and its supplements also presuppose a mathematical model of the measurement has been formulated [
16]. We agree with Cox and Harris that model formulation is the responsibility of the metrologist. However, we stress that this should involve modelling of the physical measurement. The calculation of uncertainty will ultimately use information from this model to construct a suitable computational form—a process that might itself be viewed as a kind of modelling by a statistician, because abstract statistical concepts may be introduced. We believe that maintaining a clear separation between measurement modelling and the evaluation of uncertainty is beneficial.
The international metrology community has recently embarked on a digital transformation of its systems and processes, which may entail substantial change [
17]. This initiative is motivated by a belief that significant gains in efficiency and reliability can be achieved. However, designing a digital infrastructure that simply automates the various tasks that people perform today is unlikely to foster innovation. Metrology is practised by skilled professionals throughout the world’s quality infrastructures, whose work is shaped by their interpretations of authoritative documents like the VIM and GUM. The implementation details can vary—between organisations, between economies, and between regional metrology organisations. This diversity will complicate an overarching digitalisation of quality infrastructure activities, as neither the analysts eliciting business requirements nor the metrologists describing their work have explicit guidance about the balance between practical considerations and scientific requirements. For example, the definition of traceability does not explain the purpose for measurement uncertainty or why documentation is needed [
18]. These important aspects are left to the discretion of metrologists.
This article examines traceability as a fundamental scientific principle and advocates for explicit measurement modelling, which provides direct and valuable insights into how various types of measurement achieve traceability. Starting with a few basic assumptions, we show that measurements can be modelled with mathematical expressions. These models can represent the influence quantities that ultimately determine the accuracy of measurement results at the end of a traceability chain. Traceability is established by accounting for these influences; indeed, the elements that need to be “traced” along a metrological traceability chain are the residual measurement errors arising from uncontrolled influences. Mathematical notation provides a concise, consistent, and logical structure, offering several advantages: it transcends linguistic differences, is widely understood, and facilitates rigorous analysis.
The structure of this article is as follows. The next section introduces some foundational assumptions and a notation for measurement modelling.
Section 3 illustrates modelling in a variety of scenarios, including ratio and difference measurements, international comparisons, intrinsic and quantum-based standards, and sensor networks.
Section 4 examines the possibility of evaluating models and establishes a connection between modelling and the calculation of measurement uncertainty.
Section 5 examines a way of structuring semantic model information to better align scientific concepts with digital systems development. This approach will facilitate the digitalisation of metrological processes and enhance interoperability.
Section 6 discusses our contention that residual measurement error is central to a scientific description of traceability. It highlights examples from microwave metrology, optical goniometry and an international measurement comparison where modelling has improved measurement accuracy and information flow along traceability chains. Our conclusions are summarised in
Section 7, which is followed by three appendices.
Appendix A develops a model for calibrating a simple linear measuring system,
Appendix B summarises a method for evaluating measurement uncertainty as described in the original GUM, and
Appendix C outlines a method for evaluating uncertainty provided in supplements to the GUM.
3. Different Traceability Scenarios
The principal argument of this article is that physical modelling can describe the relationship between a measurand and a measured value of that measurand. The measurand is a defined quantity, whereas a measured value is the outcome of a real-world process (a measurement) influenced by various physical factors. The challenge lies in finding a suitable model to represent the relationship between a measured value and the measurand in different situations.
3.1. Quantity Ratios
Mathematical measurement models must adhere to the rules of quantity calculus and the laws of physics. One such rule is that, for terms to be legitimately added or subtracted, they must represent quantities of the same kind. Therefore, only quantities of the same kind can be compared by difference. On the other hand, there is no such restriction on the multiplication and division of quantities. A product of quantities is understood to be proportional to its various factors. Thus, the ratio of two quantities of the same kind is sometimes said to be “dimensionless”, meaning that the ratio does not depend on the units used to express values in the numerator and denominator.
This raises an interesting question about traceability: what is an appropriate reference to establish traceability when a measurand is the ratio of two quantities of the same kind? Before addressing this, it is important to clarify a potential source of confusion. In dimensional analysis, dimensionless quantities are treated as pure numbers, which is convenient for mathematical analysis of dimensional problems; however, this is not appropriate when modelling measurements. Quantities defined as ratios of the same kind of quantity should be regarded as distinct quantities in their own right. For example, the linear scale factor, which is a ratio of lengths, is clearly not the same as emissivity, which is a ratio of energies.
When a measurand is defined as the ratio of quantities, there are two possible approaches to establish traceability to an appropriate reference, thereby anchoring the traceability chain. One approach is to trace back to a primary standard for the ratio quantity itself; the other is to trace back to standards for the individual quantities in the numerator and denominator (This is not limited to ratios of the same kind of quantity. For instance, measurements of speed can be traced back to standards of length and time). The first case is no different from establishing traceability to any quantity for which a reference of the same kind is available; the traceability chain can be straightforwardly modelled back to a primary standard.
The second case can be affected by common factors associated with the traceability chains of the numerator and the denominator. For instance, using the same system to measure both quantities may result in the cancellation of some terms. Nevertheless, it is important to consider the situation carefully.
Appendix A describes an example where a linear system measures the ratio of two quantities,
and
. The measurement model, given in Equation (
A6), is
where
G is a gain factor, and
O is a fixed offset. The gain factor cancels in the model of the ratio measurement (
A11):
However, during calibration, the measured value of the offset (A5) is actually influenced by the system gain. Equation (A12), in the appendix, provides an expression for the ratio measurement model that shows how traceability is derived from the standards used to calibrate the system. Thus, the traceability of a measurement of the ratio of
Q is established through traceability chains that refer back to
Q for both the numerator and the denominator.
3.2. Quantity Differences
In
Section 2.5, a simple mass balance was used to show how calibration creates links between the stages of a traceability chain. However, we noted that the chain was abruptly truncated when the balance was incorporated into a model of a mass difference measurement. In fact, the balance’s representation was quite simple: it accounted for a fixed offset and a repeatability error but assumed a perfect response to mass increments. This model allowed the balance to be calibrated by just measuring its offset. Since an offset does not affect the measurement of a mass difference, the representation effectively truncated the traceability chain for a mass difference.
A better representation of a balance could take account of the sensitivity, or gain, of its response to different masses. One way to do this is to introduce a gain factor,
G, to the original model. The observation equation for an indication is then
where
M,
O, and
represent the measurand, offset, and random error, respectively, as before. The parameters
G and
O must be determined by calibration, which requires at least two calibration standards,
and
(
Appendix A gives the calibration equations for a generic linear system measuring
Q, rather than
M).
The mass difference measurement model is now
which does not depend on the balance offset. However, the measurement model of
G used during calibration depends on
and
. Thus, the traceability of mass difference measurements using this model would be established in terms of the balance response to changes in mass.
3.3. Measurement Comparisons
As noted in the Introduction, the CIPM MRA [
2] provides reliable quantitative information on the metrological compatibility of similar calibration and measurement services at different NMIs. To maintain entries in the MRA, NMIs are expected to participate regularly in international measurement comparisons relevant to their services [
20]. In these
CIPM key comparisons, a group of NMIs each measure a suitable measurand—often a stable property of an artefact—and then the comparison coordinator applies an agreed method of analysis to the results.
Comparison analyses can assess the reliability of participants’ measurement capabilities. For a measurand Y, participant “a” submits a result , participant “b” submits a result , and so on, with each result accompanied by a corresponding statement of uncertainty. In modelling terms, it may be assumed that , , and so forth, where the residual errors represent the extent to which each result deviated from the measurand. A comparison analysis estimates the residuals , , etc., which are called degrees of equivalence (DoEs). DoEs can be compared with the uncertainty information provided for each result by the participants. If a DoE is larger than can be explained by a statistical interpretation of the uncertainty, it suggests a problem with the participant’s measurement analysis. Likely, some sources of measurement error have not been properly accounted for in the measurement model.
After a CIPM key comparison has been completed, similarly structured
RMO key comparisons can be carried out by regional metrology organisations (RMOs). Participation in RMO comparisons gives many more NMIs the opportunity to register and maintain claims under the MRA. To evaluate NMI performance across all comparisons, each RMO comparison must include several participants from the initial CIPM comparison. The systematic effects associated with measurements made by these linking participants introduce correlations in the results. However, such linking effects can be accounted for when measurement models are combined with the algorithms used for comparison analysis. This is described in a report on the analysis methods recommended by the Consultative Committee on Photometry and Radiometry (CCPR) [
21]. Succinct measurement models, using one residual error term to represent combined random effects and one to represent combined systematic effects, were used in that analysis. More detailed measurement models, representing the various influence quantities of each comparison participant, can be handled using specific data processing that is designed to evaluate a digital representation of measurement models [
22]. Doing so provides more insights into the comparison analysis outcomes.
3.4. Traceability of Intrinsic and Quantum-Based Standards
Intrinsic measurement standards are standards based on an inherent and reproducible property of a phenomenon or substance ([
11], clause 5.10). They serve as metrological references with assigned consensus values, such as the triple point of water.
From a modelling perspective, a measurement involving an intrinsic standard can be represented by the generic model (
1),
where the single term
represents the combined effects of all influence quantities. This term can be expanded into an appropriately detailed model of the realisation of a particular standard. It is recognised that there are generally two sources of uncertainty in the realisation of an intrinsic standard: one associated with the consensus value (common to all realisations) and the other associated with the specific implementation. In modelling terms, this means that an intrinsic standard may have an error that is common to all standards of the same type, arising from the process that fixed a consensus value (an estimate). A second, implementation-specific error, results from influence factors in the realisation of a system.
Comparison with other standards provides evidence that the system in question is adequately represented by its model—that no unaccounted-for influences introduce bias or reduce precision—and that it is metrologically compatible with the measurand. The need to compare systems is fundamentally the same as for the metrology comparisons, described in
Section 3.3. To claim traceability, the metrological compatibility of realisations must be demonstrated. Without such verification, traceability cannot be assured [
23].
Quantum-based standards are a type of intrinsic measurement standard. These standards rely on the realisation of certain physical properties with well-defined values determined by quantum mechanical phenomena, such as the Josephson effect or the quantum Hall effect. The need for calibration to establish traceability in such systems is seemingly unnecessary. However, their realisation is not immune to influence factors, and so careful characterisation is required, and comparison with independently verified systems is necessary [
24].
3.5. Traceability in Sensor Networks
Sensor networks are multiple interconnected systems of sensors, which monitor physical parameters in their environment and transmit data to a central system for aggregation and analysis. The complex topology of many sensor networks presents challenges in establishing metrological traceability. The typical hierarchical structures, where measurement standards and calibrations are used to disseminate traceability, are not easily applied to sensor networks.
Measurement modelling can help by representing sensor measurement results. For example, when sensors are manufactured in large numbers as batches, the characteristics of a batch can be estimated from a smaller sample. This characterisation can be done using traceable measuring systems. The data obtained could be incorporated in sensor models, with batch characteristics represented by common terms for all sensors, sample variability between sensors represented by sensor-dependent fixed-effect terms, and, lastly, variability between repeat observations with individual sensors represented by random effect terms. Errors due to sampling variation could also be included. Modelling in this way allows the data processing to account for systematic effects, enabling the extraction of more precise information from aggregated measurements [
25]. Many modern sensors are equipped with data processing capabilities, so sensor models could be integrated in the devices to provide plug-and-play functionality.
4. Model Evaluation
Having mathematical models that represent measurement results raises an important question: can the models be evaluated? Although all terms are assumed to have definite values, some remain unknown, making the computational task seem ill-defined. Nevertheless, terms that are not exactly known can be expressed as the sum of a (known) estimate and an (unknown) residual error. In this form, models can be evaluated by taking zero as the estimate for all residual error terms. This calculation yields the measured value—the best estimate of the measurand.
However, residual measurement errors determine the ultimate accuracy of measured values, which must be accounted for when reporting traceable measurement results. These error terms should not be overlooked. They are the subjects of interest in an evaluation of measurement uncertainty.
In metrology, measurement uncertainty is quantified using probabilistic concepts. However, since probability can be interpreted in different ways, so too can uncertainty. The frequentist interpretation, where probability represents the long-run relative frequency of events, is likely familiar to most readers and is consistent with the GUM [
16]. However, the Bayesian view, which is based on a state of knowledge, has been emphasised in later supplements to the GUM [
26,
27].
While exploring the consequences of adopting different definitions of probability—and, by extension, uncertainty—is beyond the scope of this article, this section focuses on how static measurement models can be used as a foundation for uncertainty calculations. The modelling approach described here is grounded in general physical principles, providing a robust framework for the description of measurements. Decisions about data handling—such as the choice of an appropriate probability interpretation—can be made at the end of a traceability chain based on the type of information required.
4.1. Traceability Chains
A traceability chain consists of a succession of carefully linked stages. While we may say that a “measurement” is performed at each stage, it is the combination of stages that constitutes the actual traceable measurement. The hierarchy of stages along a traceability chain is often depicted in the form of a pyramid or triangle. At the summit are the formal definitions of quantities, implemented directly below by NMIs. Second-tier calibration laboratories then provide calibration services to testing laboratories and industry organisations. As one moves down the hierarchy, traceability chains divide into more and more branches.
At the base, information is gathered about a quantity of interest and used—rather than being passed on—to make a decision. Typically, the final stage compares measured values with other measured values, or with nominal quantities. Comprehensive modelling captures the potentially complex branching structures that can arise—for example, the cases of ratio and difference measurements already mentioned and the complexities of measurement comparison analysis. Representing the complete traceability chain is essential for properly assessing the accuracy of results.
To discuss the staged nature of traceability chains, we adopt specific notation. The interpretation of upper- and lower-case terms follows the meanings provided earlier. To represent a model at a given stage, we use functional notation with a stage-index parameter, such as
where
k labels the stage,
is the measurand at that stage, and the elements of the set
are the arguments of
. These arguments may include known and unknown terms evaluated at earlier stages, as well as individually identified quantities or quantity estimates. A complete measurement model is represented by iteration through the stages:
with the final stage delivering the measurand,
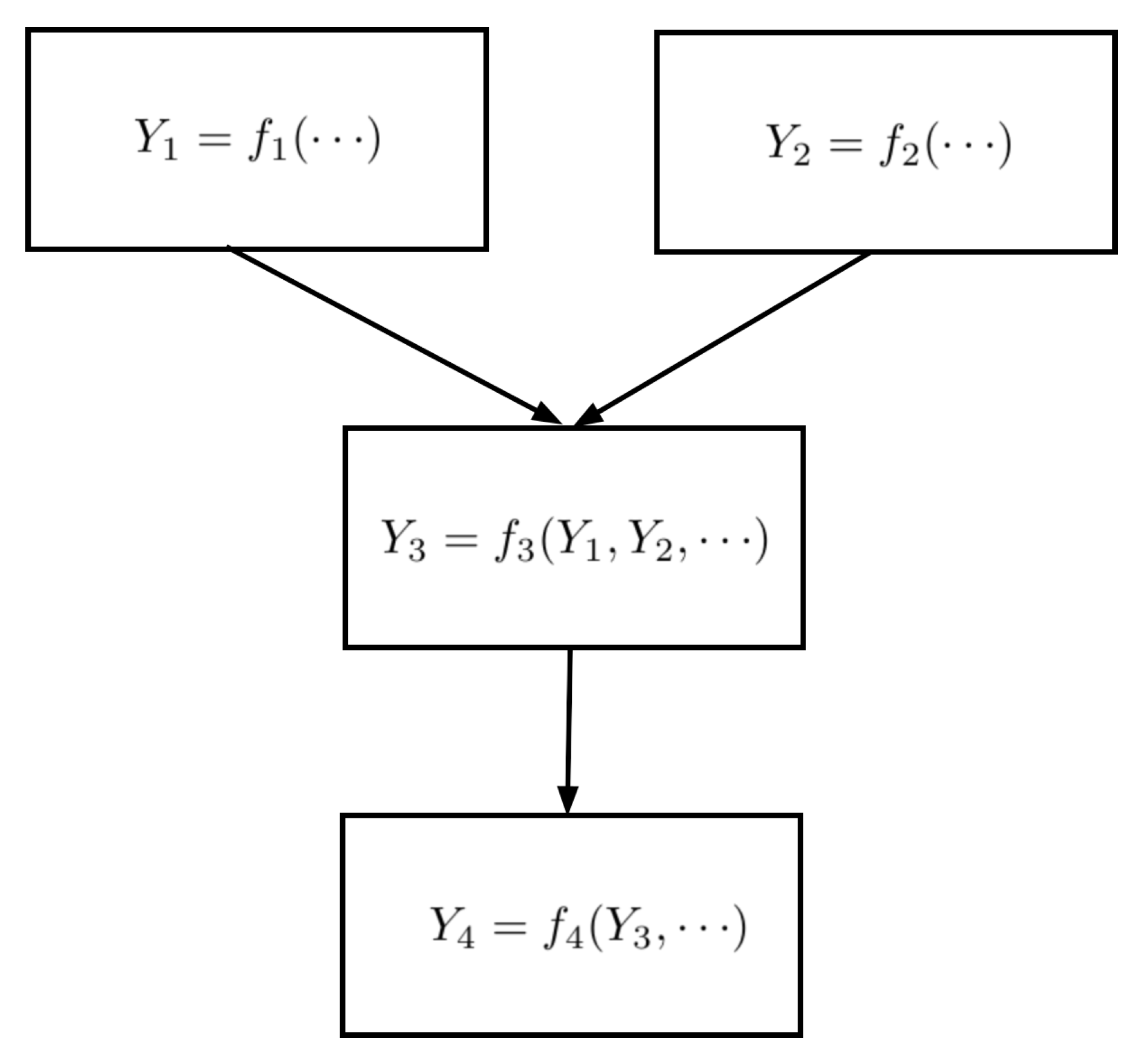
. It is worth noting that the mathematical composition of stage functions is implicit in this description: later stages are composed of earlier stages.
For instance, if the first and second stage results feed into a third stage, which, in turn, feeds the fourth (
Figure 2), the model could be expressed at the fourth stage as
which explicitly shows the composition, while omitting other arguments.
4.2. GUM Evaluation of Uncertainty
The GUM describes a method for evaluating measurement uncertainty when a function describing the measurement is available of the form
where the output quantity
Y is the measurand, and
are input quantities on which
Y depends. A summary of this method is given in
Appendix B. The GUM notation is compatible with the notation employed in this paper but is less strict, because capital letters can also denote random variables—an abstract mathematical concept.
Uncertainty arises because the values of some terms in the model are not known exactly. These terms correspond to the input quantities in Equation (
22). To evaluate the uncertainty of
y as an estimate of
Y, additional information about the input quantities is required. Specifically,
denotes the
standard uncertainty of the estimate,
, of
, expressed as a standard deviation, while
represents the
degrees of freedom associated with
. Furthermore, if there is correlation between estimates, the correlation coefficient
must be provided. Models developed using the approach described in this paper can be handled by the GUM methodology when values for these attributes are documented with the model.
The application of the GUM treatment of uncertainty to static models implies a frequentist interpretation of probability, where the variability of the data is associated with influence quantities. The GUM classifies methods for evaluating the uncertainty of input quantities into two groups: Type A, which applies statistical evaluation methods to data obtained during the measurement, and Type B, where information is obtained outside the measurement. Standard methods for evaluating sample statistics are typically used in Type A data processing and are rooted in classical frequentist approaches. Type B evaluation draws on other sources of information, such as a physical model of a process that influences the measurement. This Type B analysis aligns with the view that terms represent observable quantities that vary due to physical effects. Consequently, a frequentist interpretation of probability is also applicable for Type B uncertainties.
While it is sometimes argued that systematic errors complicate the frequentist analysis of a measurement, static modelling removes this concern. Static models do not differentiate between random and systematic errors. A static model represents all the quantities that contributed to a measurement result, with each having a definite value that may or may not be known. Influences typically classified as systematic are represented by single terms with enduring values, whereas influences typically classified as random are represented by multiple terms, each with a value associated with a different part of a measurement. In this way, static models capture the effects typically ascribed to systematic errors, as demonstrated in the simple cases of difference and ratio measurements in
Section 3.2 and
Section 3.1.
4.3. The Monte Carlo Method for Evaluating Uncertainty
A Monte Carlo simulation has many applications in computational science. It is commonly used to model dynamic stochastic behaviour, providing insights into how a system evolves over time. The Joint Committee on Guides in Metrology (JCGM) has issued supplements to the GUM that describe a method of computing uncertainty called the
Monte Carlo Method (MCM) [
26,
27]. However, this method does not model dynamic system behaviour ([
26], Note 2, p. 10). Instead, random number generation is used to evaluate Bayesian probability distributions associated with unknown fixed quantities. A brief summary of the MCM is given in
Appendix C.
As explained in
Section 4.2, the GUM notation is compatible with the notation employed in this paper. Thus, models developed using the approach described here can serve as precursors to MCM uncertainty calculations. Additional information about the input quantities in Equation (
22) is required. These terms are associated with probability distributions representing the state of knowledge about the inputs, and the result of an MCM calculation represents the state of knowledge distribution for the output quantity
Y. The interpretation of uncertainty statements produced by the MCM is different from uncertainty statements produced using the GUM method. Applying the MCM treatment of uncertainty implies a Bayesian interpretation of probability, which is not based on the variability of the data, i.e., relative frequency ([
26], Note 4, p viii).
As with the GUM method, the static modelling of the full traceability chain facilitates the formulation of MCM calculations because the distinction between random and systematic errors is unnecessary. Static modelling uniquely identifies all quantities instead of classifying some as random and others as systematic. Within the context of an MCM calculation, model terms correspond to specific realisations of random variables. Static modelling identifies common influences that affect multiple stages, enabling them to be addressed appropriately.
4.4. The Need for Documentation
The VIM definition of traceability, cited in the Introduction, refers to a “documented unbroken chain of calibrations, each contributing to the measurement uncertainty”. This phrase can now be better understood in the context of model evaluation. On one hand, calibration forges links between stages in a traceability chain. An “unbroken chain” is necessary to track and audit the effect of influences back to their origins. On the other hand, uncertainty calculations can be performed when a model is available and when probabilistic information about terms in the model has been provided. This information, along with evidence of its accuracy, must be collected and “documented”.
The documentation requirements for GUM and MCM uncertainty calculations differ, and eliciting the necessary information is beyond the scope of this article. However, an important underlying aspect of traceability, which has not been mentioned so far, pertains to the quality of information used in calculations and, consequently, the reliability of the results. One definition of traceability considered by Belanger included the following sentence [
5]:
Measurements have traceability to the designated standards if and only if scientifically rigorous evidence is produced on a continuing basis to show that the measurement process is producing measurement results (data) for which the total measurement uncertainty relative to national or other designated standards is quantified.
Although that sentence never became part of VIM definitions, a shortened version was, for a time, included in NIST traceability policy [
14,
28]:
It is noted that traceability only exists when scientifically rigorous evidence is collected on a continuing basis showing that the measurement process is producing documented results for which the total measurement uncertainty is quantified.
The idea here is that measurements must be performed with the measuring system under statistical control, ensuring that the unpredictable effects of influence quantities can be objectively described in terms of probability, and that those descriptions remain valid for a reasonable period before and after the measurement. This consistency is essential to ensure the reliability of results.
In practice, meeting this expectation involves verifying the performance of a measuring system to produce evidence of satisfactory operation, which is then documented. Ehrlich and Rasberry expand on this idea in their description of
Metrological Timelines in Traceability [
14].
5. Modelling for Digitalisation in Metrology?
This article introduced a simple and general approach to measurement modelling based on the scientific concepts of a physical quantity and quantity calculus. The notation, with clearly defined semantics, emphasised the distinction between known and unknown quantities, thereby facilitating the use of probability to describe unknown quantities.
In this section, we explore a general modelling approach in the context of the principles adopted by the Object Management Group’s Model-Driven Architecture (OMG MDA) [
29]. Our motivation stems from the potential we perceive in MDA principles for developing digital representations tailored to metrological information.
Core metrological concepts, such as traceability, can be expressed in well-defined scientific language anchored to scientific principles. By explicitly defining the semantic structure of these representations—illustrated here through the modelling of calibration scenarios using a defined notation—models of specific situations maintain strict logical relationships to foundational concepts.
In parallel, domain-specific models can be developed to represent these scenarios in digital systems, supporting such functionalities as evaluating numerical results and their associated uncertainties. If digital tools have been designed to conform to the same scientific principles, their semantic consistency facilitates interoperability across diverse systems. This section provides a broad overview of these ideas. We believe this is an area that would benefit from further research efforts.
5.1. Measurement Modelling from the MDA Perspective
The MDA approach uses a model hierarchy to achieve a clear separation between semantic layers and provide flexibility for development. This has been explained by Bézivin, whose work has been influential within the field of model-driven engineering [
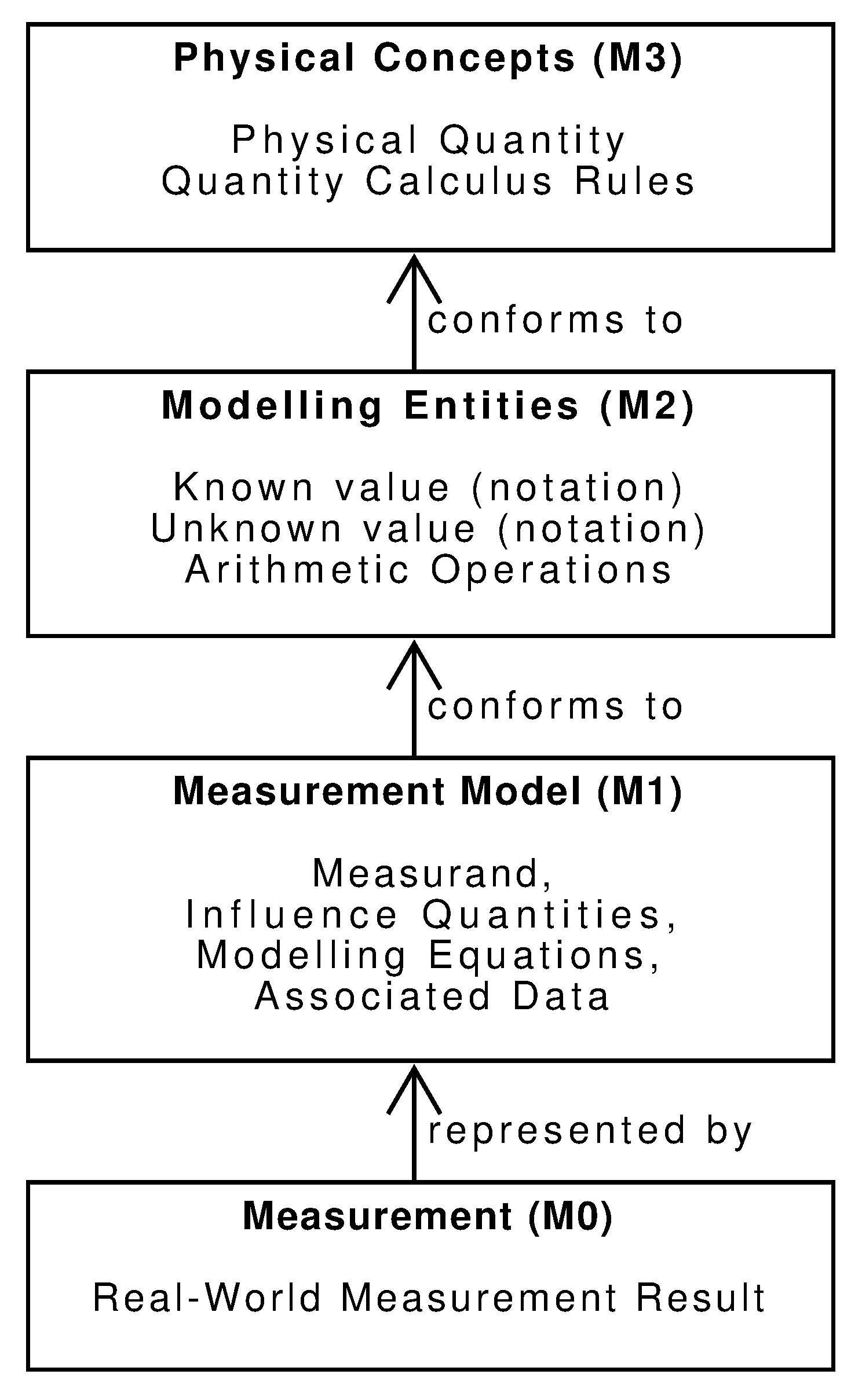
30]. The approach distinguishes four abstraction levels:
- M0:
A system (i.e., the real-world entity or phenomenon being represented).
- M1:
A model of the system, capturing its structure and behaviour in a specific context.
- M2:
A meta-model, which defines the elements, relationships, and rules used to construct models at the M1 level.
- M3:
A meta-meta-model, which provides the foundational concepts for defining meta-models.
This four-level structure aligns with the modelling approach in this paper, illustrated in
Figure 3. The real-world system of interest, at M0 in the MDA hierarchy, is a measurement result. At the opposite end, M3 in the hierarchy represents the conceptual elements needed to model a result, grounded in the concept of a physical quantity and the rules of quantity calculus, which defines the operations applicable to such quantities. These concepts form the basis for the meta-models at the M2 level, where the entities and structures used to describe measurements are formalised. The entities used for modelling include known and unknown quantities, as well as arithmetic operators, as introduced in
Section 2. These elements are identified by specific notation to facilitate the expression of quantity equations.
Models constructed at the M1 level provide concrete representations of specific measurements. Our focus is on the processes that generate a traceable result. This can be viewed as a sequence of stages, each involving definite quantities that collectively determine the final outcome. Factors such as aleatory behaviour and time dependence of quantities are not relevant.
M1 models represent specific aspects of measurement results to enable reasoning about their properties, such as traceability. In some cases, M1 models may impose additional domain-specific constraints not defined in the M2 meta-model. For example, while quantity calculus allows for the addition of quantities, intensive quantities like temperature cannot be meaningfully added.
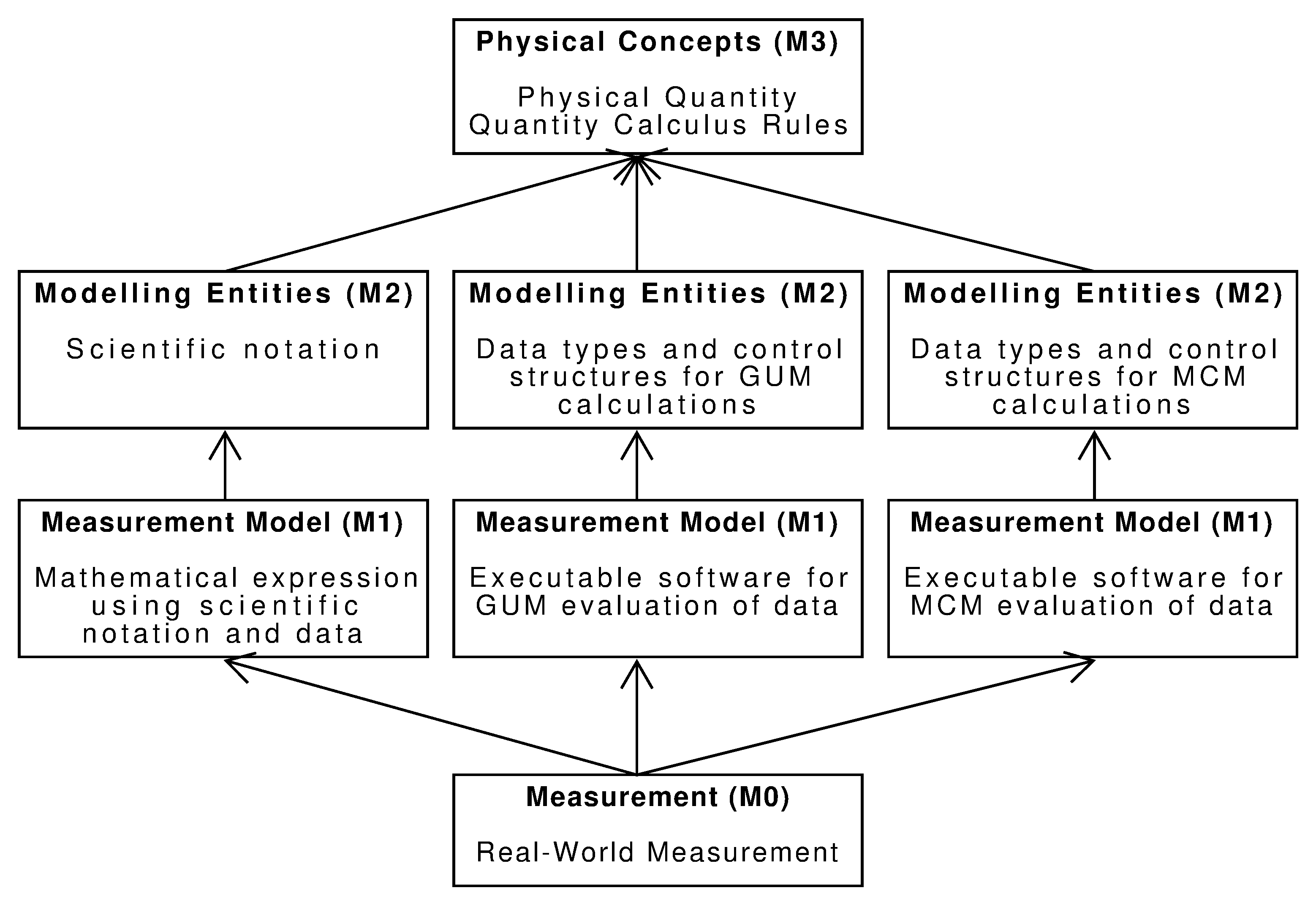
5.2. Parallel Hierarchies
Parallel model hierarchies can be developed, extending from the same foundational M3 model, but defining different software entities at the M2 level. Programs at the M1 level, built on these M2 definitions, may serve as models representing different aspects of real-world measurement results.
For instance, distinct M2-level meta-models could support the two types of uncertainty calculation discussed in
Section 4.2 and
Section 4.3 (
Figure 4). A meta-model tailored for GUM uncertainty calculations would define the data type for unknown quantities with attributes such as a value, standard uncertainty, and degrees of freedom. Conversely, a meta-model for MCM calculations would represent unknown quantities with attributes for a value, the state-of-knowledge distribution type, and its associated parameters. The GUM meta-model would also describe how uncertainty is propagated and evaluated using the LPU (
A14) and Welch–Satterthwaite (
A15) formulae. In contrast, the MCM meta-model would define control structures for Monte Carlo simulations and methods for summarising results. M2 meta-models would also identify the notion of probability applicable to M1 models.
5.3. Can the MDA Approach Help in Metrology?
The MDA approach can support the digitalisation of metrology by facilitating a clear separation of concerns. The methodology allows metrologists to focus on describing their problems using metrological principles in scientific terms, while information technologists can concentrate on the design and implementation of robust digital systems. This helps to maintain metrological understanding and scientific integrity throughout the digitalisation process, without placing unnecessary cross-disciplinary demands on either metrologists or IT developers. It also insulates the new digital metrology infrastructure from problems associated with rapid evolution of digital technologies. Flater has expressed similar ideas, observing that the conceptual foundations of a documentary standard often evolve at a different pace than the technologies used in its implementation—a challenge that MDA principles could help address [
31].
The key feature of the MDA approach that enables this separation of concerns is its establishment of a common conceptual foundation. This paper illustrated the approach using simple physical modelling applied to measurement results. This conceptual foundation is actually quite effective. Being grounded in fundamental scientific concepts, such as quantities, quantity calculus, and probability, it captures the essential elements required for modelling. Its simplicity is a strength, facilitating clear and unambiguous communication of ideas while offering the flexibility to develop more complex meta-models tailored to specific applications.
Early efforts in the digitalisation of metrology did not exploit hierarchical modelling. Instead, developers created a variety of digital systems where the conceptual foundations were implied rather than explicitly defined. This reliance on a tacit understanding of underlying concepts introduces a risk of ambiguity and inconsistency, particularly when different groups of people or systems interact.
By adopting the MDA approach, however, the metrology community can identify and apply appropriate and well-defined conceptual foundations. This clarity will foster consistency and collaboration between disciplines, reducing misunderstandings and facilitating the creation of more interoperable systems.
6. Discussion
Another perspective on the central theme of this paper is that all measured values are inherently wrong; they inevitably contain some degree of error. Metrologically traceable measurements, however, provide an objective means to quantify the magnitude of that error, enabling the accuracy of measurement to be evaluated so that the usefulness of a result can be considered. Ehrlich and Rasberry suggested that the primary use of traceability was to answer the questions ([
14], Section 1.1):
What correction should be applied to a measurement result […] to match the result that would be obtained using the instrument (standard) to which traceability is desired? What is the uncertainty of this corrected result?
These questions apply between adjacent stages in a traceability chain, where the correction required is the (unknown) value of residual error contributed by the latest stage. However, by iteratively asking these questions back along a traceability chain, we see that the idea aligns with our simple generic model (
1)
The use of “uncertainty” in the VIM definition of traceability serves a pragmatic purpose. Metrologists are accustomed to evaluating the accuracy of measurements in their specialist fields, using methods described in the GUM or its supplements. The results of these evaluations can be reported in a few different formats described in the GUM. Thus, the VIM guides people to use familiar processes that harmonise the way in which information is shared.
Nevertheless, the concept of residual measurement error is central to the scientific understanding of traceability. It is the unknown amount of residual error that leads to uncertainty in the accuracy of a result as an estimate of the measurand. Residual measurement errors can be modelled as instances of physical quantities, representing small deviations from nominal or estimated quantity values. Consequently, measurement models with terms representing errors can be analysed as physical systems. The same cannot be said about uncertainties. In metrology, “uncertainty” broadly refers both to probabilistic descriptions of terms in measurement models (e.g., standard uncertainty) and to the evaluation of statistical inferences about quantity values (e.g., expanded uncertainty) [
18]. The sense of “uncertainty” is also complicated by the various interpretations of probability employed within the metrological community.
We contend that measurement models—describing the behaviour of residual errors in traceability chains—provide a framework for understanding the scientific nature of metrological traceability. Such modelling enables a rigorous analysis of measurement scenarios, while the notation avoids some of the challenges inherent in verbal descriptions. The formal language of science, grounded in the strict logic of physical quantity equations, is well suited to this purpose.
There is ample evidence of practical applications to support this contention. The most striking example comes from the microwave metrology community, which has adopted a modelling approach to describe measurements of complex-valued transmission line components. Modelling is described in a best-practice guide for the community [
32] and has significantly enhanced the information available through traceable measurements [
33]. Modelling, supported by software, can unravel complicated effects due to common influence quantities involved in instrument calibration procedures. Information about the uncertainty components due to residual errors at each stage can be passed between stages along the traceability chain in digital form. This enables downstream users to benefit from the detailed modelling done by an NMI [
34].
Another example is a detailed study modelling a four-axis goniometric system measuring optical reflectance [
35,
36]. This system has many configuration terms that are not known exactly. Residual errors in the estimates of these parameters must be considered to account for the accuracy of the result. By modelling the set-up, the system performance in different configurations could be examined, enabling a better understanding of the correlations between various measurement errors. This understanding significantly improved the accuracy obtainable for certain measurements.
One more example relates to modelling in a recent international CIPM key comparison of the triple point of water (TPW), CCT-K7.2021 [
37]. The Measurement Standards Laboratory of New Zealand (MSL) participated in this comparison and used modelling and specialised software to account for significant correlations arising from shared influence factors. MSL submitted an uncertainty in the TPW difference between its comparison artefact and the New Zealand national reference that was less than half the uncertainties submitted by nearly all other participants. While it is unlikely that MSL can measure better than other participants, the uncertainty analysis is complex. The measurement model gives rise to correlations between terms that make rigorous uncertainty analysis by analytical methods difficult; however, these effects can easily be evaluated through automation. After the results of the comparison were published, MSL applied the modelling approach to information reported by the pilot laboratory. A mathematical model for the pilot laboratory’s measurement was derived from the written description in the report, and this model was evaluated using the published data. The result was a 2.5-fold reduction in the pilot laboratory’s uncertainty [
38].
A common feature of these examples is the use of specialised software that implicitly adopts a modelling approach similar to the one discussed in this article. Several NMIs have developed such packages [
39,
40], highlighting the benefits of adopting a clear semantic structure, in line with the MDA principles discussed in
Section 5.2. However, the overarching conceptual model is embedded within the uncertainty evaluation algorithm, rather than being explicitly specified. These software tools define an abstract data type to represent unknown quantities in a measurement model [
41]. Objects of this type possess the attributes needed for GUM-based uncertainty evaluation (
Appendix B). In this way, much of the computational complexity can be automated. Ideally, however, the definition of measurement models should be decoupled from the software responsible for uncertainty evaluation, as outlined in
Section 5.2.
7. Conclusions
The most important aspect of metrological traceability is that results can be meaningfully compared—whether with other traceable results or with nominal values expressed on the same measurement scale. To enable this, measurement results include a quantitative assessment of accuracy. Accuracy is determined by the inevitable accumulation of residual errors during measuring stages, so a measurement model that describes how these errors contribute to the final result is essential.
This paper presented a structured approach to modelling using a simple mathematical notation. A number of examples were presented that showed how to develop models using this framework. We emphasised the importance of modelling the entire traceability chain, from the realisation of primary reference standards through to the end user. This ensures that all residual errors can be properly accounted for in the accuracy assessment of a final result, wherever they arose during measuring processes. We also emphasised the need for a static model of the quantities involved. A static model consists of terms representing definite values of quantities contributing to the final result—like a snapshot of the physical situation.
The modelling approach described here is grounded in physical principles, including the concepts of physical quantities and quantity calculus. Modelling does not involve notions of probability or measurement uncertainty; however, a model serves as a precursor to uncertainty calculations. Whether the original GUM method or the GUM Supplement’s Monte Carlo Method is used, an evaluation of uncertainty requires a static model of the measurement as a starting point. Static modelling of the entire chain has the advantage of eliminating the need to explicitly distinguish between random and systematic errors, as both are inherently accounted for within the model.
The importance of clearly identifying a formal semantic basis for modelling was discussed in relation to modern methods of digital system design. We argue that creating hierarchical modelling structures, anchored in well-defined conceptual models, holds promise for the further development of digitalisation in metrology. Doing so cleanly separates the concerns of metrology from others related to computation and technology, both during the development of new digital systems and their subsequent maintenance. This is well suited to a formal, structured, enterprise-based approach to architectural planning of digital transformation in metrology. Logical next steps for the ideas discussed above will be to formalise the model notation details, allowing it to be incorporated in standardised architectural descriptions. This could be achieved by following established standards for documenting architectural descriptions, like the ISO/IEC standard 42010 [
42].