Advancing Molecular Spectroscopy Efficiency with Extensive Parallelism
Abstract
1. Introduction
2. CP-FTMW Spectroscopy
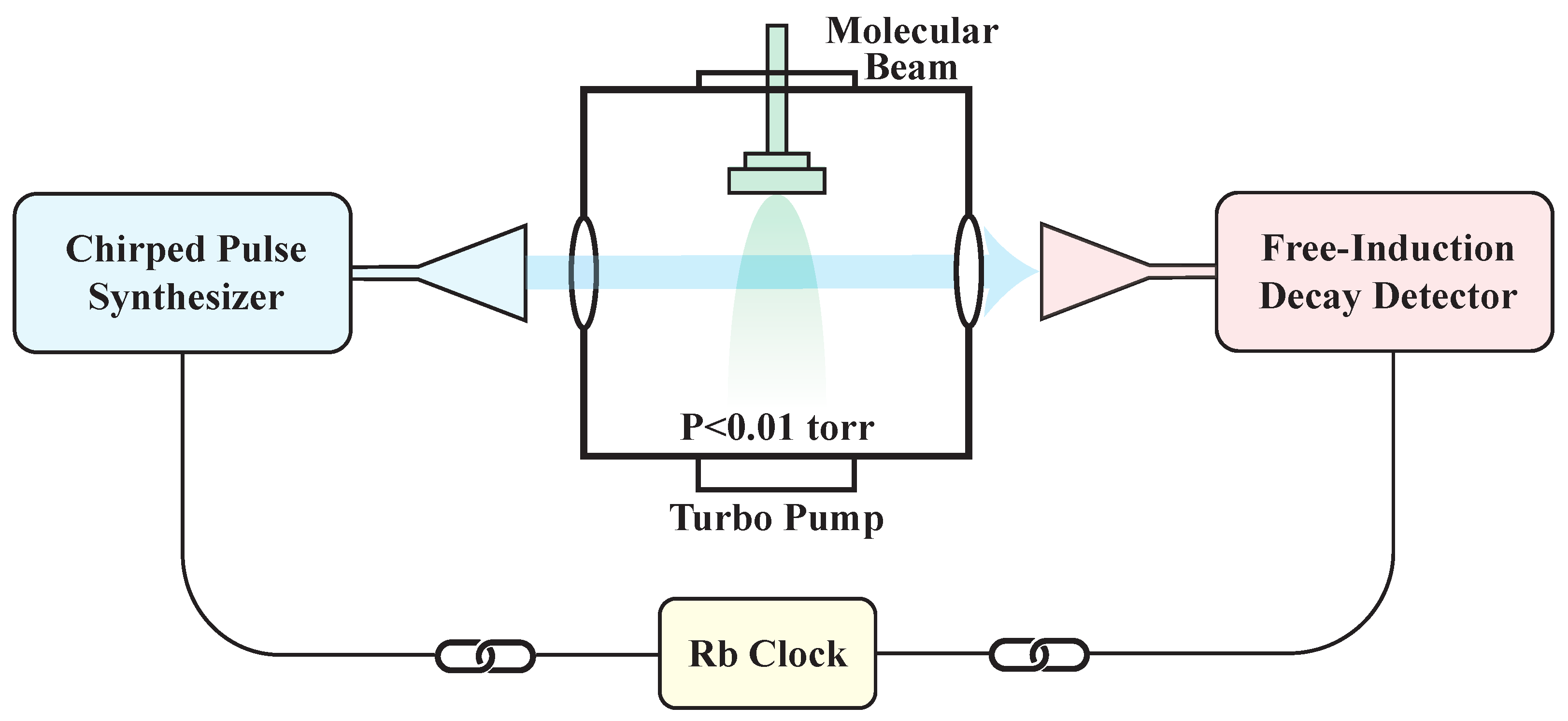
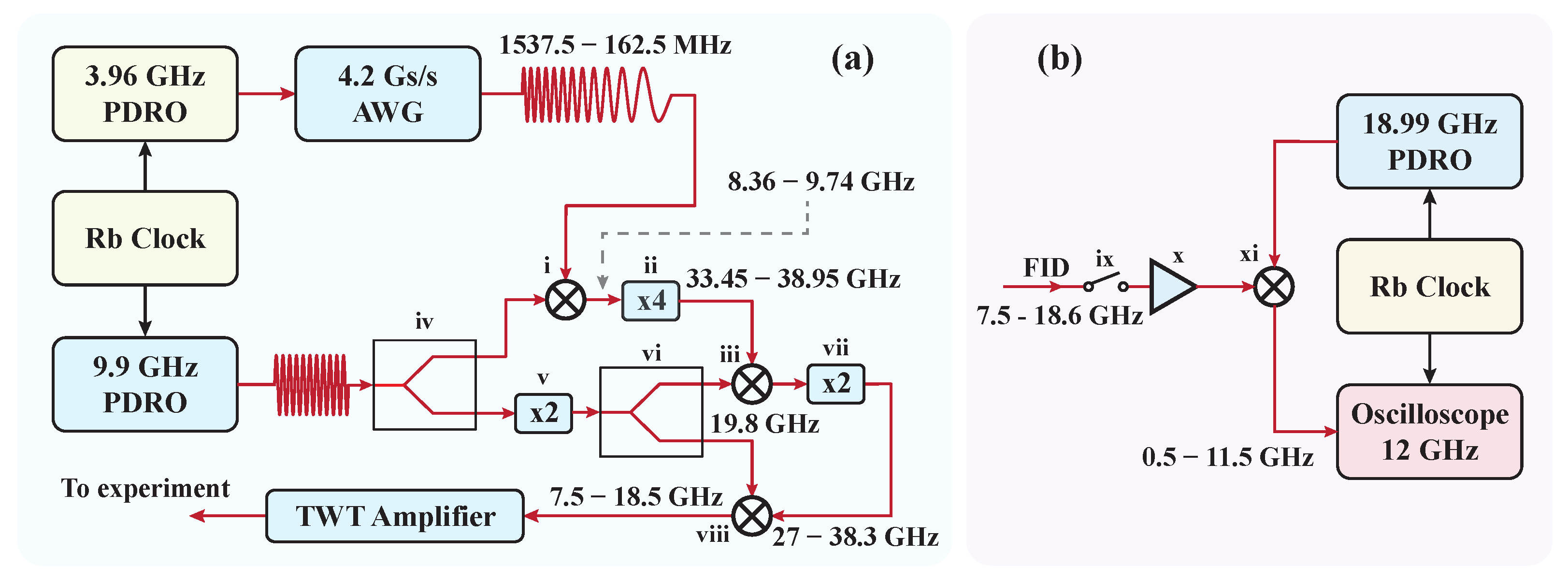
2.1. CP-FTMW Spectrometer
- The approach of using rapid frequency sweeps to generate strong polarization was first demonstrated by McGurk, Schmalz, and Flygare in 1974 [35]. At that time, however, technological limitations made it difficult to quickly adjust microwave frequencies. To overcome this, they used a ramped electric field to produce a rapid Stark shift sweep, effectively shifting the relative frequency between the microwave signal and the molecular transitions.
- To achieve broadband excitation, the chirped-pulse (CP) approach replaces ultra-short, Fourier-transform-limited pulses, which typically distribute low power across individual frequency components. In contrast, CPs have longer pulse durations (∼1 μs) and wide bandwidths (>10 GHz), providing broad spectral coverage with a more uniform power distribution. High-speed digital Arbitrary Waveform Generators (AWGs) are now commonly used to efficiently generate CPs.
- Molecules polarized by CPs emit a Free-Induction Decay (FID) signal, which can be captured and digitized in the time domain using a high-speed oscilloscope. This FID signal contains information across the entire bandwidth (>10 GHz) in a single-shot measurement. A frequency-domain spectrum is then obtained by applying a fast Fourier transform (FFT) to the FID signal.
- The devices used for generating the CPs and detecting the FID signals are phase-referenced to an accurate frequency standard. This precise synchronization ensures that the phase-reproducible FID signals are coherently averaged in the time domain, resulting in a linear enhancement of the signal-to-noise ratio (SNR).
2.2. Extensions of CP Spectrometers
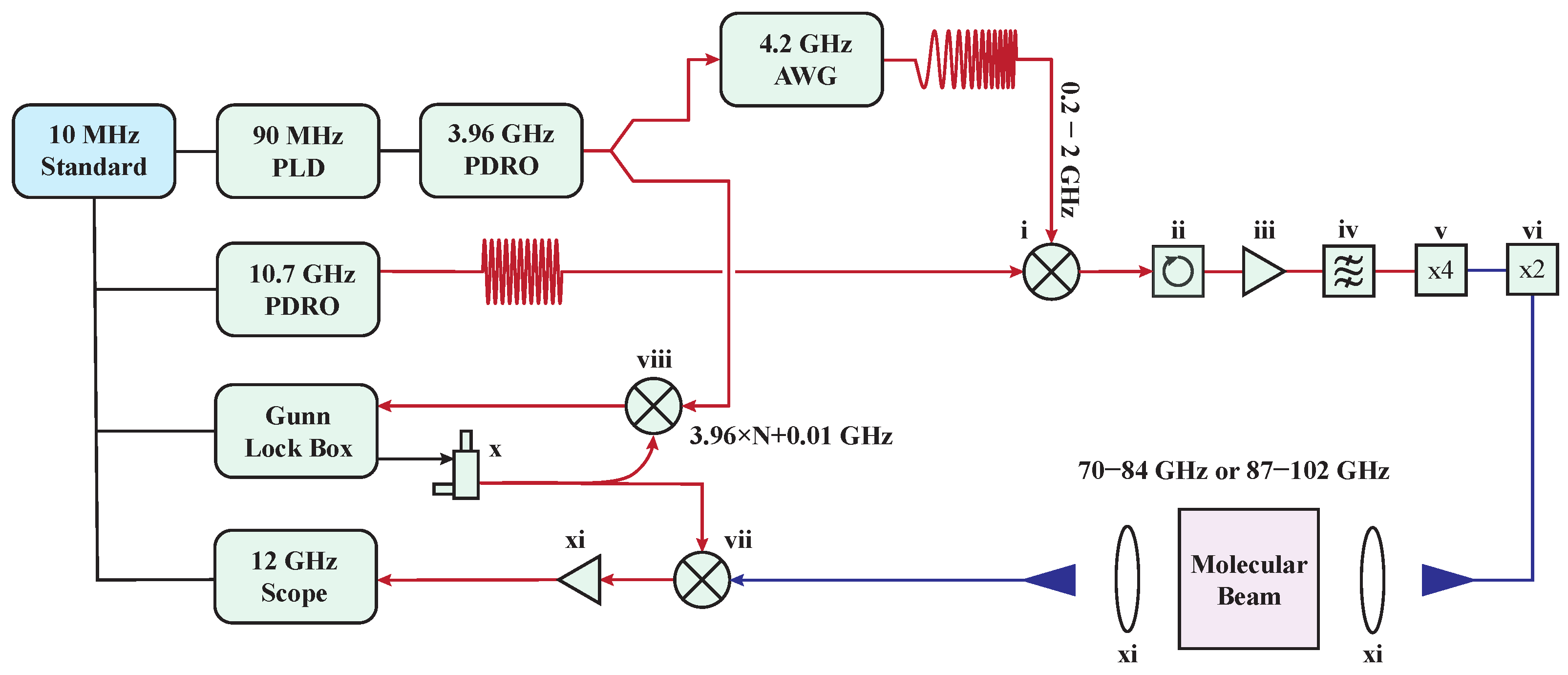
2.2.1. Spectrometers Toward Terahertz Frequencies
2.2.2. Segmented CP Spectrometers
2.2.3. Hybrid of CP-FTMW and BF-FTMW Spectrometers
2.3. Applications in Structural Determination
2.4. Applications in Investigating Dynamics
2.5. Applications in Rydberg Spectroscopy
2.6. Outlook
3. OFC Spectroscopy
3.1. Fundamental Principles of OFC
3.2. Direct Frequency Comb Spectroscopy
3.3. Dual-Comb Spectroscopy
3.4. Outlook
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Quack, M.; Merkt, F. Handbook of High-Resolution Spectroscopy; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Riyadh, S.M.S.; Telfah, H.; Jones, I.W.; Bersson, J.S.; Cheng, C.F.; Hu, S.M.; Foote, D.B.; Liu, J. Mid-infrared Doppler-free saturation absorption spectroscopy of the Q branch of CH4ν3=1 band using a rapid-scanning continuous-wave optical parametric oscillator. Opt. Lett. 2024, 49, 4230–4233. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.H.; Tan, Y.; Cheng, C.F.; Hu, S.M. Precision spectroscopy of molecular hydrogen. Phys. Chem. Chem. Phys. 2023, 25, 27914–27925. [Google Scholar] [CrossRef] [PubMed]
- Wieman, C.; Hansch, T.W. Doppler-free laser polarization spectroscopy. Phys. Rev. Lett. 1976, 36, 1170–1173. [Google Scholar] [CrossRef]
- Zalicki, P.; Zare, R.N. Cavity ring-down spectroscopy for quantitative absorption measurements. J. Chem. Phys. 1995, 102, 2708–2717. [Google Scholar] [CrossRef]
- Berden, G.; Peeters, R.; Meijer, G. Cavity ring-down spectroscopy: Experimental schemes and applications. Int. Rev. Phys. Chem. 2000, 19, 565–607. [Google Scholar] [CrossRef]
- Scherer, J.J.; Paul, J.B.; O’keefe, A.; Saykally, R.J. Cavity ringdown laser absorption spectroscopy: History, development, and application to pulsed molecular beams. Chem. Rev. 1997, 97, 25–52. [Google Scholar] [CrossRef]
- Fiedler, S.E.; Hese, A.; Ruth, A.A. Incoherent broad-band cavity-enhanced absorption spectroscopy. Chem. Phys. Lett. 2003, 371, 284–294. [Google Scholar] [CrossRef]
- Engeln, R.; Berden, G.; Peeters, R.; Meijer, G. Cavity enhanced absorption and cavity enhanced magnetic rotation spectroscopy. Rev. Sci. Instrum. 1998, 69, 3763–3769. [Google Scholar] [CrossRef]
- Schindewolf, A.; Bause, R.; Chen, X.Y.; Duda, M.; Karman, T.; Bloch, I.; Luo, X.Y. Evaporation of microwave-shielded polar molecules to quantum degeneracy. Nature 2022, 607, 677–681. [Google Scholar] [CrossRef]
- Bigagli, N.; Yuan, W.; Zhang, S.; Bulatovic, B.; Karman, T.; Stevenson, I.; Will, S. Observation of Bose–Einstein condensation of dipolar molecules. Nature 2024, 631, 289–293. [Google Scholar] [CrossRef]
- Vilas, N.B.; Hallas, C.; Anderegg, L.; Robichaud, P.; Winnicki, A.; Mitra, D.; Doyle, J.M. Magneto-optical trapping and sub-Doppler cooling of a polyatomic molecule. Nature 2022, 606, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Jin, D.S.; Ye, J. Introduction to ultracold molecules: New frontiers in quantum and chemical physics. Chem. Rev. 2012, 112, 4801–4802. [Google Scholar] [CrossRef] [PubMed]
- Tobias, W.G.; Matsuda, K.; Li, J.R.; Miller, C.; Carroll, A.N.; Bilitewski, T.; Rey, A.M.; Ye, J. Reactions between layer-resolved molecules mediated by dipolar spin exchange. Science 2022, 375, 1299–1303. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Enemali, G.; Zhang, R.; Fu, Y.; McCann, H.; Zhou, B.; Liu, C. FPGA-accelerated distributed sensing system for real-time industrial laser absorption spectroscopy tomography at kilo-hertz. IEEE Trans. Ind. Inform. 2024, 20, 2529–2539. [Google Scholar] [CrossRef]
- Davies, V.; Wandy, J.; Weidt, S.; Hooft, J.J.V.D.; Miller, A.; Daly, R.; Rogers, S. Rapid development of improved data-dependent acquisition strategies. Anal. Chem. 2021, 93, 5676–5683. [Google Scholar] [CrossRef]
- Manu, V.S.; Olivieri, C.; Veglia, G. AI-designed NMR spectroscopy RF pulses for fast acquisition at high and ultra-high magnetic fields. Nat. Commun. 2023, 14, 4144. [Google Scholar] [CrossRef]
- Angulo, A.; Yang, L.; Aydil, E.S.; Modestino, M.A. Machine learning enhanced spectroscopic analysis: Towards autonomous chemical mixture characterization for rapid process optimization†. Digit. Discov. 2022, 1, 35–44. [Google Scholar] [CrossRef]
- Crocombe, R.A. Portable spectroscopy. Appl. Spectrosc. 2018, 72, 1701–1751. [Google Scholar] [CrossRef]
- Yu, H.; Tan, Y.; Cunningham, B.T. Smartphone fluorescence spectroscopy. Anal. Chem. 2014, 86, 8805–8813. [Google Scholar] [CrossRef]
- Townes, C.; Schawlow, A. Microwave Spectroscopy; Dover books on physics; Dover Publications: Mineola, NY, USA, 2013. [Google Scholar]
- Schwarting, M.; Seifert, N.A.; Davis, M.J.; Blaiszik, B.; Foster, I.; Prozument, K. Twins in rotational spectroscopy: Does a rotational spectrum uniquely identify a molecule? arXiv 2024, arXiv:2404.04225. [Google Scholar] [CrossRef]
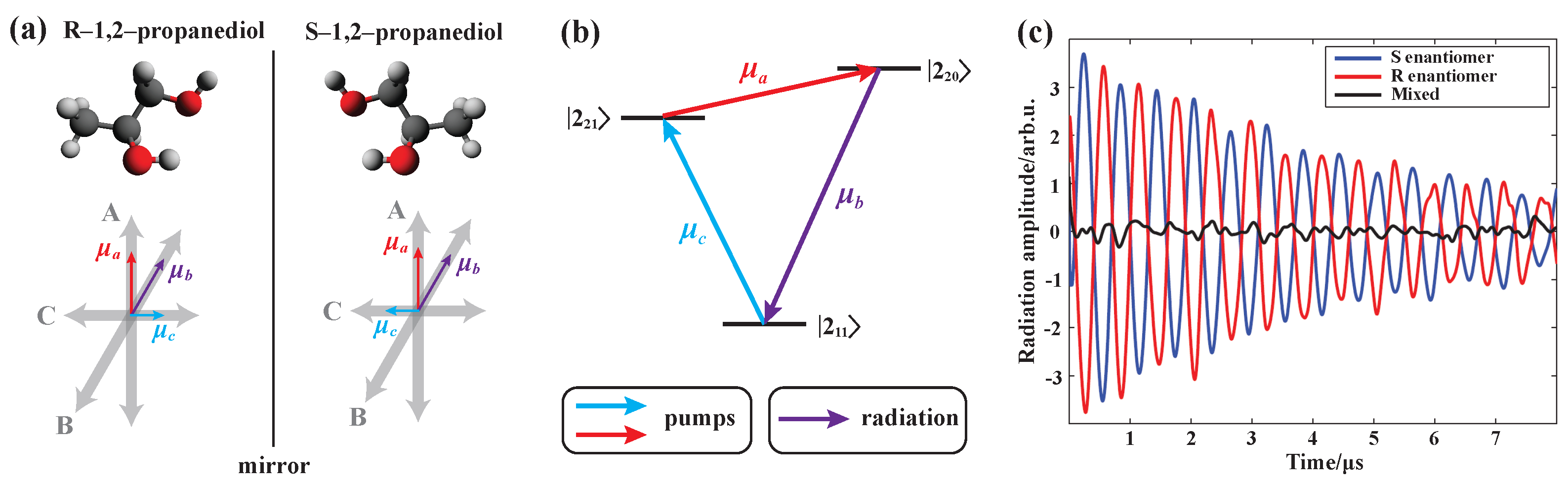
- Patterson, D.; Schnell, M.; Doyle, J.M. Enantiomer-specific detection of chiral molecules via microwave spectroscopy. Nature 2013, 497, 475–477. [Google Scholar] [CrossRef] [PubMed]
- Crabtree, K.N.; Martin-Drumel, M.A.; Brown, G.G.; Gaster, S.A.; Hall, T.M.; McCarthy, M.C. Microwave spectral taxonomy: A semi-automated combination of chirped-pulse and cavity Fourier-transform microwave spectroscopy. J. Chem. Phys. 2016, 144, 124201. [Google Scholar] [CrossRef] [PubMed]
- Balle, T.J.; Flygare, W.H. Fabry-Perot cavity pulsed Fourier transform microwave spectrometer with a pulsed nozzle particle source. Rev. Sci. Instrum. 1981, 52, 33–45. [Google Scholar] [CrossRef]
- Johnson, H.R. Backward-Wave Oscillators. Proc. IRE 1955, 43, 684–697. [Google Scholar] [CrossRef]
- Goebel, D.M.; Butler, J.M.; Schumacher, R.W.; Santoru, J.; Eisenhart, R.L. High-power microwave source based on an unmagnetized backward-wave oscillator. IEEE Trans. Plasma Sci. 1994, 22, 547–553. [Google Scholar] [CrossRef]
- Chen, C.; Liu, G.; Huang, W.; Song, Z.; Fan, J.; Wang, H. A repetitive X-band relativistic backward-wave oscillator. IEEE Trans. Plasma Sci. 2002, 30, 1108–1111. [Google Scholar] [CrossRef]
- Nusinovich, G.S.; Member, S.; Carmel, Y.; Antonsen, T.M.; Goebel, D.M.; Santoru, J. Recent progress in the development of plasma-filled traveling-wave tubes and backward-wave oscillators. IEEE Trans. Plasma Sci. 1998, 26, 151. [Google Scholar] [CrossRef]
- Hummelt, J.S.; Lewis, S.M.; Shapiro, M.A.; Temkin, R.J. Design of a metamaterial-based backward-wave oscillator. IEEE Trans. Plasma Sci. 2014, 42, 930–936. [Google Scholar] [CrossRef]
- Khodos, V.V.; Ryndyk, D.A.; Vaks, V.L. Fast-passage microwave molecular spectroscopy with frequency sweeping. Eur. Phys. J. Appl. Phys. 2004, 25, 203–208. [Google Scholar] [CrossRef]
- Brown, G.G.; Dian, B.C.; Douglass, K.O.; Geyer, S.M.; Pate, B.H. The rotational spectrum of epifluorohydrin measured by chirped-pulse Fourier transform microwave spectroscopy. J. Mol. Spectrosc. 2006, 238, 200–212. [Google Scholar] [CrossRef]
- Brown, G.G.; Dian, B.C.; Douglass, K.O.; Geyer, S.M.; Shipman, S.T.; Pate, B.H. A broadband Fourier transform microwave spectrometer based on chirped pulse excitation. Rev. Sci. Instrum. 2008, 79, 053103. [Google Scholar] [CrossRef] [PubMed]
- Park, G.B.; Field, R.W. Perspective: The first ten years of broadband chirped pulse Fourier transform microwave spectroscopy. J. Chem. Phys. 2016, 144, 200901. [Google Scholar] [CrossRef] [PubMed]
- McGurk, J.C.; Schmalz, T.G.; Flygare, W.H. Fast passage in rotational spectroscopy: Theory and experiment. J. Chem. Phys. 1974, 60, 4181–4188. [Google Scholar] [CrossRef]
- Anderegg, L.; Burchesky, S.; Bao, Y.; Yu, S.S.; Karman, T.; Chae, E.; Ni, K.K.; Ketterle, W.; Doyle, J.M. Observation of microwave shielding of ultracold molecules. Science 2021, 373, 779–782. [Google Scholar] [CrossRef] [PubMed]
- Wright, S.C.; Wall, T.E.; Tarbutt, M.R. Microwave trap for atoms and molecules. Phys. Rev. Res. 2019, 1, 033035. [Google Scholar] [CrossRef]
- Park, G.B.; Steeves, A.H.; Kuyanov-Prozument, K.; Neill, J.L.; Field, R.W. Design and evaluation of a pulsed-jet chirped-pulse millimeter-wave spectrometer for the 70–102 GHz region. J. Chem. Phys. 2011, 135, 024202. [Google Scholar] [CrossRef]
- Lauzin, C.; Schmutz, H.; Agner, J.A.; Merkt, F. Chirped-pulse millimetre-wave spectrometer for the 140–180 GHz region. Mol. Phys. 2018, 116, 3656–3665. [Google Scholar] [CrossRef]
- Gerecht, E.; Douglass, K.O.; Plusquellic, D.F. Chirped-pulse terahertz spectroscopy for broadband trace gas sensing. Opt. Express 2011, 19, 8973–8984. [Google Scholar] [CrossRef]
- Steber, A.L.; Harris, B.J.; Neill, J.L.; Pate, B.H. An arbitrary waveform generator based chirped pulse Fourier transform spectrometer operating from 260 to 295 GHz. J. Mol. Spectrosc. 2012, 280, 3–10. [Google Scholar] [CrossRef]
- Stroud, J.R.; Plusquellic, D.F. Difference-frequency chirped-pulse dual-comb generation in the THz region: Temporal magnification of the quantum dynamics of water vapor lines by >60,000. J. Chem. Phys. 2022, 156, 044302. [Google Scholar] [CrossRef]
- Neill, J.L.; Harris, B.J.; Steber, A.L.; Douglass, K.O.; Plusquellic, D.F.; Pate, B.H. Segmented chirped-pulse Fourier transform submillimeter spectroscopy for broadband gas analysis. Opt. Express 2013, 21, 19743–19749. [Google Scholar] [CrossRef] [PubMed]
- Barnum, T.J.; Lee, K.L.K.; McGuire, B.A. Chirped-Pulse Fourier transform millimeter-wave spectroscopy of Furan, isotopologues, and vibrational excited states. ACS Earth Space Chem. 2021, 5, 2986–2994. [Google Scholar] [CrossRef]
- Sironneau, V.; Chelin, P.; Tchana, F.K.; Kleiner, I.; Pirali, O.; Roy, P.; Guillemin, J.C.; Orphal, J.; Marguls, L.; Motiyenko, R.A.; et al. Reinvestigation of the microwave and new high resolution far-infrared spectra of cis-methyl nitrite, CH3ONO: Rotational study of the two first torsional states. J. Mol. Spectrosc. 2011, 267, 92–99. [Google Scholar] [CrossRef]
- Prozument, K.; Baraban, J.H.; Changala, P.B.; Park, G.B.; Shaver, R.G.; Muenter, J.S.; Klippenstein, S.J.; Chernyak, V.Y.; Field, R.W. Photodissociation transition states characterized by chirped pulse millimeter wave spectroscopy. Proc. Natl. Acad. Sci. USA 2020, 117, 146–151. [Google Scholar] [CrossRef] [PubMed]
- Fritz, S.M.; Mishra, P.; Wullenkord, J.; Fugazzi, P.G.; Kohse-Höinghaus, K.; Zwier, T.S.; Hansen, N. Detecting combustion intermediates via broadband chirped-pulse microwave spectroscopy. Proc. Combust. Inst. 2021, 38, 1761–1769. [Google Scholar] [CrossRef]
- Zou, L.; Motiyenko, R.A.; Margulès, L.; Alekseev, E.A. Millimeter-wave emission spectrometer based on direct digital synthesis. Rev. Sci. Instrum. 2020, 91, 063104. [Google Scholar] [CrossRef]
- Li, J.; Ojeda, J.M.; Letourneau, S.; Zhou, Y. Cost-effective segmented CP-FTMW spectrometers. Department of Physics and Astronomy, University of Nevada, Las Vegas, NV 89154, USA, 2024. In preparation.
- Fatima, M.; Pérez, C.; Arenas, B.E.; Schnell, M.; Steber, A.L. Benchmarking a new segmented K-band chirped-pulse microwave spectrometer and its application to the conformationally rich amino alcohol isoleucinol. Phys. Chem. Chem. Phys. 2020, 22, 17042–17051. [Google Scholar] [CrossRef]
- McCarthy, M.C.; Zou, L.; Martin-Drumel, M.A. To kink or not: A search for long-chain cumulenones using microwave spectral taxonomy. J. Chem. Phys. 2017, 146, 154301. [Google Scholar] [CrossRef]
- McGuire, B.A.; Martin-Drumel, M.A.; Lee, K.L.K.; Stanton, J.F.; Gottlieb, C.A.; McCarthy, M.C. Vibrational satellites of C2S, C3S, and C4S: Microwave spectral taxonomy as a stepping stone to the millimeter-wave band. Phys. Chem. Chem. Phys. 2018, 20, 13870–13889. [Google Scholar] [CrossRef]
- York, L.; Sorrells, C.; Dim, C.A.; Crabtree, K.N.; Hernandez-Castillo, A.O. A Tale of Two Tails: Rotational Spectroscopy of N-Ethyl Maleimide and N-Ethyl Succinimide. J. Phys. Chem. A 2024, 128, 5541–5547. [Google Scholar] [CrossRef]
- Salvitti, G.; Sigismondi, S.; Melandri, S.; López, J.C.; Blanco, S.; Maris, A. Structure and dynamics of 3’-aminoacetophenone and 4’-aminoacetophenone from rotational spectroscopy. Phys. Chem. Chem. Phys. 2024, 26, 1881–1890. [Google Scholar] [CrossRef] [PubMed]
- Landau, A.; Eduardus; Behar, D.; Wallach, E.R.; Pašteka, L.F.; Faraji, S.; Borschevsky, A.; Shagam, Y. Chiral molecule candidates for trapped ion spectroscopy by ab initio calculations: From state preparation to parity violation. J. Chem. Phys. 2023, 159, 114307. [Google Scholar] [CrossRef] [PubMed]
- Fiechter, M.R.; Haase, P.A.; Saleh, N.; Soulard, P.; Tremblay, B.; Havenith, R.W.; Timmermans, R.G.; Schwerdtfeger, P.; Crassous, J.; Darquié, B.; et al. Toward detection of the molecular parity violation in Chiral Ru(acac)3 and Os(acac)3. J. Phys. Chem. Lett. 2022, 13, 10011–10017. [Google Scholar] [CrossRef] [PubMed]
- Quack, M. On the measurement of the parity violating energy difference between enantiomers. Chem. Phys. Lett. 1986, 132, 147–153. [Google Scholar] [CrossRef]
- Quack, M.; Seyfang, G.; Wichmann, G. Perspectives on parity violation in chiral molecules: Theory, spectroscopic experiment and biomolecular homochirality. Chem. Sci. 2022, 13, 10598–10643. [Google Scholar] [CrossRef]
- Berry, M.V.; Dennis, M.R. The optical singularities of birefringent dichroic chiral crystals. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2003, 459, 1261–1292. [Google Scholar] [CrossRef]
- Hodgkinson, I.; Wu, Q.h. Inorganic Chiral Optical Materials. Adv. Mater. 2001, 13, 889–897. [Google Scholar] [CrossRef]
- Govorov, A.O.; Fan, Z.; Hernandez, P.; Slocik, J.M.; Naik, R.R. Theory of Circular Dichroism of Nanomaterials Comprising Chiral Molecules and Nanocrystals: Plasmon Enhancement, Dipole Interactions, and Dielectric Effects. Nano Lett. 2010, 10, 1374–1382. [Google Scholar] [CrossRef]
- Freedman, T.B.; Cao, X.; Dukor, R.K.; Nafie, L.A. Absolute configuration determination of chiral molecules in the solution state using vibrational circular dichroism. Chirality 2003, 15, 743–758. [Google Scholar] [CrossRef]
- Barron, L.D.; Lutz Hecht, I.H.M.; Blanch, E.W. Raman optical activity comes of age. Mol. Phys. 2004, 102, 731–744. [Google Scholar] [CrossRef]
- He, Y.; Bo, W.; Dukor, R.K.; Nafie, L.A. Determination of absolute configuration of chiral molecules using vibrational optical activity: A review. Appl. Spectrosc. 2011, 65, 699–723. [Google Scholar] [CrossRef] [PubMed]
- Patterson, D.; Doyle, J.M. Sensitive chiral analysis via microwave three-wave mixing. Phys. Rev. Lett. 2013, 111, 023008. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.H.; Bischoff, J.; Hernandez-Castillo, A.O.; Abdiha, E.; Sartakov, B.G.; Meijer, G.; Eibenberger-Arias, S. The influence of microwave pulse conditions on enantiomer-specific state transfer. New J. Phys. 2024, 26, 033015. [Google Scholar] [CrossRef]
- Lee, J.; Abdiha, E.; Sartakov, B.G.; Meijier, G.; Eibenberger-Arias, S. Near-complete chiral selection in rotational quantum states. Nat. Commun. 2024, 15, 7441. [Google Scholar] [CrossRef] [PubMed]
- Singh, H.; Berggötz, F.E.; Sun, W.; Schnell, M. Chiral control of gas-phase molecules using microwave pulses. Angew. Chem. Int. Ed. 2023, 62, e202219045. [Google Scholar] [CrossRef]
- Sun, W.; Schnell, M. Microwave three-wave mixing spectroscopy of chiral molecules in weakly bound complexes. J. Phys. Chem. Lett. 2023, 14, 7389–7394. [Google Scholar] [CrossRef]
- Domingos, S.R.; Pérez, C.; Schnell, M. Sensing Chirality with Rotational Spectroscopy. Annu. Rev. Phys. Chem. 2018, 69, 499–519. [Google Scholar] [CrossRef]
- Prozument, K.; Shaver, R.G.; Ciuba, M.; Muenter, J.S.; Park, G.B.; Stanton, J.F.; Guo, H.; Wong, B.M.; Perry, D.S.; Field, R.W. A new approach toward transition state spectroscopy. Faraday Discuss. 2013, 163, 33–57. [Google Scholar] [CrossRef]
- Prozument, K.; Park, G.B.; Shaver, R.G.; Vasiliou, A.K.; Oldham, J.M.; David, D.E.; Muenter, J.S.; Stanton, J.F.; Suits, A.G.; Ellison, G.B.; et al. Chirped-pulse millimeter-wave spectroscopy for dynamics and kinetics studies of pyrolysis reactions. Phys. Chem. Chem. Phys. 2014, 16, 15739–15751. [Google Scholar] [CrossRef]
- Zaleski, D.P.; Harding, L.B.; Klippenstein, S.J.; Ruscic, B.; Prozument, K. Time-resolved kinetic chirped-pulse rotational spectroscopy in a room-temperature flow reactor. J. Phys. Chem. Lett. 2017, 8, 6180–6188. [Google Scholar] [CrossRef]
- Schnell, M. Broadband rotational spectroscopy for molecular structure and dynamics studies. Z. Fur Phys. Chem. 2013, 227, 1–21. [Google Scholar] [CrossRef]
- Dian, B.C.; Brown, G.G.; Douglass, K.O.; Pate, B.H. Measuring picosecond isomerization kinetics via broadband microwave spectroscopy. Science 2008, 320, 924–928. [Google Scholar] [CrossRef] [PubMed]
- Gallagher, T.F. Rydberg atoms. Rep. Prog. Phys. 1988, 51, 143. [Google Scholar] [CrossRef]
- Gentile, T.; Hughey, B.; Kleppner, D.; Ducas, T. Microwave spectroscopy of calcium Rydberg states. Phys. Rev. A 1990, 42, 440. [Google Scholar] [CrossRef]
- Merkt, F. Molecules in high Rydberg states. Annu. Rev. Phys. Chem. 1997, 48, 675–709. [Google Scholar] [CrossRef]
- Hogan, S.; Seiler, C.; Merkt, F. Rydberg-state-enabled deceleration and trapping of cold molecules. Phys. Rev. Lett. 2009, 103, 123001. [Google Scholar] [CrossRef]
- Seiler, C.; Hogan, S.D.; Merkt, F. Dynamical processes in Rydberg-Stark deceleration and trapping of atoms and molecules. Chimia 2012, 66, 208. [Google Scholar] [CrossRef]
- Hogan, S.D. Rydberg-Stark deceleration of atoms and molecules. EPJ Tech. Instrum. 2016, 3, 2. [Google Scholar] [CrossRef]
- Jakubek, Z.J.; Field, R.W. Core-penetrating Rydberg series of BaF: s∼p∼d∼f supercomplexes. Phys. Rev. Lett. 1994, 72, 2167. [Google Scholar] [CrossRef]
- Kay, J.J.; Coy, S.L.; Petrović, V.S.; Wong, B.M.; Field, R.W. Separation of long-range and short-range interactions in Rydberg states of diatomic molecules. J. Chem. Phys. 2008, 128, 194301. [Google Scholar] [CrossRef]
- Altunata, S.N.; Coy, S.L.; Field, R.W. Properties of nearly one-electron molecules. II. Application to the Rydberg spectrum of CaF. J. Chem. Phys. 2005, 123, 084319. [Google Scholar] [CrossRef] [PubMed]
- Coy, S.L.; Grimes, D.D.; Zhou, Y.; Field, R.W.; Wong, B.M. Electric potential invariants and ions-in-molecules effective potentials for molecular Rydberg states. J. Chem. Phys. 2016, 145, 234301. [Google Scholar] [CrossRef] [PubMed]
- Kay, J.J.; Altunata, S.N.; Coy, S.L.; Field, R.W. Resonance between electronic and rotational motions in Rydberg states of CaF. Mol. Phys. 2007, 105, 1661–1673. [Google Scholar] [CrossRef]
- Zhou, Y.; Grimes, D.D.; Barnum, T.J.; Patterson, D.; Coy, S.L.; Klein, E.; Muenter, J.S.; Field, R.W. Direct detection of Rydberg-Rydberg millimeter-wave transitions in a buffer gas cooled molecular beam. Chem. Phys. Lett. 2015, 640, 124–136. [Google Scholar] [CrossRef]
- Wang, T.; Yelin, S.F.; Côté, R.; Eyler, E.E.; Farooqi, S.M.; Gould, P.L.; Koštrun, M.; Tong, D.; Vrinceanu, D. Superradiance in ultracold Rydberg gases. Phys. Rev. A 2007, 75, 033802. [Google Scholar] [CrossRef]
- Zhou, Y. Cooperative effects in a dense Rydberg gas. Mol. Phys. 2012, 110, 1909–1915. [Google Scholar] [CrossRef]
- Grimes, D.D.; Coy, S.L.; Barnum, T.J.; Zhou, Y.; Yelin, S.F.; Field, R.W. Direct single-shot observation of millimeter-wave superradiance in Rydberg-Rydberg transitions. Phys. Rev. A 2017, 95, 043818. [Google Scholar] [CrossRef]
- Hutzler, N.R.; Lu, H.I.; Doyle, J.M. The buffer gas beam: An intense, cold, and slow source for atoms and molecules. Chem. Rev. 2012, 112, 4803–4827. [Google Scholar] [CrossRef]
- Wright, S.C.; Doppelbauer, M.; Hofsäss, S.; Schewe, H.C.; Sartakov, B.; Meijer, G.; Truppe, S. Cryogenic buffer gas beams of AlF, CaF, MgF, YbF, Al, Ca, Yb and NO - a comparison. Mol. Phys. 2023, 121, 2146541. [Google Scholar] [CrossRef]
- Patterson, D.; Doyle, J.M. Bright, guided molecular beam with hydrodynamic enhancement. J. Chem. Phys. 2007, 126, 154307. [Google Scholar] [CrossRef]
- Lu, H.I.; Rasmussen, J.; Wright, M.J.; Patterson, D.; Doyle, J.M. A cold and slow molecular beam. Phys. Chem. Chem. Phys. PCCP 2011, 13, 18986–18990. [Google Scholar] [CrossRef] [PubMed]
- Baiz, C.R.; Błasiak, B.; Bredenbeck, J.; Cho, M.; Choi, J.H.; Corcelli, S.A.; Dijkstra, A.G.; Feng, C.J.; Garrett-Roe, S.; Ge, N.H.; et al. Vibrational spectroscopic map, vibrational spectroscopy, and intermolecular interaction. Chem. Rev. 2020, 120, 7152–7218. [Google Scholar] [CrossRef] [PubMed]
- Perakis, F.; Marco, L.D.; Shalit, A.; Tang, F.; Kann, Z.R.; Kühne, T.D.; Torre, R.; Bonn, M.; Nagata, Y. Vibrational spectroscopy and dynamics of water. Chem. Rev. 2016, 116, 7590–7607. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.X.; Xie, X.S. Vibrational spectroscopic imaging of living systems: An emerging platform for biology and medicine. Science 2015, 350, 6264. [Google Scholar] [CrossRef] [PubMed]
- Berthomieu, C.; Hienerwadel, R. Fourier transform infrared (FTIR) spectroscopy. Photosynth. Res. 2009, 101, 157–170. [Google Scholar] [CrossRef]
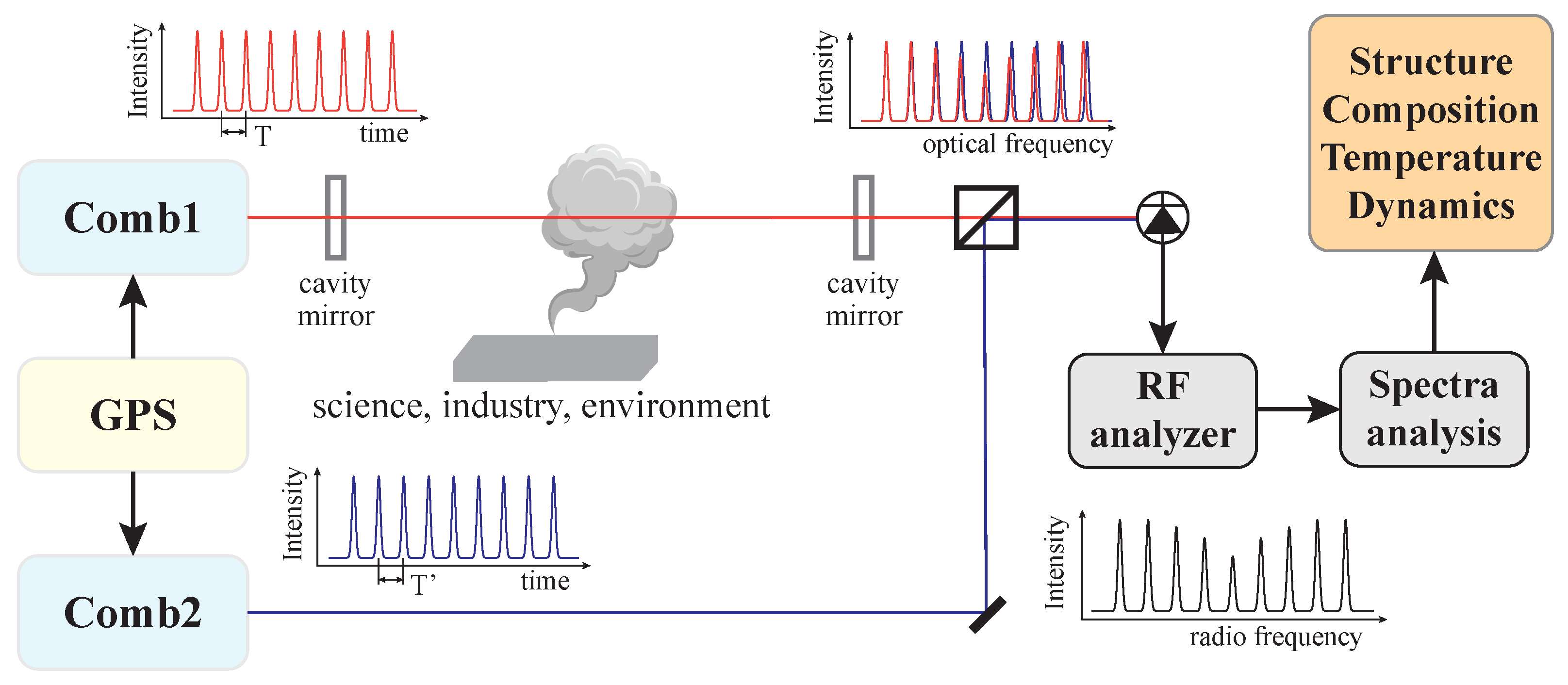
- Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef]
- Available online: https://www.menlosystems.com/products/optical-frequency-combs/fc1500-250-uln-plus/ (accessed on 15 November 2024).
- Available online: https://www.toptica.com/frequency-combs (accessed on 15 November 2024).
- Hall, J.L. Nobel Lecture: Defining and measuring optical frequencies. Rev. Mod. Phys. 2006, 78, 1279. [Google Scholar] [CrossRef]
- Picqué, N.; Hänsch, T.W. Frequency comb spectroscopy. Nat. Photonics 2019, 13, 146–157. [Google Scholar] [CrossRef]
- Hargrove, L.E.; Fork, R.L.; Pollack, M.A. Locking of hene laser modes induced by synchronous intracavity modulation. Appl. Phys. Lett. 1964, 5, 4–5. [Google Scholar] [CrossRef]
- Kuizenga, D.J.; Siegman, A.E. FM and AM mode locking of the homogeneous laser-Part I: Theory. IEEE J. Quaktum Electron. 1970, 6, 694–708. [Google Scholar] [CrossRef]
- Brabec, T.; Spielmann, C.; Curley, P.F.; Krausz, F. Kerr lens mode locking. Opt. Lett. 1992, 17, 1292–1294. [Google Scholar] [CrossRef]
- Haus, H.A. Mode-Locking of Lasers. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1173–1185. [Google Scholar] [CrossRef]
- Hudson, D.D.; Holman, K.W.; Jones, R.J.; Cundiff, S.T.; Ye, J.; Jones, D.J. Mode-locked fiber laser frequency-controlled with an intracavity electro-optic modulator. Opt. Lett. 2005, 30, 2948–2950. [Google Scholar] [CrossRef] [PubMed]
- Haus, H. A theory of forced mode locking. IEEE J. Quantum Electron. 1975, 11, 323–330. [Google Scholar] [CrossRef]
- Revin, D.G.; Hemingway, M.; Wang, Y.; Cockburn, J.W.; Belyanin, A. Active mode locking of quantum cascade lasers in an external ring cavity. Nat. Commun. 2016, 7, 11440. [Google Scholar] [CrossRef]
- Mollenauer, L.F.; Vieira, N.D.; Szeto, L. Mode locking by synchronous pumping using a gain medium with microsecond decay times. Opt. Lett. 1982, 7, 414–416. [Google Scholar] [CrossRef]
- Demaria, A.J.; Stetser, D.A.; Heynau, H. Self mode-locking of lasers with saturable absorbers. Appl. Phys. Lett. 1966, 8, 174–176. [Google Scholar] [CrossRef]
- Paschotta, R.; Keller, U. Passive mode locking with slow saturable absorbers. Appl. Phys. B Lasers Opt. 2001, 73, 653–662. [Google Scholar] [CrossRef]
- Kärtner, F.X.; Jung, I.D.; Keller, U. Soliton Mode-Locking with Saturable Absorbers. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 540–556. [Google Scholar] [CrossRef]
- Haus, H.A. Theory of mode locking with a fast saturable absorber. J. Appl. Phys. 1975, 46, 3049–3058. [Google Scholar] [CrossRef]
- Herrmann, J. Theory of Kerr-lens mode locking: Role of self-focusing and radially varying gain. JOSA b 1994, 11, 498–512. [Google Scholar] [CrossRef]
- Cerullo, G.; Silvestri, S.D.; Magni, V. Self-starting Kerr-lens mode locking of a Ti:sapphire laser. Opt. Lett. 1994, 19, 1040–1042. [Google Scholar] [CrossRef] [PubMed]
- Morgner, U.; Cho, S.H.; Chen, Y.; Haus, H.A.; Fujimoto, J.G.; Ippen, E.P.; Scheuer, V.; Angelow, G.; Tschudi, T. Sub-two-cycle pulses from a Kerr-lens mode-locked Ti : Sapphire laser. Opt. Lett. 1999, 24, 411–413. [Google Scholar] [CrossRef] [PubMed]
- Udem, T.; Holzwarth, R.; Hansch, T.W. Optical frequency metrology. Nature 2002, 416, 233–237. [Google Scholar] [CrossRef]
- Telle, H.R.; Steinmeyer, G.; Dunlop, A.E.; Stenger, J.; Sutter, D.H.; Keller, U. Carrier-envelope offset phase control: A novel concept for absolute optical frequency measurement and ultrashort pulse generation. Appl. Phys. B 1999, 69, 327–332. [Google Scholar] [CrossRef]
- Keller, U. Ultrafast solid-state laser oscillators: A success story for the last 20 years with no end in sight. Appl. Phys. B Lasers Opt. 2010, 100, 15–28. [Google Scholar] [CrossRef]
- Krauss, G.; Fehrenbacher, D.; Brida, D.; Riek, C.; Sell, A.; Huber, R.; Leitenstorfer, A. All-passive phase locking of a compact Er:fiber laser system. Opt. Lett. 2011, 36, 540–542. [Google Scholar] [CrossRef]
- Puppe, T.; Sell, A.; Kliese, R.; Hoghooghi, N.; Zach, A.; Kaenders, W. Characterization of a DFG comb showing quadratic scaling of the phase noise with frequency. Opt. Lett. 2016, 41, 1877–1880. [Google Scholar] [CrossRef]
- Thorpe, M.J.; Ye, J. Cavity-enhanced direct frequency comb spectroscopy. Appl. Phys. B 2008, 91, 397–414. [Google Scholar] [CrossRef]
- Adler, F.; Thorpe, M.J.; Cossel, K.C.; Ye, J. Cavity-enhanced direct frequency comb spectroscopy: Technology and applications. Annu. Rev. Anal. Chem. 2010, 3, 175–205. [Google Scholar] [CrossRef]
- Stowe, M.C.; Thorpe, M.J.; Pe’er, A.; Ye, J.; Stalnaker, J.E.; Gerginov, V.; Diddams, S.A. Direct frequency comb spectroscopy. Adv. At. Mol. Opt. Phys. 2008, 55, 1–60. [Google Scholar] [CrossRef]
- Cingoz, A.; Yost, D.C.; Allison, T.K.; Ruehl, A.; Fermann, M.E.; Hartl, I.; Ye, J. Direct frequency comb spectroscopy in the extreme ultraviolet. Nature 2012, 482, 68–71. [Google Scholar] [CrossRef] [PubMed]
- Cossel, K.C.; Adler, F.; Bertness, K.A.; Thorpe, M.J.; Feng, J.; Raynor, M.W.; Ye, J. Analysis of trace impurities in semiconductor gas via cavity-enhanced direct frequency comb spectroscopy. Appl. Phys. B 2010, 100, 917–924. [Google Scholar] [CrossRef]
- Coburn, S.; Alden, C.B.; Wright, R.; Cossel, K.; Baumann, E.; Truong, G.W.; Giorgetta, F.; Sweeney, C.; Newbury, N.R.; Prasad, K.; et al. Regional trace-gas source attribution using a field-deployed dual frequency comb spectrometer. Optica 2018, 5, 320–327. [Google Scholar] [CrossRef]
- Weichman, M.L.; Changala, P.B.; Ye, J.; Chen, Z.; Yan, M.; Picqué, N. Broadband molecular spectroscopy with optical frequency combs. J. Mol. Spectrosc. 2019, 355, 66–78. [Google Scholar] [CrossRef]
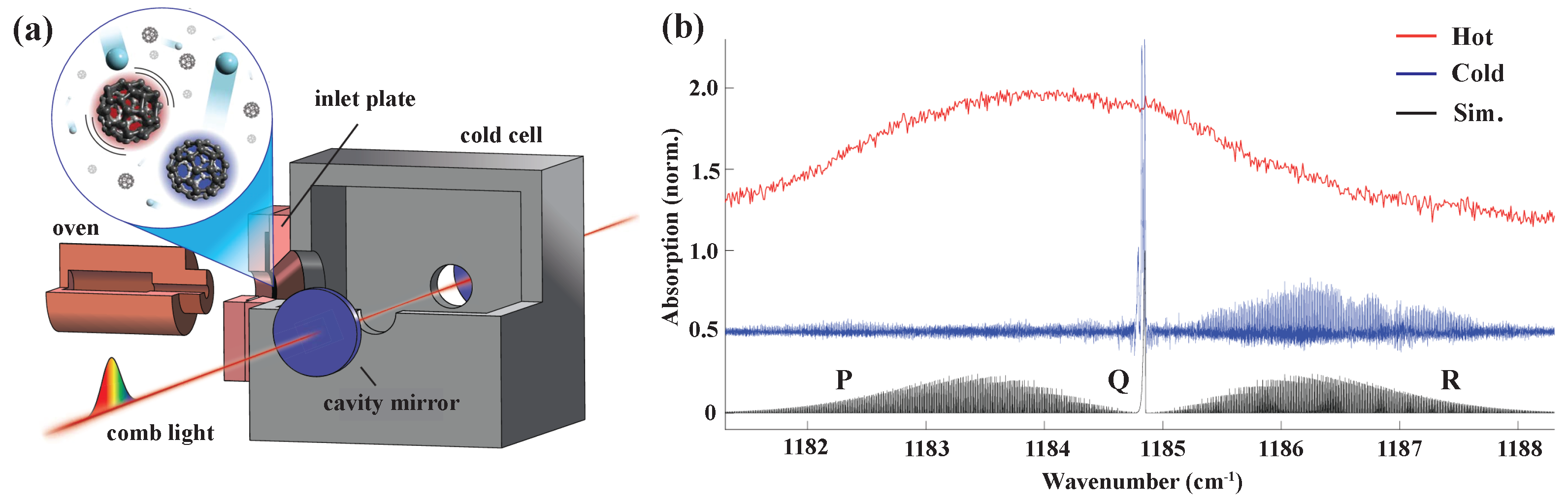
- Changala, P.B.; Weichman, M.L.; Lee, K.F.; Fermann, M.E.; Ye, J. Rovibrational quantum state resolution of the C60 fullerene. Science 2019, 363, 49–54. [Google Scholar] [CrossRef]
- Sinclair, L.C.; Cossel, K.C.; Coffey, T.; Ye, J.; Cornell, E.A. Frequency comb velocity-modulation spectroscopy. Phys. Rev. Lett. 2011, 107, 093002. [Google Scholar] [CrossRef]
- Cairncross, W.B.; Gresh, D.N.; Grau, M.; Cossel, K.C.; Roussy, T.S.; Ni, Y.; Zhou, Y.; Ye, J.; Cornell, E.A. Precision measurement of the electron’s electric Dipole moment using trapped molecular ions. Phys. Rev. Lett. 2017, 119, 153001. [Google Scholar] [CrossRef]
- Roussy, T.S.; Caldwell, L.; Wright, T.; Cairncross, W.B.; Shagam, Y.; Ng, K.B.; Schlossberger, N.; Park, S.Y.; Wang, A.; Ye, J.; et al. An improved bound on the electron’s electric dipole moment. Science 2023, 381, 46–50. [Google Scholar] [CrossRef]
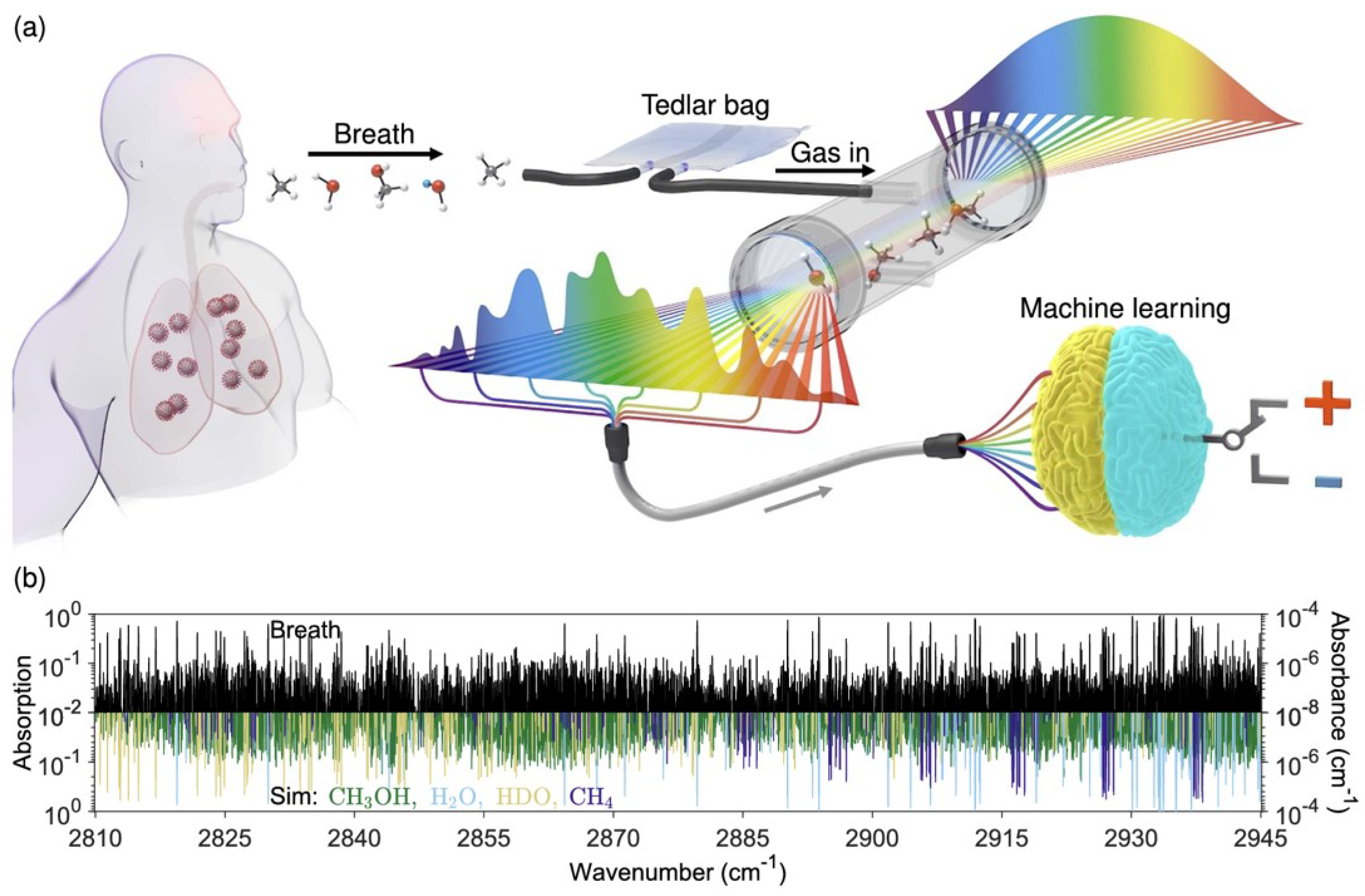
- Thorpe, M.J.; Balslev-Clausen, D.; Kirchner, M.S.; Ye, J. Cavity-enhanced optical frequency comb spectroscopy: Application to human breath analysis. Opt. Express 2008, 16, 2387–2397. [Google Scholar] [CrossRef]
- Liang, Q.; Chan, Y.C.; Toscano, J.; Bjorkman, K.K.; Leinwand, L.A.; Parker, R.; Nozik, E.S.; Nesbitt, D.J.; Ye, J. Breath analysis by ultra-sensitive broadband laser spectroscopy detects SARS-CoV-2 infection. J. Breath Res. 2023, 17, 036001. [Google Scholar] [CrossRef] [PubMed]
- Asahara, A.; Minoshima, K. Development of ultrafast time-resolved dual-comb spectroscopy. APL Photonics 2017, 2, 041301. [Google Scholar] [CrossRef]
- Fleisher, A.J.; Bjork, B.J.; Bui, T.Q.; Cossel, K.C.; Okumura, M.; Ye, J. Mid-infrared time-resolved frequency comb spectroscopy of transient free radicals. J. Phys. Chem. Lett. 2014, 5, 2241–2246. [Google Scholar] [CrossRef] [PubMed]
- Long, D.A.; Cich, M.J.; Mathurin, C.; Heiniger, A.T.; Mathews, G.C.; Frymire, A.; Rieker, G.B. Nanosecond time-resolved dual-comb absorption spectroscopy. Nat. Photonics 2024, 18, 127–131. [Google Scholar] [CrossRef]
- Bjork, B.J.; Bui, T.Q.; Heckl, O.H.; Changala, P.B.; Spaun, B.; Heu, P.; Follman, D.; Deutsch, C.; Cole, G.D.; Aspelmeyer, M.; et al. Direct frequency comb measurement of OD + CO→DOCO kinetics. Science 2016, 354, 444–448. [Google Scholar] [CrossRef]
- Makowiecki, A.S.; Herman, D.I.; Hoghooghi, N.; Strong, E.F.; Cole, R.K.; Ycas, G.; Giorgetta, F.R.; Lapointe, C.B.; Glusman, J.F.; Daily, J.W.; et al. Mid-infrared dual frequency comb spectroscopy for combustion analysis from 2.8 to 5 μm. Proc. Combust. Inst. 2021, 38, 1627–1635. [Google Scholar] [CrossRef]
- Hu, G.; Mizuguchi, T.; Oe, R.; Nitta, K.; Zhao, X.; Minamikawa, T.; Li, T.; Zheng, Z.; Yasui, T. Dual terahertz comb spectroscopy with a single free-running fibre laser. Sci. Rep. 2018, 8, 11155. [Google Scholar] [CrossRef]
- Fu, H.; Jiang, X.; Wu, J.; Qiu, L.; Yuan, Y.; Guo, X.; Zhu, Y. Terahertz dual-comb spectroscopy: A comparison between time- and frequency-domain operation modes. Infrared Phys. Technol. 2021, 115, 103699. [Google Scholar] [CrossRef]
- Giorgetta, F.R.; Peischl, J.; Herman, D.I.; Ycas, G.; Coddington, I.; Newbury, N.R.; Cossel, K.C. Open-path dual-comb spectroscopy for multispecies trace gas detection in the 4.5–5 μm spectral region. Laser Photonics Rev. 2021, 15, 2000583. [Google Scholar] [CrossRef]
- Malarich, N.A.; Washburn, B.R.; Cossel, K.C.; Mead, G.J.; Giorgetta, F.R.; Herman, D.I.; Newbury, N.R.; Coddington, I. Validation of open-path dual-comb spectroscopy against an O2 background. Opt. Express 2023, 31, 5042–5055. [Google Scholar] [CrossRef]
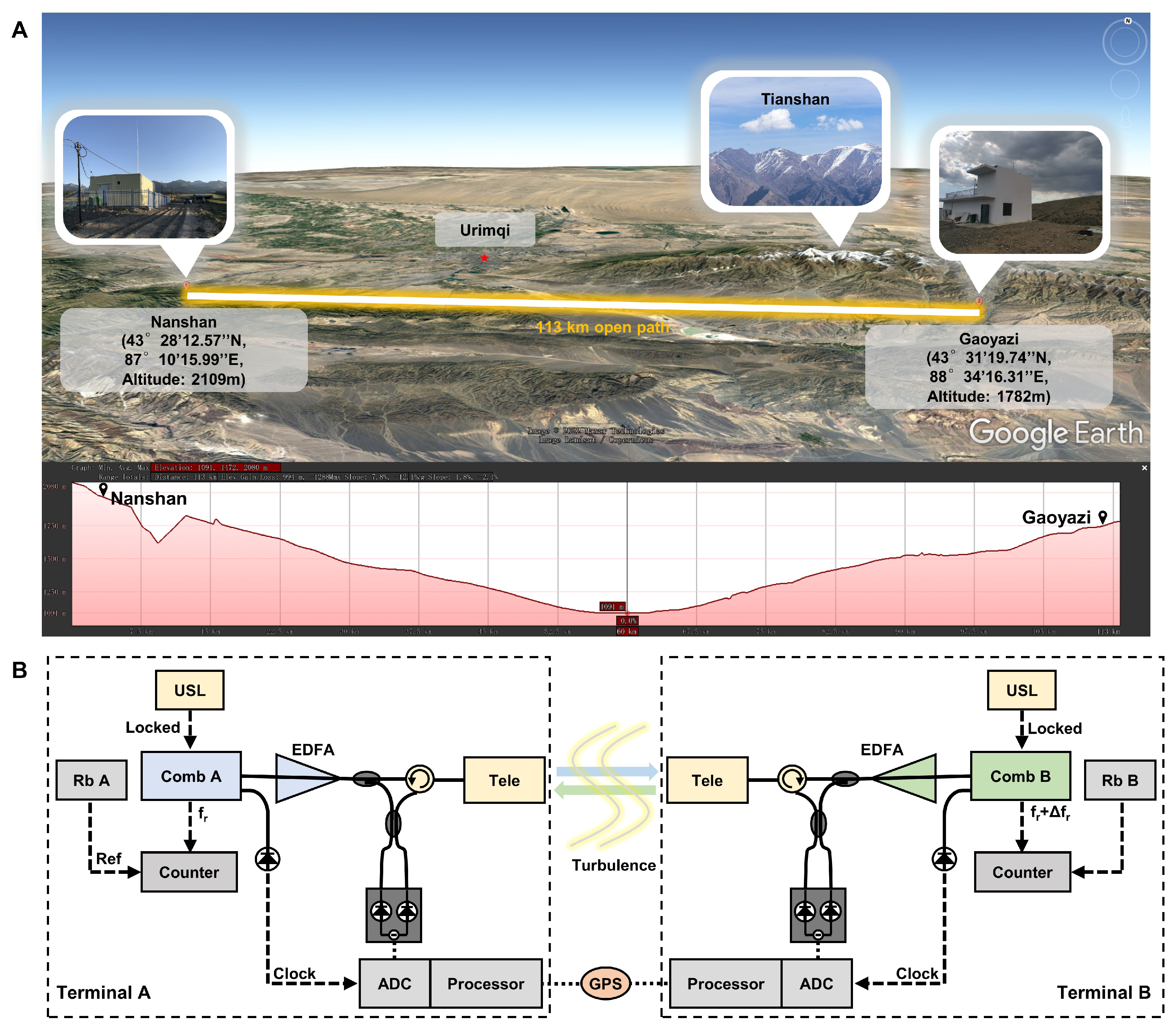
- Han, J.J.; Zhong, W.; Zhao, R.C.; Zeng, T.; Li, M.; Lu, J.; Peng, X.X.; Shi, X.P.; Yin, Q.; Wang, Y.; et al. Dual-comb spectroscopy over 100km open-air path. arXiv 2023, arXiv:2310.19294. [Google Scholar]
- Dutt, A.; Joshi, C.; Ji, X.; Cardenas, J.; Okawachi, Y.; Luke, K.; Gaeta, A.L.; Lipson, M. On-chip dual-comb source for spectroscopy. Sci. Adv. 2018, 4, e1701858. [Google Scholar] [CrossRef]
- Gaeta, A.L.; Lipson, M.; Kippenberg, T.J. Photonic-chip-based frequency combs. Nat. Photonics 2019, 13, 158–169. [Google Scholar] [CrossRef]
- Yu, M.; Okawachi, Y.; Griffith, A.G.; Picqué, N.; Lipson, M.; Gaeta, A.L. Silicon-chip-based mid-infrared dual-comb spectroscopy. Nat. Commun. 2018, 9, 1869. [Google Scholar] [CrossRef] [PubMed]
- Suh, M.G.; Yang, Q.F.; Yang, K.Y.; Yi, X.; Vahala, K.J. Microresonator soliton dual-comb spectroscopy. Science 2016, 354, 600–603. [Google Scholar] [CrossRef]
- Rueda, A.; Sedlmeir, F.; Kumari, M.; Leuchs, G.; Schwefel, H.G. Resonant electro-optic frequency comb. Nature 2019, 568, 378–381. [Google Scholar] [CrossRef]
- Long, D.A.; Bresler, S.M.; Bao, Y.; Reschovsky, B.J.; Hodges, J.T.; Lawall, J.R.; LeBrun, T.W.; Gorman, J.J. Single-modulator, direct frequency comb spectroscopy via serrodyne modulation. Opt. Lett. 2023, 48, 892–895. [Google Scholar] [CrossRef]
- Parriaux, A.; Hammani, K.; Millot, G. Electro-optic frequency combs. Adv. Opt. Photon. 2020, 12, 223–287. [Google Scholar] [CrossRef]
- Coddington, I.; Swann, W.C.; Newbury, N.R. Coherent dual-comb spectroscopy at high signal-to-noise ratio. Phys. Rev. A 2010, 82, 043817. [Google Scholar] [CrossRef]
- Phillips, C.R.; Willenberg, B.; Nussbaum-Lapping, A.; Callegari, F.; Camenzind, S.L.; Pupeikis, J.; Keller, U. Coherently averaged dual-comb spectroscopy with a low-noise and high-power free-running gigahertz dual-comb laser. Opt. Express 2023, 31, 7103–7119. [Google Scholar] [CrossRef]
- Chen, Z.; Hänsch, T.W.; Picqué, N. Mid-infrared feed-forward dual-comb spectroscopy. Proc. Natl. Acad. Sci. USA 2019, 116, 3454–3459. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Ooi, T.; Higgins, J.S.; Doyle, J.F.; von der Wense, L.; Beeks, K.; Leitner, A.; Kazakov, G.A.; Li, P.; Thirolf, P.G.; et al. Frequency ratio of the 229mTh nuclear isomeric transition and the 87Sr atomic clock. Nature 2024, 633, 63–70. [Google Scholar] [CrossRef] [PubMed]
- Ozawa, A.; Davila-Rodriguez, J.; Bounds, J.R.; Schuessler, H.A.; Hänsch, T.W.; Udem, T. Single ion fluorescence excited with a single mode of an UV frequency comb. Nat. Commun. 2017, 8, 44. [Google Scholar] [CrossRef] [PubMed]
- Nauta, J.; Borodin, A.; Ledwa, H.B.; Stark, J.; Schwarz, M.; Schmöger, L.; Micke, P.; López-Urrutia, J.R.C.; Pfeifer, T. Towards precision measurements on highly charged ions using a high harmonic generation frequency comb. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2017, 408, 285–288. [Google Scholar] [CrossRef]
- Kameyama, R.; Takizawa, S.; Hiramatsu, K.; Goda, K. Dual-comb coherent Raman spectroscopy with near 100% duty cycle. ACS Photonics 2021, 8, 975–981. [Google Scholar] [CrossRef]

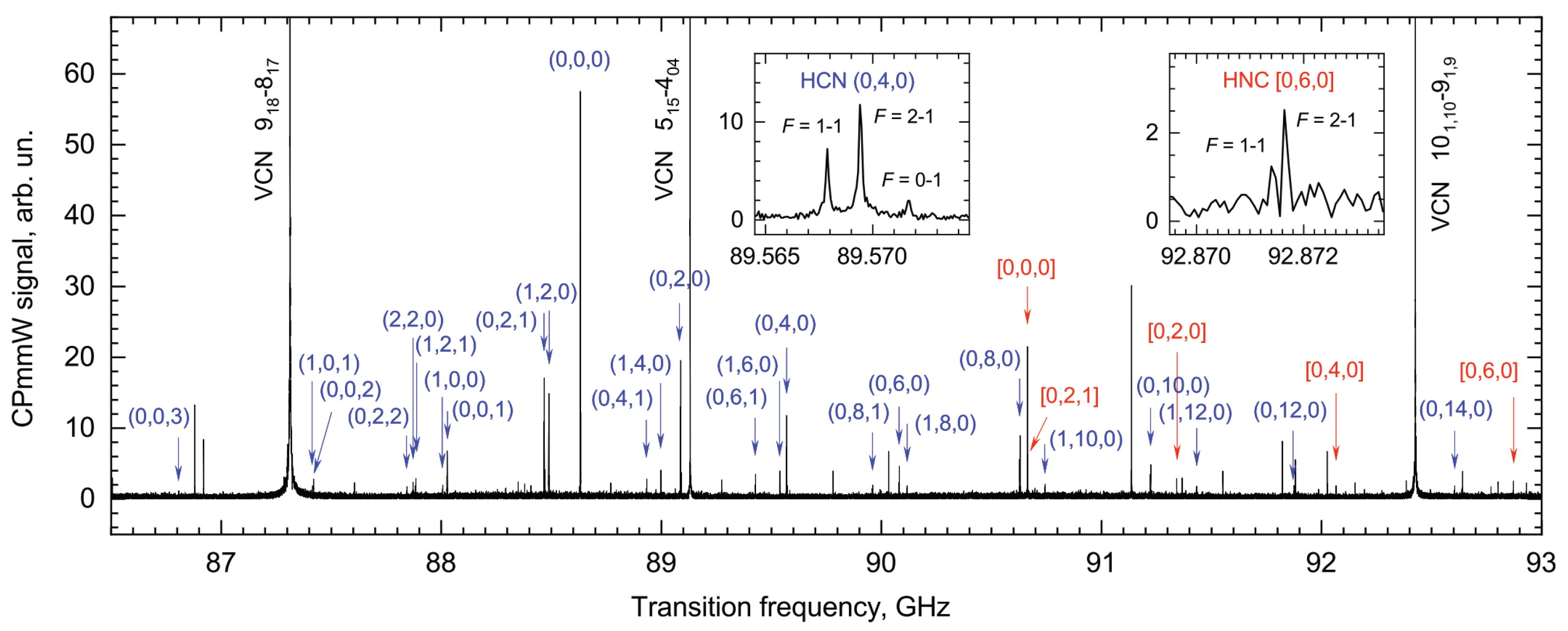
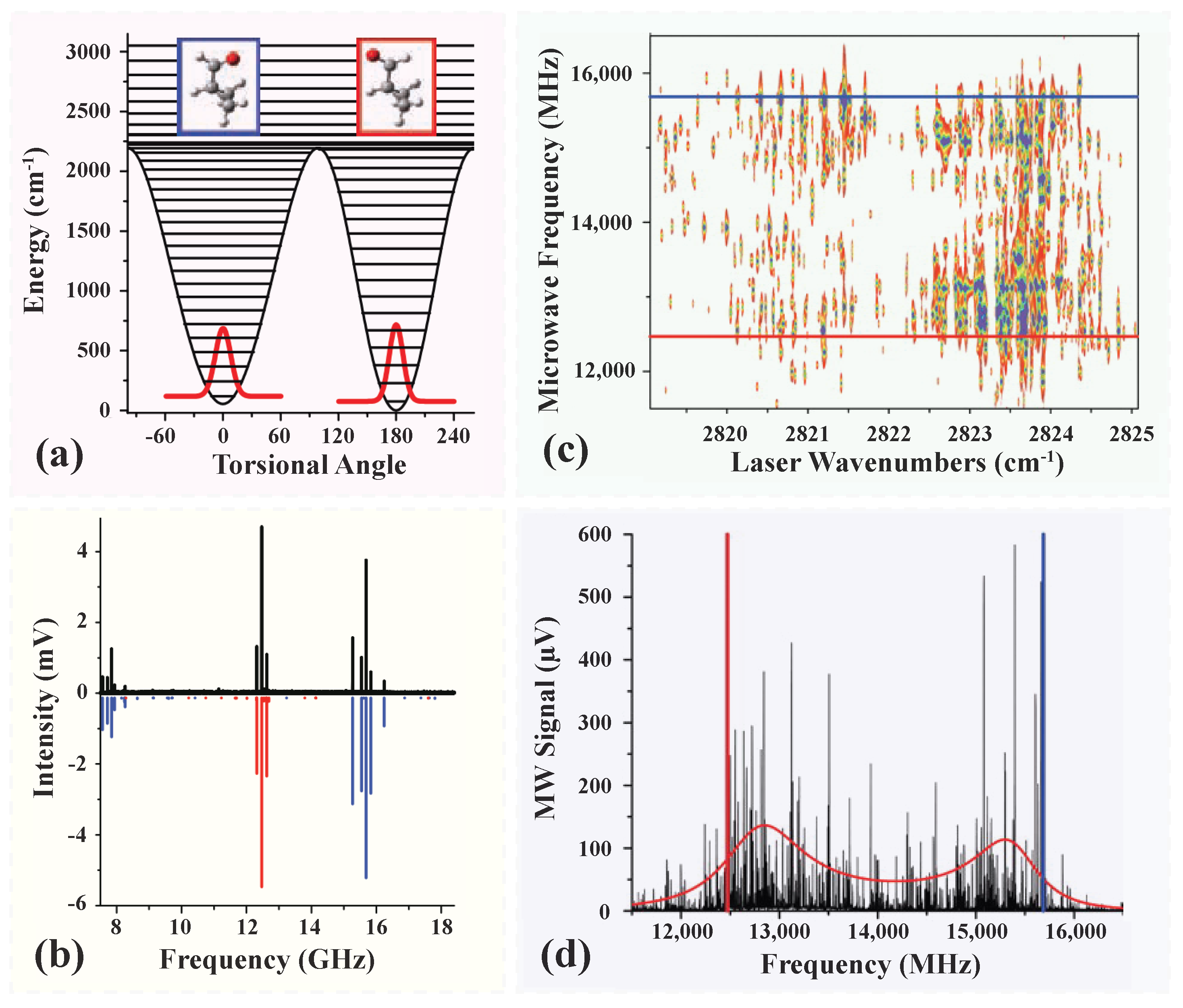

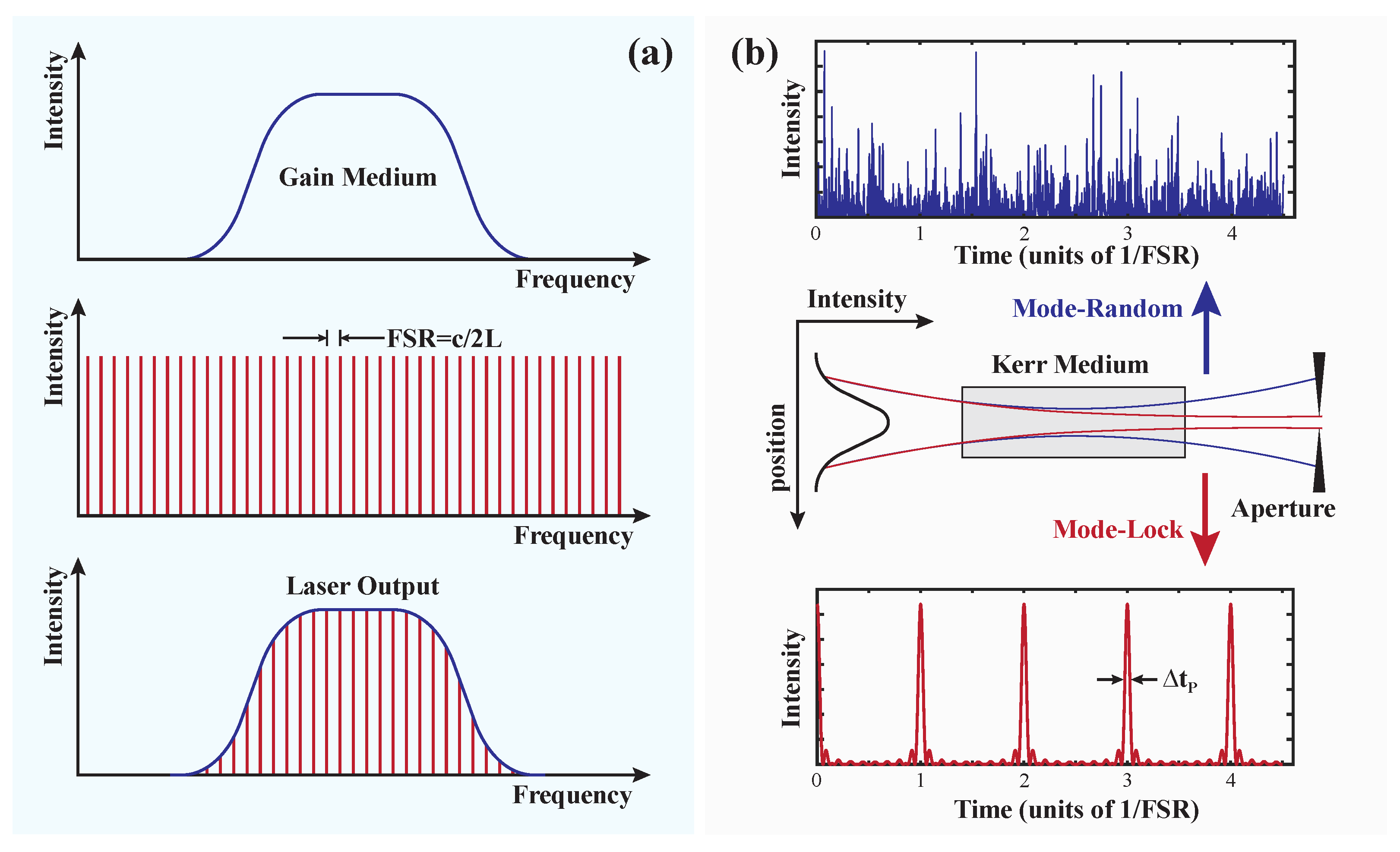
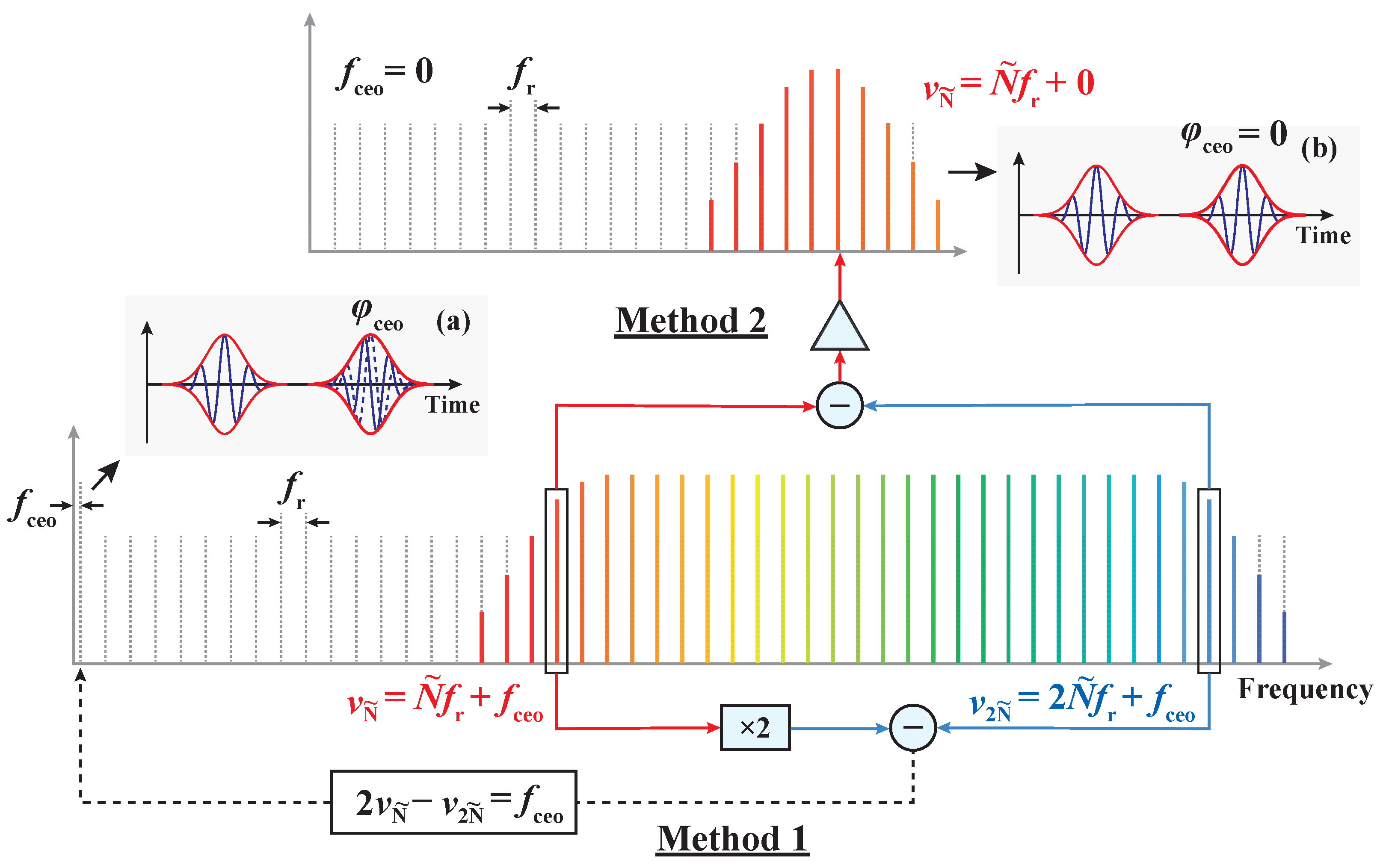


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Fernandez, R.; Gutierrez, B.; Pedersen, J.; Zhou, Y. Advancing Molecular Spectroscopy Efficiency with Extensive Parallelism. Metrology 2024, 4, 736-764. https://doi.org/10.3390/metrology4040043
Li J, Fernandez R, Gutierrez B, Pedersen J, Zhou Y. Advancing Molecular Spectroscopy Efficiency with Extensive Parallelism. Metrology. 2024; 4(4):736-764. https://doi.org/10.3390/metrology4040043
Chicago/Turabian StyleLi, Jiaqi, Rodrigo Fernandez, Bernardo Gutierrez, Jan Pedersen, and Yan Zhou. 2024. "Advancing Molecular Spectroscopy Efficiency with Extensive Parallelism" Metrology 4, no. 4: 736-764. https://doi.org/10.3390/metrology4040043
APA StyleLi, J., Fernandez, R., Gutierrez, B., Pedersen, J., & Zhou, Y. (2024). Advancing Molecular Spectroscopy Efficiency with Extensive Parallelism. Metrology, 4(4), 736-764. https://doi.org/10.3390/metrology4040043





